 |
|
���������� ������:: ��� :: ������ ����� ���� :: ������ ����� :: ������� ��� ���������� :: ������� ������ :: �������� ����� :: ������� ������ :: ����� ����� �������� :: ���� ��������� :: ������� ������ ���������� ���������� �����:: ���������� �� ������� Windows XP :: The Boarding House :: ���� (����� 1-3) :: ���������� ����� :: ����������������� ��� :: ������� ������� ����� :: �������� ������� :: ����������� ���������� :: ���� �����-������ :: ���� ������� |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 78)
A
n
m=
A n mназывают числом размещений из nэлементов по m. Число перестановок. Рассмотрим задачу: сколькими способами можно установить порядок следования друг за другом nразличных предметов? Число способов равно P n= 1Ч2Ч 3.. . n= n! (знак n!читается: « nфакториал»; оказывается удобным рассматривать также 0!, полагая его равным 1). P nназывают числом перестановок nэлементов. Число сочетаний. Пусть имеется nразличных предметов. Сколькими способами можно выбрать из них тпредметов (безразлично, в каком порядке выбираются предметы)? Число способов такого выбора равно
C
n
m=
C n mназывают числом сочетаний из nэлементов по m.Числа C n mполучаются как коэффициенты разложения n-й степени двучлена (бинома, см. Ньютона бином ) : (a+b) n=C n 0a n+ C n 1 a n-1b +C n 2a n-2b 2 +... + C n n-1ab n-1+ C n nb n, и поэтому они называются также биномиальными коэффициентами. Основные соотношения для биномиальных коэффициентов: C n m=C n n-m, C n m + C n m+1= C n+1 m+1 C n 0+ C n 1+ C n 2 +...+ C n n-1 + C n n=2 n , C n 0- C n 1+ C n 2 -...+ (-1) nC n n= 0. Числа A n m, P mи C n mсвязаны соотношением: A n m=P mC n m. Рассматриваются также размещения с повторением (т. е. всевозможные наборы из mпредметов nразличных видов, порядок в наборе существен) и сочетания с повторением (то же, но порядок в наборе не существен). Число размещений с повторением даётся формулой n m,число сочетаний с повторением - формулой C m n + m-1. Основные правила при решении задач К.: Правило суммы. Пусть некоторый предмет Аможет быть выбран из совокупности предметов mспособами, а другой предмет Вможно выбрать nспособами. Тогда имеется т+ nвозможностей выбрать либо предмет A, либо предмет В. Правило произведения. Пусть предмет Аможно выбрать mспособами и после каждого такого выбора предмет Вможно выбрать nспособами; тогда выбор пары ( А, В) вуказанном порядке можно осуществить m+ nспособами. Принцип включения и исключения. Пусть имеется Nпредметов, которые могут обладать nсвойствами a 1, a 2,..., a n.Обозначим через N(a i,a j,..., a k) число предметов, обладающих свойствами a i ,a j,...,a kи, быть может, какими-либо другими свойствами. Тогда число N'предметов, не обладающих ни одним из свойств, a 1, a 2,..., a n ,даётся формулой
Лит.:Netto E. Lehrbuch der Combinatorik, 2 Aufl., Lpz. - B., 1927. В. Е. Тараканов. Комбинаторная логика Комбинато'рная ло'гика,ветвь математической логики, изучающая комбинаторы и их свойства. В качестве основных понятий в К. л. выбираются функция и операция применения функции к аргументу (аппликация). Комбинаторами называют члены некоторого класса операций над функциями, замкнутого относительно аппликации. Сформулированное в терминах К. л. понятие «комбинаторно определимой функции» явилось одним из первых способов уточнения понятия алгоритма. Начало К. л. положено работой советского математика М. И. Шейнфинкеля (1924), большая часть результатов принадлежит американскому логику Х. Карри. К. л. находит широкое применение в теории языков программирования. Лит.:Яновская С. А., Логика комбинаторная, в кн.: Философская энциклопедия, т. 3, М., 1964; SchцnfinkeI М., Ьber die Bausteine der mathema-tischen Logik, «Mathematische Annalen», 1924, Bd 92; Curry H. B., Feys R., Combinatory logic, Amst., 1958; Curry H. B., Recent advances in combinatory logic, «Bulletin de la Sociйtй mathйmatique de Belgique», 1968, t. 20, № 3. Комбинаторная топология Комбинато'рная тополо'гия,часть топологии,в которой топологические свойства геометрических фигур изучаются при помощи их разбиений на более элементарные фигуры (например, разбиение полиэдров на симплексы ) или при помощи покрытий системами множеств. Этот метод применим, как показывают работы главным образом советских учёных, в самых широких предположениях об изучаемых фигурах. Лит.:Александров П. С., Комбинаторная топология, М. - Л., 1947; Понтрягин Л. С., Основы комбинаторной топологии, М. - Л., 1947. Комбинаторные изменения звуков Комбинато'рные измене'ния зву'ков,результат влияния окружающих звуков в речевом потоке. Таковы ассимиляция , диссимиляция , аккомодация - приспособление согласных к гласным и гласных к согласным («игры - отыгран»), выпадение звука («сонце» вместо «солнце»), гаплология - выпадение одного из одинаковых или подобных слогов («знаменосец» из «знаменоносец»), стяжение двух смежных гласных в один (русское диалектное « быват» из «бывает»), афереза - отпадение начального гласного слова после конечного гласного предшествующего слова (англ. I'm вместо I am - «я есть»), элизия - отпадение конечного гласного слова перед начальным гласным следующего слова (франц. I' ami вместо le ami - «друг»), эпентеза - вставка звуков (просторечное «Ларивон», «радиво»), метатеза - перестановка («Фрол» из лат. Florus). Комбинаторный анализ Комбинато'рный ана'лиз,комбинаторная математика, комбинаторика, отдел математики, в котором изучаются вопросы, связанные с размещением и взаимным расположением частей конечного множества объектов произвольной природы (а также бесконечных множеств, удовлетворяющих некоторым условиям конечности). Идеи комбинаторного характера имеют самое широкое распространение в математике, в таких её разделах, как теория вероятностей, теория чисел, алгебра и др. Задачи К. а. известны уже с глубокой древности. В развитие К. а. большой вклад внесли многие математики. Однако в самостоятельную научную дисциплину К. а. стал оформляться лишь в 20 в. К. а. тесно связан с теорией графов, теорией конечных автоматов и другими отраслями математики. Его результаты применяются при планировании и анализе научных экспериментов, кодировании сообщений, в линейном и динамическом программировании, в математической экономике и многих других областях науки и техники. Различают три типа проблем К. а. Задачи на перечисление. В задачах такого типа интересуются количеством возможных размещений, удовлетворяющих различным условиям, конечного множества объектов. Одним из типичных примеров такого рода задач является задача о размещении каких-либо nчастиц в Nячейках; как частицы, так и ячейки могут быть различимыми и неразличимыми, и это обусловливает различные ответы на поставленную задачу. Для решения разнообразных перечислительных задач, встречающихся на практике, разработаны мощные методы; среди них основные - метод производящих функций и метод перечисления Пойа. Задачи о существовании и построении. В задачах такого рода интересуются, существует ли конфигурация частей конечного множества, обладающая некоторыми заданными свойствами, и если да, то как её построить. Например, существует ли такая система подмножеств (блоков) данного конечного множества, что любые два различных элемента множества встречаются вместе в этих блоках заданное число раз. Такие системы называют блок-схемами. Они и им подобные конфигурации интенсивно изучаются в К. а. При этом большую роль играют теоретико-числовые и алгебраические методы. Задачи о выборе. В задачах этого типа исследуются условия, при которых можно осуществить такой выбор подмножества или некоторой совокупности частей множества, чтобы удовлетворялись некоторые требования, носящие чаще всего оптимальный характер. Например, пусть дано множество и имеется некоторая система подмножеств; при каких условиях можно выбрать по одному элементу в каждом подмножестве так, чтобы все эти элементы были попарно различны? Это - задача о системе различных представителей для системы подмножеств. При решении задач о выборе, наряду с чисто комбинаторными соображениями, также существенно применяется алгебраический аппарат. Лит.:Риордан Дж. Введение в комбинаторный анализ, пер. с англ., М., 1963; Раизер Г. Дж. Комбинаторная математика, пер. с англ., М., 1966. В. Е. Тараканов. Комбинационное рассеяние света Комбинацио'нное рассе'яние све'та,рассеяние света веществом, сопровождающееся заметным изменением частоты рассеиваемого света. Если источник испускает линейчатый спектр, то при К. р. с. в спектре рассеянного света обнаруживаются дополнительные линии, число и расположение которых тесно связаны с молекулярным строением вещества. К. р. с. открыто в 1928 советскими физиками Г. С. Ландсбергом и Л. И. Мандельштамом при исследовании рассеяния света в кристаллах и одновременно индийскими физиками Ч. В. Раманом и К. С. Кришнаном при исследовании рассеяния света в жидкостях (в зарубежной литературе К. р. с. часто называют эффектом Рамана). При К. р. с. преобразование первичного светового потока сопровождается обычно переходом рассеивающих молекул на другие колебательные и вращательные уровни (см. Молекулярные спектры ) ,причём частоты новых линий в спектре рассеяния являются комбинациями частоты падающего света и частот колебательных и вращательных переходов рассеивающих молекул - отсюда и назв. «К. р. с.». Для наблюдения спектров К. р. с. необходимо сконцентрировать интенсивный пучок света на изучаемом объекте. В качестве источника возбуждающего света чаще всего применяют ртутную лампу, а с 60-х гг. - лазерный луч. Рассеянный свет фокусируется и попадает в спектрограф, где спектр К. р. с. регистрируется фотографическим или фотоэлектрическим методами. К. р. с. наиболее часто связано с изменением колебательных состояний молекул. Такой спектр К. р. с. состоит из системы спутников, расположенных симметрично относительно возбуждающей линии с частотой n. Каждому спутнику с частотой n - n i(красный, или стоксов, спутник) соответствует спутник с частотой n + n i(фиолетовый, или антистоксов, спутник). Здесь n i- одна из собственных частот колебаний молекулы. Таким образом, измеряя частоты линий К. р. с., можно определять частоты собственных (или нормальных) колебаний молекулы, проявляющихся в спектре К. р. с. Аналогичные закономерности имеют место и для вращательного спектра К. р. с. В этом случае частоты линий определяются вращательными переходами молекул. В простейшем случае вращательный спектр К. р. с. - последовательность почти равноотстоящих симметрично расположенных линий, частоты которых являются комбинациями вращательных частот молекул и частоты возбуждающего света. Согласно квантовой теории, процесс К. р. с. состоит из двух связанных между собой актов - поглощения первичного фотона с энергией hn ( h - Планка постоянная) и испускания фотона с энергией hn '(где n' = n ± n i), происходящих в результате взаимодействия электронов молекулы с полем падающей световой волны. Молекула, находящаяся в невозбуждённом состоянии, под действием кванта с энергией hn через промежуточное электронное состояние, испуская квант h(n - n i), переходит в состояние с колебательной энергией hn i.Этот процесс приводит к появлению в рассеянном свете стоксовой линии с частотой n - n i (). Если фотон поглощается системой, в которой уже возбуждены колебания, то после рассеяния она может перейти в нулевое состояние; при этом энергия рассеянного фотона превышает энергию поглощённого. Этот процесс приводит к появлению антистоксовой линии с частотой n + n i() . Вероятность wК. р. с. (а следовательно, интенсивность линий К. р. с.) зависит от интенсивностей возбуждающего I 0и рассеянного Iизлучения: w= aI 0(b + J), где аи b -некоторые постоянные; при возбуждении К. р. с. обычными источниками света (например, ртутной лампой) второй член мал и им можно пренебречь. Интенсивность линий К. р. с. в большинстве случаев весьма мала, причём при обычных температурах интенсивность антистоксовых линий I acт, как правило, значительно меньше интенсивности стоксовых линий I cт. Поскольку вероятность рассеяния пропорциональна числу рассеивающих молекул, то отношение I acт/I cтопределяется отношением населённостей основного и возбуждённого уровней (см. Населённость уровня ) .При обычных температурах населённость возбуждённых уровней невелика и, следовательно, интенсивность антистоксовой компоненты мала. С повышением температуры их населённость возрастает (см. Больцмана статистика ) ,что приводит к увеличению интенсивности антистоксовых линий. Интенсивность линий К. р. с. I зависит от частоты n возбуждающего света: на больших расстояниях (в шкале частот) от области электронного поглощения молекул I~ n 4 ,при приближении к полосе электронного поглощения наблюдается более быстрый рост их интенсивности. В некоторых случаях при малых концентрациях вещества удаётся наблюдать резонансное К. р. с. - когда частота возбуждающего света попадает в область полосы поглощения вещества. При возбуждении К. р. с. лазерами большой мощности вероятность К. р. с. возрастает и возникает вынужденное К. р. с. (см. Вынужденное рассеяние света ) ,интенсивность которого того же порядка, что и интенсивность возбуждающего света. Линии К. р. с. в большей или меньшей степени поляризованы (см. Поляризация света ). При этом различные спутники одной и той же возбуждающей линии имеют различную степень поляризации, характер же поляризации стоксова и антистоксова спутников всегда одинаков. К. р. с., как и инфракрасная спектроскопия,является эффективным методом исследования строения молекул и их взаимодействия с окружающей средой. Существенно, что спектр К. р. с. и инфракрасный спектр поглощения не дублируют друг друга, поскольку определяются различными отбора правилами.Сопоставляя частоты линий в спектре К. р. с. и инфракрасном спектре одного и того же химического соединения, можно судить о симметрии нормальных колебаний и, следовательно, о симметрии молекулы в целом. Таким путём из нескольких предполагаемых моделей молекулы может быть выбрана реальная модель, отвечающая закономерностям в наблюдаемых спектрах. Частоты, а также другие параметры линий К. р. с. во многих случаях сохраняются при переходе от одного соединения к другому, обладающему тем же структурным элементом. Эта т. н. характеристичность параметров линий К. р. с. лежит в основе структурного анализа молекул с неизвестным строением. К. р. с. в кристаллах обладает некоторыми особенностями. Колебания атомов в кристалле можно отождествить с газом фононов,а К. р. с. в кристаллах рассматривать как рассеяние на фононах. Другие квазичастицы кристалла (поляритоны. магноны и др.) также изучаются методами К. р. с. Спектры К. р. с. каждого соединения настолько специфичны, что могут служить для идентификации этого соединения и обнаружения его в смесях. Качественный и количественный анализ по спектрам К. р. с. широко применяют в аналитической практике, особенно при анализе смесей углеводородов. Благодаря применению лазеров в качестве источников возбуждающего света () значительно расширился круг объектов, доступных для исследования методами К. р. с., стало возможным более детальное изучение газов, порошков и окрашенных веществ, например полупроводниковых материалов. Кроме того, применение лазеров резко сократило требования к количеству исследуемого вещества. Лит.:Ландсберг Г. С., Избр. труды, М., 1958, с. 101-170; Мандельштам Л. И., Полн. собр. трудов, т. 1, М., 1947, с. 293, 305; Raman С. V., Krishnan К. S., A new type of secondary radiation, «Nature», 1928, v. 121, № 3048, p. 501; Сущинский М. М., Спектры комбинационного рассеяния молекул и кристаллов, М., 1969; Light scattering spectra of solids, ed by G. B. Wright, B., 1969; Ландсберг Г. С., Бажулин П. А., Сущинский М. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313, 314 |
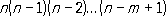

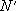 = N-N(a
1
)
- N(a
2
)
-... -N(a
n
) +
N(a
1,a
2
) +
N(a
1,a
3
) +... +
N(a
n-1,a
n
) -
N(a
1,a
2,a
3
)
-... -
N(a
n-2,a
n-1,a
n
) +... +(-1)
nN(a
1
,..., a
n
)
= N-N(a
1
)
- N(a
2
)
-... -N(a
n
) +
N(a
1,a
2
) +
N(a
1,a
3
) +... +
N(a
n-1,a
n
) -
N(a
1,a
2,a
3
)
-... -
N(a
n-2,a
n-1,a
n
) +... +(-1)
nN(a
1
,..., a
n
)