 |
|
���������� ������:: ��� :: ������ ����� ���� :: ������ ����� :: ������� ��� ���������� :: ������� ������ :: �������� ����� :: ������� ������ :: ����� ����� �������� :: ���� ��������� :: ������� ������ ���������� ���������� �����:: ���������� �� ������� Windows XP :: The Boarding House :: ���� (����� 1-3) :: ���������� ����� :: ����������������� ��� :: ������� ������� ����� :: �������� ������� :: ����������� ���������� :: ���� �����-������ :: ���� ������� |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 263)
..метр
)
,коррелограф, прибор, служащий для измерения корреляционных функций случайных процессов. Знание коэффициента корреляции позволяет анализировать физические явления, имеющие вероятностный характер, например шумы в радиоприёмных устройствах, поток космических частиц, биопотенциалы и т. п. (см.
Корреляционный анализ
)
.При подаче на выходы К. двух случайных сигналов в виде переменных электрических напряжений
U
1(t)и
U
2(t)на выходе прибора появляется напряжение, пропорциональное функции взаимной корреляции этих сигналов. Если на оба входа подан сигнал
U
k(t),К. измеряет коэффициент автокорреляции.
Наибольшее распространение получили электронные К. Индикатором К., как правило, служит стрелочный прибор, проградуированный в значениях коэффициента корреляции, или электроннолучевая трубка. В К. обычно предусматривается возможность подключения цифрового или самопишущего регистратора. К. применяют в аппаратуре радиосвязи (для измерения переходных затуханий в многоканальных системах), радиолокации, гидроакустики и радиоастрономии (для корреляционного пеленгования и увеличения разрешающей способности передачи), в медицинских электронных диагностических устройствах. Сигналы, исследуемые на взаимную корреляцию, имеют частоты от 1 гцдо 50 Мгц.Специальные методы обработки сигнала увеличивают его частотность до 500 Мгц.Коэффициент корреляции измеряется в пределах от 0,01 до 1,0; погрешность К. составляет 5-10%. Лит.:Ланге Ф., Корреляционная электроника, пер, с нем., Л., 1963; Мирский Г. Я., Радиоэлектронные измерения, 2 изд., М., 1969; Валитов Р. А., Сретенский В. Н., Радиотехнические измерения, М., 1970. Е. Г. Билык. Коррелятивное преобразование Корреляти'вное преобразова'ние(от позднелат. correlatio - соотношение), взаимно однозначное соответствие между множеством всех точек проективной плоскости и множеством всех прямых этой плоскости, при котором любым трём точкам, лежащим на одной прямой, соответствуют три прямые, проходящие через одну точку, а любым трём прямым, проходящим через одну точку, соответствуют три точки, лежащие на одной прямой. Корреляционный анализ Корреляцио'нный ана'лиз,совокупность основанных на математической теории корреляции методов обнаружения корреляционной зависимости между двумя случайными признаками или факторами. К. а. экспериментальных данных заключает в себе следующие основные практические приёмы: 1) построение корреляционного поля и составление корреляционной таблицы; 2) вычисление выборочных коэффициентов корреляции или корреляционного отношения; 3) проверка статистической гипотезы значимости связи. Дальнейшее исследование заключается в установлении конкретного вида зависимости между величинами (см. Регрессионный анализ ) .Зависимость между тремя и большим числом случайных признаков или факторов изучается методами многомерного К. а. (вычисление частных и множественных коэффициентов корреляции и корреляционных отношений). Корреляционное поле и корреляционная таблица являются вспомогательными средствами при анализе выборочных данных. При нанесении на координатную плоскость выборочных точек получают корреляционное поле. По характеру расположения точек поля можно составить предварительное мнение о форме зависимости случайных величин (например, о том, что одна величина в среднем возрастает или убывает при возрастании другой). Для численной обработки результаты обычно группируют и представляют в форме корреляционной таблицы. В каждой клетке корреляционной таблицы (см. в ст. Корреляция в математической статистике) приводятся численности гц;тех пар (х, у),компоненты которых попадают в соответствующие интервалы группировки по каждой переменной. Предполагая длины интервалов группировки (по каждому из переменных) равными между собой, выбирают центры x i(соответственно y j) этих интервалов и числа n ijв качестве основы для расчётов. Коэффициент корреляции и корреляционное отношение дают более точную информацию о характере и силе связи, чем картина корреляционного поля. Выборочный коэффициента корреляции определяют по формуле:
где
При большом числе независимых наблюдений, подчиняющихся одному и тому же распределению, и при надлежащем выборе интервалов группировки коэффициент
Выборочное значение
где числитель характеризует рассеяние условных средних значений
Проверка гипотезы значимости связи основывается на знании законов распределения выборочных корреляционных характеристик. В случае нормального распределения величина выборочного коэффициента корреляции
где t aесть критическое значение t-распределения Стьюдента с (n-2 )степенями свободы, соответствующее выбранному уровню значимости a(см. Стьюдента распределение ) .Если же известно, что r ¹0, то необходимо воспользоваться z-преобразованием Фишера (не зависящим от rи n):
Исходя из приближённой нормальности z,можно определить доверительные интервалы для истинного коэффициента корреляции r. В случае когда изучаются не количественные признаки, а качественные, обычные меры зависимости не годятся. Однако, если удаётся каким-либо образом упорядочить изучаемые объекты в отношении некоторого признака, т. е. прописать им порядковые номера - ранги (по два номера в соответствии с двумя признаками), то в качестве выборочной характеристики связи можно воспользоваться, например, т. н. коэффициентом ранговой корреляции:
где d i-разность рангов по обоим признакам для каждого объекта. По степени уклонения Rот нуля можно сделать некоторое заключение о степени зависимости качественных признаков. Проверка гипотезы независимости признаков при небольшом объёме выборки производится с помощью специальных таблиц, а при n >10 для вычисления критических значений выборочных коэффициентов пользуются тем, что эти величины распределены приближённо нормально. Лит.см. при ст. Корреляция. А. В. Прохоров. Корреляция (в биологии) Корреля'цияв биологии, взаимозависимость строения и функций клеток, тканей, органов и систем организма, проявляющаяся в процессе его развития и жизнедеятельности. К. обусловливают развитие и существование организма как единого целого. Понятие К. было введено Ж. Кювье (1800-05), однако, не принимая эволюционного учения, он придал К. статичный характер: К. - свидетельство постоянства сосуществования органов. Эволюционное учение придало К. динамический, исторический характер: взаимосвязь частей организма - результат как онтогенетический, так и филогенетический их развития. С эволюционных позиций проблема К. разрабатывалась А. Н. Северцовым;наиболее глубокое понимание её было дано И. И. Шмальгаузеном.Различается несколько форм К.: геномная К., обусловленная множественным действием наследственных факторов ( плейотропия ) ,а также действием более тесно связанных между собой генов (хромосомная К.); морфогенетическая К. - взаимозависимость во внутренних факторах индивидуального развития. При этом имеет место связь между двумя или многими морфогенетическими процессами. Так, было показано, что зачаток хордомезодермы оказывается индуктором, определяющим развитие центральной нервной системы, глазной бокал индуцирует хрусталик и т. д. Морфогенетические К. определяют место и размеры развивающегося органа. Т. к. морфогенетические процессы приводят к изменению взаимоотношений органов, то возникают и новые морфогенетические К. Т. о., в процессе индивидуального развития постепенно развёртывается последовательная система морфогенетических К., которая оказывается одним из главных факторов онтогенеза,поддерживающих в течение всего развития целостность организма. Данные, накопленные биологией развития,позволили некоторым авторам подразделить эти К. на ростовые К., зависящие от активности нервной системы, функциональные (эргонтические), гормональные и др. Филогенетические, или филетические, К. - соотносительные изменения органов в процессе эволюции организмов - А. Н. Северцов выделил как самостоятельное явление (см. Координация ) .
Лит.:Шмальгаузен И. И., Основы сравнительной анатомии позвоночных животных, 4 изд., М., 1947; его же, Организм, как целое в индивидуальном и историческом развитии, М.- Л., 1942; Северцов А. Н., Морфологические закономерности эволюции, М., 1949 (Собр. соч., т. 5); Balinsky В. Т., An introduction to embryology, 2 cd., Phil.- L., 1965. А. А. Махотин. Корреляция (в лингвистике) Корреля'цияв лингвистике, противопоставленность или сближение единиц языка по определённым свойствам (на всех уровнях языковой системы). Более всего развита теория фонологической К. (чередование фонем, с которым связано какое-либо морфологическое различие, или образующее соотносительные ряды, которые противополагаются по одному какому-либо различительному признаку). Различают понятия коррелятивной пары (франц. а - а, o - o, е - е, S - S), признака (назализация во франц., лабиовеляризация в языках шона семьи банту), ряда (a, o, e,S), пучка (в арчинском яз. шестичленный z - s - ts - ts'- `ts - `s) и др. Корреляция (в матем. статистике) Корреля'цияв математической статистике, вероятностная или статистическая зависимость, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной, корреляционная зависимость возникает тогда, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или же когда среди условий, от которых зависят и тот и другой признаки, имеются общие для них обоих условия. Пример такого рода зависимости даёт корреляционная таблица. Из таблицы видно, что при увеличении высоты сосен в среднем растет и диаметр их стволов; однако сосны заданной высоты (например, 23 м) имеют распределение диаметров с довольно большим рассеянием. Если в среднем 23-метровые сосны толще 22-метровых, то для отдельных сосен это соотношение может заметным образом нарушаться. Статистическая К. в обследованной конечной совокупности наиболее интересна тогда, когда она указывает на существование закономерной связи между изучаемыми явлениями. В основе теории К. лежит предположение о том, что изучаемые явления подчинены определённым вероятностным закономерностям (см. Вероятность, Вероятностей теория) .Зависимость между двумя случайными событиями проявляется в том, что условная вероятность одного из них при наступлении другого отличается от безусловной вероятности. Аналогично, влияние одной случайной величины на другую характеризуется законами условных распределений первой при фиксированных значениях второй. Пусть для каждого возможного значения Х = хопределено условное математическое ожидание у (х)= Е (YIX = х) величины Y(см. Математическое ожидание ) .Функция у (х)называется регрессией величины Yпо X,а её график - линией регрессии Yпо X.Зависимость Yот Хпроявляется в изменении средних значений Yпри изменении X,хотя при каждом Х = хвеличина Yостаётся случайной величиной с определенным рассеянием. Пусть m Y=Е (Y) - безусловное математическое ожидание Y. Если величины независимы, то все условные математические ожидания Yне зависят от хи совпадают с безусловными: у (х)= Е (YIX = х) =Е (Y) = m Y. Обратное заключение не всегда справедливо. Для выяснения вопроса, насколько хорошо регрессия передаёт изменение Yпри изменении X,используется условная дисперсия Yпри данном значении Х = хили её средняя величина - дисперсия Yотносительно линии регрессии (мера рассеяния около линии регрессии):
При строгой функциональной зависимости величина Yпри данном Х = хпринимает лишь одно определенное значение, то есть рассеяние около линии регрессии равно нулю. Линия регрессии может быть приближённо восстановлена по достаточно обширной корреляционной таблице: за приближённое значение у (х)принимают среднее из тех наблюдённых значений Y,которым соответствует значение Х = х.На рисунке изображена приближённая линия регрессии для зависимости среднего диаметра сосен от высоты в соответствии с таблицей. В средней части эта линия, по-видимому, хорошо выражает действительная закономерность. Если число наблюдений, соответствующих некоторым значениям X, недостаточно велико, то такой метод может привести к совершенно случайным результатам. Так, точки линии, соответствующие высотам 29 и 30 м,ненадёжны ввиду малочисленности материала. См. Регрессия. В случае К. двух количественных случайных признаков обычным показателем концентрации распределения вблизи линии регрессии служит корреляционное отношение
где
всегда -1 Ј r Ј 1. Однако практическое использование коэффициента К. в качестве меры зависимости оправдано лишь тогда, когда совместное распределение пары
(X, Y)нормально или приближённо нормально (см.
Нормальное распределение
)
;употребление
rкак меры зависимости между произвольными
Yи
Хприводит иногда к ошибочным выводам, т. к.
rможет равняться нулю даже тогда, когда
Yстрого зависит от
X. Если двумерное распределение
Хи
Yнормально, то линии регрессии
Yпо
Хи
Хпо
Yсуть прямые
у = m
Y+b
Y(x - mx)и
х = mx+b
x(у - m
Y),где
Так как в этом случае Е (Y - y (x)) 2=s 2 Y(1 -r 2) и Е (Y - x (y)) 2=s 2 X(1 -r 2) то очевидно, что r (корреляционные отношения совпадают с r 2 полностью определяет степень концентрации распределения вблизи линий регрессии: в предельном случае r = ± 1 прямые регрессии сливаются в одну, что соответствует строгой линейной зависимости между Yи X, при r =0 величины не коррелированы. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313, 314 |
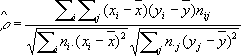 ,
,
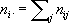 ,
,
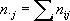 ,
,
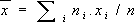 ,
,
 .
.
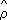 близок к истинному коэффициенту корреляции r. Поэтому использование
близок к истинному коэффициенту корреляции r. Поэтому использование
 как меры связи имеет четко определённый смысл для тех распределений, для которых естественной мерой зависимости служит r (т. е. для нормальных или близких к ним распределений). Во всех др. случаях в качестве характеристики силы связи рекомендуется использовать корреляционное отношение
h, интерпретация которого не зависит от вида исследуемой зависимости.
как меры связи имеет четко определённый смысл для тех распределений, для которых естественной мерой зависимости служит r (т. е. для нормальных или близких к ним распределений). Во всех др. случаях в качестве характеристики силы связи рекомендуется использовать корреляционное отношение
h, интерпретация которого не зависит от вида исследуемой зависимости.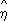 y|
xвычисляется по данным корреляционной таблицы:
y|
xвычисляется по данным корреляционной таблицы: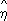 2
y|
x=
2
y|
x=
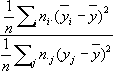
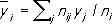 около безусловного среднего
около безусловного среднего
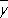 (аналогично определяется выборочное значение
(аналогично определяется выборочное значение
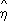 x|
y). Величина
x|
y). Величина
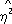 y|
x
y|
x
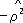 используется в качестве меры отклонения зависимости от линейной, т. к. обычно
используется в качестве меры отклонения зависимости от линейной, т. к. обычно
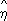 2
y|
x>r
2,
2
y|
x>r
2,
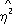 x|
y>r
2и лишь в случае линейной зависимости r
2=
x|
y>r
2и лишь в случае линейной зависимости r
2=
 2
y|
x=
2
y|
x=
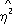 x|
y. Так, при анализе корреляции между высотой и диаметром северной сосны было обнаружено, что условные средние значения высоты сосны для заданного диаметра связаны нелинейной зависимостью. Корреляционное отношение (высоты к диаметру) в этом случае равно 0,813, а коэффициент корреляции равен 0,762.
x|
y. Так, при анализе корреляции между высотой и диаметром северной сосны было обнаружено, что условные средние значения высоты сосны для заданного диаметра связаны нелинейной зависимостью. Корреляционное отношение (высоты к диаметру) в этом случае равно 0,813, а коэффициент корреляции равен 0,762.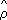 считается значимо отличной от нуля, если выполняется неравенство
считается значимо отличной от нуля, если выполняется неравенство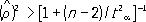 ,
,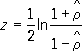 .
.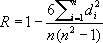 ,
,
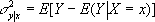 2
.
2
.
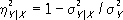 ,
,
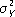 - дисперсия
Y(аналогично определяется корреляционное отношение
- дисперсия
Y(аналогично определяется корреляционное отношение
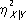 , но между
, но между
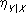 и
и
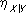 нет какой-либо простой зависимости). Величина
нет какой-либо простой зависимости). Величина
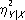 , изменяющаяся от 0 до 1, равна нулю тогда и только тогда, когда регрессия имеет вид
у (x) = m
Y,в этом случае говорят, что
Yнекоррелирована с
X,
, изменяющаяся от 0 до 1, равна нулю тогда и только тогда, когда регрессия имеет вид
у (x) = m
Y,в этом случае говорят, что
Yнекоррелирована с
X,
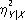 равняется единице в случае точной функциональной зависимости
Yот
X.Наиболее употребителен при измерении степени зависимости коэффициент корреляции между
Хи
Y
равняется единице в случае точной функциональной зависимости
Yот
X.Наиболее употребителен при измерении степени зависимости коэффициент корреляции между
Хи
Y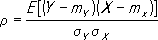
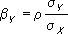 и
и
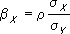 ; b
Y
и b
X
именуются коэффициентами регрессии, причём
; b
Y
и b
X
именуются коэффициентами регрессии, причём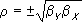 .
.