 |
|
���������� ������:: ������ ����� ���� :: ������� ������ :: ���� ��������� :: ������ ����� :: ��� :: ����� ����� �������� :: ������� ��� ���������� :: �������� ����� :: ������ ���� :: ������ ������� �������� ���������� �����:: The Boarding House :: ���� (����� 1-3) :: ���� :: ���������� ����� � ������ :: ����� �������� � ������ :: ������������ ���� ��� ������ :: �There Are More Things� :: ���������� ���-�������� :: ���� ������ ������ :: ���� �����-������ |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 262)
ко'ды,помехоустойчивые коды, коды обнаружения и исправления ошибки,
коды,позволяющие по имеющейся в кодовой комбинации
избыточности
обнаруживать и исправлять определённые ошибки, появление которых приводит к образованию ошибочных или запрещенных комбинаций. Применяются при передаче и обработке информации в вычислительной технике, телеграфии, телемеханике и технике связи, где возможны искажения сигнала в результате действия различного рода помех. Кодовые слова К. к. содержат информационные и проверочные разряды (символы). В процессе
кодирования
при передаче информации из информационных разрядов в соответствии с определёнными для каждого К. к. правилами формируются дополнительные символы - проверочные разряды. При декодировании из принятых кодовых слов по тем же правилам вновь формируют проверочные разряды и сравнивают их с принятыми; если они не совпадают, значит при передаче произошла ошибка. Существуют коды, обнаруживающие факт искажения сообщения, и коды, исправляющие ошибки, т. е. такие, с помощью которых можно восстановить первичную информацию.
В качестве примера рассмотрим код Хэмминга. Пусть требуется передать некоторое слово 1010. При кодировании оно будет представлено как 1011010, где 1-й, 2-й и 4-й разряды проверочные (слева направо 101), а остальные информационные. Если при передаче произошла ошибка, например в 3-м разряде вместо 1 получен 0, то при декодировании проверочные разряды примут значения: 1-й (младший) - 1, 2-й - 1, 4-й - 0 (т. е. 011). Несовпадение кодовых комбинаций проверочных разрядов не только сигнализирует о наличии ошибки, но и указывает номер искажённого разряда (011 - 3 в двоичном коде). Корректирующая и обнаруживающая способность кодов зависит от кодового расстояния dмежду словами, численно равного минимальному числу ошибок, которое может превратить одно слово в другое. Например, имеется кодовая комбинация: 0111100; 0100101; 0010110. Первая группа (слово) отличается от второй в трёх разрядах, вторая от третьей - в четырёх разрядах, первая от третьей - в трёх разрядах. Минимальное расстояние dмежду этими словами равно 3. Если в первом слове произойдёт 3 ошибки, то оно может превратиться либо во второе, либо в третье слово; при декодировании такая ошибка не будет обнаружена. Максимальное число ошибок, которое в данном случае может быть обнаружено, равно 2. Если в первом слове произошла ошибка во втором разряде, то полученное слово отличается от второго в четырёх разрядах, от третьего - в двух разрядах, от первого - в одном разряде. Согласно максимального правдоподобия методу, при декодировании делается вывод, что, вероятнее всего, передавалось первое слово. Для правильного декодирования необходимо, чтобы максимальное число ошибок в передаваемом слове превращало его в слово, отличающееся от исходного в наименьшем числе разрядов. Чтобы исправлять все комбинации из tошибок, необходимо и достаточно, чтобы d ³2 t+1. Ошибки в передаваемых словах могут возникать вследствие либо независимых искажений разрядов (в этом случае применяют, например, коды типа кода Хэмминга), либо искажений группы рядом стоящих разрядов (для таких случаев разработаны коды, исправляющие одиночные пачки ошибок, и коды, исправляющие более одной пачки ошибок); для обнаружения ошибок в процессе вычислений на ЭВМ разработаны так называемые арифметические коды. Лит.:Питерсон У., Коды, исправляющие ошибки, пер. с англ., М., 1964. Г. Н. Оныкий. Корректирующие цепи Корректи'рующие це'пи,электрические цепи, применяемые в аппаратуре многоканальной связи,радиоустройствах чаще всего для уменьшения искажений проходящих в них сигналов или в устройствах автоматического регулирования, следящих системах и т. п. для придания им требуемых статических и динамических характеристик. В качестве элементов К. ц. используются различные комбинации катушек индуктивности, конденсаторов и резисторов. Искажения сложных сигналов, возникающие при прохождении последними различных цепей радиоустройств, бывают двух видов: частотные, обусловленные неодинаковым усилением и ослаблением колебаний разных частот сигнала, т. е. амплитудно-частотной характеристикой цепи, и фазовые, обусловленные неодинаковым опережением и отставанием по фазе колебаний разных частот, т. е. неравномерностью группового времени распространения сигнала. В приёмниках звукового радиовещания, радиосвязи и др. исправляют лишь частотные искажения, т. к. человеческое ухо практически не ощущает небольшие фазовые искажения. В телевизионных, радиолокационных и т. п. приёмниках импульсных сигналов применяют цепи, корректирующие одновременно как частотные, так и (в большой степени) фазовые искажения (см. Видеоусилитель ) .Фазовые искажения могут быть скорректированы также отдельно. В устройствах автоматического регулирования и следящих системах наибольшее распространение получили К. ц., служащие главным образом для выполнения операций дифференцирования и интегрирования немодулированных сигналов. В системах автоматического управления К. ц. применяются для выполнения более сложных операций над сигналами. Такие К. ц. определяются по форме их амплитудно-частотных характеристик. Лит.:Корректирующие цепи в автоматике. Сб. пер. ст., под ред. М. З. Литвина-Седого, М., 1954; Артым А. Д., Электрические корректирующие цепи и усилители, М.- Л., 1965; Брауде Г. В., Коррекция телевизионных и импульсных сигналов, М., 1967. Корректирующий ракетный двигатель Корректи'рующий раке'тный дви'гатель,ракетный двигатель, включаемый в космическом полёте для коррекции направления и значения скорости полёта космического аппарата. Обычно К. р. д. - жидкостный ракетный двигатель многократного запуска, работающий на долгохранимом топливе. Корректирующий светофильтр Корректи'рующий светофи'льтр,цветной светофильтр для исправления (коррекции) цветопередачи при фотопечати (например, посредством фотографического увеличителя ) или копировании (например, посредством кинокопировального аппарата ) цветных позитивных изображений. Корректные и некорректные задачи Корре'ктные и некорре'ктные зада'чи,классы математических задач, которые различаются степенью определённости их решений. Многие математические задачи состоят в том, что по исходным данным uищется решение z.При этом считается, что uи zсвязаны функциональной зависимостью z = R (u).Задача называется корректной задачей (или корректно поставленной), если выполнены следующие условия (условия корректности): 1) задача имеет решение при любых допустимых исходных данных (существование решения); 2) каждым исходным данным uсоответствует только одно решение (однозначность задачи); 3) решение устойчиво. Смысл первого условия заключается в том, что среди исходных данных нет противоречащих друг другу условий, что исключало бы возможность решения задачи. Второе условие означает, что исходных данных достаточно для однозначной определённости решения задачи. Эти два условия обычно называют условиями математической определённости задачи. Третье условие заключается в следующем. Если u 1и u 2- два различных набора исходных данных, мера уклонения которых друг от друга достаточно мала, то мера уклонения решений z 1= R (u 1)и z 2= R (u 2)меньше любой наперёд заданной меры точности. При этом предполагается, что в многообразии U = {u}допустимых исходных данных и в многообразии возможных решений Z = {z}установлено понятие меры уклонения (или меры близости) r(u 1, u 2)и r*(z 1, z 2). Третье условие обычно трактуется как физическая детерминированность задачи. Это объясняется тем, что исходные данные физической задачи, как правило, задаются с некоторой погрешностью; при нарушении же третьего условия как угодно малые возмущения исходных данных могут вызывать большие отклонения в решении. Задачи, не удовлетворяющие хотя бы одному условию корректности, называются некорректными задачами (или некорректно поставленными). Внимание к корректности задач было привлечено французским математиком Ж. Адамаром в связи с решением краевых задач для уравнений с частными производными. Понятие корректности задач явилось, в частности, поводом для классификации краевых задач таких уравнений. Существовало мнение, что некорректные задачи не могут встречаться при решении физических и технических задач и что для некорректных задач невозможно построение приближённого решения в случае отсутствия устойчивости. Расширение средств автоматизации при получении экспериментальных данных привело к большому увеличению объёма таких данных; необходимость установления по ним информации о естественнонаучных объектах потребовала рассмотрения некорректных задач. Развитие электронной вычислительной техники и применение её к решению математических задач изменило точку зрения на возможность построения приближённых решений некорректно поставленных задач. Понятия приближённого решения для К. и н. з. существенно различны. В качестве приближённого решения
z = R (u)корректной задачи можно брать точное её решение
Т. о., приближённое решение некорректной задачи может быть сведено к нахождению регуляризирующего оператора
Примером некорректной классической математической задачи может служить задача приближённого дифференцирования при определённых (практически важных) мерах точности задания
zи
u.Именно, некорректной будет задача о нахождении равномерного приближения
Можно привести много др. примеров классических математических задач, являющихся некорректными при совершенно естественном выборе понятий меры точности как для исходных данных задачи, так и для возможных решений: решение систем линейных алгебраических уравнений с определителем, равным нулю; задача оптимального планирования; решение интегральных уравнений 1-го рода; задача аналитического продолжения; суммирование рядов Фурье; большое число краевых задач для уравнении с частными производными. Обширный класс некорректно поставленных задач в естествознании составляют задачи обработки наблюдений без дополнительной (количественной) информации о свойствах решений. Если изучается объект, количественные характеристики zкоторого недоступны для прямого изучения, то обычно исследуются некоторые проявления этого объекта u,функционально зависящие от z.Задача обработки наблюдений состоит в решении «обратной задачи», т. е. в определении характеристики zобъекта по результатам наблюдений u;при этом uзадаётся приближённо. Имеется много работ (особенно советских математиков), посвященные методам приближённого решения некорректно поставленных задач и их применений к решению обратных задач. Эти работы имеют важное значение для автоматизации обработки наблюдений, для решения проблем управления и т. д. Лит.:Тихонов Д. Н., Об устойчивости обратных задач, «Доклады АН СССР», 1943, т. 39, № 5; его же, О решении некорректно поставленных задач и методе регуляризации, там же, 1963, т. 151, № 3; Лаврентьев М. М., О некоторых некорректных задачах математической физики, Новосиб., 1962. А. Н. Тихонов. Корректура Корректу'ра(от лат. correctura - исправление, улучшение), процесс исправления грамматических и технических ошибок и недостатков в текстовом и графическом материалах, подготовленных для размножения типографским (или любым другим) способом. В более узком смысле - оттиск с типографского набора (см. Наборное производство ) ,предназначенный для внесения исправлений. Для К. с наборной формы на корректурных станках изготовляются пробные корректурные оттиски. При сличении оттиска с текстом оригинала обнаруживаются ошибки, которые могут быть результатом невнимательности и недостаточной квалификации наборщика, неправильной подготовки наборной кассы или неисправностей в наборной машине, а также низкого качества самого оригинала; наряду с орфографическими и пунктуационными ошибками в наборе могут быть и технические погрешности. Для обозначения на оттиске обнаруженных ошибок применяют систему корректурных знаков. Существуют четыре вида корректур: типографская; К. изданий, выпускаемых по оригинал-макетам; издательская К. и К. репродукционных печатных форм. Типографская К и К. изданий по оригинал-макетам предусматривают исправление ошибок в наборе, возникших на всех стадиях наборного процесса; издательская К. включает исправления автора, редактора и технического редактора; К. репродукционных печатных форм заключается в сличении пробных однокрасочных или многокрасочных оттисков с оригиналом (например, картиной, находящейся в музее) и письменном указании на полях оттиска (без специальных знаков) исправлений, которые должны быть внесены в форму (например, усилить или ослабить печатные элементы на форме). Лит.:Былинский К. И., Жилин А. Н., Справочная книга корректора, М., 1960; Каменецкий Л. М., Козоровицкая И. С., Тяпкин Б. Г., Корректура, М., 1966. А. А. Киселева. 
Илл. к ст. Корректура. Корректурный станок Корректу'рный стано'к,станок для получения корректурных оттисков с наборных полос и др. печатных форм. К. с. представляет собой упрощённую печатную машину малого формата. Наборная форма устанавливается на горизонтальном столе станка, по ней прокатываются валики, наносящие краску, и печатный цилиндр, прижимающий бумагу к печатающим элементам формы. Станок приводится в действие от электродвигателя. Применяют также ручные К. с. тигельного типа, в которых бумага прижимается к набору плоской чугунной плитой, а также станки с покрытым резиной металлическим валиком, прокатываемым вручную по форме. Коррекция динамических свойств Корре'кция динами'ческих сво'йствсистемы автоматического регулирования, изменение динамических характеристик системы с целью удовлетворения требований, предъявляемых к запасу устойчивости, поведению системы в переходном процессе, точности регулирования и др. Производится путём изменения значений параметров системы или введения корректирующих устройств. См. Регулирование автоматическое. Коррелометр Коррело'метр(от корреляция и . 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313, 314 |
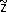 с приближёнными исходными данными
с приближёнными исходными данными
 ,т. к. для любой точности
eприближённого решения корректной задачи в силу третьего условия существует такая точность
d(e)исходных данных, что, если
,т. к. для любой точности
eприближённого решения корректной задачи в силу третьего условия существует такая точность
d(e)исходных данных, что, если
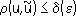 , то
, то
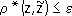 . Для некорректных задач точное решение с приближёнными исходными данными нельзя принимать в качестве приближённого решения. Однако задание приближённых исходных данных в естественных науках может быть охарактеризовано не только исходным элементом
. Для некорректных задач точное решение с приближёнными исходными данными нельзя принимать в качестве приближённого решения. Однако задание приближённых исходных данных в естественных науках может быть охарактеризовано не только исходным элементом
 ,но и мерой его точности
d. Т. о., для определения приближённого решения имеется не только элемент
,но и мерой его точности
d. Т. о., для определения приближённого решения имеется не только элемент
 ,но и параметр
d. Понятие приближённого решения задачи
z = R (u)вводится с помощью т. н. параметрического оператора
R
d(u),зависящего от параметра
dи называемого регуляризирующим (или исправляющим) оператором. Если оператор
R
d(u)определён для всех
d >0 и всех
,но и параметр
d. Понятие приближённого решения задачи
z = R (u)вводится с помощью т. н. параметрического оператора
R
d(u),зависящего от параметра
dи называемого регуляризирующим (или исправляющим) оператором. Если оператор
R
d(u)определён для всех
d >0 и всех
 ,входящих в класс допустимых исходных данных, и если
z = R (u),то для любой заданной точности
eсуществует (хотя бы в принципе) такое
d(e), что для любого элемента
,входящих в класс допустимых исходных данных, и если
z = R (u),то для любой заданной точности
eсуществует (хотя бы в принципе) такое
d(e), что для любого элемента
 решение
решение
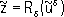 уклоняется от
zменьше, чем на заданную точность
e, т. е.
уклоняется от
zменьше, чем на заданную точность
e, т. е.
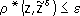 .
.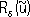 , который определяет устойчивое приближение к
z.
, который определяет устойчивое приближение к
z.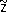 к
zпо равномерному приближению
к
zпо равномерному приближению
 к
u, т. к. здесь не выполнено первое условие корректности: не для всякой функции
к
u, т. к. здесь не выполнено первое условие корректности: не для всякой функции
 такой, что
такой, что
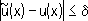 существует производная
существует производная
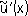 ,а также не выполняется третье условие корректности: если даже существует производная
,а также не выполняется третье условие корректности: если даже существует производная
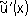 ,то из неравенства
,то из неравенства
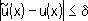 не следует близость производных
не следует близость производных
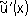 и
u'(х).Однако в качестве регуляризирующего оператора можно взять
и
u'(х).Однако в качестве регуляризирующего оператора можно взять
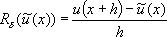 при
h >> d. Этот оператор определён для всех
при
h >> d. Этот оператор определён для всех
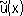 независимо от их дифференцируемости и в ограниченном промежутке даёт равномерное приближение для всякой непрерывно дифференцируемой функции
u (х).
независимо от их дифференцируемости и в ограниченном промежутке даёт равномерное приближение для всякой непрерывно дифференцируемой функции
u (х).