 |
|
���������� ������:: ��� :: ������ ����� ���� :: ������ ����� :: ������� ��� ���������� :: ������� ������ :: �������� ����� :: ������� ������ :: ����� ����� �������� :: ���� ��������� :: ������� ������ ���������� ���������� �����:: ���������� �� ������� Windows XP :: The Boarding House :: ���� (����� 1-3) :: ���������� ����� :: ����������������� ��� :: ������� ������� ����� :: �������� ������� :: ����������� ���������� :: ���� �����-������ :: ���� ������� |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 216)Д. Л. Юдин. Координатограф Координато'граф(от координаты и ...граф ) ,прибор для быстрого и точного нанесения на карту или план точек по их прямоугольным координатам. Состоит из станины, на которой наглухо прикреплена линейка с делениями, представляющая собой ось абсцисс XX. Вдоль оси абсцисс передвигается каретка, несущая на себе линейку YY,соответствующую оси ординат. По оси ординат движется малая каретка, на которой укреплена иголка для накола точек. Автоматический электронный К. имеет дополнительно счётно-решающее устройство и пульт управления. Эта система обеспечивает возможность по результатам вычислении прямоугольных координат на счётно-решающем устройстве наносить узловые точки и автоматически вычерчивать или гравировать координатные линии сетки. 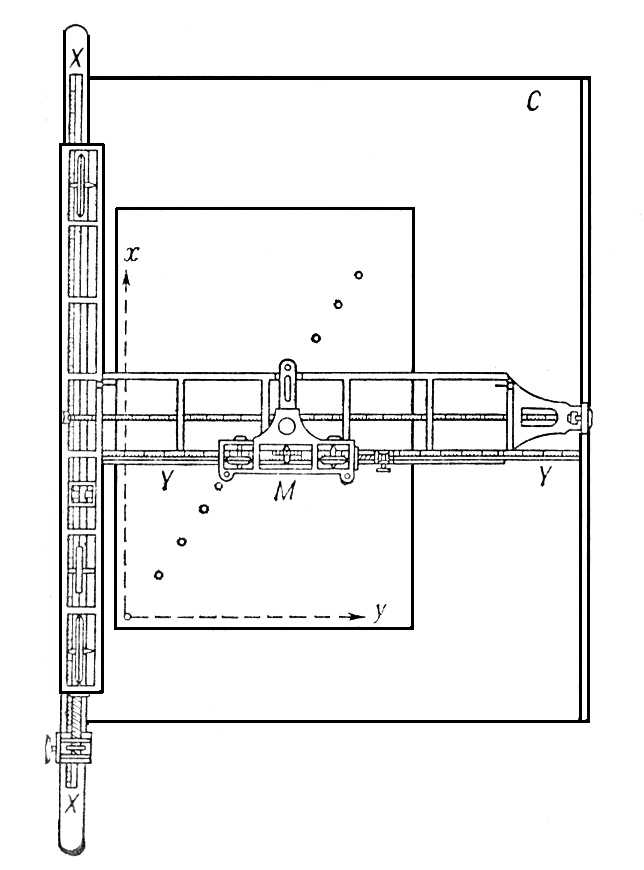
Схема координатографа. Координатомер Координатоме'р,прибор для измерения координат точек (ориентиров, целей и т. п.) на топографических картах с прямоугольной координатной сеткой. К. применяют также для нанесения на карты точек по координатам. Иногда К. представляет собой прозрачную прямоугольную плёнку (целлулоидную или др.) с квадратным вырезом посередине и нанесёнными по краям шкалами, равными по длине сторонам квадратов координатной сетки на картах масштабов 1:25000, 1:50000 и 1:100000. Координаты (в геодезии) Координа'тыв геодезии, совокупность трёх чисел, определяющих положение точки земной поверхности относительно некоторой исходной поверхности. Последняя, так называемая поверхность относимости, суть поверхность, заменяющая в некотором приближении поверхность геоида.В зависимости от целей за поверхность относимости принимают плоскость (в топографии это плоскость проекции Гаусса-Крюгера, см. Геодезические проекции, Прямоугольные координаты) ,сферу - поверхность «земного шара», поверхность референц-эллипсоида (см. также Земной эллипсоид ) . Геодезические К. точки: широта В(угол, образованный проходящей через данную точку нормалью эллипсоида с плоскостью его экватора), долгота L(угол между плоскостями меридиана данной точки и начального меридиана), высота Н(расстояние данной точки от эллипсоида по нормали к нему). Геодезические К. непосредственно из наблюдений получены быть не могут. Для любой точки, включенной в геодезическую сеть, они могут быть вычислены по данным геодезических измерений. Астрономические К. точки: широта j- угол, образованный отвесной линией в данной точке с плоскостью земного экватора; долгота l -угол между плоскостями астрономических меридианов данной точки и начального; так, определённые астрономические координаты jи lназываются также географическими координатами.К jи lприсоединяется ещё нормальная высота Н g(расстояние данной точки от квазигеоида по отвесной линии), которая часто отождествляется с высотой точки над уровнем моря. Астрономические координаты jи lполучают из астрономических наблюдений (см. Геодезическая астрономия ); высоты точек земной поверхности получают из нивелирования.Геодезические К. какой-либо точки отличаются от астрономических К. той же точки за счёт выбора эллипсоида и несовпадения отвесной линии с нормалью к эллипсоиду (см. Отклонение отвеса ) .Сравнение геодезических и астрономических К. ряда точек земной поверхности даёт возможность изучить на данном участке поверхность геоида (точнее квазигеоида) относительно применяемого эллипсоида (астрономическое нивелирование и астрономо-гравиметрическое нивелирование ) . В геодезии используют также и др. виды К. В связи с развитием космической геодезии большое значение приобрели прямоугольные геодезические координаты X, Y, Z,начало которых Осовмещено с центром эллипсоида, а ось Zнаправлена по малой его оси. Переход от В, L, Н к X, Y, Zсовершается по довольно простым формулам. При изучении многих вопросов геодезии используются также различные криволинейные К. на поверхности эллипсоида. На практике - при использовании данных геодезии и топографических карт - применяют прямоугольные К. на плоскости геодезической проекции. Лит.:Красовский Ф. Н., Руководство по высшей геодезии, ч. 2, М., 1942; 3акатов П. С., Курс высшей геодезии, 3 изд., М., 1964; Морозов В. П., Курс сфероидической геодезии, М., 1969; Грушинский Н. П., Теория фигуры Земли, М., 1963. Г. А. Мещеряков. Координаты (математ.) Координа'ты[от лат. co (cum) - совместно и ordinatus - упорядоченный, определённый], числа, заданием которых определяется положение точки на плоскости, на любой поверхности или в пространстве. Первыми вошедшими в систематическое употребление К. являются астрономические и географические К. - широта и долгота, определяющие положение точки на небесной сфере или на поверхности земного шара (см. Небесные координаты, Географические координаты) .В 14 в. французский математик Н. Орем пользовался К. на плоскости для построения графиков, называя долготой и широтой то, что теперь называют абсциссой и ординатой. Более систематически К. стали применяться к вопросам геометрии на плоскости в 17 в. Заслуга выяснения всего значения метода К., позволяющего систематически переводить задачи геометрии на язык математического анализа и, обратно, истолковывать геометрически факты анализа, принадлежит французскому учёному Р. Декарту. Кроме К. точки, рассматривают также К. прямой, плоскости и других геометрических объектов. В теоретической механике употребляют К. механических систем - числа, определяющие положение механической системы (например, некоторого твёрдого тела) в каждый момент времени.
Координаты точки на плоскости. Аффинные, или общие декартовы, К. точки на плоскости получают, выбирая точку
О(начало К.) и два не лежащих на одной прямой вектора
и ординатой
где
XPпараллельно
OBи
YPпараллельно
ОА.В частном случае, когда векторы
Полярные К. точки на плоскости получают, выбирая точку О (полюс). выходящий из неё луч
ONи единицу измерения длин. Координатами точки
Рслужат расстояние
r = OPн угол
j = РNOP.Чтобы получить возможность поставить в соответствие каждой точке плоскости
Рпару чисел (
r, j), достаточно рассматривать
rи
j, подчинённые неравенствам 0 Ј
r<Ґ, 0Ј
j<2
Из других специальных систем К. на плоскости следует отметить также эллиптические координаты. В случае аффинных К. линии х= constобразуют пучок прямых, параллельных оси Oy, а линии у = const - другой пучок прямых, параллельных оси Ox, через каждую точку плоскости Р (х 0, у 0)проходит одна прямая первого пучка ( х = x 0) и одна прямая второго пучка ( у = y 0) .В случае полярных К. линии r = constявляются окружностями, а линии j = const- лучами, выходящими из начальной точки О; через каждую точку Р, отличную от О, проходит ровно по одной линии каждого из двух семейств; отметки r 0и j 0этих двух линий и являются К. точки Р. В более общем случае можно рассмотреть в какой-либо области Gплоскости две функции точки u (Р)и u(P)такого рода, что каждая линия u (Р) = constпересекается с каждой линией семейства u(P) = constв пределах области Gне более чем в одной точке. Очевидно, что в этом случае числа u (Р)и u(Р)однозначно определяют положение точки Рв области G, т. е. являются К. точки Рв этой области; линии, определяемые уравнениями u = constили u =const, называют при этом координатными линиями. Криволинейные координаты на поверхности.Изложенная идея применима без всяких изменений и к введению криволинейных К. на произвольной поверхности. Например, для случая долготы jи широты qна сфере линиями j = constявляются меридианы, а линиями q = const- широтные круги, расположение которых всем хорошо известно из элементов географии. Криволинейные, или, как их иначе называют, гауссовы, К. на произвольной поверхности являются основным аппаратом дифференциальной геометрии поверхностей. Однородные координаты на плоскости.Евклидова плоскость, дополненная бесконечно удалёнными элементами, может рассматриваться с проективной точки зрения как замкнутая поверхность (см. Проективная плоскость ) ,на которой бесконечно удалённые точки не играют какой-либо особой роли. На всей проективной плоскости введение К., характеризующих положение точки парой чисел (u, u)с сохранением взаимной однозначности и непрерывности соответствия, невозможно. Вместо этого пользуются однородными К. При этом каждой точке ставятся в соответствие не пары, а тройки чисел (x 1, x 2, x 3),причём двум тройкам (x 1, x 2, x 3)и (x 1 ’, x 2 ’, x 3 ’)соответствует одна и та же точка только тогда, когда входящие в них числа пропорциональны, т. е. существует такой множитель l,что x 1 ’= lx 1, x 2 ’= lx 2, x 3 ’= lx 3. Такие системы координат играют большую роль в геометрии.
Координаты точки в пространстве.Аффинные, или общие декартовы, К. в трёхмерном пространстве вводятся заданием точки
Ои трёх векторов
В простейшем случае прямоугольных К. векторы e x, е у, e zпопарно перпендикулярны и имеют единичную длину. В пространстве возможны два существенно различных типа систем прямоугольных К.: правая система (где е уи e zлежат в плоскости чертежа, а e x направлен вперёд, к читателю) и левая система (где e xи e zлежат в плоскости чертежа, а е у направлен к читателю). В пространстве пользуются также системами криволинейных К., общая схема которых такова: в какой-либо области Gпространства рассматриваются три функции точки u (P), u(P), w(P),подчинённые условию, чтобы через каждую точку Робласти Gпроходила одна поверхность семейства u = const, одна поверхность семейства u = constи одна поверхность семейства w = const. Тем самым каждой точке ставятся в соответствие три числа (u, u, w) -её К. Поверхности, определяемые уравнениями u = const,или u = const,или w = const, называют координатными. В приложениях (к механике, математической физике и пр.) наиболее употребительны некоторые специальные системы криволинейных К., а именно: сферические координаты, цилиндрические координаты. Координаты прямой, плоскости ит. п. Принцип двойственности (см. Двойственности принцип ) ,устанавливающий равноправность точек и прямых в геометрии двух измерений и равноправность точек и плоскостей в геометрии трёх измерений, подсказывает ту мысль, что с помощью особых К. могут быть определены положения прямых и плоскостей. Действительно, если, например, в прямоугольных К. уравнение прямой (не проходящей через начало К.) приведено к виду ux + uy + 1 = 0,то числами uи u ( u = - 1/ a, u = - 1/ b,где аи bсуть «отрезки», отсекаемые прямой на осях) вполне определяется положение прямой; можно принять ( u, u) за К. (так называемые тангенциальные К.) прямой линии. Симметричность уравнения ux + uy + 1 = 0относительно пар (х, у)и (u, u)является аналитическим выражением принципа двойственности. Вполне аналогично случаям n = 2(плоскость, поверхность) и n = 3(трёхмерное пространство) употребление К. в n-мepном пространстве. Лит.см. при ст. Аналитическая геометрия. А. Н. Колмогоров. 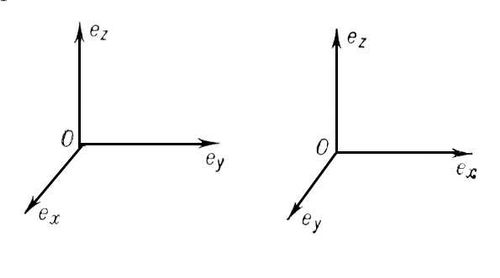
Рис. 3 (слева) и рис. 4 (справа) к ст. Координаты. 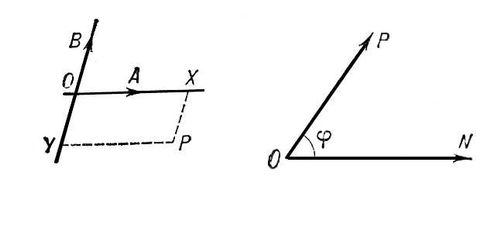
Рис. 1 (слева) и рис. 2 (справа) к ст. Координаты. Координационно-вычислительный центр Координацио'нно-вычисли'тельный центр,часть командно-измерительного комплекса,предназначенный для проведения расчётов, связанных с полётом космических кораблей (вывод корабля на орбиту, изменение траектории полёта, коррекция орбиты и др.). К.-в. ц. обрабатывает данные, полученные с корабля, и анализирует их. К.-в. ц. оснащен быстродействующими универсальными ЦВМ. Координационное число Координацио'нное число'в кристаллографии, число ближайших к данному атому или иону соседних одинаковых атомов или ионов в кристалле. Прямые линии, соединяющие центры ближайших атомов или ионов в кристалле, образуют координационный многогранник, в центре которого находится данный атом. Одному и тому же К. ч. могут соответствовать разные многогранники. В структурах алмаза, кремния, германия, сфалеритаК. ч. равно 4, а координационный многогранник - тетраэдр. В структуре NaCI каждый ион Na окружен шестью ионами Cl, а каждый ион Cl - шестью ионами Na, т. е. для обоих типов ионов К. ч. равно 6, многогранник - октаэдр. В структуре флюорита CaF 2для ионов Са К. ч. равно 8, многогранник - куб; для ионов F К. ч. равно 4, многогранник - тетраэдр. Наивысшее возможное К. ч. равно 12, что характерно для металлов с плотнейшей кубической или гексагональной упаковкой. Для металлов с объёмно-центрированной решёткой К. ч. равно 8. Для полупроводниковых кристаллов, не имеющих плотнейшей упаковки атомов, характерны К. ч., равные 4 или 6. В химии К. ч. - число атомов или атомных групп, непосредственно присоединённых к данному атому в комплексных соединениях.Понятие К. ч. применяется также при описании структуры жидкостей и аморфных тел. В этом случае К. ч. - среднее число ближайших соседей атома, оно может быть дробным. К. ч. является мерой ближнего порядка в жидкостях и аморфных телах (см. Жидкость, Аморфное состояние, Дальний порядок и ближний порядок) .
Лит. см.при ст. Кристаллохимия. М. П. Шаскольская. Координация (биол.) Координа'ция, 1) соотносительное развитие органов и частей организма в филогенезе.Термин предложен А. Н. Северцовым. Немецким зоолог Л. Плате назвал это явление филетической корреляцией.И. И. Шмальгаузен рассматривал К. как закономерную зависимость изменений частей (органов) в ходе эволюции. Различают: топографическую К., выражающуюся в устойчивых соотношениях между органами, хотя непосредственной функциональной связи между ними нет (например, К. между редукцией крайних и прогрессивным развитием средних пальцев в филогенетическом ряду копытных); динамическую, или конструктивную, К., определяющуюся постоянством функциональных зависимостей между различными органами (например, органами чувств и соответствующими нервными центрами или летательными мышцами и килем грудной кости у птиц и т. д.); биологическую К., или коадаптацию,к которой относится большинство корреляций, установленных Ж. Кювье. 2) В физиологии согласование деятельности различных органов и систем организма, обусловленное сочетанием процессов возбуждения и торможения в центральной нервной системе. Например, при сгибании конечности возбуждение нервных клеток, посылающих импульсы к мышцам-сгибателям, вызывает одновременно торможение клеток, связанных с мышцами-разгибателями; возникающее при этом расслабление разгибателей облегчает сгибание конечности (см. Реципрокная иннервация ) . 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313, 314 |
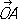 и
и
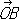 ,исходящих из точки
О. Положение точки
Ропределяется (в выбранной системе К.) двумя К.: абсциссой
,исходящих из точки
О. Положение точки
Ропределяется (в выбранной системе К.) двумя К.: абсциссой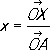
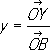 ,
,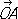 и
и
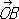 перпендикулярны и имеют одну и ту же длину, получают наиболее употребительные прямоугольные К. Если угол между
перпендикулярны и имеют одну и ту же длину, получают наиболее употребительные прямоугольные К. Если угол между
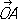 и
и
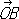 произволен, но длины этих векторов одинаковы, то получают те косоугольные К., рассмотрением которых ограничивался сам Декарт (часто только их и называют декартовыми, сохраняя для общих декартовых К. название аффинные К.).
произволен, но длины этих векторов одинаковы, то получают те косоугольные К., рассмотрением которых ограничивался сам Декарт (часто только их и называют декартовыми, сохраняя для общих декартовых К. название аффинные К.). . За исключением точки
О, для которой
r
=0, а угол
jне определён, соответствие между точками
Р,отличными от
О, и парами (
r, j), подчинёнными указанным условиям, взаимно однозначно.
. За исключением точки
О, для которой
r
=0, а угол
jне определён, соответствие между точками
Р,отличными от
О, и парами (
r, j), подчинёнными указанным условиям, взаимно однозначно.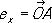 ,
,
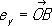 ,
,
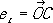 , не лежащих в одной плоскости. Для получения К.
х, у, zточки
Рвектор
, не лежащих в одной плоскости. Для получения К.
х, у, zточки
Рвектор
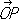 представляют в виде
представляют в виде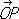 = xex+ уе
у+ze
z.
= xex+ уе
у+ze
z.