 |
|
���������� ������:: ��� :: ������ ����� ���� :: ������ ����� :: ������� ��� ���������� :: ������� ������ :: �������� ����� :: ������� ������ :: ����� ����� �������� :: ���� ��������� :: ������� ������ ���������� ���������� �����:: ���������� �� ������� Windows XP :: The Boarding House :: ���� (����� 1-3) :: ���������� ����� :: ����������������� ��� :: ������� ������� ����� :: �������� ������� :: ����������� ���������� :: ���� �����-������ :: ���� ������� |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 197)Конфликты пограничные Конфли'кты пограни'чные,см. Пограничные конфликты. Конфлюэнтная ступень Конфлюэ'нтная ступе'нь(от лат. confluens, род. падеж confluentis - соединение, слияние), ступень слияния поперечных уступов на дне ледниковой долины в месте бывшего слияния двух ледников, где мощность ледника и его эрозионная способность резко возрастали. Конфокальные кривые Конфока'льные кривы'е[от лат. con (cum) - вместе, сообща и focus (в математике) - фокус, буквально - очаг], кривые, имеющие общие фокусы. См. Софокусные кривые. Конформационный анализ Конформацио'нный ана'лиз,область стереохимии,исследующая конформации молекул и связи их с физическими и химическими свойствами веществ. Голландский химик Я. Х. Вант-Гофф в основу разработанной им (1874-75) стереохимической гипотезы положил два основных постулата: валентности насыщенного атома углерода направлены в пространстве к вершинам тетраэдра; атомы или группы атомов (заместители) в молекуле способны свободно вращаться вокруг простых связей без их разрыва (в отличие от двойных связей, жёсткость которых служит причиной появления геометрии изомеров; см. Изомерия ) .Впоследствии тетраэдрическая модель атома углерода была подтверждена прямыми рентгенографическими определениями. Положение же о свободном вращении вокруг простых связей подверглось пересмотру, поскольку было установлено, что вращение вокруг простых связей происходит не вполне свободно; при таком вращении возникают энергетически неравноценные геометрические формы - конформации, или поворотные изомеры, некоторые из них энергетически предпочтительнее других. Большинство молекул существует преимущественно в одной или немногих устойчивых (предпочтительных) конформациях. Энергетические барьеры, разделяющие разные конформации одного и того же вещества, обычно составляют 20,9-62,7 кдж/моль(5-15 ккал/моль) ;отдельные конформации постоянно переходят друг в друга. Особое значение имели исследования английского химика Д. Бартона о конформациях в ряду циклогексана; этот автор и ввёл термин «К. а.» (1950). В ряду парафиновых углеводородов необходимость конформационного рассмотрения возникает уже в случае этана, для которого возможны две конформации: т. н. заслонённая (или чётная) и заторможенная (или нечётная), образующиеся при вращении одной метильной группы относительно другой В чётной конформации этана атомы водорода расположены наиболее близко один к другому («друг за другом») и, следовательно, отталкивание между ними наибольшее; поэтому энергия этой конформации максимальна [она на 12,5кдж/моль(3 ккал/моль) больше энергии нечётной конформации]. Из этого энергетически невыгодного состояния молекула стремится перейти в более устойчивое состояние, в нечётную конформацию, атомы водорода в которой находятся на наибольшем возможном расстоянии друг от друга. В этом более благоприятном положении вращение вокруг связи С-С «тормозится» (отсюда и второе название - заторможенная). Заместители более объёмные, чем водород, не могут занимать чётных (заслонённых) положений. Поэтому, например, для бутана CH 3-CH 2-СН 2-CH 3следует рассматривать лишь три нечётные конформации, из которых наиболее выгодна трансоидная. С увеличением длины углеродной цепи, с появлением заместителей число возможных конформации, которые может принять молекула, быстро возрастает. Обычно из них более благоприятны те, в которых объёмные заместители максимально удалены друг от друга (как в трансоидной конформации бутана). Однако если между заместителями возникает электростатическое притяжение или водородная связь, то более выгодной может оказаться скошенная конформация, как, например, у этиленхлор-гидрина HOCH 2-CH 2CI. Характер химических превращений вещества часто зависит от конформации его молекул. Так, дебромирование 2,3-дибром-бутана металлическим цинком возможно лишь при трансоидном положении отщепляющихся атомов брома. Поэтому два диастереомера 2,3-дибромбутана дают геометрически изомерные олефины. Большое значение имеют конформационные представления для объяснения свойств циклических соединений, особенно в ряду циклогексана. Последний существует главным образом в форме «кресла», которая особенно выгодна, т. к. валентные углы в ней не искажены, а конформации по всем связям С - С нечётные. Оставшиеся две валентности каждого из входящих в цикл атомов углерода ориентированы или перпендикулярно к кольцу (аксиальные связи - а), или направлены по его периферии (экваториальные связи - е). Более выгодно экваториальное расположение заместителей. Например, при комнатной температуре конформационное равновесие хлорциклогексана е: а =70: 30. При понижении температуры до -150° С скорость взаимопревращения сильно уменьшается; в этих условиях можно изолировать чистую е-форму хлорциклогексана. Конформационное рассмотрение циклогексанового кольца позволяет, например, понять, почему как цис-,так и транс -циклогексан-1,2-дикарбоновая кислота способна к образованию ангидрида (в обоих случаях диэдральный угол между связями, ведущими к группам COOH, составляет 60°). Для исследования конформации, помимо химических методов, широко используются и физические, особенно метод ядерного магнитного резонанса. Полученные данные о конформациях органических соединений служат важной основой для истолкования и предсказания их свойств. Большое значение конформационные представления приобрели в химии синтетических и природных высокомолекулярных соединений, в области физиологически активных веществ. Лит.:Конформационный анализ, пер. с англ., М., 1969; Илиел Э., Основы стереохимии, пер. с англ., М., 1971; Терентьев А. П., Потапов В. М., Основы стереохимии, М. - Л., 1964. В. М. Потапов. 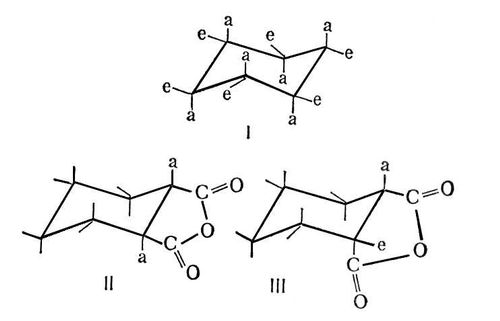
Рис. 5. Кресловидные конформации: циклогексана с аксиальными (а) и экваториальными (е) связями (I), ангидрида транс-циклогексан-1,2-дикарбоновой кислоты (II) и ангидрида цис-циклогексан-1,2-дикарбоновой кислоты (III). 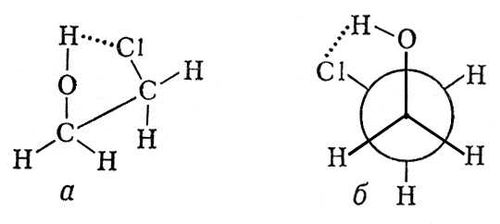
Рис. 3. Перспективная формула (а) и формула Ньюмена (б) для этиленхлоргидрина (скошенная конформация). 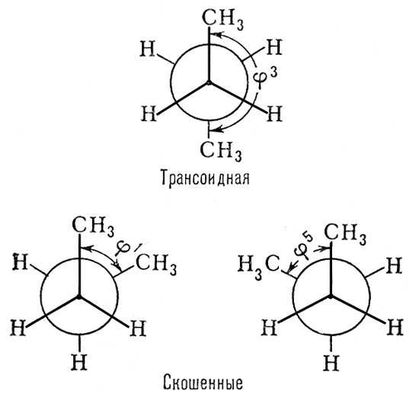
Рис. 2. Формулы Ньюмена, изображающие три заторможенные (нечётные) конформации бутана. 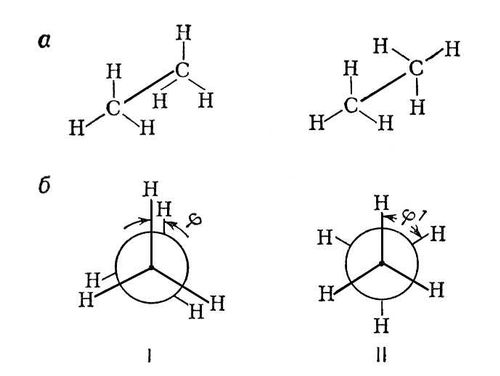
Рис. 1. Перспективные формулы (а) и проекционные (вид на молекулу «сверху» вдоль связи С - С) формулы Ньюмена (б), изображающие заслонённую, или чётную (I), и заторможенную, или нечётную (II), конформации этана, j- угол между заместителями, т. н. двугранный (или диэдральный) угол. 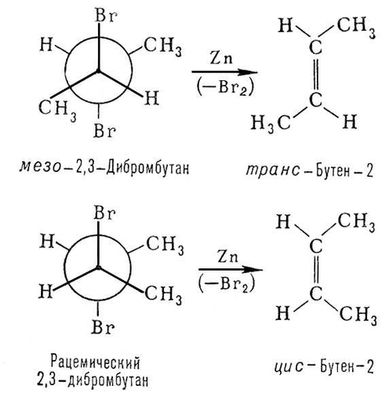
Рис. 4. Схемы реакций дебромирования 2,3-дибромбутана. Конформация Конформа'ция(от лат. conformatio - форма, построение, расположение) молекул, геометрические формы, которые могут принимать молекулы органических соединений при вращении атомов или групп атомов (заместителей) вокруг простых связей при сохранении неизменными порядка химической связи атомов (химического строения), длины связей и валентных углов. Молекулы, отличающиеся только своими К., называются конформерами, или поворотными изомерами. Существование конформации обусловлено пространственным взаимодействием (например, отталкиванием, притяжением, образованием водородных связей) не связанных между собой заместителей, в т. ч. и атомов водорода. Примером могут служить нисколько плоских конформации молекул пентана: CH 3-CH 2-CH 2-CH 2-CH 3 В отличие от геометрических и оптических изомеров (см. Изомерия химических соединений), конформеры при обычных условиях легко переходят друг в друга (без разрыва связей) и поэтому их нельзя изолировать (ср. Конфигурация ) .Молекулы органических соединений обычно существуют в виде смеси находящихся в равновесии конформеров, среди которых преобладают энергетически наиболее выгодные, т. е. обладающие наименьшей энергией. Конформационное состояние молекул влияет на физические свойства веществ, на направление и скорость их химических превращений (см. Конформационный анализ ) . В. М. Потопов. 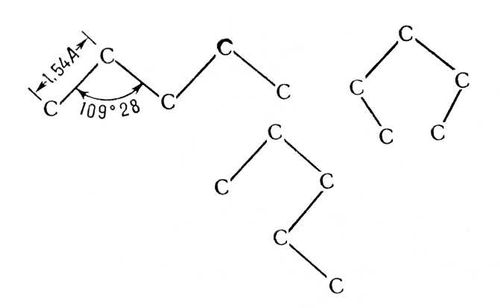
Плоские конформации молекул пентана: а - зигзагообразная; б - клешневидная; в - нерегулярная. Конформизм Конформи'зм(от позднелат. conformis - подобный, сообразный), морально-политический термин, обозначающий приспособленчество, пассивное принятие существующего порядка вещей, господствующих мнений и т. д. К. означает отсутствие собственной позиции, беспринципное и некритическое следование любому образцу, обладающему наибольшей силой давления (мнение большинства, признанный авторитет, традиция и т. п.). В современном буржуазном обществе К. по отношению к существующему социальному строю и господствующим ценностям насаждается системой воспитания и идеологического воздействия; он является типичной чертой деятельности бюрократических организаций. В отличие от К., социалистический коллективизм предполагает активное участие индивида в выработке групповых норм, сознательное усвоение коллективных ценностей и вытекающее отсюда соотнесение собственного поведения с интересами коллектива, общества и - в случае необходимости - подчинение последним. От К. следует отличать конформность (конформные реакции), изучаемую социальной психологией. Усвоение определённых групповых норм, привычек и ценностей - необходимый аспект социализации личности и предпосылка нормального функционирования любой социальной системы. Но социально-психологические механизмы такого усвоения и степень автономии личности по отношению к группе бывают различными. Социологов и психологов издавна интересовали такие вопросы, как подражание, социальное внушение, «психическое заражение» и т. п. С 50-х гг. 20 в. предметом интенсивных экспериментальных психологических исследований стали способы отбора и усвоения индивидом социальной информации и мера его отношения к групповому давлению. Выяснилось, что они зависят от целой совокупности факторов - личностных (степень внушаемости индивида, устойчивость его самооценок, уровень самоуважения, тревожность, интеллект, потребность в одобрении окружающих и т. д.; у детей конформные реакции выше, чем у взрослых, а у женщин - выше, чем у мужчин), групповых (положение индивида в группе, её значимость для него, степень сплочённости и структура группы), ситуационных (содержание задачи и заинтересованность в ней испытуемого, его компетентность, принимается ли решение публично, в узком кругу или наедине и т. п.) и общекультурных (насколько вообще в данном обществе ценится личная самостоятельность, независимость суждений и т. д.). Поэтому, хотя высокая конформность ассоциируется с определённым типом личности, её нельзя считать самостоятельной личностной чертой; её соотношение с другими социально-психологическими явлениями, такими, как внушаемость, ригидность (жёсткость) установок, стереотипность мышления, авторитарный синдром и др., требует дальнейших исследований. Лит.:Кон И. О., Социология личности, М., 1967; Общая психология, под ред. А. В. Петровского, М., 1970, с. 109-11; Me Guire W. J., Personality and susceptibility to social influence, в кн.: Handbook of personality theory and research, ed. E. F. Borgatta and W. W. Lambert, Chi., 1968; Marlowe D., Gergen K. J., Personality and social interaction, в кн.: The handbook of social psychology, ed G. Lindzey, E. Aronson, v. 3, N. Y., 1968. И. С. Кон. Конформисты Конформи'сты(conformist, буквально - согласный), распространённое название сторонников государственной англиканской церкви в Англии, принимающих все её догматы и обряды и выступающих против их изменения. Конформная проекция Конфо'рмная прое'кция(от позднелат. conformis - подобный), равноугольная проекция, одна из картографических проекций. Конформное отображение Конфо'рмное отображе'ние,конформное преобразование (математическое), отображение одной фигуры (области) на другую, при котором две любые кривые, пересекающиеся под некоторым углом во внутренней точке первой фигуры, преобразуются в кривые второй фигуры, пересекающиеся под тем же углом. Простейший пример К. о. представляет подобие. Другой пример - К. о. прямого угла на полуплоскость. Его можно получить, если каждый луч, выходящий из точки Опод углом aк Ox,преобразовать в луч, выходящий из O'под углом 2 aк O'x',и притом так, что каждая точка М,для которой OM = r,преобразуется в точку M',для которой O'M' = r 2.Т. к. Мизображает комплексное число z = r (cos a+ isin a), а M' -число z' = r (cos2a + isin2a ) = z 2,то можно сказать, что рассматриваемое К. о. осуществляется посредством функции комплексного переменного z' = z 2.Нетрудно убедиться в том, что полупрямые, параллельные сторонам угла, преобразуются при этом в полупараболы с общим фокусом в O'. Нужно заметить, что углы с вершиной в точке Оизменяются, увеличиваясь вдвое; это не противоречит определению К. о., т. к. Оне является внутренней точкой области. В общем случае К. о. любой криволинейный многоугольник Р,лежащий внутри отображаемой области, преобразуется в криволинейный многоугольник P'с соответственно равными углами, но длины сторон изменяются непропорционально. Если многоугольник Руменьшается, стягиваясь в некоторую точку A, то и P'уменьшается, стягиваясь в соответствующую точку A',при этом отношения длин сторон стремятся к одному и тому же числу:
которое зависит только от положения точки А(но не от рассматриваемых многоугольников); оно называется растяжением в данной точке. Указанный факт позволяет приближённо рассматривать любое К. о. «в малом» (т. е. в достаточно малой окрестности каждой точки A) как преобразование подобия, соединённое, вообще говоря, ещё с поворотом (например, четырёхугольники Ри P'). К. о. применяется с давних пор в картографии, когда требуется часть поверхности земного шара изобразить на плоскости (на карте) с сохранением величин всех углов; примерами таких К. о. являются стереографическая проекция и Меркатора проекция . Более общая задача К. о. произвольной поверхности (или её части) на другую поверхность (или её часть) изучается в дифференциальной геометрии. Особое место занимают К. о. одних областей плоскости на другие; их теория имеет существенные приложения в гидро- и аэромеханике, электростатике и теории упругости. Решение многих важных задач получается без труда, когда область, для которой ставится задача, имеет достаточно простой вид (например, круг или полуплоскость). Если задача ставится для другой, более сложной области, то оказывается достаточным отобразить конформно простейшую область на данную, чтобы получить решение новой задачи из известного решения. Так, например, задача об определении потока несжимаемой однородной жидкости или газа, обтекающего цилиндр с круговым сечением, решается сравнительно легко. Линии тока (т. е. линии, вдоль которых направлены скорости частиц жидкости), для этого случая, здесь представлено течение при наличии циркуляции.Если отобразить конформно внешность кругового сечения цилиндра на внешность поперечного сечения крыла самолёта (профиля крыла), то линии тока для случая круглого цилиндра перейдут, как можно показать, в линии тока при обтекании крыла. Знание отображающей функции z' = f (z)позволяет подсчитать скорость потока в любой точке, вычислить подъёмную силу крыла самолёта и т. д. Именно таким путём шёл Н. Е. Жуковский,создавая теорию крыла самолёта. Не всякие области плоскости допускают К. о. друг на друга. Так, например, круговое кольцо, ограниченное концентрическими окружностями радиусов
R
1и
R
2,где
R
1 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313, 314 |
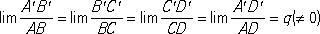 ,
,