 |
|
���������� ������:: ��� :: ������ ����� ���� :: ������ ����� :: ������� ��� ���������� :: ������� ������ :: �������� ����� :: ������� ������ :: ����� ����� �������� :: ���� ��������� :: ������� ������ ���������� ���������� �����:: ���������� �� ������� Windows XP :: The Boarding House :: ���� (����� 1-3) :: ���������� ����� :: ����������������� ��� :: ������� ������� ����� :: �������� ������� :: ����������� ���������� :: ���� �����-������ :: ���� ������� |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 180)
Клуциса, А. М. Родченко), конструирования книги (новые приёмы использования выразительных возможностей шрифта и наборных материалов в работах А. М. Гана, Л. М. Лисицкого). В театре вместо традиционных декораций конструктивисты создавали подчинённые задачам сценические действия «станки» для работы актёров, одетых в прозодежду (работы Л. С. Поповой, А. А. Веснина и др. над постановками В. Э. Мейерхольда, А. Я. Таирова).
Применительно к зарубежным пластическим искусствам термин «К.» в значительной мере условен: в архитектуре он обозначает течение внутри функционализма,стремящееся подчеркнуть экспрессию современных конструкций, в живописи и скульптуре - одно из авангардистских течений, использовавшее некоторые формальные поиски раннего советского К. (скульпторы Н. Габо, А. Певзнер). В литературе конструктивистские тенденции, отвечавшие «левым» требованиям «революции формы» (преобразования языка, стиха, жанров), стимулировались лозунгами ЛЕФа.(ориентация на «конструкцию материалов» вместо интуитивно найденного стиля, монтаж или «кинематографичность» в прозе, «агит-поэзию», газетный язык). Как самостоятельное, преимущественно поэтическое течение К. провозглашен К. Л. Зелинским, И. Л. Сельвинским и А. Н. Чичериным в 1923 (манифест - в их сборнике «Мена всех», 1924). В 1924 оформился Литературный центр конструктивистов (ЛЦК), в котором участвовали наряду с И. Л. Сельвинским и К. Л. Зелинским (теоретик группы) В. А. Луговской, В. М. Инбер, Б. Н. Агапов, Е. И. Габрилович, Туманный (Н. Н. Панов), А. П. Квятковский и др.; организационно примыкал Э. Г. Багрицкий. В теоретических установках К. (в противовес ЛЕФу) признавал суверенные права поэзии, однако закономерности её развития как явления духовной культуры во многом подменялись ориентацией на прогресс «технической оснастки культуры» [например, принцип «грузофикации слова», или «конструкторского» распределения материала: «максимальная нагрузка потребности на единицу его, т. е. коротко, сжато, в малом - многое, в точке - всё» («Мена всех», [сб.], 1924, с. 8), что в крайнем выражении приводило к стилю лозунга и рекламы (опыты А. Н. Чичерина)]. С другой стороны, выражением конструктивной «организованности» явился «локальный принцип» - «конструирование» темы из наиболее сопричастных ей слов и ритмов; в поэтической лаборатории И. Л. Сельвинского авторская речь растворялась в языке перспнажа или описываемой среды (стихотворение «Вор», 1922, целиком на воровском жаргоне), применялась фонетическая транскрипция с обозначением тона для передачи «ритмических соответствий» произношению (например, песенного или плясового лада). Конструктивисты осваивали в поэзии приёмы прозы («инфляция прозы»), особые пласты лексики и др. (профессиональная речь, жаргоны); отказываясь от лирических эмоций, предпочитали четко организованную фабульную поэзию, эпические жанры. Но «стиля эпохи», как замышляли, они не создали. В 1930 группа ЛЦК самораспустилась. Роль ЛЦК в советской поэзии определяется не ошибочными теоретическими установками, а самим творчеством входивших в него талантливых поэтов (во главе с И. Л. Сельвинским), оставивших живое поэтическое наследие. Лит.:Ган А., Конструктивизм, Тверь, 1922; «Кино-фот», 1922-23; «Современная архитектура», 1926-30; Литературные манифесты (от символизма к Октябрю), М., 1929; Из истории советской архитектуры. 1917-1925 гг. Документы и материалы, М., 1963; Советское литературоведение и критика. Библиографический указатель, М., 1966; Из истории советской архитектуры. 1926-1932 гг. Документы и материалы, М., 1970. С. О. Хан-Магомедов(введение, архитектура), В. И. Ракитин(художественное конструирование, графика, театрально-декорационное искусство), А. А. Морозов (литература). 
А. М. Родченко. Оформление и мебель рабочего клуба, экспонировавшиеся на Международной выставке декоративного искусства в Париже. 1925. 
В. Ф. Степанова. Проекты спортивной одежды. Гуашь. 1920-е гг. Собственность В. А. Родченко. Москва. 
М. О. Барщ, М. Я. Гинзбург, М. А. Охитович и др. Проект жилого здания («товарищеская коммуна»). 1929. 
Н. Д. Колли. Проект трансформаторной станции. 1-я пол. 1920-х гг. 
И. И. Леонидов. Проект «Института Ленина» (Института библиотековедения им. В. И. Ленина). 1927. Фрагмент. 
М. Я. Гинзбург. Проект дома акционерного общества «Оргметалл» в Москве. 1926-27. 
А. А., В. А. и Л. А. Веснины. Проект Дворца Труда в Москве. 1922-23. 
А. М. Ган. Киоск Всероссийского комитета помощи инвалидам войны… (слева - в подготовленном для работы виде; справа - в сложенном виде). 1-я пол. 1920-х гг. 
Эскизы рисунков для тканей: 1 - В. Ф. Степановой (гуашь, 1924, собрание В. А. Родченко, Москва); 2 - Л. С. Поповой (гуашь, 1924, собрание Д. В. Сарабьянова и Е. Б. Муриной, Москва). 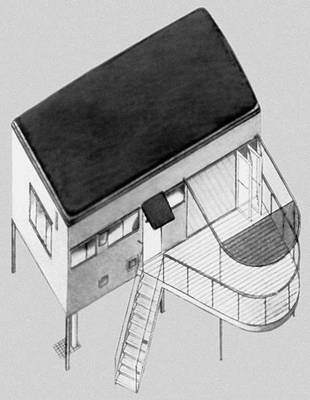
М. О. Барщ, М. Я. Гинзбург, М. А. Охитович и др. Проект однокомнатной ячейки для «семейного коллектива». 1929. 
В. А. и Г. А. Стенберги. Экспериментальная конструкция. Металл, стекло. 1919. 
И. А. Глосов. Проект клуба им. Зуева в Москве. 1927. 
Л. М. Лисицкий. «Ленинская трибуна». Проект. Цветная тушь. 1920-24. Научно-исследовательский музей архитектуры им. А. В. Щусева. Москва. 
А. К. Буров. Проект центрального вокзала в Москве. 1925. 
Г. Г. Клуцис. «Спорт». Фотомонтаж. 1923. 
Л. С. Попова. Макет установки для трагического фарса Кроммелинка «Великодушный рогоносец» в Театре им. В. Э. Мейерхольда в Москве. 1922. Центральный театральный музей им. А. А. Бахрушина. Москва. 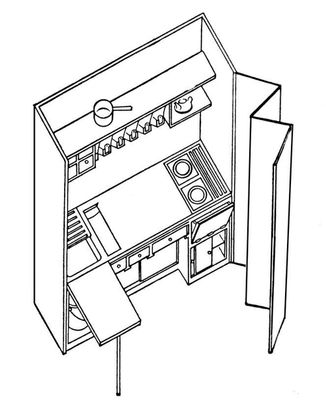
М. О. Барщ, В. Н. Владимиров, М. Я. Гинзбург, А. Л. Пастернак, Г. А. Сум-Шик. Типовой проект шкафа-кухни. 1928-29. Конструктивная логика Конструкти'вная ло'гика,логика, развиваемая в соответствии с принципами т. н. конструктивного направления,отличающимися требованием конструктивности (возможности эффективного построения) объектов, существование которых утверждается в высказываниях (предложениях). См. Конструктивные объекты.
Лит.см. при ст. Логика. Конструктивная математика Конструкти'вная матема'тика,абстрактная наука о конструктивных процессах, человеческой способности осуществлять их и о их результатах - конструктивных объектах. Абстрактность К. м. проявляется прежде всего в том, что в ней систематически применяются две абстракции: абстракция потенциальной осуществимости и абстракция отождествления. Абстракцию потенциальной осуществимости используют, когда отвлекаются от практических ограничений конструктивных возможностей в пространстве, времени и материале. Абстракцию отождествления используют, когда говорят о двух в том или ином смысле одинаковых объектах как об одном и том же объекте. В К. м. не применяется характерная для теоретико-множественной математики абстракция актуальной бесконечности, связанная с рассмотрением никогда не завершаемых процессов как бесконечно продолженных и тем самым как бы завершенных. Конструктивный процесс, результатом которого является объект, одинаковый с А,называется построением объекта А. Высказывания, связанные с человеческой способностью осуществлять конструктивные процессы, часто формулируются в К. м. в виде теорем существования, утверждающих, что существует объект, удовлетворяющий каким-то требованиям. Под этим подразумевают, что построение такого объекта потенциально осуществимо, т. е. что владеют способом его построения. Это понимание теорем существования отличается от их понимания в теоретико-множественной математике, что вынуждает строить для К. м. свою логику, отличную от обслуживающей теоретико-множественную математику классической математической логики, - конструктивную математическую логику. Понятия конструктивного процесса и конструктивного объекта не определяются в К. м. В таких общих определениях и нет надобности, поскольку в К. м. обычно имеют дело не с конструктивными процессами и конструктивными объектами вообще, а с определёнными видами тех и других. Простейшим видом конструктивных объектов являются слова в фиксированном алфавите, т. е. ряды букв этого алфавита (слово «буква» понимается здесь как «элементарный знак», т. е. как «знак, частями которого мы не интересуемся»; алфавит - это набор букв). Конструктивный процесс, результатом которого является слово, состоит в данном случае в выписывании этого слова буква за буквой. Частным случаем слов являются натуральные числа, которые мы рассматриваем как слова в алфавите 01, начинающиеся с нуля и, кроме того, нуля не содержащие, т. е. как слова 0, 01, 011, 0111,... Добавляя к этому алфавиту знак минус «-» и знак дроби «/», получают возможность строить рациональные числа как некоторые слова в алфавите 01 - /. Т. о., рациональные числа оказываются конструктивными объектами. Естественно, возник вопрос о построении действительных чисел в рамках К. м. и, далее, вопрос о включении математического анализа в эти рамки. Эти цели достигнуты на основе уточнённого понятия алгоритма.Каким из известных уточнений этого понятия ( Тьюринга машина , рекурсивные функции, нормальные алгорифмы) здесь пользоваться, при этом несущественно. В дальнейшем под «алгорифмом» будет пониматься нормальный алгорифм.
Конструктивной последовательностью рациональных (натуральных) чисел будет называться алгорифм, перерабатывающий всякое натуральное число в рациональное (натуральное) число. Без существенного ограничения общности можно считать конструктивную последовательность рациональных чисел алгорифмом в алфавите 01 -
/ab.Запись такого алгорифма будет осуществляться как слово в алфавите 01. О конструктивной последовательности рациональных чисел
|( n) - ( n+1)|Ј 2 - n-1. Записи регулярно сходящихся последовательностей рациональных чисел называют конструктивными действительными числами (КДЧ). Естественным образом определяются равенство двух КДЧ, порядковые отношения между ними, а также арифметическими действия над ними и операция взятия абсолютной величины. Арифметические операции оказываются алгорифмическими: имеется, например, алгорифм, перерабатывающий всякую пару КДЧ в сумму этих КДЧ. С другой стороны, невозможен алгорифм, распознающий КДЧ среди слов в алфавите 01; невозможен алгорифм, распознающий равенство КДЧ. Далее, на основе алгоритмов теории можно определить понятие конструктивной последовательности КДЧ. Для всякой такой последовательности оказывается возможным построить КДЧ, не равное ни одному члену этой последовательности. Это - конструктивный аналог теоремы Кантора о несчётности континуума. Могут быть определены понятия конструктивной сходимости конструктивной последовательности КДЧ в себе и к КДЧ. Имеет место теорема полноты, утверждающая, что всякая конструктивная последовательность КДЧ, конструктивно сходящаяся в себе, конструктивно сходится к некоторому КДЧ. Однако конструктивный аналог известной теоремы о сходимости ограниченной возрастающей последовательности опровергается на примере. Согласно определению, КДЧ - слова в алфавите 01. Алгорифмы над этим алфавитом можно применять к КДЧ, что открывает возможность строить функцию от действительного переменного как алгорифм, перерабатывающий КДЧ в КДЧ. Надо только, чтобы такой алгорифм был согласован с равенством - равные КДЧ он должен перерабатывать в равные КДЧ. Т. о., получается следующее определение - алгорифм Fнад алфавитом 01 есть конструктивная функция действительного переменного, если соблюдаются следующие условия: 1) Fперерабатывает всякое КДЧ, к которому он применим, в КДЧ; 2) всякий раз, когда Fприменим к каким-либо КДЧ х,он применим и ко всякому КДЧ у,равному х,и КДЧ F( x) и F( y) равны. На основе этого определения была разработана конструктивная теория функций действительного переменного. Одним из наиболее интересных её результатов является теорема о непрерывности конструктивных функций: всякая конструктивная функция действительного переменного непрерывна всюду, где она определена. Вместе с тем выяснено, что в теории конструктивных функций не имеют место аналоги классических теорем Вейерштрасса и Кантора о непрерывных функциях на сегменте. В частности, были построены: 1) неограниченная конструктивная (и потому непрерывная) функция на сегменте [0,1]; 2) ограниченная на этом сегменте конструктивная функция, не имеющая точной верхней границы; 3) конструктивная функция, имеющая на сегменте [0,1] точную верхнюю границу, но не достигающая её; 4) ограниченная на сегменте [0,1] конструктивная функция, не являющаяся равномерно непрерывной ни на каком сегменте, содержащемся в сегменте [0,1]. Эти результаты выявляют глубокое отличие конструктивного математического анализа от анализа теоретико-множественного. В настоящее время (70-е гг. 20 в.) успешно разрабатываются многие отделы К. м.: конструктивные теории дифференцирования и интегрирования, конструктивная теория метрических пространств, конструктивный функциональный анализ, конструктивная теория функций комплексного переменного и др. Лит.:Марков А. А., Теория алгорифмов, «Тр. Математического института АН СССР», 1954, т. 42; Проблемы конструктивного направления в математике, в. 1-5, там же, 1958, т. 52; 1962, т. 67; 1964, т. 72; 1967, т. 93; 1970, т. 113; Фан Динь Зиеу, Некоторые вопросы конструктивного функционального анализа, там же, 1970, т. 114. А. А. Марков. Конструктивная теория функций Конструкти'вная тео'рия фу'нкций,раздел теории функций, в котором изучаются как приближённые представления функций, так и сами функции, исходя из свойств их приближённых представлений. К. т. ф. оформилась в самостоятельную дисциплину в трудах С. Н. Бернштейна (термин «К. т. ф.» принадлежит ему же), который исходил из идей П. Л. Чебышева,относящихся к наилучшим приближениям функций, интерполированию по способу наименьших квадратов и проблеме моментов. Лит.:Бернштейн С. Н., Собр. соч., т. 1 - Конструктивная теория функций [1905-1930], М., 1952; Натансон И. П., Конструктивная теория функций, М.- Л., 1949; Смирнов В. И., Лебедев Н. А., Конструктивная теория функций комплексного переменного, М.- Л., 1964. Конструктивное направление Конструкти'вное направле'ниев математике, математическое мировоззрение, связанное с признанием исследования конструктивных процессов и конструктивных объектов основной задачей математики. К концу 19 в. в математике возникло неконструктивное, теоретико-множественное направление, получившее существенное развитие в трудах К. Вейерштрасса,Р. Дедекинда и особенно Г. Кантора.Началось построение теории множеств, претендовавшей на роль фундамента всей математики. В этой теории, в соответствии с изречением Кантора «сущность математики в её свободе», допускался большой произвол при введении «множеств», которые затем рассматривались как законченные «объекты». Однако в начале 20 в. в теории множеств были открыты т. н. антиномии, т. е. противоречия, показавшие, что нельзя любым образом объединить «объекты» в «множества». Попытки преодолеть возникшие трудности были сделаны на пути аксиоматизации теории множеств, т. е. превращения её в аксиоматическую науку наподобие геометрии (см. Аксиоматическая теория множеств ) .Это осуществляется так, чтобы всё, требуемое для обоснования математики, получалось на основе аксиом, тогда как известные до сих пор антиномии не проходили бы. Первая попытка в этом направлении была предпринята Э. Цермело,опубликовавшим свою систему аксиом теории множеств в 1908. Известные антиномии теории множеств не проходили в системе Цермело, однако гарантий против появления противоречий не было. Возникла проблема обеспечения непротиворечивости аксиоматически построенной теории множеств. Эту проблему выдвинул и пытался решить Д. Гильберт,основная идея которого состояла в полной формализации аксиоматической теории множеств, в трактовке её как формальной системы (см. в ст. Логика ) .Задача установления непротиворечивости рассматриваемой теории сводилась бы тогда к доказательству формальной недоказуемости формул определённого вида. Это доказательство должно было быть убедительным рассуждением о конструктивных объектах - формальных доказательствах. Оно, таким образом, должно было укладываться в рамки конструктивной математики. Цепь,поставленная Гильбертом, оказалась недостижимой, что было доказано К. Гёделем в 1931. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180, 181, 182, 183, 184, 185, 186, 187, 188, 189, 190, 191, 192, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 230, 231, 232, 233, 234, 235, 236, 237, 238, 239, 240, 241, 242, 243, 244, 245, 246, 247, 248, 249, 250, 251, 252, 253, 254, 255, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 269, 270, 271, 272, 273, 274, 275, 276, 277, 278, 279, 280, 281, 282, 283, 284, 285, 286, 287, 288, 289, 290, 291, 292, 293, 294, 295, 296, 297, 298, 299, 300, 301, 302, 303, 304, 305, 306, 307, 308, 309, 310, 311, 312, 313, 314 |
 говорят, что она регулярно сходится, если для всякого натурального числа
nсоблюдается условие
говорят, что она регулярно сходится, если для всякого натурального числа
nсоблюдается условие