Большая Советская Энциклопедия (КО)

  Лит.:Колосов Н. А., Георгий Конисский, архиепископ белорусский, М., 1895; УкраЇнськi письменники. Бio-бiблioграфiчний словник, т. 1, К., 1960.

Кониферин

Конифери'РЅ,C ₁₆H ₂₂O ₈Р§H ₂O, фенольный гликозид.Впервые выделен РёР· СЃРѕРєР° хвойных растений (Coniferales); содержится РІ тканях РјРЅРѕРіРёС… растений. РџСЂРё ферментативном гидролизе Рљ. распадается РЅР° глюкозу Рё конифериловый СЃРїРёСЂС‚ - РѕРґРёРЅ РёР· исходных продуктов РїСЂРё биосинтезе лигнина.

Коничев Константин �ванович

Ко'ничевКонстантин �ванович [13 (26).2.1904, деревня Поповская, ныне Усть-Кубинского района Вологодской области, - 2.5.1971, Ленинград], русский советский писатель. Член КПСС с 1926. Окончил Литературный институт имени М. Горького (1940). Участник Великой Отечественной войны 1941-45. Автор книг: «Тропы деревенские» (1929), «Лесная быль» (1934), «К северу от Вологды» (1954), «В году 30-ом» (1964) и др., цикла историко-биографических повестей «Повесть о Федоте Шубине» (1941-51), «Повесть о Верещагине» (1956), «Повесть о Воронихине» (1959-64), «Русский самородок. Повесть о Сытине» (1966). Основные темы произведений К.- русский Север, судьбы его исторических деятелей. Награжден 2 орденами, а также медалями.

  Соч.: Песни Севера, частушки, пословицы, загадки, 2 изд., [Архангельск], 1955; �з жизни взятое. [Вступит. ст. В. Гуры], Вологда, 1964.

Лит.:Фрумкин Л., Характер русского северянина. (О творчестве Константина Коничева), «Север». 1969, № 12.

Коническая поверхность

Кони'ческая пове'рхность(математика), то же, что конус.

Конические проекции

Кони'ческие прое'кции(нормальные), картографические проекции,в которых параллели изображаются концентрическими окружностями, меридианы - ортогональными им прямыми. В К. п. искажения не зависят от долготы. Особо пригодны для территорий, вытянутых вдоль параллелей. Карты всей территории СССР часто составляются в равноугольных и равнопромежуточных К. п.

Конические сечения

Кони'ческие сече'ния,линии, которые получаются сечением прямого кругового конуса плоскостями, не проходящими через его вершину. К. с. могут быть трёх типов:

  1) секущая плоскость пересекает все образующие конуса в точках одной его полости ;линия пересечения есть замкнутая овальная кривая - эллипс;окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса.

  2) Секущая плоскость параллельна одной из касательных плоскостей конуса; в сечении получается незамкнутая, уходящая в бесконечность кривая - парабола,целиком лежащая на одной полости.

  3) Секущая плоскость пересекает обе полости конуса; линия пересечения - гипербола-состоит из двух одинаковых незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса.

С точки зрения аналитической геометрии К. с.- действительные нераспадающиеся линии второго порядка.

В тех случаях, когда К. с. имеет центр симметрии (центр), т. е. является эллипсом или гиперболой, его уравнение может быть приведено (путём перенесения начала координат в центр) к виду:

a ₁₁x ²+2a ₁₂xy + a ₂₂y ²= a ₃₃.

Дальнейшие исследования таких (называемых центральными) К. с. показывают, что их уравнения могут быть приведены к ещё более простому виду:

РђС… ²+ Р’Сѓ ²= РЎ,В В В В В В В В В В В В В (1)

если за направления осей координат выбрать т. н. главные направления - направления главных осей (осей симметрии) К. с. Если Аи Вимеют одинаковые знаки (совпадающие со знаком С), то уравнение (1) определяет эллипс; если Аи Вразного знака, то - гиперболу.

Уравнение параболы привести к виду (1) нельзя. При надлежащем выборе осей координат (одна ось координат - единственная ось симметрии параболы, другая - перпендикулярная к ней прямая, проходящая через вершину параболы) её уравнение можно привести к виду:

y ²= 2СЂС….

К. с. были известны уже математикам Древней Греции (например, Менехму, 4в. до н. э.); с помощью этих кривых решались некоторые задачи на построение (удвоение куба и др.), оказавшиеся недоступными при использовании простейших чертёжных инструментов - циркуля и линейки. В первых дошедших до нас исследованиях греческие геометры получали К. с., проводя секущую плоскость перпендикулярно к одной из образующих, при этом, в зависимости от угла раствора при вершине конуса (т. е. наибольшего угла между образующими одной полости), линия пересечения оказывалась эллипсом, если этот угол -острый, параболой, если - прямой, и гиперболой, если - тупой. Наиболее полным сочинением, посвященным этим кривым, были «Конические сечения» Аполлония Пергского (около 200 до н. э.). Дальнейшие успехи теории К. с. связаны с созданием в 17 в. новых геометрических методов: проективного (французские математики Ж. Дезарг, Б. Паскаль) и в особенности координатного (французские математики Р. Декарт, П. Ферма).

При надлежащем выборе системы координат уравнение К. с. может быть приведено к виду:

y ²= 2px + lx ²( СЂРё lпостоянные).

Если СЂ ¹ 0,то РѕРЅРѕ определяет параболу РїСЂРё l= 0, эллипс РїСЂРё l< 0, гиперболу РїСЂРё l> 0. Геометрическое свойство Рљ. СЃ., содержащееся РІ последнем уравнении, было известно уже древнегреческим геометрам Рё послужило для Аполлония Пергского РїРѕРІРѕРґРѕРј присвоить отдельным типам Рљ. СЃ. названия, сохранившиеся РґРѕ СЃРёС… РїРѕСЂ: слово «парабола» (греческого parabole) означает приложение (С‚. Рє. РІ греческой геометрии превращение прямоугольника данной площади y ²РІ равновеликий ему прямоугольник СЃ данным основанием 2pназывалось приложением данного прямоугольника Рє этому основанию); слово «эллипс» (греческий Р№lleipsis) - недостаток (приложение СЃ недостатком), слово «гипербола» (греческий hyperbole) - избыток (приложение СЃ избытком).

С переходом к современным методам исследования стереометрическое определение К. с. было заменено планиметрическими определениями этих кривых как геометрических мест на плоскости. Так, например, эллипс определяется как геометрическое место точек, для которых сумма расстояний от двух данных точек (фокусов) имеет данное значение.

Можно дать другое планиметрическое определение К. с., охватывающее все три типа этих кривых: К. с.- геометрическое место точек, для каждой из которых отношение её расстояний до данной точки («фокуса») к расстоянию до данной прямой («директрисы») равно данному положительному числу («эксцентриситету») е. Если при этом е< 1, то К. с.- эллипс; если е> 1, то - гипербола; если е= 1, то - парабола.

�нтерес к К. с. всегда поддерживался тем, что эти кривые часто встречаются в различных явлениях природы и в человеческой деятельности. В науке К. с. приобрели особенное значение после того, как немецкий астроном �. Кеплер открыл из наблюдений, а английский учёный �. Ньютон теоретически обосновал законы движения планет, один из которых утверждает, что планеты и кометы Солнечной системы движутся по К. с., в одном из фокусов которого находится Солнце. Следующие примеры относятся к отдельным типам К. с.: параболу описывает снаряд или камень, орошенный наклонно к горизонту (правильная форма кривой несколько искажается сопротивлением воздуха); в некоторых механизмах пользуются зубчатыми колёсами эллиптической формы («эллиптическая зубчатка»); гипербола служит графиком обратной пропорциональности, часто наблюдающейся в природе (например, закон Бойля - Мариотта).

Лит.:Александров П. С., Лекции по аналитической геометрии, М., 1968; Ван дер Варден Б. Л., Пробуждающаяся наука, пер. с голл., М., 1959.

В. �. Битюцков.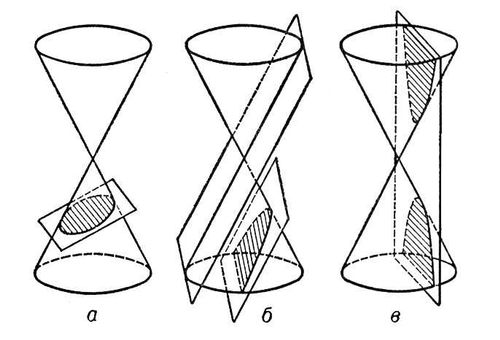

Рис. к ст. Конические сечения.

РљРѕРЅРєР°

РљРѕ'РЅРєР°,Конская, река РІ Запорожской области РЈРЎРЎР , левый приток СЂ. Днепр. Длина 146 РєРј,площадь бассейна 2580 РєРј ².Берёт начало РЅР° Приазовской возвышенности, впадает РІ Каховское водохранилище, СЃ образованием которого связано затопление долины нижнего течения Рљ. Питание РІ РѕСЃРЅРѕРІРЅРѕРј снеговое. Весеннее половодье сменяется глубокой летней меженью. РќР° Рљ. - РіРі. Пологи, Орехов.

Конкиста

Конки'ста(испанский conquista - завоевание), термин, употребляющийся в исторической литературе применительно к периоду завоевания Центральной и Южной Америки испанцами и португальцами в конце 15-16 вв. См. Конкистадоры.

Конкистадоры

Конкистадо'ры(от испанского conquistador - завоеватель), участники испанских завоевательных походов в Южную и Центральную Америку в конце 15-16 вв. Походы К. сопровождались истреблением и порабощением племён и народов Вест-�ндии, Центральной и Южной Америки, опустошением и разграблением целых областей, актами вандализма, насилий и массовых пыток. Награбленное золото, рабы и земли делились между К. Наиболее известные предводители К. - П. Альварадо, Нуньес де Бальбоа,П. Вальдивия,Д. Веласкес,Г. Х. Кесада, Э. Кортес,Ф. Писарро.

  Лит.:Лас Касас Б. де, �стория �ндий, пер. с исп., Л., 1968; Бартоломе де Лас-Касас. К истории завоевания Америки. [Сб. статей], М., 1966; Kirkpatrick F. A., The Spanish conquistadores, 3 ed., L., 1963.

Конклав

Конкла'РІ(РѕС‚ латинского conclave - запертая комната), собрание кардиналов, созываемое после смерти папы СЂРёРјСЃРєРѕРіРѕ для избрания РЅРѕРІРѕРіРѕ папы; РїСЂРѕС…РѕРґРёС‚ РІ изолированном РѕС‚ внешнего РјРёСЂР° помещении (двери его наглухо закрываются). Выборы производятся закрытым голосованием; для избрания необходимо собрать РЅРµ менее ²/ ₃голосов плюс ещё РѕРґРёРЅ голос. Помещение открывают лишь после избрания папы. Этот РїРѕСЂСЏРґРѕРє Рљ. был утвержден РЅР° 2-Рј Лионском СЃРѕР±РѕСЂРµ 1274.

Конкорд и Лексингтон

Ко'нкорд и Ле'ксингтон(Concord, Lexington), города в США (штат Массачусетс), в районе которых 19 апреля 1775 произошли первые бои во время Войны за независимость в Северной Америке 1775-83 . 2-тысячный английский отряд подполковника Ф. Смита выступил из Бостона в Конкорд (30 кмсеверо-западней Бостона) с задачей захватить склад оружия восставших колонистов. На марше английские войска подверглись нападениям в К. и Л. и на участках дороги между ними со стороны американских колонистов, действовавших в рассыпном строю и стрелявших из-за укрытий. Только при поддержке подкрепления английскому отряду, потерявшему около 300 человек, удалось отойти к Бостону. Американцы потеряли 100 человек из 400. Эти бои показали преимущество действий стрелков в рассыпном строю против пехоты в линейном боевом порядке.

Конкордат

Конкорда'т(позднелатинское concordatum - соглашение, от латинского concordo - нахожусь в согласии), соглашение между папой римским как главой католической церкви и католическим государством, регулирующее положение католической церкви в этом государстве, её права в области брачно-семейных отношений, в школьном вопросе и т. д. Впервые К. был заключён в 1122 ( Вормсский конкордат 1122) между папой римским и германским императором, разграничивший функции светской и церковной власти при назначении епископов, чем была завершена борьба за инвеституру.Наиболее известны Болонский конкордат 1516, К. папы Пия VII и Наполеона 1801, определявший положение католической церкви во Франции. В 1929 папой был заключён К. с правительством Б. Муссолини (одновременно с Латеранскими соглашениями, признававшими суверенитет папы над территории Ватикана).

  Лит.:Лаврецкий �. Р., Ватикан, М., 1957; Шейнман М., Ватикан между двумя мировыми войнами, М.- Л., 1948.

Конкордат семи

Конкорда'т семи',Зибенбунд (немецкий Siebenbund), союз 7 швейцарских кантонов (Ааргау, Берн, Золотурн, Люцерн, Санкт-Галлен, Тургау, Цюрих), основан 17 марта 1832. К. с., во главе которого стояли представители либеральной швейцарской буржуазии, выдвинул программу проведения умеренных реформ, предусматривавших пересмотр федерального договора Швейцарского союза (1815), создание централизованного государства, демократизацию политического строя. В 1832 швейцарский сейм разработал проект нового федерального договора, который в 1833 был отвергнут большинством экономически отсталых кантонов, где преобладали клерикалы, выступавшие против централизации страны. Буржуазно-либеральные преобразования, выдвинутые К. с., были закреплены в конституции 1848.

РљРѕРЅРєРѕСЂРґРёСЏ

Конко'рдия(Concordia), город на востоке Аргентины, в провинции Энтре-Риос. 61,9 тысяч жителей (1960). Порт на правом берегу р. Уругвай, начальный пункт судоходства. Ж.-д. узел. Мясохладобойная, маслобойная промышленность.

Конкременты

Конкреме'нты(от латинского concrementum - скопление, срастание), камни, плотные образования, встречающиеся в полостных органах и выводных протоках желёз человека. Могут быть разной величины, формы и консистенции. Химический состав К. зависит от места их образования и состава жидкости, в которой происходит камнеобразование. В жёлчном пузыре и протоках К. состоят из холестерина, жёлчных пигментов, фосфорнокислого и углекислого кальция; мочевые К. образуются в мочевыводящих путях и по кислотным остаткам делятся на ураты (самый частый вид мочевых К.), оксалаты, фосфаты и карбонаты. Мочевые К. могут содержать ксантин, цистин, индиго, серу, мыла, холестерин. Причины образования К. могут быть общими (нарушение обмена веществ, беременность и т. п.) и местными (изменение химизма секрета, в частности его защитных коллоидов и рН, застой секрета, воспалительные процессы); чаще камнеобразование обусловлено сочетанием этих факторов. Образование жёлчных камней лежит в основе желчно-каменной болезни,мочевых - мочекаменной болезни.

Конкретная музыка

Конкре'тная му'зыка(французский musique concrete), музыкальные произведения, создаваемые посредством записи на магнитофонную ленту природных или искусственных звучаний которые по усмотрению автора могут подвергаться различным акустическим преобразованиям и смешиваться. В К. м. используются преимущественно разнообразные шумы, изредка звучание человеческих голосов и музыкальных инструментов. �зобретателем К. м. является французский инженер-акустик П. Шеффер, создавший свои первые «конкретные» сочинения в 1948. В 50-е гг. 20 в. во Франции при Центральном радиовещании была создана экспериментальная студия К. м., вокруг которой объединилась группа музыкантов; группы деятелей К. м. возникли также в �талии, Западной Германии, США. Сторонники К. м. полагают, что она «безгранично расширяет» выразительные средства музыкального искусства, вводя в композицию весь мир звучаний, окружающих человека. В действительности произведения К. м., порывающие с системой звуковысотной организации, предельно обедняют возможности выражения определённого художественного содержания и способны выполнять лишь чисто прикладную роль (шумовое оформление кинокартин, драматических спектаклей и пр.). К. м. представляет собой одно из проявлений кризиса музыкальной культуры в буржуазном обществе

  Лит.:Шнеерсон Г., О музыке живой и мертвой, 2 изд., М., 1964; его же, Французская музыка ХХ века, 2 изд., М., 1970.

  Г. М. Шнеерсон.

Конкретная флора

РљРѕРЅРєСЂРµ'тная фло'СЂР°,элементарная флора, совокупность РІРёРґРѕРІ растений, приуроченная Рє ограниченной (примерно РѕС‚ 100 РґРѕ 1000 РєРј ²) части земной поверхности Рё целостная РІ генетическом отношении. Распределение РІРёРґРѕРІ Рљ. С„. РІ пределах занимаемого ею участка зависит РѕС‚ РёС… связей СЃ условиями местообитания. Р�зучение Рљ. С„. - удобный метод сравнительной флористики.

Конкретное

Конкре'тное(от латинского concretus, буквально - сгущенный, уплотнённый, сросшийся), единое в многообразном, общее в единичном, реальная связь сторон, граней объекта, знание его во всём богатстве существ. отношений, взаимодействий, противоречий. Представители идеализма, например �. Кант, �. Фихте, Г. Гегель, исходили из понимания К. как только духовной в своей основе связи эмпирически данных явлений. С их точки зрения К. существует лишь в абсолютизированном понятии. Сторонники эмпиризма сводят К. лишь к единичным чувственно-воспринимаемым вещам, а различные школы позитивизма - к индивидуальному объекту, понимаемому субъективно-идеалистически, как комплекс ощущений. В диалектическом материализме понятие К. употребляется в двух смыслах: как непосредственно данное, чувственно-воспринимаемое и представляемое целое. В этом смысле К. - исходный пункт познания. В теоретическом мышлении К. выступает уже концептуально, как система научных определений, выявляющих существующие связи и отношения вещей, событий, единство в многообразном, закономерности, тенденции развития явлений.