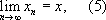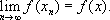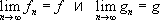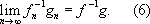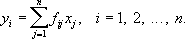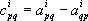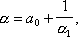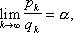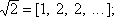|
|
���������� ������:: �������� ������ ������� :: �������� ��� ������ :: ������� ������ :: ����� ��� :: ������ ������ ����� :: ���� ����� ����� :: ������� ��������� :: ��� :: ������� ������ :: ����� ���� ���������� �����:: ���������� �� ������� Windows XP :: ����� ���� :: ��������� ��������� :: ���� � ������� :: ��� - ���� ���� :: ������, ����� �� �������� :: ����������� ��� :: ������� ������ :: ���� ����� ���-����� [���� ��������] :: ������� |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 60)
Непредельные углеводороды Непредёльные углеводоро'ды,то же, что ненасыщенные углеводороды. Непредикативное определение Непредикати'вное определе'ние,определение, посредством которого создаётся или вводится в рассмотрение предмет, являющийся одним из значений неопределённого имени («переменной»), участвующего в определяющем выражении. Некорректность Н. о. состоит в том, что предмет, вводимый посредством такого определения, своим появлением может изменить смысл определяющего выражения, а тем самым и самого определяемого предмета. Когда эта возможность не реализуется (что бывает, если все вхождения упомянутого неопределённого имени несущественны, т. е. устранимы логическими средствами), некорректностью Н. о. можно пренебречь, но в таких случаях не возникает и проблемы Н. о. Если же хоть одно вхождение неопределённого имени неустранимо, то создаваемый определением объект сам участвует в своём определении в качестве одного из значений смысла этого имени - и определение прочно, поскольку оно не даёт редукции определяемого объекта к ранее известным объектам и понятиям. С точки зрения теории определений,подобные порочные Н. о. следует считать столь же недопустимыми, как и круги в доказательствах.Впервые на Н. о. в математическом анализе указал А. Пуанкаре.Он же ввёл и сам термин «Н. о.». Наиболее известные примеры Н. о. встречаются при «наивных» классических попытках обоснования аксиоматической теории множеств. Например, доказательство существования объединения («теоретико-множественной суммы») произвольного множества множеств является непредикативным (так как при определении множества слово «множество» входит, и притом дважды, в определяющее выражение). В целях избежания связанных с этим трудностей были предложены различные средства (модификация наивной теории множеств), в частности типов теория. Непременный совет Непреме'нный сове'т,высший совещательный орган в царствование Александра I в России. Существовал в 1801-10. Состоял из 12 представителей титулованной знати (Д. И. Трощинский, П. В. Завадовский, А. Р. Воронцов, П. и В. Зубовы и др.); председатель - граф Н. И. Салтыков. В начале деятельности Н. с. был рассмотрен ряд важных вопросов. С учреждением министерств и Комитета министров в 1802 на рассмотрение Н. с. поступали маловажные и запутанные дела. Упразднён при учреждении Государственного совета. Непреодолимая сила Непреодоли'мая си'ла(лат. vis major, франц. force majeure), в гражданском праве - обстоятельство, освобождающее от ответственности. Под Н. с. понимается чрезвычайное событие, вредные последствия которого не могло предотвратить лицо, обязанное это сделать. К таким событиям относятся стихийные бедствия (например, землетрясения, наводнения), общественные явления (например, война). Будучи непредотвратимой, Н. с. обладает тем не менее относительным характером: событие, непреодолимое в одних условиях, может стать преодолимым в других. Как правило, Н. с. освобождает от имущественной ответственности, если именно Н. с. - причина правонарушения и отсутствует вина обязанного лица. В некоторых случаях правонарушитель несёт имущественную ответственность даже при наличии Н. с. (например, согласно ст. 101 Возд. кодекса СССР). Н. с. является также основанием приостановления срока течения исковой давности. Непрерывная группа Непреры'вная гру'ппа,математическое понятие, как и понятие обыкновенной группы,возникающее при рассмотрении преобразований. Пусть М -множество элементов хкакого-либо рода, например чисел, точек пространства, функций и т.п. Говорят, что имеется преобразование fмножества М,если каждому элементу xиз Мпоставлен в соответствие определённый элемент y= f( x) , (1) также принадлежащий М;при этом предполагается, что для каждого унайдётся такой элемент х,и притом единственный, который удовлетворяет уравнению (1). Т. о., уравнение (1) разрешимо относительно х: x= f --1( y) , и f --1также есть преобразование множества М.Преобразование f -1называется обратным к преобразованию f. Преобразование е,переводящее каждый элемент хв себя, е( х) = х,называется тождественным. Если имеется два преобразования fи g,то последовательное их применение даёт новое преобразование k: k( x) = f[ g( x)] . Преобразование kназывается произведением преобразований fи g: k= fg. Умножение некоторого преобразования fна тождественное ене меняет его: fe= ef= f. (2) Произведение преобразования fна его обратное f --1даёт тождественное: ff -1= f -1f= e. (3) Для любых трёх преобразований имеет место ассоциативный закон: ( fg) h= f( gh) . (4) Совокупность всех преобразований множества Мявляется группой. Можно, однако, рассматривать совокупность не всех преобразований, а любую такую совокупность преобразований, что наряду с каждым преобразованием в неё входит обратное к нему, а наряду с каждыми двумя - их произведение. Тогда мы также имеем группу преобразований (подгруппу группы всех преобразований множества М) .Если множество Мявляется непрерывной средой ( топологическим пространством ) ,точнее говоря, если известно, что значит
где x 1, x 2,..., x n,... -некоторая последовательность элементов из М, а xтакже принадлежит М(как это имеет место, например, в множестве чисел или точек), то можно выделить непрерывные преобразования. Преобразование fназывается непрерывным, если из (5) следует
Множество всех непрерывных преобразований составляет группу непрерывных преобразований. Во многих случаях (но не всегда) группа непрерывных преобразований сама естественным образом оказывается непрерывной средой, т. е. в ней определяется понятие предельного перехода: можно говорить о том, что некоторая последовательность преобразований сходится к преобразованию. При этом оказывается, что из
следует
Такая группа называется Н. г. преобразований. Пусть Месть множество точек плоскости. Преобразование fназывается движением плоскости, если для каждой пары точек хи уиз Мрасстояние между хи уравно расстоянию между f( x) и f( y). Преобразование плоскости называется проективным, если точки, лежащие на одной прямой, переходят в точки, также лежащие на одной прямой. Частным случаем проективного преобразования является аффинное, при котором параллельные прямые переходят в параллельные. Здесь мы имеем три простейших геометрических примера Н. г. преобразований: группу движений, группу проективных преобразований и группу аффинных преобразований. Если рассматривать те свойства геометрических фигур на плоскости, которые не меняются при движениях плоскости, то мы получим обычную элементарную геометрию. Аналогично возникают геометрии проективная и аффинная, Ф. Клейном была выдвинута общая точка зрения (см. Эрлангенская программа ) ,согласно которой геометрия есть наука, изучающая те свойства фигур, которые не меняются при заданной группе непрерывных преобразований. Отсюда - роль теории Н. г. в геометрии. Примем за множество Мвсевозможные упорядоченные системы по nчисел x 1, x 2,..., x n,которые будем трактовать как компоненты вектора х.Рассмотрим т. н. линейное преобразование f, переводящее вектор хв вектор ус компонентами y 1, y 2,..., y n,причём преобразование задаётся формулой
Множество всех линейных преобразований составляет Н. г. преобразований. Можно рассматривать не все линейные преобразования, а, например, такие, которые не меняют длины векторов, т. е. для которых выполнено условие x 1 2+ x 2 2+... + x n 2= y 1 2+ y 2 2+... + y n 2. Такие преобразования составляют группу линейных ортогональных преобразований. Группы линейных преобразований играют весьма важную роль, в частности находят своё приложение в квантовой механике. Современное развитие теории групп показало, что при изучении группы целесообразно бывает отвлечься от того факта, что элементы её являются преобразованиями, а следует трактовать группу просто как множество элементов, в котором установлена операция умножения, т. е. каждой паре элементов группы поставлен в соответствие элемент, называемый произведением исходных: k= fg,причём в качестве аксиом выдвигаются условия (2), (3), (4). Элемент e, раньше бывший тождественным преобразованием, теперь называется единицей группы. Вместо обратного преобразования появляется обратный элемент. Существование единицы и обратного элемента теперь являются аксиомами. Если для любых двух элементов fи gверно fg= gf,то группа называется коммутативной. Для того чтобы получить Н. г., следует предположить, что элементы её составляют топологическое пространство и что операция умножения непрерывна, т. е. выполнено условие (6), которое теперь выдвигается как аксиома. Так возникло в математике новое, абстрактное понятие непрерывной, или, что то же самое, топологической группы. Логически оно слагается из операции перемножения и операции предельного перехода. Так как обе эти операции весьма часто встречаются в математике, то понятие Н. г. принадлежит к числу важных и находит многочисленные приложения. Важнейшим типом Н. г. являются группы Ли (С. Ли-основоположник теории Н. г.). Если в окрестности единицы группы можно ввести координаты, т. е. каждый элемент fзадать числами f 1, f 2,..., f r-его координатами, то закон умножения k= fgможно записать для элементов, близких к единице, в координатной форме: k i= j i ( f 1, f 2,..., f r, g 1, g 2,..., g r) , (7) i= 1, 2,..., r, где j i-непрерывная функция всех переменных. Если ещё предположить, что функции j, трижды непрерывно дифференцируемы, то мы придём к понятию группы Ли. Если считать, что координаты единицы все равны нулю, т. е. если принять единицу за начало координат, то, разлагая в ряд Тейлора правую часть соотношения (7), получим
Числа
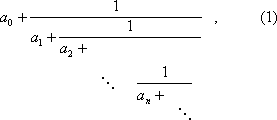
называются структурными константами группы Ли, и к изучению их полностью сводится изучение группы Ли. Лит.:Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1973 (имеется библ.). Л. С. Понтрягин. Непрерывная дробь Непреры'вная дробь,цепная дробь, один из важнейших способов представления чисел и функций. Н. д. есть выражение вида
где a 0- любое целое число, a 1, a 2,..., a n,... - натуральные числа, называемые неполными частными, или элементами, данной Н. д. К Н. д., изображающей некоторое число a, можно прийти, записывая это число в виде
где a 0- целое число и 0 < 1/a 1< 1, затем, записывая в таком же виде a 1и т. д. Число элементов Н. д. может быть конечным или бесконечным; в зависимости от этого Н. д. называют конечной или бесконечной. Н. д. (1) часто символически обозначают так: [ а 0; a 1, a 2 ,..., a n,...] (бесконечная Н. д.) (2) или [ а 0; а 1, a 2 ,..., a n] (конечная Н. д.). (3) Конечная Н. д. всегда представляет собой рациональное число; обратно, каждое рациональное число может быть представлено в виде конечной Н. д. (3); такое представление единственно, если потребовать, чтобы a n¹ 1. Н. д. [ а 0; a 1, a 2,..., a k] ( kЈ n), записанную в виде несократимой дроби p k/ q k,называют подходящей дробью порядка kданной Н. д. (2). Числители и знаменатели подходящих дробей связаны рекуррентными формулами: p k +1= a k +1 p k+ p k -1 , q k +1= a k +1 q k+ q k -1 , которые служат основанием всей теории Н. д. Из этих формул непосредственно вытекает важное соотношение p kq k -1- q kp k- 1= ± 1. Для каждой бесконечной Н. д. существует предел
называемый значением данной Н. д. Каждое иррациональное число является значением единственной бесконечной Н. д., получаемой разложением a указанным выше образом, например ( е- 1)/2 = [0, 1,6, 10,14, 18,...];
квадратичные иррациональности разлагаются в периодические Н. д. Основное значение Н. д. для приложений заключается в том, что подходящие дроби являются наилучшими приближениями числа a, то есть, что для любой другой дроби m/ n,знаменатель которой не более g kимеет место неравенство | na - m| > | g ka - p kl; при этом | q k. - p k| < 1 /q k+ 1 .Нечётные подходящие дроби больше a, а чётные - меньше. При возрастании kнечётные подходящие дроби убывают, а чётные возрастают. Н. д. используются для приближения иррациональных чисел рациональными. Например, известные приближения 22/ 7, 355/ 113для числа p (отношения длины окружности к диаметру) суть подходящие дроби для разложения p в Н. д. Следует отметить, что первое доказательство иррациональности чисел еи p было дано в 1766 немецким математиком И. Ламбертом с помощью Н. д. Французский математик Ж. Лиувилль доказал: для любого алгебраического числа a степени nможно найти такую постоянную l, что для любой дроби x/ yвыполняется неравенство |a - x/ y| > l/ у n. С помощью Н. д. можно построить числа a такие, что разность |a - p k/ q k| делается меньше a/ g k, какую бы постоянную l мы ни взяли. Так, используя Н. д., можно строить трансцендентные числа. Недостатком Н. д. является чрезвычайная трудность арифметических действий над ними, равносильная практической невозможности этих действий; например, зная элементы двух дробей, мы не можем сколько-нибудь просто получить элементы их суммы или произведения. Н. д. встречаются уже в 16 в. у Р. Бомбелли . В 17 в. Н. д. изучал Дж. Валлис ; ряд важных свойств Н. д. открыл Х. Гюйгенс , занимавшийся ими в связи с теорией зубчатых колёс. Многое сделал для теории Н. д. Л. Эйлер в 18 в. В 19 в. П. Л. Чебышев , А. А. Марков и др. применили Н. д., элементами которых являются многочлены, к изучению ортогональных многочленов .
Лит.:Чебышев П. Л., Полное собрание сочинений, 2 изд., т. 1, М. - Л., 1946; Хинчин А. Я., Цепные дроби, 2 изд., М. - Л., 1949; Эйлер Л., Введение в анализ бесконечно малых, пер. с лат., т. 1, М. - Л., 1936; Стилтьес Т. И., Исследования о непрерывных дробях, пер. с франц., Хар. - К., 1936; Perron О., Die Lehre von den Kettenbrьchen, 2 Aufl., Lpz. - B., 1929; Wall Н. S., Analytic theory of continued fractions, Toronto - N. Y. - L., 1948. Непрерывная разливка стали Непреры'вная разли'вка ста'ли,процесс получения из жидкой стали слитков-заготовок (для прокатки, ковки или прессования), формируемых непрерывно по мере поступления жидкого металла с одной стороны изложницы-кристаллизатора и удаления частично затвердевшей заготовки с противоположной стороны. Н. р. с. имеет следующие преимущества перед обычной разливкой: на 10-15% сокращается расход металла на 1 тгодного проката вследствие уменьшения обрези головной и донной частей заготовки; сокращаются капитальные затраты на сооружение металлургического завода, так как исключаются парк чугунных изложниц, отделения для их подготовки и извлечения слитков из изложниц, дорогостоящие блюминги или слябинги , на которых крупные слитки обжимаются в заготовку для последующей прокатки; создаются условия для полной механизации и автоматизации процесса разливки; благодаря ускорению затвердевания повышается степень однородности металла, улучшается его качество. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91 |
|||||||