 |
|
Популярные авторы:: Картленд Барбара :: Громов Дмитрий :: Твен Марк :: БСЭ :: Горький Максим :: Андреев Леонид Николаевич :: Лесков Николай Семёнович :: Ламур Луис :: Станюкович Константин Михайлович :: СССР Внутренний Предиктор Популярные книги:: Справочник по реестру Windows XP :: Бурый волк :: Мясоеды :: Течет река Волга… :: Информационный листок украинской фантастики N 17-2003 (157) :: Похититель талантов :: Агент галактики :: Нежеланная невеста :: Туманная грань :: Протокол допроса военнопленного генерал-лейтенанта Красной Армии М Ф Лукина 14 декабря 1941 года |
Большая Советская Энциклопедия (СТ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (СТ) - Чтение (стр. 19)
Лит.:Струмилин С. Г., Избр. произведения, т. 1(с. 171-81), т. 2 (с. 310-22, 407-10), т. 3 (с. 7-507), т. 4 (с. 29-37, 44-67,310-36), т. 5 (с. 230-44, 338-51, 364-381), М., 1963-64; Минц Л. Е., Проблемы баланса труда и использования трудовых ресурсов в СССР, М., 1967: Еремина Н. М., Маршалова В. П., Статистика труда, 2 изд., М., 1971; Шевчепко Н. Н., Кошелюк С. А., Нелюбин Н. И., Статистика труда, М.,1972. См. также лит. при ст. . Н. М. Еремина. Статистика финансов Стати'стика фина'нсов,отрасль , предметом изучения которой являются закономерности и массовые процессы, происходящие в области финансов, денежного обращения и кредита. Основными задачами советской С. ф. являются сбор, обработка и анализ показателей, характеризующих финансовые отношения в народном хозяйстве, наблюдение за ходом выполнения финансовых планов. Сов. С. ф. подразделяется на статистику государственного бюджета, банковскую статистику, статистику сберегательного дела, государственного социального страхования, а также статистику финансов предприятия и отраслей народного хозяйства. Статистика государственного бюджета рассматривает структуру и динамику доходов и расходов бюджетов (государственных, республиканских и местных), даёт характеристику финансовых процессов в развитии экономики и культуры страны. Банковская статистика разрабатывает систему статистических показателей, характеризующих кредитные и расчётные отношения банков с предприятиями, а также денежные обращения в стране. В число этих показателей входят объём и структура выданных ссуд, объекты кредита, своевременность возврата ссуд, оборачиваемость и динамика ссудной задолженности, объём и распределение расчётных операций по способам расчётов, денежная масса в стране и др. Статистика сберегательного дела изучает состояние сети сберегательных касс, динамику и структуру сбережений населения, выявляет тенденции их изменения по территории страны и во времени. Основные её показатели: сеть, объём вкладов и численность вкладов в группировке по ряду признаков, средний срок хранения вкладов, операции по государственным займам и денежно-вещевым лотереям, по кассовому обслуживанию населения, предприятий и организаций, показатели, характеризующие деятельность сберегательных касс, и др. Статистика государственного страхования изучает объём и источники образования страховых фондов и данные о выплатах страховых возмещений и страховых сумм в группировке по ряду признаков (по территории, видам страхования, типам хозяйств и др.). В статистике социального страхования наряду с другими учитываются показатели частоты, тяжести и опасности страховых событий, даётся характеристика бюджета социального страхования и обеспечения. Большое значение в С. ф. имеют показатели, характеризующие финансовую деятельность отдельных предприятий и организаций, целых отраслей и всего народного хозяйства (прибыль, рентабельность, фонды экономического стимулирования, оборачиваемость оборотных средств, платежи в бюджет и др.). В связи с осуществляемой в стране экономической реформой роль финансовой статистики предприятий и организаций возрастает, а система её показателей и методы их анализа совершенствуются. Характерна интеграция финансовых показателей с др. показателями деятельности предприятий и организаций (см. ). Важным разделом С. ф. является разработка показателей отчётных финансовых балансов народного хозяйства СССР, республик, отраслей, предприятий. Составная часть финансовых балансов - отчётный баланс денежных доходов и расходов населения. Основным источником данных С. ф. являются материалы бухгалтерской и статистической отчётности, регулярно разрабатываемые в соответствии с инструкциями ЦСУ СССР и министерства финансов СССР. Данные сплошного наблюдения дополняются материалами выборочного наблюдения. С. ф. СССР развивается в тесной связи с С. ф. др. социалистических стран, в частности стран - членов СЭВ. Совместную работу в области С. ф. (регулярно и по единому плану) социалистические страны осуществляют через постоянные комиссии СЭВ по статистике и финансам. Основным источником данных С. ф. капиталистических стран являются сведения бухгалтерских балансов предприятий и материалы различных обследований финансовых органов, финансовые отчёты корпораций, а также переписи (цензы) коммерческих учреждений, которые проводятся один раз в 5 лети реже. Др. источник - материалы, собираемые и публикуемые государственными финансовыми службами (в США, например, Федеральным резервным управлением), преимущественно на выборочной основе. Ценным источником сведений являются также биржевые сообщения и публикации (курсы валют, курсы акций). Материалы, характеризующие результаты финансовой деятельности частных компаний (основной и наиболее важный раздел С. ф.), собираются на урезанной основе (закон коммерческой тайны) и поэтому не дают полного представления о результатах их деятельности. При сопоставлениях показателей С. ф. различных капиталистических стран эти показатели пересчитываются по единой методологии. Большое значение имеет также пересчёт сопоставимых национальных показателей в единую валюту. и - основные организации, занимающиеся международной С. ф. Большое внимание С. ф. уделяют также статистические службы ООН. Лит.:Карпенко Б. И., Финансовая статистика, М., 1929; Лившиц Ф. Д., Банковская статистика с основами общей теории, 2 изд., М., 1948; Ряузов Н. Н., Шор Ю. Л., Статистика в кредитных учреждениях, М., 1973; Статистика финансов, подред. П. П. Маслова, М., 1974. В. М. Симчера. Статистическая гипотеза
Статисти'ческая
гипо'теза,предположительное суждение о вероятностных закономерностях, которым подчиняется изучаемое явление. Как правило, С. г. определяет значения параметров закона распределения вероятностей или его вид. С. г. называется простой, если она определяет единственный закон распределения; в ином случае С. г. называется сложной и может быть представлена как некоторый класс простых С. г. Например, гипотеза о том, что распределение вероятностей является
с математическим ожиданием
а=
а
0и некоторой (неизвестной) дисперсией s
2
будет сложной, составленной из простых гипотез
а =
а
0,
Статистическая лингвистика Статисти'ческая лингви'стика,дисциплина, изучающая количественные закономерности естественного языка, проявляющиеся в текстах. В основе С. л. лежит предположение, что некоторые численные характеристики и функциональные зависимости между ними, полученные для ограниченной совокупности текстов, характеризуют язык в целом или его функциональные стили (публицистический, научный, художественный и т.п.). Практически важной и наиболее изученной числовой характеристикой является относительная частота употребления различных лингвистических единиц (букв, фонем, слогов, слов, синтаксических конструкций), их классов (например, гласных, согласных, частей речи) и сочетаний (например, последовательностей из n букв). Данные о частоте слов (иногда словосочетаний) отражаются в . Важную роль в С. л. играет функциональная зависимость, приближённо описывающая связь между частотой слова и его номером (рангом) в последовательности по убыванию частот - Ципфа - Мандельброта закон. С. л. изучает также зависимости между частотой и длиной слова (в числе слогов), числом его значений и возрастом. Накопленные данные используются для выявления особенностей стиля отдельных авторов, атрибуции текстов, дешифровки исторических письменностей, для решения задач стенографии, теории связи, а также . С. л. при получении численных характеристик использует методы и некоторые методы теории информации (для определения энтропии и избыточности языка, см. ), а для установления связи между наблюдаемыми характеристиками и выбора наиболее существенных из них - метод математических моделей, базирующихся на понятиях теории вероятностей (см. ) и . Возможно более широкое понимание С. л. как использования методов статистики для проверки лингвистических гипотез, которые могут носить и качественный характер. Лит.:Головин Б. Н., Язык и статистика, М., 1971; Фрумкина Р. М., Статистические методы и стратегия лингвистического исследования, «Изв. АН СССР. Серия литературы и языка». 1975, т. 34, №2; Штейнфельдт Э. А., Частотный словарь современного русского языка, Таллин, 1963; Herdan G., The advanced theory of language as choice and chance, B.,1966; Mulier Ch., Initiation a la statistique linguistique, P., 1968. М. В. Арапов. Статистическая механика Статисти'ческая меха'ника,тоже, что . Статистическая проверка гипотез
Статисти'ческая прове'рка гипо'тез,система приёмов в
, предназначенных для проверки соответствия опытных данных некоторой
. Процедуры С. п. г. позволяют принимать или отвергать статистические гипотезы, возникающие при обработке или интерпретации результатов измерений во многих практически важных разделах науки и производства, связанных с экспериментом. Правило, по которому принимается или отклоняется данная гипотеза, называется статистическим критерием. Построение критерия определяется выбором подходящей функции
Тот результатов наблюдений, которая служит мерой расхождения между опытными и гипотетическими значениями. Эта функция, являющаяся случайной величиной, называется статистикой критерия, при этом предполагается, что распределение вероятностей
Тможет быть вычислено при допущении, что проверяемая гипотеза верна. По распределению статистики
Тнаходится значение
Т
0, такое, что если гипотеза верна, то вероятность неравенства
T>
T
0равна a, где a - заранее заданный
. Если в конкретном случае обнаружится, что
Т>
T
0, то гипотеза отвергается, тогда как появление значения
ТЈ
T
0не противоречит гипотезе. Пусть, например, требуется проверить гипотезу о том, что независимые результаты наблюдений
x
1,..., x
nподчиняются
со средним значением
а = a
0и известной дисперсией s
2
. При этом предположении среднее арифметическое
и подчинена с n- 1 степенями свободы (подобную задачу см. в ст. , табл. 1a). Такого рода критерии называются критериями согласия и используются как для проверки гипотез о параметрах распределения, так и гипотез о самих распределениях (см. ). При решении вопроса о принятии или отклонении какой-либо гипотезы H 0с помощью любого критерия, основанного на результатах наблюдения, могут быть допущены ошибки двух типов. Ошибка «первого рода» совершается тогда, когда отвергается верная гипотеза H 0. Ошибка «второго рода» совершается в том случае, когда гипотеза H 0принимается, а на самом деле верна не она, а какая-либо альтернативная гипотеза Н. Естественно требовать, чтобы критерий для проверки данной гипотезы приводил возможно реже к ошибочным решениям. Обычная процедура построения наилучшего критерия для простой гипотезы заключается в выборе среди всех критериев с заданным уровнем значимости и (вероятность ошибки первого рода) такого, который приводил бы к наименьшей вероятности ошибки второго рода (или, что то же самое, к наибольшей вероятности отклонения гипотезы, когда она неверна). Последняя вероятность (дополняющая до единицы вероятность ошибки второго рода) называется мощностью критерия. В случае, когда альтернативная гипотеза Нпростая, наилучшим будет критерий, который имеет наибольшую мощность среди всех других критериев с заданным уровнем значимости а (наиболее мощный критерий). Если альтернативная гипотеза Нсложная, например зависит от параметра, то мощность критерия будет функцией, определенной на классе простых альтернатив, составляющих Н, т. е. будет функцией параметра. Критерий, имеющий наибольшую мощность при каждой альтернативной гипотезе из класса Н, называется равномерно наиболее мощным, однако следует отметить, что такой критерий существует лишь в немногих специальных ситуациях. В задаче проверки гипотезы о среднем значении нормальной совокупности а= а 0против альтернативной гипотезы а> a 0 равномерно наиболее мощный критерий существует, тогда как при проверке той же гипотезы против альтернативы а¹ a 0его нет. Поэтому часто ограничиваются поиском равномерно наиболее мощных критериев в тех или иных специальных классах (Инвариантных, несмещенных критериев и т.п.). Теория С. п. г. позволяет с единой точки зрения трактовать выдвигаемые практикой различные задачи математической статистики (оценка различия между средними значениями, проверка гипотезы постоянства дисперсии, проверка гипотезы независимости, проверка гипотез о распределениях и т.п. Идеи , примененные к С. п. г., указывают на возможность связать решение о принятии или отклонении гипотезы с результатами последовательно проводимых наблюдений (в этом случае число наблюдений, на основе которых по определённому правилу принимается решение, не фиксируется заранее, а определяется в ходе эксперимента) (см. также ). Лит.:Kpamep Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975; Леман Э., Проверка статистических гипотез, пер. с англ., М., 1964. Л. В. Прохоров. Статистическая радиофизика Статисти'ческая радиофи'зика,раздел радиофизики, посвященный изучению флуктуационных явлений при генерации, излучении, распространении и приёме радиоволн. В более широком смысле С. р. охватывает исследования статистических закономерностей в колебательных и волновых процессах ( , проблемы взаимодействия сигналов и шумов в нелинейных системах и т.п.). Практическое значение С. р. связано с тем, что в системах , , и др. флуктуации играют важную и во многих случаях определяющую роль на основных этапах передачи информации. Электрические флуктуации, обусловленные фундаментальными физическими процессами в веществе, являются причиной возникновения флуктуационных напряжений и токов в радиоприёмных устройствах (см. ). Флуктуационные токи и напряжения, неизбежные в реальных генераторах колебаний, определяют предельно достижимые монохроматичность и стабильность частоты генератора радиопередающих устройств. Флуктуационные явления при в атмосфере связаны с тем, что показатель преломления тропосферы и ионосферы испытывает нерегулярные изменения, носящие флуктуационный характер. Идеи и методы С. р. проникают в оптику. Лит.:Рытов С. М. Введение в статистическую радиофизику, М., 1966; Вандер-Зил А., Флуктуации в радиотехнике и физике, пер. с англ., М., 1958: Малахов А. Н., Флуктуации в автоколебательных системах, М., IJ68; Татарский В. И., Распространение волн в турбулентной атмосфере, М., 1967. С. Л. Ахманов. Статистическая сумма Статисти'ческая су'мма,величина, обратная нормирующему множителю канонического в квантовой . В классической статистической физике такая величина называется статистическим интегралом. С. с. (статистический интеграл) позволяет вычислить все . Статистическая термодинамика Статисти'ческая термодина'микаравновесная, раздел , дающий статистическое обоснование законов основе статистической механики Дж. У. и посвященный вычислениям термодинамических характеристик системы ( , ) на основе законов взаимодействия составляющих систему частиц. Неравновесная С. т. даёт статистическое обоснование (уравнений переноса энергии, импульса, массы) и позволяет получить выражения для входящих в уравнения коэффициентов (кинетических коэффициентов, или коэффициентов переноса) на основе законов взаимодействия и движения частиц системы. Статистическая физика Статисти'ческая фи'зика,раздел физики, задача которого - выразить свойства макроскопических тел, т. е. систем, состоящих из очень большого числа одинаковых частиц (молекул, атомов, электронов и т.д.), через свойства этих частиц и взаимодействие между ними. Изучением макроскопических тел занимаются и др. разделы физики - , механика сплошных сред, электродинамика сплошных сред. Однако при решении конкретных задач методами этих дисциплин в соответствующие уравнения всегда входят неизвестные параметры или функции, характеризующие данное тело. Так, для решения задач гидродинамики необходимо знать уравнение состояния жидкости или газа, т. е. зависимость плотности от температуры и давления, теплоёмкость жидкости, её коэффициент вязкости и т.п. Все эти зависимости и параметры можно, разумеется, определять экспериментально, поэтому методы, о которых идёт речь, называются феноменологическими. Статистическая же физика позволяет, по крайней мере в принципе, а во многих случаях и фактически, вычислить все эти величины, если известны силы взаимодействия между молекулами. Т. о., С. ф. использует сведения о «микроскопическом» строении тел - о том, из каких частиц они состоят, как эти частицы взаимодействуют, поэтому её называют микроскопической теорией. Если в какой-то момент времени заданы координаты и скорости всех частиц тела и известен закон их взаимодействия, то, решая уравнения механики, можно было бы найти эти координаты и скорости в любой последующий момент времени и тем самым полностью определить состояние исследуемого тела. (Для простоты изложение ведётся на языке классической механики. Но и в ситуация та же: зная начальную системы и закон взаимодействия частиц, можно, решая , найти волновую функцию, определяющую состояние системы во все будущие моменты времени.) Фактически, однако, такой путь построения микроскопической теории невозможен, т.к. число частиц в макроскопических телах очень велико. Например, в 1 см 3газа при температуре 0 °С и давлении в 1 атмсодержится примерно 2,7Ч10 19молекул. Невозможно решить такое число уравнений, а начальные координаты и скорости всех молекул всё равно неизвестны. Однако именно большое число частиц в макроскопических телах приводит к появлению новых - статистических - закономерностей в поведении таких тел. Это поведение в широких пределах не зависит от конкретных начальных условий - от точных значений начальных координат и скоростей частиц. Важнейшее проявление этой независимости - известный из опыта факт, что система, предоставленная самой себе, т. е. изолированная от внешних воздействий, с течением времени приходит в некоторое равновесное состояние (термодинамическое, или статистическое, равновесие), свойства которого определяются только такими общими характеристиками начального состояния, как число частиц, их суммарная энергия и т.п. (см. ). В дальнейшем речь будет идти главным образом о С. ф. равновесных состояний. Прежде чем сформулировать теорию, описывающую статистические закономерности, следует разумно ограничить сами требования к теории. Именно, задачей теории должно являться вычисление не точных значений различных физических величин для макроскопических тел, а средних значений этих величин по времени. Рассмотрим, например, молекулы, находящиеся в некотором выделенном в газе достаточно большом - макроскопическом - объёме. Число таких молекул с течением времени будет меняться из-за их движения, и его можно было бы найти точно, если были бы известны все координаты молекул во все моменты времени. В этом, однако, нет необходимости. Изменение числа молекул в объёме будет носить характер беспорядочных колебаний - флуктуаций - относительно некоторого среднего значения. При большом числе частиц в объёме эти колебания будут малы по сравнению со средним числом частиц, так что для характеристики макроскопического состояния достаточно знать именно это среднее значение. Для уяснения характера статистических закономерностей рассмотрим ещё один простой пример. Пусть в некоторый сосуд помещено большое число зёрен двух сортов, каждого сорта поровну, и содержимое сосуда тщательно перемешано. Тогда на основании повседневного опыта можно быть уверенным, что во взятой из сосуда пробе, содержащей всё ещё большое число зёрен, будет обнаружено примерно равное число зёрен каждого сорта независимо от того, в каком порядке засыпались зёрна в сосуд. На этом примере хорошо видны два важных обстоятельства, обеспечивающих применимость статистической теории. Во первых, необходимость большого числа зёрен как во всей «системе» - сосуде с зерном, так и в выбранной для опыта «подсистеме» - пробе. (Если проба состоит всего из двух зёрен, то нередко оба будут одного сорта.) Во-вторых, ясно, что существенную роль играет сложность движения зёрен при перемешивании, обеспечивающая их равномерное распределение в объёме сосуда. Функция распределения.Рассмотрим систему, состоящую из Nчастиц, для простоты считая, что частицы не имеют внутренних степеней свободы. Такая система описывается заданием 6Nпеременных - 3Nкоординат q iи 3Nимпульсов p i, частиц [совокупность этих переменных сокращённо будет обозначаться ( р, q)]. Вычислим среднее значение по интервалу временит некоторой величины F( р, q), являющейся функцией этих координат и импульсов. Для этого разобьем интервал (0, t) на sравных малых отрезков D t a( а= 1,2,....... s). Тогда по определению
или (1)
где q aи p a- значения координат и импульсов в моменты времени t a. В пределе s® Ґ сумма переходит в интеграл:
Понятие функции распределения естественным образом, возникает, если рассмотреть пространство 6 Nизмерений, на осях которого отложены значения координат и импульсов частиц системы; оно называется фазовым пространством. Каждому значению времени tсоответствуют определённые значения всех qи р, т. е. некоторая точка в фазовом пространстве, изображающая состояние системы в данный момент времени t. Разобьем всё фазовое пространство на элементы, размер которых мал по сравнению с характерными для данного состояния системы значениями qи р, но ещё настолько велик, что в каждом из них находится много точек, изображающих состояние системы в различные моменты времени t. Тогда число таких точек в элементе объёма будет примерно пропорционально величине этого объёма dpdq. Если обозначить коэффициент пропорциональности через sw( p, q), то это число для элемента с центром в некоторой точке ( р, q) запишется в виде: da = sw( р, q) dpdq, (2) где dpdq = dp 1dq 1dp 2dq 2... dp 3Ndq 3N - объём выбранного элемента фазового пространства. Среднее значение (1) с учётом малости этих элементов объёма можно переписать как
(интегрирование по координатам производится по всему объёму системы, по импульсам - от -Ґ до Ґ). Функция w( p, q, t) носит название функции распределения по координатами импульсам частиц. Поскольку полное число выбранных точек равно s, функция wудовлетворяет условию нормировки:
Из (3) и (4) видно, что w dpdqможно рассматривать как вероятность системе находиться в элементе dpdqфазового пространства. Введённой таким образом функции распределения можно дать и др. истолкование. Для этого будем рассматривать одновременно большое число одинаковых систем и примем, что каждая точка в фазовом пространстве изображает состояние одной такой системы. Тогда усреднение по времени в (1)-(1a) можно понимать как усреднение по совокупности этих систем, или, как говорят, по . Проведённые до сих пор рассуждения носили чисто формальный характер, т.к. нахождение функции распределения, согласно (2), требует знания всех ри qво все моменты времени, т. е. решения уравнений движения с соответствующими начальными условиями. Основным положением С. ф. является, однако, утверждение о возможности определить эту функцию из общих соображений для системы, находящейся в состоянии термодинамического равновесия. Прежде всего можно показать, исходя из сохранения числа систем при движении, что функция распределения является интегралом движения системы, т. е. остаётся постоянной, если ри qменяются в соответствии с уравнениями движения (см. ). При движении замкнутой системы не меняется её энергия, поэтому все точки в фазовом пространстве, изображающие состояние системы в разные моменты времени, должны лежать на некоторой «гиперповерхности», соответствующей начальному значению энергии Е. Уравнение этой поверхности имеет вид; H( p, q) = E, где Н( р, q) - энергия системы, выраженная через координаты и импульсы, т. е. её функция Гамильтона. Далее, движение системы из многих частиц носит крайне запутанный характер. Поэтому с течением времени точки, описывающие состояние, распределятся по поверхности постоянной энергии равномерно, подобно тому как равномерно распределяются зёрна при перемешивании в сосуде в упомянутом выше примере (см. также ). Такое равномерное распределение по изоэнергетической поверхности описывается функцией распределения вида: w( p, q) = Ad[ H( p, q) - E], (5) где d[ Н( р, q) - E] - , отличная от нуля только при Н = Е, т. е. на этой поверхности, А- постоянная, определяемая из условия нормировки (4). Функция распределения (5), называется микроканонической, позволяет вычислять средние значения всех физических величин по формуле (3), не решая уравнений движения. При выводе выражения (5) предполагалось, что единственная сохраняющаяся при движении системы величина, от которой зависит w, - это энергия системы. Разумеется, сохраняются также импульс и момент импульса, но эти величины можно исключить, предположив, что рассматриваемое тело заключено в неподвижный ящик, которому частицы могут отдавать импульс и момент. Фактически обычно рассматриваются не замкнутые системы, а макроскопические тела, являющиеся макроскопически малыми частями, или подсистемами, какой-либо замкнутой системы. Функция распределения для подсистемы будет отлична от (5), но не будет зависеть от конкретного характера остальной части системы - т. н. термостата. Поэтому функцию распределения подсистемы можно определить, считая, например, что термостат состоит просто из Nчастиц идеального газа, координаты и импульсы которых будем обозначать через Qи Р, в отличие от обозначений qи рдля подсистемы, тогда микроканоническое распределение: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73 |
|||||||
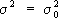 (
а
0и
(
а
0и
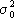 - заданные числа). См.
.
- заданные числа). См.
.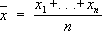 результатов наблюдений распределено нормально со средним
а = a
0и дисперсией s
2/n, а величина
результатов наблюдений распределено нормально со средним
а = a
0и дисперсией s
2/n, а величина
 распределена нормально с параметрами (0, 1). Полагая
распределена нормально с параметрами (0, 1). Полагая
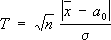 можно найти связь между
T
0и a по таблицам нормального распределения. Например, при гипотезе
а=
a
0событие
Т> 1, 96 имеет вероятность а = 0,05. Правило, рекомендующее считать, что гипотеза
а = a
0неверна, если
Т> 1,96, будет приводить к ложному отбрасыванию этой гипотезы в среднем в 5 случаях из 100, в которых она верна. Если же
ТЈ 1,96, то это ещё не означает, что гипотеза подтверждается, т.к. указанное неравенство с большой вероятностью может выполняться при
а, близких к
a
0. Следовательно, при использовании предложенного критерия можно лишь утверждать, что результаты наблюдений не противоречат гипотезе
а=
a
0. При выборе статистики
Твсегда явно или неявно учитывают гипотезы, конкурирующие с гипотезой
а = a
0. Например, если заранее известно, что
а ³ a
0, т. е. отклонение гипотезы
а = a
0влечёт принятие гипотезы
а > a
0, то вместо
Тследует взять
можно найти связь между
T
0и a по таблицам нормального распределения. Например, при гипотезе
а=
a
0событие
Т> 1, 96 имеет вероятность а = 0,05. Правило, рекомендующее считать, что гипотеза
а = a
0неверна, если
Т> 1,96, будет приводить к ложному отбрасыванию этой гипотезы в среднем в 5 случаях из 100, в которых она верна. Если же
ТЈ 1,96, то это ещё не означает, что гипотеза подтверждается, т.к. указанное неравенство с большой вероятностью может выполняться при
а, близких к
a
0. Следовательно, при использовании предложенного критерия можно лишь утверждать, что результаты наблюдений не противоречат гипотезе
а=
a
0. При выборе статистики
Твсегда явно или неявно учитывают гипотезы, конкурирующие с гипотезой
а = a
0. Например, если заранее известно, что
а ³ a
0, т. е. отклонение гипотезы
а = a
0влечёт принятие гипотезы
а > a
0, то вместо
Тследует взять
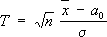 . Если дисперсия s
2неизвестна, то вместо данного критерия для проверки гипотезы
а = a
0можно воспользоваться т. н. критерием Стьюдента, основанным на статистике
. Если дисперсия s
2неизвестна, то вместо данного критерия для проверки гипотезы
а = a
0можно воспользоваться т. н. критерием Стьюдента, основанным на статистике
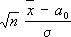 которая включает несмещенную оценку дисперсии
которая включает несмещенную оценку дисперсии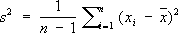
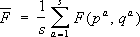 ,
,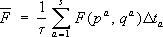 ,
,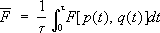 (1a)
(1a)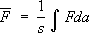 , т. е.
, т. е.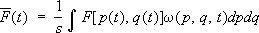 (3)
(3)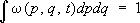 (4)
(4)