Большая Советская Энциклопедия (СО)

Национальная художественная галерея (б. царский дворец). Перестроена в 1877-87. Архитектор П. Момчилов.

Софокл

Софо'кл(Sophokles) (около 496-406 до н. э.). Древнегреческий драматург. Родился в предместье Афин - Колоне. Избирался на важные государственные должности, был близок к кругу .По античным свидетельствам, написал свыше 120 драм; первую победу на состязаниях трагических поэтов одержал в 468. Целиком дошли до нас трагедии «Аякс» (до 442), «Антигона» (около 441), «Царь Эдип» (около 425), «Филоктет» (409), «Трахинянки» и «Электра» (даты обеих неизвестны), «Эдип в Колоне» (поставлена в 401). От прочих произведений сохранилось много фрагментов.

  Мировоззрение С. отражает сложность и противоречивость афинской демократии периода её высшего расцвета. С одной стороны, демократическая идеология, выросшая на основе «... совместной частной собственности активных граждан государства...» (Маркс К. и Энгельс Ф., Соч., 2 изд., т. 3, с. 21), видела свой оплот во всевластии божественного промысла, в незыблемости традиционных установлений; с другой стороны - в условиях наиболее свободного для того времени развития личности всё настойчивее становилась тенденция к её высвобождению из полисных связей. Испытания, выпадающие на долю человека, не могли найти удовлетворительного объяснения в божественной воле, и С., озабоченный сохранением полисного единства, не пытался обосновать божественное управление миром какими-либо этическими соображениями. В то же время его привлекал активный, отвечающий за свои решения человек. В «Аяксе» герой осознаёт несовместимость содеянного им с нравственным кодексом доблестного вождя и в добровольной смерти находит освобождение от позора и бесчестья. В «Царе Эдипе» непреклонное расследование героем тайны своего рождения и прошлого возлагает на него объективную ответственность за невольные преступления, хотя и не даёт основания толковать трагедию в категориях субъективной вины и божественного возмездия. Цельным, неколебимым в своём решении человеком предстаёт Антигона с её героической защитой «неписаных» законов от произвола отдельной личности, прикрывающейся авторитетом государства. Герои С. свободны от всего второстепенного и слишком личного, в них сильно идеальное начало. Введение третьего актёра позволило С. усилить напряжение в развитии действия, обогатить изображение вовлечённых в него лиц. Несмотря на увеличившийся состав хора (15 человек), объём и значение хоровых партий в трагедиях С. существенно сократились по сравнению с произведениями Эсхила.

  Сюжеты и образы С. использовались как в последующей античной (Акций, Сенека), так и в новой европейской литературе от эпохи классицизма (Ж. Ротру, П. Корнель) вплоть до 20 в. (Ж. Жироду, Ж. Ануй, Б. Брехт и др.). Глубокий интерес к творчеству С. проявлялся в исследованиях и высказываниях по теории трагедии (Г. Э. Лессинг, И. В. Гёте, братья Шлегель, Ф. Шиллер, В. Г. Белинский). С середины 19 в. трагедии С. ставятся в театрах всего мира.

  Соч.: Sophocle, Tragйdies, t. 1-3, P., 1955-60: в рус. пер. - Драмы. Пер. Ф. Зелинского, т. 1-3, М., 1914-15; Трагедии. Пер. С. Шервинского, М., 1958.

  Лит.:Радциг С. И., К вопросу о мировоззрении Софокла, «Вестник древней истории». 1957, № 4; Lesky A., Die tragische Dichtung der Hellenen, 3 Aufl., Gott., 1972, S. 169-274.

  В. Н. Ярхо.

Софокусные кривые

Софо'кусные кривы'е,конфокальные кривые [от лат. con (cum) - с, вместе и ] , ,имеющие общие фокусы. Если Fи F'- две данные точки плоскости, то через каждую точку плоскости проходит один эллипс и одна гипербола, имеющие F и F'своими фокусами (рис. 1).

  Каждый эллипс ортогонален любой софокусной с ним гиперболе, т. е. пересекается с ней (в четырёх точках) под прямым углом (углом между двумя кривыми в точке пересечения называется угол между их касательными). Всё множество софокусных эллипсов и гипербол в надлежащей системе координат определяется уравнением

 (*)

где с -расстояние фокусов от начала координат, а l - переменный параметр. При l > с ²это уравнение определяет эллипс, при 0< l< с ²-гиперболу (при l < 0 - мнимую линию 2-го порядка). Если один из фокусов стремится к бесконечности, то в пределе получаются два семейства софокусных парабол (рис. 2); любые две параболы, относящиеся к разным семействам, также ортогональны друг другу. При помощи софокусных эллипсов и гипербол на плоскости вводится система т. н. .Именно, если М( х, у) -произвольная точка плоскости, то, подставляя ее координаты хи ув уравнение (*), получим квадратное уравнение для l; корни его l ₁, l ₂ называются эллиптическими координатами точки М.Сами софокусные эллипсы и гиперболы составляют координатную сеть эллиптической координатной системы, т. с. определяются уравнениями l = const. l ₂= const.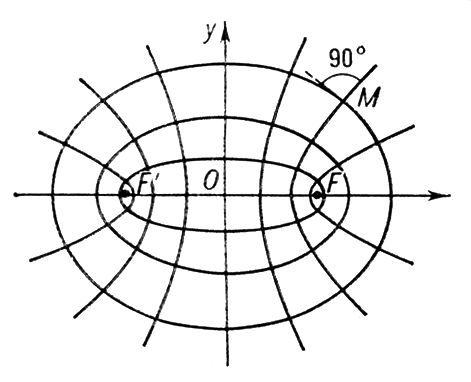

Рис. 1 к ст. Софокусные кривые.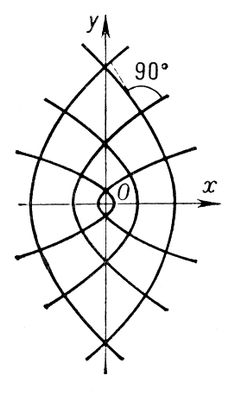

Рис. 2 к ст. Софокусные кривые.

Софора

Софо'ра(Sophora), род листопадных или вечнозелёных деревьев и кустарников, реже - многолетних трав семейства бобовых. Листья непарноперистые. Цветки белые, желтоватые, розовые, синевато-фиолетовые, длина около 10-18 мм,в кистях или метёлках. Бобы четковидные, цилиндрические или почти четырёхгранные, иногда крылатые, большей частью невскрывающиеся. Около 20 (по др. данным, до 70) видов, растущих в тропиках и субтропиках, реже - в умеренном поясе обоих полушарий. В СССР 5 видов. С. толстоплодная (S. pachycarpa - Средняя Азия) и С. лисохвостная, или обыкновенная (S. alopecuroides - юг Европейской части, Кавказ, Западная Сибирь, Средняя Азия) - опасные и трудноискоренимые карантинные сорняки полей. Примесь измельченных семян С. к муке делает хлеб горьким и ядовитым. Все виды С. ядовиты, содержат алкалоиды a-спартеин, софокарпин, матрин и могут быть использованы как инсектицидные, лекарственные, красильные и медоносные. С. японскую (S. japonica) широко разводят на юге СССР как декоративное растение.

  Лит.:Котт С. А., Карантинные сорные растения и меры борьбы с ними, 2 изд., М., 1953; Деревья и кустарники СССР, т. 4, М. - Л., 1958.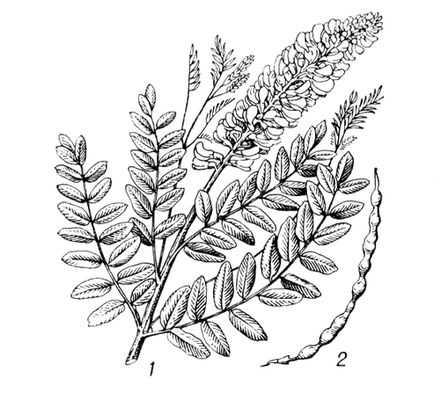

Софора обыкновенная: 1 - верхняя часть цветущего растения; 2 - плод.

Софрино

Со'фрино,посёлок городского типа в Пушкинском районе Московской области РСФСР. Ж.-д. станция в 46 кмк С. от Москвы. Предприятие ж.-д. транспорта, заводы: стройматериалов, строительных деталей и экспериментально-механический.

Софроний Врачанский

Софро'ний Врача'нский(церковное имя; до пострижения - Стойко Владиславов) (1739, г. Котел, - 22 или 23.9.1813, Бухарест), деятель болгарского национального возрождения и народного просвещения; ученик и последователь .В 1762 стал священником; многие годы учительствовал в Котеле. Преследования турецких властей и греческого архиепископа побудили С. В. уехать во Врацу (1792). С 1794 епископ Врачанский. Спасаясь от преследований ,бежал (1803) в Бухарест. В период русско-турецкой войны 1806-12 призывал болгар содействовать русским. С. В. выступал против засилья греческого духовенства, за просвещение болгарского народа, сыграл важную роль в развитии болгарского литературного языка. С. В. - автор первой печатной книги в новоболгарской литературе «Неделник».

  Соч.: Избрани творения, София, 1946.

  Лит.:Державин Н. С., Софроний Врачанский. Его жизнь и литературная деятельность, в кн.: Державин Н. С., Сборник статей и исследований в области славянской филологии, М. - Л., 1941, с. 125-69; Киселков В., Софроний Врачански, София, 1963.

Софроницкий Владимир Владимирович

Софрони'цкийВладимир Владимирович [25.4(8.5).1901, Петербург, - 29.8.1961, Москва], советский пианист и педагог, заслуженный деятель искусств РСФСР (1942). Учился у А. Михаловского в Варшаве, у Л. В. Николаева в Петроградской консерватории (1916-21). Концертировал с 1919 (в Ленинграде, Москве, в 1928-29 - в Варшаве, Париже). В конце 30-х гг. дал 12 т. н. исторических концертов (цикл). В 1936 - 42 профессор Ленинградской, в 1942-61 Московской консерваторий. Игра С. отличалась образной силой, остротой чувств, одухотворённостью, блеском техники. Исполнял главным образом произведения А. Н. Скрябина, а также Ф. Шопена, Ф. Листа, Р. Шумана. Государственная премия СССР (1943). Награжден орденом Ленина, 2 др. орденами, а также медалями.

  Лит.:Дельсон В., В. Софроницкий, М., 1959; Рабинович Д., Портреты пианистов, 2 изд., М,, 1970: Воспоминания о Софроницком, [сб.], М., 1970.

Софронов Анатолий Владимирович

Софро'новАнатолий Владимирович [р. 6(19).1.1911, Минск], русский советский писатель, драматург. Член КПСС с 1940. Окончил литературный факультет Ростовского педагогического института (1937). В годы Великой Отечественной войны 1941-45 специальный корреспондент «Известий». Главный редактор журнала «Огонёк» (с 1953). Печатается с 1929. Автор сборников стихов: «Солнечные дни» (1934), «Над Доном-рекой» (1938), «Ковыли» (1944), «Я вас люблю» (1962), «Мы с тобою из Ростова» (1964), «Всё это было на войне» (1972) и др., главные мотивы которых - любовь к родному краю, борьба за мир. Написал тексты песен «Шумел сурово брянский лес» (музыка С. Каца), «От Волги до Дона» (музыка С. Заславского) и др. Автор многих пьес: «В одном городе» (1946; пост. Театра им. Моссовета, 1948, Государственная премия СССР, 1948), «Московский характер» (1948; пост. Малого театра, 1949, Государственная премия СССР, 1949), «Карьера Бекетова» (1949; 2-я ред. 1972), «Сердце не прощает» (1953), «Деньги» (1954), «Миллион за улыбку» (1959), «Стряпуха» (1959; пост. Театра им. Евг. Вахтангова, 1959), «Стряпуха замужем» (1961), «Берегите живых сыновей» (1963), «Судьба - индейка» (1963), «Павлина» (1964), «Лабиринт» (1968), «Наследство» (1970), «Ураган» (1972) и др. Пьесы С., основу которых часто составляют комедийные и водевильные ситуации, касаются нравственных норм поведения сов. человека; они широко ставятся театрами страны. Опубликовал книги очерков «Путешествие, которое хочется повторить» (1964), «Наследство» (1973) и др. Некоторые произведения С. переведены на иностранные языки. В 1948-1953 секретарь СП СССР. Заместитель председателя Советского комитета солидарности стран Азия и Африки (с 1958). Награжден 2 орденами Ленина, орденом Октябрьской Революции и медалями.

  Соч.: Собр. соч. [Вступ. ст. Вас. Федорова], т. 1-5, М., 1971-72.

  Лит.:Толченова Н., Веление времени. Очерк творчества А. Софронова, М., 1972.

  В. А. Калашников.

Софронов Анемподист Иванович

Софро'новАнемподист Иванович [2(14).11.1886 - 24.10.1935], якутский советский писатель. Родился в Ботурусском улусе (Якутия). Занимался самообразованием. Печатался с 1912. Как писатель развивался под влиянием русской классической литературы. В поэмах «Родина» (1912), «Ангел и Демон» (1914), в драмах «Бедный Яков» (1914), «Любовь» (1916), «Манчары» (1920), «Тина жизни» (1921) изображены жизнь якутов до революции, гнёт местных феодалов и царизма, семейный деспотизм. С. выступил как критический реалист, демократ и просветитель. После революции С. основал национальный театр, был редактором первой якутской советской газеты «Манчары», первого литературного журнала «Чолбон». Избирался членом ЦИК Якутской АССР.

  Соч.: Талыллыбыт айымньылар, т. 1-2, Якутскай, 1964-65; Торообут дойду, Якутскай, 1966.

  Лит.:Башарин Г. П., А. И. Софронов. Жизнь и творчество. [1886-1935], Якутск, 1969.

Софронов Василий Яковлевич

Софро'новВасилий Яковлевич [18(30).1.1884, Петербург, - 10.10.1960, Ленинград], русский советский актёр, народный артист СССР (1956). Артистическую деятельность начал, будучи студентом университета. В 1907-10 учился при театре Литературно-художественного общества, затем вступил в его труппу. В 1918 участвовал в создании Петроградского Большого драматического театра (ныне Ленинградский Большой драматический театр им. М. Горького). Сыграл роли: Доминго, Шпигельберг («Дон Карлос», «Разбойники» Шиллера), Шут, Ричард III («Король Лир», «Ричард III» Шекспира), Барон, Сальери («Скупой рыцарь», «Моцарт и Сальери» Пушкина). Внёс значительный вклад в сценическое воплощение советской драматургии: создал образ В. И. Ленина («Человек с ружьем» Погодина), играл Кошкина («Любовь Яровая» Тренева), Забелина («Кремлёвские куранты» Погодина), Годуна и Берсенева («Разлом» Лавренева). В пьесах Горького исполнял роли Рябинина («Достигаев и другие»), Суслова («Дачники») и др. Государственная премия СССР (1951). Награжден 2 орденами, а также медалями.

В. Я. Софронов.

Софтбол

Со'фтбол(англ. softball, буквально - мягкий мяч), спортивная игра с мячом, представляющая собой разновидность ;в отличие от него, проводится на небольшой площадке. Появился в США в начале 20 в. как одна из форм зимней тренировки бейсболистов. Первые официальные правила опубликованы в 1906. Основанная в 1952 Международная федерация С. (ISF) объединяла в 1974 свыше 50 национальных федераций (28 млн. спортсменов). С 60-х гг. раз в два года проводятся чемпионаты мира (для мужчин и женщин). Наибольшее развитие С. получил в США, Японии, Канаде, Австралии, Мексике, Кубе и ряде др. стран Латинской Америки. В 1967 ISF признана Международным олимпийским комитетом. В СССР С. не культивируется.

Софья Алексеевна

Со'фья Алексе'евна[17(27).9.1657, Москва, - 3(14).7.1704, там же], правительница России в 1682-89, дочь царя от брака с М. И. Милославской. С. А. отличалась умом, энергией и честолюбием, была образованной женщиной. После смерти своего брата - царя Федора Алексеевича (27 апреля 1682), С. А. активно участвовала в борьбе придворных партий, т.к. была недовольна избранием на царский престол 10-летнего Петра I. Воспользовавшись ,партия Милославских захватила власть. «Первым» царём был провозглашен Иван V Алексеевич, а С. А. 29 мая - регентшей при обоих царях. С. А. фактически возглавила правительство, опираясь на В. В. Голицына, Ф. Л. и др. Осенью 1682 правительство С. А., находившееся в Троице-Сергиевом монастыре, с помощью дворянского войска подавило восстание в Москве. В годы правления С. А. были сделаны небольшие уступки посадам и ослаблен сыск беглых крестьян, что вызвало недовольство дворян. Во внешней политике наиболее значительными акциями правительства С. А. были заключение с Польшей, с Китаем, вступление в войну с Турцией и Крымским ханством (см. ) .В 1689 произошёл разрыв между С. А. и боярско-дворянской группировкой, поддерживавшей Петра I. Партия Петра I одержала победу. С. А. была заточена в Новодевичий монастырь. Во время сторонники С. А. намеревались «выкликнуть» её на царство. После подавления восстания С. А. была пострижена под именем Сусанны в монахини Новодевичьего монастыря, где и умерла.

  В. И. Буганов.

Софья Палеолог

Со'фья Палеоло'г,Зоя Палеолог (умерла 7.4.1503), племянница последнего византийского императора Константина XI Палеолога, с ноября 1472 жена великого князя .Имя Софьи она получила в России. Брак с С. П. Иван III использовал для укрепления престижа Руси в международных отношениях и авторитета великокняжеской власти внутри страны.

Сох

Сох,река в Киргизской ССР и Узбекской ССР. Длина 124 км,площадь бассейна 3510 км ².Берёт начало на северных склонах Алайского хребта, заканчивается в Ферганской долине обширным конусом выноса, прорезанным оросительными каналами. Питание ледниково-снеговое. Половодье с июня по сентябрь. Средний расход воды в 44 кмот устья (у кишлака Сарыконда) 42,1 м ³/сек.Воды используются для орошения и не доходят до р. Сырдарьи.

Соха (единица податного обложения)

Соха',единица податного обложения на Руси в 13-17 вв., с которой собирался государственный поземельный налог - .До середины 16 в. С. измерялась количеством рабочей силы. В 13-15 вв. 2-3 крестьянина-работника составляли С. При сборе податей к С. приравнивались и другие хозяйственные единицы: чан кожевничий, невод, лавка, кузница и т.п. В конце 15 в. новгородская С. равнялась 3 .Московская С. равнялась 10 новгородским и являлась податным округом разных размеров в различных районах государства. Т. о., в московской С. в каждом конкретном случае входило разное количество деревень, дворов, людей и пашен. С середины 16 в. в Московском государстве все С. были заменены т. н. большой С., состоящей из того или иного количества четвертей земли (см. ) .В конце 16-17 вв. на посадах повсеместно существовала большая С., состоящая из определённого числа дворов. В 1679 посошное было заменено .

Соха (земледельч. орудие)

Соха',земледельческое пахотное орудие. Известна с конца 4 - начала 3 тыс. до н. э. в Древнем Египте, Месопотамии, Средиземноморье (о. Крит). В средние века была распространена у многих народов Евразии. Первоначально была целиком деревянной, позже стала снабжаться железными сошниками. В русских письменных памятниках упоминается только с 14 в., однако применялась значительно раньше, о чём свидетельствуют находки железных сошников 7-8 вв. Наиболее распространены были двузубые С. От пахотных орудий плужного типа С. отличается тем, что отвал её не пригоден к опрокидыванию пласта и она не имеет подошвы. Производительность и качество работы С. очень низкие. С. сохраняется у некоторых народов Южной и Передней Азии.

  В СССР с конца 20-х гг. С. не применяется.

Сохаг

Соха'г,город в Египте, административный центр губернаторства Сохаг. 74,9 тыс. жителей (1966). Ж.-д. станция. Порт на левом берегу Нила. Торговый центр с.-х. района. Хлопкоочистительная, пищевая, кожевенно-обувная промышленность.

Сохатый

Соха'тый,парнокопытное животное семейства оленей; то же, что .

Сохё

Сохё,Сохио (сокращенное от Нихон родокумиай сохёгикай - Генеральный совет профсоюзов Японии), крупнейший в Японии профсоюзный центр. Образован в июле 1950 из профсоюзов, отколовшихся от прогрессивного профсоюзного центра Самбэцу кайги [Всеяпонского (или Национального) конгресса производственных профсоюзов, основан в 1946], и ряда профсоюзов соглашательского толка. В ходе дальнейшего развития С. постепенно сам стал на путь боевой защиты интересов рабочего класса. В 1951 принял «четыре принципа мира», обязывающие профсоюзы бороться за заключение Японией мирных договоров со странами, против которых она воевала во 2-й мировой войне 1939-45, против милитаризации, размещения иностранных военных баз, за нейтралитет. В 1953 от С. отмежевались профсоюзы, возглавляемые правореформистским руководством, что положило начало образованию нового профсоюзного объединения - Дзэнро (в 1964 преобразовано в Домэй - Вееяпонскую конфедерацию труда), стоящего на позициях сотрудничества с капиталом. С 1955 С. выступает инициатором ежегодных «весенних наступлений», организуемых совместно с другими профсоюзами в защиту условий жизни трудящихся и нередко выдвигающих политические требования. Для этих выступлений трудящихся характерны согласованность и применение забастовочных методов борьбы. С. совместно с Коммунистической партией Японии (КПЯ) и Социалистической партией Японии (СПЯ) являлся главной силой борьбы против японо-американского «договора безопасности» в 1959-60, а также активно участвовал в других массовых политических кампаниях, проводившихся в Японии со 2-й пол. 50-х гг. Выступая за единство профдвижения в Японии, отвергает предложения Домэй об объединении на соглашательских принципах. Руководство С. тесно связано с СПЯ, внутри его профсоюзов имеется значительное влияние КПЯ.

  В международном профдвижении С. придерживается принципа организационного нейтралитета, но разрешает входящим в него профсоюзам участвовать в любом 113 международных профсоюзных центров. С. установил постоянные контакты с ВФП. Имеет регулярные контакты с сов. профсоюзами, с 1966 проводятся встречи постоянной японо-советской профсоюзной комиссии с участием руководителей С. и ВЦСПС. На конец 1974 объединял 4,4 млн. чел. (около 36% всех членов японских профсоюзов).

  Лит.:Топеха П. П., Рабочее движение в Японии (1945-1971), М., 1973.

  Л. Иванов.

Сохио

Сохио,см. .

Сохондо

Сохондо',самая высокая вершина Хэнтэй на территории СССР, в Забайкалье, в верховьях р. Ингоды (бассейн Амура). Высота 2499 м.Широкий купол сложен дацитами. На склонах до высоты 2000 мкедрово-лиственничная тайга, выше - заросли кедрового стланика, ерника и даурского можжевельника, на вершине - россыпи, высокогорная тундра.

Сохоцкий Юлиан Васильевич

Сохо'цкийЮлиан Васильевич [24.1(5.2).1842, Варшава, - 14.12.1927, Ленинград], русский математик. В 1866 окончил Петербургский университет. С 1873 профессор там же. Основные труды по теории функций комплексного переменного. В магистерской диссертации «Теория интегральных вычетов с некоторыми приложениями» (1868) сформулировал и доказал теорему о поведении аналитических функции в окрестности существенно особой точки (см. ) .В докторской диссертации «Об определённых интегралах и функциях, употребляемых при разложениях в ряды» (1873) изучил граничные значения интегралов типа интеграла Коши при весьма общих условиях. Эти результаты имеют важное значение для приложений к механике. Автор оригинального курса «Высшая алгебра» (ч. 1 - «Решение численных уравнений», 1882; ч. 2 - «Начала теории чисел», 1888).

  Лит.:Маркушевич А. И., Вклад Ю. В. Сохоцкого в общую теорию аналитических функций, в кн.: Историко-математические исследования, в. 3, М. - Л., 1950.

Сохоцкого-Вейерштрасса теорема

Сохо'цкого - Вейерштра'сса теоре'ма,теорема теории ;всякая однозначная аналитическая функция в каждой окрестности принимает значения, сколь угодно близкие к любому наперёд заданному комплексному числу. Эта теорема была установлена Ю. В. в 1868 и одновременно с ним итальянским математиком Ф. Казорати. На 8 лет позже опубликовал теорему К. .Впервые же она встречается в «Теории эллиптических функций» (1859) францepcrb[ математиков Ш. Брио и Ж. К. Буке.

Сохранения законы

Сохране'ния зако'ны,физические закономерности, согласно которым численные значения некоторых физических величин не изменяются со временем в любых процессах или в определённом классе процессов. Полное описание физической системы возможно лишь в рамках динамических законов, которые детально определяют эволюцию системы с течением времени. Однако во многих случаях динамический закон для данной системы неизвестен или слишком сложен. В такой ситуации С. з. позволяют сделать некоторые заключения о характере поведения системы. Важнейшими С. з., справедливыми для любых изолированных систем, являются законы сохранения энергии, количества движения (импульса), момента количества движения и электрического заряда. Кроме всеобщих, существуют С. з., справедливые лишь для ограниченных классов систем и явлений.

  Идея сохранения появилась сначала как чисто философская догадка о наличии неизменного, стабильного в вечно меняющемся мире. Ещё античные философы-материалисты пришли к понятию материи - неуничтожимой и несотворимой основы всего существующего ( , , , , ) .С другой стороны, наблюдение постоянных изменений в природе приводило к представлению о вечном движении материи как важнейшем её свойстве ( , , , Эфесский, ,Демокрит). С появлением математической формулировки механики на этой основе появились законы сохранения массы (М. В. ,А. ) и механической энергии (Г. ) .Затем Ю. Р. ,Дж. и Г. был экспериментально открыт закон сохранения энергии в немеханических явлениях. Т. о., к середине 19 в. оформились законы сохранения массы и энергии, которые трактовались как сохранение материи и движения.

  Однако в начале 20 в. оба эти С. з. подверглись коренному пересмотру в связи с появлением специальной теории относительности (см. ) ,которая заменила классическую, ньютоновскую, механику при описании движений с большими (сравнимыми со скоростью света) скоростями. Оказалось, что ,определяемая по инерционным свойствам тела, зависит от его скорости и, следовательно, характеризует не только количество материи, но и её движение. С другой стороны, и понятие энергии подверглось изменению: полная энергия (Е) оказалась пропорциональной массе ( m) ,согласно известному соотношению Эйнштейна Е = mс ²( с -скорость света). Т. о., закон сохранения энергии в специальной теории относительности естественным образом объединил законы сохранения массы и энергии, существовавшие в классической механике; по отдельности эти законы не выполняются, т. е. невозможно охарактеризовать количество материи, не принимая во внимание её движения.

  Эволюция закона сохранения энергии показывает, что С. з., будучи почерпнуты из опыта, нуждаются время от времени в экспериментальной проверке и уточнении. Нельзя быть уверенным, что данный закон или его конкретная формулировка останутся справедливыми всегда, несмотря на расширение пределов человеческого опыта. Закон сохранения энергии интересен ещё и тем, что в нём теснейшим образом переплелись физика и философия. Этот закон, всё более уточняясь, постепенно превратился из неопределённого и абстрактного философского высказывания в точную количественную формулу. Другие С. з. возникали сразу в количественной формулировке. Таковы законы сохранения импульса, момента количества движения, электрического заряда, многочисленные законы сохранения в теории .В современной физике С. з. - необходимая составная часть рабочего аппарата.

  Большую роль С. з. играют в квантовой теории, в частности в теории элементарных частиц. Например, С. з. определяют ,согласно которым некоторые реакции с элементарными частицами (именно те, которые привели бы к нарушению С. з.) не могут осуществляться в природе. Кроме С. з., имеющихся и в физике макроскопических тел (сохранение энергии, импульса, момента, электрического заряда), в теории элементарных частиц возникло много специфических С. з., позволяющих объяснить экспериментально наблюдаемые правила отбора. Таковы законы сохранения и ,являющиеся точными, т. е. выполняющимися во всех видах взаимодействий, во всех процессах. Кроме точных, в теории элементарных частиц существуют и приближённые С. з., выполняющиеся в одних процессах и нарушающиеся в других. Такие С. з. имеют смысл, если можно точно указать класс процессов и явлений, в которых они выполняются. Примером приближённых С. з. являются законы сохранения (или ) ,изотопического спина (см. ) , .Все эти законы строго выполняются в процессах, протекающих за счёт (с характерным временем 10 ^-23-10 ^-24 сек) ,но нарушаются в процессах (характерное время которых примерно 10 ^-10 сек) . нарушают закон сохранения изотопического спина. Т. о., исследования элементарных частиц вновь напомнили о необходимости проверять существующие С. з. в каждой области явлений.

  С. з. тесно связаны со свойствами симметрии физических систем. При этом симметрия понимается как инвариантность физических законов относительно некоторых преобразований входящих в них величин (см. в физике). Наличие симметрии приводит к тому, что для данной системы существует сохраняющаяся физическая величина (см. ) .Т. о., если известны свойства симметрии системы, можно найти для неё законы сохранения, и наоборот.

  Как уже было сказано, С. з. механических величин (энергии, импульса, момента) обладают всеобщностью. Это связано с тем, что соответствующие симметрии можно рассматривать как симметрии пространства-времени (мира), в котором движутся материальные тела. Так, сохранение энергии связано с однородностью времени, т. е. с инвариантностью физических законов относительно изменения начала отсчёта времени (сдвигов во времени).
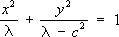