 |
|
Популярные авторы:: Борхес Хорхе Луис :: Горький Максим :: Азимов Айзек :: Раззаков Федор :: Грин Александр :: Толстой Лев Николаевич :: Чехов Антон Павлович :: Шукшин Василий Макарович :: Сименон Жорж :: Картленд Барбара Популярные книги:: Рагнарёк :: Скандальная леди :: The Boarding House :: Дочь Льва :: Валгалла (Калибан - 3) :: Елка для взрослых :: Дюна (Книги 1-3) :: Справочник по реестру Windows XP :: Трое суток из жизни оперуполномоченного :: У любви свои законы |
Большая Советская Энциклопедия (СО)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (СО) - Чтение (стр. 58)
Диапазон: до
1- до (ре - фа)
3. Необходимое качество С. - хорошо развитый т. н. головной регистр. С. обладают обычно женщины и дети. В хоре особенно красиво звучат голоса мальчиков (т. н. дискантистов). В 16-18 вв. было широко распространено пение
(называемых также сопранистами). Существует 3 основных разновидности женских С.: драматическое, лирическое и колоратурное. Бывает также лирико-драматическое и лирико-колоратурное С. Драматическое С. отличается силой звучания на всём диапазоне, плотным нижним регистром; лирическому С. свойственны мягкость тембра, гибкость и большая выразительность в кантилене; для колоратурного С. характерны подвижность в исполнении фиоритур, пассажей и т.п., прозрачность тембра, лёгкость и свобода звучания в верхнем регистре. 2) Самая высокая партия в хоре. 3) Высокие по регистру разновидности некоторых музыкальных инструментов.
Соприкасающаяся окружность Соприкаса'ющаяся окру'жностьв точке Мкривой l,окружность, имеющая с / в точке Мкасание порядка n³ 2 (см. ). Если кривой lв точке Мравна нулю, то С. о. вырождается в прямую. Т. к. порядок касания / и С. о. в точке Мне ниже двух, то С. о. воспроизводит ход кривой вблизи точки касания с точностью до малых 3-го порядка по сравнению с размерами участка кривой. На рисунке изображено обычное (порядок касания кривой и С. о. равен двум) взаимное расположение кривой и её С. о.: кривая пронизывает С. о. в точке соприкосновения. Радиус С. о. называют радиусом кривизны кривой / в точке М,а центр С. о. - центром кривизны. Если кривая lплоская и задана уравнением у = f( x) ,то радиус С. о. определяется формулой:
Если кривая l -пространственная и задана уравнениями х = х( u) , у = у( u) , z = z( u) ,то радиус С. о. определяется формулой:
(здесь штрихи означают дифференцирование по параметру u) . Иногда С. о. называют соприкасающимся кругом. См. также .
Лит.:Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956. 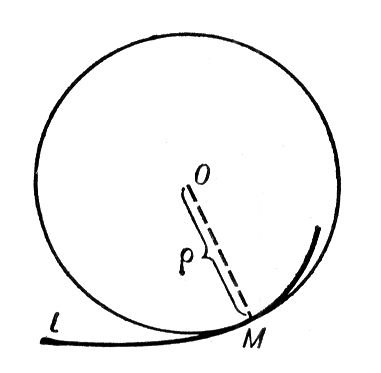
Рис. к. ст. Соприкасающаяся окружность. Соприкасающаяся плоскость Соприкаса'ющаяся пло'скостьв точке М кривой l,плоскость, имеющая с lв точке Мкасание порядка n³ 2 (см. ) .С. п. может быть также определена как предел переменной плоскости, проходящей через три точки кривой /, когда эти точки стремятся к точке М.С механической точки зрения С. п. может быть охарактеризована как плоскость ускорений: при произвольном движении материальной точки по кривой lвектор ускорения лежит в С. п. Обычно кривая, кроме исключит, случаев, пронизывает свою С. п. в точке соприкосновения (см. рис.). Если кривая lзадана уравнениями х = х( u) , у= у( u) , z = z( u) ,то уравнение С. п. имеет вид:
где X, Y, Z- текущие координаты, а х, у, z, х', у', z', х’’, у’’, z’’вычисляются в точке соприкосновения; если все три коэффициента при X, У, Zв уравнении С. п. исчезают, то С. п. делается неопределённой (может совпадать с любой плоскостью, проходящей через касательную). См. также .
Лит.:Рашевский П. К., Курс дифференциальной геометрии. 4 изд., М., 1956. 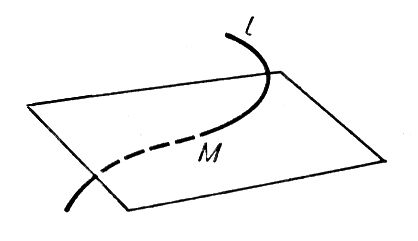
Рис. к ст. Соприкасающаяся плоскость. Соприкасающаяся сфера Соприкаса'ющаяся сфе'ра вточке М кривой l,сфера, имеющая с / в точке Мкасание порядка n³ 3 (см. ) .С. с. может быть также определена как предел переменной сферы, проходящей через четыре точки кривой /, когда эти точки стремятся к точке М.Если радиус кривой / в точке Мравен r, а s - кручение, то формула для вычисления радиуса С. с. имеет вид:
( ds -дифференциал дуги кривой /). Лит.:Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956. Соприкасающийся круг Соприкаса'ющийся кругв дифференциальной геометрии, см. . Соприкосновение Соприкоснове'ниекривой qс кривой / в данной точке М,геометрическое понятие, означающее, что qимеет с lв точке Мкасание максимального порядка по сравнению с любой кривой из некоторого заранее данного семейства кривых { q} ,включающего q.Порядок касания кривых qи / считается равным п,если отрезок QLесть величина n+ 1 порядка малости по отношению к отрезку МК(см. рис., где отрезок QLперпендикулярен к общей касательной кривых qи / в точке М). Таким образом, среди всех кривых семейства { q} С. с кривой / имеет та кривая, которая наиболее тесно прилегает к l(для неё отрезок QLимеет максимальный порядок малости). Кривая семейства { q} ,которая имеет С. с кривой lв данной её точке М,называется соприкасающейся кривой данного семейства в указанной точке кривой /. Например, в точке Мкривой / является окружность, которая в этой точке имеет с / максимальный порядок касания по сравнению с любой другой окружностью. Аналогично вышеизложенному определяется понятие соприкосновения поверхности q,принадлежащей данному семейству поверхностей { q} ,с какой-нибудь кривой / (или с поверхностью) в некоторой её точке М(в этих случаях порядок касания определяется также аналогично предыдущему; следует только вместо касательной прямой МК,изображенной на рисунке, рассматривать касательную плоскость поверхности qв точке М). См. , .
Лит.:Ла Валле-Пуссен Ш. Ж., Курс анализа бесконечно малых, пер. с франц., т. 2, Л. - М., 1933: Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., ч. 1, М., 1971. 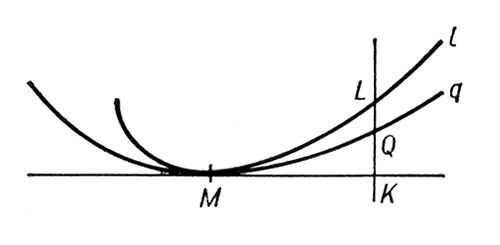
Рис. к ст. Соприкосновение. Сопротивление активное Сопротивле'ние акти'вноеэлектрическое, величина, характеризующая сопротивление цепи (её участка) ,обусловленное необратимым превращением электрической энергии в др. формы энергии (преимущественно в тепловую); выражается отношением ,поглощаемой на участке цепи, к квадрату действующего значения тока на этом участке; измеряется в .На участках цепи, содержащих проводники большого поперечного сечения, С. а. больше при постоянном токе (из-за поверхностного эффекта, см. ,и потерь в магнитном поле на и ) . Сопротивление акустическое Сопротивле'ние акусти'ческое,характеристика, вводимая при рассмотрении колебаний акустических систем, равная отношению звукового давления к объёмной колебательной скорости. Активное и реактивное С. а. образуют комплексный . Сопротивление ёмкостное Сопротивле'ние ёмкостное,величина, характеризующая сопротивление, оказываемое переменному току цепи (её участка); измеряется в .В случае синусоидального тока С. ё. - x cвыражается в виде отношения 1/w С, где w - угловая частота тока, С- ёмкость цепи. С. ё. равно отношению амплитуды напряжения на зажимах цепи, имеющей ёмкостный характер (обладающей малыми и ,такую цепь можно считать эквивалентной ) ,к амплитуде тока в ней. Если w ¹ 0, изменение напряжения на конденсаторе вызывает изменение заряда на его обкладках; в силу этого в цепи конденсатора непрерывно течёт зарядный (разрядный) ток. В процессе перезарядки конденсатора электрическая энергия периодически передаётся от источника тока электрическому полю конденсатора и затем обратно, причём средняя за период мощность равна нулю, поэтому С. ё. называют реактивным. Сопротивление индуктивное Сопротивле'ние индукти'вное,величина, характеризующая сопротивление, оказываемое переменному току цепи (её участка); измеряется в .В случае синусоидального тока С. и. x Lвыражается в виде произведения w L,где w - угловая частота тока, L -индуктивность цепи. С. и. равно отношению амплитуды напряжения на зажимах цепи, имеющей индуктивный характер (обладающей малым и достаточно большой индуктивностью: такую цепь можно считать эквивалентной ) ,к амплитуде тока в ней. При постоянном токе в катушке (w =0) С. и. равно нулю. Когда через катушку протекает переменный ток, электрическая энергия передаётся от источника тока магнитному полю катушки и затем обратно, причём средняя за период мощность равна нулю, поэтому С. и. называется реактивным. Сопротивление магнитное Сопротивле'ние магни'тное,характеристика .См. . Сопротивление материалов Сопротивле'ние материа'лов,наука о прочности и деформируемости элементов (деталей) сооружений и машин. Основные объекты изучения С. м. - стержни и пластины, для которых устанавливаются соответствующие методы расчёта на прочность, жёсткость и устойчивость при действии статических и динамических нагрузок. С. м. базируется на законах и выводах теоретической ,но, помимо этого, учитывает способность материалов деформироваться под действием внешних сил. Физико-механические характеристики (предел текучести, предел прочности, модуль упругости и т.п.), необходимые для оценки прочности и деформативности материалов, определяются при помощи испытательных машин и специальных измерительных приборов - .При испытаниях обеспечиваются требуемые условия загружения и высокая точность измерения деформаций испытываемых образцов материалов. Наиболее характерно испытание на растяжение образцов, представляющих собой стержни круглого сечения или полосы с сечением в виде узкого прямоугольника. По результатам этих испытаний строится т. н. диаграмма .Располагая диаграммой испытания и пользуясь разработанными в С. м. методами расчёта, можно предсказать, как будет вести себя реальная конструкция, изготовленная из того же материала. Основное содержание и методы С. м.При деформации твёрдого тела под нагрузкой изменяется взаимное расположение его микрочастиц, вследствие чего в теле возникают внутренние напряжения. В С. м. определяются наибольшие напряжения в элементах сооружений или деталях машин. Они сравниваются с нормативными величинами, т. е. с напряжениями, которые можно допустить, не опасаясь повреждения или разрушения этих элементов (деталей). Проверке подлежат также деформации тела и перемещения его отдельных точек. Помимо необходимой прочности, конструкция должна быть также устойчивой, т. е. обладать способностью при малых случайных кратковременных воздействиях, нарушающих её равновесие, лишь незначительно отклоняться от исходного состояния. Выполнение этого требования зависит от внешних сил, геометрии элемента (детали) и от физических констант материала. Для расчёта элементов конструкций в С. м. разрабатываются приближённые инженерные методы, использующие кинематические и статические гипотезы, которые в большинстве случаев оказываются достаточно близкими к действительности. При выводе расчётных формул для определения напряжений и перемещений производится схематизация рассчитываемого элемента сооружения, его опорных закреплений и действующей нагрузки, иначе говоря, создаётся (модель) объекта. При построении общей теории расчёта в С. м. рассматриваются т. н. идеализированные тела со свойствами, лишь приближённо отражающими поведение реальных объектов. Тела считаются однородными (со свойствами, одинаковыми во всех точках), сплошными (без пустот), обладающими упругостью (способностью восстанавливать свои размеры после снятия нагрузки), изотропными (с одинаковыми упругими свойствами по всем направлениям). На основе изучения простейших деформаций - растяжения-сжатия, , в С. м. выводятся формулы, позволяющие для каждого из этих видов деформаций определять напряжения, перемещения и деформации в отдельных точках тела. При наличии одновременно двух или нескольких простейших деформаций, протекающих в упругой стадии (для которой справедлива линейная зависимость между напряжением и деформациями), напряжения и деформации, найденные отдельно для каждого вида, суммируются. Многие материалы (например, бетон) обладают свойством ползучести (см. материалов), вследствие которой деформации могут возрастать со временем при неизменной нагрузке. В С. м. устанавливаются законы развития ползучести и время, в течение которого она заметно проявляется, а также рассматривается воздействие на стержень ударной нагрузки, при которой возникают динамические напряжения; последние определяются по приближённым формулам, выведенным на основе ряда допущений. При расчёте элементов сложной формы, для которых аналитические формулы вывести не удаётся, применяют экспериментальные методы (например, оптический, лаковых покрытий, муаровых полос и др.), позволяющие получать наглядную картину распределения деформаций по поверхности исследуемого элемента (детали) и вычислять напряжения в его отдельных точках. Наибольшую трудность представляет определение т. н. остаточных напряжений, которые могут возникать в элементах конструкций, не несущих нагрузки (например, при сварке или в процессе прокатки стальных профилей). Одна из важных задач С. м. состоит в создании т. н. теорий прочности, на основе которых можно проверить прочность элементов в сложном напряжённом состоянии, исходя из прочностных характеристик, полученных опытным путём для простого растяжения-сжатия. Существует ряд теорий прочности; в каждом отдельном случае пользуются той из них, которая в наибольшей степени отвечает характеру нагружения и разрушения материала. Историческая справка.История С. м., как и многих др. наук, неразрывно связана с историей развития .Зарождение науки о С. м. относится к 17 в.; её основоположником считается ,который впервые обосновал необходимость применения аналитических методов расчёта взамен эмпирических правил. Важным шагом в развитии С. м. явились экспериментальные исследования Р. (60-70-е гг. 17 в.), установившего линейную зависимость между силой, приложенной к растянутому стержню, и его удлинением (закон Гука). В 18 в. большой вклад в развитие аналитических методов в С. м. был сделан Д. ,Л. и Ш. ,сформулировавшими важнейшие гипотезы и создавшими основы теории расчёта стержня на изгиб и кручение. Исследования Эйлера в области продольного изгиба послужили основой для создания теории устойчивости стержней и стержневых систем. Т. ввёл (1807) понятие о модуле упругости при растяжении и предложил метод его определения. Важный этап в развитии С. м. связан с опубликованием (в 1826) Л. первого курса С. м., содержавшего систематизированное изложение теории расчёта элементов конструкций и сооружений. Принципиальное значение имели труды А. (2-я половина 19 в.). Им впервые были выведены точные формулы для расчёта на изгиб и сформулирован принцип, согласно которому распределение напряжений в сечениях, отстоящих на некотором расстоянии от места приложения нагрузки, не связано со способом её приложения, а зависит только от равнодействующей этой нагрузки. Большие заслуги в развитии С. м. принадлежат русскому учёным М. В. ,исследования которого в области С. м., строительной механики, математики и теории упругости приобрели мировую известность, и Д. И. ,впервые установившему (1855) наличие касательных напряжений в продольных сечениях бруса и получившему формулу для их определения (эта формула применяется и в современной практике инженерных расчётов). Всеобщее признание получили исследования Ф. С. ,разработавшего (1893) теорию продольного изгиба в упругой стадии и за её пределами (рекомендации Ясинского послужили основой для разработки современных нормативных документов в СССР и за рубежом). В начале 20 в. расширение масштабов применения железобетонных и стальных конструкций, появление сложных машин и механизмов обусловили быстрое развитие науки о С. м. Были опубликованы классические учебники С. П. по С. м. и строительной механике, труды А. Н. по продольному изгибу, устойчивости сжатых стержней и др. Дальнейшему совершенствованию методов С. м. способствовало создание в СССР ряда научно-исследовательских учреждений для проведения исследований в области расчёта конструкций. Появились новые разделы С. м. Большое влияние на развитие С. м. оказали труды Н. М. в области пластических деформаций, А. А. по теории пластичности, Ю. Н. и А. Р. Ржаницына по теории ползучести. Значительным вкладом в науку о С. м. явилась созданная В. З. теория расчёта тонкостенных стержней и оболочек. Важные фундаментальные исследования выполнены советскими учёными Н. И. Безуховым, В. В. Болотиным, А. Ф. ,В. И. Феодосьевым и др. Современные тенденции развития науки о С. м.Одна из важнейших задач С. м. - установление причин и характера разрушения материалов, требующее всестороннего теоретического и экспериментального изучения процессов, происходящих в микрообъёмах тела, в частности характера возникновения и развития трещин. Установлено существование таких (предельных) напряжений, превышение которых влечёт за собой прогрессирующий рост уже появившихся трещин, приводящий в конечном счёте к разрушению тела. Если напряжения меньше указанного предела, то тело, имеющее трещины, находится в состоянии трещиноустойчивости. В некоторых случаях под действием нагрузки разрушения в микроэлементах распространяются на весь объём тела (особенно при высоких температурах). Исследование этих вопросов требует создания нового важного раздела механики деформируемого тела - механики разрушения. Ещё недостаточно изучен ряд вопросов т. н. усталостной прочности материалов, в частности прочность элементов (деталей) машин при их длительном циклическом нагружении. В связи с появлением новых (например, пластмасс, лёгких сплавов) возникла необходимость создания теорий прочности, отражающих специфические свойства этих материалов. Современные технологические процессы (например, с применением высоких давлений) позволяют получать материалы с весьма высокой прочностью, поведение которых под нагрузкой недостаточно изучено и требует целенаправленных исследований. Лит.:Тимошенко С. П., История науки о сопротивлении материалов с краткими сведениями из истории теории упругости и теории сооружений, М., 1957; Работнов Ю. Н., Сопротивление материалов, М.. 1962; Феодосьев В. И., Сопротивление материалов, М., 1974; Сопротивление материалов, М., 1975. Под редакцией А. Ф. Смирнова. Сопротивление омическое Сопротивле'ние оми'ческое,прежнее название предельного значения при w ® 0, где w - частота переменного тока. Термином «С. о.» подчёркивается выполнение ,т. е. наличие линейной зависимости между током и напряжением. Сопротивление реактивное
Сопротивле'ние реакти'вноеэлектрическое, величина, характеризующая сопротивление, оказываемое переменному току
и
цепи (её участка); измеряется в
.В случае синусоидального тока при последовательном соединении индуктивного и ёмкостного элементов цепи С. р. выражается в виде разности
и
:
Сопротивление электрическое Сопротивле'ние электри'ческое,см. . Сопротивление электрической цепи
Сопротивле'ние электри'ческой цепи,полное электрическое сопротивление, величина, характеризующая сопротивление цепи электрическому току; измеряется в
.В случае синусоидального переменного тока С. э. ц. выражается отношением амплитуды напряжения на зажимах цепи к амплитуде тока в ней и равно
Сопротивления электрического измерители Сопротивле'ния электри'ческого измери'тели,электро- и радиоизмерительные приборы для измерения активного сопротивления электрической цепи (см. , , , ) . Сопряжение контуров Сопряже'ние ко'нтуров,обеспечение согласованного изменения резонансных частот какого-либо устройства (например, ) ,перестраиваемых посредством одной ручки настройки. При настройке супергетеродинного приёмника на определённый сигнал резонансная частота контуров входной цепи и усилителя радиочастоты f oустанавливается равной частоте принимаемого радиосигнала f c,а резонансная частота контура гетеродина f r- такой, чтобы промежуточная частота (равная обычно разности частот f cи f r) совпадала с резонансной частотой контуров усилителя промежуточной частоты. Для С. к. преимущественно используют метод, при котором во всех перестраиваемых контурах применяют одинаковые конденсаторы переменной ёмкости, но в контур гетеродина, частота которого должна отличаться от f o,дополнительно включают постоянные конденсаторы, называемые конденсаторами сопряжения (см. рис.). Получаемые в этом случае зависимости частот f oи f rот угла поворота ручки настройки несколько отличаются от требуемых т. е. С. к. является лишь приближённым (однако с достаточной степенью точности). В современных (середина 70-х гг.) приёмниках при С. к. в качестве конденсаторов переменной ёмкости используют конденсаторы с механическим изменением ёмкости либо варакторы ( ) .
Лит.:Радиоприемные устройства, под ред. В. И. Сифорова, М., 1974; Чистяков Н. И., Сидоров В. М., Радиоприемные устройства, М., 1974. В. М. Сидоров 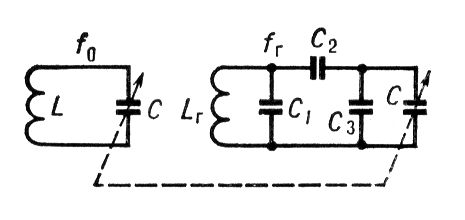
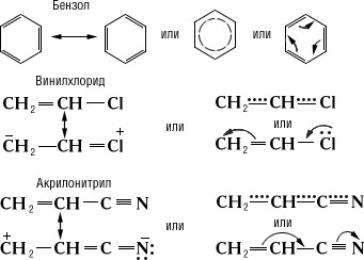
Принципиальная схема одного из контуров, содержащихся во входной цепи и в усилителе радиочастоты, и контура гетеродина: Lи L r- катушки индуктивности контуров; С- конденсаторы переменной ёмкости; C 1, С 2, С 3- конденсаторы сопряжения; f oи f r- резонансные частоты контуров; пунктир означает, что ёмкости конденсаторов изменяются при помощи одной ручки настройки. Сопряжение связей Сопряже'ние свя'зей,один из важнейших видов внутримолекулярного взаимного влияния атомов и связей в органических соединениях; обусловлено взаимодействием электронных систем атомов (прежде всего валентных электронов, см. ) .Главный признак сопряжения - распределение по всей сопряжённой системе электронной плотности, создаваемой р-и p-электронами. Такими системами являются: чередующиеся простая и кратные связи - двойные или тройные; см. , (p,p-сопряжение, как, например, в бутадиене, I; здесь и далее жирными штрихами, а также точками выделена сопряжённая система); кратная связь и атом со свободной электронной парой (р, p-сопряжение, например в винилхлориде, II); крестная связь и способная к сопряжению простая связь (s, p-сопряжение, например в хлормеркурацетальдегиде, III); две способные к сопряжению простые связи (s, s-сопряжение, например в этанолмеркурхлориде, IV). Такая классификация сопряжённых систем предложена в начале 50-х гг. 20 в. А. Н. .
Общая особенность всех сопряжённых систем - «растекание» электронной плотности
р-и p-электронов (см.
) по всей сопряжённой системе - определяет их физические и химические свойства. Так, простые связи приобретают некоторую «двоесвязность», выражающуюся, в частности, в уменьшении их длины. Например, в бутадиене длина центральной С - С-связи 1,46
Количество образующихся продуктов 1,2-и 1,4-присоединения зависит от природы сопряжённой системы, от реагента и условий реакции. Сопряжение снижает внутреннюю энергию молекул и, следовательно, делает их более устойчивыми: величина энергии сопряжения колеблется между несколькими единицами и десятками ккал/моль(например, для бутадиена 3,6 ккал/моль,для бензола 35 ккал/моль,1 ккал/моль=4,19 кдж/моль) . Истинное распределение электронной плотности в сопряжённых системах нельзя выразить простейшими структурными формулами. Их строение более точно передаётся наборами предельных структур (см. , ) ,формулами с пунктирными («полуторными») связями или с изогнутыми стрелками, указывающими направление сдвига электронов, например:
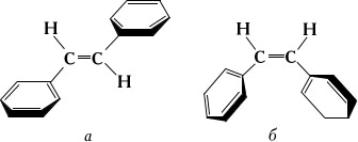
Для проявления С. с. необходимо, чтобы участвующие в нём электронные системы находились в одной плоскости. Если структура молекулы не допускает этого, то говорят о пространственных препятствиях сопряжению. Так, у стильбена (а), по данным УФ-спектров, обнаруживается более сильное сопряжение, чем у стильбена (б), у которого бензольные ядра не могут разместиться в одной плоскости с двойной связью:
Сопряжённые гиперболы Сопряжённые гипе'рболы,две ,которые в одной и той же системе прямоугольных координат при одних и тех же значениях аи bопределяются уравнениями:
и
С. г. имеют общие асимптоты и общий основной прямоугольник (см. рис.). 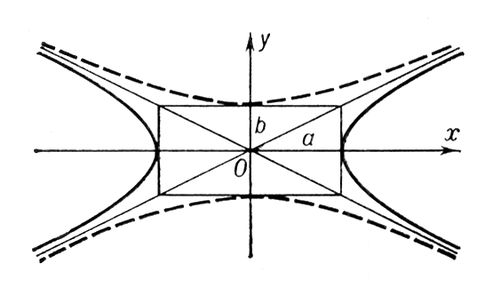
Рис. к ст. Сопряжённые гиперболы. Сопряжённые диаметры Сопряжённые диа'метрылинии второго порядка, два диаметра, каждый из которых делит пополам хорды этой кривой, параллельные другому. С. д. играют важную роль в общей теории линий второго порядка. При параллельном проектировании эллипса в окружность его С. д. проектируются в пару взаимно перпендикулярных диаметров окружности. Сопряжённые дифференциальные уравнения Сопряжённые дифференциа'льные уравне'ния,понятие теории дифференциальных уравнений. Уравнением, сопряжённым с дифференциальным уравнением
называется уравнение
Соотношение сопряженности взаимно. Для С. д. у. имеет место тождество 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88 |
|||||||
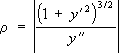 .
.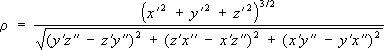
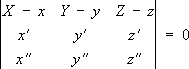 ,
,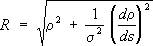
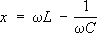 ,где w - угловая частота тока,
Lи
С- индуктивность и ёмкость цепи; С. р. равно отношению амплитуды напряжения на зажимах цепи, обладающей малым
,к амплитуде тока в ней. В цепи, обладающей только С. р., при протекании переменного тока происходит передача энергии источника тока электрическому или магнитному полю, создаваемому соответственно ёмкостным или индуктивным элементом цепи, и затем обратно, причём средняя за период мощность равна нулю. Наличие у цепи С. р. вызывает
между напряжением и током. В цепях несинусоидального тока С. р. различно для отдельных гармонических составляющих тока.
,где w - угловая частота тока,
Lи
С- индуктивность и ёмкость цепи; С. р. равно отношению амплитуды напряжения на зажимах цепи, обладающей малым
,к амплитуде тока в ней. В цепи, обладающей только С. р., при протекании переменного тока происходит передача энергии источника тока электрическому или магнитному полю, создаваемому соответственно ёмкостным или индуктивным элементом цепи, и затем обратно, причём средняя за период мощность равна нулю. Наличие у цепи С. р. вызывает
между напряжением и током. В цепях несинусоидального тока С. р. различно для отдельных гармонических составляющих тока.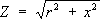 ,где
r -
, х -
.При несинусоидальном переменном токе С. э. ц. определяется отдельно для каждой
к-той гармонической составляющей:
,где
r -
, х -
.При несинусоидальном переменном токе С. э. ц. определяется отдельно для каждой
к-той гармонической составляющей:
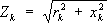 .
.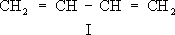
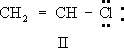
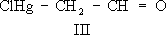
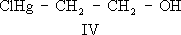
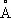 вместо обычной 1,54
вместо обычной 1,54
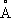 . С. с. проявляется также, например, в УФ- и ИК-спектрах, дипольных моментах. Наиболее характерная химическая особенность сопряжённых систем - способность вступать в реакции не только с участием одной кратной связи, но и всей сопряжённой системы как единого целого. Примером может служить, например, присоединение к бутадиену хлористого водорода:
. С. с. проявляется также, например, в УФ- и ИК-спектрах, дипольных моментах. Наиболее характерная химическая особенность сопряжённых систем - способность вступать в реакции не только с участием одной кратной связи, но и всей сопряжённой системы как единого целого. Примером может служить, например, присоединение к бутадиену хлористого водорода: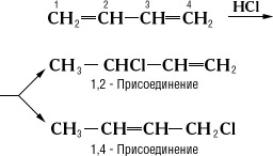
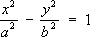
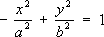
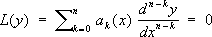 , (1)
, (1)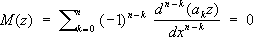 , (2)
, (2)