 |
|
Популярные авторы:: БСЭ :: Борхес Хорхе Луис :: Азимов Айзек :: Грин Александр :: Чехов Антон Павлович :: Раззаков Федор :: Толстой Лев Николаевич :: Горький Максим :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Справочник по реестру Windows XP :: Дюна (Книги 1-3) :: Полуночный маскарад :: 200 км танков. О российско-грузинской войне :: The Boarding House :: Агнесса. Том 1 :: Полет :: Ящик Пандоры :: Змея из ночного кошмара :: Омен. Последняя битва. |
Моделирование рассуждений. Опыт анализа мыслительных актовModernLib.Net / Научно-образовательная / Поспелов Дмитрий Александрович / Моделирование рассуждений. Опыт анализа мыслительных актов - Чтение (стр. 3)
7. На последующих страницах книги мы столкнемся с немалым количеством других особенностей человеческих рассуждений: размытостью и неточностью посылок, своеобразными «рассуждениями по дереву», рефлексивными рассуждениями и многими иными видами человеческих способов утверждать то или иное. А начнем мы с удивительного открытия – силлогистики Аристотеля. Глава вторая. СИЛЛОГИСТИКА И ГЕРМЕНЕВТИКА РАССУЖДЕНИЙ В то время как заурядный наблюдатель видит Лишь ряд разрозненных, отдельных сцен И бродит ощупью средь них всю жизнь, Способны вы сводить их воедино, Одною мерой мерите вы всё. Что сделал Аристотель? Развитие всех наук протекает в условиях возникновения множества новых идей, многие из которых оказываются ошибочными. Рождаются и умирают десятки, а то и сотни теорий, бывает, что новые данные опровергают ранее сложившиеся убеждения. Нередки случаи, когда на этих убеждениях покоилось стройное здание данной науки. Лишенное их, оно рассыпается, как карточный домик, а на его месте начинает возводиться новое здание. Так в драматических столкновениях, среди которых изредка вспыхивают гениальные открытия, кропотливым трудом десятков поколений исследователей создается и модернизируется здание той или иной науки. Но из всего всеобщего процесса есть одно парадоксальное исключение. Существует теория, построенная одним человеком и практически сразу, которую никто не пытался критиковать или опровергать. Ее лишь уточняли и модернизировали. И хотя со времени ее создания прошло уже значительно больше двух тысяч лет, она по-прежнему занимает почетное место в науке. В средние века автор этой теории пользовался такой популярностью, что его наверняка бы причислили к святым, если бы он не родился за четыреста лет до рождения основателя этой религии. Это исключение – силлогистика, созданная гениальным мыслителем древности Аристотелем. На протяжении многих столетий силлогистика была единственной моделью дедуктивных рассуждений. В этом смысле она сыграла исключительную роль в становлении всех наук вообще, ибо стала для них методологией научного мышления. Прежде, чем пояснить вновь появившиеся понятия, попробуем ответить на вопрос: какую задачу хотел решить Аристотель, создавая свою теорию? Он жил в те времена, когда научные споры были основным видом научной деятельности. «В споре рождается истина» – выражение, пришедшее к нам из эпохи этой седой древности. Только в дискуссиях и спорах можно было отстоять свою точку зрения и усвоить, что хочет сказать твой коллега. Со времен Сократа получили широкое распространение специальные виды спора – сократические беседы. В ходе такого спора доказательство выдвинутого положения защищалось с помощью ответов двух типов («согласен» или «не согласен») на любые высказывания оппонентов выдвинутого положения. Искусство вести подобные беседы высоко ценилось. И, по-видимому, одной из первопричин исследований Аристотеля было стремление найти такие формы рассуждений, которые при правильном их использовании не нарушали бы истинности исходного положения. Истинность тут понималась не как некоторый абсолют. Идея была в другом. Как строить рассуждения, чтобы они лишь поддерживали исходное положение (в его истинности надо было убедить оппонентов), а не опровергали его? Помня о весьма популярном Сократе, Аристотель не мог не знать, что часто для показа силы своей логики этот мыслитель выдвигал заведомо ложное положение, но с помощью специально построенных софистических рассуждений убеждал слушателей в истинности выдвинутого ложного положения. Конечно, софистические рассуждения содержали скрытую ошибку, нарушали какие-то фундаментальные законы логики человеческих рассуждений. Но вскрыть их было невозможно, пока эта логика сама была не описана и не формализована. Аристотель и его современники уже знали, что существует по крайней мере три типа рассуждений: от общего к частному, от частного к общему и от частного к частному. Идея первого типа рассуждений основывалась на том явном для людей положении, что если общее утверждение верно, то должно быть верными и частные утверждения, определяемые этим общим рассуждением. Именно такого типа рассуждения и называют дедуктивными. Два других типа рассуждений с точки зрения истинности вывода куда менее ясны. Рассуждения от частного к общему отражают наш путь постижения окружающего мира и нас самих в нем. Общие утверждения возникают на пути обобщения частных, отражающих совокупность наших единичных опытных фактов. Такие рассуждения называются индуктивными. Истинность общего результата таких рассуждений для людей становится очевидной, если частных утверждений, подтверждающих этот результат, довольно много, а опровергающих утверждений нет. Еще более сложная ситуация складывается при переходе от одних частных утверждений к другим частным, как-то связанным с исходными. Здесь человеческая интуиция в оценке истинности результата почти бессильна. Такие рассуждения, которые мы будем в этой книге называть правдоподобными, лежат где-то на границе между допустимыми и недопустимыми формами человеческих рассуждений Исходя из этих соображений (не по форме, конечно, а по существу) Аристотель выбрал для формализации именно дедуктивные рассуждения. Хотя и в область индуктивных рассуждений Аристотель внес определенный вклад, но он, конечно, не может сравниться с тем, что удалось сделать этому философу в области дедуктивных рассуждений. Еще раз зафиксируем два положения, связанные с работой Аристотеля в интересующей нас области: 1) исходные посылки рассуждения являются истинными; 2) правильно применяемые приемы перехода от посылок к другим вытекающим из них утверждениям и из посылок и ранее полученных утверждений к новым вытекающим из них утверждениям должны сохранять истинность всех получаемых утверждений, т.е. истинные посылки порождают только истинные следствия. Именно это свойство силлогистики Аристотеля, как со временем стала называться созданная им система, позволила средневековому философу и богослову Фоме Аквинату использовать теорию Аристотеля для обоснования всей христианской теологии. Сделал это он с помощью следующего приема. Поскольку по учению христианской церкви определенная часть сочинений, составляющая книги Ветхого и Нового Заветов, является боговдохновенной, то все утверждения, содержащиеся в них, являются абсолютно истинными. Их истинность не меняется. А значит, они образуют посылочный базис логической системы, в которой невозможны противоречия. Из них можно с помощью силлогистики Аристотеля порождать новые утверждения, которые также будут истинны. И если многие из этих утверждений человеческий рассудок отказывается принимать, сомневается в их допустимости, то, следовательно, рассудок земного человека слаб и не дорос еще до истинных откровений. Ведь еще на заре распространения христианского учения один из его апологетов Тер…[3] …их больше двух. Для получения заключения в сорите нужен многошаговый процесс, а для проверки истинности заключения не два шага (как на рис. 11–13), а столько шагов, сколько посылок имеется в сорите. На каждом шаге при поиске заключения в сорите выбирается пара посылок, которые могут образовать одну из четырех силлогистических фигур (верхних частей схем на рис. 10). Если такая пара найдена, то она порождает по законам силлогистики заключение. Если к этому моменту еще не все множество исходных посылок использовано, то использованные на данном шаге посылки вычеркиваются из списка посылок, а вместо них добавляется найденное промежуточное заключение. Новое множество посылок рассматривается как исходное для следующего шага вывода. Рассмотрим два примера получения заключения в соритах. Первый сорит содержит три посылки: Малые дети неразумны. Тот, кто может укрощать крокодилов, заслуживает уважения. Неразумные люди не заслуживают уважения. Чтобы начать процесс вывода, необходимо сначала привести все посылки к нормальной форме, принятой в схемах базовых высказываний в силлогистике. После этого преобразования посылки сорита примут вид: Всякие малые дети есть неразумные люди. Всякий, укрощающий крокодилов, есть заслуживающий уважения. Всякие неразумные люди не есть заслуживающие уважения. Возьмем первую и третью посылки. Если обозначить через Р класс сущностей с именем «малые дети», через М – с именем «неразумные люди», а через S – с именем «заслуживающие уважения», то получим схему взаимного расположения Р, М и S, которая соответствует схеме четвертой фигуры на рис. 10. 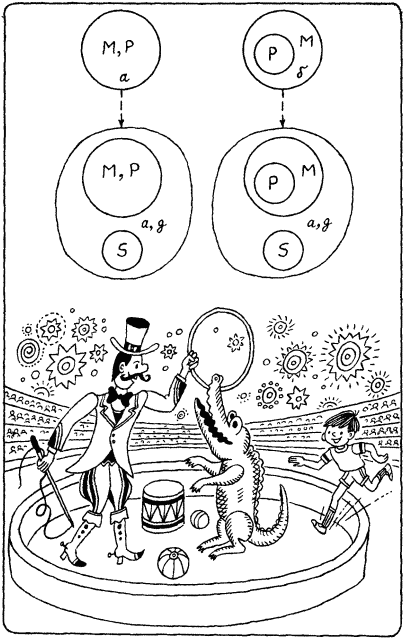
Рис. 15. На рис. 15 в верхнем ярусе показаны два возможных варианта областей истинности для первой посылки. Вторая посылка такова, что ее добавление к каждой из областей первой посылки дает только одну альтернативу. Обе области, показанные в нижнем ярусе, есть области типа g (рис. 8). Это означает, что в качестве заключительного высказывания силлогизма может выступать лишь высказывание типа Е. Само заключение при этом имеет вид «Всякие, заслуживающие уважения, не есть малые дети». После этого промежуточного вывода мы имеем две посылки: Всякие, заслуживающие уважения, не есть малые дети. Всякий, укрощающий крокодилов, есть заслуживающий уважения. Если теперь М – класс с именем «заслуживающие уважения» (надо помнить, что М – единственный класс, имя которого встречается в обеих посылках), то Р соответствует классу «малые дети», a S – классу «укрощающий крокодилов». Такое введение классов сущностей приводит нас к первой фигуре силлогистики Аристотеля (рис. 10). Для получения вывода можно воспользоваться тем, что показано на рис. 16. В верхнем ярусе возможна только одна область истинности, а добавление к первой посылке второй приводит к появлению двух вариантов. Эти два варианта дают область истинности, соответствующую схеме базового высказывания Е. Таким образом, окончательное заключение разбираемого нами сорита выглядит следующим образом: «Всякий, укрощающий крокодилов, не есть малые дети». 
Рис. 16. При получении заключений мы из соображений наглядности каждый раз обращались к графической интерпретации областей истинности. На самом деле для правильных модусов силлогистики Аристотеля (поскольку схемы посылок однозначно определяют схему заключения в каждой из четырех фигур) эти заключительные схемы могут при необходимости выдаваться автоматически. Например, для первой фигуры если посылки имеют тип АА, то заключение имеет тип А, а если посылки имеют тип EI, то заключение имеет тип О. Значит, при определении высказывания, стоящего в заключении, нет никакой необходимости строить области истинности высказываний-посылок. Переход к заключению может происходить чисто механически. Надо только определить по виду выбранных посылок номер фигуры, а затем обратиться к таблице правильных силлогизмов, в которой находится ответ по номеру фигуры и типам посылок. Вот эта таблица: Первая фигура: AAA, EAE, ЕIO, AII, AAI, EAO. Вторая фигура: ЕАЕ, АЕЕ, ЕIO, АОО, ЕАО, АЕО. Третья фигура: AAI, IАI, АII, ЕАО, ОАО, ЕIO. Четвертая фигура: AAI, AEE, IAI, ЕАО, ЕIO, АЕО. Проиллюстрируем процесс такого механического перехода на примере следующего сорита: 1. Те, кто нарушает свои обещания, не заслуживают доверия. 2. Любители выпить очень общительны. 3. Человек, выполняющий свои обещания, честен. 4. Ни один трезвенник не ростовщик. 5. Тому, кто очень общителен, всегда можно верить. Если читатели попробуют «с ходу» сказать, какое заключение следует из этих посылок, то они тут же поймут, что сделать это практически невозможно. Поэтому будем двигаться постепенно, выполняя все необходимые в силлогистике шаги. Постепенность весьма важна, ибо она позволит впоследствии сделать из анализа этого процесса важные выводы для автоматизации вывода рассуждений. Прежде всего преобразуем все посылки сорита в нормальную форму. 1. Всякий, кто нарушает свои обещания, есть не заслуживающий доверия. 2. Всякий любитель выпить есть человек очень общительный. 3. Всякий, кто выполняет свои обещания, есть человек честный. 4. Всякий трезвенник не есть ростовщик. 5. Всякий общительный человек есть человек, заслуживающий доверия. Обратим внимание на то, что переход к нормальной форме для посылок требует прежде всего уточнения того, что за универсум объединяет все имеющиеся посылки. Каков он для нашего сорита? О каких сущностях идет в посылках речь? По-видимому, общей сущностью для всех, о ком говорится в посылках сорита, является сущность с именем «люди», как это было и в предшествующем сорите. Заметим, что если мы не хотим оперировать с «отрицательными классами» сущностей, то надо провести дальнейшую нормализацию посылок, ибо в силлогистике Аристотеля должно неукоснительно выполняться правило, согласно которому при n посылках должен быть выделен в точности n+1 класс сущностей (в силлогизме соответственно три класса S, М и Р). Посчитаем, сколько классов получилось в примере после перехода к нормальной форме представления: W1 – «нарушающие свои обещания», W2 – «не заслуживающие доверия», W3 – «любители выпить», W4 – «очень общительные люди», W5 – «те, кто выполняют свои обещания», W6 – «честные люди», W7 – «трезвенники», W8 – «ростовщики», W9 – «заслуживающие доверия». Итак, девять классов сущностей вместо полагающихся шести. Какие из классов можно исключить из рассмотрения? Анализируя семантику имен классов, можно прийти к тому, что имеют место соотношения: W5= Сохраним все высказывания, в которые не входят классы W2, W5 и W7, а высказывания, в которые они входят, подвергнем преобразованию. Тогда получим следующую систему высказываний, в которой классы сущностей обозначены соответствующими Wi, а около тех высказываний, которые подверглись пре…[4] На рис. 18 показана общая структура системы, позволяющей получать силлогистические выводы. Четыре блока системы выполняют следующие функции. Новые факты, поступающие в систему, попадают в лингвистический блок, который преобразует их в нормальную форму. Если вспомнить первоначальную форму посылок в сорите о ростовщиках и любителях выпить, то становится понятным, что работа лингвистического блока не столь проста. В его задачу входит не только «навешивание» кванторов «всякий» и «некоторые», но и вычленение имен классов сущностей, а также освобождение высказываний от тех слов, которые не влияют на суть той информации, которая в высказывании содержится. Лингвистический блок должен определить, говорит ли высказывание о некоторой единичной сущности или о совокупности таких сущностей. 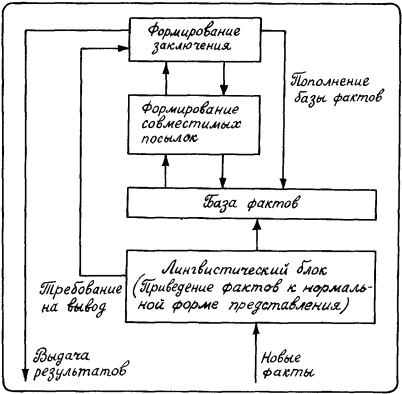
Рис. 18. Наконец, в задачу лингвистического блока входит расшифровка входного сообщения. Эти сообщения могут быть двух типов: факты для пополнения базы фактов системы и факты, истинность которых хотелось бы установить. В первом случае факт после его перевода в нормальную форму передается в базу фактов, а во втором – поступает в блок формирования заключения, где он выступает в качестве задания на вывод. Значительные проблемы возникают при исключении омонимии в названиях классов сущностей. Лингвистический блок должен, например, установить, что в рамках некоторого определенного универсума «люди» имена «трезвенники» и «те, кто не пьют» относятся к одному и тому же классу сущностей. Установление подобных соотношений невозможно без учета специфики той проблемной области, к которой относятся силлогистические утверждения. В памяти лингвистического блока должна храниться достаточная информация о возможных преобразованиях имен классов сущностей. Если очередной факт, переведенный в нормальную форму, поступает в базу фактов, то прежде чем занять в ней свое место, он подвергается проверке с помощью процедур, встроенных в базу фактов. Сначала проверяется, не содержится ли такой же факт в базе. Если подобный факт уже есть, то он не дублируется. Затем проверяется, не противоречит ли вновь поступивший факт тем, которые уже хранятся в базе фактов. Противоречивыми являются пары, отмеченные крестиком в табл. 2. Таблица 2 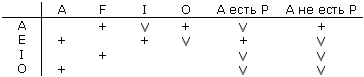 Они противоречивы тогда, когда в обоих высказываниях речь идет об одинаковых классах сущностей S и Р. Галочкой в таблице отмечены те пары, для которых тип высказывания, стоящий в столбце, есть следствие того типа высказывания, которым отмечена строка таблицы. Поэтому если, например, на вход базы фактов поступил факт Asp, а в базе до этого существовал факт Isp, то производится замена Isp на Asp. Если же в базе хранился факт Asp, а на вход поступил факт Isp, то вновь поступивший факт в базу не записывается. Высказывания с единичными сущностями всегда записываются в базу фактов, если проверка их на противоречивость прошла успешно. При проверке их на противоречивость, кроме случаев, показанных в табл. 2, анализируется еще случай возникновения двух высказываний «a есть Р» и «a не есть Р», касающихся одного и того же a. Какие решения принимает система, если она обнаруживает противоречие между вновь поступившим фактом и теми, которые до этого хранились в базе фактов? Какому из двух выявившихся противоречивых фактов система должна верить? На эти вопросы практически нет ответа. Возможные альтернативы: хранение всех фактов при условии, что противоречивые факты относятся к различным возможным мирам; исключение этой пары фактов из базы фактов, так как в системе нет средств для определения предпочтительности истинности того или иного факта; привлечение дополнительной информации для выбора из двух противоречащих фактов одного, истинность которого обоснована больше. Поясним эти альтернативы на следующем примере. Пусть в базе фактов хранился факт Asp: «Всякие лошади не есть летающие существа». И пусть на вход базы фактов поступили новые факты «Пегас есть лошадь» и «Пегас есть летающее существо». Эти факты входят в противоречие с ранее имевшимся фактом о том, что лошади не летают. Принятие первой альтернативы заключается в том, что класс сущностей с именем «лошади» делится на два класса с именами «лошади, которые не есть Пегас» и «пегасы». В качестве единичных сущностей первого класса выступают те конкретные сущности, о которых системе было известно ранее (если их в системе не было, то класс «лошади» не имеет в системе конкретных представителей). В качестве единичной сущности класса «пегасы» выступает тот Пегас, который был упомянут в поступившем в систему сообщении. Факт Asp сохраняется с учетом, что S есть имя класса «лошади, которые не есть Пегас», и вводится высказывание Aq При выборе второй альтернативы система должна будет стереть из базы фактов информацию о классе сущностей «лошади» или убрать из нее факт Asp. Обе эти возможности осуществить не так просто. Если производится удаление какой-то части базы фактов, то необходимо удалить и все те факты, которые прямо не связаны с классом сущности «лошади», но при образовании которых при силлогистическом выводе использовались факты, связанные с лошадьми. Ведь следы прямого упоминания класса «лошади» при таком выводе могут исчезнуть, если класс «лошади» в силлогистической фигуре занимал позицию М. Поэтому вторая альтернатива всегда требует глобальной перепроверки всех фактов, хранимых в базе, а на это уходит немалое время. Наконец, если используется третья альтернатива, то система может, например, не воспринять факт, касающийся Пегаса, зная из каких-то побочных источников, что в памяти хранятся лишь факты, относящиеся к области коневодства, и что Пегас не является именем конкретной сущности. Кроме чистого противоречия, выявить которое принципиально несложно, при вводе нового факта в базу фактов приходится сталкиваться и с проблемами пресуппозиции. Эти проблемы занимали важное место в исследованиях средневековых логиков. Они связаны, в частности, с тем, что истинность некоторого факта неразрывно связана с истинностью некоторых других фактов. Особенно это касается фактов, описывающих динамику событий во внешнем мире. Если, например, в систему поступает факт «Петров заболел», то после приведения его к нормальной форме мы будем иметь: «Петров тот, кто есть больные люди». Этот факт можно ввести в память системы, но при этом сама истинность этого факта предполагает, что некоторое время тому назад был истинен другой факт: «Петров тот, кто не есть больные люди». Этот факт, вытекающий из явления пресуппозиции, формально противоречит вновь вводимому факту. Здесь мы сталкиваемся со случаем третьей альтернативы. Из двух противоречивых фактов надо убрать из памяти системы первый, а второй записать в нее. С тем же явлением пресуппозиции связан и факт введения новых классов сущностей, о которых известно системе. Факт «Петр дал Ивану билет на поезд» по принципу пресуппозиции порождает совокупность высказываний вида: «Петр существует» или «Петр есть человек», «Иван есть человек», «Иван обладает билетом» или «Иван тот, кто есть люди, обладающие билетом» и т.п. Продолжим обсуждение работы системы, структура которой показана на рис. 18. Возможны два режима работы системы: режим пополнения базы фактов и режим доказательства теоремы. В первом случае происходит добавление в базу фактов всех тех фактов, которые с помощью силлогистического вывода получаются из вновь введенного факта, и всех фактов, ранее хранившихся в базе фактов. Во втором случае формулируется теорема в виде вопроса о возможности вывода факта, поступившего на вход системы, из фактов, хранящихся в базе фактов. В процессе вывода блок формирования совместимых посылок выбирает из базы фактов пары посылок, которые образуют одну из четырех фигур силлогизма, т.е. посылок, сцепленных между собой общим классом сущностей М. После нахождения такой пары она передается в блок формирования заключения. В этом блоке проверяется возможность вывода, т.е. возможность того, что пара типов посылок в данной фигуре силлогизма образует правильный модус. Если правильный модус не образуется, то вырабатывается требование на поиск новой пары посылок. Если же вывод возможен, то его результат сравнивается с высказыванием, являющимся целью доказательства теоремы. Если полученное заключение есть искомое высказывание, то процесс доказательства обрывается и результат, говорящий о том, что теорема верна, выдается из системы. Если этого не произошло, то полученное заключение добавляется в базу фактов и процесс поиска доказательства продолжается. В рассмотренной процедуре возникает проблема остановки. Если нужный факт не выводится из той системы посылок, которая имеется в базе фактов, то как это узнать? Единственный возможный ответ связан с полным перебором всех сочетаний посылок, дающих фигуры силлогизма. Это же касается и случая прекращения процесса пополнения базы фактов после введения нового факта в систему. Суммируя все сказанное, необходимо отметить, что, несмотря на внешнюю простоту процедуры вывода в силлогистике, в ней, как в капле воды, отражаются все те трудности, которые связаны с поиском вывода. Прежде всего это трудности понимания поступающих в систему сообщений, истолкования их в терминах, понятных на уровне внутреннего языка (в нашем случае это необходимость в процедурах нормализации сообщений). Затем это ряд трудностей, вызываемых процедурами проверки поступающего сообщения на согласованность содержащейся в нем информации с той информацией, которая ранее хранилась в памяти системы. Это трудности поиска, не опирающегося на какую-то цель, или при известной цели (в случае доказательства теоремы) не опирающегося на какие-либо соображения о путях движения по дереву вывода. Наконец, это трудности, связанные с прекращением процедур вывода и формированием отрицательного ответа на поставленный перед системой вопрос о выводимости. Все эти трудности в той или иной форме будут присущи и другим системам моделирования человеческих рассуждений, ибо они являются принципиальными для всех формальных систем, частным случаем которых является силлогистика Аристотеля. Формальная система – это четверка вида Ф=<T,L,Q,R>. Множество Т есть множество базовых элементов, исходных кирпичиков, не расчленяемых на более простые. Примерами таких элементов служат буквы (графемы) или детали в детском конструкторе. Единственное требование к элементам множества Т состоит в том, что для любого элемента за конечное число шагов можно узнать, принадлежит он Т или нет, а также отличить одни элементы от других, отождествляя одинаковые элементы. Множество L есть множество синтаксических правил. С их помощью из элементов множества Т строятся более сложные образования, которые называются синтаксически правильными. Так, из графем возникают линейно упорядоченные сочетания, называемые словами, предложениями (для их образования используется специальный знак – пробел и знаки пунктуации), текстами; из деталей детского конструктора возникают более сложные образования, в которых отдельные элементы набора соединяются крепежными элементами. Множество Q состоит из выделенных на основе некоторого соображения синтаксически правильных образований. Такое множество называется начальным или априорно принимаемым. Часто синтаксически правильные образования, входящие в Q, называют аксиомами. Тогда Q называют множеством аксиом. Наконец, R представляет собой совокупность процедур, с помощью которых можно получать одни синтаксически правильные совокупности из других. Эти процедуры носят название правил вывода. Формальные системы обладают одним общим свойством – автономностью. Если в такой системе задать все четыре множества, то она самостоятельно начнет генерировать множество выводимых в ней синтаксически правильных совокупностей. Они будут порождаться в результате применения различными способами правил вывода к совокупностям из множества Q. Сами элементы Q считаются в данной формальной системе выведенными всегда, т.е. априорно выведенными. Легко усмотреть, что силлогистика Аристотеля и ее расширения, описанные нами, являют собой пример формальной системы. В качестве элементов Т выступают буквы, символизирующие имена конкретных сущностей и имена классов, а также символы А, Е, I и О. Синтаксические правила образуют из этих элементов нормальные формы представления высказываний Asp, Esp и т.п. В качестве исходных аксиом выступают законы силлогистики. Наконец, правилами вывода являются фиксированные выводы с одной посылкой, предназначенные для эквивалентных преобразований высказываний (например, Esp Другие подходы к моделированию человеческих рассуждений, возникшие в столь же давние времена, что и силлогистика, не сумели достигнуть ее уровня. Но анализ их достижений полезен, ибо позволяет ввести некоторые типы нестрогих человеческих рассуждений, которые были отброшены силлогистикой как не отвечающие строгим логическим принципам. Ибо истина и ложь в человеческих рассуждениях это не Истина и Ложь с большой буквы, о которых говорят строгие логические теории. Но и они имеют право говорить об Истине лишь тогда, когда исходные факты, служащие посылками, не могут быть подвергнуты никакой критике. А возможно ли это? Во всяком случае, возможно ли это, когда мы рассуждаем о проблемных областях, знание о которых у нас не абсолютно? Ответ, как мне кажется, дан героем повести «Сказка о тройке» А. и Б. Стругацких Фарфуркисом: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 |
|||||||
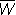 1, W7=
1, W7=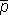 , в котором Q есть имя класса сущностей «пегасы».
, в котором Q есть имя класса сущностей «пегасы».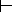 Eps), а также таблица получения заключений в правильных модусах при наличии посылок для этих заключений. Такая силлогистическая система способна при заданном множестве, в состав которого кроме законов силлогистики входит некоторое число высказываний, принятых в этой системе за априорно выведенные, породить все высказывания, которые вытекают из Q и правил вывода для силлогизмов.
Eps), а также таблица получения заключений в правильных модусах при наличии посылок для этих заключений. Такая силлогистическая система способна при заданном множестве, в состав которого кроме законов силлогистики входит некоторое число высказываний, принятых в этой системе за априорно выведенные, породить все высказывания, которые вытекают из Q и правил вывода для силлогизмов.