 |
|
Популярные авторы:: БСЭ :: Борхес Хорхе Луис :: Азимов Айзек :: Грин Александр :: Раззаков Федор :: Горький Максим :: Чехов Антон Павлович :: Толстой Лев Николаевич :: Станюкович Константин Михайлович :: Лондон Джек Популярные книги:: Справочник по реестру Windows XP :: The Boarding House :: Мертвые души :: Дюна (Книги 1-3) :: Полет :: Малинник Якобсона :: Омен. Последняя битва. :: По заданию преступного синдиката :: Повесть о том, как один мужик двух генералов прокормил :: «Фирма приключений» |
Какой сейчас век?ModernLib.Net / Альтернативная история / Носовский Глеб Владимирович / Какой сейчас век? - Чтение (стр. 11)
В 1978– 1985 годах нами был проведен первый обширный вычислительный эксперимент по подсчету чисел р(Х, Y) для нескольких десятков пар конкретных исторических текстов -хроник, летописей и т. п. Оказалось, что коэффициент р(Х, Y) достаточно хорошо различает заведомо зависимые и заведомо независимые пары исторических текстов. Было обнаружено, что для всех исследованных нами пар реальных летописей X, Y, описывающих заведомо разные события (разные исторические эпохи или разные государства) – то есть для НЕЗАВИСИМЫХ текстов, – число р(Х, Y) колеблется от 1 до 1/100 при количестве локальных максимумов от 10 до 15. Напротив, если исторические летописи X и Y ЗАВЕДОМО ЗАВИСИМЫ, то есть описывают одни и те же события, то числор(Х, Y) не превосходит 108 для того же количества максимумов. Таким образом, между значениями коэффициента для зависимых и независимых текстов обнаруживается разрыв примерно на 5-6 порядков. Подчеркнем, что здесь важны не абсолютные величины получающихся коэффициентов, а тот факт, что "зона коэффициентов для заведомо зависимых текстов" отделена несколькими порядками от "зоны коэффициентов для заведомо независимых текстов". Приведем типичные примеры. Точные значения функций объемов для особо интересных летописей мы приводим в ХРОН1. На рис. 5.6-5.8 показаны графики объемов двух заведомо зависимых исторических текстов. А именно, в качестве текста X мы взяли историческую монографию современного автора В. С. Сергеева "Очерки по истории древнего Рима", тома 1-2, М., 1938, ОГИЗ. В качестве текста Y мы взяли "античный" источник, а именно "Римскую историю" Тита Ливия, тома 1-6, М., 1897-1899. 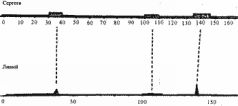 Рис. 5.6 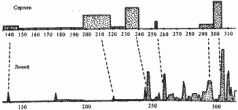 Рис. 5.7 
Согласно скалигеровской хронологии, эти тексты описывают события на интервале якобы 757-287 годы до н. э. Итак, здесь A = 757 год до н. э., В= 287 год до н. э. Оба текста описывают одну и ту же историческую эпоху, примерно одни и те же события. Наглядно видно, что графики объемов делают свои основные всплески практически одновременно. Для количественного сравнения функций следует предварительно сгладить "мелкую зыбь", то есть вторичные всплески, накладывающиеся на основные, первичные колебания графиков. При вычислении коэффициента р(Х, Y) мы сгладили, усреднили эти графики, чтобы выделить лишь их основные локальные максимумы в количестве, не превышающем пятнадцати. Оказалось, что здесь р(Х, Y) = 210-12. Малая величина коэффициента указывает на зависимость сравниваемых текстов. В данном случае это неудивительно. Как мы уже отмечали, оба текста описывают один и тот же период в истории "античного" Рима. Малое значение коэффициента р(Х, Y) показывает, что если рассматривать наблюдаемую близость точек всплесков обоих графиков как случайное событие, то его вероятность чрезвычайно мила. Как мы видим, современный автор В. С. Сергеев достаточно аккуратно воспроизвел в своей книге "античный" оригинал. Конечно, он дополнил его своими соображениями и комментариями, но, как выясняется, они не влияют на характер зависимости этих текстов. Теперь в качестве "летописи" X' возьмем снова книгу В. С. Сергеева, а в качестве "летописи" Y' – ее же, но заменив порядок лет в тексте на противоположный. То есть, грубо говоря, прочитав книгу Сергеева "задом наперед". Оказывается, в этом случае р(Х' Y) будет равняться 1/3. Таким образом, получается значение, существенно более близкое к единице, чем предыдущее, и указывающее на независимость сравниваемых текстов. Что и неудивительно, так как проведенная нами операция "перевертывания летописи" очевидно дает два заведомо независимых текста. Еще пример. Возьмем следующие заведомо зависимые исторические тексты, две русские летописи: X – Никифоровская летопись, Y – Супрасльская летопись. В обеих летописях описан следующий интервал времени: якобы 850-1256 годы н. э. Графики их объемов приведены на рис. 5.9. Оба графика объемов "глав" на интервале якобы 850-1256 годы н. э. имеют 31 всплеск и делают эти всплески практически одновременно, в одни и те же годы. Подсчет дает, что здесь р(Х, Y) = 10-24. Это значение весьма мало, что подтверждает зависимость этих текстов. Рассмотрим еще две русские летописи: X – Холмогорская летопись, Y – Повесть Временных лет. 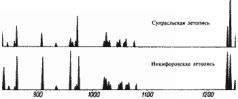 Рис. 5.9 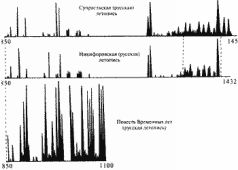 Рис. 5.10
Следующий интервал времени описан в обеих летописях: якобы 850-1000 годы н. э. Графики объемов летописей также достигают локальных максимумов практически одновременно. И снова это не случайно, а закономерно, иначе реализовался бы единственный шанс из 1015 шансов. Здесь р(Х, Y) = 10-15. На указанном временном интервале эти две летописи зависимы. На рис. 5.10 представлены сразу три графика объемов: для Супрасльской летописи, для Никифоровской летописи и для Повести Временных лет. Последняя летопись "богаче", поэтому ее график имеет больше локальных максимумов и зависимость не столь очевидна. Тем не менее после сглаживания выясняется, что между этими тремя графиками также имеется ярко выраженная зависимость. Выше мы использовали такую числовую характеристику "главы", как ее объем. Однако, как показали наши исследования, аналогичные статистические закономерности для достаточно больших исторических текстов обнаруживаются и при использовании других числовых характеристик. Например, можно рассматривать количество имен в каждой "главе", количество ссылок на другие летописи и т. п. В нашем вычислительном эксперименте сравнивались: а) древние тексты с древними, б) древние с современными, в) современные с современными. Как мы уже сказали, наряду с графиками объемов "глав" исследовались и другие количественные характеристики текстов. Например, графики числа упомянутых имен, графики числа упоминаний данного года в тексте, графики частот ссылок на какой-либо другой фиксированный текст и т. п. Оказалось, что для всех этих характеристик выполняется тот же принцип корреляции максимумов. А именно, графики зависимых текстов делают всплески практически одновременно, а для независимых текстов точки всплесков графиков никак не коррелируют. Сформулируем еще одно следствие из нашей основной модели, статистической гипотезы. А именно, если два исторических текста заведомо зависимы, то есть описывают один и тот же "поток событий" на одном и том же интервале времени в истории одного и того же государства, то для любой пары указанных выше числовых характеристик соответствующие им графики делают всплески приблизительно в одни и те же годы. Другими словами, если какой-то год в обеих летописях описан подробнее, чем соседние годы, то увеличится (локально) число упоминаний этого года в обеих летописях, увеличится количество имен персонажей, упомянутых в этом году в обеих летописях, и т. п. Напротив, если тексты заведомо зависимы, то никакой корреляции между указанными числовыми характеристиками быть не должно. 1.4. Метод датирования исторических событий Поскольку наша теоретическая модель подтвердилась на экспериментальном материале, мы можем теперь предложить новую методику датирования древних событий. Хотя она, конечно, не универсальна. Опишем идею метода. Пусть Y – исторический текст, описывающий неизвестный нам "поток событий" с утраченными абсолютными датировками. Пусть годы t отсчитываются в тексте от какого-то события местного значения, например от основания какого-то города или от момента воцарения какого-то царя, абсолютные датировки которых нам неизвестны. Подсчитаем для текста Y его график объема "глав" и сравним его с графиками объема других текстов, для которых абсолютная датировка событий, описанных в них, нам известна. Если среди этих текстов обнаружится текст X, для которого число р(Х, Y) мало – то есть имеет такой же порядок, как и для пар зависимых текстов (не превосходит, например, числа 10"8 для соответствующего количества локальных максимумов), – то можно с достаточно большой вероятностью сделать вывод о совпадении или близости описываемых в этих текстах "потоков событий". Причем эта вероятность тем больше, чем меньше число р(Х, Y). При этом оба сравниваемых текста могут быть внешне совершенно несхожи. Например, они могут быть двумя вариантами одной и той же летописи, но написанными в разных странах, разными летописцами, на разных языках. Эта методика датирования была экспериментально проверена на текстах XVI-XX веков с заранее известной датировкой. Полученные даты совпали с этими датировками. 2. Метод распознавания и датирования династий правителей 2.1. Принцип малых династических искажений Принцип малых династических искажений и основанный на нем метод был предложен и разработан А. Т. Фоменко. Пусть обнаружен исторический текст, описывающий неизвестную нам династию правителей с указанием длительностей их правлений. Возникает вопрос: является ли эта династия новой, ранее нам неизвестной и, следовательно, нуждающейся в датировке, или это одна из известных нам династий, но описанная в непривычных для нас терминах с видоизмененными именами правителей? Ответ дается при помощи излагаемой ниже методики. Рассмотрим к любых последовательных реальных правителей, ца-рей в истории какого-то государства, области. Условно назовем эту последовательность реальной династией. При этом ее члены отнюдь не обязаны быть родственниками. Часто одна и та же реальная династия описывается в разных документах и разными летописцами. При этом описывается с разных точек зрения. Например, по-разному оцениваются деятельность правителей, их значение, их личные качества и т. д. Тем не менее существуют "инвариантные" факты, описания которых в меньшей степени зависят от симпатий или антипатий летописцев. К таким более или менее "инвариантным фактам" относится, например, длительность правления царя. Обычно нет особых причин, по которым хронист значительно и намеренно исказил бы это число. Однако перед летописцами часто возникали естественные трудности в подсчете длительности правления того или иного царя. Эти естественные трудности таковы: неполнота информации, искажения в документах и т. д. Поэтому разные летописцы приводят в своих хрониках или таблицах разные данные длительности правления одного и того же царя. Такие расхождения, иногда значительные, характерны, например, для фараонов в таблицах Г. Бругша и в "Хронологических таблицах" Ж. Блера. Например, в таблицах Ж. Блера, доведенных до начала XIX века, собраны все основные исторические династии, с датами правлений, сведения о которых дошли до нас. Таблицы Ж. Блера ценны для нас тем, что они были составлены в эпоху, достаточно близкую ко времени создания скалигеровской хронологии. Поэтому они несут в себе более явственные отпечатки "скалигеровской деятельности", позднее затушеванные, заштукатуренные историками XIX-XX веков. 
Итак, каждый летописец, описывая реальную династию М, по-своему, в меру своих способностей и возможностей, вычисляет длительности правлений ее царей. В результате он получает некоторую последовательность чисел а = (а1, а2,… ак), где число а. изображает – быть может, с ошибкой – реальную длительность правления царя с номером i. Напомним, что число к – это общее число царей в данной династии. Эту последовательность чисел, извлекаемую из летописи, мы условно называем летописной династией. Ее удобно изображать вектором а в евклидовом пространстве. Другой летописец, описывая ту же самую реальную династию М, возможно, припишет этим же царям несколько другие длительности правлений. В результате получится другая летописная династия b = (bv bv… bk). Таким образом, одна и та же реальная династия М, но описанная в разных летописях, может изображаться в них разными летописными династиями а и b. Спрашивается, насколько велики возникающие искажения? При этом существенную роль играют ошибки и объективные трудности, препятствующие точному определению реальных длительностей правлений. Основные типы ошибок мы опишем ниже. Сформулируем статистическую модель, гипотезу, которую мы условно назовем принципом малых искажений. Если две летописные династии а и b "мало" отличаются друг от друга, то они изображают одну и ту же реальную династию М, то есть являются двумя вариантами ее описания в разных летописях. В этом случае летописные династии назовем зависимыми. Напротив, если же две летописные династии а и b изображают две различные реальные династии M и N, то они "значительно" отличаются друг от друга. В этом случае назовем их независимыми. Остальные пары династий мы назовем нейтральными. Другими словами, согласно этой гипотезе-модели, разные летописцы "мало" искажали одну и ту же реальную династию при написании своих летописей. Во всяком случае, возникавшие разночтения оказывались "в среднем" меньше, чем имеющиеся различия между заведомо разными, то есть независимыми, реальными династиями. Сформулированная выше гипотеза-модель нуждается в экспериментальной проверке. В случае ее справедливости мы обнаруживаем важное и отнюдь не очевидное свойство, характеризующее деятельность древних летописцев. А именно, летописные династии, возникавшие при описании одной и той же реальной династии, отличаются друг от друга и от своего прототипа меньше, чем отличаются друг от друга две действительно разные реальные династии. Существует ли естественный числовой коэффициент, мера с(а, b), вычисляемый для каждой пары летописных династий а и b и обладающий тем свойством, что он "мал" для зависимых династий и, напротив, "велик" для независимых? Другими словами, этот коэффициент должен различать зависимые и независимые династии. Такой коэффициент был нами найден. Оказывается, для оценки "близости" двух династий а и b можно ввести числовой коэффициент с(а, b), аналогичный описанному выше коэффициенту р(Х, Y), – вероятность случайного совпадения династий. Этот коэффициент с(а, b) также имеет смысл вероятности. Сначала опишем грубую идею определения коэффициента с(а, b). Летописную династию удобно изображать в виде графика, отложив по горизонтали номера царей, а по вертикали – длительности их правлений. Мы скажем, что династия q "похожа" на две династии а и b, если график династии q отличается от графика династии а не больше, чем график династии отличается от графика династии а. В качестве с(а, b) берется доля, которую династии, "похожие" на династии аи b, составляют во множестве всех династий. Другими словами, подсчитывается отношение: 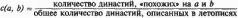
Длительности правлений царей могут определяться летописцами с ошибкой. Фактически мы извлекаем из летописей лишь некоторые приближенные их значения. Можно математически описать вероятностные механизмы, приводящие к появлению этих ошибок. Кроме того, мы учитывали еще две возможные ошибки летописцев: перестановку двух соседних царей и замену двух соседних царей одним "царем" с суммарной длительностью правления. 2.2. Уточнения модели и вычислительного эксперимента Сформулированный выше принцип малых искажений проверялся на основе коэффициента с(а, b). 1. Для проверки были использованы хронологические таблицы Ж. Блера, содержащие практически все основные хронологические данные, в скалигеровской версии, из истории Европы, Средиземноморья, Ближнего Востока, Египта, Азии от якобы 4000 года до н. э. до 1800 года н. э. Эти данные были затем дополнены списками правителей и их правлений, взятых нами из других таблиц и монографий, как средневековых, так и современных (Ш. Бемон, Г. Моно, Э. Бикерман, Г. Бругш, А. А. Васильев, Ф. Грегоровиус, Д. Эссад, Ш. Диль, Кольрауш, С. Г. Лозинский, Б. Низе, В. С. Сергеев, Chronologie egiptienne, F. К. Ginzel, L. Ideler, L'art de verifier les dates faites historiques, T. Mommsen, Isaac Newton, D. Petavius, I. Scaliger и другие). 2. Как мы уже отмечали, под династией мы понимаем последовательность фактических правителей страны, безотносительно к их титулатуре и родственным связям. В дальнейшем мы иногда будем, для краткости, условно называть их царями. 3. Из-за наличия соправителей иногда возникают трудности при расположении этих династов в ряд. Мы приняли простейший принцип их упорядочения – по серединам периодов правлений. 4. Последовательность чисел, выражающих длительности правлений всех правителей на протяжении всей истории данного государства (то есть длина последовательности априори не ограничивается), будем называть династическим потоком. Подпоследовательности, получающиеся отбрасыванием тех или иных соправителей, назовем династическими струями. От каждой такой струи требуется, чтобы она была монотонной, то есть чтобы середины периодов правлений монотонно возрастали. Требуется также, чтобы династическая струя была полной, то есть чтобы она без пропусков и разрывов покрывала весь исторический период, охваченный данным потоком. Перекрытия периодов правлений при этом допускаются. 5. В реальных ситуациях по понятным причинам перечисленные выше требования могут быть несколько нарушены. Например, из рассказа летописца может выпасть год или несколько лет междуцарствия. Поэтому приходится разрешать незначительные пробелы. Мы допускали лишь такие пробелы, длительность которых не превышает одного года. Кроме того, при анализе династических потоков и струй приходится постоянно иметь в виду возможность искажения подлинной картины в результате описанных выше ошибок, допускаемых летописцами. 6. Имеется еще одна причина нарушения четкой формальной картины. Она заключается в том, что иногда трудно с определенностью установить время начала правления царя. Например, считать ли его от момента фактического прихода к власти или от момента формальной интронизации. Для начала правления Фридриха II, например, в разных таблицах приводятся различные варианты: 1196, 1212, 1215, 1220 годы н. э. В то же время с концом правления обычно никаких трудностей нет. Чаще всего это смерть царя. Таким образом, мы приходим к необходимости "раздвоения" царя или даже к рассмотрению его в трех вариантах. Большее число вариантов на прак-хике, к счастью, появлялось исключительно редко. Все эти варианты включались в общий династический поток. При этом требовалось, чтобы ни одна из выделяемых в дальнейшем для исследования династических струй не содержала двух различных вариантов одного и того же правления царя. 7. Для всех государств из указанных выше географических регионов был составлен – на основе собранных нами хронологических данных в скалигеровской версии – полный список D всех летописных династий длиной 15. То есть был составлен список всех династий из 15 последовательных царей. Каждый царь может при этом попасть в несколько 15-членных династий, то есть династии могут "перекрываться". Перечислим основные династические потоки, подвергнутые статистическому анализу. Это: епископы и папы в Риме, патриархи Византии, сарацины, первосвященники в Иудее, грекобактрийцы, экзархи в Равенне, фараонские династии Египта, средневековые династии Египта, династии Византии, Римской империи, Испании, России, Франции, Италии, Османской = Оттоманской империи, Шотландии, Лакедемона, Германии, Швеции, Дании, Израиля, Иудеи, Вавилона, Сирии, Португалии, Парфии, Боспорского царства, Македонии, Польши, Англии. 8. Получилось примерно 15*1011(11 это степень и далее все степени)виртуальных династий. То есть в множестве vir(Z) оказывается примерно 15*1011 точек. Вычислительный эксперимент, проведенный в 1977-1979 годах А. Т. Фоменко совместно с М. Замалетдиновым и П. Пучковым, подтвердил принцип малых искажений. А именно, оказалось, что для заведомо зависимых летописных династий а и b число с(а, b) всегда не превышает 108 и обычно колеблется от 10-12 до 10-10. При вероятностной интерпретации это означает, что если рассматривать наблюдаемую близость двух зависимых летописных династий как случайное событие, то его вероятность мала, событие исключительно редкое, поскольку реализуется единственный из ста миллиардов шансов. Выяснилось далее, что если две летописные династии а и b изображают две заведомо разные реальные династии, то коэффициент с(а, b) "существенно больше". А именно, он всегда не меньше чем 10-3, то есть "велик". Как и в случае с коэффициентом р(Х, Y) здесь важны, конечно, не абсолютные значения с(а, b), а разница в несколько порядков между "зависимой зоной" и "независимой зоной" (рис. 5.11). 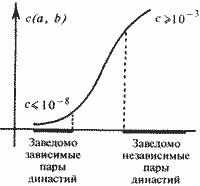
Итак, при помощи коэффициента с(а, b) удалось обнаружить существенное различие между заведомо зависимыми и заведомо независимыми летописными династиями. 2.3. Метод датирования царских династий и метод обнаружения фантомных династических дубликатов Итак, при помощи коэффициента с(а, b) можно достаточно уверенно различать зависимые и независимые пары летописных династий. Важный экспериментальный факт состоит в том, что летописцы ошибаются "не слишком сильно". Во всяком случае, их ошибки существенно меньше величины, различающей независимые династии. Это позволяет, в рамках проведенного эксперимента, предложить новый метод распознавания зависимых летописных династий и методику датировки неизвестных династий. Поступая по аналогии с предыдущим пунктом, вычисляем для неизвестной династии d коэффициент с(а, d), где а – известные, уже датированные летописные династии. Допустим, что мы обнаружили династию а, для которой коэффициент с(а, d) мал, то есть не превышает 10-8 Это дает нам основание утверждать, что династии а и d зависимы с вероятностью 1 – с(а, d). To есть летописные династии and, по-видимому, соответствуют одной реальной династии М, датировка которой нам уже известна. Тем самым мы датируем летописную династию d. Эта методика была проверена на средневековых династиях с заранее известной датировкой. Эффективность методики полностью подтвердилась. Этот же метод позволяет обнаруживать в "скалигеровском учебнике по истории" фантомные дубликаты. А именно, если мы найдем две летописные династии а и b, для которых коэффициент с(а, b) не превышает 10-8, это дает нам основания предполагать, что перед нами – просто два экземпляра, две версии описания какой-то одной и той же реальной династии М. Которая размножилась на страницах разных летописей, помещенных затем в разные места "скалигеровского учебника". Повторим еще раз, что любые выводы или гипотезы, опирающиеся на "похожесть" или, напротив, "непохожесть" династий, могут считаться осмысленными только в том случае, когда они опираются на обширные численные эксперименты, подобные проведенным нами. В противном случае на первое место выступают туманные субъективные соображения, обсуждать которые вряд ли стоит. 3. Принцип затухания частот. Метод упорядочивания исторических текстов во времени Принцип затухания частот и основанный на нем метод был предложен и разработан А. Т. Фоменко. Он позволяет находить хронологически правильный порядок отдельных фрагментов текста, обнаруживать в нем дубликаты на основе анализа, например, совокупности собственных имен, упомянутых в тексте. Как и в предыдущих методиках, мы стремимся к созданию метода датировки, основанного на численных, количественных характеристиках текстов и не обязательно требующего анализа смыслового содержания текстов, которое может быть весьма многозначно и расплывчато. Если в документе упомянуты какие-либо "знаменитые", ранее известные нам персонажи, описанные в других, уже датированных хрониках, то это позволяет датировать описанные в тексте события. Однако если такое отождествление сразу не удается и если, кроме того, описаны события нескольких поколений с большим количеством ранее неизвестных действующих лиц, то задача установления тождества персонажей с ранее известными усложняется. Для краткости назовем фрагмент текста, описывающий события одного поколения, "главой-поколением". Будем считать, что средняя длительность одного "поколения" – это средняя длительность правления реальных царей, упомянутых в дошедших до нас летописях. Эта средняя длительность правления царей была вычислена А. Т. Фоменко при обработке хронологических таблиц Блера. Она оказалась равной 17, 1 года. При работе с реальными историческими текстами выделение в них "глав-поколений" иногда наталкивается на трудности. В таких случаях мы ограничивались лишь приблизительным разбиением текста на последовательные фрагменты. Пусть летопись X описывает события на достаточно большом интервале времени (А, В), на протяжении которого менялось по крайней мере несколько поколений персонажей. Пусть летопись X разбита на "главы-поколения" Х(Т), где Г – порядковый номер поколения, описанного во фрагменте Х(Т), в той нумерации "глав", которая фиксирована в тексте. Возникает вопрос: правильно ли занумерованы, упорядочены эти "главы-поколения" в летописи? Или же если эта нумерация утрачена или сомнительна, то как ее восстановить? Другими словами, как правильно расположить во времени "главы" относительно друг друга? Оказывается, для реальных исторических текстов в подавляющем большинстве случаев выполняется следующая "формула"-правило: полное имя = персонаж. Это означает следующее. Пусть интервал времени, описываемый летописцем, достаточно велик, например составляет несколько десятков или сотен лет. Тогда – как было проверено нами в результате анализа большого набора исторических документов – в подавляющем большинстве случаев разные персонажи имеют в одном и том же тексте разные полные имена. Полное имя может состоять из нескольких слов, например, Карл Плешивый. Другими словами, число разных лиц с одинаковыми полными именами ничтожно мало по сравнению с количеством всех персонажей. Это верно для всех нескольких сотен исследованных нами исторических текстов, описывающих Рим, Грецию, Германию, Италию, Россию, Англию и т. д. Ничего удивительного в этом нет. В самом деле, летописец заинтересован в различении разных персонажей, чтобы избежать путаницы. Простейший способ добиться этого – присвоить разным лицам разные полные имена. Это простое психологическое обстоятельство и подтверждается подсчетами. Сформулируем теперь принцип затухания частот, описывающий хронологически правильный порядок "глав-поколений". При правильной нумерации "глав-поколений" летописец, переходя от описания одного поколения к следующему, сменяет и персонажей. А именно, при описании поколений, предшествующих поколению с номером Q, он ничего не говорит о персонажах этого поколения, так как они еще не родились. Затем, при описании поколения Q, летописец именно здесь больше всего говорит о персонажах этого поколения, поскольку с ними напрямую связаны описываемые им события. Наконец, переходя к описанию последующих поколений, летописец все реже и реже упоминает о прежних персонажах, так как описывает новые события, персонажи которых вытесняют умерших. Здесь важно подчеркнуть, что мы имеем в виду не какие-то отдельные имена, а полный резервуар всех имен, использовавшихся в поколении с номером Q. Вкратце наша модель формулируется так. Каждое поколение рождает новые исторические лица. При смене поколений эти лица сменяются. Несмотря на внешнюю простоту, этот принцип оказался полезен при создании метода датировки. Принцип затухания частот имеет эквивалентную переформулировку. Так как персонажи практически однозначно определяются своими полными именами (имя = персонаж), то мы будем изучать резервуар всех полных имен текста. Термин "полное" будем обычно опускать, постоянно подразумевая его. Более того, оказалось, что подавляющее большинство исторических имен являются "простыми", состоящими из одного слова. Поэтому при обработке больших исторических текстов со значительным запасом имен можно рассматривать лишь "элементарные имена – кирпичи", разбивая редкие полные имена на отдельные составляющие их слова. Рассмотрим группу всех имен, впервые появившихся в тексте, в "главе-поколении" с номером Q. Условно назовем эти имена Q-именами, а соответствующие им персонажи Q-персонажами. Количество всех упоминаний, с кратностями, всех этих имен в данной "главе" обозначим через K(Q, Q). Подсчитаем затем, сколько раз эти же имена упомянуты в "главе" с номером Т. Получившееся число обозначим через K(Q, 7). При этом если одно и то же имя повторяется несколько раз, то есть с кратностью, то все эти упоминания подсчитываются. Построим график, отложив по горизонтали номера "глав", а по вертикали – числа K(Q, T), где номер Q фиксирован, а Г меняется. Для каждого Q мы получаем свой график. Принцип затухания частот тогда формулируется так. При хронологически правильной нумерации "глав-поколений" каждый график К(Q, T) должен иметь следующий вид. Слева от точки Q график равен нулю, в точке Q – абсолютный максимум графика, потом график постепенно падает, более или менее монотонно затухает (рис. 5.12). Этот график (на рис. 5.12) мы назовем идеальным. 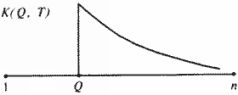 Рис. 5.12
Сформулированный принцип должен быть проверен экспериментально. Если он верен и если "главы" в летописи упорядочены хронологически правильно, то все экспериментальные графики должны быть близки к идеальному. Проведенная экспериментальная проверка полностью подтвердила принцип затухания частот. Всего нами было обработано несколько десятков больших исторических текстов. Во всех случаях, когда тексты описывают события эпохи XVI-XX веков, принцип затухания частот подтвердился. Отсюда вытекает методика хронологически правильного упорядочивания "глав-поколений" в тексте, или в наборе текстов, где этот порядок нарушен или неизвестен. Рассмотрим совокупность "глав-поколений" летописи X и занумеруем их в каком-нибудь порядке. Для каждой "главы" X(Q) подсчитаем число K(Q, T) при заданной нумерации "глав". Все числа K(Q, T), при переменных Q и Т, естественно организуются в квадратную матрицу К{T} размера n*n, где n – общее число "глав". В идеальном теоретическом случае частотная матрица К{T} имеет вид, показанный на рис. 5.13. На рис. 5.13 ниже главной диагонали стоят нули, на главной диагонали расположен абсолютный максимум в каждой строке. Затем каждый график, в каждой строке, монотонно падает, затухает. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 |
|||||||