 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ПР)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ПР) - Чтение (стр. 27)
Возможность характеризовать классы функций с помощью приближений их полиномами нашла приложение в ряде вопросов математического анализа. Развивая исследования по наилучшим приближениям функций многих переменных полиномами, С. М. построил теорию вложений важных для анализа классов дифференцируемых функций многих переменных, в которой имеют место не только прямые, но и полностью обращающие их обратные теоремы. Для приближений в метрике L 2полином наилучшего приближения может быть легко построен. Для других пространств нахождение полиномов наилучшего приближения является трудной задачей и её удаётся решить только в отдельных случаях. Это привело к разработке разного рода алгоритмов для приближённого нахождения полиномов наилучшего приближения. Трудность нахождения полиномов наилучшего приближения отчасти объясняется тем, что оператор, сопоставляющий каждой функции её полином наилучшего приближения, не является линейным: полином наилучшего приближения для суммы f+ gне обязательно равен сумме полиномов наилучшего приближения функций fи g.Поэтому возникла задача изучения (по возможности простых) линейных операторов, сопоставляющих каждой функции полином, дающий хорошее приближение. Например, для периодической функции f( x) можно брать частные суммы её ряда Фурье S n( f, х) .При этом справедлива оценка (теорема А. ) ||
f - S
n
где
L
n-числа, растущие при
n®
Ґ как (4/p
2) ln
n. Они получили название констант Лебега. Эта оценка показывает, что полиномы
S
n
А. Н.
начал изучение нового вопроса теории приближений - задачи о нахождении при фиксированном
nтакой системы функций j
1,..., j
n,для которой наилучшие приближения функций заданного класса полиномами
Теория приближений функций является одним из наиболее интенсивно разрабатываемых направлений в теории функций. Идеи и методы теории приближений являются отправной точкой исследования в ряде вопросов вычислительной математики. С 1968 в США издаётся специализированный журнал «Journal of Approximation Theory». См. также .
Лит.: Монографии. Ахиезер Н. И., Лекции по теории аппроксимации, 2 изд., М., 1965; Гончаров В. Л., Теория интерполирования и приближения функций, 2 изд., М., 1954; Натансон И. П., Конструктивная теория функций, М. - Л., 1949; Никольский С. М., Приближение функций многих переменных и теоремы вложения, М., 1969; Тиман А. Ф., Теория приближения функций действительного переменного, М., 1960. Обзоры.Математика в СССР за тридцать лет. 1917-1947, М. - Л., 1948, с. 288-318; Математика в СССР за сорок лет. 1917-1957, т. 1, М., 1959, с. 295-379; История отечественной математики, т. 3, К., 1968, с. 568-588. С. А. Теляковский. Приближение функций комплексного переменного Приближе'ние фу'нкций ко'мплексного переме'нного,раздел комплексного анализа, изучающий вопросы приближённого представления (аппроксимации) функций комплексного переменного посредством специальных классов. Центральная проблематика относится к приближению функций полиномами и рациональными функциями. Основными являются задачи о возможности приближения, скорости приближения и аппроксимационных свойствах различных способов представления функций (интерполяционных последовательностей и рядов, рядов по ортогональным полиномам и полиномам Фабера, разложений в непрерывные дроби и т.п.). Теория приближений тесно связана с др. разделами комплексного анализа (теорией конформных отображений, интегральными представлениями, теорией потенциала и др.); многие теоремы, формулируемые в терминах теории приближений, являются, по существу, глубокими результатами о свойствах аналитических функций и природе аналитичности. Одним из первых результатов о полиномиальной аппроксимации является теорема Рунге, согласно которой любая функция, голоморфная в односвязной области плоскости комплексного переменного z,может быть равномерно аппроксимирована на компактных подмножествах (см. ) этой области посредством полиномов от z.Общая задача о возможности равномерного приближения полиномами ставится так: для каких компактов Кв комплексной плоскости любая функция f,непрерывная на Ки голоморфная на множестве внутренних точек К,допускает равномерную аппроксимацию на К(с любой степенью точности) посредством полиномов от z.Необходимым и достаточным условием возможности такой аппроксимации является связность дополнения компакта К.Эта теорема для компактов без внутренних точек была доказана М. А. (1934), для замкнутых областей - М. В. (1945) и в общем случае - С. Н. (1951). Пусть
Е
п=
E
n(
f, K)
-наилучшее приближение функции
fна компакте
Кпосредством полиномов от
zстепени не выше
n(в равномерной метрике). Если
К -компакт со связным дополнением и функция
f голоморфна на
К,то последовательность {
Е
п} стремится к нулю быстрее некоторой геометрической прогрессии:
E
n<
q
n,0
<
q=
q
Другие направления исследований - равномерные и наилучшие приближения рациональными функциями, приближения целыми функциями, весовые приближения полиномами, приближения полиномами и рациональными функциями в интегральных метриках. Большое внимание уделяется проблематике, связанной с приближением функций нескольких комплексных переменных. Лит.:Уолш Д.-Л., Интерполяция и аппроксимация рациональными функциями в комплексной области, пер. с англ., М,, 1961; Маркушевич А. И., Теория аналитических функций, т. 2, М., 1968; Смирнов В. И.. Лебедев Н. А., Конструктивная теория функций комплексного переменного, М. - Л., 1964; Мергелян С. Н., Приближения функций комплексного переменного. в кн.: Математика в СССР за сорок лет. 1917-1957, т. 1, М., 1959, с. 383-98; Гончар А. А., Мергелян С. Н., Теория приближений функций комплексного переменного, в кн.: История отечественной математики, т. 4, кн. 1, К,, 1970, с. 112-78. А. А. Гончар. Приближённое интегрирование Приближённое интегри'рованиеопределённых интегралов, раздел вычислительной математики, занимающийся разработкой и применением методов приближённого вычисления определённых . Пусть y= f( x) -непрерывная функция на отрезке [ a, b] и интеграл
Если для функции f( x) известны значения первообразной F( x) при x= аи х= b,то по формуле Ньютона - Лейбница I( f) = F( b) - F( a)
В противном случае приходится искать др. пути вычисления
l
S
n
в котором точки x k, k= 1, 2,..., n, x kО [ a, b] ,называют узлами, а коэффициенты A k-весами. Для каждой непрерывной функции
f(
x) значение
I
R
n
Квадратурная формула содержит 2
n+ 1 не зависящих от функции
f(
x) параметров:
n, x
k, A
k(
k= 1, 2,...,
n)
,которые выбирают так, чтобы при
fО W погрешность её была допустимо малой. Точность квадратурной формулы для
fО W характеризует величина
rn(W) - точная верхняя грань ½
Rn
Пусть
Квадратурная формула, для которой W n(W) = r n(W), называется оптимальной на классе П. Веса и узлы в оптимальной квадратурной формуле могут быть произвольными или подчинёнными определённым связям. Различают два класса квадратурных формул: элементарные и составные. Разработано несколько методов построения элементарных квадратурных формул. Пусть w q ( x) , q= 0, 1,..., - в классе W, и любая f( x) О Q достаточно хорошо приближается линейными комбинациями первых функций w q ( x) .Пусть l(w q ) , q= 0, 1, 2,..., можно вычислить точно. Для каждого nпараметры квадратурной формулы можно определить из требования, чтобы I(w q ) = S n(w q ) , q= 0, 1,..., m, для возможно большего значения m.В методе Ньютона - Котеса в квадратурной формуле выбираются узлы x k,а определению подлежат веса A k.В методе Чебышева на веса A kзаранее накладываются некоторые связи [например, A k= ( b - а) /n] ,а определению подлежат узлы x k.В методе Гаусса определяются и веса A kи узлы x k.В методе Маркова jузлов ( j< n) считают заранее известными, а определяют веса и оставшиеся узлы. Точность полученных такими методами квадратурных формул существенно повышается при удачном выборе функций w q ( x) . Формулы Ньютона - Котеса строятся на основе системы функций w q = x q, q= 0 ,1,...; узлы x kразбивают отрезок интегрирования на равные части. Примерами таких формул являются , и . Поскольку заменой переменной интегрирование по [ а, b] сводится к интегрированию по отрезку [-1, 1], то для определения весов и узлов элементарных формул на [ а, b] достаточно знать их для отрезка [-1, 1]. В случае составных формул исходный интеграл представляется в виде:
и для вычисления интегралов по отрезкам [ a i, a i+1] применяются элементарные квадратурные формулы. В формулах Гаусса m= 2 n- 1, а при а= -1, b= 1 узлы x kявляются корнями P n( x) степени n,а A k=2(1 - x 2 k) -1( P’ n( x k)) -2 Квадратурная формула Чебышева существует при A k= l/n, l= b - аи x kО [ a, b] лишь для n= 1,..., 7, 9; в ней m= n -1. Применение равных весов минимизирует вероятностную ошибку, если значения f( x) содержат независимые случайные ошибки с одинаковой дисперсией. При вычислении интегралов от функций с периодом lнаиболее употребительны квадратурные формулы типа Гаусса:
Существуют квадратурные формулы для вычисления интегралов вида
где р( х) -фиксированная, т. н. весовая функция. Её подбирают так, чтобы для всех fО W функции f( x) хорошо приближалась линейными комбинациями функций w q ( x) . Для приближённого вычисления неопределённых интегралов их представляют как определённые интегралы с переменным верхним пределом и далее применяют указанные выше формулы. Таблицы узлов и весов, а также оценки погрешности квадратурных формул приводятся в специальных справочниках. Квадратурные формулы вычисления кратных интегралов иногда называются кубатурными формулами. Кратные интегралы можно вычислять как повторные интегралы, применяя описанные квадратурные формулы. Т. к. при увеличении кратности существенно возрастает количество узлов, то для вычисления кратных интегралов разработан ряд специальных формул. Вычисление интегралов на ЭВМ обычно осуществляется с помощью стандартных программ. В случае однократных интегралов наиболее употребительны стандартные программы с автоматическим выбором шага. Лит.:Крылов В. И., Приближенное вычисление интегралов, 2 изд., М., 1967; Бахвалов Н. С., Численные методы, М., 1973; Никольский С. М., Квадратурные формулы, М., 1958; Березин И. С., Жидков Н. П., Методы вычисления, 3 изд., ч. 1, М., 1966; Соболев С. Л., Введение в теорию кубатурных формул, М., 1974; Коробов Н. М., Теоретикочисловые методы в приближенном анализе, М., 1963. В. И. Лебедев. Приближённое решение Приближённое реше'ниедифференциальных уравнений, получение аналитических выражений (формул) или численных значений, приближающих с той или иной степенью точности искомое частное решение дифференциального уравнения. П. р. дифференциальных уравнений в виде аналитического выражения может быть найдено методом рядов (степенных, тригонометрических и др.), методом малого параметра, , , . Каждый из этих методов определяет один или несколько бесконечных процессов, с помощью которых при выполнении определённых условий можно получить точное решение задачи. Для получения П. р. останавливаются на некотором шаге процесса. Если решение ищется в виде бесконечного ряда, то за П. р. принимают конечный отрезок ряда. Например, пусть требуется найти решение дифференциального уравнения y'= f( x, у) ,удовлетворяющее начальным условиям у( х 0) = y 0,причём известно, что f( x, у) -аналитическая функция х, ув некоторой окрестности точки ( х 0, y 0) .Тогда решение можно искать в виде степенного ряда:
y(
x)
- y(
x
0)
=
Коэффициенты A kряда могут быть найдены либо по формулам: A 1= y’ 0= f( x 0, y 0) ;
либо с помощью .Метод рядов позволяет находить решение лишь при малых значениях величины х - х 0. Часто (например, при изучении периодических движений в небесной механике и теории колебаний) встречается случай, когда уравнение состоит из членов двоякого вида: главных и второстепенных, причём второстепенные члены характеризуются наличием в них малых постоянных множителей. Обычно после отбрасывания второстепенных членов получается уравнение, допускающее точное решение. Тогда решение основного уравнения можно искать в виде ряда, первым членом которого является решение уравнения без второстепенных членов, а остальные члены ряда расположены по степеням малых постоянных величин, входящих во второстепенные члены (малых параметров). При этом уравнения для коэффициентов при степенях малых параметров линейны, что облегчает их решение. В роли малого параметра иногда выступают начальные значения (например, при изучении колебаний около положения равновесия). Метод малого параметра был использован при решении задачи о возмущённом движении в небесной механике Л. и П. .Теоретическое обоснование этого метода дали А. М. и А. . К численным методам относятся методы, позволяющие находить П. р. при некоторых значениях аргумента (т. е. получать таблицу приближённых значений искомого решения), пользуясь известными значениями решения в одной или нескольких точках. Такими методами являются, например, метод Эйлера, метод Рунге и целый ряд разностных методов. Поясним эти методы на примере уравнения y’’ = f( x, у) с начальным условием у( х 0) = y 0. Пусть точное решение этого уравнения представлено в некоторой окрестности точки х 0в виде ряда по степеням h= х- х 0Основной характеристикой точности формул П. р. дифференциальных уравнений является требование, чтобы первые kчленов разложения в ряд по степеням hП. р. совпадали с первыми kчленами разложения в ряд по степеням hточного решения. Основная идея метода Эйлера заключается в применении метода рядов для вычисления приближённых значений решения у( х) в точках x 1, x 2,..., x nнекоторого фиксированного отрезка [ х 0, b] Так, для того чтобы вычислить у( х 1) ,где х 1= х 0+ h, h= ( b - x 0) /n,представляют у( х 1) в виде конечного числа членов ряда по степеням h= х 1- х 0. Например, ограничиваясь первыми двумя членами ряда, получают для вычисления у( xk) формулы:
Это т. н. метод ломаных Эйлера (на каждом отрезке [ xk ,x k+1] интегральная кривая заменяется прямолинейным отрезком - звеном ломаной Эйлера). Погрешность метода пропорциональна h 2. В методе Рунге вместо того, чтобы отыскивать производные, находят такую комбинацию значений f( x, у) в некоторых точках, которая даёт с определённой точностью несколько первых членов степенного ряда для точного решения уравнения. Например, правая часть формулы Рунге:
где
дает первые пять членов степенного ряда с точностью до величин порядка h 5. В разностных формулах П. р. удаётся несколько раз использовать уже вычисленные значения правой части. Решение ищется в виде линейной комбинации у( xi), h i и разностей D ih j, где h j= hf( x j, y j); Dh j= h j+1- h j; D ih j= D i-1h j+1- D i-1h j. Примером разностной формулы П. р. является экстраполяционная формула Адамса. Так, формула Адамса, учитывающая «разности» 3-го порядка:
даёт решение у( х) в точке x kсточностью до величин порядка h 4. Для уравнений 2-го порядка можно получить формулы численного интегрирования путём двукратного применения
формулы Адамса. Норвежский математик К. Стёрмер получил формулу:
особенно удобную для решения уравнений вида у''= f( x, у) .По этой формуле находят D 2 y n-1,а затем y n+1= y n+D y n+ 1+ D 2 y n-1. Найдя y n+1, вычисляют y’’ n+1= f( x n+1, y n+1) ,находят разности и повторяют процесс далее. Указанные выше численные методы распространяются и на системы дифференциальных уравнений. Значение численных методов решения дифференциальных уравнений особенно возросло с распространением ЭВМ. Кроме аналитических и численных методов, для П. р. дифференциальных уравнений применяются графические методы. В простейшем из них строят поле направлений, определяемое дифференциальным уравнением, т. е. в некоторых точках рисуют направления касательной к интегральной кривой, проходящей через эту точку. Затем проводят кривую так, чтобы касательные к ней имели направления поля (см. ). Лит.:Березин И. С., Жидков Н. П., Методы вычислений, 2 изд., т. 2, М.. 1962; Бахвалов Н. С., Численные методы, М., 1973: Коллатц Л., Численные методы решения дифференциальных уравнений, пер. с нем., М., 1953; Милн В. Э., Численное решение дифференциальных уравнений, пер, с англ., М., 1955. Приближённые вычисления Приближённые вычисле'ния,вычисления, в которых данные и результат (или по крайней мере только результат) являются числами, лишь приближённо представляющими истинные значения соответствующих величин. П. в. возникают в связи с численным решением задач и обусловлены неточностями, которые присущи формулировке задачи и способам её решения. Общие правила и теорию методов П. в. принято называть . Приближённые формулы Приближённые фо'рмулы,математические формулы, получаемые из формул вида f( x) = f*( x) + e( х), где e( х) рассматривается как погрешность и после оценки отбрасывается. Таким образом, П. ф. имеет вид f( x) » f*( x) .
Например, П. ф. (1 +
х)
2» 1 + 2
xполучается из точной формулы для (1 +
х)
2
при малых |
x|; этой формулой можно пользоваться при вычислении с точностью до сотых, тысячных, десятитысячных, если |
x| соответственно не больше 0,0707..., 0,0223..., 0,00707... Эта П. ф. даёт результат тем более точный, чем
хближе к 0. Но так бывает не всегда. Например, точность П. ф. tg
Выше (стр. 555) приведено несколько наиболее употребительных П. ф., причём показано, какого числа не должно превосходить | x| ,чтобы формула давала kточных десятичных знаков. Часто П. ф. получают с помощью разложения функций в ряды, например в ряд Тейлора. Чтобы уверенно применять П. ф., необходимо иметь оценку разности между точным и приближённым выражениями функции. Зная, например, что разность между sin
xи двучленом
«Прибой» «Прибо'й», легальное большевистское издательство, создано в ноябре 1912 в Петербурге во время (1912-1914), с 1913 начало выпуск литературы по вопросам социального страхования рабочих; с июля 1913 стало издательством ЦК РСДРП, по указанию которого главное внимание уделяло изданию политической агитационно-пропагандистской литературы по вопросам рабочего движения. Вышли сборники: «Марксизм и ликвидаторство» со статьями В. И. Ленина, «Страхование рабочих в России и на Западе» (2-й и 3-й выпуски), календарь «Спутник рабочего на 1914» (со статьей Ленина «Стачки в России») и др. В работе издательства участвовали А. И. Ульянова-Елизарова, М. С. Ольминский, Ф. И. Драбкина и др. В начале 1-й мировой войны 1914-18 в связи с цензурными репрессиями «П.» прекратил свою деятельность; издательство возобновило работу в марте 1917. Были выпущены работы Ленина «Письма о тактике». Письмо 1-е с приложением Апрельских тезисов; «Задачи пролетариата в нашей революции»; «Уроки революции»; «Материалы по пересмотру партийной программы»; «Грозящая катастрофа и как с ней бороться». В 1918 влилось в книгоиздательство «Коммунист». Лит.:Шварцман С. М., Книгоиздательство «Прибой» (1913-1914), в сборнике: «Книга», № 13, М., 1966. Прибой (в ткачестве) Прибо'йв ткачестве, продвижение уточной нити вдоль основы к опушке (краю) ткани. Одна из основных операций при формировании ткани на .Наиболее распространённый рабочий орган для П. - ;перемещающее уточную нить одновременно по всей ширине основы. П. на некоторых станках осуществляется непрерывно с помощью прижимов-уплотнителей утка ( ) ,профилированных дисков (многозевные ткацкие машины). Прибой (морской) Прибо'й, явление разрушения морской (озёрной) волны, происходящее в результате разбивания волн непосредственно у берега, при этом колебательные движения воды сменяются возвратно-поступательным движением .П. - основной фактор разрушения абразионных берегов и образования пляжей, сопровождаемый перемещением наносов на пляжах на аккумулятивных берегах. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
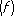 ||
c
Ј (
L
n
+ 1)
E
n
||
c
Ј (
L
n
+ 1)
E
n
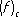 ,
,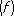 доставляют приближение, не очень сильно отличающееся от наилучшего. Подобная оценка имеет место и для приближений интерполяционными тригонометрическими полиномами с равноотстоящими узлами интерполирования, а также для приближений интерполяционными алгебраическими многочленами на отрезке [-1, 1] с узлами
доставляют приближение, не очень сильно отличающееся от наилучшего. Подобная оценка имеет место и для приближений интерполяционными тригонометрическими полиномами с равноотстоящими узлами интерполирования, а также для приближений интерполяционными алгебраическими многочленами на отрезке [-1, 1] с узлами
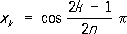 , k=
1, 2
,..., n,т. е. в нулях полинома Чебышева cos
narccos
x.Для основных встречающихся в анализе классов функций известны такие линейные операторы, построенные с помощью рядов Фурье или на основе интерполяционных полиномов, что значениями этих операторов являются полиномы, дающие на классе тот же порядок убывания приближений при
n® Ґ, что и наилучшие приближения.
, k=
1, 2
,..., n,т. е. в нулях полинома Чебышева cos
narccos
x.Для основных встречающихся в анализе классов функций известны такие линейные операторы, построенные с помощью рядов Фурье или на основе интерполяционных полиномов, что значениями этих операторов являются полиномы, дающие на классе тот же порядок убывания приближений при
n® Ґ, что и наилучшие приближения.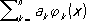 были бы наименьшими (т. н. задача о поперечнике класса функций). В этом направлении в дальнейшем было выяснено, например, что для ряда важных классов периодических функций наилучшими в указанном смысле системами являются тригонометрические полиномы.
были бы наименьшими (т. н. задача о поперечнике класса функций). В этом направлении в дальнейшем было выяснено, например, что для ряда важных классов периодических функций наилучшими в указанном смысле системами являются тригонометрические полиномы. < 1 (
n>
N)
.Если
f непрерывна на
Ки голоморфна во внутренних точках
К,то скорость её полиномиальной аппроксимации зависит как от свойств
f на границе
К(модуль непрерывности, дифференцируемость), так и от геометрических свойств границы
К.
< 1 (
n>
N)
.Если
f непрерывна на
Ки голоморфна во внутренних точках
К,то скорость её полиномиальной аппроксимации зависит как от свойств
f на границе
К(модуль непрерывности, дифференцируемость), так и от геометрических свойств границы
К.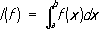
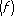 .Одним из путей является построение квадратурных формул, приближённо выражающих значение
I
.Одним из путей является построение квадратурных формул, приближённо выражающих значение
I
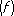 в виде линейной функции некоторого числа значений функции
f(
x)
и её производных. Квадратурной формулой, содержащей только значения функции
f(
x)
,называют выражение вида
в виде линейной функции некоторого числа значений функции
f(
x)
и её производных. Квадратурной формулой, содержащей только значения функции
f(
x)
,называют выражение вида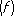 =
=
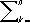 A
kf(
x
k)
,
A
kf(
x
k)
, может быть вычислено с помощью сумм
S
n
может быть вычислено с помощью сумм
S
n
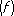 слюбой точностью. Выбор квадратурной формулы определяется классом W, к которому относят конкретную функцию
f(
x)
,способом задания функции и имеющимися вычислительными средствами. Погрешностью квадратурной формулы называется разность
слюбой точностью. Выбор квадратурной формулы определяется классом W, к которому относят конкретную функцию
f(
x)
,способом задания функции и имеющимися вычислительными средствами. Погрешностью квадратурной формулы называется разность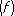 =
I
=
I
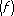 - S
n
- S
n
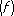 .
.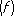 ½ на множестве W:
½ на множестве W: .
.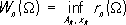
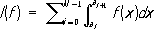
 .
.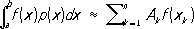
 .
.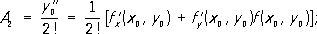
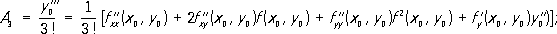
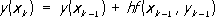 ,
,
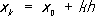
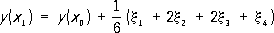 ,
,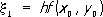 ;
;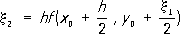 ;
;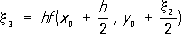 ;
;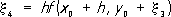
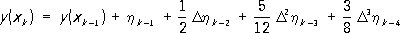
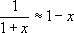
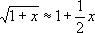

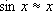

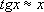

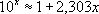


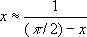 тем больше, чем
хближе к p/2.
тем больше, чем
хближе к p/2.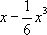 не превосходит по абсолютному значению
не превосходит по абсолютному значению
 ,легко убедиться, что П. ф.
,легко убедиться, что П. ф.
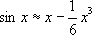 даёт значения sin
xс точностью до сотых, тысячных, десятитысячных, если
хсоответственно меньше 0,89 (51°), 0,55 (32°), 0,34 (20°).
даёт значения sin
xс точностью до сотых, тысячных, десятитысячных, если
хсоответственно меньше 0,89 (51°), 0,55 (32°), 0,34 (20°).