 |
|
Популярные авторы:: Горький Максим :: Желязны Роджер :: БСЭ :: Борхес Хорхе Луис :: Андреев Леонид Николаевич :: Чехов Антон Павлович :: Азимов Айзек :: Картленд Барбара :: Толстой Лев Николаевич :: Раззаков Федор Популярные книги:: The Boarding House :: Зовите меня Джо :: Дневник писателя :: Бурый волк :: Справочник по реестру Windows XP :: Великие неторопливые короли :: Подземная Москва :: Зимнее пламя :: Авторитет :: О мальчике и девочке, которые не замёрзли |
Большая Советская Энциклопедия (ПР)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ПР) - Чтение (стр. 11)
В условиях социализма предвидение основных тенденций и событий общественной жизни составляет основу научного руководства обществом. Методология П. н., включая исследование логических структур, применяемых в различных схемах предвидения и предсказания, необходима для разработки специальных методик точного количественного прогнозирования. При этом необходимо учитывать, что каждый акт П. н. по схеме может оказывать влияние на ход исторических событий, видоизменяя их в рамках объективных закономерностей. В условиях буржуазного общества предвидение социальных процессов и событий осложняется анархией производства, неконтролируемыми социально-экономическими кризисами, волюнтаризмом и др. факторами, характерными для экономики, политики и культуры капитализма. Это привело к появлению концепций, отрицающих возможность предвидения развития общественных явлений. Главными направлениями в исследовании основ П. н. являются: логическое исследование его структур; сравнительные исследования П. н. в естественных и общественных науках; методология П. н. основных социальных процессов в современном обществе; методика и техника различных специальных видов предвидения, предсказания и прогнозирования, применяемых в народном хозяйстве, политике, культуре, в области индивидуального поведения людей. Лит.Виноградов В. Г., Гончарук С. И., Законы общества и научное предвидение, М., 1972; Виноградов В. Г., Научное предвидение (Гносеологический анализ), М., 1973; Руденко К. П., Логika i наукове передбачення. Логiкo-гносеологiчний аналiз, Кипв, 1972; SiciDski A., Prognozy a nauka, Warsz., 1969. А. И. Ракитов. Предводителев Александр Саввич Предводи'телевАлександр Саввич [30.8(11.9).1891, село Букрино, ныне Старожиловского района Рязанской области, - 27.12.1973, Москва], советский физик, член-корреспондент АН СССР (1939). Окончил Московский университет (1915), с 1935 профессор там же. Одновременно с 1939 заведующий лабораторией Энергетического института АН СССР. Основные труды по молекулярной физике, гидродинамике, теплофизике. Исследовал процессы горения, распространения волн в жидких и газовых средах, физические свойства жидкостей и др. Разрабатывал теорию гетерогенного горения. Совместно с другими исследовал процессы горения углерода (результаты этих исследований изложены в монографии «Горение углерода», 1949; Государственная премия СССР, 1950). Предложил методы расчёта констант рабочих веществ. Награжден 2 орденами Ленина, 5 др. орденами, а также медалями. Лит.:Александр Саввич Предводителев (К 80-летию со дня рождения), «Успехи физических наук», 1971, т. 105, в. 3. Предвыходные и предпраздничные дни Предвыходны'е и предпра'здничные дни, по советскому праву накануне праздничных дней продолжительность работы рабочих и служащих (кроме тех, кто уже имеет ) сокращается на 1 чкак при 5-, так и при 6-дневной рабочей неделе. В предвыходные дни продолжительность работы при 6-дневной рабочей неделе не может превышать 6 ч. Предгорные лестницы Предго'рные ле'стницы, выровненные поверхности, расположенные в виде ступеней по окраинам наиболее высокой и расчленённой центральной части горной страны. Понятие о П. л. введено в 20-х гг. 20 в. В. ,который развивал представление о П. л. как о разновозрастных ,образующихся при непрерывном равномерном поднятии горной страны и одновременном вовлечении в поднятие всё новых территорий прилегающих равнин. Как показали последующие исследования, П. л. не типичны для внешнего облика горных стран; в том случае, когда многоярусные выровненные поверхности всё же имеют место, они являются принадлежностью горного рельефа, а не предгорий; т. о., неточен сам термин «П. л.» (правильнее было бы говорить о горной лестнице). Объяснение, которое дал Пенк происхождению П. л., неудовлетворительное, т.к. непрерывное плавное поднятие горной страны не может сопровождаться образованием «ступеней». Множественность денудационных поверхностей обычно является следствием смены периодов быстрого поднятия земной коры периодами относительного покоя или результатом деформации одной и той же денудационной поверхности тектоническими процессами, благодаря чему различные её части оказываются на разных высотах. Предгорный прогиб Предго'рный проги'б,то же, что или . Предгорья Предго'рья, пониженные окраинные части ,характеризующиеся холмистым или низкогорным рельефом. Преддверноулитковый нерв Преддверноули'тковый нерв(n. vestibulo-cochlearis) у человека (устаревшее - слуховой и статический нерв), 8-я пара черепно-мозговых нервов. Состоит из двух функциональных частей - вестибулярной (проводник импульсов от органа равновесия) и улитковой, воспринимающей звуковые раздражения (см. ) .Вестибулярная часть начинается от узла преддверия, лежащего на дне внутреннего слухового прохода. Периферические отростки нервных клеток этого узла подходят к рецепторным элементам мешочка, маточки и ампул перепончатых полукружных каналов внутреннего уха. Улитковая часть берёт начало от спирального узла, залегающего в основании костной пластинки улитки. Периферические отростки клеток данного узла вступают в тесные связи с рецепторными аппаратами спирального (кортиева) органа, расположенного по всей длине улиткового канала перепончатого лабиринта. Центральные отростки преддверного и спирального узлов выходят из внутреннего уха и в составе соответствующих частей нерва направляются к основанию мозга, кнаружи от оливы продолговатого мозга они вступают в него и после объединения достигают своих ядер, локализованных в углах ромбовидной ямки. При поражении волокон улитковой части П. н. (инфекционном или травматическом) могут наступить расстройства слуха (вплоть до глухоты), при нарушениях вестибулярной части - нарушение равновесия, головокружение. Преддоговорные споры Преддогово'рные спо'ры,в СССР споры, возникающие при заключении гражданско-правовых договоров между государственными, кооперативными и общественными организациями в случае недостижения соглашения о содержании конкретного договора. Порядок разрешения П. с. регулируется Основами гражданского законодательства 1961, ГК союзных республик и др. нормативными актами (например, Положением о порядке предъявления и рассмотрения претензий предприятиями, учреждениями и организациями и урегулирования разногласий по хозяйственными договорам, 1973). Разногласия при заключении договора, основанного на обязательном для обеих сторон плановом задании, разрешаются соответствующим арбитражем, а также судом, если хотя бы одной из сторон является колхоз или межколхозная организация. При заключении договора, не основанного на плановом задании, П. с. могут разрешаться соответственно арбитражем или судом при условии, если это специально предусмотрено законом либо соглашением сторон (например, ст. 166 ГК РСФСР). В установленных законодательством случаях П. с. разрешаются в особом порядке (например, разногласия между поставщиками и покупателями при заключении договоров поставки на ярмарках по оптовой продаже товаров народного потребления разрешаются ярмарочными комитетами). Непременному урегулированию подлежат разногласия, возникающие при заключении хозяйственного договора, даже если обязательными для организаций правилами не предусмотрены порядок и сроки согласования условий договора. В основе решения по П. с. лежит рассмотрение компетентным органом т. н. протокола разногласий, представляемого, как правило, стороной, от которой исходит инициатива заключения договора. В протоколе излагается (в редакции каждой из сторон) содержание условий договора, по которым обнаружились расхождения. Если в процессе рассмотрения спора арбитражем (судом) соглашение между сторонами не достигнуто, арбитраж (суд) сам принимает решение по спорным вопросам, обязательное для сторон, и тем самым договор считается заключённым. Предел Преде'л,одно из основных понятий математики. П. - постоянная, к которой неограниченно приближается некоторая переменная величина, зависящая от другой переменной величины, при определённом изменении последней. Простейшим является понятие П. числовой последовательности, с помощью которого могут быть определены понятия П. функции, П. последовательности точек пространства, П. интегральных сумм. Предел последовательности.Пусть задана последовательность действительных чисел x n, n= 1 ,2,... Число аназывается пределом этой последовательности, если для любого числа e > 0 существует такой номер n e,что для всех номеров n³ n eвыполняется неравенство | x n- a| < e. В этом случае пишется
(lim - первые буквы латинского слова limes), или x n® aпри n® Ґ. Если последовательность имеет П., то говорят, что она сходится. Так, последовательность 1/ n, n= 1, 2,..., сходится и имеет своим П. число 0. Не всякая последовательность имеет П., например последовательность 1, -1, 1,..., (-1) n+1,... не имеет П. Последовательность, не имеющая П., называется расходящейся. На геометрическом языке существование у последовательности П., равного а,означает, что каждая окрестность точки асодержит все члены данной последовательности, за исключением, быть может, их конечного числа. Для П. последовательностей имеют место формулы
Эти формулы справедливы в предположении, что П., стоящие в их правых частях, существуют, причём в формуле для П. частного
x
n/
y
nнадо ещё дополнительно потребовать, чтобы
т. е. при предельных переходах нестрогие неравенства сохраняются (но из
x
n<
y
nне вытекает
Последовательность a n, n= 1, 2,..., сходящаяся к нулю, называется бесконечно малой. Последовательность сходится к какому-либо числу тогда и только тогда, когда разность между членами последовательности и этим числом является бесконечно малой последовательностью (т. о., общее понятие П. последовательности сводится к понятию ) .Так, например, последовательность 1/ 2, 2/ 3, 3/ 4, ..., n/( n+ 1),... имеет своим П. единицу, поскольку разность 1 - n/( n+ 1) = 1/( n+ 1), n= 1, 2,... является бесконечно малой последовательностью. Всякая возрастающая (убывающая) последовательность, ограниченная сверху (соответственно снизу), сходится. Например, если для заданного числа
аобозначить через a
nприближённое значение его корня
Для того чтобы сходилась произвольная последовательность x n,необходимо и достаточно, чтобы она удовлетворяла критерию Коши: для любого числа e > 0 существует такой номер N e ,что для всех номеров m³ N eи n³ N eвыполняется неравенство | x n- x m| < e. Если последовательность x n, n= 1, 2,..., такова, что для числа e > 0 существует такой номер n e,что для всех номеров n³ n eвыполняется неравенство | x n| > e ,то последовательность x n, называется бесконечно большой и пишется
Если же при этом для любого e > 0 существует такой номер
n
e,что
x
n>
e
(соответственно
x
n< -e) для всех
n³
n
e,то пишется
Эти П. называются бесконечными. Например,
Частичные пределы. Верхний и нижний пределы. П. (конечный и бесконечный) какой-либо подпоследовательности называется частичным пределом последней. Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность (теорема Больцано - Вейерштрасса), а из всякой неограниченной - бесконечно большую. В множестве всех частичных П. последовательности всегда имеется как наибольший, так и наименьший (конечный или бесконечный). Наибольший (соответственно наименьший) частичный П. последовательности
x
n, n =1, 2,..., называют её верхним (соответственно нижним) пределом и обозначается
Последовательность имеет конечный или бесконечный П. тогда и только тогда, когда её верхний П. совпадает с нижним, при этом их общее значение и является её П. Конечный верхний П. последовательности можно также определить как такое число а, что при любом e > 0 существует бесконечно много членов последовательности, больших, чем а -e, и лишь не более, чем конечное число членов, больших, чем a+ e . Предел функции. Пусть функция f, принимающая действительные значения, определена в некоторой окрестности точки x 0,кроме, быть может, само'й точки x 0.Функция fимеет П. в точке x 0,если для любой последовательности точек x n, n= 1, 2,..., x n¹ x 0,стремящейся к точке x 0,последовательность значений функции f( x n) сходится к одному и тому же числу А,которое и называется пределом функции fв точке x 0,(или при x® x 0) при этом пишется
или f( x) ® Aпри x ® x 0 В силу этого определения на П. функций переносятся свойства П. суммы, произведения и частного последовательностей, а также сохранение неравенств при предельном переходе. Определение П. функции можно сформулировать и не прибегая к понятию П. последовательности: число Аназывается пределом функции fв точке x 0,если для любого числа e > 0 существует такое число d > 0, что для всех точек х¹ x 0,удовлетворяющих условию ½ х - x 0½ < d , x¹ x 0,выполняется неравенство ½ f( x) -A½ < e. Все основные элементарные функции: постоянные, х a , a x, sin x,cos x,tg xи ctg xи arcsin x,arccos x,arctg xи arcctg xво всех внутренних точках своих областей определения имеют П., совпадающие с их значениями в этих точках. Но это не всегда бывает так. Функция
являющаяся суммой бесконечной геометрической прогрессии со знаменателем q= 1/(1 + x 2) ,0 < q< 1 ,в точке х= 0 имеет П., равный 1, ибо f( x) = 1 + x 2при x¹ 0 .Этот П. не совпадает со значением функции fв нуле: f(0) = 0. Функция же
вовсе не имеет П. при х® 0 ,ибо уже для значений x n= 1 /(p/2 + p n) последовательность соответствующих значений функции f( x n) = ( -1) n не имеет П. Если П. функции при х® х 0равен нулю, то она называется бесконечно малой при х® х 0.Например, функция sin xбесконечно мала при х® 0 .Для того чтобы функция fимела при х® х 0П., равный А,необходимо и достаточно, чтобы f( x) = A+ a( x) ,где a( х) является бесконечно малой при х® х 0
Если при определении П. функции
fв точке
x
0рассматриваются только точки
х,лежащие левее (правее) точки
x
0,то получающийся П. называется пределом слева (справа) и обозначается
Функция имеет П. в некоторой точке, если её П. слева в этой точке равен её П. справа. Понятие П. функции обобщается и на случай, когда аргумент стремится к бесконечности:
Например,
означает, что для любого e > 0 существует такое d > 0, что для всех х,удовлетворяющих условию x > d, выполняется неравенство ½ f( x) - А½ < e. Примером функций, всегда имеющих П., являются
.Так, если функция
fопределена на интервале (
а, b) и не убывает, то в каждой точке
х, а<
х<
b,она имеет конечный П. как слева, так и справа; в точке в П. справа, который конечен тогда и только тогда, когда функция
fограничена снизу, а в точке
bП. слева, конечный в том и только в том случае, когда функция ограничена сверху. В общем же случае стремление к П. может носить разный, необязательно монотонный характер. Например, функция
f(
x)
=
x
Т. н. внутренний критерий (критерий Коши) существования П. функции в точке состоит в следующем: функция fимеет в точке x 0П. в том и только в том случае, если для любого e > 0 существует такое d > 0, что для всех точек х'и х'',удовлетворяющих условию ½ х’ - x 0½ < d, ½ x'' - x 0½ < d, x' ¹ x 0, x'’¹ x 0,выполняется неравенство ½ f( x'') - f( x')½ < e. Для функций, как и для последовательностей, определяются понятия бесконечных П. вида
означает, что для любого e > 0 существует такое d > 0, что для всех х,удовлетворяющих условию х< -d, выполняется неравенство f( x) > e . Расширение понятия предела функции. Если функция fопределена на некотором множестве Ечисловой прямой и точка x 0такова, что в любой её окрестности имеются точки множества Е,то аналогично данному выше определению П. функции, заданной в некоторой окрестности точки x 0,кроме, быть может, самой точки x 0,определяется понятие предела функции по множеству Е
для этого следует лишь в определении П. всегда дополнительно требовать, чтобы точка хпринадлежала множеству Е: хО Е. П. последовательности x n, n= 1, 2 ,..., является при таком определении понятия П. частным случаем П. функции по множеству, а именно функции f,определённой на множестве натуральных чисел n формулой f( n) = x n, n= 1, 2 ,.... Функция, равная нулю при рациональных
хи единице при иррациональных, не имеет П. при
х® 0
,однако по множеству рациональных чисел она при
х® 0 имеет П., равный нулю. Понятие П. числовой функции по множеству переносится и на функции многих переменных. В этом случае можно говорить, в частности, о П. в данном направлении, о П. по данной кривой, по данной поверхности и т.д. Кроме того, для функций многих переменных возникает понятие повторного предела, когда предельный переход совершается последовательно по разным переменным, например
Предел интегральных сумм. Ещё одно важное понятие П. возникает при определении .Пусть, например, функция fопределена на отрезке [ a, b] .Совокупность { x i} таких точек x i,что a= x 0< x 1< ...< x i< ...< x n-1< x n = b, наз. разбиением отрезка [ a, b]. Пусть x i-1 Ј x I < x i,D x i = x i- x i-1, i= 1, 2,..., n.Тогда сумма f(x 1 )D x 1+ f(x 2 )D x 2+ ...+ f(x n )D x nназывается интегральной суммой функции f. Число Аявляется пределом интегральных сумм и называется определённым интегралом:
если для любого e > 0 существует такое d > 0, что каково бы ни было разбиение { xi} отрезка [ a, b] ,для которого D x i < d, и каковы бы ни были точки x i, x i-1 Ј x I Ј x i, i= 1, 2,..., n,выполняется неравенство ½ f(x 1)D x 1+ f(x 2)D x 2+... + f(x n)D x n - A| < e. Понятие П. интегральных сумм может быть введено и с помощью П. последовательности. Обобщения понятия предела. Ввиду разнообразия употребляемых в математике специальных видов понятия П. естественно возникло стремление включить их как частный случай в то или иное общее понятие П. Например, можно ввести понятие П., обобщающее как понятие П. функции, так и понятие П. интегральных сумм. Система S непустых подмножеств некоторого множества Еназывается направлением, если для каждых двух подмножеств Аи Вэтой системы выполняется одно из включений АМ Вили BМ Aи пересечение всех множеств из S пусто. Пусть на множестве Езадана числовая функция f.Число аназывается пределом функции fпо направлению S, если для любого e > 0 существует такое множество Аиз S, что во всех его точках выполняется неравенство | f( x) - а| < e .При определении П. функции fв точке x 0за направление следует взять совокупность всех окрестностей этой точки с достаточно малыми радиусами за вычетом самой точки х 0 .При определении П. интегральных сумм функции f, заданной на отрезке [ а, b] ,следует рассмотреть множество Е,элементами которого являются всевозможные разбиения отрезка [ а, b] с выбранными в них точками x i. Подмножества E hмножества Е,отвечающие разбиениям, длины D x i, отрезков которых не превышают h, образуют направление. П. интегральных сумм (которые, очевидно, являются функциями, определёнными на множестве Е) по указанному направлению является интеграл. Понятие П. обобщается на более широкие классы функций, например на функции, заданные на частично упорядоченных множествах, или на функции, являющиеся отображениями одного пространства (метрического или, более общо, топологического) на другое. Наиболее полно задача определения П. решается в топологии и означает в общем случае, что некоторый объект, обозначенный f( x) ,меняющийся при изменений др. объекта, обозначенного через х,при достаточно близком приближении объекта хк объекту х 0сколь угодно близко приближается к объекту А.Основным в такого рода понятиях П. является понятие близости объектов хи x 0 , f( x) и А,которые нуждаются в математическом определении. Только после того как это будет сделано, высказанному определению П. можно будет придать чёткий смысл и оно станет содержательным. Различные понятия близости и изучаются, в частности, в топологии. Встречаются, однако, понятия П. др. природы, не связанные с топологией, например понятие П. последовательности множеств. Последовательность множеств A n, n= 1, 2,..., называется сходящейся, если существует такое множество А,называемое её пределом, что каждая его точка принадлежит всем множествам A n ,начиная с некоторого номера, и каждая точка из объединения всех множеств A n ,не принадлежащая A, принадлежит лишь конечному числу A n . Историческая справка. К понятию П. вплотную подошли ещё древнегреческие учёные при вычислении площадей и объёмов некоторых фигур и тел с помощью .Так, ,рассматривая последовательности вписанных и описанных ступенчатых фигур и тел, с помощью метода исчерпывания доказывал, что разность между их площадями (соответственно объёмами) может быть сделана меньше любой наперёд заданной положительной величины. Включая в себя представление о бесконечно малых, метод исчерпывания являлся зародышем теории П. Однако в явном виде в древнегреческой математике понятие П. не было сформулировано, не было создано и каких-либо основ общей теории. Новый этап в развитии понятия П. наступил в эпоху создания дифференциального и интегрального исчислений. Г. ,И. ,Б. ,Б. и др. широко используют при вычислении площадей и объёмов , метод актуальных бесконечно малых, т. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 |
|||||||
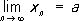
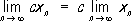 (
c- постоянная)
(
c- постоянная)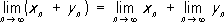
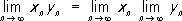
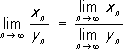
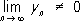 . Если
x
nЈ
y
nи последовательности
x
nи
y
n, n= 1, 2,... сходятся, то
. Если
x
nЈ
y
nи последовательности
x
nи
y
n, n= 1, 2,... сходятся, то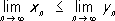
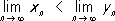 ,например, 1/
n> 0,
n=
1, 2,... однако
,например, 1/
n> 0,
n=
1, 2,... однако
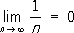 ). Если
). Если
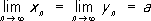 и
x
nЈ
z
nЈ
y
n,то последовательность
z
n, n= 1,
2,
...,сходится к тому же П.:
и
x
nЈ
z
nЈ
y
n,то последовательность
z
n, n= 1,
2,
...,сходится к тому же П.: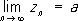
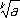 (
k- натуральное число) с
nдесятичными знаками после запятой, вычисленное с недостатком, то
a
nЈ
a
n+1Ј
(
k- натуральное число) с
nдесятичными знаками после запятой, вычисленное с недостатком, то
a
nЈ
a
n+1Ј
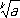 ,
n= 1, 2, …, поэтому последовательность
a
n,сходится, причём из неравенства 0 Ј
,
n= 1, 2, …, поэтому последовательность
a
n,сходится, причём из неравенства 0 Ј
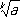 -
a
nЈ 10
-nследует, что
-
a
nЈ 10
-nследует, что
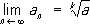 . Др. примером возрастающей ограниченной сверху последовательности является последовательность длин периметров правильных многоугольников, вписанных в данную окружность, к длине которой сходится эта последовательность.
. Др. примером возрастающей ограниченной сверху последовательности является последовательность длин периметров правильных многоугольников, вписанных в данную окружность, к длине которой сходится эта последовательность.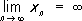
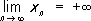 (соответственно
(соответственно
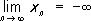 )
)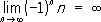 . В случае же последовательности
n
2, n= 1, 2, …,, можно написать не только
. В случае же последовательности
n
2, n= 1, 2, …,, можно написать не только
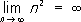 но и более точное равенство
но и более точное равенство
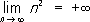 . Само собой разумеется, что бесконечно большие последовательности не являются сходящимися в смысле данного выше определения этого понятия. На бесконечные П. переносятся далеко не все свойства конечных П. Например, последовательности x
n
=
nи
y
n=
. Само собой разумеется, что бесконечно большие последовательности не являются сходящимися в смысле данного выше определения этого понятия. На бесконечные П. переносятся далеко не все свойства конечных П. Например, последовательности x
n
=
nи
y
n=
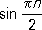 - nбесконечно большие, а последовательность
x
n+
y
n,, n= 1, 2,..., ограниченная и к тому же расходящаяся.
- nбесконечно большие, а последовательность
x
n+
y
n,, n= 1, 2,..., ограниченная и к тому же расходящаяся. (соответственно
(соответственно
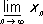 )
.Например,
)
.Например,
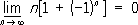

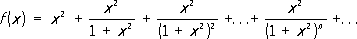 ,
,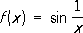 ,
x¹ 0,
,
x¹ 0,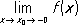 (соответственно
(соответственно
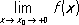 ).
). ,
,
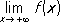 ,
,
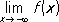

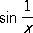 при
х® 0 стремится к нулю, бесконечное число раз переходя от возрастания к убыванию и обратно.
при
х® 0 стремится к нулю, бесконечное число раз переходя от возрастания к убыванию и обратно.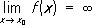 ,
,
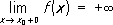 ,
,
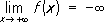 и т.д.; в этих случаях функция
f называется бесконечно большой при
х®
х
0,При
х®
х
0+ 0 или При
х® +Ґ
соответственно и т.д. Например,
и т.д.; в этих случаях функция
f называется бесконечно большой при
х®
х
0,При
х®
х
0+ 0 или При
х® +Ґ
соответственно и т.д. Например,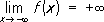
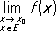 ,
, . Распространяется понятие П. и на функции, которые могут принимать не только действительные, но и комплексные значения.
. Распространяется понятие П. и на функции, которые могут принимать не только действительные, но и комплексные значения.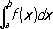 ,
,