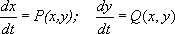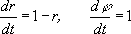|
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ПР)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ПР) - Чтение (стр. 12)
е. таких бесконечно малых, которые, по их представлению, являются неизменными величинами, не равными нулю и вместе с тем меньшими по абсолютной величине любых положительных конечных величин. Продолжает в этот период применяться и развиваться и метод исчерпывания (
из Сен-Винцента, П.
,Х.
и др.). На основе интуитивного понятия П. появляются попытки создать общую теорию П. Так, И.
первый отдел первой книги («О движении тел») своего труда «Математические начала натуральной философии» посвящает своеобразной теории П. под названием «Метод первых и последних отношений», которую он берёт за основу своего
.В этой теории Ньютон взамен актуальных бесконечно малых предлагает концепцию «потенциальной» бесконечно малой, которая лишь в процессе своего изменения становится по абсолютной величине меньше любой положит, конечной величины. Точка зрения Ньютона была существенным шагом вперёд в развитии представления о П. Понятие П., намечавшееся у математиков 17 в., в 18 в. постепенно всё больше анализировалось (Л.
,Ж.
, Л.
,братья
и др.) и уточнялось. В этот период оно служило лишь для попыток объяснить правильность дифференциального и интегрального исчисления и ещё не являлось методом разработки проблем математического анализа.
Современная теория П. начала формироваться в начале 19 в. в связи с изучением свойств различных классов функций, прежде всего непрерывных, а также в связи с попыткой доказательства существования ряда основных объектов математического анализа (интегралов функций действительных и комплексных переменных, сумм рядов, алгебраических корней и более общих уравнений и т.п.). Впервые в работах О. понятие П. стало основой построения математического анализа. Им были получены основные признаки существования П. последовательностей, основные теоремы о П. и. что очень важно, дан внутренний критерий сходимости последовательности, носящий теперь его имя. Наконец, он определил интеграл как П. интегральных сумм и изучил его свойства, исходя из этого определения. Окончательно понятие П. последовательности и функции оформилось на базе теории действительного числа в работах Б. и К. .Из дальнейших обобщений понятия П. следует отметить понятия П., данные в работах С. О. (опубликовано в 1923), американских математиков Э. Г. Мура и Г. Л. Смита (1922) и французского математика А. Картана (1937). Лит.:Александров П. С., Введение в общую теорию множеств и функций, М. - Л., 1948; Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., т. 1-2, М., 1971-73; Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1-2, М., 1970; Никольский С. М., Курс математического анализа, т. 1-2, М., 1973; Смирнов В. И., Курс высшей математики, 22 изд., т. 1, М., 1967. Л. Д. Кудрявцев. Предельная равнина Преде'льная равни'на,почти равнина, то же, что . Предельная точка Преде'льная то'чкамножества А,такая точка x пространства, сколь угодно близко от которой имеются отличные от x точки множества А,т. е. в любой которой содержится бесконечное множество точек из А.Характеристическим свойством П. т. множества Aявляется существование по крайней мере одной сходящейся к ней различных точек множества А.П. т. множества Ане обязана ему принадлежать. Так, например, всякая точка числовой прямой является П. т. для множества Арациональных её точек: ко всякому как рациональному, так и иррациональному числу можно подобрать сходящуюся к нему последовательность различных рациональных чисел. Не всякое бесконечное множество имеет П. т. - таково, например, множество всех целых чисел. Однако всякое бесконечное и ограниченное множество любого евклидова пространства имеет по крайней мере одну П. т. Лит.:Александров П. С., Введение в общую теорию множеств и функций, М. - Л., 1948. Предельная эффективность капитала Преде'льная эффекти'вность капита'ла(англ. marginal efficiency of capital), термин буржуазной политической экономии, означающий ожидаемую на дополнительный капитал. Это понятие наиболее четко сформулировано Дж. М. (Великобритания) и получило распространение в работах представителей .По Кейнсу, П. э. к. - первое определяющее, которым руководствуется капиталист при решении вопроса об ,т.к. их размер зависит от той нормы прибыли, которую он рассчитывает получить. Вторым определяющим выступает процентная ставка на капитал. Капиталист проводит сравнение между П. э. к. и нормой .Инвестирование осуществляется лишь в том случае, если процентная ставка на капитал ниже нормы прибыли, ожидаемой от капиталовложений. Чем больше разрыв между этими показателями, тем сильнее побуждение капиталиста к инвестированию. Т. о., объём текущих инвестиций зависит от соотношения между П. э. к. и нормой процента: повышение нормы процента вызывает понижение П. э. к. и уменьшение инвестиций, понизившаяся норма процента и повысившаяся доступность ,наоборот, вызывают рост инвестиций. Кейнс исходит из предположения, что предприниматель расширяет свои инвестиции до тех пор, пока П. э. к. не снизится до уровня нормы процента. Однако такое предположение несостоятельно. Во-первых, Кейнс считает, что предприниматель применяет только .В действительности же самая возможность использования ссудного капитала обусловлена наличием собственного капитала. Поэтому вопрос о норме процента имеет подчинённое значение для предпринимателя. Во-вторых, Кейнс признаёт распространённый в буржуазной политической экономии закон убывающей производительности капитала, согласно которому с увеличением вложения каждой дополнительной единицы капитала его производительность или эффективность снижается. Однако Кейнс не отвечает на вопрос, почему с увеличением применяемого в производстве капитала норма прибыли должна снижаться и почему в конечном счёте она должна снизиться до нормы процента. Теория П. э. к. Кейнса является вульгарным истолкованием имеющейся в капиталистической действительности и вскрытой ещё К. Марксом тенденции нормы прибыли к понижению (см. ) .Кейнс назвал эту тенденцию снижением П. э. к. и связал её с избыточным предложением капитала. По Кейнсу, рост инвестиций приводит к созданию новых капитальных благ, конкурирующих со старыми. Расширение выпуска продукции, считает он, неминуемо должно привести к снижению цен, что уменьшит ожидаемую прибыль. Такое явление может продолжаться до тех пор, пока норма процента не превысит П. э. к. Если же норма процента упадёт до нуля, капиталы будут непрерывно предлагаться до тех пор, пока они не насытят до предела рынок. В этом случае возникнут избыточные капиталы, не находящие применения, и норма прибыли катастрофически снизится. Т. о., Кейнс даёт искажённый анализ тенденции нормы прибыли к понижению, сохраняющей свою силу и в условиях монополистического капитализма. В его толковании не проводится чёткого различия между нормой и массой прибыли, превратно объясняются причины, вызывающие снижение нормы прибыли, неправильно показывается влияние этого понижения на капиталистическое накопление. Лит.:Кейнс Дж. М., Общая теория занятости, процента и денег, пер. с англ., М., 1948; Хаберлер Г., Процветание и депрессия, пер, с англ., М., 1960; Блюмин И. Г., Критика буржуазной политической экономии, т. 2, М., 1962. С. С. Носова. Предельно-допустимая концентрация Преде'льно-допусти'мая концентра'ция(ПДК), максимальное количество вредного вещества в единице объёма (воздуха, воды или др. жидкостей) или веса (например, пищевых продуктов), которое при ежедневном воздействии в течение неограниченно продолжительного времени не вызывает в организме каких-либо патологических отклонений, а также неблагоприятных наследственных изменений у потомства. Для установления ПДК используют расчётные методы, результаты биологических экспериментов, а также материалы динамических наблюдений за состоянием здоровья лиц, подвергшихся воздействию вредных веществ. Уровни ПДК одного и того же вещества различны для разных объектов внешней среды (например, в СССР для свинца и его неорганических соединений ПДК в воде водоёмов хозяйственно-питьевого назначения - 0,1 мг/л,в воздухе производственных помещений - 0,01 мг/м 3,в атмосферном воздухе - 0,007 мг/м 3) .В СССР при нормировании ПДК учитывают воздействие вещества на людей любого возраста (в т. ч. и больных) в течение всей жизни, а также др. факторы (например, влияние на общий санитарный режим водоёма, возможности возникновения неприятных запахов в окружающем воздухе и т.д.). Правилами по охране поверхностных вод определены раздельные ПДК для водоёмов хозяйственно-питьевого и рыбопромыслового назначения. Установлено, что принятые уровни ПДК веществ в атмосферном воздухе, рассчитанные на охрану здоровья человека, в ряде случаев недостаточны для охраны зелёных насаждений; современной разрабатываются нормативы ПДК, учитывающие вредные влияния соответствующих веществ и на зелёные насаждения. Уровни ПДК включены в ГОСТы, санитарные нормы и др. нормативные документы, обязательные для исполнения на всей территории СССР; их учитывают при проектировании технологических процессов, оборудования, очистных устройств и пр. в порядке санитарного надзора систематически контролирует соблюдение нормативов ПДК в воде водоёмов хозяйственно-питьевого водопользования (см. ) ,атмосферном воздухе (см. ) и в воздухе производственных помещений; контроль за состоянием водоёмов рыбопромыслового назначения осуществляют органы рыбнадзора. В зарубежных социалистических странах перечень нормируемых веществ и уровни их ПДК аналогичны нормативам в СССР. В некоторых капиталистических странах также установлены ПДК для отдельных вредных веществ в водоёмах хозяйственно-питьевого водопользования, атмосферном воздухе и воздухе рабочих помещений. Однако, по мнению сов. учёных-гигиенистов, количество нормируемых веществ является недостаточным, а уровни их ПДК в большинстве случаев завышены. А. М. Сточик. Предельное состояние Преде'льное состоя'ниев строительной технике, состояние строительной конструкции или основания здания (сооружения), при котором они перестают удовлетворять эксплуатационным требованиям. Понятием «П. с.» пользуются при расчёте конструкций по методу того же названия, разработанному в СССР и введённому (СНиП) в 1955. По сравнению с ранее применявшимися методами (по допускаемым напряжениям и по разрушающим нагрузкам) метод расчёта по П. с. является более совершенным; он отличается полнотой оценки несущей способности и надёжности конструкций благодаря учёту вероятностных свойств действующих на конструкции нагрузок и сопротивлений этим нагрузкам, особенностей работы отдельных видов конструкций, а также пластических свойств материалов. В методе расчёта по П. с. вместо ранее применявшегося единого коэффициента запаса прочности используют несколько независимых коэффициентов, каждый из которых имеет определенное значение в обеспечении надёжности конструкции и гарантии от возникновения П. с. Основной из них: коэффициент безопасности по материалу (и грунту), учитывающий статистическую изменчивость прочностных свойств материалов (грунтов), а также некоторые др. факторы, исключающие или сильно затрудняющие возможность статистической оценки, например отличие сопротивлений материалов в конструкциях от определяемых испытаниями контрольных образцов; коэффициент перегрузки, учитывающий возможное отклонение величин нагрузок от исходных (нормативных) значений из-за изменчивости нагрузок и отступления от условий нормальной эксплуатации; коэффициент условий работы, учитывающий особенности действительные работы элементов конструкций, оснований, а также зданий и сооружений в целом, не отражаемые непосредственно в расчётах; коэффициент надёжности, учитывающий степень капитальности зданий и сооружений, а также значимость последствий наступления тех или иных П. с. Различают П. с., при которых конструкция становится непригодной к нормальной эксплуатации, и П. с., при которых она полностью утрачивает несущую способность. Пригодность к нормальной эксплуатации обычно определяется требованиями жёсткости, ограничениями осадок, трещиностойкостью и т.д. Потеря несущей способности может проявляться в виде хрупкого, вязкого, усталостного разрушения материала, изменения конфигурации конструкции, а также потери устойчивости её формы, положения и т.д. Основная цель расчёта по П. с. - предотвратить их возникновение в течение всего срока службы здания (сооружения). Метод расчёта по П. с. получил широкое распространение в СССР, странах - членах СЭВ и странах, входящих в Международную организацию по стандартизации и Европейский комитет по бетону. В СССР этот метод применяется также при расчёте некоторых машиностроительных конструкций, например металлических конструкций мостовых, подвесных и башенных грузоподъёмных кранов. Лит.:Строительные нормы и правила, ч. 2, раздел А, гл. 10. Строительные конструкции и основания. Основные положения проектирования, М., 1972; Балдин В. А. [и др.], К выходу СНиП II - А. 10-71, «Строительная механика и расчет сооружений», 1972, № 4. А. А. Бать, В. А. Отставнов. Предельной полезности теория Преде'льной поле'зности тео'рия,буржуазная теория, пытающаяся дать объяснение процессам ценообразования в условиях капиталистического хозяйства. Возникла в последней трети 19 в. в противовес теории трудовой стоимости К. Маркса. Разрабатывалась У. С. (Великобритания), Л. (Швейцария), К. ,Э. (Австрия). Буржуазные экономисты не могли примириться с тем, что марксистская теория не только даёт объяснение процессам ценообразования, но и вскрывает источник капиталистической эксплуатации в виде и тем самым показывает основу непримиримых противоречий между двумя основными классами капиталистического общества. Конкретно-исторические условия, способствовавшие возникновению и развитию П. п. т., были связаны с вовлечением в сферу действия капиталистического рынка новых территорий и сфер хозяйства. Усиление рыночных отношений затушёвывало производственную основу ценообразования и способствовало буржуазной фетишизации рыночных процессов. Методологии П. п. т. присущи: 1) субъективно-психологический взгляд на действующие в рыночном хозяйстве механизмы, в основу которых кладутся оценки агентов рыночного хозяйства (продавца, покупателя), а не объективные процессы, формирующие в конечном счёте психологические оценки этих агентов. 2) Потребительский подход к объяснению сил, воздействующих на формирование цены. В этом П. п. т. коренным образом отличается от классической буржуазной политической экономии, рассматривавшей в качестве основы и связывавшей эту категорию с процессами производства и трудовыми затратами в ходе производства, хотя часто объяснения классиков буржуазной политической экономии страдали эклектизмом и не вскрывали единого источника стоимости, заключённого в затратах абстрактного труда. На место категории стоимости П. п. т. ставит категорию полезности, выводя последнюю из процессов потребления. В этом едином источнике формирования цен, исходящем из потребления, из полезности, состоит монизм П. п. т. 3) Априорно-дедуктивный метод построения теории. П. п. т. исходит из ограниченного набора постулатов, имеющих характер очевидности с точки зрения «здравого смысла», и, пользуясь ими, стремится к построению теории, не противоречащей законам формальной логики. Однако коренным пороком такого метода является отсутствие практической проверки теоретической конструкции. К числу основных постулатов П. п. т. относятся .Процесс установления цены на рынке наиболее подробно описывается в работах представителей (Менгера, Ф. ,Бём-Баверка). На основе взаимоотношений т. н. рыночных пар (продавец - покупатель) пока на рынке оценки полезности товара со стороны продавца ниже, чем оценки покупателя, обмен идёт беспрепятственно. Это способствует вовлечению в обмен продавцов с более высокой оценкой полезности товара и покупателей с более низкой оценкой. Процесс обмена продолжается до тех пор, пока не встречается т. н. предельная пара, чьи субъективные оценки полезности, выраженные в деньгах, совпадают. Субъективная оценка полезности товара этой последней пары продавец - покупатель и есть та предельная полезность, которая определяет рыночную цену товара. Это - цена равновесия, определяющая в дальнейшем течение всех сделок на рынке. Апологетическая сущность П. п. т. состоит в том, что она выводит проблему измерения и соизмерения цен из области общественно-производственных отношений в область субъективно-психологических оценок. Непротиворечивость П. п. т. оказывается мнимой, поскольку оценки полезности носят конкретно-исторический характер и зависят от сложившейся в тот или иной период структуры цен. Т. о. возникает порочный логический круг: цены - полезности - цены. Полезность и предельная полезность есть не что иное, как свойства потребительной стоимости (см. ) .Между тем потребительные стоимости невозможно соизмерить непосредственно. Соизмерению они подвергаются в той мере, в какой они являются носителями стоимости, т. е. определённого количества абстрактного труда, выраженного в единицах общественно необходимого рабочего времени. В марксистской литературе даётся также критика модификаций П. п. т. (метода кривых безразличия, теории выявленных предпочтений). Лит.:Hilferding R., Bцhm-Bawerks Marx-Kritik, «Marx - Studien», Bd 1, W., 1904; Блюмин И. Г., Критика буржуазной политической экономии, т. 1, М., 1962; Козлова К., Энтов Р., Теории цены, М., 1972. Ю. Б. Кочеврин. Предельной производительности теория Преде'льной производи'тельности тео'рия, см. в ст. . Предельные теоремы
Преде'льные теоре'мытеории вероятностей, общее название ряда теорем
,указывающих условия возникновения тех или иных закономерностей в результате действия большого числа случайных факторов. Исторически первые П. т. - теорема Бернулли (1713) и теорема Лапласа (1812) - относятся к распределению отклонений частоты появления некоторого события
Епри
nнезависимых испытаниях от его вероятности
р(0 <
р< 1). Частотой называется отношение
m/n,где
m -число наступлений события
Епри
nиспытаниях (точные формулировки см. в ст.
и
). С.
(1837) распространил эти теоремы на случай, когда вероятность
p
kнаступления
Ев
k-м испытании может зависеть от
k,описав предельное поведение при
n® Ґ распределения отклонений частоты
m/nот среднего арифметического
(см. ) .Если обозначить через X kслучайную величину, принимающую значение, равное единице при появлении события Ев k-м испытании, и значение, равное нулю при его непоявлении, то mможно представить в виде суммы m= X 1+ X 2+... + X n, что позволяет рассматривать перечисленные теоремы как частные случаи общих П. т., относящихся к суммам независимых случайных величин (закона больших чисел и центральной предельной теоремы). Закон больших чисел. Пусть X 1, X 2,..., X n,... (*) - какая-либо последовательность независимых случайных величин, s n-сумма первых nиз них s n= X 1+ X 2+ ...+ X n, A nи B 2 n-соответственно A n= Е s n= Е X 1+ E X 2+... + E X n, и B 2 n= D s n-= D X 1+ D X 2+... + D X n, суммы s n.Говорят, что последовательность (*) подчиняется закону больших чисел, если при любом e > 0 вероятность неравенства
стремится к нулю при n® Ґ. Широкие условия приложимости закона больших чисел найдены впервые П. Л. (в 1867) (см. ) .Эти условия затем были обобщены А. А. (старшим). Вопрос о необходимых и достаточных условиях приложимости закона больших чисел был окончательно решен А. Н. (1928). В случае, когда величины X nимеют одну и ту же функцию распределения, эти условия, как показал А. Я. (1929), сводятся к одному: величины X n должны иметь конечные математические ожидания. Центральная предельная теорема. Говорят, что к последовательности (*) применима центральная предельная теорема, если при любых z 1и z 2вероятность неравенства z 1B n< s n- A n< z 2B n имеет пределом при n® Ґ -величину
(см. ) .Довольно общие достаточные условия применимости центральной предельной теоремы были указаны Чебышевым (1887), но и в его доказательстве обнаружились пробелы, восполненные лишь позже Марковым (1898). Решение вопроса, близкое к окончательному, было получено А. М. (1901). Точная формулировка теоремы Ляпунова такова: пусть c k= E| X k- Е Х к| 2+ d, d > 0 C n= c 1+ c 2+... + c n.
Если отношение
Из др. направлений работ в области П. т. можно отметить следующие. 1) Начатые Марковым и продолженные Бернштейном и др. исследования условий приложимости закона больших чисел и центральной предельной теоремы к суммам зависимых величин. 2) Даже в случае последовательности одинаково распределённых случайных величин можно указать простые примеры, когда суммы имеют в пределе распределение, отличное от нормального (речь идёт о невырожденных распределениях, т. е. о распределениях, не сосредоточенных целиком в одной точке). В работах советских математиков А. Я. Хинчина, Б. В. Гнеденко, французских математиков П. Леви, В. Дёблина и др. полностью изучены как класс возможных предельных распределении для сумм независимых случайных величин, так и условия сходимости распределений сумм к тому или иному предельному распределению. 3) Значительное внимание уделяется т. н. локальным П. т. Пусть, например, величины X nпринимают лишь целые значения. Тогда суммы s nпринимают также только целые значения и естественно поставить вопрос о предельном поведении вероятностей P n( m) того, что s n= m(где m -целое). Простейшим примером локальной П. т. может служить локальная теорема Лапласа (см. ) . 4) П. т. в их классической постановке описывают поведение отдельной суммы s nс возрастанием номера n.Достаточно общие П. т. для вероятностей событий, зависящих сразу от нескольких сумм, получены впервые Колмогоровым (1931). Так, например, из его результатов следует, что при весьма широких условиях вероятность неравенства
имеет пределом величину
5) Перечисленные выше П, т. относятся к суммам случайных величин. Примером П. т. иного рода могут служить П. т. для членов .Эти П. т. подробно изучены советскими математиками Б. В. Гнеденко и Н. В. Смирновым. 6) Наконец, к П. т. относят также и теоремы, устанавливающие свойства последовательностей случайных величин, имеющие место с вероятностью, равной единице (см., например, ) .
Лит.:Гнеденко Б. В., Колмогоров А. Н., Предельные распределения для сумм независимых случайных величин, М. - Л., 1949; Ибрагимов И. А., Линник Ю. В., Независимые и стационарно связанные величины, М., 1965; Прохоров Ю. В., Розанов Ю. А., Теория вероятностей. Основные понятия. Предельные теоремы. Случайные процессы, 2 изд., М., 1973. Ю. В. Прохоров. Предельные углеводороды Преде'льные углеводоро'ды, то же, что . Предельный цикл Преде'льный циклсистемы дифференциальный уравнений 2-го порядка
- замкнутая траектория в фазовом пространстве xOy, обладающая тем свойством, что все траектории, начинающиеся в достаточно узкой кольцеобразной ее окрестности, неограниченно приближаются к этой траектории или при t® +Ґ (устойчивый П. ц.), или при t® -Ґ (неустойчивый П. ц.), или часть из них при t® +Ґ, а остальные - при t® -Ґ (полуустойчивый П. ц.). Например, система
( rи j - полярные координаты), общее решение которой r= 1 – (1 – r 0) e -t, j = j 0+ t(где r 0³ 0), имеет устойчивый П. ц. r= 1 ( см. рис. ). Понятие П. ц. переносится также на систему n-го порядка. С механической точки зрения устойчивый П. ц. соответствует устойчивому периодическому режиму системы. Поэтому разыскание П. ц. имеет важное значение в теории нелинейных колебаний. Лит.:Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 3 изд., М., 1970; Андронов А. А., Витт А. А., Хайкин С. Э., Теория колебаний, 2 изд., М., 1959. 
Рис. к ст. Предельный цикл. Предивинск Преди'винск, посёлок городского типа в Большемуртинском районе Красноярского края РСФСР. Расположен на правом берегу Енисея, в 183 кмниже Красноярска. Леспромхоз. Предикат (свойство отд. предмета) Предика'т(от позднелат. praedicatum- сказанное), то же, что свойство; в узком смысле - свойство отдельного предмета, например «быть человеком», в широком смысле - свойство пары, тройки, вообще n-ки предметов, например «быть родственником». П. в широком смысле называют также отношениями. Исторически понятие о П. явилось следствием логического анализа высказываний естественного языка, т. е. выяснения их логической структуры, выяснения того, какой логикой может быть выражен (формализован) смысл этих высказываний. Идея выделения логической структуры речи, в отличие от грамматической, для нужд логической дедукции принадлежит Аристотелю. В аристотелевской и в последующей «традиционной» логике П. понимался в узком смысле как один из двух терминов суждения, а именно тот, в котором нечто говорится о предмете речи - субъекте. Форма сказывания - предикативная связь - сводилась при этом к атрибутивной связи, т. е. выражала «присущность» предмету некоторого признака. Аристотель выделял 4 типа признаков, способных играть роль П.: родовые, видовые, собственные и случайные. Это т. н. предикабилии - типы сказуемых. Логический анализ фраз естественного языка на том уровне представлений о логической дедукции, который был характерен для аристотелевской (и традиционной) логики, ограничивался, т. о., для выражения смысла высказываний логикой одноместных П. (логикой свойств в узком смысле). Это существенно ослабляло «выразительные возможности» логики и служило препятствием для адекватной формализации тех объективных связей между предметами, которые, будучи мыслимыми в виде отношений (свойств в широком смысле) между соответствующими понятиями, лежат в основе логической правильности умозаключений об отношениях - основных умозаключений в науке. Устранение указанного препятствия и усиление выразительных средств формализма современной логики связано, в частности, с восходящей к работе Г. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99 |
|||||||
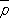 вероятностей
p
k(1 Ј
kЈ
n):
вероятностей
p
k(1 Ј
kЈ
n):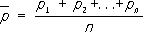
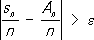

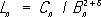 стремится к нулю при
n® Ґ, то к последовательности (*) применима центральная предельная теорема. Окончательное решение вопроса об условиях приложимости центральной предельной теоремы получено в основных чертах С. Н.
(1926) и дополнено В.
(1935).
стремится к нулю при
n® Ґ, то к последовательности (*) применима центральная предельная теорема. Окончательное решение вопроса об условиях приложимости центральной предельной теоремы получено в основных чертах С. Н.
(1926) и дополнено В.
(1935).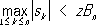
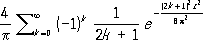 (
z> 0)
(
z> 0)