 |
|
���������� ������:: ��� :: ������� ��� ���������� :: �������� ����� :: ������ ����� :: ����� ����� �������� :: ���� ��������� :: ������ ����� ���� :: ������� ������ :: ������� ������ ���������� :: ������� ���� ���������� �����:: �������� ������ :: ������ � ������ ��� ����� (��������� ��. ����������� � �������� ������ ������) :: �������� ���� :: � ����� ������ �. �������� :: ����� ���� (��� 1) :: ���� (����� 2) :: ������� ����� :: ������ � �� ����� :: ��� �� ������ �� ������� ������ :: ������ ����� ������ |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 60)
Соч.: Собр. соч., т. 1-2, СПБ, 1911. Лит.:Ленин В. И., Что такое «друзья народа» и как они воюют против социал-демократов?, Полн. собр. соч., 5 изд., т. 1; его же, Экономическое содержание народничества и критика его в книге г. Струве, там же; Валк С. Н., С. Н. Кривенко в нелегальной литературе, в сб.: Из истории рабочего класса и революционного движения, М., 1958. Ю. Н. Коротков. Кривизна Кривизна'(матем.), величина, характеризующая отклонение кривой (поверхности) от прямой (плоскости). Отклонение дуги MNкривой Lот касательной МРв точке Мможно охарактеризовать с помощью т. н. средней кривизны k cpэтой дуги, равной отношению величины ее угла между касательными в точках Ми Nк длине D sдуги MN:
Для дуги окружности средняя кривизна равна обратной величине радиуса этой окружности и, т. о., наглядно характеризует степень искривлённости окружности - с уменьшением радиуса увеличивается искривлённость дуги. Предельное значение средней кривизны при стремлении точки Nкривой к точке М,т. е. при D s®0, называется кривизной kкривой Lв точке М:
Величина R,обратная кривизне, обычно называется радиусом кривизны кривой Lв точке М. Если кривая Lявляется графиком функции у = f( x) ,то кривизна kэтой кривой может быть вычислена по формуле
Кривизна kкривой Lпредставляет собой, вообще говоря, функцию длины дуги s, отсчитываемой от некоторой точки Мэтой кривой. Если для двух плоских кривых L 1и L 2К. как функции длины дуги одинаковы, то кривые L 1и L 2конгруэнтны - они могут быть совмещены движением. Поэтому задание К. плоской кривой как функции длины дуги обычно называется натуральным (внутренним) уравнением этой кривой. Для характеристики отклонения пространственной кривой Lот плоскости вводят понятие т. н. кручения,которое иногда называют второй К. Кручение s в точке Мкривой определяется как предел отношения угла bмежду соприкасающимися плоскостями к кривой в точках Ми Nк длине D sдуги MNпри стремлении точки Nк М:
При этом угол bсчитается положительным, если поворот соприкасающейся плоскости в Nпри стремлении Nк Мпроисходит против часовой стрелки при наблюдении из точки М.К. и кручение, заданные как функции длины дуги, определяют кривую Lс точностью до положения в пространстве. Исследование отклонения поверхности от плоскости может быть проведено следующим образом. Через нормаль в данной точке Мповерхности проводят всевозможные плоскости. Сечения поверхности этими плоскостями называют нормальными сечениями, а кривизны нормальных сечений в точке М -нормальными кривизнами поверхности в этой точке. Максимальная и минимальная из нормальных кривизн в данной точке Мименуются главными кривизнами. Если k 1 и к 2-главные кривизны, то величины K=k 1Чk 2и Н = 1/ 2( k 1+ k 2) называют соответственно полной кривизной (или гауссовой кривизной) и средней кривизной поверхности в точке М.Эти К. поверхности определяют нормальные К., поэтому могут служить характеристикой отклонения поверхности от плоскости. В частности, если К =0 и Н =0 во всех точках поверхности, то поверхность представляет собой плоскость. Полная К. не меняется при изгибаниях поверхности (деформациях поверхности, не меняющих длин линий на ней). Если, например, полная К. равна нулю во всех точках поверхности, то каждый достаточно малый её кусок может быть изогнут на плоскость. Полная К. на поверхности без обращения к объемлющему пространству составляет объект т. н. внутренней геометрии поверхности. Средняя К. связана с внешней формой поверхности. Понятие К. обобщается на объекты более общей природы. Например, понятие К. возникает в т. н. римановых пространствах , представляя собой меру отклонения этих пространств от евклидовых. Лит.:Бляшке В., Дифференциальная геометрия и геометрические основы теории относительности Эйнштейна, пер. с нем., т.1, М.- Л., 1935; Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969. Э. Г. Позняк. 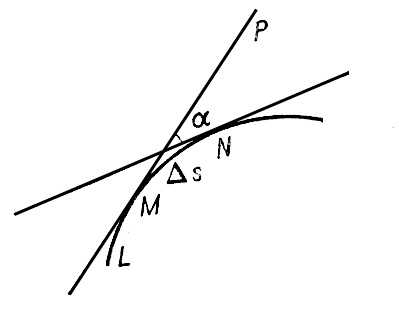
Рис. к ст. Кривизна. Кривизна поля Кривизна' по'ляизображения, одна из аберраций оптических систем ; заключается в том, что изображение плоского предмета получается резким не в плоскости, как это должно быть в идеальной системе, а на искривленной поверхности. Если линзы, входящие в состав центрированной системы, имеют сферические преломляющие поверхности радиусов r k( k -номер поверхности по ходу светового луча) и, кроме того, в системе исправлен астигматизм,то изображение плоскости, перпендикулярной оси системы, представляет собой сферу. Её радиус Rопределяется соотношением
где
n
k, n
k+1-показатели преломления сред, расположенных перед и за
k-той преломляющей поверхностью. В случае, когда линзы в системе можно считать тонкими (см.
Линза
)
,(*) сводится к более простой формуле:
Лит.:Тудоровский Д. И., Теория оптических приборов, 2 изд., М.- Л., 1948; Слюсарев Г. Г., Методы расчёта оптических систем, 2 изд., Л., 1969, Кривизна пространства-времени Кривизна' простра'нства-време'ни,в общей теории относительности (теории тяготения ) величина, характеризующая меру отклонения свойств пространства-времени от свойств так называемого плоского пространства-времени специальной теории относительности. Понятие К. н.-в. возникло по аналогии с понятием полной кривизны в геометрии поверхностей. К. п.-в. описывается тензором кривизны (см. Римановы геометрии ) .От вида тензора К. п.-в. существенно зависит тип космологических моделей (см. Космология ) . Кривичи (вост.-слав. племенное объединение) Кривичи',восточнославянское племенное объединение 6-10 вв., занимавшее обширные области в верхнем течении Днепра, Волги и Западной Двины, а также южную часть бассейна Чудского озера. Археологические памятники - курганы (с трупосожжениями) в виде длинных валообразных насыпей, остатки земледельческих поселений и городища, где обнаружены следы железоделательного, кузнечного, ювелирного и др. ремёсел. Главные центры - гг. Смоленск, Полоцк, Изборск и, возможно, Псков. В состав К. входили многочисленные балтийские этнические группы. В конце 9-10 вв. появились богатые погребения дружинников с вооружением; особенно много их в Гнездовских курганах.По летописи, К. до включения их в состав Киевского государства (во 2-й половине 9 в.) имели своё княжение. Последний раз имя К. упоминается в летописи под 1162, когда на земле К. уже сложились Смоленское и Полоцкое княжества, а северо-западная её часть вошла в состав Новгородских владений. К. сыграли большую роль в колонизации Волго-Клязьминского междуречья. Лит.:Довнар-Запольский М., Очерк истории Кривичской и Дреговичской земель до конца XII ст., К., 1891; Третьяков П. Н., Восточнославянские племена, 2 изд., М., 1953; Седов В. В., Кривичи, «Советская археология», 1960, № 1. П. Н. Третьяков. Кривичи (пос. гор. типа в Минской обл.) Кривичи',посёлок городского типа в Мядельском районе Минской области БССР, на р. Сервечь (правый приток р. Вилия), в 3 кмот ж.-д. станции Кривичи (на линии Молодечно - Полоцк). Молокозавод, промкомбинат. Предприятия местной промышленности. Кривов Тимофей Степанович Криво'вТимофей Степанович [21.2(5.3).1886, село Старое Ерёмкино Мелекесского уезда Самарской губернии, - 16.8.1966, Москва], советский государственный и партийный деятель, Герой Социалистического Труда (1966). Член Коммунистической партии с 1905. Родился в крестьянской семье. Был батраком, рабочим. Учился в Симбирской учительской школе (1899), работал учителем. Участник Революции 1905-07 в Уфе и Златоусте, был членом боевых дружин. Подвергался репрессиям. В январе 1910 эмигрировал. После возвращения в 1911 в Россию арестован и приговорён к бессрочной каторге. После Февральской революции 1917 на партийной и советской работе в Уфе. С 1920 секретарь Уральского бюро ЦК РКП (б). С 1922 ответственный инструктор ЦК партии, затем работал в ЦКК ВКП (б). С 1927 заместитель наркома РКИ РСФСР и член партколлегии ЦКК. В 1934-35 главный арбитр при СНК РСФСР. В 1936 заместитель наркомфина РСФСР. С 1936 работал в ЦК профсоюза рабочих коммунальных предприятий СССР. С 1940 персональный пенсионер. Делегат 10-12-го, 14-17-го съездов партии; на 10-м, 12-16-м съездах избирался членом ЦКК, на 11-м - кандидат в члены ЦК партии. Награжден 2 орденами Ленина. Лит.:Муратов Х. И., Липкина А. Г., Т. С. Кривов, Уфа, 1968. Н. М. Юрова. Кривоголовка Кривоголо'вка,анкилостома (Ancylostoma duodenale), паразитический круглый червь семейства анкилостомид. «Кривое зеркало» «Криво'е зе'ркало»,театр малых форм, существовавший в Петербурге (Ленинграде) в 1908-31. Возник как театр-кабаре по инициативе артистки З. В. Холмской при Театральном клубе. Руководитель (1908-28) - критик А. Р. Кугель.«К. з.» был театром пародий, общественно-политической сатиры, «скепсиса и отрицания» (Кугель), «игривой и тонкой иронии» (А. В. Луначарский). Большой успех имел спектакль «Вампука, невеста африканская» (1909, режиссер Р. А. Унгерн), высмеивавший оперные штампы. В театре работали: актёры М. К. Яроцкая, С. И. Антимонов, К. Э. Гибшман, Л. А. Фенин, Ф. Н. Курихин, В. А. Лепко; режиссёры Н. Н. Евреинов, Н. М. Фореггер и др. Лит.:Кугель А. Р., Листья с дерева, Л., 1926, гл. 9, с. 195-209; Боровский В. В., Несколько слов о «Кривом зеркале», Соч., т. 2, Л., 1931. Кривой брус Криво'й брусв сопротивлении материалов и в теории упругости, тело, геометрическая форма которого образуется движением в пространстве плоской фигуры (называемом поперечным сечением К. о.), при этом центр её тяжести всегда остаётся на некоторой кривой (оси К. б.), а плоскость фигуры нормальна этой кривой. В зависимости от вида поперечного сечения различают: К. б. постоянного сечения (пример - звено цепи, составленной из овальных или круглых колец) и К. б. переменного сечения (пример - крюк подъёмного крана). По виду оси К, б. может быть плоским (если его ось - плоская кривая) и пространственным (ось - пространственная кривая). Разновидностью К. б. является естественно закрученный К. б., отличающийся тем, что плоская фигура поперечного сечения при своём движении по оси К. б. одновременно вращается вокруг касательной к ней (пример - лопасть воздушного винта самолёта или вентилятора). Расчёт плоского К. б. ( рис. ) симметричного поперечного сечения (ось симметрии лежит в плоскости кривизны) на действие нагрузки, лежащей в плоскости симметрии, заключается в определении напряжений (нормальных его поперечному сечению) по формуле:
где F -площадь поперечного сечения, N -продольная сила, М -изгибающий момент в сечении, определяемый относительно оси z 0,проходящей через центр тяжести поперечного сечения ( С), у -расстояние до рассматриваемого волокна от нейтральной оси z, r -радиус кривизны рассматриваемого волокна, S z= Fy 0-статический момент площади сечения относительно оси z.Смещение y 0нейтральной оси относительно центра тяжести сечения всегда направлено к центру кривизны К. б. и обычно определяется по специальным таблицам. Для круглого сечения y 0» d 2/16R,для прямоугольного - у 0» h 2/12R( R -радиус кривизны оси К. б., d -диаметр, h -высота поперечного сечения К. б.). Нормальные напряжения в К. б. имеют наибольшие по абсолютной величине значения у вогнутого края бруса и меняются в сечении по гиперболическому закону. При малой кривизне ( R > 5h) определение нормальных напряжений может производиться, как и в прямом брусе (см. Изгиб ) .
Лит.:Беляев Н. М., Сопротивление материалов, 14 изд., М., 1965. Л. В. Касабьян. 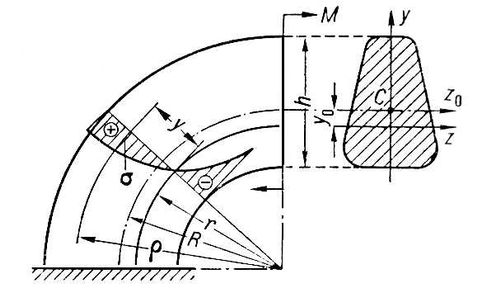
Распределение нормальных напряжений в сечении кривого бруса при чистом изгибе. Кривой Рог Криво'й Рог,город в Днепропетровской области УССР. Расположен в верховьях р. Ингулец при впадении в неё р. Саксагань. Узел железных дорог (линии на Знаменку, Пятихатки, Запорожье, Днепропетровск). 600 тыс. жителей в 1972 (192 тыс. в 1939; 401 тыс. в 1959). Делится на 5 районов. К. Р. возник из почтовой станции, основанной 27 апреля 1775 в урочище Кривой Рог. С 20-х гг. 19 в. К. Р. - военное поселение; с 1860 - местечко. Начало промышленного развития связано с добычей железной руды (80-е гг. 19 в.) и постройкой железной дороги, связавшей Криворожский бассейн с Донбассом. Большинство рудников К. Р. принадлежало иностранным (главным образом французам) капиталистам, часть которых в 1907 объединилась в синдикат «Продаруд». Первые с.-д. кружки в К. Р. возникли в начале 1903. Советская власть в городе была установлена 9(22) января 1918 и окончательно упрочена в 1920. С 14 августа 1941 по 22 февраля 1944 К. Р. был оккупирован немецко-фашистскими войсками, которые нанесли городу крупный ущерб. В послевоенные годы К. Р. восстановлен и является крупным индустриальным и культурным центром Украины. К. Р. - центр Криворожского железорудного бассейна.В К. Р. - мощные шахты, оборудованные новейшей техникой (среди них - «Гигант-Глубокая», им. В. И. Ленина, Гвардейская и др.). Большое развитие получила металлургическая ( Криворожский металлургический завод им. В. И. Ленина; горнообогатительные комбинаты - Северный, Центральный, Южный, Новокриворожский, Ингулецкий), машиностроительный и металлообрабатывающий (завод горного оборудования «Коммунист»), энергетическая, коксохимическая промышленность. Выросла промышленность стройматериалов (цементный, кирпичные заводы); заводы крупнопанельного домостроения. Предприятия лёгкой (обувная фабрика), пищевой и деревообрабатывающей промышленности. В 1970 жилой фонд города составил свыше 5 млн. м 2(против 833 тыс. м 2в 1940). Имеются горнорудный, педагогический институты, вечерний факультет Днепропетровского металлургического института, филиал Донецкого института советской торговли, 15 техникумов (в т. ч. рудничной автоматики, политехнический, горной электромеханики, металлургический, коксохимический, горно-механический и др.); авиационное училище специальных служб гражданской авиации, медицинское, музыкальное училища. Русский музыкально-драматический театр им. Т. Г. Шевченко, цирк. Историко-краеведческий музей. Среди отдельных зданий и комплексов послевоенного периода: Русский музыкально-драматический театр им. Т. Г. Шевченко (1949-50, архитектор В. А. Зуев), Дворец культуры металлургов (1952-54, архитектор К. С. Барташевич), здание Горнорудного института (1960-64), цирк (1968-69, архитектор Г. В. Наприенко, С. М. Гельфер), шахта «Родина» (1972, архитектор Е. Г. Пестрякова, инженер В. А. Бондаренко и др.), здание института «Гипрорудмаш» (1972, архитектор Д. А. Лившиц). Город награжден орденом Ленина (1971). 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112 |
|||||||
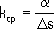 .
.
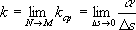 .
.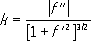 .
.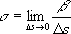 .
.
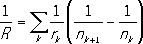 ,
,
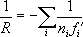 , где
f’
i- фокусное расстояние
i-той линзы,
n
i-показатель преломления её материала. В сложных оптических системах (например, в фотографических
объективах
) К. п. исправляют, сочетая линзы с поверхностями разной кривизны так, чтобы правая часть формулы (*) стала равна нулю (т. н. условие Пецваля).
, где
f’
i- фокусное расстояние
i-той линзы,
n
i-показатель преломления её материала. В сложных оптических системах (например, в фотографических
объективах
) К. п. исправляют, сочетая линзы с поверхностями разной кривизны так, чтобы правая часть формулы (*) стала равна нулю (т. н. условие Пецваля).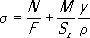 ,
,