Большая Советская Энциклопедия (ПО)

  В 1968 американо-канадская экспедиция в составе 6 человек во главе с Р. Плейстедом на малогабаритных моторных санях от Канадского Арктического архипелага за 44 дня достигла Северного полюса. В 1968-1969 четверо англичан во главе с У. Хербертом пересекли на собачьих упряжках Арктический бассейн от Аляски (мыс Барроу) до Шпицбергена через Северный полюс (были там 5 апреля 1969).

  Первая попытка достичь Южного полюса была предпринята англичанином Р. Скоттом (совместно с Э. Шеклтоном и Э. Уилсоном) в 1902; в 1907-09 вторую попытку сделал английский исследователь Э.Шеклтон (88°23’ ю. ш.), но вернулся из-за недостатка продовольствия. Впервые Южного полюса удалось достичь 14 декабря 1911 норвежской экспедиции под руководством Р. Амундсена, которая на месяц опередила английскую экспедицию Р. Скотта (18 января 1912). В 30-х гг. в связи с развитием авиации начался новый период в исследовании Антарктиды. 29 ноября 1929 американский адмирал Р. Бэрд первым достиг на самолёте Южного полюса; второй полёт был осуществлен им же в 1947. В период Международного геофизического года (1957-58) США организовали научную базу на Южном полюсе. В одном из разведочных полётов 8 января 1956 здесь впервые приземлился американский самолёт, а в январе 1957 была открыта научная станция Амундсен - Скотт.

  В ноябре 1957 начался трансконтинентальный поход англо-новозеландской экспедиции по маршруту станция Шеклтон - Юж. полюс - станция Скотт. Вспомогательная партия во главе с новозеландцем Э. Хиллари 4 января 1958 на тягачах достигла Южного полюса со стороны моря Росса. 20 января 1958 через Южный полюс прошёл основной отряд под руководством англичанина В. Фукса. Переход длился 99 сут.

 Для изучения рельефа Восточной Антарктиды в октябре 1958 был совершен трансконтинентальный полёт (на самолёте ИЛ-12) сов. лётчика В. М. Перова по маршруту станция Мирный - станция Советская - Южный полюс - станция Мак-Мердо.

  26 декабря 1959 Южного полюса достигли совнтские исследователи - участники санно-тракторного похода (руководитель похода начальник 4-й Антарктической экспедиции А. Г. Дралкин) по маршруту станция Комсомольская - станция Восток - Южный полюс. В 1961 американские учёные осуществили внутриконтинентальный поход (под руководством А. Крэри) на вездеходах по маршруту станция Мак-Мердо - Южный полюс.

  Лит.:Визе В. Ю., Моря Советской Арктики. Очерки по истории исследования, [3 изд.], М. - Л., 1948; Зубов Н. Н., В центре Арктики. Очерки по истории исследования и физической географии Центральной Арктики, М. - Л., 1948; Лактионов А. ф.. Северный полюс, [3 изд.], М., 1960; Мотрохов А. Н., Советские подводники на Северном полюсе, «Морской сборник», 1964, № 2; Вокруг света под водой, пер. с англ., М., 1965; Магидович И. П., Очерки по истории географических открытий, М., 1967; Херберт У., Пешком через Ледовитый океан, пер. с англ., М., 1972; Пири Р. Э., Северный полюс, пер. с англ., М., 1972; Папанин И. Д., Жизнь на льдине. Дневник, М., 1972; Райт Т., Большой гвоздь, пер. с англ. Л., 1973. Берд Р. Э., Над Южным полюсом, пер. с англ., Л., 1935; Амундсен Р., Южный полюс. Плавание «Фрама» в Антарктике. 1910-12, Собр. соч., пер. с норв., т. 2, Л., 1937; Скотт Р. Ф.. Последняя экспедиция Р. Скотта, М., 1955; Борхгревинк К. Э., У Южного полюса, пер. с норв., М., 1958; Трешников А. Ф., История открытия и исследования Антарктиды, М., 1963; Fuchs V. Е., Hillary Ed., The crossing of Antarctica, L., 1958.

  Н. Г. Дубровская.

  Движение географических полюсов.Мгновенная ось вращения Земли не сохраняет в теле Земли неизменного направления, вследствие чего происходит перемещение П. г. по земной поверхности; это явление называется движением полюсов Земли. Сведения о движении полюсов имеют важное значение в астрономии и геодезии, т.к. оно вызывает непрерывные изменения координат точек поверхности Земли и азимутов земных предметов, что сказывается на результатах астрономических и геодезических измерений. Для получения этих сведений в 1899 была создана Международная служба широты,переименованная в 1961 в Международную службу движения полюсов Земли (см. Служба движения полюса международная ) .В её состав входят 5 станций, ведущих наблюдения изменений широт, и Центральное бюро, которое на основе этих наблюдений вычисляет координаты П. г. Станции расположены на одной географической параллели 39° 8’ с. ш. и снабжены однотипными инструментами. В число их входят станции: Мидзусава (Япония), Китаб (СССР), Карлофорте (Италия), Гейтерсберг (США), Юкайа (США). В СССР наблюдения для службы движения полюсов Земли ведутся также в Пулкове, Москве, Полтаве, Казани, Горьком, Иркутске, Благовещенске.

  Движение полюсов Земли изучается относительно т. н. условного международного начала координат Сев. полюса Земли (ему соответствует «условный» экватор), положение которого установлено решением 13-й Генеральной ассамблеи Международного астрономического союза в 1967. В этой точке (О, рис. 1 ) проводится плоскость К,касательная к поверхности земного сфероида. По результатам астрономических наблюдений широты j на станциях определяется плоскость мгновенного экватора Земли. Перпендикуляр СР к этой плоскости практически совпадает с мгновенной осью вращения Земли, а точка Р, в которой он пересекает плоскость К, -с мгновенным полюсом Земли. В плоскости Квводят координатную систему: ось ОХпроводят в направлении меридиана Гринвича, OY -под углом 90° к З. от него. Координаты точки Рв этой системе называется координатами мгновенного полюса Земли. Они связаны с широтой пункта наблюдений формулой, предложенной в 1893 С. К. Костинским:

хcos l + уsin l = j -j ₀,

где l - долгота пункта наблюдения.

  Данные о движении П. г. показывают, что полюс Рдвижется по поверхности Земли в направлении её суточного вращения вокруг полюса инерции I, в которой наименьшая ось эллипсоида инерции Земли пересекает плоскость Ки при этом описывает неправильную спиралевидную кривую - полодию ( рис. 2 ), витки которой постепенно смещаются относительно условного международного начала О в сторону Гренландии. Полодия Южного полюса имеет такую же форму, как и Северного.

  Периодическая составляющая движения П. г. слагается из двух частей: движения по кривой, близкой к окружности, с периодом 1,2 года, которое называется свободным движением П. г. или свободной нутацией, и годового движения. Амплитуда свободного движения П. г. значительно меняется, приближаясь в максимуме к 0,3’’ (например, в 1910, 1955, 1965) и уменьшаясь почти до нуля в минимуме (в 1927, 1935, 1961, 1968). Годовое движение П. г. происходит по эллипсу, полуоси которого, по определению А. Я. Орлова,равны 0,088’’ и 0,075’’ (1’’ соответствует примерно 31 мна поверхности Земли). В теории движения П. г. рассматривались различные модели Земли. Считая её абсолютно твёрдым телом, Л. Эйлер вывел (опубликовал 1790) формулу, связывающую период свободного движения П. г. со значениями главных моментов инерции Земли, из которой следовало, что этот период должен равняться 305 сут(период Эйлера). Но в действительности, как установил из анализа наблюдений американский астроном С. Чендлер (1892), он значительно больше и близок к 433 сут(период Чендлера). Расхождение между периодами Эйлера и Чендлера С. Ньюком объяснил влиянием упругих деформаций Земли и перемещений воды в океане, которые происходят под действием изменений центробежной силы, обусловленной движением П. г. Так была установлена зависимость периода свободного движения П. г. от механических свойств Земли, а вместе с тем и возможность применения данных о движении П. г. к изучению внутреннего строения Земли. В частности, они использовались при проверке выводов теории вращения Земли с жидким ядром, которой занимались Ф. А. Слудский,А. Пуанкаре , Х. Джефрис,М. С. Молоденский и др. Согласно этой теории, кроме уже упомянутых составляющих движения П. г., может происходить движение с периодом, близким к суткам (по расчётам Молоденского он равен 23 ^h56 ^m54 ^sзвёздного времени). Подтверждение существования такого движения было получено Н. А. Поповым из наблюдений двух зенитных звёзд в Полтаве.

  Годовое движение П. г. вызывается сезонным перераспределением масс на поверхности Земли, главным образом масс воздуха, вследствие чего меняются центробежные моменты инерции. Х. Джефрис выяснил, что нарушение правильного годового хода этого процесса может возбуждать и поддерживать свободное движение П. г.; напротив, вязкость Земли вызывает затухания движения полюсов. При такой трактовке явления оказалось возможным применять к анализу движения П. г. аппарат теории случайных функций.

  Для каждого витка полодии можно найти центр - средний полюс эпохи наблюдений, который, как показывает теория, у любой модели Земли всегда должен находиться вблизи полюса инерции I. А. Я. Орлов разработал метод вычислений, позволяющий находить координаты мгновенного полюса относительно среднего полюса эпохи наблюдений непосредственно по результатам определений изменения широт. Выдвинута гипотеза о значительных перемещениях П. г. в геологическом прошлом. Делаются попытки проследить движение полюсов Земли вплоть до докембрия по данным об остаточной намагниченности горных пород (см. Палеомагнетизм ) .

  Лит.:Орлов А. Я., Служба широты. Избр. труды, т. 1, К., 1961; Куликов К. А., Изменяемость широт и долгот, М., 1962; Манк У., Макдональд Г., Вращение Земли, пер. с англ., М., 1964.

  Е. П. Федоров.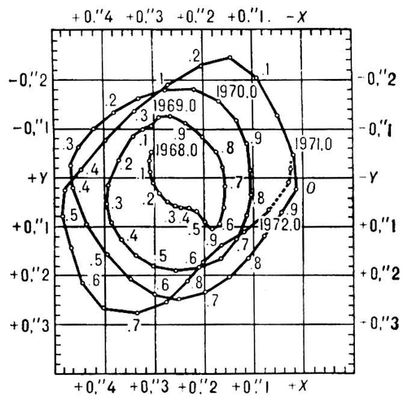

Рис. 2. Движение Северного полюса Земли с 1968 по 1972. Положения полюса отмечены через десятую часть года. Координатная сетка проведена через 0'', 1 (315 см).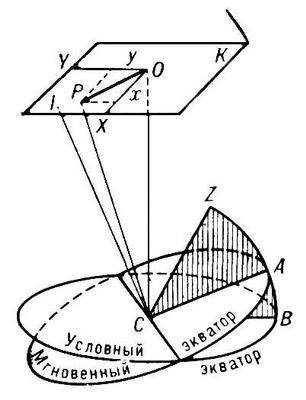

Рис. 1 к ст. Полюсы географические.

Полюсы геомагнитные

По'люсы геомагни'тные, точки пересечения магнитной оси Земли с её поверхностью. В первом приближении магнитное поле Земли описывается как поле однородно намагниченного шара ( диполя ) ,магнитная ось которого составляет угол около 11,5° с осью вращения Земли. В этом приближении П. г. - полюсы однородно намагниченного земного шара. В П. г. сходятся все геомагнитные меридианы. Местоположение П. г. определяется по данным о компонентах основного (главного) магнитного поля Земли (см. Земной магнетизм ) .Координаты П. г. на 1970 (по уточнённым данным): Северное полушарие j = 78° 31' с. ш., l = 70° 01’ з. д.; Южное полушарие (j = 78° 31' ю. ш., l = 109° 59' в. д.

Полюсы и поляры

По'люсы и поля'ры. Полярой точки Р относительно линии 2-го порядка Lназывается множество точек Q таких, что точки Р, О и точки пересечения прямой PQ с линией Lобразуют гармоническую четвёрку (см. Гармоническое расположение ) .Поляра является прямой линией. Точка Р по отношению к своей поляре называется полюсом. Аналогично определяются полюсы и полярные плоскости относительно поверхности 2-го порядка. П. и п. удовлетворяют принципу взаимности, т. е., если поляра точки Р проходит через точку Q, то поляра точки Q проходит через точку Р. Если линия Lявляется невырожденной, то относительно этой линии любая прямая имеет определённый полюс и любому полюсу соответствует определённая поляра. Т. о. устанавливается взаимно однозначное соответствие между точками и прямыми (являющееся частным случаем коррелятивного преобразования ) .П. и п. применяются в проективной геометрии при классификации линий и поверхностей 2-го порядка.

  Лит.см. при ст. Проективная геометрия.

Полюсы магнитные Земли

По'люсы магни'тные Земли', точки на поверхности Земли, в которых вектор индукции магнитного поля Земли направлен вертикально: вниз на Северном полюсе и вверх на Южном (в районе некоторых очень сильных магнитных аномалий,например Курской, Восточно-Сибирской, наблюдаются локальные магнитные полюсы). П. м. З. находятся вблизи географических полюсов Земли. В П. м. З. сходятся все изогоны и меридианы магнитные.Со временем координаты и знак полярности П. м. З. меняются (см. Земной магнетизм ) .Координаты П. м. З. на 1970 (по уточнённым данным): Северное полушарие (j = 75,0 ± 0,5° с. ш., l = 99,0 ± 1,0° з. д.; Южное полушарие (j = 66,5 ± 0,5° ю. ш., l = 140,0 ± 1,0° в. д.

  Полярность магнитного поля Земли в текущую эпоху такова, что в Северном полушарии находится южный (отрицательный) магнитный полюс,в Южном полушарии - северный (положительный, см. Палеомагнетизм ) ,однако общепринято П. м. З. называть в соответствии с полушарием, в котором каждый из полюсов находится.

  Лит.:Яновский Б. М., Земной магнетизм, ч. 1-2, Л., 1963-64; Медведев Н. Д., К вопросу современного положения магнитной оси Земли, «Бюллетень Советской Антарктической экспедиции», 1972, № 84, с. 89.

Полюсы мира

По'люсы ми'ра(Северный и Южный), две точки небесной сферы,в которых её пересекает ось мира, т. е. прямая, параллельная оси вращения Земли и проходящая через центр сферы. Не участвуя в суточном вращении небесной сферы, П. м., вследствие прецессии,медленно перемещаются относительно звёзд по окружностям радиусом около 23 ¹/ ₂° с центром в полюсе эклиптики, совершая полный оборот за 26 тыс. лет. Двигаясь вдоль этой окружности, П. м. совершают мелкие колебательные движения с амплитудой около 9’’ и периодом в 18,6 года вследствие нутации.В 1975 Северный П. м. находится на угловом расстоянии 51’ от звезды a Малой Медведицы, называемой вследствие этого Полярной. Через 5500 лет он приблизится к звезде a Цефея.

Поля напряжённости измеритель

По'ля напряжённости измери'тель, прибор для измерения напряжённости электрической (реже магнитной) составляющей поля или плотности потока энергии электромагнитного излучения, создаваемого источниками синусоидальных и модулированных колебаний, в том числе радиопомех. Различают П. н. и. для измерения слабых и сильных полей. Первые применяют при исследовании распространения радиоволн,для определения качества экранирования источников излучения, измерения диаграмм направленности антенн,обнаружения и измерения побочных излучений передающих устройств, а также при поиске источников радиопомех и измерении интенсивности их излучения. Основное назначение П. н. и. второго типа - измерение плотности потока энергии СВЧ излучения для определения, находится ли она в пределах, допускаемых медико-биологическими нормами безопасности для обслуживающего персонала.

  П. н. и. состоит из антенны, обычно широкополосной (штыревой, дипольной или ферритовой, а в диапазоне СВЧ - рупорной), калиброванной по значению действующей высоты либо по площади эффективной поверхности, и устройства, измеряющего напряжение или мощность принятых колебаний. В П. н. и. для слабых полей такими устройствами являются частотно-избирательные супергетеродинные радиоприёмники, работающие обычно в диапазоне частот 0,015-1000 Мгци выше; их чувствительность 0,5-10 мкв,суммарная погрешность измерения 2-4 дб.Результат измерения отсчитывают по стрелочному прибору на выходе радиоприёмника; для индикации радиопомех часто пользуются головными телефонами. Средние и сильные сигналы (от 0,1 мквтдо 10 мвт) в диапазоне частот 0,1-40 Ггцизмеряют термисторными или термоэлектрическими мощности измерителями;суммарная погрешность измерений такими П. н. и. 20-30%.

  Лит.:Валитов Р. А., Сретенский В. Н., Радиотехнические измерения, М., 1970; Измерители радиопомех. Сб., под ред. И. А. Фастовского, М., 1973.

  Е. Г. Билык.

Поля орошения

Поля' ороше'ния, участки земли, подготовленные для естественной биологической очистки сточных вод и выращивания с.-х. растений. Различают П. о. коммунальные - выполняют в основном санитарные функции, устройством почти не отличаются от полей фильтрации,в СССР организуются на землях, находящихся в ведении коммунальных органов; П. о. земледельческие (сезонные - действуют летом, и круглогодовые) - устраиваются для выращивания с.-х. культур, потребляющих питательные вещества, содержащиеся в сточных водах, на землях колхозов и совхозов.

  Использование сточных вод в сельском хозяйстве известно с древнейших времён (Рим, Афины, Вавилон и др.). В Германии (Бунцлау) П. о. существовали с 1559, в Великобритании (Эдинбург) с 1709, во Франции (Париж) с 1868; в России - с 1887 в Одессе, с 1895 в Киеве, с 1898 в Москве. В СССР орошение сточными водами в сельском хозяйстве применяется с 1922, в 1931 под Москвой организован совхоз «Люберецкие поля орошения». Земледельческие П. о. существуют под Киевом (Бортнические), в Ухтомском районе Московской области, в Кустанайской области (г. Рудный) и др. местах. В 1973 площадь их в СССР - более 60 тыс. га.Орошение с.-х. культур сточными водами распространено во многих странах.

  На П. о. возделывают в основном кормовые растения - кукурузу на силос, корнеплоды (урожаи их достигают 1000 цс 1 га) ,многолетние травы. П. о. устраивают на почвах (грунтах) разного механического состава, желательно на лёгких песчаных и супесчаных. Оросительная сеть состоит из трубопроводов, отстойников, насосной станции, регулирующих ёмкостей и каналов, поливной сети. Суточные нормы нагрузки (зависят от потребности растений во влаге и питательных веществах) - 15-20 м ³/гана лёгких почвах и 5-7 м ³/гана тяжёлых. Оросительные нормы и поливные нормы на П. о. устанавливают, исходя из потребностей с.-х. культуры во влаге. Основной способ полива - самотёчный по бороздам или полосам, зимой - затопление (см. Полив поверхностный ) .На П. о. используют также жидкий навоз, получаемый на животноводческих фермах, при применении гидросмыва. Устройство П. о. тесно связано с проектированием и строительством канализации, что позволяет комплексно решать вопросы благоустройства городов и сельских населённых мест.

  Лит.:Орлов В. П., Земледельческие поля орошения, 3 изд., М., 1961; Использование сточных вод в орошении, М., 1964; Шульц М., Круглогодовое орошение сточными водами, М., 1965; Львович А. И., Практика проектирования земледельческих полей орошения, М., 1968.

  В. М. Новиков.

Поля погребальных урн

Поля' погреба'льных урн, см. Полей погребений культуры.

Поля теория

По'ля тео'рия, математическая теория, изучающая свойства скалярных, векторных (в общем случае - тензорных) полей, т. е. областей пространства (или плоскости), каждой точке Мкоторых поставлено в соответствие число u( М) (например, температура, давление, плотность, магнитная проницаемость) или вектор а( М) (например, скорость частицы текущей жидкости, напряжённость силового поля, в частности электрического или магнитного поля) или тензор (например, напряжение в точке упругого тела, проводимость в анизотропном теле). Основным аппаратом П. т. является векторный и тензорный анализ (см. Векторное исчисление, Тензорное исчисление) .

 Многие понятия дифференциального и интегрального исчисления функций нескольких переменных переносятся в П. т. Среди них важное значение для описания скалярных полей имеет производная по направлению максимального изменения скалярного поля - т. н. градиент-вектор, инвариантный относительно выбора системы координат. Изменения векторного поля в 1-м приближении характеризуются двумя величинами: скаляром, называется дивергенцией (или расхождением) поля, который характеризует изменение интенсивности (плотности) поля, и вектором, называется вихрем (или ротором) поля, который представляет собой векторную характеристику «вращательной составляющей» векторного поля (его «скручивание»). Операцию перехода от скалярного поля к его градиенту и операцию перехода от векторного поля к его дивергенции часто обозначают Гамильтона оператором.Градиент скалярного поля, дивергенция и вихрь векторного поля обычно называют основными дифференциальными операциями П. т. К ним иногда относят операцию последовательного выполнения градиента и дивергенции, которая обозначается Лапласа оператором.При применении основных дифференциальных операций к полям с определёнными видами симметрий (сферических, цилиндрических и др.) используют специальные виды криволинейных координат (полярные, цилиндрические и др.), что упрощает вычисления.

  В П. т. используется ряд интегральных соотношений и понятий, связывающих дифференцирование и интегрирование при изучении частей (или в целом) полей. Так, потоком векторного поля через поверхность называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к поверхности. Поток векторного поля связывается с дивергенцией при помощи Остроградского формулы : поток векторного поля через поверхность равен интегралу от дивергенции по объёму, ограниченному этой поверхностью. Др. важной характеристикой векторных полей является циркуляция векторного поля по замкнутому контуру - интеграл по контуру от скалярного произведения векторного поля на единичный вектор касательной к контуру. Циркуляция вектора по замкнутому контуру равна интегралу от вихря поля по любой поверхности, ограниченной данным контуром ( Стокса формула ) .По вихрю и дивергенции различают потенциальные поля (rot a= 0), соленоидальные (div a = 0) и лапласовы (Dj = 0).

  Лит.см. при статьях Векторное исчисление, Тензорное исчисление.

  А. Б. Иванов.

Поля физические

Поля' физи'ческие, особая форма материи; физическая система, обладающая бесконечно большим числом степеней свободы. Примерами П. ф. могут служить электромагнитное и гравитационное поля, поле ядерных сил, а также волновые (квантованные) поля, соответствующие различным частицам.

  Впервые (30-е гг. 19 в.) понятие поля (электрического и магнитного) было введено М. Фарадеем.Концепция поля была принята им как альтернатива теории дальнодействия, т. е. взаимодействия частиц на расстоянии без какого-либо промежуточного агента (так интерпретировалось, например, электростатическое взаимодействие заряженных частиц по закону Кулона или гравитационное взаимодействие тел по закону всемирного тяготения Ньютона). Концепция поля явилась возрождением теории близкодействия, основоположником которой был Р. Декарт (1-я половина 17 в.). В 60-х гг. 19 в. Дж. К. Максвелл развил идею Фарадея об электромагнитном поле и сформулировал математически его законы (см. Максвелла уравнения ) .

 Согласно концепции поля, частицы, участвующие в каком-либо взаимодействии (например, электромагнитном или гравитационном), создают в каждой точке окружающего их пространства особое состояние - поле сил, проявляющееся в силовом воздействии на др. частицы, помещаемые в какую-либо точку этого пространства. Первоначально выдвигалась механистическая интерпретация поля как упругих напряжений гипотетической среды - «эфира». Однако наделение «эфира» свойствами упругой среды оказалось в резком противоречии с результатами проведённых позднее опытов. С точки зрения современных представлений, такая механистическая интерпретация поля вообще бессмысленна, поскольку сами упругие свойства макроскопических тел полностью объясняются электромагнитными взаимодействиями частиц, из которых состоят эти тела. Теория относительности, отвергнув концепцию «эфира» как особой упругой среды, вместе с тем придала фундаментальный смысл понятию П. ф. как первичной физической реальности. Действительно, согласно теории относительности, скорость распространения любого взаимодействия не может превышать скорости света в вакууме. Поэтому в системе взаимодействующих частиц сила, действующая в данный момент времени на какую-либо частицу системы, не определяется расположением др. частиц в этот же момент времени, т. е. изменение положения одной частицы сказывается на др. частице не сразу, а через определённый промежуток времени. Т. о., взаимодействие частиц, относительная скорость которых сравнима со скоростью света, можно описывать только через создаваемые ими поля. Изменение состояния (или положения) одной из частиц приводит к изменению создаваемого ею поля, которое отражается на др. частице лишь через конечный промежуток времени, необходимый для распространения этого изменения до частицы.

  П. ф. не только осуществляют взаимодействие между частицами; могут существовать и проявляться свободные П. ф. независимо от создавших их частиц (например, электромагнитные волны ) .Поэтому ясно, что П. ф. следует рассматривать как особую форму материи.

  Каждому типу взаимодействий в природе отвечают определённые П. ф. Описание П. ф. в классической (не квантовой) теории поля производится с помощью одной или нескольких (непрерывных) функций поля, зависящих от координаты точки ( х, у, z) ,в которой рассматривается поле, и от времени ( t) .Так, электромагнитное поле может быть полностью описано с помощью четырёх функций: скалярного потенциала j( х, у, z, t) и вектор-потенциала А( х, у, z, t) ,которые вместе составляют единый четырёхмерный вектор в пространстве-времени. Напряжённости электрического и магнитного полей выражаются через производные этих функций. В общем случае число независимых полевых функций определяется числом внутренних степеней свободы частиц, соответствующих данному полю (см. ниже), например их спином, изотопическим спиноми т.д. Исходя из общих принципов - требований релятивистской инвариантности и некоторых более частных предположений (например, для электромагнитного поля - суперпозиции принципа и т. н. градиентной инвариантности), можно из функций поля составить выражение для действия и с помощью наименьшего действия принципа (см. также Вариационные принципы механики ) получить дифференциальные уравнения, определяющие поле. Значения функций поля в каждой отдельной точке можно рассматривать как обобщённые координаты П. ф. Следовательно, П. ф. представляется как физическая система с бесконечным числом степеней свободы. По общим правилам механики можно получить выражение для обобщённых импульсов П. ф. и найти плотности энергии, импульса и момента количества движения поля.

  Опыт показал (сначала для электромагнитного поля), что энергия и импульс поля изменяются дискретным образом, т. е. П. ф. можно поставить в соответствие определённые частицы (например, электромагнитному полю - фотоны,гравитационному - гравитоны ) .Это означает, что описание П. ф. с помощью полевых функций является лишь приближением, имеющим определённую область применимости. Чтобы учесть дискретные свойства П. ф. (т. е. построить квантовую теорию поля), необходимо считать обобщённые координаты и импульсы П. ф. не числами, а операторами,для которых выполняются определённые перестановочные соотношения.(Аналогично осуществляется переход от классической механики к квантовой механике.)

 В квантовой механике доказывается, что систему взаимодействующих частиц можно описать с помощью некоторого квантового поля (см. Квантование вторичное ) .Т. о., не только каждому П. ф. соответствуют определённые частицы, но и, наоборот, всем известным частицам соответствуют квантованные поля. Этот факт является одним из проявлений корпускулярно-волнового дуализма материи. Квантованные поля описывают уничтожение (или рождение) частиц и одновременно рождение (уничтожение) античастиц.Таким полем является, например, электрон-позитронное поле в квантовой электродинамике.

  Вид перестановочных соотношений для операторов поля зависит от сорта частиц, соответствующих данному полю. Как показал В. Паули (1940), для частиц с целым спином операторы поля коммутируют и указанные частицы подчиняются Бозе-Эйнштейна статистике,в то время как для частиц с полуцелым спином они антикоммутируют и соответствующие частицы подчиняются Ферми-Дирака статистике . Если частицы подчиняются статистике Бозе-Эйнштейна (например, фотоны и гравитоны), то в одном и том же квантовом состоянии может находиться много (в пределе - бесконечно много) частиц. В указанном пределе средние величины квантованных полей переходят в обычные классические поля (например, в классические электромагнитное и гравитационное поля, описываемые непрерывными функциями координат и времени). Для полей, отвечающих частицам с полуцелым спином, не существует соответствующих классических полей.