Большая Советская Энциклопедия (ПО)

  Может оказаться, что в П. равно нулю целое кратное naкакого-либо отличного от нуля элемента а.В этом случае существует такое простое число р,что р-кратное paлюбого элемента аэтого П. равно нулю. Говорят, что в этом случае характеристика П. равна р(пример 6). Если na ¹0 ни для каких отличных от нуля nи а,то считают характеристику П. равной нулю (примеры 1-5).

  Если часть Fэлементов поля Gсама образует П. относительно тех же операций сложения и умножения, то Fназывается подполем поля G, а G -надполем, или расширением поля F.П., не имеющее подполей, называется простым. Все простые П. исчерпываются П. примеров 1 и 6 (при всевозможных выборах простого числа р) .В каждом П. содержится единственное простое подполе (П. примеров 2-5 содержат П. рациональных чисел). Естественно было бы поставить такую задачу: отправляясь от простого П., получить описание всех П., изучив структуру расширений; приводимая ниже теорема Штейница делает шаг именно в этом направлении.

  Некоторые расширения имеют сравнительно простое строение. Это - а) простые трансцендентные расширения, которые сводятся к тому, что за поле Gберётся П. всех рациональных функций от одного переменного с коэффициентами из F,и б) простые алгебраические расширения (пример 5), которые получаются, если совокупность Gвсех многочленов степени nскладывать и умножать по модулю данного неприводимого над Fмногочлена f( x) степени n(конструкция, аналогичная примеру 6). Расширения второго типа сводятся к тому, что мы добавляем к Fкорень многочлена f( x) и все те элементы, которые можно выразить через этот корень и элементы F;каждый элемент надполя Gявляется корнем некоторого многочлена с коэффициентами из F.Расширения, обладающие последним свойством, называется алгебраическими. Любое расширение можно выполнить в два приёма: сначала совершить трансцендентное расширение (образовав П. рациональных функций, не обязательно от одной переменной), а затем алгебраическое (теорема Штейница). Алгебраических расширений не имеют только такие П., в которых каждый многочлен разлагается на линейные множители. Такие П. называются алгебраически замкнутыми. П. комплексных чисел является алгебраически замкнутым ( алгебры основная теорема ) .Любое П. можно включить в качестве подполя в алгебраически замкнутое.

  Некоторые П. специального вида подверглись более детальному изучению. В теории алгебраических чисел рассматриваются главным образом простые алгебраические расширения П. рациональных чисел. В теории алгебраических функций исследуются простые алгебраические расширения П. рациональных функций с комплексными коэффициентами; значительное внимание уделяется конечным расширениям П. рациональных функций над произвольным П. констант (т. е. с произвольными коэффициентами). Конечные расширения П., в особенности их автоморфизмы (см. Изоморфизм ) ,изучаются в теории Галуа (см. Галуа теория ) ;здесь находят ответ многие вопросы, возникающие при решении алгебраических уравнений. Во многих вопросах алгебры, особенно в различных отделах теории П., большую роль играют нормированные поля. В связи с геометрическими исследованиями появились и изучались упорядоченные П.

  См. также Алгебра, Алгебраическое число, Алгебраическая функция, Кольцоалгебраическое.

  Лит.:Курош А. Г., Курс высшей алгебры, 10 изд., М., 1971; Ван дер Варден Б. Л., Современная алгебра, пер. с нем., [2 изд.], ч. 1-2, М. - Л., 1947; Чеботарев Н. Г., Теория алгебраических функций, М.- Л., 1948; его же, Основы теории Галуа. ч. 1-2, Л. - М., 1934-37; Вейль Г., Алгебраическая теория чисел, пер. с англ., М., 1947.

Поле (в биологии)

По'лев биологии, понятие, описывающее биологическую систему, поведение частей которой определяется их положением в этой системе. Наличие таких систем следует прежде всего из многочисленных опытов по перемещению, удалению и добавлению частей у зародышей. Во многих случаях из таких зародышей развиваются нормальные организмы, т.к. их составные части изменяют прежний путь развития согласно своему новому положению в целом. В 1912-22 А. Г. Гурвич ввёл понятие П. (морфогенетического П.) в эмбриологию и поставил задачу отыскания его законов. Последние сначала отождествлялись им с нерасчленимым фактором, управляющим формообразованием, позже - с системой межклеточных взаимодействий, определяющих движение и дифференцировку клеток зародыша. В 1925 австрийский учёный П. Вейс применил понятие П. к процессам регенерации;в 1934 английские учёные Дж. Хаксли и Г. де Вер объединили его с понятием градиента.Английский биолог К. Уоддингтон и французский математик Р. Том (40-60-е гг. 20 в.) создали представления об эмбриональном развитии как о векторном П., разделённом на ограниченное число зон «структурной устойчивости». Этот круг понятий интенсивно разрабатывается в современной теоретической биологии, но единого мнения о внутренних закономерностях явлений, описываемых понятием П., не выработано.

  Лит.:Гурвич А. Г., Теория биологического поля, М., 1944; Уоддингтон К. Морфогенез и генетика, пер. с англ., М., 1964; На пути к теоретической биологии, пер. с англ., [т.] 1, М., 1970; Towards a theoretical biology, v. 2-4, Edin., 1969-72.

  Л. В. Белоусов.

Поле (в сельском хоз-ве)

По'ле, 1) обширное, ровное, безлесное пространство. 2) В сельском хозяйстве участки пашни, на которые разделены площадь севооборота,а также внесевооборотные (запольные) участки, используемые для выращивания с.-х. растений. 3) Ограниченный определёнными пределами объект наблюдения, обозрения (П. зрения); часть пространства, плоскости, которая изображается оптической системой, например поле зрения оптической системы. 4) Район боевых операций (П. битвы, П. обстрела). 5) В русских юридических источниках 13-16 вв. судебный поединок (см. Поле юридическое). 6) Основной цвет, тон, на котором что-либо изображено; задний план изображения, то же, что фон. 7) Полоса вдоль края листа бумаги, оставляемая свободной от письма и печати (тетрадь с П., П. книги, П. рукописи). 8) В переносном смысле - область, сфера человеческой деятельности, поприще. 9) Поля - а) земельные участки, специально приспособленные для определённых целей, например для приёма сточных вод (см. Поля фильтрации, Поля орошения) ;б) широкий край шляпы. О применении термина «П.» в математике см. Поле алгебраическое, Поле направлений, Поля теорияи др.; в физике - Поля физические, Электромагнитное полеи др.; в астрономии и геофизике - Электрическое поле в атмосфере, Электрическое поле Земли. См. также Поле в биологии, Поле семантическое.

Поле (грамматич.)

По'ле(Feld, field, champ) семантическое, совокупность слов, объединяемых смысловыми связями по сходным признакам их лексических значений. Например, П. немецкого глагола fehlen охватывает 7 глаголов, объединяемых признаком «отсутствовать»: fehlen, abgehen, mangeln, gebrechen, vermissen, entbehren, missen. Понятие П. позволяет адекватно описывать микроструктурные системные семантические взаимодействия языковых единиц. Разрабатывается с конца 20-х - начала 30-х гг. 20 в. немецкими учёными И. Триром (изучал совокупность слов в их предметно-понятийных связях), В. Порцигом (исследовал одно слово в его семантико-синтаксических связях), А. Йоллесом (связал П. с этимолого-словообразовательным анализом слова), Г. Ипсеном. В 50-е гг. 20 в. теорию П. разрабатывает Л. Вайсгербер (ФРГ). Концепции немецких учёных подвергаются критике за использование понятия П. для доказательства идеалистического тезиса о «промежуточном языковом мире» (die sprachliche Zwischenwelt), субъективизм в выделении полей, невозможность охватить ими всю лексику, умаление самостоятельной роли отдельного слова.

  С 60-х гг. 20 в. исследуются лексико-семантические поля слов и синтактико-семантические П. одного слова. Понятие П. расширяется: выделяются лексико-грамматические, функционально-семантические, словообразовательные и др. виды полей.

  Лит.:Уфимцева А. А., Опыт изучения лексики как системы, М., 1962; Кузнецова А. И., Понятие семантической системы языка и методы её исследования, М., 1963; Васильев Л. М., Теория семантических полей, «Вопросы языкознания», № 5, 1971; Щур Г. С., Теории поля в лингвистике, М. - Л., 1974; Trier J., Der deutsche Wortschatz im Sinnbezirk des Verstandes, Hdlb., 1931; Porzig W., Das Wunder der Sprache, 3 Aufl., Bern, 1962; Weisgerber L., Grundzьge der inhaitbezogenen Grammatik, 3. Aufl., Dьsseldorf, 1962: Hoberg R., Die Lehre vom sprachlichen Feld, Dьsseldorf, 1970; Minina N., Semantische Felder, Moskau, 1973.

  Н. М. Минина.

Поле зрения

По'ле зре'нияоптической системы, часть пространства (плоскости), изображаемая этой системой. Величина П. з. определяется входящими в систему деталями (такими, как оправы линз, призм и зеркал, диафрагмы и пр.), которые ограничивают пучок лучей света. Различают измеряемое в угловых единицах угловое П. з. систем, предназначенных для наблюдения за очень (практически - бесконечно) удалёнными объектами ( телескопы, зрительные трубы,многие фотографические аппараты), и измеряемое в ммили см. линейное П. з. систем, в которых расстояние до объекта невелико (например, микроскопов ) .Если А( рис. ) - центр входного зрачка системы (см. Диафрагма в оптике), то П. з. - это либо угол 2w, под которым из Авиден входной люк S ₁S ₂и соответствующая часть плоскости объекта O ₁O ₂, либо сами линейные размеры O ₁O ₂( OO- ось симметрии системы). В общем случае плоскости O ₁O ₂и S ₁S ₂не совпадают и имеет место виньетирование (с шириной кольца BB ₁). Если же S ₁S ₂совмещена с плоскостью объекта, граница П. з. резка. Этого стараются добиться во многих телескопах, зрительных трубах и др., помещая диафрагму П. з. в фокальную плоскость объектива. Угол П. з. (в пространстве предметов, см. Изображение оптическое ) обратно пропорционален угловому увеличению оптическому системы. В биноклях он составляет 5-10°, а в самых больших телескопах не превышает несколько дуговых минут. В специальных (т. н. широкоугольных) фотообъективах он достигает 120-140° и даже 180° (см. Объектив ) .Подавляющее большинство микроскопов снабжается набором сменных окуляров,увеличения которых и, следовательно, линейные П. з. в пространстве объектов 2 lразличны. Очень часто используются окуляры с 2 l= 18 мм;однако у многих окуляров П. з. больше или меньше этой величины. В поляризационных микроскопах и стереомикроскопах зачастую применяют окуляры с П. з. до 25 мм(широкоугольные). Линейное П. з. микроскопа в целом равно 2 l/b, где b - линейное увеличение объектива микроскопа.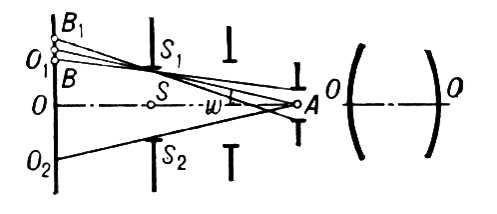

Рис. к ст. Поле зрения.

Поле направлений

По'ле направле'ний,совокупность точек плоскости хОу,в каждой из которых задано определённое направление, изображающееся обычно стрелкой (небольшим отрезком), проходящей через данную точку. Если дано уравнение y'= -f( x, у) ,то в каждой точке ( х _0,у ₀) некоторой области плоскости хОуизвестно значение углового коэффициента k= f( x ₀, y ₀) касательной к интегральной кривой,проходящей через эту точку; направление касательной можно изобразить стрелкой (небольшим отрезком). Таким образом, это дифференциальное уравнение определяет П. н.; наоборот, П. н., заданное в некоторой области плоскости хОу,определяет дифференциальное уравнение вида y'= f( x, y) .Проводя достаточно густую сеть изоклин [линий одинакового наклона П. н. f( x, у) = С,где С- постоянная], можно приближённо построить семейство интегральных кривых как совокупность линий, имеющих в каждой своей точке направление, совпадающее с направлением поля (метод изоклин) .На рис. изображено П. н. уравнения у'= х ²+ у ²;тонкие линии (окружности) - изоклины; жирные линии - интегральные кривые.

  Лит.:Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959; Петровский И. Г., Лекции по теории обыкновенных дифференциальных уравнений, 6 изд., М., 1970.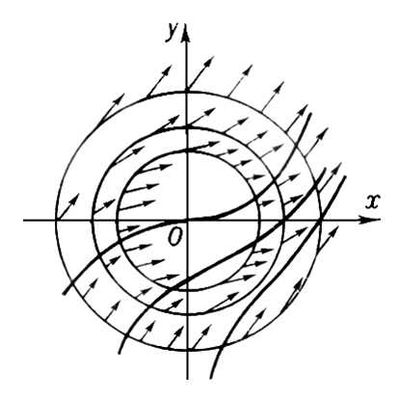

Рис. к ст. Поле направлений.

Поле (юридич.)

По'леюридическое, в русских источниках 13-16 вв. судебный поединок. Обычно П. предусматривалось как альтернатива присяге (крестному целованию), причём в качестве противоборствующих могли выступить и свидетели обеих сторон. Инициатива решения дела П. принадлежала участникам процесса. Престарелые, малолетние и духовные лица имели право выставлять за себя «наймита». Проигрыш поединка или отказ от П. со стороны участника процесса означал проигрыш им дела. Стороны имели право помириться как до поединка, так и выйдя на него. К середине 16 в. П. - юридический анахронизм (хотя и упомянуто в Судебниках 1550 и 1589), оно почти полностью исчезает из судебной практики.

  Лит.:Судебники XV-XVI вв., М. - Л., 1952.

Полевая

Полева'я,посёлок городского типа в Дергачёвском районе Харьковской области УССР, в 7 кмот ж.-д. станции Пересечная (на линии Харьков - Готня). Отделение совхоза «Южный» овоще-молочного направления.

Полевая артиллерия

Поле'вая артилле'рия,артиллерия, организационно входящая в состав общевойсковых подразделений, частей и соединений. В Советских Вооруженных Силах П. а. именуется войсковой артиллерией.

Полевая всхожесть семян

Полева'я всхо'жесть семя'н,отношение числа появившихся всходов к числу высеянных в поле всхожих семян, выраженное в процентах. П. в. с. зависит от качества и биологических особенностей семян, условий их хранения, почвенных и метеорологических условий периода «посев - всходы», сроков посева, глубины заделки семян и др. При прочих равных условиях чем выше лабораторная всхожесть семян и энергия прорастания, тем выше и П. в. с. При низкой П. в. с. получаются редкие всходы и большая засорённость посевов, увеличивается повреждение болезнями и вредителями, растения оказываются ослабленными и менее продуктивными.

Полевая горчица

Полева'я горчи'ца,однолетнее сорное растение семейства крестоцветных; см. Горчица.

Полевица

Полеви'ца(Agrostis), род многолетних, реже однолетних трав семейства злаков. Мелкие одноцветковые колоски собраны в рыхлое, метельчатое соцветие. Около 200 видов, произрастающих в умеренном и холодном поясе, главным образом в Сев. полушарии, и в горах тропиков. В СССР свыше 30 видов, преимущественно в лесной зоне; растут по лугам (часто в массе), полянам, кустарникам, берегам водоёмов. Среди П. много кормовых растений. П. побегообразующая (A. stolonifera, прежде A. alba) и П. гигантская (A. gigantea), распространённые по влажным лугам, - пастбищные и сенокосные растения; оба вида используют в травосмесях для низинных лугов. П. собачья (A. canina), произрастающая в Европейской части, сибирские виды - П. булавовидная (A. clavata) и П. Триниуса (A. trinii), кавказская П. плосколистная (A. planifolia) и др. также имеют кормовое значение. П. тонкая (A. tenius, прежде А. capillaris), часто встречающаяся по суходольным лугам, скотом почти не поедается. П. собачью, П. тонкую и др. используют для газонов, П. альпийскую (А. alpina), П. ажурную (A. nebulosa), П. наскальную (A. rupestris) и др. - как декоративные растения.

  Лит.:Кормовые растения сенокосов и пастбищ СССР, под ред. И. В. Ларина, т. 1, М. - Л., 1950.

  Т. В. Егорова.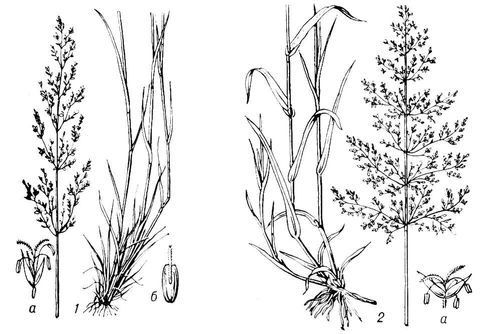

Полевица: 1 - собачья (а - колосок, б - нижняя цветковая чешуя с остью); 2 - побегообразующая (а - колосок).

Полевичка

Полеви'чка(Eragrostis), род растений семейства злаков. Одно- или многолетние травы с узколинейными плоскими листовыми пластинками. Соцветие метельчатое. Колоски трёх- или многоцветковые. Около 500 видов, растут в субтропической, тропической и отчасти умеренных областях. В СССР около 10 видов. В их числе П. мятликовидная, или малая (Е. poaeoides, прежде Е. minor), и П. волосистая (Е. pilosa) - однолетники, растущие преимущественно в сухих степях и полупустынях по песчаным местам и как сорняки на полях; оба вида хорошо поедаются скотом на пастбище и в сене. П. холмовая, или тростниковидная (Е. collina, прежде Е. arundinaceae), - многолетник высотой до 1,5 м,обитающий в степях и полупустынях на солончаках и солонцах; солевыносливое кормовое растение. П. тефф возделывается как хлебная и кормовая культура в Эфиопии, Индии и ряде др. стран (см. Тефф ) .П. волосовидную (Е. capillaris), П. изящную (Е. elegans) и некоторые другие иногда разводят как декоративные.

Полёвки

Полёвки(Microtinae), подсемейство грызунов семейства хомяков; некоторые зоологи выделяют семейства полёвковых (или полёвок). Длина тела в среднем 10-12 см,у некоторых до 36 см,хвост - в половину длина тела, иногда короче. Окраска верха обычно однотонная - серая или буроватая. Коренные зубы у большинства без корней, постоянно растущие, реже с корнями (у большинства вымерших); на их жевательной поверхности - чередующиеся треугольные петли. Свыше 40 родов, в том числе более половины вымерших. В СССР 12 современных родов с 43 видами. Населяют материки и многие острова Северного полушария к югу до Северной Африки, северной части Индии, Японских, Курильских и Командорских островов, сев. части Мексики. В горах - до верхнего предела растительности, к С. - до океанического побережья. Наибольшего видового разнообразия и высокой численности достигают в открытых ландшафтах умеренной зоны. Большинство П. селится колониями. Активны круглый год. В пище преобладают надземные части растений, некоторые виды П. делают запасы. Размножаются весь тёплый период года, часть видов - и зимой. Численность может резко колебаться в разные годы. Большинство П. - серьёзные вредители с.-х. культур и природные носители возбудителей туляремии, лептоспирозаи др. заболеваний. Шкурки крупных видов (например, ондатры ) используются как меховое сырьё.

  И. М. Громов.

Полеводство

Полево'дство, одна из отраслей земледелия ; производство продукции полевых, преимущественно однолетних яровых и озимых, культур (зерновых, технических - сахарная свёкла, лён, хлопчатник и др., кормовых, бахчевых, картофеля). Часто отождествляется с растениеводством (в связи с выделением из последнего специальных отраслей - овощеводства, плодоводства, виноградарства и т.п.).

Полеводческая бригада

Полево'дческая брига'да, см. Бригада производственная в сельском хозяйстве.

Полевой Борис Николаевич

Полево'й(псевдоним; настоящая фамилия - Кампов) Борис Николаевич [р. 4(17).3.1908, Москва], русский советский писатель, общественный деятель, Герой Социалистического Труда (1974). Член КПСС с 1940. Окончил промышленный техникум в Твери (1926). Участник советско-финляндской войны 1939-40. В годы Великой Отечественной войны 1941-1945 военный корреспондент «Правды». Первая очерковая повесть - «Мемуары вшивого человека» (1927). Автор повести «Горячий цех» (1939). Широкую известность в стране и за рубежом завоевала книга «Повесть о настоящем человеке» (1946; Государственная премия СССР, 1947; одноименный фильм, 1948), в основе которой - реальный подвиг Героя Советского Союза лётчика А. П. Маресьева.Темы героизма советских людей в годы войны и послевоенного строительства нашли воплощение в сборнике очерков и рассказов «Мы - советские люди» (1948; Государственная премия СССР, 1949); в романах «Золото» (1949-50, одноименный фильм, 1970), «Глубокий тыл» (1958), «На диком бреге...» (1962; одноименный фильм, 1966), «Доктор Вера» (1966; одноименный фильм, 1968) и др. Поездкам за рубеж посвящены сборники очерков: «Американские дневники» (1956; Международная премия Мира, 1959), «По белу свету» (1958), «30 тысяч ли по Китаю» (1957) и др. С 1962 главный редактор журнала «Юность», с 1967 секретарь правления Союза писателей СССР. Член бюро Всемирного Совета Мира и Президиума Советского комитета защиты мира. Вице-президент Европейского общества культуры (с 1952). Награжден 2 орденами Ленина, орденом Октябрьской Революции, 6 др. орденами, а также медалями, Золотой медалью Мира (1968), иностранными орденами и медалями. Многие произведения П. переведены на иностранные языки.

  Соч.: Избр. произв., т. 1-2, М., 1969; Человек - человеку. Повести, М., 1971; Эти четыре года. Из записок военного корреспондента, т. 1-2, М., 1974.

  Лит.:Галанов Б., Борис Полевой, М. - Л., 1957; Леонов Б., Красота подвига, «Знамя», 1971, №3; Михайлова Л., Отражение истории в человеке, «Новый мир», 1974, № 5; Русские советские писатели-прозаики, Биобиблиографический указатель, т. 3, М., 1964.

  В. А. Калашников.

 

Б. Н. Полевой.

Полевой жаворонок

Полево'й жа'воронок, птица семейства жаворонков отряда воробьиных.

Полевой Николай Алексеевич

Полево'йНиколай Алексеевич [22.6(3.7).1796, Иркутск, - 22.2(6.3).1846, Петербург], русский писатель, критик, журналист и историк. Родился в купеческой семье. Систематического образования не получил. Начал печататься в 1817. В 1820-1836 жил в Москве. П. явился одним из первых буржуазных идеологов в России 20-30-х гг.; был сторонником конституционной монархии. Издавал журнал «Московский телеграф» (1825-34), в котором с либерально-буржуазных позиций выступал против феодализма и дворянства, подчёркивал гражданскую честность, заслуги и монархический патриотизм купечества. В журнале печаталось много статей по истории и этнографии; в литературно-критических статьях (о романах В. Гюго, о состоянии драматического искусства во Франции и др.) П. опровергал эстетику классицизма, защищал романтизм,в котором видел средство утверждения демократического искусства. Антиаристократические тенденции характерны для П. - автора романтических повестей «Живописец» (1833), «Эмма» (1834), романа «Аббаддонна» (1834), исторического романа «Клятва при гробе Господнем» (1832) и др. После запрещения в 1834 журнала в условиях николаевской реакции П. отошёл от своих прежних взглядов, сильно эволюционировал вправо (участие в «Сыне отечества» и «Северной пчеле»). Переехав в Петербург, П. занял критическую позицию в отношении Н. М. Карамзина,в противовес его «Истории государства Российского» написал свою «Историю русского народа» (т. 1-6, 1829-33). П. старался обнаружить и показать органическое развитие народного начала в истории. Вместо главного внимания к придворной, военной, дипломатической истории, рассуждений о достоинствах и недостатках князей и царей П. предложил обратиться к раскрытию внутренних закономерностей русского исторического процесса. Но реализация новых и важных общих установок, им самим провозглашенных, оказалась для П. непосильной. Вместо обещанной истории народа у П. на первом месте также оказалась история государственной власти. П. принадлежит прозаический перевод «Гамлета» У. Шекспира (1837). Статьи П. о Г. Р. Державине, В. А. Жуковском, А. С. Пушкине и др. собраны в его книгу «Очерки русской литературы» (ч. 1-2, 1839). В последние годы жизни выступал против В. Г. Белинского и гоголевского направления в литературе.

  Соч.: Соч., кн. 1-3, М., 1903.

  Лит.:Полевой К. А., Записки, СПБ, 1888; Н. Полевой. Материалы из истории русской литературы и журналистики 30-х гг., Л., 1934; Евгеньев-Максимов В. Е., Березина В. Г., Н. А. Полевой, [Иркутск], 1947; Белинский В. Г., Н. А. Полевой, Полн. собр. соч., т. 9, М., 1955; Очерки истории исторической науки в СССР, т. 1, М., 1955, с. 331-34; Гуляев Н. А., Литературно-эстетические взгляды Н. А. Полевого, «Вопросы литературы», 1964, № 12; Кулешов В. И., История русской критики XVIII-XIX вв., М., 1972, с. 103-07; История русской литературы XIX в. Библиографический указатель, М. - Л., 1962.

Н. А. Полевой.

Полевой опыт

Полево'й о'пыт, постановка эксперимента в полевых условиях, близких к производственным, для выяснения зависимости величины и качества урожая с.-х. растений от условий и технологии возделывания; вид агрономического исследования.

  П. о. закладывают по определённой методике, предусматривающей число вариантов, повторность, площадь, форму и направление делянок, размещение их на участке, методы учёта урожая. Результаты П. о. служат основанием для широкого внедрения в с.-х. производство новых агротехнических приёмов, сортов и др.

  П. о. должен проводиться в типичных для с.-х. производства условиях, т. е. на типичной для конкретного района почвенной разности, в условиях применяемого в районе севооборота, с соблюдением высокого уровня агротехники. Закладывают П. о. по определённой схеме, состоящей из ограниченного числа вариантов, отличающихся только одним изучаемым в опыте фактором (агротехническим приёмом, сортом и др.). Число делянок и вариантов определяется принятой в опыте повторностью. Повторность является средством повышения точности результатов П. о. и даёт возможность оценить степень достоверности полученных в опыте разниц между средними урожаями сравниваемых вариантов. Для получения надёжных результатов П. о. закладывают с повторностью не меньше 4-кратной, а в отдельных случаях (когда требуется более высокая точность опыта) - с 6-8-кратной. Участок под П. о. должен быть однородным по рельефу, почвенной разности, предшествующей истории за последние 3-4 года (одинаковые обработки, удобрения, чередования культур и т.д.). Размеры участка зависят от величины делянки, числа вариантов и принятой в опыте повторности. При установлении размеров делянки и числа повторностей учитывают особенности культуры, тему опыта, характер рельефа, пестроту почвенного покрова, орудия и машины, которыми будут выполняться работы, а также требования к точности опыта. Обычно величину делянки принимают равной минимальной площади, обеспечивающей в данных условиях необходимую точность опыта и проведение всех полевых работ, включая учёт урожая, с максимальной механизацией. В практике опытного дела наиболее часто применяются делянки квадратной или прямоугольной формы площадью 50-200 м ²(иногда 300 м ²и более). В зависимости от рельефа и конфигурации участка делянки располагают в один ряд или в несколько рядов так, чтобы они соприкасались длинными сторонами. При многорядном расположении делянок в каждом ряду помещают целое число повторностей. Внутри повторности расположение вариантов на делянках может быть различным: систематическим, рендомизированным (случайным) или стандартным. Наибольшее значение имеют методы, основанные на принципе рендомизированного размещения вариантов.

  По краям делянок и по краям участка П. о. заранее выделяют т. н. защитные полосы, урожай с которых убирают отдельно. Они необходимы для устранения погрешностей, вызванных влиянием смежных делянок (например, внесённых удобрений). В программу П. о. наряду с учётом урожая включаются наблюдения за динамикой роста и развития растений, за состоянием почвы, учёт метеорологических условий и т.д. Содержание программы изменяется в зависимости от цели П. о.

  Урожай на делянке определяют методом сплошного учёта (со всей площади делянки). В опытах с зерновыми, прядильными культурами и травами применяют также учёт по пробному снопу. Данные урожая статистически обрабатывают, что позволяет установить степень точности опыта и показать, что разницы, полученные в опыте при сравнении средних урожаев различных вариантов, являются достоверными, т. е. они значительно превосходят величину случайных ошибок, или же недостоверными, если они находятся в пределах ошибки. Один из наиболее распространённых методов статистической обработки данных П. о. - дисперсионный анализ, позволяющий находить общую ошибку средних урожаев в целом для всего опыта и одну общую ошибку разности для средних урожаев любой пары сравниваемых вариантов в опыте.