 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (ПО)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ПО) - Чтение (стр. 114)
Соч.: Клинические лекции (о болезнях сердца и их лечении), пер. с франц., СПБ 1898. Лит.:Менье Л., История медицины, пер. с франц., М. - Л., 1926, с. 193; Vaquez М. Н., Pierre-Carl Potain (1825-1901), «Bulletin de l'Akadйmie de mйdicine», 1927, 3 sйr., t. 98, № 41. Потенциал действия Потенциа'л де'йствия(физиологический), быстрое колебание мембранного потенциала, возникающее при возбуждении нервных и мышечных клеток (волокон); активный электрический сигнал, с помощью которого осуществляется передача информации в организме человека и животных. Основан на быстро обратимых изменениях ионной проницаемости клеточной мембраны (см. Биоэлектрические потенциалы ) ,связанных с активацией и инактивацией ионных мембранных каналов. В нервных волокнах восходящая фаза П. д. связана с активацией т. н. быстрых натриевых каналов (БНК), а нисходящая фаза - с инактивацией БНК и активацией калиевых каналов (КК). На таком же механизме основана генерация П. д. в волокнах скелетных мышц позвоночных. В мышечных волокнах сердца активация БНК обеспечивает только начальный подъём П. д. Характерное же для этих волокон плато П. д. связано с активированием медленных натрий-кальциевых каналов (МНК). В мембранах волокон гладких мышц внутренних органов и сосудов позвоночных, а также мышечных волокон членистоногих (ракообразных, насекомых) и ряда нейронов моллюсков БНК не обнаружены. П. д. в этих клетках связан с активацией МНК или медленных кальциевых каналов (МКК). Нисходящая фаза П. д. обеспечивается КК. Изучение физико-химических свойств ионных каналов важно не только для расшифровки их молекулярной структуры, но и для разработки методов управления генерацией П. д. в различных клетках. Установлено, что БНК специфически блокируются тетродотоксином (ядом японской рыбы-шар и калифорнийских саламандр), а также новокаином, кокаином и др. местными анестезирующими средствами. МНК и МКК к этим агентам нечувствительны, но блокируются ионами Mn 2+, Со 2+, Ni 2+, La 3+и органическими соединениями - изоптином (используемым в кардиологической практике) и его дериватом Д-600. Большинство КК эффективно блокируется тетраэтиламмонием. Пусковое влияние П. д. на такие внутриклеточные процессы, как сокращение миофибрилл (в скелетных, гладких и сердечной мышцах), нейросекреция (в некоторых специализированных нейронах и нервных окончаниях) и т.д., осуществляется в результате прямого воздействия электрического импульса; на внутриклеточные структуры (выброс) ионов Ca 2+из саркоплазматической сети мышцы) и влияния на эти структуры ионов Ca 2+ ,проникающих внутрь клетки во время П. д. Лит.см. при ст. Биоэлектрические потенциалы. Б. И. Ходоров. Потенциал зажигания Потенциа'л зажига'ния,см. Зажигания потенциал. Потенциал запаздывающий Потенциа'л запа'здывающий,см. Запаздывающие потенциалы. Потенциал ионизации Потенциа'л иониза'ции,см. Ионизационный потенциал. Потенциал (математич., физич.) Потенциа'л,потенциальная функция, понятие, характеризующее широкий класс физических силовых полей (электрическое, гравитационное и т.п.) и вообще поля физических величин, представляемых векторами (поле скоростей в жидкости и т.п.). В электростатическое поле П. вводится как вспомогательная функция, пространственные производные которой - компоненты напряжённости электрического поля в данной точке; в гидродинамике - компоненты скорости в данной точке и т.п. При этом П. в ряде случаев имеет и др. важный физический смысл. Так, в электростатическом поле он численно равен энергии, необходимой для удаления единичного положительного заряда из данной точки в бесконечность (с обратным знаком). В общем случае П. векторного поля
а(
х, у, z)
-скалярная функция
u(
х, у, z)
,такая, что
а =grad
u,т. е.
Для поля тяготения, образованного помещенной в точку A(x, h, x) точечной массой m,П. (ньютонов П.) имеет в точке Р( х, у, z) вид: u( х, у, z) = Gm/r, (1) где
П. u( х, у, z) - непрерывная функция во всём пространстве вместе со своими частными производными 1-го порядка; вне тела объёма Т функция u( х, у, z) удовлетворяет Лапласа уравнению,внутри - Пуассона уравнению. Если притягивающие массы распределены с плотностью r повпо поверхности S(простой слой), то П. образованного ими поля выражается интегралом
П. простого слоя u(
x, у, z)
-непрерывная во всём пространстве функция; при пересечении поверхности S нормальная производная функции w(
х, у, z) испытывает разрыв, равный 4pG/r
пов. Неограниченно сближая две поверхности, на которых расположены простые слои с плотностями r
пови -r
пов, и одновременно увеличивая r
повдо бесконечности, но так, чтобы был конечным предел
П. двойного слоя w( х, у, z) - непрерывная функция во всём пространстве вне S;при пересечении поверхности Sфункция w( х, у, z) испытывает разрыв, равный 4pGm. Функции u( х, у, z) и w( х, у, z) удовлетворяют уравнению Лапласа. Если тело объёма Т -бесконечный цилиндр с поперечным сечением Dи плотность r вещества цилиндра постоянна вдоль каждой прямой, параллельной образующим цилиндра, то формула (2) приводит к понятию логарифмического потенциала:
u(
х, у)
=
В виде суммы П. простого и двойного слоев может быть представлена любая гармоническая функция;этим объясняется важность теории П. Лит.:Гюнтер Н. М., Теория потенциала и её применение к основным задачам математической физики, М., 1953; Сретенский Л. Н., Теория ньютоновского потенциала, М. - Л., 1946; Тамм И. Е., Основы теории электричества, 7 изд., М., 1957; Идельсон Н. И., Теория потенциала с приложениями к теории фигуры Земли и геофизике, 2 изд., Л. - М., 1936. В. И. Битюцков. Потенциал нулевого заряда Потенциа'л нулево'го заря'да,«нулевая точка» в электрохимии, особое для каждого металла значение электродного потенциала,при котором его чистая поверхность при соприкосновении с электролитом не приобретает электрического заряда. При этом электролит не должен содержать поверхностно-активные вещества.Если электродный потенциал положительнее, чем П. н. з., то к металлу из раствора притягиваются отрицательные ионы, если отрицательнее, то - положительные. В обоих случаях уменьшается обычная тенденция частиц вещества уходить с поверхности фазы в её объём, т. е. понижается поверхностное натяжение на границе металла с раствором. На жидком, например ртутном, электроде это легко наблюдать с помощью т. н. электрокапиллярных кривых, показывающих, как потенциал металлического мениска, соприкасающегося с электролитом, влияет на высоту его капиллярного поднятия или опускания. При П. н. з. поверхностное натяжение максимально, а электрическая ёмкость границы минимальна. Знание П. н. з. необходимо при изучении кинетики электродных реакций, при подборе ингибиторов коррозии и в др. случаях, когда важно учитывать адсорбцию компонентов на металлической поверхности. Потенциал повреждения Потенциа'л поврежде'ния(физиологическая), разность потенциалов, регистрируемая между поврежденным (механически, термически, электрически и т.д.) и интактным (неповрежденным) участками клетки (ткани). П. п. обусловлен потенциалом покоя и связан с ним. Поврежденный участок отрицательно заряжен по отношению к неповрежденному. Наибольшую величину П. п. имеет в момент нанесения повреждения; с течением времени вследствие формирования мембраноподобных структур в месте повреждения П. п. снижается. Электрический ток между поврежденным и интактным участками нервного или мышечного волокна оказывает раздражающее и повреждающее действие на соседние участки клеточной мембраны. См. Биоэлектрические потенциалы. Потенциал покоя Потенциа'л поко'я(физиологический), разность потенциалов между содержимым клетки (волокна) и внеклеточной жидкостью; скачок потенциала локализуется на поверхностной мембране, при этом её, внутренняя сторона заряжена электроотрицательно по отношению к наружной. П. п. обусловлен неравенством концентраций, ионов Na +, К +и Cl -по обе стороны клеточной мембраны и неодинаковой её проницаемостью для этих ионов (см. Биоэлектрические потенциалы, Деполяризация) .В нервных и мышечных клетках П. п. участвует в поддержании состояния готовности молекулярной структуры мембраны к возбуждению в ответ на действие раздражителя. Все воздействия на клетку, вызывающие длительное стойкое снижение П. п. (например, нарушение обмена веществ, повышение внеклеточного содержания ионов К +, действие сильного электрического тока и т.д.), ведут к снижению возбудимости клетки или к полной утрате ею способности к генерации потенциалов действия. Б. И. Ходоров. Потенциал (средства) Потенциа'л(от лат. potentia - сила), в широком смысле - средства, запасы, источники, имеющиеся в наличии и могущие быть мобилизованы, приведены в действие, использованы для достижения определённой цели, осуществления плана, решения какой-либо задачи; возможности отдельные лица, общества, государства в определённой области: экономический П. (см. Экономический потенциал ) ,производственный П. О применении термина «П.» в математике, физике, технике, биологии и химии см. Запаздывающий потенциал, Потенциал, Потенциал действия, Потенциал повреждения, Химический потенциал, Потенциалы электромагнитного поляи др. Потенциал химический Потенциа'л хими'ческий, см. Химический потенциал. Потенциал экономический Потенциа'л экономи'ческий, см. Экономический потенциал. Потенциал электростатический Потенциа'л электростати'ческий, скалярная энергетическая характеристика электростатического поля. П. э. равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда. Напряжённость электростатического поля Е и потенциал j связаны соотношением: Е = -gradj. П. э. удовлетворяет Пуассона уравнению.Непосредственный физический смысл имеет не сам потенциал, определяемый, подобно потенциальной энергии, с точностью до произвольной постоянной, а разность потенциалов. Потенциалоскоп Потенциалоско'п(от потенциал и греч. skopйo - смотрю, наблюдаю) с видимым изображением, электроннолучевой прибор,предназначенный для записи информации, подаваемой на его входной электрод в виде электрических сигналов, её хранения и последующего воспроизведения на люминесцентном экране. Записывающий электронный луч П. ( рис. ), модулированный сигналом, подлежащим записи, перемещаясь по мишени, выбивает с её диэлектрической поверхности вторичные электроны (см. Вторичная электронная эмиссия ) и создаёт на ней переменный потенциал. Изменения потенциала пропорциональны силе тока и времени действия записывающего луча. Полученный на мишени т. н. потенциальный рельеф модулирует воспроизводящий пучок электронов, создающий изображение на экране. В т. н. полутоновых П. потенциал мишени отрицателен по отношению к потенциалу катода воспроизводящего прожектора, поэтому электроны воспроизводящего пучка не попадают на мишень и записанное изображение сохраняется на ней в течение некоторого времени (до нескольких мин) .В бистабильных П. потенциал мишени положителен по отношению к потенциалу катода воспроизводящего прожектора и воспроизводящий пучок приводит её потенциал к двум стабильным значениям, благодаря чему изображение сохраняется длительное время (до нескольких часов). П. с видимым изображением применяют для наблюдения однократных и редко повторяющихся сигналов в осциллографах, радиолокационных индикаторах, устройствах вывода информации ЭВМ и т.д. В осциллографах П. имеют яркость свечения 2-150 нт,разрешающую способность (определяемую числом линий, приходящихся на диаметр или какую-либо сторону изображения на экране П.) 60-200 линий и полное время воспроизведения (считывания) 1-600 мин;в радиолокационных устройствах - соответственно 100-5000 нт,150-600 линий и 0,2-2,0 мин. П. называют также любую запоминающую электроннолучевую трубку,последний термин в 70-е гг. 20 в. получает преимущественное распространение. Лит.:Котовщиков Г. С., Кондратенков В. М., Запоминающие трубки с видимым изображением, М., 1970; Жигарев А. А., Электронная оптика и электроннолучевые приборы, М., 1972; Денбновецкий С. В., Семенов Г. Ф., Запоминающие электроннолучевые трубки в устройствах обработки информации, М., 1973 (лит.). Г. С. Котовщиков. 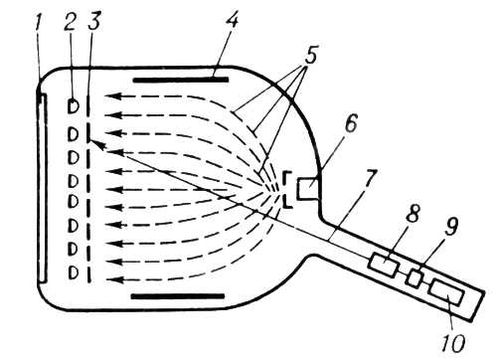
Схема потенциалоскопа с видимым изображением: 1 - люминесцентный экран; 2 - мишень в виде металлической мелкоструктурной сетки, покрытой слоем диэлектрика; 3 - коллекторная сетка; 4 - электрод, формирующий воспроизводящий пучок электронов; 5 - воспроизводящий пучок электронов, облучающий равномерно всю поверхность мишени; 6 - электронный прожектор воспроизводящего пучка; 7 - записывающий луч; 8 - отклоняющая система записывающего луча; 9 - электрод, к которому подводится записываемый сигнал; 10 - электронный прожектор записывающего луча. Потенциалы постсинаптические Потенциа'лы постсинапти'ческие(физиологические), относительно кратковременные колебания мембранного потенциала (чаще десятки миллисекунд, реже секунды), возникающие в результате местного воздействия медиатора на постсинаптическую мембрану нервной, мышечной, железистой клетки (см. Синапсы ) .Амплитуда П. п. зависит от количества выделенного медиатора. Взаимодействуя со специфическими рецепторами постсинаптические мембраны, медиаторы увеличивают её проницаемость для определённых ионов, которые входят в клетку или выходят из неё в соответствии с электрохимическим градиентом. Если этот процесс приводит к уменьшению трансмембранной разности потенциалов ( деполяризации ) ,П. п. являются возбуждающими (ВПСП). Тормозные П. п. (ТПСП) выражаются в гиперполяризации клетки, обусловленной действием тормозного медиатора. Как правило, нервная клетка имеет большое число синаптических входов; приходящие к ней сигналы алгебраически суммируются. В клетках, спонтанно генерирующих потенциалы действия, ВПСП увеличивает, а ТПСП уменьшает частоту разрядов. В «молчащих» клетках ВПСП может вызвать одиночный или групповой разряд, а одновременно возникший ТПСП блокировать этот эффект. Т. о., с помощью П. п. осуществляется управление возбудимостью нервных клеток. См. также статьи Биоэлектрические потенциалы, Мембранная теория возбужденияи литературу при них. Л. Г. Магазаник. Потенциалы термодинамические Потенциа'лы термодинами'ческие, определённые функции объёма ( V), давления ( р) ,температуры ( Т), энтропии ( S), числа частиц системы ( N) и др. макроскопических параметров ( x i) ,характеризующих состояние термодинамической системы. К П. т. относятся: внутренняя энергияU= U( S, V, N, x i) ; энтальпияН= Н( S, р, N, x i) ; Гельмгольцева энергия(свободная энергия, или изохорно-изотермический потенциал, обозначается Аили F) F= F( V, T, N, x i) , Гиббсова энергия(изобарно-изотермический потенциал, обозначается Ф или G) G= G( p, Т, N, x i) и др. Зная П. т. как функцию указанных параметров, можно получить путём дифференцирования П. т. все остальные параметры, характеризующие систему, подобно тому как в механике можно определить компоненты действующих на систему сил, дифференцируя потенциальную энергию системы по соответствующим координатам. П. т. связаны друг с другом следующими соотношениями: F= U- TS, Н= U+ pV, G= F+ pV.Если известен какой-либо один из Т. п., то можно определить все термодинамические свойства системы, в частности получить уравнение состояния.При помощи П. т. выражаются условия термодинамического равновесия системы и критерии его устойчивости (см. Равновесие термодинамическое ) . Совершаемая термодинамической системой в какой-либо процессе работа определяется убылью П. т., отвечающего условиям процесса. Так, в условиях теплоизоляции ( адиабатический процесс , S= const) элементарная работа dAравна убыли внутренней энергии: dA= - dU.При изотермическом процессе ( Т= const) dA= - dF(в этом процессе работа совершается не только за счёт внутренней энергии, но и за счёт поступающей в систему теплоты). Часто процессы в системах, например химические реакции, идут при постоянных ри Т. Вэтом случае элементарная работа всех термодинамических сил, кроме сил давления, равна убыли термодинамического потенциала Гиббса (G), т. е. dA'= - dG. Равенство dA= - dUвыполняется как для квазистатических (обратимых) адиабатических процессов, так и для нестатических (необратимых). В остальных же случаях работа равна убыли П. т. только при квазистатических процессах, при нестатических процессах совершаемая работа меньше изменения П. т. Теоретическое определение П. т. как функций соответствующих переменных составляет основную задачу статистической термодинамики (см. Статистическая физика ) . Метод П. т. широко применяется для получения общих соотношений между физическими свойствами макроскопических тел и анализа термодинамических процессов и условий равновесия в физико-химических системах. Термин «П. т.» ввёл французский физик П. Дюгем (1884), сам же основатель метода П. т. Дж. У. Гиббс пользовался в своих работах термином «фундаментальные функции». Лит.:Ландау Л. Д., Лифшиц Е. М., Статистическая физика, 2 изд., М., 1964 (Теоретическая физика, т. 5); Леонтович М. А., Введение в термодинамику, 2 изд., М. - Л., 1952; Рейф Ф., Статистическая физика, пер. с англ., М., 1972 (Берклеевский курс физики, т. 5); Гиббс Д. В., Термодинамические работы, пер. с англ., М. - Л., 1950. Г. Я. Мякишев. Потенциалы электромагнитного поля Потенциа'лы электромагни'тного по'ля, величины, характеризующие электромагнитное поле. В электростатике векторное электрическое поле можно характеризовать одной скалярной функцией - потенциалом электростатическим.В общем случае для описания произвольного электромагнитного поля вместо двух векторов - магнитной индукцииВи напряжённости электрического поляЕможно ввести две др. величины: векторный потенциал А( х, у, z, t) и скалярный потенциал j(x, у, z, t) (где х, у, z -координаты, t -время), при этом Ви Еоднозначно выражаются через Аи j В= rot А,
E= -gradj
где с - скорость света в вакууме. Уравнения для потенциалов поля имеют более простую форму, чем исходные Максвелла уравнения,и поэтому введение П. э. п. упрощает задачу нахождения переменных электромагнитных полей. Существенное упрощение уравнений для П. э. п. возможно благодаря тому, что потенциалы определяются неоднозначно. Если вместо Аи j выбрать новые потенциалы А'= А+ gradc ,
где c -произвольная функция координат и времени, то векторы Ви Е,определяемые уравнениями (1), не изменятся. Инвариантность электромагнитного поля по отношению к преобразованиям потенциалов (2) носит название калибровочной или градиентной инвариантности. Калибровочная инвариантность позволяет наложить на П. э. п. дополнительное условие. Обычно таким дополнительным условием является условие Лоренца: div
A+
где e и m- диэлектрическая и магнитная проницаемости среды. При использовании условия (3) уравнения для П. э. п. в однородной среде (e = const, m = const), получаемые из уравнений Максвелла, приобретают одинаковую форму:
здесь D-
Лапласа оператор,r и
j- плотности заряда и тока, a u
=
Уравнения (4) позволяют определить потенциалы Аи j по известному распределению зарядов и токов, а следовательно, с помощью формул (1) - характеристики электромагнитного поля Ви Е.Частные решения уравнений (4), удовлетворяющие причинности принципу,называют запаздывающими потенциалами. Запаздывающие потенциалы в точке с координатами х, у, zв момент времени tопределяются плотностями заряда и тока в точке с координатами х’, у’, z'в предшествующий момент времени t = t - R/u ,где
-расстояние от источника поля до точки наблюдения. Если заряды и токи распределены в конечной области пространства G,то запаздывающие потенциалы определяются суммированием (интегрированием) элементарных потенциалов от зарядов и токов, сосредоточенных в бесконечно малых объёмах dx'dy'dz’,с учётом времени запаздывания: j (
х, у, z, t) =
A(
х, у, z, t) =
Через П. э. п. выражается функция Гамильтона Нзаряженной частицы, движущейся в электромагнитном поле:
где p- импульс частицы, eи m -ее заряд и масса. Соответственно через П. э. п. выражается оператор Гамильтона (гамильтониан) в квантовой механике.
Лит.см. при ст. Максвелла уравнения. Г. Я. Мякишев. Потенциальная энергия Потенциа'льная эне'ргия,часть общей механической энергии системы, зависящая от взаимного расположения частиц, составляющих эту систему, и от их положений во внешнем силовом поле (например, гравитационном; см. Поля физические ) .Численно П. э. системы в данном её положении равна работе, которую произведут действующие на систему силы при перемещении системы из этого положения в то, где П. э. условно принимается равной нулю (П = 0). Из определения следует, что понятие П. э. имеет место только для консервативных систем,т. е. систем, у которых работа действующих сил зависит только от начального и конечного положения системы. Так, для груза весом Р,поднятого на высоту h,П. э. будет равна П = Ph(П = 0 при h= 0); для груза, прикрепленного к пружине, П = 0,5 сl 2, где l - удлинение (сжатие) пружины, с- её коэффициент жёсткости (П = 0 при l = 0); для двух частиц с массами m 1и m 2,притягивающихся по закону всемирного тяготения, П = -fm 1m 2/r,где f -гравитационная постоянная, r -расстояние между частицами (П = 0 при r= Ґ); аналогично определяется П. э. двух точечных зарядов e 1и e 2. С. М. Тарг. Потенциальная яма Потенциа'льная я'мав физике, ограниченная область пространства, в которой потенциальная энергия частицы меньше, чем вне её. Термин «П. я.» происходит от вида графика, изображающего зависимость потенциальной энергии Vчастицы, находящейся в силовом поле, от её положения в пространстве (в случае одномерного движения - от координаты х; рис. 1). Такая форма зависимости V( x) возникает в поле сил притяжения. Характеристики П. я. - ширина (расстояние, на котором проявляется действие сил притяжения) и глубина (равная разности потенциальных энергий частицы на «краю» ямы и на её «дне», соответствующем минимальной потенциальной энергии). Основное свойство П. я. - способность удерживать частицу, полная энергия Eкоторой меньше глубины ямы V 0; такая частица внутри П. я. будет находиться в связанном состоянии. В классической механике частица с энергией E< V 0не сможет вылететь из П. я. и будет всё время двигаться в ограниченной области пространства внутри ямы; устойчивому равновесию отвечает положение частицы на «дне» ямы (оно достигается при кинетической энергии частицы Екин= E- V= 0). Если же E> V 0,то частица преодолеет действие сил притяжения и покинет яму. Примером может служить движение упругого шарика, находящегося в поле сил земного притяжения, в чашке с пологими стенками ( рис. 2 ). В квантовой механике, в отличие от классической, энергия частицы, находящейся в связанном состоянии в П. я., может принимать лишь определённые дискретные значения, т. е. существуют дискретные
уровни энергии
(см., например, рис. 6 к ст.
Квантовая механика
)
.Однако такая дискретность уровней становится заметной лишь для систем, имеющих микроскопические размеры и массы. По порядку величины расстояние D
Eмежду уровнями энергии для частицы массы
mв «глубокой» яме ширины
аопределяется величиной D
E ~
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127 |
|||||||
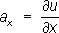 ,
,
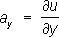 ,
,
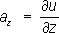 , где
a
x, a
y, a
z; -компоненты поля
aв системе декартовых координат
Oxyz.Если такую функцию можно ввести, то векторное поле
аназывают потенциальным. Иногда П. называют функцию
U=
-
u(например, в электростатике). П. векторного поля
аопределяется не однозначно, а с точностью до постоянного слагаемого. Поэтому при изучении потенциального поля представляют интерес лишь разности П. в различных точках поля. Уравнение
u(
х, у, z)
=
сгеометрически представляет поверхность, во всех точках которой П. имеет одинаковую величину; такие поверхности называют поверхностями уровня, или эквипотенциальными поверхностями.
, где
a
x, a
y, a
z; -компоненты поля
aв системе декартовых координат
Oxyz.Если такую функцию можно ввести, то векторное поле
аназывают потенциальным. Иногда П. называют функцию
U=
-
u(например, в электростатике). П. векторного поля
аопределяется не однозначно, а с точностью до постоянного слагаемого. Поэтому при изучении потенциального поля представляют интерес лишь разности П. в различных точках поля. Уравнение
u(
х, у, z)
=
сгеометрически представляет поверхность, во всех точках которой П. имеет одинаковую величину; такие поверхности называют поверхностями уровня, или эквипотенциальными поверхностями.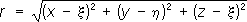 ,
G- постоянная тяготения. При наложении полей их П. алгебраически складываются. Если поле тяготения обусловлено некоторой массой плотности r(x, h, x), занимающей объём
Т,то его можно рассматривать как результат наложения элементарных полей, образованных бесконечно малыми телами массы r
dx
dh
dx
.Ньютонов П. такого поля представляется интегралом
,
G- постоянная тяготения. При наложении полей их П. алгебраически складываются. Если поле тяготения обусловлено некоторой массой плотности r(x, h, x), занимающей объём
Т,то его можно рассматривать как результат наложения элементарных полей, образованных бесконечно малыми телами массы r
dx
dh
dx
.Ньютонов П. такого поля представляется интегралом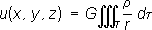 . (2)
. (2)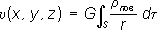 . (3)
. (3)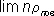 = m, где
n -нормальное расстояние между поверхностями, приходят к понятию П. двойного слоя:
= m, где
n -нормальное расстояние между поверхностями, приходят к понятию П. двойного слоя: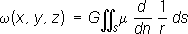 (4)
(4)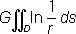 . (5)
. (5)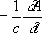 , (1)
, (1)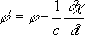 , (2)
, (2)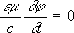 , (3)
, (3) , (4)
, (4)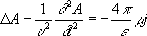 ;
;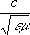 - скорость распространения электромагнитного поля в среде. Если r = 0 и
j=
0
,то П. э. п. удовлетворяют
волновым уравнениям.
- скорость распространения электромагнитного поля в среде. Если r = 0 и
j=
0
,то П. э. п. удовлетворяют
волновым уравнениям.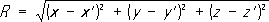
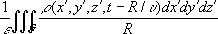 ,
,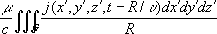 ,
,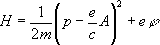 , (6)
, (6)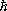 /ma
2(
/ma
2(
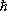 -
Планка постоянная
)
.Наинизший (основной) уровень энергии лежит выше «дна» П. я. (см.
Нулевая энергия
)
.В П. я. малой глубины (
V
oЈ
-
Планка постоянная
)
.Наинизший (основной) уровень энергии лежит выше «дна» П. я. (см.
Нулевая энергия
)
.В П. я. малой глубины (
V
oЈ
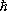 /ma
2) связанное состояние может вообще отсутствовать (так, протон и нейтрон с параллельными
спинами
не образуют связанной системы, несмотря на существование сил притяжения между ними).
/ma
2) связанное состояние может вообще отсутствовать (так, протон и нейтрон с параллельными
спинами
не образуют связанной системы, несмотря на существование сил притяжения между ними).