 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (ПО)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ПО) - Чтение (стр. 108)
При П. с. приёмников тока (нагрузок) напряжение на них распределяется пропорционально их сопротивлениям. Выключение одного элемента прерывает ток во всей цепи. 2) Соединение
четырехполюсников,при котором напряжение и ток на выходе предыдущего четырехполюсника равны соответственно напряжению и току на входе последующего. П. с. четырехполюсников применяют для увеличения затухания или усиления в устройствах преобразования сигналов и при электрическом моделировании соединения звеньев систем автоматического управления.
Последовательное сосредоточение огня После'довательное сосредото'чение огня'(ПСО), вид огня наземной артиллерии, применяемый с целью огневой поддержки наступающих войск сосредоточенным огнем. Ведётся 1-2 дивизионами по заранее намеченным участкам подавления. Огневой налёт начинается при подходе наступающих подразделений на 800-1000 мк участку огня и прекращается с выходом их на рубеж безопасного удаления от разрывов снарядов (мин). Данный вид огня широко применялся советской артиллерией в Великую Отечественную войну 1941-45. Последовательность После'довательность, одно из основных понятий математики. П. образуется из элементов любой природы, занумерованных натуральными числами 1, 2,..., n,...,и записывается в виде x 1, x 2, …, x n,… или коротко, { x n} .Элементы, из которых составляется П., называются её членами. Члены П., стоящие на разных местах, могут совпадать. П. можно рассматривать как функцию от натурального аргумента (т. е. функцию, определённую на множестве натуральных чисел). Обычно П. определяется заданием n-го члена или рекуррентной формулой,по которой каждый следующий член определяется через предыдущий (см., например, Фибоначчи числа ) .Наиболее часто встречаются числовые и функциональные П. (т. е. П., членами которых являются числа или функции). Примеры: 1, 2, …, n, …, то есть x n= n; (1)
то есть
то есть
Если элементы числовой П. при достаточно больших номерах nсколь угодно мало отличаются от числа а,то П. называется сходящейся, а число а -её пределом (аналогично определяется предел при функциональных П.). Например, П. (2) и (4) - сходящиеся, и их пределами служат число 0 и функция 1/(1 + x 2) .Несходящиеся П., например (1) и (3), называются расходящимися. Последовательные реакции После'довательные реа'кции, химические процессы, в которых продукт одной реакции является исходным веществом др. реакции. К П. р. относятся такие важные химические процессы, как полимеризация,термический крекинг углеводородов, хлорирование углеводородов и т.д. Так, при крекинге происходят последовательное превращение высокомолекулярных соединений во всё более низкомолекулярные и в то же время последовательные процессы образования высокомолекулярных соединений, бедных водородом (например, кокс). При хлорировании метана последовательно образуются CH 3Cl, CH 2Cl 2, CHCl 3и CCl 4. Пример простой П. р. - последовательное протекание двух необратимых реакций первого порядка: А® В® С, где A, В, С -некоторые вещества. Изменение концентраций веществ во времени можно получить, интегрируя систему двух кинетических уравнений. Расчёт показывает, что концентрация промежуточного вещества Всначала растет, достигает некоторого максимального значения, а затем убывает. Более сложное описание П. р. получается в тех случаях, когда учитываются обратимость отдельных реакций, участие в них различных исходных веществ и т.п. Лит.:Эмануэль Н. М., Кнорре Д. Г., Курс химической кинетики, М., 1962; Родигин Н. М., Родигина Э. Н., Последовательные химические реакции. Математический анализ и расчёт, М., 1960; Бенсон С., Основы химической кинетики, пер. с англ., М., 1964. Последовательный анализ После'довательный ана'лизв математической статистике, способ статистической проверки гипотез,при котором необходимое число наблюдений не фиксируется заранее, а определяется в процессе самой проверки. Во многих случаях для получения столь же обоснованных выводов применение надлежащим образом подобранного способа П. а. позволяет ограничиться значительно меньшим числом наблюдений (в среднем, т.к. число наблюдений при П. а. есть величина случайная), чем при способах, в которых число наблюдений фиксировано заранее. Пусть, например, задача состоит в выборе между гипотезами H 1и H 2по результатам независимых наблюдений. Гипотеза H 1заключается в том, что случайная величина Химеет распределение вероятностей с плотностью f 1(x), a H 2-в том, что Химеет плотность f 2( x) .Для решения этой задачи поступают следующим образом. Выбирают два числа Аи В(0 < A< B) .После первого наблюдения вычисляют отношение l 1= f 2( x 1) /f 1( x 1) ,где x 1 -результат первого наблюдения. Если l 1< A, принимают гипотезу H 1;если l 1> B,принимают H 2,если AЈ l 1Ј B, производят второе наблюдение и так же исследуют величину l 2= f 2( x 1) f 2( x 2) /f 1( x 1) f 1( x 2) ,где x 2-результат второго наблюдения, и т.д. С вероятностью, равной единице, процесс оканчивается либо выбором H 1,либо выбором H 2.Величины Аи Вопределяются из условия, чтобы вероятности ошибок первого и второго рода (т. е. вероятность отвергнуть гипотезу H 1, когда она верна, и вероятность принять H 1,когда верна H 2) имели заданные значения a 1и a 2. Для практических целей вместо величины l n удобнее рассматривать их логарифмы. Пусть, например, гипотеза H 1состоит в том, что Химеет нормальное распределение
с a= 0 ,s = 1, гипотеза H 2-в том, что Xимеет нормальное распределение с a= 0,6, s = 1, и пусть a 1= 0,01, a 2= 0,03. Соответствующие подсчёты показывают, что в этом случае
и logl
n= 0.6
Поэтому неравенства
соответственно. Процесс П. а. допускает при этом простое графическое изображение (см.
рис.
). На плоскости (
хОу) наносятся две прямые
y= 0.3
x- 5.83 и
y= 0.3
x+ 7.62 и ломаная линия с вершинами в точках (
n,
Лит.:Блекуэлл Д., Гиршик М. А., Теория игр и статистических решений, пер. с англ., М., 1958: Вальд А., Последовательный анализ, пер. с англ., М., 1960; Ширяев А. Н., Статистический последовательный анализ, М., 1969. Ю. В. Прохоров. 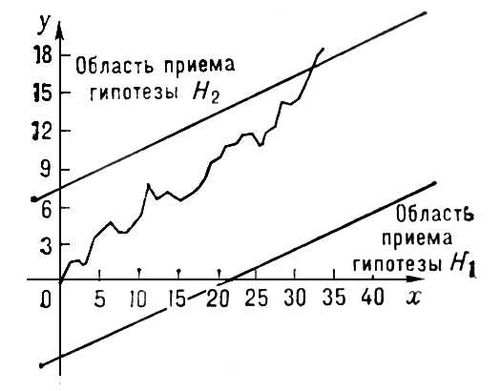
Графическое изображение процесса последовательного анализа. Последовательных приближении метод После'довательных приближе'нии ме'тод,метод решения математических задач при помощи такой последовательности приближении, которая сходится к решению и строится рекуррентно (т. е. каждое новое приближение вычисляют, исходя из предыдущего; начальное приближение выбирается в достаточной степени произвольно). П. п. м. применяется для приближённого нахождения корней алгебраических и трансцендентных уравнений, для доказательства существования решения и приближённого нахождения решений дифференциальных, интегральных и интегро-дифференциальных уравнений, для качественной характеристики решения и в ряде др. математических задач. 1) Для решения уравнения f( x) =0 (1) составляют ему равносильное
х =j(х)
,обозначив, например, через j(x) разность
х - kf(
x)
(
k -постоянное). Выбрав
a
0-начальное приближение к корню уравнения, составляют последовательность чисел
a
0, a
1=
j(
a
0)
, a
2=
j(
a
1)
, …, a
n=
j(
a
n-1)
,…; предел
а=
и в качестве начального приближения a 0взято любое число. Обычно, когда надо найти приближённое значение корня уравнения, устанавливают достаточно узкий интервал, в котором лежит корень (например, с помощью графических методов); затем подбирают
kтак, чтобы условие (2) выполнялось на всём интервале; за начальное приближение
a
0выбирают любое число из этого интервала и применяют П. п. м. Практически, после того как два последовательных приближения
a
n-1и
a
nсовпадут с заданной степенью точности, вычисление прекращают и полагают
a
n»
а.Пусть дано, например, уравнение
f(
x) =
2) П. п. м. применяют для приближённого решения систем линейных алгебраических уравнений с большим числом неизвестных. Пусть дана система трёх уравнений с тремя неизвестными:
Строят ей эквивалентную систему:
полагая, например,
и, пользуясь рекуррентными формулами: x j= c 11x j-1+ c 12y j-1+ c 13z j-1+ d 1 y j= c 21x j-1+ c 22y j-1+ c 23z j-1+ d 2 z j= c 31x j-1+ c 32y j-1+ c 33z j-1+ d 3 составляют последовательность ( x 0, у 0, z 0) ,( x 1, у 1, z 1) ,...,( x n, y n, z n) ,...Если x n® a , y n® b , z n® gпри неограниченном увеличении n,то тройка чисел х= a , у= b , z= g будет решением системы (3). Пределы a, b, g заведомо существуют, каковы бы ни были начальные приближения x 0, у 0, z 0,если, например, в каждом уравнении системы (4) сумма абсолютных величин коэффициентов c ijменьше единицы. 3) Для того чтобы найти решение
у = у(
х) дифференциального уравнения
и, пользуясь рекуррентной формулой
составляют последовательность функций y 1( x) , у 2( х) ,..., y n( x),... Если она равномерно сходится, то предел её будет искомым решением. 4) Чтобы найти решение первой краевой задачи для уравнения
выбирают произвольную дважды дифференцируемую функцию u 0( x, у) и составляют затем линейное уравнение
Пусть u 1( х, у) -решение первой краевой задачи для уравнения (5); считая u 1первым приближением, составляют уравнения типа (5) для последующих приближений. Полученная последовательность { u n( x, у)} при некоторых предположениях сходится и даёт решение задачи. О применимости П. п. м. см. статью Сжатых отображений принцип. Послезародышевое развитие Послезаро'дышевое разви'тие,то же, что постэмбриональное развитие. Послеледниковая эпоха Послеледнико'вая эпо'ха,то же, что голоцен. Послелог Послело'г,разряд служебных слов,соответствующих по значению предлогу,но занимающих постпозитивное положение (после того слова, к которому относятся). П. распространены в угро-финских, тюркских, монгольских, кавказских, тунгусо-маньчжурских и др. языках, например: в татарском тавлар арасында - «между гор» (ара-сында - «между»), в чувашском шыв урла - «через реку» (урла - «через»), в венгерском a talla mellett - «около доски» (mellett - «около»). Некоторые П. могут принимать падежное окончание, например: в языке коми пу вылын - «на дереве» (местный падеж), пу вылысь - «с дерева» (исходный падеж), пу выло - «на дереве» (направительный падеж). В некоторых случаях П. употребляются и как имена существительные с самостоятельным значением, например: в татарском языке ара - «промежуток» и арасында - «между», в удмуртском языке выдан - «на» и выл - «поверхность». Послеродовой период Послеродово'й пери'од,начинается с момента рождения плаценты и продолжается 6-8 нед.В П. п. в организме родильницы почти все изменения в системах и органах, возникшие при беременности и родах, подвергаются обратному развитию (инволюции). Матка, дно которой после родов находится на 15 смнад лоном, сокращается и к 10-12-м сутисчезает за лоном; масса её с 1000 гк концу 8-й неддоходит до 50-60 г.Внутренний зев шейки матки закрывается к 10-м сутпосле родов, наружный - к концу 3-й нед.Одновременно с сокращением матки происходит восстановление её слизистой оболочки, которая начинает постепенно покрывать внутреннюю поверхность матки; полное восстановление эпителиального покрова завершается к концу 3-й недпосле родов. До завершения этого процесса внутренняя поверхность матки представляет собой обширную раневую поверхность с характерным отделяемым (лохии), которое постепенно к 10-му дню из кровянистого становится светлым, без примеси крови. В П. п. восстанавливается тонус влагалища, заживают ссадины и разрывы в области наружных половых органов, влагалища и шейки матки. Постепенно укорачиваются перерастянутые связки матки, маточные трубы и яичники приобретают обычное состояние. На 3-4-е сут после родов начинается лактация. При нормальном течении П. п. общее состояние родильницы хорошее: пульс ритмичный, редко бывает замедленным (физиологическая брадикардия), артериальное давление в пределах нормы. Температура тела обычно нормальная, возможно однократное незначительное повышение её (непосредственно после родов). Во время П. п. должны строго соблюдаться правила асептики и антисептики,так как раневая поверхность матки, ссадины и разрывы мягких тканей родовых путей и трещины сосков могут служить местом проникновения для возбудителей инфекции, что приводит к развитию послеродовых септических заболеваний.В П. п. необходимо производить ежедневный тщательный туалет наружных половых органов и молочных желёз. Здоровым женщинам со второго дня нормальных родов назначают специальный комплекс гимнастических упражнений, способствующих повышению тонуса организма, более быстрому сокращению матки и т.д. Выписка из родильного дома при нормальном течении П. п. и физиологическом развитии новорождённого осуществляется на 6-7-е сут после родов. Родильниц с повышенной температурой, катаром верхних дыхательных путей, гнойничковыми заболеваниями кожи и др. признаками инфекции госпитализируют в специальное отделение родильного дома. Лит.:Коган А. А., Нормальный послеродовой период, в кн.: Многотомное руководство по акушерству и гинекологии, т. 2, кн. 2, М., 1963. Л. П. Кирющенков. Послеродовые септические заболевания Послеродовы'е септи'ческие заболева'ния,инфекционные заболевания в послеродовом периоде.Возбудители инфекции проникают в половые пути женщины во время осложнённых родов. Процесс начинается с воспаления матки или её шейки, влагалища и может принять генерализованный характер ( сепсис ) .По степени распространённости процесса и его тяжести различают несколько этапов П. с. з.: инфекция ограничена воспалительным процессом в области родовой раны (послеродовой эндометрит,послеродовая язва); процесс распространяется за пределы раны, но остаётся локализованным (воспаление околоматочной клетчатки, придатков матки, тромбофлебиты вен матки, таза, бедренных вен и пр.); инфекция по тяжести стоит близко к распространённой (разлитой перитонит,септический шок,прогрессирующий тромбофлебит и др.); генерализованная инфекция (сепсис). Чаще всего встречаются инфекционные поражения матки (эндомиометрит). Заболевание начинается на 3-4-е сутпосле родов с недомогания, слабости, подъёма температуры до 37,5-38 °С, болей в животе, усиления послеродовых выделений. Обратное развитие матки замедляется. Длительность заболевания до 10-12 сут.При распространении инфекции за пределы матки возникает поражение придатков - сальпингоофорит.В послеродовом периоде часто развивается мастит.Особая форма П. с. з. - септический эндотоксиновый шок, развивающийся при попадании в кровь микробов группы кишечной палочки, при разрушении которых выделяется сильный эндотоксин, вызывающий состояние шока. Шок сравнительно быстро сменяется состоянием недостаточности кровообращения. Нередко заболевание заканчивается развитием острой почечной недостаточности.Лечение стационарное; покой, антибиотики, сульфаниламиды, десенсибилизирующая терапия, введение средств, повышающих защитные силы организма (дробные переливания крови, плазмы и пр.), антикоагулянты и др. При диффузном перитоните - хирургическое вмешательство. Профилактика: строгое соблюдение правил санитарно-гигиенического режима в родильных домах, выявление и лечение бациллоносителей среди медицинского персонала, ранняя диагностика и лечение начальных форм заболеваний. Лит.:Бартельс А. В., Послеродовые инфекционные заболевания, М., 1973. А. П. Кирющенков. Пословица Посло'вица,краткое, ритмически организованное, устойчивое в речи, образное изречение народа. Обладает способностью к многозначному употреблению по принципу аналогии. Суждение «Лес рубят - щепки летят» интересно не прямым смыслом, а тем, что может быть применено к др. аналогичным ситуациям. Предмет высказывания рассматривается в свете общепризнанной истины, выраженной П. Отсюда её идейно-эмоциональная характерность. Композиционное членение суждения в П., часто подкрепляемое ритмом, рифмой, ассонансами, аллитерациями, совпадает с синтаксическим. Лит.:Потебня А. А., Из лекций по теории словесности. Басня. Пословица. Поговорка, Хар., 1914; Даль В. И., Пословицы русского народа, [4 изд.], М., 1957; Пермяков Г. Л., От поговорки до сказки, М., 1970; «Proverbium», Hels., 1965-1974: № 1-24. В. П. Аникин. Послух По'слух,в древнерусском праве свидетель «доброй славы» (заслуживающий доверия) в отличие от видока-свидетеля-очевидца. По Русской правде,П. могли быть, как правило, только свободные люди. Позднее П. стали также называть свидетелей, подтверждавших существование письменных юридических актов. По Судебнику 1497,П. запрещалось давать показания в суде, если они сами не видели обстоятельств дела. Посмитный Макар Анисимович Посми'тныйМакар Анисимович [19(31).1.1895, село Джугастрово, ныне Березовского района Одесской области, - 3.4.1973, село Рассвет того же района], организатор колхозного производства на Украине, председатель ордена Ленина колхоза им. 21-го съезда КПСС Березовского района Одесской области Украинской ССР, дважды Герой Социалистического Труда (1949, 1958), заслуженный работник сельского хозяйства УССР. Член КПСС с 1931. В 1924 организовал в селе Розквит Березовского района Одесской области товарищество по совместной обработке земли, которое под руководством П. превратилось в образцовое коллективное хозяйство. В 1941-45 участник Великой Отечественной войны. С 1945 председатель колхоза им. Буденного, переименованного позднее в колхоз им. 21-го съезда КПСС. В 1935-37 член ЦИК СССР. Делегат 19-24-го съездов КПСС. Депутат Верховного Совета СССР 4-8-го созывов. Неоднократно избирался членом ЦК КП Украины. Делегат 1-3-го Всесоюзных съездов колхозников. В 1969 был избран членом Союзного совета колхозов. Награжден 3 орденами Ленина, орденом Октябрьской Революции, 4 др. орденами, а также медалями. Соч.: В черноморских степях, М., 1955; Колхоз имени Буденного, М., 1955 (совм. с И. П. Луговым). 
М. А. Посмитный. Посников Александр Сергеевич По'сниковАлександр Сергеевич [14(26).12.1846 - 1921], русский экономист. Родился в г. Вязьма, ныне Смоленской области. В 1869 окончил юридический факультет Московского университета. В 1876-82 профессор политической экономии Новороссийского университета (Одесса) и Петроградского политехнического института. В работе «Начала поземельного кредита» отстаивал либерально-народническое требование предоставления дешёвого кредита крестьянским хозяйствам. Во время поездки за границу (1873-76) участвовал в съезде либеральных экономистов (организованном Н. И. Зибером, А. И. Чупровым и др.), выступавших за демократизацию государственного строя в России и сочувственно относившихся к экономической теории марксизма. В 1875 вышла первая часть основного труда П. - «Общинное землевладение»; вторая часть этого труда (1878) явилась его докторской диссертацией. В 1886-96 редактор «Русских ведомостей». В 1912 П. избран членом Государственной думы (примыкал к прогрессистам). В 1917 председатель Главного земельного комитета при Временном правительстве. После Октябрьской революции 1917 П. - преподаватель Политехнического института. Был близок к либеральному народничеству и выступал в защиту общинной формы землевладения, утверждая, что она не препятствует прогрессу в с.-х. производстве. Путём сравнения общины с фермерским хозяйством доказывал превосходство общинного землевладения и видел в нём спасение крестьянских масс от пролетаризации. Защищая теорию «устойчивости» мелкого крестьянского хозяйства, П. не видел процесса концентрации и централизации в сельском хозяйстве и полагал, что организация разного рода кооперативов и товариществ на базе общинного землевладения способна придать крестьянскому хозяйству все преимущества крупного производства. П. активно выступал против Столыпинской аграрной реформы. Н. С. Шухов. Пособие Посо'бие,в СССР денежная выплата, которая производится гражданам в случаях, предусмотренных законодательством; одна из форм материального обеспечения в старости, при болезни и потере трудоспособности, а также в некоторых др. случаях. В зависимости от цели выплаты П. делятся на 3 группы: 1) П. престарелым и инвалидам, не получающим государственную пенсию и не имеющим др. источников средств к существованию; инвалидам с детства; больным лепрой.В отличие от пенсии, назначение и выплата этих П. не обусловлены прежней трудовой или иной общественно полезной деятельностью, они устанавливаются лишь в связи с наступлением нетрудоспособности с тем, чтобы материально обеспечить граждан, которые по каким-либо причинам не получают пенсию, но в силу старости либо плохого состояния здоровья нуждаются в заботе общества. 2) П. временно нетрудоспособным, а также беременным женщинам и роженицам. Их цель - возместить (полностью либо в значительной части) заработок, утраченный работающим вследствие временной нетрудоспособности, а женщиной, кроме того, вследствие освобождения её от работы на период отпуска по беременности и родам. П. по временной нетрудоспособности выплачиваются рабочим, служащим, колхозникам при болезни или увечье, санаторно-курортном лечении (если отпуска недостаточно для лечения и проезда в санаторий и обратно), при уходе за заболевшим членом семьи, карантине, временном переводе на др. работу в связи с заболеванием туберкулёзом или профессиональным заболеванием, при протезировании в стационаре протезно-ортопедического предприятия. П. выдаётся, как правило, с 1-го дня утраты трудоспособности и до её восстановления либо с установления врачебно-трудовой экспертной комиссией инвалидности. При временной нетрудоспособности вследствие бытовой травмы П. выплачивается начиная с 6-го дня нетрудоспособности. При помещении в стационар протезно-ортопедического предприятия П. выдаётся за всё время нахождения в стационаре, но не более чем за 30 дней. П. по уходу за заболевшим членом семьи выдаётся по общим правилам не более чем за 3 дня, а по уходу за больным ребёнком в возрасте до 14 лет - за более длительный период (см. также ст. Листок нетрудоспособности ) . Размер П. зависит от причины наступления временной нетрудоспособности. При трудовом увечье или профессиональном заболевании П. выдаётся в размере полного заработка. При общем заболевании или увечье, не связанном с работой, размер П. дифференцируется в зависимости от длительности непрерывного стажа: при непрерывном стаже до 3 лет П. составляет 50% заработка; от 3 до 5 лет - 60% как для рабочих (служащих), так и для колхозников; от 5 до 8 лет - 80% для рабочих и служащих, 70% - для колхозников; свыше 8 лет - 100% для рабочих и служащих и 90% - для колхозников. В соответствии с постановлением Совета Министров СССР от 13 декабря 1974 рабочим и служащим, имеющим на иждивении 3 и более детей, не достигших 16 лет (учащихся - 18 лет), с 1 декабря 1975 П. по временной нетрудоспособности во всех случаях выплачивается в размере 100% заработка, независимо от продолжительности трудового стажа. Размер П. рабочим (служащим), колхозникам, не достигшим 18 лет, во всех случаях не может быть менее 60% заработка; инвалидам войны выплачивается 100% заработка независимо от продолжительности непрерывного стажа. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127 |
|||||||
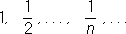 , то есть
, то есть
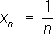 ; (2)
; (2)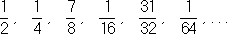 ,
,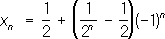 ; (3)
; (3)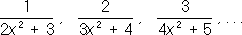 ,
,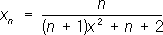 ; (4)
; (4)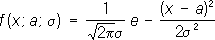
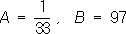
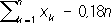
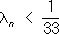 и
и
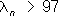 равносильны неравенствам
равносильны неравенствам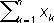 < 0.3
n- 5.83
< 0.3
n- 5.83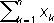 > 0.3
n+ 7.62
> 0.3
n+ 7.62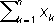 )
, n=
1
,2,.... Если ломаная впервые выходит из полосы, ограниченной этими прямыми, через верхнюю границу, то принимается
H
2,если через нижнюю, -
H
1.В приведённом примере для различения
H
1и
H
2методом П. а. требуется в среднем не более 25 наблюдений. В то же время для указанного различения гипотез
H
1и
H
2по выборкам фиксированного объёма потребовалось бы более 49 наблюдений.
)
, n=
1
,2,.... Если ломаная впервые выходит из полосы, ограниченной этими прямыми, через верхнюю границу, то принимается
H
2,если через нижнюю, -
H
1.В приведённом примере для различения
H
1и
H
2методом П. а. требуется в среднем не более 25 наблюдений. В то же время для указанного различения гипотез
H
1и
H
2по выборкам фиксированного объёма потребовалось бы более 49 наблюдений.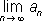 ,если он существует, является корнем уравнения (1), а числа
a
0, a
1, a
2,..., a
n,... - приближёнными значениями этого корня. Предел
абудет существовать, например, если
,если он существует, является корнем уравнения (1), а числа
a
0, a
1, a
2,..., a
n,... - приближёнными значениями этого корня. Предел
абудет существовать, например, если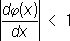 (2)
(2)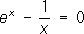 .Так как
.Так как
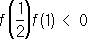 ,
то корень уравнения лежит в интервале
,
то корень уравнения лежит в интервале
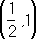 . Положив
. Положив
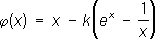 , непосредственной проверкой убеждаемся, что для
k =
, непосредственной проверкой убеждаемся, что для
k =
 условие (2) выполняется на всём интервале
условие (2) выполняется на всём интервале
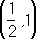 . Выбирем
a
0=
. Выбирем
a
0=
 и применим П. п. м. к уравнению
и применим П. п. м. к уравнению
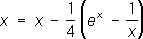 . Получим
a
1= 0,554,
a
2= 0,570,
a
3= 0,566 (на самом деле корень уравнения с тремя верными десятичными знаками равен
a
4» 0,567).
. Получим
a
1= 0,554,
a
2= 0,570,
a
3= 0,566 (на самом деле корень уравнения с тремя верными десятичными знаками равен
a
4» 0,567).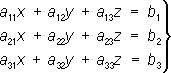 (3)
(3)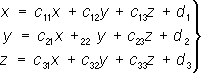 (4)
(4)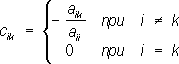
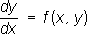 , удовлетворяющее условию
у
0= у(
х
0)
,записывают это уравнение в виде
, удовлетворяющее условию
у
0= у(
х
0)
,записывают это уравнение в виде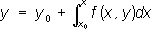
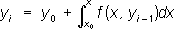
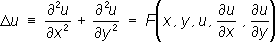
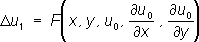 .
.