 |
|
���������� ������:: ��� :: ������� ��� ���������� :: �������� ����� :: ������ ����� :: ����� ����� �������� :: ���� ��������� :: ������� ������ :: ������ ����� ���� :: ������� ������ ���������� :: ������� ���� ���������� �����:: �������� ������ :: �������� ���� :: � ����� ������ �. �������� :: ����� ���� (��� 1) :: ���� (����� 2) :: ��� �� ������ �� ������� ������ :: ������ ����� ������ :: ������ � ������ ��� ����� (��������� ��. ����������� � �������� ������ ������) :: ������� ����� :: ������ � �� ����� |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 3)
Центры К. б. в СССР - республиканские, областные и краевые библиотеки. Работу в этой области ведут также библиотеки университетов и некоторых научно-исследовательских учреждений. Крупнейший библиографический центр Сибири и Дальнего Востока - Государственная публичная научно-техническая библиотека Сибирского отделения АН СССР выпускает библиографические ежеквартальники «История Сибири» (с 1966), «Народное хозяйство Сибири и Дальнего Востока» (с 1967). Многие библиотеки издают общие и отраслевые указатели литературы о крае (например, «Внутренние воды Карелии и их использование» С. В. Григорьева, Петрозаводск, 1964), краеведческие библиографические ежегодники и ежеквартальники (например, «Литература о Свердловской области», издаётся ежеквартально с 1951), краеведческие биобиблиографические словари и персональные пособия (например, «В. И. Ленин и Сибирь», Библиографический указатель, 2 изд., Новосибирск, 1970) и др. Государственная публичная библиотека им. Салтыкова-Щедрина в Ленинграде с 1963 выпускает многотомную серию «Библиография краеведческой библиографии РСФСР». Во многих зарубежных странах информацию о краеведческих изданиях дают нередко библиографические пособия, посвященные стране в целом или её крупным частям. Такие пособия обычно называются региональными. Лит.:Здобнов Н. В., Библиография и краеведение. Сб. статей, М., 1963; Николаев В. А., Краеведческая библиография, М., 1961; Шапиро А. Л., Библиография истории СССР, М., 1968, с. 252-74; Справочники по истории дореволюционной России. Библиография, М., 1971, с. 347-479. В. А. Николаев. Краеведческие музеи Краеве'дческие музе'и,научно-исследовательские и культурно-просветительные учреждения, которые собирают, сохраняют, изучают, экспонируют и пропагандируют исторические памятники, естественнонаучные и художественные коллекции, произведения народного искусства определённых географических или административных территорий. К. м. - один из наиболее распространённых музеев комплексного профиля. В России возникновение «местных» комплексных музеев относится к концу 18 - началу 19 вв. Они создавались при учебных заведениях, палатах государственных имуществ,. отделениях Русского географического общества. В середине 19 в. насчитывалось 12 К. м. (в Барнауле, Иркутске, Минусинске, Красноярске, Оренбурге, Тбилиси и др.). Основная сеть К. м. сформировалась в пореформенный период. В начале 20 в. функционировало 60 К. м. в губернских и уездных городах. В национальных районах число их было невелико: 14 на Украине и в Молдавии, 2 в Закавказье, 4 в Средней Азии. После Октябрьской революции 1917 проводимая Коммунистической партией и Советским правительством ленинская национальная политика обусловила рост К. м. Они создавались главным образом в ранее обездоленных в культурном отношении районах (Мордовский музей в Саранске, Горно-Марийский музей в Козьмодемьянске, Чувашский музей в Чебоксарах, Наманганский музей в Узбекистане и многие др.). За первое пятилетие Советской власти было организовано свыше 250 К. м. Развитию К. м. способствовал общий подъём краеведческого движения (см. Краеведение ) .В 1920 было создано Центральное бюро краеведения, в 1931 - Научно-исследовательский институт методов краеведческой работы; издавались журналы «Краеведение», «Советское краеведение», получила широкое развитие краеведческая библиография. За годы предвоенных пятилеток 1929-40 во всех союзных республиках создана развитая сеть К. м.; в 1940 насчитывалось свыше 400 К. м. Во время Великой Отечественной войны 1941-45 немецко-фашистскими захватчиками был нанесён огромный ущерб К. м., находившимся на оккупированной территории: разграблены ценнейшие коллекции, многие К. м. полностью уничтожены. В послевоенные годы сеть К. м. восстановлена. В 1970 функционировало 493 государственных К. м. В музеях имеются отделы природы края, истории дореволюционного прошлого, истории советского общества, а в некоторых К. м. также художественные, литературные и этнографические отделы. Многие К. м. издают каталоги, путеводители, публикации памятников, «Краеведческие записки». За рубежом местные музеи комплексного профиля носят название региональных. Лит.:Ионова О. В., Создание сети краеведческих музеев РСФСР в первые 10 лет Советской власти, в кн.: История музейного дела в СССР, М., 1957; Равикович Д. А., Музеи местного края во второй половине XIX - нач. XX в., в кн.: Очерки истории музейного дела в России, М., 1960; Мезенцева Г. Г., Музеи Украины, К., 1959; Моисеев А. М., Краеведческие музеи за 50 лет, «История СССР», 1967, № 6; Лурье В., Обзор литературы, выпущенной краеведческими музеями РСФСР за 1953- 1959 гг., М., 1960. А. М. Разгон. Краевой прогиб Краево'й проги'б,прогиб земной коры, образующийся на границе геосинклинали (геосинклинальной системы) и платформы в позднюю стадию развития геосинклинали, когда во внутренней части её происходит горообразование. К. п. обычно заполнены осадками главным образом лагунной и моллассовой формаций, слои которых дислоцированы в виде глыбовых складок и диапировых куполов. К К. п. приурочены месторождения углей, нефти, природных газов. См. также Передовой прогиб. Краевой суд Краево'й суд,см. в ст. Областной суд . Краевский Андрей Александрович Крае'вскийАндрей Александрович [5(17).2.1810, Москва, - 8(20).8.1889, Павловск], русский издатель и журналист. Окончил Московский университет (1828). В 1839-67 издавал журнал «Отечественные записки»,привлек в него лучшие литературные силы, в том числе В. Г. Белинского. В 1846 Белинский порвал с К.; журнал постепенно утратил прогрессивное направление. После 1848 К. занял откровенно консервативные позиции. Был редактором ряда газет. Как издатель К. проявил себя способным организатором, вместе с тем имел репутацию человека, наживавшегося на эксплуатации литературных сотрудников. Особенной популярностью пользовалась умеренно-либеральная газета К. «Голос» (1863-84). Лит.:Козьмин Б. П., Русская журналистика 70-х и 80-х гг. XIX в., М., 1948; Кулешов В. И., «Отечественные записки» и литература 40-х годов XIX в., М., 1958; Орлов В. Н., Молодой Краевский, в его кн.: Пути и судьбы, М.- Л., 1963. В. И. Кулешов. Краевые валы Краевы'е ва'лы,пологие слаборасчленённые поднятия на окраинах океанических котловин, вытянутых вдоль океанического края глубоководных желобов; то же, что океанические окраинные валы. Краевые задачи Краевы'е зада'чи,задачи, в которых из некоторого класса функций, определённых в данной области, требуется найти ту, которая удовлетворяет на границе (крае) этой области заданным условиям. Функции, описывающие конкретные явления природы (физические, химические и др.), как правило, представляют собой решения уравнений математической физики, выведенных из общих законов, которым подчиняются эти явления. Когда рассматриваемые уравнения допускают целые семейства решений, дополнительно задают так называемые краевые или начальные условия, позволяющие однозначно выделить интересующее нас решение. В то время, как краевые условия задаются исключительно на граничных точках области, где ищется решение, начальные условия могут оказаться заданными на определённом множестве точек внутри области. Например, уравнение
имеет бесконечное множество решений u (x 1, х 2) = f (x 1+x 2) + f 1(x 1-x 2), где fи f 1-произвольные дважды непрерывно дифференцируемые функции. Однако в прямоугольнике - аЈ x 2 Ј a, 0Ј x 1Ј l,плоскости с прямоугольными декартовыми координатами x 1, x 2уравнение (1) имеет единственное решение u (x 1, x 2),удовлетворяющее краевым u(0, x 2) = 0, u( l, x 2) = 0, - аЈ x 2 Ј a,(2) и начальным u( x 1,0) = j( x 1) ,
условиям. При этом дважды непрерывно дифференцируемые функции j и y считаются наперёд заданными. Если переменное x 2есть время t,то решение u( х, t) уравнения (1), удовлетворяющее условиям (2) и (3), описывает колебание упругой струны длины lс концами, закрепленными в точках (0, 0) и (0, l). Изложенная задача нахождения решения уравнения (1) при условиях (2) и (3) - простейший пример так называемой смешанной задачи. Вообще краевыми называют задачи, в которых в заданной области Gпространства независимых переменных ( x 1,..., x n) = хищется решение u( х) = u( x 1,..., x n) уравнения Du( x) = 0, xО G(4) при требовании, что искомая функция u( х) на границе Sобласти Gудовлетворяет краевому (граничному) условию Bu( у) = 0, yО S,(5) где Dи В- заданные операторы, причём, как правило, D- дифференциальный или интегро-дифференциальный оператор. Граница Sназывается носителем краевых данных (5). Когда операторы Dи Влинейны, К. з. (4), (5) называется линейной. В предположениях, что Sявляется ( n - 1)-мерной гиперповерхностью, D -линейным дифференциальным оператором второго порядка
а
где A i, j, B i, C, F, f -заданные функции, задача (4), (5) называется первой краевой задаей Дирихле. Если же
где a i, i= 1,..., n, f -заданные функции, то задача (4), (5) называется задачей наклонной (косой) производной. В частности, когда вектор ( a 1,..., a n) совпадает с конормалью к S,задача наклонной производной носит название второй краевой задачи, или задачи Неймана. Задача Дирихле (Неймана) называется однородной, если F( x) =0, f( y) =0 . Задачи Дирихле и Неймана хорошо исследованы в ограниченных областях с достаточно гладкой границей в случае равномерной эллиптичности оператора D сдействительными коэффициентами, т. е. при соблюдении условий
где l 1,..., l n-произвольные действительные параметры, а k 0и k 1- фиксированные отличные от нуля числа одинакового знака. При требовании достаточной гладкости коэффициентов операторов Dи Ви равномерной эллиптичности оператора Dсправедливы следующие утверждения: 1) число kлинейно независимых решений однородной задачи Дирихле (Неймана) конечно; 2) для разрешимости задачи Дирихле (Неймана) необходимо и достаточно, чтобы функции F( x) и f( y) были подчинены дополнительным ограничениям типа условий ортогональности, число которых равно k; 3) при соблюдении условия С( x) Ј 0, xО G, задача Дирихле всегда имеет и притом единственное решение; 4) в области Gдостаточно малого диаметра задача Дирихле всегда имеет и притом единственное решение и 5) при однозначной разрешимости задачи Дирихле (Неймана) малое изменение краевых данных вызывает малое изменение решения (т. е. решение устойчиво). Когда
Dпредставляет собой оператор Лапласа
u(
х)
=
где f 1= u( -1), f 2= u(1), а при n= 2 и n =3, соответственно, в круге | x| < 1 и шаре | x| < 1
где | х-у| -расстояние между точками хи у.Линейную К. з. называют фредгольмовой, если для неё имеют место сформулированные выше утверждения 1) - 5). В К. з. для эллиптических уравнений обычно предполагается, что носителем краевого условия является вся граница Sобласти G. Если условие (6) равномерной эллиптичности не удовлетворено, но оператор
Dявляется эллиптическим в том смысле, что квадратичная форма
Линейная К. з. даже при требовании равномерной эллиптичности дифференциального оператора D,вообще говоря, не является фредгольмовой. В частности, задача наклонной производной может не оказаться фредгольмовой, если вектор ( a 1..., a n) в некоторых точках границы Sлежит в касательной к Sплоскости. Когда дифференциальный оператор Dне является эллиптическим, К. з. (4), (5) может вовсе не иметь содержательного смысла, если часть границы Sобласти Gне освободить от краевых данных и на структуру носителя краевых данных не наложить определённые (порой весьма сильные) ограничения. Так, например, уравнение теплопроводности
являющееся типичным представителем уравнений параболического типа, в квадрате, ограниченном прямыми: x 1 =0 , x 1=1 , x 2=0 , x 2=1 ,имеет единственное решение u( x 1, x 2) ,удовлетворяющее краевым условиям: u(0 , x 2) = f( x 2) ,0 Ј x 2Ј 1 u( x 1,0) =j( x 1) ,0 Ј x 1Ј 1 u(1 , x 2) =y( x 2) ,0 Ј x 2Ј 1 f(0) =j(0) ,y(0) =j( 1) при произвольных достаточно гладких данных f, j. y. Следовательно, краевое условие u( x 1,1) = q( x 1) ,0 Ј x 1Ј 1, уже нельзя задавать произвольно. Точно так же рассмотренное выше простейшее уравнение гиперболического типа (1) в квадрате, ограниченном прямыми: x 1+ x 2=0, x 1- x 2=0, x 1+ x 2=1, x 1- x 2=-1, имеет единственное решение u( x 1, x 2) ,удовлетворяющее краевым условиям: u( x 1, x 1) = f( x 1) ,0 Ј x 1Ј 1/ 2 u( x 1,-x 1) =j( x 1) ,- 1/ 2 Ј x 1Ј 0 f(0) =j(0) при произвольных достаточно гладких данных f и j. Очевидно, что в рассмотренном случае краевые значения u( x 1,1+x 1) ,- 1/ 2Ј x 1Ј 0, и u( х 1,1-x 1) ,0 Ј x 1Ј 1/ 2, не могут быть заданы произвольно. Особо ставятся К. з., когда в разных частях рассматриваемой области Gдифференциальный оператор Dпринадлежит различным (эллиптическим, гиперболическим и параболическим) типам [т. е. когда уравнение (4) является уравнением смешанного типа]. Для исследования К. з. широко используются методы интегральных уравнений (потенциала), априорных оценок и конечных разностей. Лит.:Бернштеин С. Н., Собр. соч., т. 3, [М.], 1960; Бицадзе А. В., Краевые задачи для эллиптических уравнений второго порядка, М., 1966; Векуа И. Н., Новые методы решения эллиптических уравнений, М.- Л., 1948; Владимиров В. С., Уравнения математической физики, М., 1967; Мусхелишвили Н. И., Сингулярные интегральные уравнения, 3 изд., М., 1968; Петровский И. Г., Лекции об уравнениях с частными производными, 3 изд., М., 1961; Соболев С. Л., Некоторые применения функционального анализа в математической физике, Новосибирск, 1962; Тихонов А. Н., Самарский Д. А., Уравнения математической физики, 3 изд., М., 1966. А. В. Бицадзе. Кража Кра'жа,в уголовном праве тайное похищение имущества. Тайный способ изъятия имущества, предполагающий наличие у преступника уверенности, что он действует незаметно для потерпевшего и др. лиц, отличает К. от грабежа и разбоя. В СССР УК союзных республик устанавливают раздельную ответственность за К. с целью завладения государственным или общественным имуществом и за К. с целью завладения личным имуществом (например, УК РСФСР, ст. ст. 89 и 144). За К. государственного или общественного имущества установлено более строгое наказание, чем за К. личного имущества. Ответственность за К. государственного или общественного имущества в особо крупных размерах и за мелкую К. этого же имущества предусмотрена специальными нормами (например, ст. ст. 93 1и 96 УК РСФСР). К обстоятельствам, отягощающим ответственность за К., закон относит: совершение К. повторно; по предварительному сговору группой лиц; с применением технических средств (только в УК РСФСР, Грузинской ССР и Таджикской ССР); причинение значительного ущерба потерпевшему (при К. личного имущества). Особо отягчающими обстоятельствами являются совершение К. особо опасным рецидивистом или в крупных размерах (при К. государственного или общественного имущества). 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112 |
|||||||
 (1)
(1)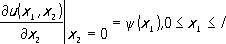 (3)
(3)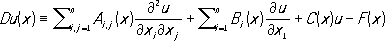 ,
,
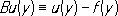 ,
,
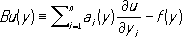 ,
,
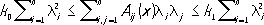 , x О
G
, x О
G
 S (6)
S (6)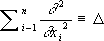 , решение задачи Дирихле в ограниченной области с достаточно гладкой границей всегда существует и единственно, причём для некоторых областей частного вида оно выписывается в явном виде. Так, например, при
n= 1 в интервале -1 <
х <1 это решение имеет вид
, решение задачи Дирихле в ограниченной области с достаточно гладкой границей всегда существует и единственно, причём для некоторых областей частного вида оно выписывается в явном виде. Так, например, при
n= 1 в интервале -1 <
х <1 это решение имеет вид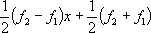 ,
,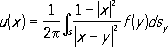 ,
,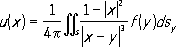 ,
,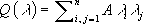 в области
Dположительно (или отрицательно) определена, то иногда для сохранения фредгольмовости К. з. вполне определённую часть границы
Sобласти
Gследует освободить от краевых данных.
в области
Dположительно (или отрицательно) определена, то иногда для сохранения фредгольмовости К. з. вполне определённую часть границы
Sобласти
Gследует освободить от краевых данных.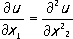 ,
,