George Gamow

Mr. Tompkins in Wonderland, 1939 (The Mr. Tompkins Series #1)

Mr. Tompkins Explores the Atom, 1944 (The Mr. Tompkins Series #2)

Предисловие

Зимой 1938 года я написал короткий фантастический с точки зрения науки (но не научно-фантастический) рассказ, в котором предпринял попытку объяснить доступно для неспециалиста основные идеи теории искривленного пространства и расширяющейся Вселенной. Я решил, что для этого лучше всего сильно увеличить масштабы реально существующих релятивистских явлений и тем самым сделать их легко наблюдаемыми для героя моего рассказа — некоего Ц. Г. Х. Томпкинса [1], скромного банковского служащего, интересующегося современной наукой.

Рукопись я отослал в редакцию журнала «Harper's Magazine» и, как и все начинающие авторы, в скором времени получил ее обратно вместе с уведомлением об отказе. Попробовал было послать рукопись в редакции полдюжины других журналов — результат оказался таким же. Тогда я засунул рукопись в ящик своего письменного стола и забыл о ней.

Летом того же года мне довелось побывать на международном конгрессе по теоретической физике, происходившем в Варшаве под эгидой Лиги Наций. Как-то раз я разговорился там за стаканом превосходного потьского меда с моим давним приятелем сэром Чарлзом Дарвином, внуком того самого Чарлза Дарвина (автора «Происхождения видов»). Речь зашла о популяризации науки. Я поведал Дарвину о постигшей меня неудаче на поприще популяризации, и тот посоветовал мне в ответ:

— Знаете, что я вам скажу, Гамов? По возвращении в Соединенные Штаты разыщите свою рукопись и пошлите ее доктору Чарлзу Сноу. Он сейчас редактирует научно-популярный журнал «Discovery», выпускаемый издательством Кембриджского университета.

Так я и поступил. А через неделю пришла телеграмма от Сноу. В ней значилось: «Ваша статья будет опубликована в следующем номере. Присылайте еще». Вскоре в выпусках журнала «Discovery» одна за другой появились повести о мистере Томпкинсе, в которых популярно излагались теория относительности и квантовая механика. А затем я получил письмо от издательства Кембриджского университета, в котором мне предлагалось, дополнив уже вышедшие статьи несколькими новыми для большего объема, опубликовать повести о мистере Томпкинсе в виде отдельной книжки. Эта книжка под названием «Мистер Томпкинс в Стране Чудес» вышла в издательстве Кембриджского университета в 1940 г. и с тех пор выдержала 16 изданий. За первой книжкой последовало продолжение — «Мистер Томпкинс исследует атом». Вторая книжка вышла впервые в 1944 г. и с тех пор успела выдержать 10 изданий. Обе книжки были переведены на все европейские языки (кроме русского), а также — на китайский и хинди.

Недавно издательство Кембриджского университета решило выпустить обе книжки под одной обложкой и обратилось ко мне с просьбой обновить устаревший материал и добавить несколько историй о событиях, которые произошли в физике и смежных областях науки со времени выхода первых изданий моих повестей. Так, мне пришлось добавить истории о делении и синтезе ядер, стационарной Вселенной и увлекательных проблемах физики элементарных частиц. Весь материал вместе составил содержание этой книги.

Не могу не сказать несколько слов об иллюстрациях. Все иллюстрации к моим статьям, опубликованным в журнале «Discovery», и к первой книжке были выполнены художником Джоном Хукхэмом, наделившим Мистера Томпкинса определенными портретными чертами. Когда я написал вторую книжку, мистер Хукхэм удалился от дел и мне пришло в голову самому проиллюстрировать книжку в духе Хукхэма. Новые иллюстрации к предлагаемой читателю книге также выполнены мной. Стихи и песенки написаны моей женой Барбарой.

Георгий Гамов

Университет Колорадо, Боулдер, штат Колорадо, США

Введение

С детства мы привыкаем к окружающему миру, каким он воспринимается нашими пятью чувствами; именно в детстве у нас формируются фундаментальные представления о пространстве, времени и движении. Наш разум вскоре настолько осваивается с этими понятиями, что впоследствии мы склонны считать единственно возможным наше основанное на них представление о внешнем мире и любая мысль об изменении этих понятий кажется нам парадоксальной. Однако развитие точных физических методов наблюдения и более глубокий анализ наблюдаемых соотношений привели современную науку к вполне определенному выводу о том, что ее «классические» основы оказываются совершенно несостоятельными, когда их пытаются применить к подробному описанию явлений, обычно недоступных наблюдениям, и что для правильного и непротиворечивого описания нашего утонченного опыта совершенно необходимо внесение некоторых изменений в фундаментальные понятия — пространство, время и движение.

Вместе с тем расхождения между понятиями, основанными на обыденном здравом смысле, и понятиями, введенными современной физикой, пренебрежимо малы, пока речь идет о нашем повседневном житейском опыте. Но стоит лишь нам вообразить иные миры, в которых действуют такие же физические законы, как в нашем собственном мире, но с другими числовыми значениями физических констант, устанавливающих пределы применимости старых понятий, как новые (правильные) представления о пространстве, времени и движении, к которым современная наука пришла в результате долгих и кропотливых исследований, становятся достоянием обычного здравого смысла. Можно утверждать, что в таких мирах даже первобытный дикарь был бы знаком с принципами теории относительности и использовал бы их на охоте и для удовлетворения других повседневных потребностей.

Герой историй, с которыми вы познакомитесь в этой книге, переносится во сне в несколько таких миров, где явления, обычно недоступные нашим чувствам, усиливаются до такой степени, что их можно наблюдать как события повседневной жизни. В фантастических, но вполне реальных («правильных») с научной точки зрения снах нашему герою помогает старый профессор физики (на дочери которого по имени Мод наш герой в конце концов женится), просто и доходчиво объясняющий необычные явления, наблюдаемые героем в мире теории относительности, космологии, квантовой механики, атомной и ядерной физики, теории элементарных частиц и т. д.

Надеемся, что необычные путешествия мистера Томпкинса помогут интересующемуся читателю составить более ясное представление о том реальном физическом мире, в котором мы живем.

Глава 1

Ограничение скорости

В тот день все банки были закрыты — выходной, и мистер Томпкинс, скромный служащий солидного городского банка, встал позже обычного и не спеша позавтракал. Пора было позаботиться о досуге, и мистер Томпкинс решил, что было бы неплохо сходить на дневной сеанс в кино. Развернув утреннюю газету на той полосе, где публиковалась информация о развлечениях, он углубился в изучение репертуара кинотеатров. Ни один из рекламируемых фильмов не показался мистеру Томпкинсу достаточно привлекательным. Он терпеть не мог всю эту голливудскую дребедень с нескончаемыми любовными историями, разыгрываемыми популярными кинозвездами. Вот если бы нашелся хотя бы один фильм с сюжетом, заимствованным из реальной жизни, быть может, с примесью чего-нибудь необычного или даже фантастического! Но таких фильмов — увы! — не было. Неожиданно внимание мистера Томпкинса привлекло небольшое объявление в самом углу газетной полосы. Местный университет доводил до сведения всех желающих, что в его помещении будет прочитан цикл лекций по проблемам современной физики. Ближайшая лекция состоится сегодня вечером и будет посвящена теории относительности Эйнштейна. Вот это стоящее дело! Мистеру Томпкинсу частенько приходилось слышать, что во всем мире едва ли дюжина людей по-настоящему понимают теорию Эйнштейна! А что если он, мистер Томггкинс, станет тринадцатым? Ясное дело: он непременно отправится на лекцию. Это как раз то, что ему нужно! Когда мистер Томпкинс вошел в большую университетскую аудиторию, лекция уже началась. Все помещение было битком набито студентами (в основном это были молодые люди), с неподдельным интересом внимавшими высокому седобородому человеку у доски, который пытался объяснить аудитории основные идеи теории относительности. Из слов лектора мистер Томпкинс понял только, что основной пункт теории Эйнштейна — существование максимальной скорости — скорости света, которую не может превзойти ни одно движущееся материальное тело, и что это обстоятельство приводит к весьма странным и необычным следствиям. Правда, профессор заметил, что, поскольку скорость света составляет 300000 километров в секунду, релятивистские (т.е. связаннее с теорией относительности) эффекты едва ли могут наблюдаться в явлениях повседневной жизни. Что же касается природы этих необычных эффектов, то понять ее было несравненно труднее, и мистеру Томпкинсу показалось, что все, о чем говорит лектор, противоречило здравому смыслу. Он попытался мысленно представить себе сокращение измерительных стержней и странное поведение часов — эффекты, которых следовало бы ожидать при движении со скоростью, близкой к скорости света, но тут голова его медленно склонилась на плечо.

Когда мистер Томпкинс снова открыл глаза, он обнаружил, что сидит не на скамье в университетской аудитории, а на скамейках, установленных городскими властями для удобства пассажиров, ожидающих автобус. Кругом простирался красивый старинный городок со средневековыми зданиями колледжей, выстроившимися вдоль улицы. Мистер Томпкинс заподозрил было, что видит все это во сне, но к его удивлению ничего необычного вокруг не происходило, даже полисмен, стоявший на противоположном углу, выглядел так, как обычно выглядят полисмены. Стрелки больших часов на башне в конце улицы показывали пять часов, и улицы были почти пустынными. Одинокий велосипедист показался вдали и стал медленно приближаться. Когда он подъехал поближе, мистер Томпкинс вытаращил глаза от изумления: и велосипед, и восседавший на нем молодой человек были невероятно сокращены в направлении движения, как будто их рассматривали через цилиндрическую линзу. Часы на башне пробили пять, и велосипедист, по-видимому, куда-то спешивший, приналег на педали. Мистер Томпкинс не заметил, чтобы скорость от этого прибавилась, но усилия велосипедиста не прошли бесследно: он сократился еще сильнее и отправился дальше, в точности напоминая картинку, вырезанную из картона. Тут мистер Томпкинс ощутил необычный прилив гордости, ибо ему было совершенно ясно, что происходило с велосипедистом — это было не что иное, как сокращение движущихся тел в направлении движения, о котором только что рассказывал лектор.

— Должно быть, естественная предельная скорость здесь поменьше, чем у нас, — подумал мистер Томпкинс, — поэтому полицейский на углу выглядит таким ленивым: ему не нужно следить, чтобы никто не нарушал ограничений на скорость.

Действительно, появившееся на улице такси производило грохот и скрежет, способные разбудить и мертвого, но продвигалось не намного быстрее, чем велосипедист, и, если сказать честно, ползло еле-еле. Мистер Томпкинс решил догнать велосипедиста, который на вид был симпатичным малым, и расспросить его обо всем. Убедившись, что полисмен отвернулся и смотрит в другую сторону, мистер Томпкинс воспользовался чьим-то велосипедом, стоявшим у края тротуара, и помчался по улице. Он ожидал, что сразу же сократится в направлении движения и даже был очень рад этому, так как начавшая расползаться за последнее время фигура причиняла ему некоторые неприятности. Но к величайшему удивлению мистера Томпкинса ни с ним самим, ни с велосипедом ничего не произошло. Сократились улицы, витрины лавок и магазинов превратились в узкие щели, а полисмен на углу стал самым тощим человеком, которого приходилось когда-нибудь видеть мистеру Томпкинсу.

— Клянусь Юпитером, — радостно воскликнул мистер Томпкинс, — я, кажется, понял, в чем дело! Вот где появляется словечко «относительность». Все, что движется относительно меня, кажется мне сокращенным, кто бы ни крутил педали!

Мистер Томпкинс был неплохим велосипедистом и изо всех сил старался догнать молодого человека. Однако он обнаружил, что развить приличную скорость на угнанном им велосипеде совсем нелегко. Хотя мистер Томпкинс крутил педали что было сил, скорость от этого прибавлялась едва заметно. Ноги у него уже начало сводить от напряжения, а ему никак не удавалось миновать фонарный столб на углу быстрее, чем когда он только пустился в путь. Казалось, все его усилия ехать быстрее тщетны. Теперь он отлично понял, почему велосипедист и встретившееся ему только что такси ползли с такой черепашьей скоростью. Вспомнились ему и слова профессора о том, что ни одно движущееся тело не может превзойти предельную скорость — скорость света. Правда, мистер Томпкинс заметил, что городские кварталы сокращались все больше и до ехавшего впереди велосипедиста теперь казалось не так далеко. У второго поворота мистеру Томпкинсу удалось догнать велосипедиста и в тот самый момент, когда они поровнялись, ехали рядом, мистер Томпкинс, взглянув на того, к своему удивлению увидел, что перед ним обычный молодой человек спортивного вида.

— Должно быть, это от того, что мы не движемся друг относительно друга,

— подумал мистер Томпкинс и обратился к молодому человеку:

— Прошу прощения, сэр! — сказал он. — Не находите ли вы, что жизнь в городе со столь низкой предельной скоростью сопряжена с некоторыми неудобствами?

— О какой предельной скорости вы говорите? — с недоумением спросил молодой человек. — У нас в городе нет никаких ограничений на скорость. Я могу ехать где угодно и куда угодно с любой скоростью, какая мне только заблагорассудится или по крайней мере с какой мог бы двигаться, будь у меня мотоцикл, а не эта допотопная развалина, из которой, как ни старайся, приличной скорости не выжмешь!

— Но когда вы недавно проезжали мимо меня, — продолжал мистер Томпкинс,

— то тащились еле-еле. Я обратил на это внимание.

— В самом деле? — молодой человек был явно задет подобным замечанием. — В таком случае вы, вероятно, заметили, что впервые обратились ко мне, когда мы были отсюда в пяти кварталах. Для вас это недостаточно быстро?

— Но с тех пор улицы значительно сократились, — продолжал настаивать мистер Томпкинс.

— А какая разница, движемся ли мы быстрее или улица становится короче? Мне нужно проехать десять кварталов, чтобы попасть на почту, и если я буду прилежнее крутить педали, то кварталы станут короче и я быстрее попаду на почту. Впрочем, вот мы и доехали.

С этими словами молодой человек соскочил с велосипеда.

Мистер Томпкинс взглянул на часы на здании почты: они показывали полшестого.

— Вот видите, — заметил он торжествующе, — чтобы проехать каких-нибудь десять кварталов, вам понадобилось полчаса. Ведь когда я впервые увидел вас, было ровно пять!

— И вы почувствовали, что прошло полчаса? — спросил его собеседник. Мистеру Томпкинсу пришлось признать, что по его ощущениям прошло всего несколько минут. Кроме того, взглянув на свои ручные часы, он увидел, что они показывают только пять минут шестого.

— О! — только и смог вымолвить он. — Часы на здании почты спешат?

— Разумеется, спешат или — ваши часы отстают, потому что вы двигаетесь слишком быстро. Да что с вами в самом деле? Вы что, с Луны свалились? — и молодой человек вошел в здание почты.

После этого разговора мистер Томпкинс пожалел, что рядом нет старого профессора, который бы объяснил ему эти странные события. Молодой человек, по-видимому, был местным жителем и привык к такому состоянию вещей прежде, чем научился ходить. Мистеру Томпкинсу не оставалось ничего другого, как самому приняться за исследование окружавшего его странного мира. Он поставил свои часы по часам на здании почты и, чтобы убедиться в том, что его часы идут правильно, выждал минут десять. Его ручные часы не отставали. Продолжив свое путешествие по улице, мистер Томпкинс, наконец, добрался до вокзала и решил снова сверить свои часы. К его удивлению, часы снова немного отстали.

— Должно быть, это также какой-то релятивистский эффект, — решил мистер Томпкинс и подумал, что было бы недурно расспросить об этом кого-нибудь поумнее юного велосипедиста.

Удобный случай представился очень скоро. Джентльмен, на вид лет сорока, сошел с поезда и направился к выходу. Его встречала леди весьма преклонного возраста, которая, к удивлению мистера Томпкинса, называла его не иначе, как «мой дорогой дедушка». Для мистера Томпкинса это было уже чересчур. Под предлогом помочь поднести вещи он вмешался в разговор.

— Прошу извинить меня за то, что вмешиваюсь в ваши семейные дела, — начал он, — но действительно ли вы приходитесь дедушкой этой милой пожилой леди? Видите ли, я в этих местах человек новый и не знаю местных обычаев, но мне никогда не доводилось…

— Понимаю ваше затруднение, — улыбнулся в усы джентльмен. — Должно быть, вы принимаете меня за Вечного Жида или кого-нибудь в том же духе. Но в действительности все обстоит очень просто. Моя профессия вынуждает меня много ездить, и большую часть своей жизни я провожу в поезде и поэтому, естественно, старею гораздо медленнее, чем мои родственники, проживающие в городе. Я так рад, что сумел вернуться вовремя и застал еще в живых мою любимую внучку! Но прошу меня извинить, мне нужно проводить ее до такси, — и джентльмен поспешил прочь, оставив мистера Томпкинса один на один с его проблемами. Пара бутербродов из вокзального буфета несколько подкрепили его умственные способности, и он зашел в своих рассуждениях так далеко, что заявил, будто ему удалось обнаружить противоречие в знаменитом принципе относительности.

— Если бы все было относительно, — размышлял он, отхлебывая кофе, — то путешественник казался бы своим оседлым родственникам очень старым, а они в свою очередь казались бы очень старыми ему, хотя в действительности обе стороны были бы достаточно молодыми, Но то, что я утверждаю теперь, кажется совершеннейшей чепухой: ни у кого не может быть «относительно седых волос!»

Тут мистер Томпкинс решил предпринять последнюю попытку разобраться в том, как обстоит дело в действительности, и обратился к человеку в железнодорожной форме, одиноко сидевшему в буфете.

— Не будете ли вы так любезны, — начал он, — не будете ли вы так добры сказать, кто виноват в том, что пассажиры в поезде стареют гораздо медленнее тех людей, которые остаются дома?

— Во всем виноват я, сэр, — очень спокойно ответил незнакомец.

— О! — воскликнул мистер Томпкинс. — Так вам удалось разрешить проблему философского камня, над которой в старину столько бились алхимики. Должно быть, вы очень знамениты в медицинском мире. Вы возглавляете где-нибудь кафедру?

— Нет, — ответил незнакомец, необычайно удивленный тем, что сказал мистер Томпкинс. — Я тормозной кондуктор и в мои обязанности входит вовремя тормозить.

— Тормозной кондуктор! — воскликнул мистер Томпкинс, чувствуя, что почва уходит у него из-под ног. — Так вы думаете, что вы … Вы действительно только нажимаете на тормоз, когда поезд подходит к станции?

— Совершенно верно! Именно это я и делаю, и всякий раз, когда поезд замедляет свой ход, пассажиры становятся чуть старше других людей.

— Разумеется, — скромно добавил кондуктор, — машинист, который разгоняет поезд, также выполняет свою часть работы.

— А какое отношение торможение и разгон поезда имеют к тому, что одни остаются молодыми, а другие стареют? — в изумлении спросил мистер Томкинс.

— Какая тут связь, мне доподлинно неизвестно, — сказал кондуктор, — знаю только, что она есть. Однажды среди пассажиров мне встретился профессор из университета, и я спросил у него, как это получается. Он пустился в длинные и маловразумительные объяснения, а под конец упомянул о каком-то «гравитационном красном смещении (кажется, он выразился именно так) на Солнце». Приходилось ли вам слышать о чем-нибудь подобном? Что это за зверь такой — красное смещение?

— Не-ет, — задумчиво протянул мистер Томпкинс, и кондуктор пошел своей дорогой, качая головой.

Вдруг чья-то тяжелая рука опустилась на плечо мистера Томпкинса, и, очнувшись, он обнаружил, что сидит не в вокзальном буфете, а на скамье в той самой университетской аудитории, где он слушал лекцию профессора. Свет уже был потушен, и аудитория опустела. Разбудивший его университетский служитель мягко заметил:

— Мы закрываемся, сэр! Если хотите спать, ступайте лучше к себе домой.

Мистер Томпкинс встал и направился к выходу.

Глава 2

Лекция профессора о теории относительности, на которой заснул мистер Томпкинс

Леди и джентльмены!

Человеческий разум сформировал определенные представления о пространстве и времени как о вместилище или арене, на которой происходят различные события. Эти представления без особых изменений передавались из поколения в поколение, а со времени зарождения точных наук были включены в самые основы математического описания окружающего нас мира. Великий Ньютон, по-видимому, первым дал четкую формулировку классических понятий пространства и времени, написав в своих «Математических началах»:

«Абсолютное пространство по самой своей сущности, безотносительно к чему бы то ни было внешнему, остается всегда одинаковым и неподвижным» и «Абсолютное, истинное математическое время само по себе и по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно и иначе называется длительностью» [2].

— Убеждение в абсолютной правильности этих классических представлений о пространстве и времени было столь сильным, что философы часто считали их априорными и ни одному ученому-естествоиспытателю даже в голову не приходило усомниться в них. Однако в начале XX века стало ясно, что ряд результатов, полученных с помощью чувствительных и тонких методов экспериментальной физики, приводят к противоречиям, если их интерпретировать в рамках классических представлений о пространстве и времени. Это обстоятельство привело одного из величайших современных физиков Альберта Эйнштейна к революционной идее: не существует никаких причин, кроме традиции, по которым классические представления о пространстве и времени следовало бы считать абсолютно правильными; в эти понятия можно и должно вносить изменения, чтобы они соответствовали нашему новому, более точному опыту. Действительно, классические понятия пространства и времени были сформулированы на основе человеческого опыта, почерпнутого из повседневной жизни. Нужно ли удивляться, что тонкие и точные современные методы наблюдения, основанные на использовании высокоразвитой экспериментальной техники, указывают на то, что старые понятия пространства и времени слишком грубы, неточны и могли использоваться в повседневной жизни и на более ранних стадиях развития физики только потому, что их отклонения от правильных понятий достаточно малы. Не следует удивляться и тому, что расширение области исследований современной науки рано или поздно должно было привести нас в такие области, где эти отклонения весьма велики и классические понятия вообще не применимы.

Самым важным экспериментальным результатом, приведшим к коренному пересмотру наших классических представлений, стало открытие того факта, что скорость света в пустоте представляет собой верхний предел всех возможных физических скоростей. Такой важный и неожиданный вывод был сделан главным образом на основании экспериментов американского физика Майкельсона, который в конце прошлого века предпринял попытку наблюдать влияние движения Земли на скорость распространения света и к своему великому удивлению и к удивлению всего научного мира обнаружил, что никаких эффектов, свидетельствующих о влиянии скорости движения Земли на скорость света, не существует и что скорость света в пустоте оказывается всегда одной и той же, независимо от системы, в которой производится измерение, или от движения источника, испускающего свет. Нет необходимости объяснять, почему такой результат весьма необычен и противоречит нашим фундаментальным представлениям о движении. Действительно, если какой-то объект быстро движется в пространстве, а вы движетесь навстречу ему, то движущийся объект столкнется с вами с большей относительной скоростью, равной сумме скоростей объекта и наблюдателя. С другой стороны, если вы удаляетесь от объекта, то он, догнав вас сзади, столкнется с вами с меньшей относительной скоростью, равной разности скоростей.

Например, если вы движетесь, скажем, едете в автомашине, навстречу распространяющемуся в воздухе звуку, то измеренная из машины скорость звука будет больше на величину, равную скорости, развиваемой вашей машиной, или, соответственно, меньше, если звук догоняет вас. Мы называем это теоремой сложения скоростей. Всегда считалось, что эта теорема самоочевидна.

Однако, как показали самые тщательные эксперименты, в случае света теорема сложения скоростей нарушается: скорость света в пустоте всегда остается одной и той же и равна 300000 км/с (скорость света принято обозначать строчной латинской буквой с) независимо от того, как быстро движется наблюдатель.

— Все это хорошо, — скажете вы, — но разве нельзя построить сверхсветовую скорость, складывая несколько меньших, физически достижимых скоростей?

Можем же мы представить себе движущийся очень быстро (например, со скоростью, равной 3/4 скорости света) поезд и бродягу, бегущего по крышам вагонов также со скоростью, равной 3/4 скорости света.

По теореме сложения скоростей, общая скорость бродяги была бы равна полутора скоростям света, и бродяга мог бы обогнать свет, испускаемый сигнальным фонарем. Однако истина состоит в том, что, поскольку постоянство скорости света есть экспериментальный факт, результирующая скорость в нашем случае должна быть меньше, чем мы ожидаем, — она не может превосходить критического значения с. Таким образом, мы приходим к выводу о том, что и при меньших скоростях классическая теорема сложения скоростей должна быть неверна.

Математический анализ проблемы, в который я не хочу здесь вдаваться, приводит к очень простой новой формуле для вычисления результирующей скорости двух складываемых движений.

Если u1 и u2 — две подлежащие сложению скорости, то результирующая скорость оказывается равной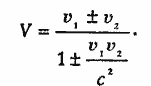

(1)

Вы видите из этой формулы, что если обе подлежащие сложению скорости малы (я имею в виду «малы по сравнению со скоростью света»), то вторым членом в знаменателе формулы (1) можно пренебречь по сравнению с единицей и вы получаете классическую теорему сложения скоростей. Если же скорости u1, и u2 не малы, то результат будет несколько меньше арифметической суммы скоростей. Так, в нашем примере с бродягой, бегущим по крышам вагонов мчащегося поезда, u1 = (3/4)c и u2 = (3/4)c и наша формула позволяет найти результирующую скорость F = (24/25) с, которая, как и складываемые скорости, меньше скорости света.

В частности, когда одна из исходных скоростей равна скорости света с, из формулы (1) следует, что результирующая скорость также равна с, независимо от того, какова вторая скорость. Поэтому, складывая любое число скоростей, мы никогда не можем превзойти скорость света.

Возможно, вам будет интересно узнать, что формула (1) была подтверждена экспериментально и действительно было обнаружено, что результирующая двух скоростей всегда несколько меньше их арифметической суммы.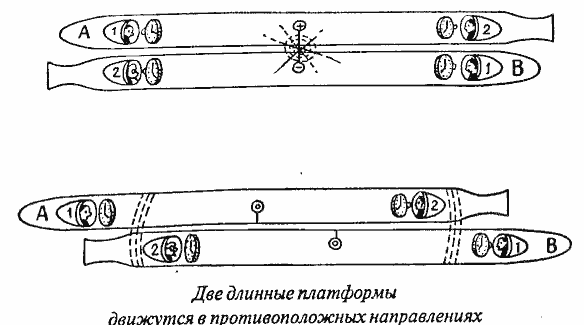

Признав существование верхнего предела скорости, мы можем приступить к анализу классических представлений о пространстве и времени. Свой первый удар мы направим против понятия одновременности, основанном на этих классических представлениях. Когда вы заявляете:

— Взрыв на шахте неподалеку от Кейптауна произошел в тот самый момент, когда в моей лондонской квартире мне на завтрак подали яичницу с ветчиной, — вам кажется, будто вы высказываете вполне осмысленное утверждение. Однако я попытаюсь показать, что в действительности вы не знаете, о чем, собственно, идет речь и, более того, что ваше утверждение, строго говоря, не имеет точного смысла. В самом деле, как бы вы стали проверять одновременность двух событий, происходящих в двух различных местах? Возможно, вы скажете, что такие два события одновременны, если местные часы показывают одно и то же время, но тогда возникает вопрос, как установить часы, разнесенные в пространстве на большое расстояние друг от друга, так, чтобы они одновременно показывали одно и то же время, и мы снова возвращаемся к исходному вопросу.

Поскольку независимость скорости света в пустоте от движения источника или системы, в которой производится измерение, принадлежит к числу наиболее точно установленных экспериментальных фактов, следующий метод измерения расстояний и правильной установки часов на различных наблюдательных станциях следует признать наиболее разумным и, поразмыслив немного, вы согласитесь со мной, что это — единственно приемлемый способ.

Световой сигнал отправляется со станции А и, как только он принимается на станции В, посылается обратно на станцию А. Половина времени (по измерениям, производимым на станции А) между отправлением сигнала и его приемом на станции А, умноженная на скорость света, определяет расстояние между станциями А и В.

Условимся говорить, что часы на станциях А и В установлены правильно, если в момент приема сигнала на станции В местные часы показывали время, равное полусумме показаний часов на станции А в момент отправления и приема сигнала. Применяя этот способ правильной установки часов к двум различным наблюдательным станциям, сооруженным на одной платформе (одном и том же твердом теле), мы получаем столь желанную систему отсчета и обретаем возможность отвечать на вопросы об одновременности событий или временном интервале между двумя событиями, происходящими в различных местах.

Но признают ли одновременными те же события и согласятся ли с оценкой временных интервалов наблюдатели в других системах отсчета? Чтобы ответить на этот вопрос, представим себе две системы отсчета, сооруженные на двух различных платформах (твердых телах), например на двух длинных космических ракетах, летящих в противоположных направлениях каждая со своей постоянной скоростью. Как результаты измерений, производимых в одной системе отсчета, будут соотноситься с результатами аналогичных измерений, производимых в другой системе отсчета? Предположим, что в носовой и кормовой части каждой ракеты находится по наблюдателю и что все четыре наблюдателя хотят прежде всего правильно установить свои часы. Каждая пара наблюдателей, находящихся на борту одной и той же ракеты, может, несколько видоизменив описанный выше способ правильной установки часов, поставить нуль на своих часах в тот момент, когда световой сигнал, посланный из середины ракеты (середина ракеты может быть установлена с помощью мерного стержня), достигнет соответственно носа или кормы ракеты. Таким образом, каждая пара наших наблюдателей устанавливает в соответствии с принятым выше определением критерий одновременности в своей собственной системе отсчета и «правильно» (разумеется, со своей точки зрения) свои часы.

Предположим теперь, что наши наблюдатели решили выяснить, согласуются ли показания часов на борту их ракеты с показанием часов на борту другой ракеты. Например, будут ли часы двух наблюдателей, находящихся на борту различных ракет, показывать одно и то же время, когда ракетам случится пролетать мимо друг друга? Проверить это можно следующим способом. В центре (геометрической середине) каждой ракеты наблюдатели, устанавливают заряженный конденсатор с таким расчетом, что когда ракеты пролетают мимо друг друга, между конденсаторами проскакивает искра и из центра каждой платформы к ее концам (носу и корме) одновременно начинают распространяться световые сигналы. К тому времени, когда световые сигналы, распространяющиеся с конечной скоростью, достигнут наблюдателей, ракеты изменят свое относительное расположение и наблюдатели 2А и 2В окажутся ближе к источнику света, чем наблюдатели 1А и 1В.

Ясно, что когда световой сигнал достигнет наблюдателя 2А, наблюдатель 1B будет позади него и, чтобы достигнуть наблюдателя 1B, световому сигналу понадобится некоторое дополнительное время. Следовательно, если часы наблюдателя 1В поставлены так, что показывают ноль часов ноль минут в момент прихода сигнала, то наблюдатель 2А будет настаивать на том, что часы его коллеги 1В отстают от правильного времени.

Точно так же другой наблюдатель 1А придет к заключению, что часы наблюдателя 2В, до которого световой сигнал дойдет раньше, чем до него, спешат. Поскольку согласно принятому определению одновременности каждый из наблюдателей считает, что его часы поставлены правильно, наблюдатели на борту ракеты А согласятся с тем, что между часами наблюдателей на борту ракеты В имеется различие. Не следует, однако, забывать о том, что наблюдатели на борту ракеты В по точно тем же причинам будут считать, что их часы поставлены правильно, а часы наблюдателей на борту ракеты А рассогласованы.

Поскольку обе ракеты совершенно эквивалентны, разногласия между двумя группами наблюдателей можно разрешить, только если признать, что правы обе группы — каждая со своей точки зрения, но что вопрос о том, кто из них прав, «абсолютно» не имеет физического смысла.

Боюсь что я утомил вас этими длинными рассуждениями, но если вы внимательно следили за ходом моей мысли, то вам должно быть ясно, что как только наш способ пространственно-временных измерений принят, понятие абсолютной одновременности полностью утрачивает смысл и два события, происходящие в различных местах и одновременные с точки зрения одной системы отсчета, разделены конечным временным интервалом с точки зрения другой системы отсчета.

Это утверждение звучит весьма странно, в особенности для тех, кто слышит его впервые, но так ли странно покажется вам, если я скажу, что, обедая в вагоне-ресторане идущего поезда, вы съедаете свой суп и десерт в одной и той же точке вагона-ресторана, но в различных точках железнодорожного полотна, разделенных достаточно большим расстоянием? Между тем утверждение о вашей трапезе в поезде можно сформулировать и так: два события, происходящие в различное время в одной и той же точке одной системы отсчета, разделены конечным пространственным интервалом с точки зрения другой системы отсчета.

Сравнив это «тривиальное» утверждение с предыдущим «парадоксальным» утверждением, вы увидите, что они совершенно симметричны и переходят друг в друга, если слово «временной» заменить на «пространственный» (и наоборот).

В этом и состоит вся суть точки зрения Эйнштейна: если в классической физике время рассматривалось как нечто совершенно независимое от пространства и движения и считалось, что оно «по самой своей сущности, без всякого отношения к чему-либо внешнему, протекает равномерно» (Ньютон), то в новой физике пространство и время тесно взаимосвязаны и представляют собой два различных сечения одного однородного «пространственно-временного континуума», в котором разыгрываются все наблюдаемые события. Разделение этого четырехмерного континуума на трехмерное пространство и одномерное время совершенно произвольно и зависит от системы отсчета, в которой производятся наблюдения.

Два события, разделенные в пространстве расстоянием l и во времени интервалом t по наблюдениям в одной системе отсчета, по наблюдениям в другой системе отсчета разделены другим расстоянием l' в пространстве и другим временным интервалом t' что позволяет в определенном смысле говорить о преобразовании пространства во время и наоборот. Нетрудно также понять, почему преобразование времени в пространство, как в примере с обедом в вагоне-ресторане, для нас обычное дело, тогда как преобразование пространства во время, порождающее относительность понятия одновременности, кажется весьма необычным. Дело в том, что если расстояния мы измеряем, например, в «сантиметрах», то соответствующей единицей времени должна быть не привычная «секунда», а «рациональная единица времени» — интервал времени, который необходим световому сигналу для того, чтобы преодолеть расстояние в один сантиметр, т.е. 0,00000000003 секунды.

Следовательно, в сфере нашего обычного опыта преобразование пространственных интервалов во временные интервалы приводит к практически ненаблюдаемым результатам, что, казалось бы, подкрепляет классический взгляд на природу вещей, согласно которому время есть нечто абсолютно независимое и неизменяемое.

Но при изучении движений с очень большими скоростями, например, движения электронов, испускаемых радиоактивными элементами, или движения электронов внутри атома, где расстояния, покрываемые за определенный интервал времени, — величины того же порядка, как время, выраженное в рациональных единицах, мы непременно сталкиваемся с обоими эффектами, о которых шла речь выше, и теория относительности приобретает важное значение. Релятивистские эффекты могут наблюдаться даже в области сравнительно малых скоростей, например, при движении планет в нашей Солнечной системе из-за необычайно высокой точности астрономических измерений (однако наблюдение релятивистских эффектов в подобных случаях требует измерений изменений движения планеты, доходящих до доли угловой секунды за год).

Как я пытался объяснить вам, критический анализ понятий пространства и времени приводит к заключению, что пространственные интервалы могут быть частично превращены во временные интервалы и наоборот. Это означает, что числовые значения данного расстояния или периода времени, измеряемые в различных движущихся системах отсчета, могут расходиться.

Сравнительно простой математический анализ этой проблемы, в который, однако, я не хотел бы входить на этих лекциях, приводит к вполне определенным формулам для изменения длин пространственных и временных интервалов. Из них следует, что любой объект длины l, движущийся относительно наблюдателя со скоростью u, сократится на величину, зависящую от скорости, и измеренная длина объекта окажется равной

(2)

Аналогично, любой процесс, длящийся время t, при наблюдении из движущейся относительно него системы отсчета, будет длиться дольше — время t', которое может быть вычислено по формуле

(3)

Это и есть знаменитое «сокращение пространства» и «замедление времени» в теории относительности.

Обычно, когда скорость u гораздо меньше скорости света с, эти эффекты очень малы, но при достаточно больших скоростях длины, наблюдаемые из движущейся системы отсчета, могут быть сделаны сколь угодно малыми, а временные интервалы — сколь угодно продолжительными.

Я хочу, чтобы вы не забывали, что оба эффекта — и сокращение пространственных интервалов, и замедление времени — совершенно симметричны и, если пассажиры быстро мчащегося поезда будут удивляться, почему пассажиры стоящего поезда такие тощие и движутся так медленно, пассажиры стоящего поезда будут размышлять о том же, глядя на пассажиров мчащегося поезда.

Еще одно следствие существования максимальной достижимой скорости относится к массе движущихся тел. Как явствует из общих основ механики, масса тела определяет, насколько трудно привести его в движение или, если оно уже движется, ускорить его: чем больше масса, тем труднее увеличить скорость тела на данную величину.

То, что ни одно тело ни при каких обстоятельствах не может двигаться со скоростью, большей скорости света, приводит нас непосредственно к выводу, что его сопротивление дальнейшему ускорению, или, иначе говоря, его масса, неограниченно возрастает, когда скорость тела приближается к скорости света. Математический анализ позволяет вывести формулу зависимости массы тела от его скорости, аналогичную формулам (2) и (3). Если m0 — масса тела при очень малых скоростях, то масса m тела при скорости u определяется по формуле

(4)

Мы видим, что сопротивление тела дальнейшему ускорению становится бесконечно большим, когда и стремится к c. Этот эффект релятивистского изменения массы может быть легко наблюдаем экспериментально на частицах, движущихся с очень большими скоростями. Например, масса электронов, испускаемых радиоактивными телами (со скоростью, составляющей 99 % скорости света), в несколько раз больше, чем в состоянии покоя, а массы электронов, образующих так называемые космические ливни и нередко движущихся со скоростью 99,98 % скорости света, в 1000 раз больше. К таким скоростям классическая механика становится абсолютно неприменимой, и мы вступаем в область чистой теории относительности.

Глава 3

Мистер Томпкинс берет отпуск

Мистеру Томпкинсу очень понравились приключения в релятивистском городе, огорчало только, что с ним не было профессора, который мог бы объяснить необычные явления, которые ему, мистеру Томпкинсу, довелось там наблюдать, например, помочь разрешить загадку, особенно занимавшую его: каким образом тормозному кондуктору удавалось предупредить старение пассажиров? Много ночей подряд мистер Томпкинс укладывался в постель с надеждой снова увидеть полюбившийся ему город, но сны мистер Томпкинс видел редко и, в основном, довольно неприятные. Например, в последний раз мистеру Томпкинсу приснилось, что управляющий банком уволил его за небрежность в ведении банковских счетов. Проснувшись, мистер Томпкинс счел за благо взять отпуск и отправиться на недельку куда-нибудь на море. Так мистер Томпкинс оказался в купе поезда, наблюдая в окно, как серые крыши пригорода постепенно уступают место зеленым лужайкам сельской местности. Мистер Томпкинс достал газету и попытался сосредоточиться на последних корреспонденциях с театра военных действий во Вьетнаме. Но все сообщения показались ему невыносимо скучными, а железнодорожный вагон так приятно покачивало…

Когда Томпкинс опустил газету и снова выглянул в окно, пейзаж сильно изменился. Телеграфные столбы стояли так близко друг от друга, что напоминали гигантскую изгородь, а кроны деревьев были такими узкими, что деревья напоминали итальянские кипарисы. Напротив мистера Томпкинса в купе сидел его старый знакомый — профессор и с живейшим интересом смотрел в окно. По-видимому, он вошел в купе, пока мистер Томпкинс был занят чтением газеты.

— Мы находимся в стране относительности, если я не ошибаюсь, — заметил мистер Томпкинс.

— О! — воскликнул профессор. — Не ожидал встретить попутчика, обладающего столь глубокими познаниями! А по какому учебнику вы изучали теорию относительности?

— Мне уже доводилось бывать здесь, хотя я не имел чести быть вашим попутчиком.

— На этот раз вам придется быть моим гидом, — сказал старый профессор.

— Боюсь, что мне придется отказаться от этой почетной роли, — отклонил лестное предложение мистер Томпкинс. — Я действительно видел множество необычных вещей, но местные жители, к которым я обращался за разъяснениями, никак не могли взять в толк, что меня смущает.

— Вполне естественно, — заметил профессор. — Ведь они родились в этом мире, и все происходящие вокруг них явления кажутся им самоочевидными. Представляю, как они удивились бы, если бы им довелось побывать в том мире, где привыкли жить вы. Думаю, он показался бы им весьма необычным.

— Позвольте задать вам один вопрос, — сказал мистер Томпкинс. — В прошлый раз, когда я был здесь, мне встретился тормозной кондуктор с железной дороги. Он утверждал, будто из-за того, что поезд останавливается и трогается в путь, пассажиры старятся быстрее, чем люди в городе. Что это — чудеса или явление, которое согласуется с современной наукой?

— Ссылаться на чудеса при объяснении чего угодно — прием запрещенный, — ответил профессор. — Явление, о котором говорил ваш кондуктор, следует из законов физики. Анализируя новые (или, лучше сказать, старые, но лишь незадолго до того открытые) понятия пространства и времени, Эйнштейн показал, что все физические процессы замедляются, когда система, в которой они происходят, изменяет свою скорость. В нашем мире такие эффекты почти незаметны, но здесь из-за малой скорости света они становятся легко наблюдаемыми. Например, если вы попытаетесь здесь сварить себе на завтрак яйцо и вместо того, чтобы дать кастрюльке спокойно стоять на огне, начнете двигать ее то в одну, то в другую сторону, то сварить яйцо вкрутую вам удастся не за пять, а, скажем, за шесть минут. Все процессы в человеческом теле также замедляются, если, например, человек качается в кресле-качалке или сидит в купе поезда, который замедляет или ускоряет ход: в такого рода условиях мы живем медленнее. Но поскольку все процессы замедляются одинаково, физики предпочитают говорить, что в неравномерно движущейся системе время течет медленнее.

— А наблюдают ли такие явления ученые в нашем мире, так сказать, у нас дома?

— Наблюдают, хотя для этого им приходится проявлять недюжинное экспериментальное искусство. Технически очень трудно достичь необходимых ускорений, а физические условия в неравномерно движущейся системе аналогичны, я бы даже сказал «тождественны», результату воздействия очень большой силы тяжести. Вам, должно быть, приходилось замечать, что в кабине поднимающегося с ускорением лифта вам кажется, что вы становитесь тяжелее. Наоборот, если лифт опускается (например, если оборвался трос и лифт падает), то вы ощущаете как бы потерю веса. Объяснение изменений веса состоит в том, что создаваемое ускорением гравитационное поле добавляется или вычитается из силы тяжести Земли. Потенциал силы тяжести на Солнце во много раз больше, чем на поверхности Земли, и поэтому все процессы на Солнце немного замедляются. Астрономы наблюдают это.

— Но ведь они не могут отправиться на Солнце, чтобы наблюдать замедление всех процессов?

— Им и не нужно туда отправляться. Они наблюдают свет, приходящий к нам от Солнца. Этот свет порождается колебаниями различных атомов в солнечной атмосфере. Если все процессы на Солнце идут медленнее, то скорость атомных колебаний также убывает и, сравнивая свет, испускаемый Солнцем и земными источниками, астрономы могут заметить разницу.

— Кстати, вы не знаете, как называется небольшая станция, мимо которой мы сейчас проезжаем? — прервал себя профессор.

Поезд катился вдоль перрона маленькой захолустной станции. Перрон был совершенно пуст, если не считать начальника станции и молодого носильщика, сидевшего на багажной тележке и читавшего газету. Вдруг начальник станции как-то нелепо взмахнул руками и упал ничком. Мистер Томкинс не слышал звука выстрела, должно быть, заглушенного стуком колес поезда, но лужа крови у тела начальника станции не оставляла сомнений в том, что произошло убийство. Профессор не медля дернул стоп-кран, и поезд рывком остановился. Когда мистер Томпкинс и профессор вышли из вагона, носильщик бежал к телу и на перроне появился местный полисмен.

— Убит выстрелом в сердце, — констатировал полисмен, осмотрев тело, и, положив тяжелую руку на плечо носильщика, продолжил:

— Вы арестованы за убийство начальника станции.

— Не убивал я его, — закричал несчастный носильщик. — Я читал газету, как вдруг услышал выстрел. Возможно, эти джентльмены с поезда видели, как все произошло и могут подтвердить, что я не виновен.

— Действительно, — подтвердил мистер Томпкинс, — я видел своими собственными глазами, как этот человек читал газету в тот момент, когда был застрелен начальник станции. Могу поклясться на Библии.

— Но вы находились в движущемся поезде, — заметил полисмен, обретая начальственный тон, — и поэтому ваши показания не имеют доказательной силы. С точки зрения наблюдателя на перроне этот человек мог быть застрелен в тот же самый момент. Разве вы не знаете, что одновременность событий зависит от системы отсчета, из которой вы ее наблюдаете? Пройдем без лишнего шума, — обратился он к носильщику.

— Прошу извинить меня, констебль, — прервал его профессор, — но вы совершенно не правы и я не думаю, что в полицейском управлении очень обрадуются, узнав о вашем невежестве. Никто не спорит: в вашей стране понятие одновременности в высшей степени относительно. Это правда. Верно и то, что два события, происходящих в различных местах, могут быть одновременными или не одновременными в зависимости от движения наблюдателя. Но даже в вашей стране ни один наблюдатель не может видеть следствие раньше, чем причину. Вам же никогда не случалось получать телеграмму до того, как та была отправлена, ведь верно? Не случалось и пить до того, как бутылку откупорили. Насколько я вас понимаю, вы полагаете, что из-за движения поезда мы, пассажиры, наблюдали выстрел гораздо позже, чем его следствие, поскольку, выскочив из вагона тотчас же после экстренной остановки поезда, мы увидели начальника станции лежащим на земле, но еще не видели самого выстрела. Я знаю, что в полиции вас учат верить только тому, что написано в ваших инструкциях. Взгляните в них и вы, вероятно, отыщите что-нибудь подходящее к случаю.

Тон профессора произвел неизгладимое впечатление на полисмена и, вытащив карманный свод инструкций, он принялся медленно, страница за страницей изучать их. Вскоре по его широкой красной физиономии разлилась улыбка облегчения.

— Вот, — сказал он, — раздел 37, часть 12, параграф е: «В качестве абсолютно надежного алиби следует считать любое авторитетное доказательство того, что из любой движущейся системы отсчета в момент совершения преступления или в течение интервала времени +-cd (где с — скорость света, а d — расстояние от места преступления) подозреваемого видели в другом месте».

— Вы свободны, мой милый, — обратился полисмен к носильщику и добавил, повернувшись к профессору:

— Очень признателен вам, сэр, что вы избавили меня от неприятностей с полицейским управлением. Я в полиции служу недавно и еще не выучил назубок все правила. Но мне все равно необходимо доложить об убийстве. И полисмен поспешил к телефонной будке. Через минуту он закричал на весь перрон:

— Все в порядке! Они поймали настоящего убийцу, когда тот бежал со станции. Еще раз благодарю вас, сэр!

— Должно быть, я непроходимо глуп, — заметил мистер Томпкинс, когда поезд снова тронулся, — но что означает вся эта неразбериха с одновременностью? Имеет ли одновременность вообще какой-нибудь смысл в этой стране?

— Имеет, — гласил ответ профессора, — но лишь в определенной степени, иначе я не смог бы помочь бедняге-носильщику. Дело в том, что если существует естественный предел скорости для движения любого тела или распространения любого сигнала, то одновременность в обычном смысле этого слова утрачивает смысл. Вам, вероятно, будет легче понять суть дела на следующем примере. Предположим, что у вас есть друг, живущий в далеком городе, с которым вы переписываетесь, и почтовый поезд, который отправляется раз в сутки, — самое быстрое средство сообщения. Предположим теперь, что какое-то происшествие случилось с вами в воскресенье и вы узнали, что аналогичное происшествие должно произойти с вашим другом. Ясно, что вы не можете уведомить его об этом раньше вторника. С другой стороны, если бы он знал заранее о том, что произойдет с вами, то последний день, когда он мог предупредить вас о грядущем событии, был четверг на прошлой неделе. Таким образом, в течение шести дней — с четверга на прошлой неделе до вторника на будущей неделе — ваш друг не способен ни повлиять на вашу судьбу в воскресенье, ни узнать о том, что с вами произошло. С точки зрения причинности он изъят из общения с вами, или, так сказать, экскоммуницирован.

— А что если ему послать телеграмму? — предложил мистер Томпкинс.

— Но ведь я предположил, что скорость почтового поезда — максимально возможная. Примерно так и обстоит дело в этой стране. У нас на родине максимальной скоростью является скорость света, и вы не можете послать сигнал, которой распространялся бы быстрее, чем радиосигнал.

— Пусть так, — согласился мистер Томпкинс, — но даже если ничто не может превзойти скорость почтового поезда, я все равно не понимаю, какое это имеет отношение к одновременности. Мой друг и я по-прежнему обедаем по воскресеньям в одно и то же время. Разве не так?

— Нет, не так. Ваше утверждение вообще не имело бы смысла: один наблюдатель согласился бы с тем, что вы с приятелем обедаете одновременно, а другие наблюдатели, производившие свои наблюдения из других поездов, утверждали бы, что вы обедаете по воскресеньям в то самое время, когда ваш друг завтракает по пятницам или ужинает по вторникам. Но никто не может наблюдать вас и вашего друга за одновременной трапезой, если вас разделяет временной интервал более трех дней.

— Но как это может быть? — воскликнул недоверчиво мистер Томпкинс.

— Происходит все это точно так, как вы, возможно, уяснили себе из моих лекций. Верхний предел скорости должен оставаться одним и тем же при наблюдении из различных движущихся систем отсчета. Приняв такое предположение, мы с необходимостью приходим к заключению о том, что…

Тут разговор, к сожалению, прервался, так как поезд прибыл на ту станцию, где мистеру Томпкинсу нужно было сходить.

Когда мистер Томпкинс спустился к завтраку на длинную застекленную веранду отеля на следующее утро после своего прибытия на побережье, его ожидал приятный сюрприз: на противоположном конце стола против него восседал старый профессор с красивой молодой девушкой, которая оживленно что-то говорила ему, часто поглядывая в ту сторону, где сидел мистер Томпкинс.

— Должно быть, я совершил большую глупость, когда заснул в поезде, — подумал мистер Томпкинс, сердясь на себя все больше и больше, — а профессор все еще помнит тот глупый вопрос, который я задал ему о молодеющих пассажирах. Но по крайней мере это позволяет мне продолжить знакомство с профессором и расспросить его о том, что мне по-прежнему непонятно.

Даже самому себе мистер Томпкинс не хотел признаться, что думает не только о профессоре, но и о его хорошенькой спутнице.

— Да, да, конечно, я помню, что видел вас на своих лекциях, — сказал профессор, когда они выходили из обеденного зала. — Познакомьтесь, это моя дочь Мод. Она занимается живописью.

— Рад познакомиться с вами, мисс Мод, — ответил мистер Томпкинс и подумал, что никогда не слышал более красивого имени. — Думаю, что здешние красоты дадут вам немало материала для ваших этюдов.

— Мод непременно покажет их вам когда-нибудь, — пообещал профессор. — А сейчас скажите мне лучше, много ли вы почерпнули из моей лекции?

— О да, очень много! Более того, я на себе прочувствовал все эти релятивистские сокращения материальных объектов и сумасшедшее поведение часов, когда побывал в городе, где скорость света составляла только километров десять в час.

— Жаль, что вы пропустили мою следующую лекцию о кривизне пространства и ее связи с силами ньютоновской гравитации, — задумчиво произнес профессор.

— Но здесь, на побережье, у нас хватит времени, и я надеюсь объяснить вам все это. Например, понимаете ли вы, в чем разница между положительной и отрицательной кривизной пространства?

— Папочка, — вмешалась мисс Мод, капризно надув губы, — если вы собираетесь снова беседовать о физике, то я лучше займусь этюдами.

— Хорошо, девочка, иди, — согласился профессор, опускаясь в легкое кресло. — Я вижу, что вы молодой человек, не очень сведущи в математике, но думаю, что удастся объяснить вам все очень просто. Для большей наглядности я буду говорить о поверхности. Представьте себе, что мистер Шелл (вы знаете, о ком я говорю, — это тот самый господин, который владеет бензозаправочными станциями «Шелл Ойл») решил как-то раз проследить за тем, чтобы его заправочные станции были равномерно распределены по территории какой-нибудь страны, например, Америки. Для этого мистер Шелл отдал правлению своей фирмы, расположенному где-то в центре страны (если я не ошибаюсь, многие склонны думать, что сердце Америки находится в Канзас-Сити), распоряжение сосчитать число станций на расстоянии сто, двести, триста и т. д. миль от центра. Со школьной скамьи мистер Шелл вынес воспоминания о том, что площадь круга пропорциональна квадрату его радиуса, и ожидает, что в случае равномерного распределения заправочных станций число их в результате подсчетов будет возрастать, как последовательность чисел 1; 4; 9; 16 и т.д. Когда в правление «Шелл Ойл» стали поступать отчеты, глава фирмы к своему великому удивлению обнаружил, что число станций возрастает гораздо медленнее, например, как числа, образующие последовательность 1; 3,8; 8,5; 15,0 и т.д.

— Что за дьявольщина, — воскликнул мистер Шелл, — мои управляющие в Америке ничего не смыслят в своем деле! Ну скажите на милость, зачем им понадобилось сосредотачивать заправочные станции в окрестностях Канзас-Сити?

Прав ли мистер Шелл в своем заключении?

— В самом деле, прав ли он? — повторил мистер Томпкинс, мысли которого где-то витали.

— Мистер Шелл глубоко заблуждается, — мрачно изрек профессор. — Он упустил из виду, что поверхность Земли не плоская, а сферическая, а на сфере площадь, заключенная внутри круга данного радиуса, растет медленнее, чем на плоскости. Можете вы представить себе это наглядно? Нет? Тогда возьмите глобус и убедитесь сами в том, что я прав. Например, если вы находитесь на Северном полюсе, то окружность радиусом в половину меридиана есть не что иное, как экватор, а заключенная внутри нее площадь поверхности Земли есть площадь северного полушария. С увеличением радиуса площадь на поверхности сферы возрастает только вдвое, а не вчетверо, как было бы на плоскости. Теперь, надеюсь, ясно?

— О, да, — кивнул мистер Томпкинс, делая вид, будто он внимательно следит за объяснениями. — А что такое положительная или отрицательная кривизна?

— У сферы кривизна считается положительной. Как вы видели на примере земного шара, положительная кривизна соответствует конечной поверхности, имеющей конечную площадь. Примером поверхности с отрицательной кривизной может служить седло.

— Седло? — переспросил мистер Томпкинс.

— Да, седло, или на поверхности Земли седлообразный перевал между двумя горными вершинами. Предположим, что некий ботаник обитает в горной хижине, расположенной на таком седловидном перевале, и занимается изучением плотности сосен, растущих вокруг его жилища. Подсчитав число сосен, растущих не далее ста, двухсот, трехсот и т. д. футов от хижины, он обнаружит, что число сосен возрастает быстрее, чем квадрат расстояния, поскольку на седловидной поверхности площадь, заключенная внутри данного радиуса, растет быстрее, чем на плоскости. О таких поверхностях говорят, что они обладают отрицательной кривизной. Если вы попытаетесь, растянув, наложить седловидную поверхность на плоскость, то вам придется сделать складки. Если же вы задумаете наложить на плоскость сферическую поверхность, то вам придется где-то проделать в ней дырочку.

— Кажется, я начинаю понимать, — задумчиво произнес мистер Томпкинс. — Вы хотите сказать, что седловидная поверхность бесконечная, хотя и искривленная.

— Вот именно! — одобрительно кивнул профессор. — Седловидная поверхность простирается во все стороны до бесконечности и нигде не замыкается. Разумеется, в моем примере с седловидным перевалом поверхность перестает быть поверхностью отрицательной кривизны, как только вы спускаетесь с гор, и переходит в искривленную поверхность земного шара с положительной кривизной. Но, разумеется, ничто не мешает вам вообразить поверхность, сохраняющую повсюду отрицательную кривизну.

— Но какое отношение имеет все это к искривленному трехмерному пространству?

— Самое непосредственное. Представьте себе, что какие-то ваши объекты равномерно распределены по всему пространству. Под равномерным я понимаю такое распределение, при котором расстояние между любыми соседними объектами всегда одно и то же. Предположим, что вы подсчитываете число объектов, расположенных не далее того или иного расстояния от вас. Если это число растет как квадрат расстояния, то пространство плоское. Если же число объектов растет медленнее или быстрее, то пространство обладает соответственно положительной или отрицательной кривизной.

— Значит, в случае пространства положительной кривизны объем, заключенный в пределах данного расстояния, меньше, а в случае пространства отрицательной кривизны — больше, чем в случае плоского пространства? — с удивлением спросил мистер Томпкинс.

— Вот именно! — улыбнулся профессор. — Я вижу, что теперь вы поняли меня правильно. Чтобы определить знак кривизны той огромной Вселенной, в которой мы живем, необходимо лишь производить такие подсчеты удаленных объектов. Большие туманности, о которых вы, возможно, слышали, рассеяны равномерно в космическом пространстве, и их можно наблюдать вплоть до расстояний в несколько миллионов световых лет. Для исследования кривизны Вселенной это очень удобные объекты.

— И получается, что наша Вселенная конечна и замкнута?

— Видите ли, — ответил профессор, — в действительности эта проблема все еще не решена. В своих работах по космологии Эйнштейн утверждал, что наша Вселенная имеет конечные размеры, замкнута и не изменяется во времени. Однако в более поздней работе русского математика Ал. Фридмана было показано, что фундаментальные уравнения Эйнштейна допускают такую возможность, как расширение или сжатие Вселенной на более позднем этапе развития. Это математическое заключение было подтверждено американским астрономом Э. Хабблом, который, используя стодюймовый телескоп обсерватории Маунт Вилсон, обнаружил, что галактики разлетаются, т.е. наша Вселенная расширяется. Существует, однако, все еще нерешенная проблема относительно того, будет ли это расширение продолжаться неограниченно или радиус Вселенной достигнет своего максимального значения, после чего в отдаленном будущем расширение сменится сжатием. Ответ на этот вопрос могут дать только более подробные астрономические наблюдения.

Пока профессор говорил, вокруг стали происходить весьма необычные изменения: один конец коридора сжался и стал крохотным, сдавив всю стоявшую там мебель, зато другой конец расширился и продолжал увеличиваться в размерах, хотя уже сейчас, как показалось мистеру Томпкинсу, он мог вместить всю Вселенную. Ужасная мысль пронеслась в голове мистера Томпкинса: что если кусочек пространства с пляжем, где мисс Мод рисовала свои этюды, оторвался от основной части Вселенной? — Тогда, — подумал мистер Томпкинс, — я никогда не увижу ее снова!

Мистер Томпкинс бросился к выходу. Последнее, что он услышал, был голос профессора, кричавшего ему вслед:

— Осторожнее! Квантовая постоянная также сходит с ума!

Когда мистер Томпкинс достиг пляжа, ему показалось, что он переполнен. Тысячи девушек носились по всем направлениям, создавая дикую неразбериху.

— Как же я смогу найти мою Мод в этой толпе? — растерянно подумал мистер Томпкинс. Но приглядевшись, он заметил, что все девушки выглядели точно так же, как дочь профессора, и понял, что это необычайное сходство было игрой принципа неопределенности. В следующий момент волна аномально большой квантовой постоянной прошла, и перед мистером Томпкинсом на пляже оказалась мисс Мод с испуганным выражением в глазах.

— Ах, это вы! — вздохнула она с облегчением. — А мне показалось, что огромная толпа затопчет меня. Должно быть, я перегрелась на солнце и это мне померещилось. Подождите, пожалуйста, меня здесь, я только на минутку сбегаю в отель за шляпой.

— Нет-нет, мы не должны расставаться, — запротестовал мистер Томпкинс.

— Мне кажется, что скорость света также меняется. Вернувшись со шляпой, вы можете застать меня дряхлым стариком.

— Не говорите чепухи, — возразила девушка, но взяла мистера Томпкинса под руку. А на полпути к отелю новая волна неопределенности накрыла их, и мистер Томпкинс и его спутница оказались размазанными по всему берегу. Одновременно с окрестных холмов начала распространяться складка пространства, причудливо искажая очертания прибрежных скал и рыбацких домиков. Лучи Солнца, отраженные от интенсивного гравитационного поля, полностью исчезли за горизонтом, и мистер Томпкинс погрузился в кромешную тьму.

Прошла целая вечность, прежде чем столь милый его сердцу голос не привел его в чувство.

— О, я вижу мой папочка совсем усыпил вас своими разговорами о физике,

— прощебетала мисс Мод. — Не хотите ли вы пойти со мной поплавать? Вода сегодня просто великолепная.

Мистер Томпкинс подпрыгнул со своего легкого кресла, как на пружинах.

— Так это был только сон, — подумал он, когда они спускались к пляжу. — Или сон только теперь начинается?

Глава 4

Лекция профессора об искривленном пространстве, гравитации и вселенной

Леди и джентльмены!

Сегодня я намереваюсь рассмотреть проблему искривленного пространства и ее связь с явлениями гравитации. Не сомневаюсь, что каждый из вас без труда может представить себе искривленную линию (кривую) или искривленную поверхность, но при упоминании об искривленном трехмерном пространстве ваши лица вытягиваются и вы склонны думать, что это нечто весьма необычное и почти сверхъестественное. Почему искривленное пространство вызывает всеобщий «ужас»? Действительно ли понятие искривленного пространства труднее для понимания, чем понятие искривленной поверхности? Многие из вас, поразмыслив немного над этими вопросами, вероятно, скажут, что представить искривленное трехмерное пространство труднее по одной-единственной причине: мы не можем взглянуть на пространство «со стороны», как мы смотрим на искривленную поверхность шара, или, если обратиться к другому примеру, на такую особым образом изогнутую поверхность, как седло. Но те, кто так говорят, обрекают себя на незнание строго математического смысла кривизны, существенно отличающегося от общеупотребляемого значения этого слова. Мы, математики, называем поверхность искривленной, если свойства геометрических фигур, начерченных на ней, отличны от свойств фигур на плоскости, и измеряем кривизну отклонением от классических правил Евклида. Если вы начертите треугольник на плоском листе бумаги, то, как известно из элементарной геометрии, сумма его внутренних углов равна двум прямым. Вы можете изогнуть этот лист бумаги, придав ему форму цилиндра, конуса или какой-нибудь более сложной фигуры, но сумма углов начерченного на нем треугольника неизменно будет оставаться равной двум прямым углам.

Геометрия поверхности не меняется при этих деформациях и с точки зрения «внутренней» кривизны получающиеся поверхности (искривленные в обычном смысле) такие же плоские, как обычная плоскость. Но вы не можете наложить лист бумаги, не растягивая его, на поверхность сферы или седла, а если вы начертите треугольник на поверхности сферы (т.е. построите сферический треугольник), то простые теоремы евклидовой геометрии выполняться не будут. Например, треугольник, образованный северными половинами меридианов и заключенной между ними дугой экватора, имеет два прямых угла при основании и произвольный угол при вершине.

Возможно, вы удивитесь, когда узнаете, что на седловидной поверхности сумма углов треугольника, наоборот, всегда меньше двух прямых.

Таким образом, чтобы определить кривизну поверхности, необходимо изучить геометрию на этой поверхности. Взгляд же извне на поверхность часто бывает ошибочным. Глядя на поверхность извне, вы скорее всего отнесли бы поверхность цилиндра к тому же классу, что и поверхность обручального кольца. Между тем первая поверхность плоская, а вторая неизлечимо искривлена. Как только вы привыкните к этому новому строгому понятию кривизны, у вас не будет более никаких трудностей в понимании того, что имеют в виду физики, рассуждая о том, искривлено или плоско пространство, в котором мы живем. Проблема заключается только в выяснении того, подчиняются или не подчиняются обычным правилам евклидовой геометрии геометрические фигуры, построенные в физическом пространстве.

Но поскольку мы говорим о реальном физическом пространстве, нам необходимо прежде всего дать физическое определение терминов, используемых в геометрии, и, в частности, указать, что мы понимаем под прямыми, из которых построены фигуры.

Думаю, все вы знаете, что прямую чаще всего определяют как кратчайшее расстояние между двумя точками. Прямую можно построить, либо натянув нить между двумя точками, либо с помощью какого-нибудь эквивалентного, но более сложного процесса, установив опытным путем линию между двумя данными точками, вдоль которой минимальное число раз укладывается мерный стержень данной длины.

Чтобы показать, что результаты построения прямой с помощью такого метода зависят от физических условий, представим себе большую круглую платформу, равномерно вращающуюся вокруг своей оси [3], и пусть экспериментатор Э2 пытается найти кратчайшее расстояние между двумя точками на краю платформы. У экспериментатора имеется коробка с огромным числом стержней, каждый длиной 5 дюймов, и он пытается выложить из минимального числа этих стержней линию, соединяющую две данные точки А и В. Если бы платформа не вращалась, то наш экспериментатор расположил бы стержни вдоль штриховой линии между точками А и В. Но из-за вращения платформы его мерные стержни претерпевают релятивистское сокращение, о котором я рассказал вам в моей предыдущей лекции, причем те из них, которые расположены ближе к краю платформы (и, следовательно, обладают большими линейными скоростями), сокращаются сильнее, чем стержни, расположенные ближе к центру. Ясно, что для того чтобы каждый стержень покрывал как можно большее расстояние, стержни необходимо располагать как можно ближе к центру. Но поскольку оба конца линии закреплены на краю платформы, сдвигать все стержни от середины линии слишком близко к центру невыгодно.

В результате наш физик достигнет некоего компромисса между этими двумя условиями, и кратчайшее расстояние будет в конце концов представлено кривой, слегка выпуклой в сторону центра.

Если наш экспериментатор вместо отдельных стержней натянет между двумя данными точками А и В нить, то результат, как нетрудно понять, получится прежним, поскольку каждый отрезок нити претерпевает такое же релятивистское сокращение, как отдельные стержни. Я хочу особо подчеркнуть, что релятивистская деформация натянутой нити, происходящая, когда платформа начинает вращаться, не имеет ничего общего с обычными эффектами центробежной силы. Релятивистская деформация остается неизменной, как бы сильно ни была натянута нить, не говоря уже о том, что обычная центробежная сила действует в противоположном направлении.

Если наблюдатель, находящийся на платформе, вздумает проверить результат своих построений, сравнив полученную «прямую» с лучом света, то он обнаружит, что свет действительно распространяется вдоль построенной им линии. Разумеется, для наблюдателей, стоящих у платформы, луч света вообще не будет искривлен. Они будут интерпретировать результаты движущегося наблюдателя путем суперпозиции, или наложения, вращения платформы и прямолинейного распространения света. Они скажут вам, что если вы нанесете царапину на вращающуюся граммофонную пластинку, двинув рукой по прямой, то царапина на пластинке, конечно же, будет искривленной.

Но для наблюдателя, находящегося на вращающейся платформе, название «прямая» для построенной им кривой вполне разумно: эта кривая дает кратчайшее расстояние и совпадает с лучом света в системе отсчета нашего наблюдателя. Предположим, что он выбрал на краю платформы три точки и соединил их прямыми, построив тем самым треугольник. Сумма углов в этом треугольнике меньше двух прямых, из чего наш наблюдатель заключает (и совершенно справедливо), что пространство вокруг него искривлено.

Рассмотрим другой пример. Предположим, что два других наблюдателя на платформе (Э3 и Э4) решили оценить число пи, измеряя длину окружности платформы и ее диаметр. На мерный стержень наблюдателя Э3 вращение не влияет, поскольку движение стержня всегда перпендикулярно его длине. С другой стороны, мерный стержень наблюдателя Э4 всегда будет сокращен, и для длины окружности платформы этот наблюдатель получит большее значение, чем в случае невращающейся платформы. Деля результат, полученный наблюдателем 4, на результат, полученный наблюдателем 3, мы получим значение, превышающее значение пи, обычно приводимое в учебниках. Это также является следствием кривизны пространства.

Вращение влияет не только на измерения длин. Часы, расположенные на краю платформы, будут двигаться с большей скоростью и, как было показано в предыдущей лекции, их ход замедлится по сравнению с ходом часов, установленных в центре платформы.

Если два экспериментатора (Э4 и Э5) сверят часы в центре платформы, а затем экспериментатор Э5 на какое-то время отнесет свои часы на край платформы, то по возвращении в центр он обнаружит, что его часы отстают по сравнению с часами, все время остававшимися в центре платформы. Из этого экспериментатор Э5 сделает вывод, что в различных местах платформы все физические процессы идут с различными скоростями. Предположим теперь, что наши экспериментаторы остановились и немного поразмыслили над причиной необычных результатов, только что полученных ими в геометрических измерениях. Предположим также, что вращающаяся платформа закрыта со всех сторон и представляет собой вращающуюся комнату без окон, чтобы экспериментаторы не могли наблюдать свое движение относительно окружающих предметов. Могли бы в этом случае экспериментаторы объяснить все полученные результаты чисто физическими условиями на платформе без учета ее вращения относительно «твердой основы», на которой установлена платформа?

Глядя на различия между физическими условиями на платформе и на «твердой основе», посредством которых можно было бы объяснить наблюдаемые изменения в геометрии, наши экспериментаторы сразу же заметили бы, что существует какая-то новая сила, которая стремится отбросить все тела от центра платформы к ее окружности. Вполне естественно, что они приписали бы наблюдаемые эффекты действию этой силы, утверждая, например, что из двух часов те будут идти медленнее, которые расположены дальше от центра в направлении новой силы.

Но действительно ли эта новая сила нова, т. е. не наблюдаема на «твердой основе»? Разве мы не наблюдаем, как все тела притягиваются к центру Земли силой, которая получила название силы тяжести? Разумеется, в одном случае мы имеем притяжение к окружности диска, в другом — притяжение к центру Земли, но это означает только различие в распределении силы. Нетрудно, однако, привести другой пример, когда «новая» сила, порождаемая неравномерным движением системы отсчета, выглядит точно так же, как сила тяжести в этой лекционной аудитории.

Предположим, что космический корабль, предназначенный для межзвездных перелетов, свободно летит где-то в космическом пространстве настолько далеко от различных звезд, что внутри корабля сила тяжести не действует. Все предметы внутри космического корабля и сами путешествующие в нем экспериментаторы невесомы и свободно плавают в воздухе примерно так же, как Мишель Ардан и его спутники во время путешествия на Луну в знаменитом романе Жюля Верна.

Но вот двигатели включены и космический корабль приходит в движение, постепенно набирая скорость. Что происходит внутри него? Нетрудно видеть, что пока космический корабль ускоряется, все предметы внутри него обнаруживают стремление двигаться к полу, или, что то же, пол движется навстречу этим предметам. Например, если наш экспериментатор держит в руке яблоко и выпускает его, то яблоко продолжает двигаться (относительно окружающих корабль звезд) с постоянной скоростью — той самой, с которой двигался космический корабль, когда экспериментатор выпустил из рук яблоко. Но космический корабль ускоряется. Следовательно, пол кабины, двигаясь все быстрее и быстрее, в конце концов догонит яблоко и стукнет его. С этого момента яблоко останется в постоянном контакте с полом, будучи прижато к полу постоянно действующим ускорением.

Но для экспериментатора, находящегося внутри космического корабля, все выглядит иначе: яблоко «падает» с каким-то ускорением и, ударившись об пол, остается лежать на полу, придавленное к нему собственным весом. Бросая различные предметы, наш экспериментатор заметит, что все они падают с совершенно одинаковым ускорением (если пренебречь трением о воздух) и вспомнит, что это — закон свободного падения, открытый Галилео Галилеем. Но наш экспериментатор так и не сможет заметить ни малейшего различия между явлениями, происходящими в движущейся с ускорением кабине космического корабля и обычными явлениями гравитации. Он может пользоваться маятниковыми часами, ставить книги на полку, не боясь, что те улетят прочь, и повесить на гвоздь портрет Альберта Эйнштейна, который первым указал на эквивалентность ускорения системы отсчета и гравитации и на этой основе развил так называемую общую теорию относительности.

Но тут, как и в первом примере с вращающейся платформой, мы замечаем явления, оставшиеся неизвестными Галилею и Ньютону, когда те изучали гравитацию. Луч света, посланный через кабину, искривляется и освещает в зависимости от ускорения космического корабля каждый раз другое место экрана, висящего на противоположной стене. Разумеется, внешний наблюдатель интерпретирует это как суперпозицию равномерного прямолинейного движения света и ускоренного движения кабины, где производятся наблюдения. Геометрия также нарушается: сумма углов треугольника, образованного тремя лучами света, будет больше двух прямых углов, а отношение длины окружности к диаметру — больше числа пи. Мы рассмотрели лишь два из простейших примеров ускоренно движущихся систем отсчета, но установленная выше эквивалентность остается в силе для любого движения твердой или деформируемой системы отсчета.

Тут мы подходим к вопросу величайшей важности. Как мы только что видели, в ускоренно движущейся системе отсчета может наблюдаться ряд явлений, оставшихся неизвестными для обычного гравитационного поля. Существуют ли эти новые явления, такие как искривление луча света или замедление часов, и в гравитационных полях, порождаемых тяжелыми массами? Или, иначе говоря, существуют ли эффекты ускорения и эффекты гравитации, которые не только очень похожи, но и тождественны? Разумеется, ясно, что хотя с эвристической точки зрения весьма соблазнительно принять полное тождество этих двух разновидностей эффектов, окончательный ответ может быть дан только с помощью прямых экспериментов. И к величайшему удовлетворению нашего человеческого разума, требующего простоты и внутренней непротиворечивости законов Вселенной, эксперименты подтверждают существование новых явлений, о которых идет речь, и в обычном гравитационном поле. Разумеется, эффекты, предсказываемые гипотезой об эквивалентности полей ускорения и гравитационного поля, очень малы. Именно поэтому они и были открыты только после того, как ученые специально занялись их поиском.

Используя приведенный выше пример ускоренно движущихся систем отсчета, мы можем легко оценить два наиболее важных релятивистских гравитационных явления по порядку величины: изменение скорости хода часов и искривление луча света.

Рассмотрим сначала пример с вращающейся платформой. Из элементарной механики известно, что на частицу с единичной массой, расположенную на расстоянии r от центра, действует центробежная сила, вычисляемая по формуле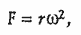

(1)

где омега — постоянная угловая скорость вращения нашей платформы.

Полная работа, совершаемая этой силой при движении частицы от центра до края платформы, равна величине

(2)

где R — радиус платформы.

Согласно сформулированному выше принципу эквивалентности мы должны отождествить центробежную силу F с силой тяжести на платформе, а работу W — с разностью значений гравитационного потенциала в центре и на краю платформы.

Напомним, что, как было показано в предыдущей лекции, часы, движущиеся со скоростью u, замедляют свой ход в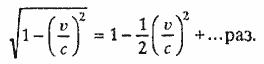

(3)

Если скорость u мала по сравнению со скоростью света с, то остальными членами можно пренебречь. По определению угловой скорости получаем r = R*омега, и «коэффициент замедления» можно представить в виде

(4)

Формула (4) показывает, как изменяется скорость хода часов в зависимости от разности значений гравитационного потенциала в местах расположения часов.

Если мы поместим одни часы у основания, а другие — на вершине Эйфелевой башни (высота башни 300 м), то разность значений гравитационного потенциала между ними будет так мала, что часы у подножия будут идти медленнее, чем часы на вершине башни, только в 0,99999999999997 раз.

С другой стороны, разность значений гравитационного потенциала между поверхностью Земли и поверхностью Солнца гораздо больше и порождает коэффициент замедления, равный 0,9999995, что может быть подтверждено высокоточными измерениями. Разумеется, никто не собирается помещать обычные часы на поверхность Солнца и наблюдать за их ходом! У физиков для этого имеются гораздо лучшие средства. С помощью спектроскопа мы можем наблюдать колебания различных атомов на поверхности Солнца и сравнивать их с периодами колебаний атомов тех же элементов, помещенных в пламя бунзеновской горелки в лаборатории. Колебания атомов на поверхности Солнца должны замедляться в число раз, задаваемое формулой (4), и поэтому испускаемый ими свет должен быть чуть более красноватым, чем в случае земных источников. Такое «красное смещение» действительно наблюдается в спектрах Солнца и нескольких других звезд, спектры которых легко поддаются измерениям, и результаты экспериментов согласуются со значением, которое дает наша теоретическая формула.

Таким образом, существование красного смещения доказало, что процессы на Солнце происходят действительно несколько медленнее, чем на Земле, из-за более высокого гравитационного потенциала на поверхности Солнца.

Чтобы измерить кривизну луча света в гравитационном поле, более удобно воспользоваться примером с космическим кораблем (с.51). Если l — расстояние от одной стенки кабины до другой, то время, за которое свет преодолевает это расстояние, определяется величиной

(5)

За это время космический корабль, двигаясь с ускорением g, пройдет расстояние L, величина которого может быть вычислена по формуле

(6)

известной из элементарной механики. Следовательно, угол, задающий изменение направления луча, есть величина порядка

(7)

Угол ф тем больше, чем больше расстояние l, проходимое светом в гравитационном поле, В формуле (7) ускорение g космического корабля может быть интерпретировано как ускорение силы тяжести. Если я посылаю луч света через эту аудиторию, то величину l можно считать примерно равной 1000 см. Ускорение силы тяжести g на поверхности Земли составляет 981 см/с2, и при с = 3 * 10^10 см/с мы получаем

(8)

Ясно, что при таких условиях наблюдать кривизну луча света заведомо невозможно. Но вблизи поверхности Солнца g = 27000 см/с2, а общий путь, проходимый светом в гравитационном поле Солнца, очень велик. Как показывают точные вычисления, отклонение луча света, проходящего вблизи поверхности Солнца, достигает величины 1,75». Такое отклонение наблюдали астрономы по смещению видимого положения звезд вблизи солнечного диска во время полного затмения Солнца. Вы видите, и в этом случае наблюдения подтверждают абсолютное тождество эффектов ускорения и гравитации.

Теперь мы можем снова вернуться к проблеме кривизны пространства. Как вы помните, используя наиболее разумное определение прямой, мы пришли к заключению, что геометрия, возникающая в неравномерно движущихся системах отсчета, отличается от геометрии Евклида и что пространства с такой геометрией следовало бы считать искривленными. Поскольку любое гравитационное поле эквивалентно некоторому ускорению системы отсчета, это означает, что любое пространство с гравитационным полем является искривленным пространством. Сделав еще один шаг вперед, можно утверждать, что гравитационное поле есть не что иное, как физическое проявление кривизны пространства. Таким образом, кривизна в каждой точке пространства должна определяться распределением масс, и вблизи тяжелых тел кривизна пространства должна быть максимальной. Я не могу вдаваться здесь в весьма сложную математическую теорию, описывающую свойства искривленного пространства и их зависимость от распределения масс. Упомяну только о том, что кривизна пространства, вообще говоря, описывается не одним числом, а десятью различными числами, общеизвестными под названием компонент гравитационного потенциала g и представляющими собой обобщение гравитационного поля классической физики, который ранее я обозначил W. Соответственно, кривизна в каждой точке описывается десятью различными радиусами кривизны, обычно обозначаемыми R. Эти радиусы кривизны связаны с распределением масс фундаментальным уравнением Эйнштейна

(9)

где T зависит от плотностей, скоростей и других свойств гравитационного поля, порождаемого тяжелыми массами.

В заключение лекции я хотел бы обратить ваше внимание на одно из наиболее интересных следствий из уравнения (9). Если мы рассмотрим пространство, равномерно заполненное массами, как, например, наше пространство заполнено звездами и звездными системами, то придем к заключению, что помимо случайно большой кривизны вблизи отдельных звезд пространство должно обладать вполне закономерной тенденцией к равномерному искривлению на больших расстояниях. С точки зрения математики существует несколько различных решений фундаментального уравнения Эйнштейна. Одни из них соответствуют пространству, которое замыкается и поэтому обладает конечным объемом, другие — бесконечному пространству, аналогичному седловидной поверхности, о которой я упоминал в начале этой лекции. Второе важное следствие из уравнения (9) состоит в том, что такие искривленные пространства должны находиться в состоянии непрестанного расширения или сжатия. Физически это означает, что заполняющие пространство частицы должны были бы разлетаться или, наоборот, слетаться. Кроме того, можно показать, что в случае замкнутых пространств с конечным объемом стадии расширения и сжатия должны были бы периодически чередоваться. Такие пространства получили название пульсирующих вселенных. С другой стороны, бесконечные «седловидные» пространства постоянно находятся в состоянии сжатия или расширения.

Ответ на вопрос о том, какое из этих различных математически возможных решений соответствует пространству, в котором мы живем, должен быть найден не физикой, а астрономией, и я не буду рассматривать его здесь. Упомяну лишь о том, что все имеющиеся астрономические данные вполне определенно свидетельствуют о том, что наша Вселенная расширяется, хотя вопрос о том, не сменится ли когда-нибудь расширение сжатием, а также о конечности или бесконечности Вселенной, остается пока открытым.

Глава 5

Пульсирующая вселенная

Первый вечер своего пребывания в гостинице «На берегу Канала» [4] мистер Томпкинс завершил ужином в ресторане, разумеется, в обществе старого профессора и его очаровательной дочери. Ужин удался на славу. Профессор без умолку разглагольствовал о космологии, мисс Мод премило болтала об искусстве. Когда мистер Томпкинс добрался, наконец, до своего номера, он едва успел раздеться и, без сил рухнув на постель, с головой накрылся одеялом. В его усталом мозгу перемешались Боттичелли и Бонди, Сальвадор Дали и Фред Хойл, Леметр и Лафонтен. Поворочавшись некоторое время с боку на бок, мистер Томпкинс, наконец, забылся глубоким сном…

Среди ночи он вдруг проснулся от неожиданного ощущения: ему показалось, что вместо мягкого пружинного матраца он лежит на чем-то необычайно твердом. Мистер Томпкинс открыл глаза и увидел себя простертым на чем-то, показавшемся ему сначала скалой на берегу океана. Однако чуть позже он обнаружил, что действительно возлежит на скале, метров этак девять в поперечнике, которая без всякой видимой опоры висела в пространстве. Скала была местами покрыта зеленым мхом, а кое-где из расселин на ней росли небольшие кустики. Пространство вокруг скалы было освещено каким-то странным мерцающим светом и изрядно забито пылью. Мистеру Томпкинсу еще никогда не приходилось видеть, чтобы в воздухе было столько пыли, даже в фильмах, изображавших пыльные бури на Среднем Западе. Он сделал себе защитную маску из носового платка и почувствовал изрядное облегчение. Но в окружающем пространстве были вещи и поопаснее пыли. Очень часто камни размером с голову мистера Томпкинса и поболее проносились в пространстве у самой скалы и время от времени врезались в нее с непривычно глухим стуком. Но и это еще не все: обозревая окрестности, мистеру Томпкинсу приходилось изо всех сил цепляться за выступы скалы и прижиматься к ней, опасаясь сорваться со скалы и сгинуть в пыльной бездне. Но вскоре мистер Томпкинс набрался храбрости и попытался взобраться на край скалы, чтобы убедиться в том, что под ней действительно нет никакой опоры. Подползая к краю скалы, мистер Томпкинс к своему великому удивлению заметил, что не падает со скалы. Наоборот, его вес постоянно прижимает его к поверхности скалы, хотя сама скала невелика и он успел проползти уже не менее четверти ее охвата. Взглянув из-за груды камней на то место, которое расположено в аккурат под тем местом, где мистер Томпкинс первоначально оказался, он убедился, что скала свободно висит в пространстве и ее ничто не поддерживает. К своему великому изумлению, мистер Томпкинс внезапно увидел в мерцающем свете своего друга — старого профессора, стоявшего на скале, как показалось мистеру Томпкинсу, вниз головой и делавшего какие-то заметки в записной книжке.

Теперь до мистера Томпкинса медленно стало доходить, что происходит. Он вспомнил, как в детстве учил в школе, что Земля — огромная круглая скала, свободно обращающаяся в космическом пространстве вокруг Солнца. Мистер Томпкинс вспомнил также рисунок из школьного учебника: два антипода, стоящие на противоположных сторонах Земли. Ну конечно же! Его скала была небесным телом очень малых размеров, притягивавшим все к своей поверхности, а он сам и старый профессор составляли все население этой крохотной планеты. Размышления несколько утешили мистера Томпкинса: по крайней мере не было опасности свалиться со скалы в космическое пространство!

— Доброе утро, — произнес мистер Томпкинс, чтобы отвлечь внимание старого профессора от вычислений, в которые тот ушел с головой.

Профессор оторвал глаза от записной книжки.

— Здесь нет никаких утр, — сказал он, — нет Солнца, как нет ни одной светящейся звезды во всей этой вселенной. Хорошо еще, что на поверхности тел здесь не протекают кое-какие химические процессы, иначе я просто не смог бы наблюдать за расширением этого участка вселенной. — И с этими словами профессор снова уткнулся в свою записную книжку.

Мистер Томпкинс очень расстроился: подумать только, встретить единственное живое существо во всей вселенной и обнаружить, что оно так необщительно! Неожиданно мистеру Томпкинсу на помощь пришел один из мелких метеоритов: со стуком ударившись о записную книжку, он выбил ее из рук профессора и унес ее в космические дали, прочь от маленькой планеты.

— Больше вы ее не увидите, — заметил мистер Томпкинс, глядя, как записная книжка, становясь все меньше и меньше, скрылась из виду.

— Наоборот! — живо возразил профессор. — Видите ли, пространство, где мы с вами находимся, имеет не бесконечную протяженность. О да, да! Я знаю, что в школе вас учили, будто пространство бесконечно и две параллельные прямые никогда не пересекаются. Но это неверно ни для пространства, в котором обитает остальное человечество, ни для пространства, в котором находимся сейчас мы с вами. Разумеется, пространство, в котором живет все остальное человечество, очень велико, и, по оценкам ученых, простирается примерно на 10000000000000000000000 километров, что для заурядного ума вполне может сойти за бесконечность. Если бы я потерял свою записную книжку в той Вселенной, то ждать бы ее пришлось невероятно долго. Здесь же, где мы с вами находимся, ситуация совершенно иная. Как раз перед тем, как записная книжка была столь неожиданно вырвана из моих рук, я подсчитал, что это пространство имеет поперечник всего лишь около десяти километров, хотя и быстро расширяется. Думаю, что моя записная книжка вернется примерно через полчаса.

— Вы полагаете, — робко подал голос мистер Томпкинс, — что ваша записная книжка поведет себя, как бумеранг аборигенов Австралии, и, описав искривленную траекторию, упадет к вашим ногам?

— Ничего подобного, — возразил профессор. — Если хотите понять, что произойдет в действительности, подумайте о каком-нибудь древнем греке, который не знал, что Земля круглая. Предположим, что наш грек отдал кому-нибудь инструкции двигаться все время на север. Представьте себе его изумление, когда посланец вернется к нему с юга. Ведь наш древний грек не имеет ни малейшего понятия о кругосветном путешествии (говоря о путешествии вокруг света, я, конечно, имею в виду путешествие вокруг Земли) и будет пребывать в полной уверенности, что посланец сбился с истинного пути и, описав искривленный маршрут, вернулся в исходную точку. В действительности же его посланец все время двигался по кратчайшей линии, какую только можно провести на поверхности Земли, но, обойдя вокруг земного шара, вернулся в исходную точку с противоположной стороны. То же самое произойдет и с моей записной книжкой, если только по дороге она не столкнется с каким-нибудь камнем и не отклонится от правильного пути. Вот, возьмите этот бинокль. Может быть, вам удастся разглядеть ее.

Мистер Томпкинс поднес к глазам бинокль и, хотя пыль несколько затемняла общую картину, действительно разглядел записную книжку профессора, плывущую далеко от них в глубине космического пространства. Мистера Томпкинса несколько удивило, что все далекие предметы, в том числе и записная книжка, имеют розовый цвет.

— Ваша записная книжка возвращается, — воскликнул он чуть позже, — я вижу, как она увеличивается в размерах.

— Нет, — откликнулся профессор, — она все еще удаляется от нас. То, что вы видите, как она увеличивается в размерах, объясняется особым фокусирующим действием замкнутого сферического пространства на лучи света. Вернемся к нашему древнему греку. Если бы лучи света, например с помощью атмосферной рефракции, можно было заставить распространяться вдоль искривленной поверхности Земли, то наш грек, будь у него мощный бинокль, мог бы следить за своим посланцем на протяжении всего путешествия. Взглянув на глобус, вы заметите, что прямейшие линии на его поверхности — меридианы — сначала расходятся от одного полюса, но после прохождения через экватор начинают сходиться к противоположному полюсу. Если бы лучи света распространялись вдоль меридианов, то вы находясь, например, на одном полюсе, увидели, как посланец, удаляясь от вас, уменьшается в размерах только до тех пор, пока не пересечет экватор. Затем вы увидите, как он увеличивается в размерах, и вам будет казаться, что он возвращается, тогда как в действительности он будет двигаться все дальше и дальше от вас. Когда посланец достигнет противоположного полюса, вы увидите его в натуральную величину — таким, как если бы он стоял рядом с вами. Однако вы не могли бы коснуться его, как не могли бы потрогать изображение в сферическом зеркале. Опираясь на эту двумерную аналогию, вы можете теперь представить, что произойдет с лучами света в необычно искривленном трехмерном пространстве.

— Взгляните, — прервал себя на полуслове профессор, — изображение моей записной книжки совсем рядом.

Действительно, без всякого бинокля мистер Томпкинс мог видеть, что записная книжка находилась не более чем в метре от них. Но выглядела она весьма странно! Контуры ее были не резкими, а сильно размытыми, формулы, которыми профессор исписал странички, были едва различимы, а вся записная книжка в целом выглядела, как фотография, снятая не в фокусе и к тому же еще недопроявленная.

— Теперь вы сами можете убедиться, — заметил профессор, — что перед вами не сама записная книжка, а всего лишь ее изображение, сильно искаженное светом, которому пришлось пройти полмира. Если хотите окончательно убедиться в том, что перед вами изображение, взгляните в страницы повнимательнее и вы увидите сквозь них камни, летящие в космическом пространстве за книжкой.

Мистер Томкинс попытался было схватить записную книжку, но рука его без всякого сопротивления прошла сквозь изображение.

— Сама записная книжка, — продолжал профессор, — находится сейчас очень близко от противоположного полюса вселенной. Второе изображение книжки сейчас прямо у вас за спиной, и когда оба изображения совпадут, настоящая книжка окажется на противоположном полюсе.

Но мистер Томпкинс уже ничего не слышал. Он глубоко погрузился в размышления, пытаясь припомнить, как строятся изображения объектов в элементарной оптике с помощью вогнутых зеркал и линз. Когда мистер Томпкинс очнулся, изображения снова расходились в противоположные стороны.

— А что искривляет пространство и порождает все эти забавные эффекты? — спросил мистер Томпкинс профессора.

— Наличие тяжелой материи, — последовал ответ. — Когда Ньютон открыл закон всемирного тяготения, он видел в гравитации обычную силу, такую же, как, например, сила, порождаемая упругой нитью, натянутой между двумя телами. Однако всегда остается загадкой то обстоятельство, что все тела независимо от их массы и размера обладают одним и тем же ускорением и, если исключить сопротивление воздуха и тому подобные эффекты, под действием сил тяготения движутся одинаково. Эйнштейн первым ясно и определенно показал, что тяжелая материя прежде всего порождает кривизну пространства и что траектории всех тел, движущихся в гравитационном поле, искривлены только потому, что искривлено само пространство. Боюсь однако, что вам без достаточной математической подготовки трудно разобраться во всем этом.

— Нелегко, — согласился мистер Томпкинс. — Но скажите мне, пожалуйста, была бы у нас та геометрия, которой меня учили в школе, если бы материи вообще не было, и пересекались бы тогда параллельные прямые?

— Параллельные не пересекались бы, — подтвердил профессор, — но ни одно материальное существо не могло бы проверить это.

— Может быть, никакого Евклида в действительности не было и поэтому он не мог создать геометрию абсолютно пустого пространства?

Но профессор явно не желал вдаваться в метафизическую дискуссию.

Между тем изображение записной книжки удалилось в первоначальном направлении и начало приближаться во второй раз. Теперь оно было искажено еще больше, чем прежде, и узнать в нем «призрак» записной книжки было почти невозможно. По мнению профессора, столь сильное искажение объяснялось тем, что лучам света на этот раз приходилось обходить весь мир.

— Если вы еще раз оглянетесь, — обратился профессор к мистеру Томпкинсу, — то увидите мою записную книжку, которая, наконец, возвращается ко мне, совершив кругосветное путешествие.

Профессор протянул руку, поймал записную книжку и засунул ее в карман.

— В этой вселенной, как вы можете убедиться сами, так много пыли и камней, — сказал профессор, — что почти невозможно окинуть взглядом весь мир. Эти бесформенные тени, которые вы видите вокруг нас, скорее всего наши изображения и изображения окружающих предметов. Однако они так сильно искажены пылью и дефектами кривизны пространства, что я не берусь сказать, чему соответствует каждое такое изображение.

— А не наблюдается ли такой же эффект в большой Вселенной, где мы с вами жили раньше? — спросил мистер Томпкинс.

— Конечно, наблюдается, — последовал ответ, — но та Вселенная настолько велика, что свету требуются миллиарды лет, чтобы обойти ее. Вы могли бы, не пользуясь зеркалом, увидеть, как парикмахер постриг вас сзади, но лишь через миллиарды лет после того, как побываете у парикмахера. Кроме того, вероятнее всего межзвездная пыль полностью затемнит изображение. Кстати сказать, один английский астроном предположил даже как-то раз, скорее в шутку, чем всерьез, что видимые сейчас звезды на небе — не более чем изображения звезд, существовавших в очень далекую эпоху.

Устав от усилий понять все эти объяснения, мистер Томпкинс оглянулся и к своему большому удивлению заметил, что картина неба значительно изменилась. Пыли стало заметно меньше, и он снял с лица маску, которую смастерил из носового платка. Небольшие камешки пролетали значительно реже и стукались о поверхность скалы с гораздо меньшей энергией. Что же касается нескольких больших скал, наподобие той, на которой нашли приют и он сам, мистер Томпкинс, и старый профессор, то теперь большие скалы не маячили поблизости, как в самом начале, а удалились на большие расстояния друг от друга и стали едва различимыми.

— Жизнь явно идет на лад, — подумал мистер Томпкинс, — а то я все опасался, как бы один из этих блуждающих камней не врезался в меня.

— Можете ли вы объяснить изменения, происходящие вокруг нас? — спросил он, повернувшись к профессору.

— Очень даже просто, — с готовностью ответил тот. — Наша маленькая вселенная очень быстро расширяется и с тех пор, как мы здесь оказались, ее размеры увеличились с десяти до примерно сотни километров. Как только я здесь очутился, расширение было мне заметно по покраснению далеких объектов.

— Я тоже заметил, что на большом расстоянии все становится розовым, — подтвердил мистер Томпкинс, — но почему это свидетельствует о расширении вселенной?

— Должно быть, вы замечали, — начал профессор, — что гудок приближающегося поезда звучит высоко, но значительно понижается, когда поезд проносится мимо вас? Это так называемый эффект Доплера: зависимость высоты звука от скорости источника. Когда расширяется все пространство, каждый объект, расположенный в нем, удаляется со скоростью, пропорциональной расстоянию от наблюдателя до объекта. Свет, испускаемый такими объектами, краснеет, что в акустике соответствует понижению высоты тона. Чем дальше объект, тем быстрее он движется и тем краснее кажется нам. В нашей доброй старой Вселенной, которая также расширяется, это покраснение, или, как мы его называем, красное смещение, позволяет астрономам оценивать расстояния до очень далеких звездных облаков. Например, одно из таких ближайших облаков — так называемая Туманность Андромеды — обнаруживает 0,05 %-ное покраснение, что соответствует расстоянию, проходимому светом за восемьсот тысяч лет. Но существуют также туманности на пределе разрешающей способности современных телескопов, которые обнаруживают 15 %-ное покраснение, что соответствует расстоянию в несколько сотен миллионов световых лет. Предполагается, что эти туманности расположены почти на середине экватора нашей большой Вселенной и весь объем космического пространства, известного земным астрономам, составляет значительную часть полного объема Вселенной. Современная скорость ее расширения составляет 0,00000001 % в год, каждую секунду радиус Вселенной возрастает примерно на десять миллионов километров. Наша малая вселенная растет (по сравнению с большой) гораздо быстрее, и ее размеры увеличиваются примерно на 1 % в минуту.

— И такое расширение никогда не прекратится? — спросил мистер Томпкинс.

— Разумеется, прекратится, — сказал профессор, — а затем начнется сжатие. Каждая вселенная пульсирует между наименьшим и наибольшим радиусом. Для большой Вселенной период колебаний очень велик и составляет что-нибудь около нескольких тысяч миллионов лет, но для нашей маленькой вселенной период колебаний составляет всего лишь каких-нибудь два часа. Думаю, что сейчас мы наблюдали состояние ее наибольшего расширения. Вы заметили, как похолодало?

Действительно, тепловое излучение, заполняющее вселенную и теперь распределенное по очень большому объему, отдавало маленькой планете, на которой находились мистер Томпкинс и старый профессор, лишь небольшую толику тепла и температура была близка к точке замерзания.

— Хорошо еще, — сказал профессор, — что когда мы здесь оказались, теплового излучения было столько, что немного тепла оно отдавало даже на стадии расширения. В противном случае в нашей маленькой вселенной было бы настолько холодно, что воздух вокруг нашей скалы сконденсировался бы в жидкость и мы бы насмерть замерзли. Но сжатие уже началось и скоро снова будет тепло.

Взглянув на небо, мистер Томпкинс заметил, что все далекие объекты изменили свой цвет с розового на фиолетовый. По мнению профессора, это означало, что все небесные тела начали приближаться к ним. Мистер Томпкинс вспомнил приведенную профессором аналогию с высотой звучания гудка приближающегося поезда и содрогнулся от страха.

— Если все теперь сжимается, не следует ли ожидать, что вскоре огромные скалы, заполняющие вселенную, сблизятся и раздавят нас? — с беспокойством спросил он профессора.

— Вы совершенно правы, так и произойдет, — спокойно ответил профессор,

— но я думаю, что еще до того, как это произойдет, мы оба распадемся на отдельные атомы из-за необычайно высокой температуры. Это миниатюрная копия картины конца большой Вселенной, все смешается в однородный шар раскаленного газа и только после того, как наступит стадия нового расширения, начнется новая жизнь.

— Ничего себе перспектива! — пробормотал мистер Томпкинс. — В большой Вселенной у нас было до ее конца, как вы упоминали, миллиарды лет, а здесь все происходит слишком быстро для меня! Мне жарко даже в пижаме!

— Пижаму лучше не снимать, — посоветовал профессор. — Все равно этим не поможешь. Лучше лечь и наблюдать за происходящим вокруг, пока вы сможете.

Мистер Томпкинс ничего не ответил. Жара становилась нестерпимой. Пыль, сильно уплотнившаяся, стала собираться вокруг него, и он почувствовал себя как бы завернутым в мягкое теплое одеяло. Мистер Томпкинс сделал движение, чтобы освободиться из этого кокона, и рука его неожиданно оказалась в холодном воздухе.

— Уж не проделал ли я дыру в негостеприимной вселенной? — было его первой мыслью. Он хотел спросить об этом профессора, но того нигде не было. Вместо ставшей уже привычной скалы мистер Томпкинс различил в предрассветной мгле смутные очертания гостиничного номера. Он лежал на кровати, плотно завернутый в шерстяное одеяло, выпростав из-под одеяла одну лишь руку.

— Новая жизнь начнется с расширения! — подумал он, вспомнив слова старого профессора. — Слава Богу, мы все еще расширяемся!

И мистер Томпкинс направился в ванную, чтобы принять утренний душ.

Глава 6

Космическая опера

Когда утром за завтраком мистер Томпкинс поведал профессору о своем сне, приснившемся прошлой ночью, тот выслушал его весьма скептически.

— Коллапс нашей Вселенной, — заметил он, — разумеется, был бы весьма драматическим концом, однако скорости разбегания галактик настолько велики, что переживаемая нами стадия расширения никогда не перейдет в коллапс, наша Вселенная будет неограниченно расширяться, а распределение галактик в космическом пространстве становиться все более разреженным. Когда все звезды, образующие галактики, погаснут из-за исчерпания ядерного топлива, наша Вселенная превратится в набор холодных и темных скоплений небесных тел, рассеянных в бесконечных просторах.

Впрочем, некоторые астрономы думают иначе. Они выдвигают теорию так называемой космологии стационарного состояния, согласно которой Вселенная остается неизменной во времени: она существовала примерно в том же состоянии, в каком мы видим ее сегодня, в бесконечно далеком прошлом и будет существовать в таком же состоянии в бесконечно далеком будущем. Разумеется, такая теория великолепно согласуется со старым добрым принципом Британской империи — сохранять в мире статус кво, однако я склонен думать, что теория стационарного состояния неверна. Кстати сказать, один из создателей этой новой теории — профессор теоретической астрономии Кембриджского университета — написал оперу о стационарной Вселенной, премьера которой состоится в Ковент-Гарден на следующей неделе. Почему бы вам не заказать билеты для Мод и для себя и не послушать столь необычную оперу?

Через несколько дней после возвращения в Лондон с южного побережья, где, как это часто бывает, стало холодно и пошли дожди, мистер Томпкинс и Мод сидели в удобных креслах красного бархата, ожидая, когда взовьется занавес и начнется опера.

Прелюдия была исполнена в темпе precipitevol issimevolmente, и дирижер дважды менял свой воротничок, прежде чем прелюдия подошла к концу. Наконец, когда занавес рывком поднялся, все, кто находился в зале, вынуждены были закрыть глаза руками — столь ослепительно ярким светом была залита сцена. Потоки света, изливавшиеся со сцены, вскоре заполнили весь зрительный зал от партера до балкона самого верхнего яруса, превратив его в один ослепительный океан света. Но вот свет стал постепенно меркнуть, и мистер Томпкинс внезапно обнаружил, что как бы плавает в темном пространстве, освещенном множеством быстро вращающихся крошечных горящих факелов, напоминающих огненные колеса, используемые при фейерверках. Музыка невидимого оркестра сменилась звучанием органа, и мистер Томпкинс увидел неподалеку от себя человека в черной сутане и белом воротничке, который носят священнослужители. Взглянув в либретто, мистер Томпкинс узнал, что это был аббат Жорж Леметр из Бельгии, который первым предложил теорию расширяющейся Вселенной (эту теорию нередко называют теорией «Большого Взрыва»).

Первые куплеты из арии Леметра мистер Томпкинс помнит и поныне:

После того как отец Леметр закончил свою арию, откуда ни возьмись появился высокий мужчина, который (судя по либретто) оказался русским физиком Георгием Гамовым, вот уже три десятилетия проводящим свой отпуск в Соединенных Штатах. Вот что он запел:

Третью арию, запавшую в память мистеру Томпкинсу, исполнил автор оперы, внезапно материализовавшийся из ничего в пространстве между ярко сиявшими галактиками. Он вынул из кармана едва народившуюся галактику и запел:

Все было и будет навсегда.

Несмотря на столь вдохновляющие слова, все галактики в окружающем пространстве стали меркнуть. Наконец, бархатный занавес опустился, и в зрительном зале оперного театра зажглись канделябры.

— О, Сирил, — услышал мистер Томпкинс голос Мод, — я знаю, что ты способен уснуть где угодно и когда угодно, но засыпать в Ковент-Гарден тебе все-таки не следовало! Ты проспал весь спектакль!

Когда мистер Томпкинс проводил Мод до дома ее отца, старый профессор, удобно расположившись в кресле, просматривал только что доставленный выпуск «Monthly Notices» (журнала «Ежемесячные заметки»).

— Ну и как вам понравилась опера? — осведомился профессор.

— Великолепно! — отозвался мистер Томпкинс. — На меня особенно сильное впечатление произвела ария о вечно существующей Вселенной. Она звучит так успокаивающе!

— Поосторожней с этой теорией, — предостерег профессор. — Разве вы не знаете пословицу «Не все то золото, что блестит»? Я как раз читал статью кембриджского астронома Мартина Райла, который построил гигантский радиотелескоп, позволяющий обнаруживать галактики на расстояниях, в несколько раз превышающих радиус действия двухсотдюймового оптического телескопа обсерватории Маунт Паломар. Наблюдения Райла показывают, что очень далекие галактики расположены гораздо ближе друг к другу, чем соседние галактики.

— Вы хотите сказать, — попробовал уточнить мистер Томпкинс, — что область Вселенной, в которой мы обитаем, населена галактиками весьма редко и что плотность населения возрастает по мере того, как мы удаляемся от Земли?

— Ничего подобного, — возразил профессор. — Не следует забывать о том, что из-за конечности скорости света, когда вы смотрите далеко в глубь космического пространства, вы как бы заглядываете далеко назад во времени. Например, так как свету требуется восемь минут, чтобы дойти до нас от Солнца, вспышку на Солнце земные астрономы наблюдают с запозданием в восемь минут. Фотографии нашего ближайшего космического соседа — спиральной галактики в созвездии Андромеды (которую вы, наверное, видели в книгах по астрономии; она расположена от нас на расстоянии примерно в один миллион световых лет) — в действительности показывают, как эта галактика выглядела миллион лет назад. То, что Райл видит или, лучше сказать, слышит с помощью своего радиотелескопа, соответствует ситуации, существовавшей в той далекой части Вселенной многие тысячи миллионов лет назад. Если бы наша Вселенная находилась в стационарном состоянии, то картина не должна была бы изменяться во времени и очень далекие галактики, наблюдаемые с Земли, должны были бы быть распределены в космическом пространстве не плотнее и не реже, чем галактики в ближайшей космической окрестности Земли. Следовательно, если наблюдения Райла показывают, что далекие галактики расположены в космическом пространстве плотнее, чем более близкие галактики, то это эквивалентно утверждению о том, что в далеком прошлом, тысячи миллионов лет назад, галактики были распределены в пространстве плотнее, чем теперь. Ясно, что такое утверждение противоречит теории стационарного состояния Вселенной и подкрепляет первоначальную гипотезу, согласно которой галактики разбегаются и плотность их населения убывает. Но, разумеется, мы должны соблюдать осторожность и подождать, пока результаты Райла не будут подтверждены.

— Кстати сказать, — продолжал профессор, доставая из кармана сложенный листок бумаги, — один из моих ученых коллег, обладающий поэтическими наклонностями, недавно написал на эту тему стихотворение. Вот послушайте:

— Мне очень хотелось бы узнать, — заметил мистер Томпкинс, — чем закончится этот не на шутку разгоревшийся спор.

С этими словами он, поцеловав на прощанье мисс Мод в щеку, пожелал ей и старому профессору спокойной ночи и отправился к себе домой.

Глава 7

Квантовый бильярд

Однажды мистер Томпкинс возвращался к себе домой страшно усталый после долгого рабочего дня в банке, где он служил. Проход мимо паба, мистер Томпкинс решил, что было бы недурственно пропустить кружечку эля. За первой кружкой последовала другая, и вскоре мистер Томпкинс почувствовал, что голова у него изрядно кружится. В задней комнате паба была бильярдная, где игроки в рубашках с засученными рукавами толпились вокруг центрального стола. Мистер Томпкинс стал смутно припоминать, что ему уже случалось бывать здесь и прежде, как вдруг кто-то из его приятелей-клерков потащил мистера Томпкинса к столу учиться играть в бильярд. Приблизившись к столу, мистер Томпкинс принялся наблюдать за игрой. Что-то в ней показалось ему очень странным! Играющий ставил шар на стол и ударял по шару кием. Следя за катящимся шаром, мистер Томпкинс к своему большому удивлению заметил, что шар начал «расплываться». Это была единственное выражение, которое пришло ему на ум при виде странного поведения бильярдного шара; который, катясь по зеленому полю, казался все более и более размытым, на глазах утрачивая четкость своих контуров. Казалось, что по зеленому сукну катится не один шар, а множество шаров, к тому же частично проникающих друг в друга. Мистеру Томпкинсу часто случалось наблюдать подобные явления и прежде, но сегодня он не принял ни капли виски и не мог понять, почему так происходит.

— Посмотрим, — подумал мистер Томпкинс, — как эта размазня из шара столкнется с другой такой же размазней.

Должно быть, игрок, нанесший удар по шару, был знатоком своего дела: катящийся шар столкнулся с другим шаром в лобовом ударе, как это и требовалось. Послышался громкий стук, и оба шара — покоившийся и налетевший (мистер Томпкинс не мог бы с уверенностью сказать, где какой шар) — разлетелись «в разные стороны». Выглядело это, что и говорить, весьма странно: на столе не было более двух шаров, выглядевших несколько размазанно, а вместо них бесчисленное множество шаров (все — с весьма смутными очертаниями и сильно размазанные) поразлеталось по направлениям, составлявшим от 0 o до 180 o с направлением первоначального соударения. Бильярдный шар скорее напоминал причудливую волну, распространяющуюся из точки соударения шаров.

Присмотревшись повнимательнее, мистер Томпкинс заметил, что максимальный поток шаров направлен в сторону первоначального удара.

— Рассеяние S-волны, — произнес у него за спиной знакомый голос, и мистер Томпкинс, не оборачиваясь, узнал профессора.

— Неужели и на этот раз что-нибудь здесь искривилось, — спросил мистер Томпкинс, — хотя поверхность бильярдного стола мне кажется гладкой и ровной?

— Вы совершенно правы, — подтвердил профессор, — пространство в данном случае совершенно плоское, а то, что вы наблюдаете, в действительности представляет собой квантовое явление.

— Ах, эти матрицы! — рискнул саркастически заметить мистер Томпкинс.

— Точнее, неопределенность движения, — заметил профессор. — Владелец этой бильярдной собрал здесь коллекцию из нескольких предметов, страдающих, если можно так выразиться, «квантовым элефантизмом». В действительности квантовым законам подчиняются все тела в природе, но так называемая квантовая постоянная, управляющая всеми этими явлениями, чрезвычайно мала: ее числовое значение имеет двадцать семь нулей после запятой. Что же касается бильярдных шаров, которые вы здесь видите, то их квантовая постоянная гораздо больше (около единицы), и поэтому вы можете невооруженным глазом видеть явления, которые науке удалось открыть только с помощью весьма чувствительных и изощренных методов наблюдения.

Тут профессор умолк и ненадолго задумался.

— Не хочу ничего критиковать, — продолжал он, — но мне очень хотелось бы знать, откуда у владельца бильярдной эти шары. Строго говоря, они вообще не могут существовать, поскольку для всех тел в мире квантовая постоянная имеет одно и то же значение.

— Может быть, их импортировали из какого-нибудь другого мира, — высказал предположение мистер Томпкинс, но профессор не удовлетворился такой гипотезой и не избавился от охвативших его подозрений.

— Вы заметили, что шары «расплываются», — начал он. — Это означает, что их положение на бильярдном столе не вполне определенно. Вы не можете точно указать, где именно находится шар. В лучшем случае вы можете утверждать лишь, что шар находится «в основном здесь» и «частично где-то там».

— Все это в высшей степени необычно, — пробормотал мистер Томпкинс.

— Наоборот, — возразил профессор, — это абсолютно обычно в том смысле, что всегда происходит с любым материальным телом. Лишь из-за чрезвычайно малого значения квантовой постоянной и неточности обычных методов наблюдения люди не замечают этой неопределенности и делают ошибочный вывод о том, что положение и скорость тела всегда представляют собой вполне определенные величины. В действительности же и положение, и скорость всегда в какой-то степени неопределенны, и чем точнее известна одна из величин, тем более размазана другая. Квантовая постоянная как раз и управляет соотношением между этими двумя неопределенностями. Вот взгляните, я накладываю определенные ограничения на положение этого бильярдного шара, заключая его внутрь деревянного треугольника.

Как только шар оказался за деревянным заборчиком, вся внутренность треугольника заполнилась блеском слоновой кости.

— Видите! — обрадовался профессор. — Я ограничил положение шара размерами пространства, заключенного внутри треугольника, т. е. какими-то несколькими дюймами. И в результате — значительная неопределенность в скорости, шар так бегает внутри периметра треугольника!

— А разве вы не могли бы остановить шар? — удивленно спросил мистер Томпкинс.

— Ни в коем случае! Это физически невозможно, — последовал ответ. — Любое тело, помещенное в замкнутое пространство, обладает некоторым движением. Мы, физики, называем такое движение нулевым. Таково, например, движение электронов в любом атоме.

Пока мистер Томпкинс наблюдал за бильярдным шаром, мечущимся в треугольной загородке, как тигр в клетке, произошло нечто весьма необычное: шар «просочился» сквозь стенку деревянного треугольника и в следующий момент покатился в дальний угол бильярдного стола. Самое странное было в том, что шар не перепрыгнул сквозь деревянную стенку, а прошел сквозь нее, не поднимаясь над уровнем бильярдного стола.

— Вот вам ваше «нулевое движение», — с упреком сказал мистер Томпкинс.

— Не успели оглянуться, а шар «сбежал». Это как, по правилам?

— Разумеется, в полном соответствии с правилами, — согласился профессор. — В действительности вы видите перед собой одно из наиболее интересных следствий квантовой теории. Если энергии достаточно для того, чтобы тело могло пройти сквозь стенку, то удержать его за стенкой невозможно: рано или поздно объект «просочится» сквозь стенку и будет таков.

— В таком случае я ни за что на свете не пойду в зоопарк, — решил про себя мистер Томпкинс, и его живое воображение тотчас же нарисовало ужасающую картину львов и тигров, «просачивающихся» сквозь стенки своих клеток. Затем мысли мистера Томпкинса приняли несколько иное направление: ему привиделся автомобиль, «просочившийся» из гаража сквозь стены, как доброе старое привидение во времена Средневековья.

— А сколько мне понадобится ждать, — поинтересовался мистер Томпкинс у профессора, — пока автомашина, сделанная не из того, из чего делают автомашины здесь, а из обычной стали, «просочится» сквозь стену гаража, построенного, скажем, из кирпичей? Хотел бы я своими глазами увидеть такое «просачивание»!

Наскоро произведя в уме необходимые вычисления, профессор привел ответ:

— Ждать вам придется каких-нибудь 1 000 000 000…000 000 лет.

Даже привыкший к внушительным числам в банковских счетах мистер Томпкинс потерял счет нулям в числе, приведенном профессором. Впрочем, он несколько успокоился: число было достаточно длинным для того, чтобы можно было не беспокоиться о том, как бы автомашина не сбежала, «просочившись» сквозь стенку в гараже.

— Предположим, что все, о чем вы мне рассказали, не вызывает у меня ни малейших сомнений. Однако мне все же остается непонятно, как можно было бы наблюдать такие вещи (разумеется, я не говорю об этих бильярдных шарах).

— Разумное выражение, — заметил профессор. — Конечно, я не утверждаю, будто квантовые явления можно было бы наблюдать на таких больших телах, с какими вам обычно приходится иметь дело. Действие квантовых законов становится гораздо более заметным применительно к очень малым массам — таким, как атомы или электроны. Для таких частиц квантовые эффекты настолько сильны, что обычная механика становится совершенно неприменимой. Столкновение двух атомов выглядит точно так же, как столкновение двух бильярдных шаров, которое вы здесь наблюдали, а движение электронов в атоме очень напоминает «нулевое движение» бильярдного шара, который я поместил внутрь деревянного треугольника.

— А часто ли атомы выбегают из своего гаража? — спросил мистер Томпкинс.

— О да, весьма часто. Вам, конечно, приходилось слышать о радиоактивных веществах, атомы которых претерпевают спонтанный распад, испуская при этом очень быстрые частицы. Такой атом или, точнее, его центральная часть, называемая атомным ядром, очень напоминает гараж, в котором стоят автомашины, т. е. другие частицы. И частицы убегают из ядра, просачиваясь через стенки, — порой внутри ядра они не остаются ни секунды! В атомных ядрах квантовые явления — дело совершенно обычное!

Мистер Томпкинс порядком устал от столь длинной беседы и рассеянно оглянулся по сторонам. Его внимание привлекли большие дедовские часы, стоявшие в углу комнаты. Их длинный старомодный маятник совершал медленные колебания то в одну, то в другую сторону.

— Я вижу, вы заинтересовались часами, — сказал профессор. — Перед вами не совсем обычный механизм, хотя ныне он несколько устарел. Эти часы могут служить прекрасной иллюстрацией того, как люди сначала мыслили себе квантовые явления. Маятник часов устроен так, что амплитуда его колебаний может возрастать только конечными шагами. Теперь все часовщики предпочитают пользоваться патентованными расплывающимися маятниками.

— О, как бы я хотел разобраться в столь сложных вопросах! — воскликнул мистер Томпкинс.

— Нет ничего проще, — ответствовал профессор. — Я зашел в паб по пути на свою лекцию о квантовой теории, потому что увидел в окно вас. А теперь мне пора отправляться дальше, чтобы не опоздать на лекцию. Не хотите ли пойти со мной?

— С превеликим удовольствием! — согласился мистер Томпкинс.

Большая аудитория как обычно была до отказа заполнена студентами, и мистер Томпкинс считал, что ему очень повезло, когда он кое-как примостился на ступенях прохода.

— Леди и джентльмены, — начал профессор. — В двух моих предыдущих лекциях я попытался показать вам, каким образом открытие существования верхнего предела всех физических скоростей и анализ понятия прямой привел нас к полному пересмотру классических представлений о пространстве и времени.

Однако критический анализ основ физики не остановился на этой стадии и привел к еще более поразительным открытиям и выводам. Я имею в виду раздел физики, получивший название квантовой теории. Этот раздел занимается изучением не столько самих пространства и времени, сколько взаимодействия и движения материальных объектов в пространстве и времени. В классической физике всегда считалось самоочевидным, что взаимодействие между любыми двумя материальными телами может быть сделано настолько малым, насколько это требуется по условиям эксперимента, и даже, если это необходимо, практически сведено к нулю. Например, если при исследовании тепла, выделяющегося в некоторых процессах, возникает опасение, что вводимый термометр может забрать на себя некоторое количество теплоты и тем самым внести возмущение в нормальное течение процесса, то экспериментатор пребывает в уверенности, что, используя термометр меньших размеров или миниатюрную термопару, он всегда сможет понизить вносимое возмущение до уровня, который укладывается в пределы допустимой точности измерений.

Убеждение в том, что любой физический процесс может быть в принципе наблюдаем с любой требуемой точностью без каких-либо возмущений, вносимых наблюдением, было весьма сильным, и никому даже в голову не приходило сформулировать столь очевидное допущение в явном виде. Все проблемы, связанные с вносимыми при наблюдении возмущениями, считались чисто техническими трудностями. Однако новые экспериментальные факты, накопленные с начала XX столетия, постоянно вынуждали физиков приходить к выводу, что в действительности все обстоит гораздо сложнее и в природе существует определенный нижний предел взаимодействия, который никогда не может быть превзойден. Этот естественный предел точности пренебрежимо мал для всевозможных процессов, с которыми мы сталкиваемся в повседневной жизни, но становится существенным при рассмотрении взаимодействий, происходящих в таких микроскопически-механических системах, как атомы и молекулы.

В 1900 г. немецкий физик Макс Планк, занимаясь теоретическими исследованиями условий равновесия между излучением и веществом, пришел к удивительному выводу: такое равновесие невозможно, если взаимодействие между излучением и веществом происходит не непрерывно, как всегда предполагалось, а в виде последовательности отдельных «соударений". При каждом таком элементарном акте взаимодействия от вещества излучению и от излучения веществу передается определенное количество — «порция» — энергии. Для достижения требуемого равновесия и согласия с экспериментальными фактами Планку понадобилось ввести простое математическое соотношение — предположить, что между количеством энергии, передаваемом при каждом элементарном акте взаимодействия, и частотой (величиной, обратной периоду) процесса, приводящего к передаче энергии, существует прямая пропорциональность.

Иначе говоря, если коэффициент пропорциональности обозначить через h, то, согласно принятой Планком гипотезе, минимальная порция, или квант, передаваемой энергии определяется выражением

где v — частота. Постоянная Л имеет числовое значение 6,547 х 10^27 эрг.с и обычно называется постоянной Планка, или квантовой постоянной. Малое числовое значение постоянной Планка объясняет, почему квантовые явления обычно не наблюдаются в повседневной жизни.

Дальнейшее развитие идей Планка связано с именем Эйнштейна, который через несколько лет пришел к выводу, что излучение не только испускается определенными дискретными порциями, но и всегда существует в виде таких дискретных «порций энергии», которую Эйнштейн назвал квантами света.

Поскольку кванты света движутся, они помимо энергии hv должны обладать и определенным механическим импульсом, который, согласно релятивистской механике, должен быть равен их энергии, деленной на скорость света с. Вспоминая, что частота света связана с его длиной волны лямбда соотношением v = с/(лямбда), механический импульс кванта света можно записать в виде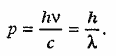

(2)

Поскольку механическое действие, производимое соударением движущегося объекта, определяется его импульсом, мы заключаем, что действие квантов света возрастает при убывании длины волны.

Одно из лучших экспериментальных подтверждений правильности представления о квантах света, а также о приписываемых им энергии и импульсе было получено в работе американского физика Артура Комптона. Исследуя столкновение квантов света и электронов, Комптон показал, что электроны, приведенные в движение под действием луча света, ведут себя точно так же, как если бы столкнулись с частицей, обладающей энергией и импульсом, задаваемыми формулами (1) и (2). Как показали эксперименты Комптона, сами кванты претерпевают после столкновения с электронами некоторые изменения (изменяется их частота) в полном согласии с предсказанием теории.

В настоящее время мы вправе утверждать, что в части, касающейся взаимодействия с веществом, квантовые свойства излучения надлежит считать твердо установленным экспериментальным фактом.

Дальнейшее развитие квантовых идей связано с именем знаменитого датского физика Нильса Бора, который в 1913 г. впервые высказал идею о том, что внутреннее движение любой механической системы может обладать только дискретным набором допустимых значений энергии и движение может изменять свое состояние только конечными шагами, причем при каждом из таких переходов излучается лишь определенное количество энергии. Математические правила, определяющие возможные состояния механических систем, более сложные, чем в случае излучения, и мы не будем приводить их здесь. Упомянем лишь о том, что, как и в случае квантов света, импульс определяется длиной волны света, поэтому в механической системе импульс любой движущейся частицы связан с геометрическими размерами той области пространства, в которой она заключена, и составляет величину порядка

, (3)

где l — линейные размеры области, в которой происходит движение. Из-за чрезвычайно малого значения квантовой постоянной квантовые явления становятся существенными только для движений, происходящих в очень малых областях пространства, например внутри атомов и молекул, и играют важную роль в наших знаниях о внутреннем строении вещества.

Одно из наиболее прямых доказательств существования последовательности дискретных состояний этих крохотных механических систем было получено в экспериментах Джеймса Франка и Густава Герца. Бомбардируя атомы электронами различной энергии, эти физики заметили, что определенные изменения в состоянии атома происходят, только когда энергия налетающих электронов достигала определенных дискретных значений. Если энергия электронов была ниже определенного предела, то соударения вообще никак не сказывались на состоянии атома, так как энергия, переносимая каждым электроном, была недостаточна для того, чтобы поднять атом с первого квантового состояния во второе.

Резюмируя, можно сказать, что к концу описанной мной первой, предварительной стадии развития квантовой теории была достигнута не модификация фундаментальных понятий и принципов классической физики, а более или менее искусственное ограничение весьма загадочными квантовыми условиями, выбирающими из непрерывного множества классически возможных движений дискретное подмножество «разрешенных», или «допустимых», движений. Однако если мы глубже вникнем в связь между законами классической механики и квантовыми условиями, налагаемыми нашим обобщенным опытом, то обнаружим, что теория, получаемая при объединении классической механики с квантовыми условиями, страдает логической непоследовательностью и что эмпирические квантовые ограничения делают бессмысленными те фундаментальные понятия, на которых основана классическая механика. Действительно, основное представление классической механики относительно движения заключается в том, что любая движущаяся частица занимает в любой данный момент времени определенное положение в пространстве и обладает определенной скоростью, характеризующей временные изменения в положении частицы на траектории.

Такие фундаментальные понятия, как положение, скорость и траектория, на которые опирается все величественное здание классической механики, построены (как и все другие наши понятия) на наблюдении явлений в окружающем мире и, подобно классическим понятиям пространства и времени, должны быть существенно модифицированы, когда наш опыт вторгается в новые, не исследованные ранее, области.

Если я спрошу кого-нибудь, почему он (или она) верит, что любая движущаяся частица занимает в любой данный момент определенное положение, описывает во время движения определенную линию, то в ответ мой собеседник скорее всего скажет: «Потому, что я вижу все это именно так, когда наблюдаю за движением». Проанализируем такой метод образования классического понятия траектории и попытаемся выяснить, действительно ли он приводит к определенному результату. Для этого представим себе мысленно физика, оснащенного всевозможной чувствительнейшей аппаратурой и пытающегося проследить движение маленького материального тела, брошенного со стены лаборатории. Наш физик решает производить наблюдения, глядя, как движется тело, и использует для этого небольшой, но очень точный теодолит. Разумеется, чтобы увидеть движущееся тело, физику необходимо освещать его. Зная, что свет оказывает давление на освещаемое тело и поэтому возмущает движение тела, физик решает освещать тело короткими вспышками только в те моменты, когда он производит наблюдения. В первом эксперименте физик намеревается наблюдать только десять положений тела на траектории и выбирает источник, дающий вспышки света, настолько слабый, что интегральный эффект светового давления в течение десяти последовательных сеансов наблюдения лежит в пределах требуемой точности эксперимента. Таким образом, освещая падающее тело десятью вспышками, наш физик получает в пределах требуемой точности десять точек на траектории.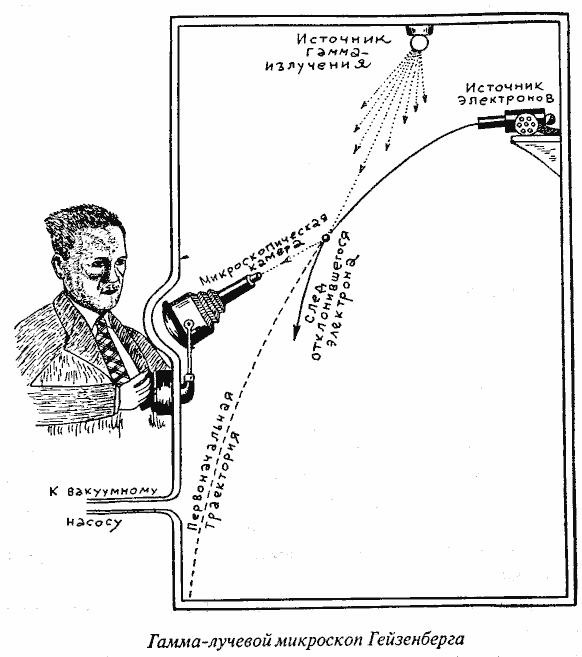

Затем он хочет повторить эксперимент и получить сто точек. Физик знает, что сто последовательных вспышек слишком сильно возмутят движение и, готовясь ко второй серии наблюдений, выбирает фонарь, дающий в десять раз менее интенсивное освещение. Для третьей серии наблюдений, готовясь получить тысячу точек на траектории, физик выбирает фонарь, дающий в сто раз менее интенсивное освещение, чем источник света, который был использован в первой серии наблюдений.

Продолжая в том же духе и постоянно уменьшая интенсивность освещения, даваемого источником, физик может получить на траектории столько точек, сколько сочтет нужным, не увеличивая экспериментальную ошибку выше установленного с самого начала предела. Описанная мной сильно идеализированная, но принципиально вполне осуществимая процедура представляет собой строго логический способ, позволяющий построить движение по траектории, «глядя на движущееся тело», и, как вы видите, в рамках классической физики такое построение вполне возможно.

Попытаемся теперь выяснить, что произойдет, если мы введем квантовые ограничения и учтем, что действие любого излучения может передаваться только в форме квантов света. Мы видели, что наблюдатель постоянно уменьшал количество света, падающего на движущееся тело, и теперь нам следует ожидать, что, дойдя до одного кванта, наш физик не сможет продолжать в том же духе и дальше. От движущегося тела будет отражаться либо весь квант света целиком, либо ничего, и в последнем случае наблюдение становится невозможным. Мы знаем, что в результате столкновения с квантом света длина волны света уменьшается и наш наблюдатель, также зная об этом, заведомо попытается использовать для своих наблюдений свет со все увеличивающейся длиной волны, чтобы компенсировать число наблюдений. Но тут его подстерегает другая трудность.

Хорошо известно, что при использовании света определенной длины волны невозможно различить детали, размеры которых меньше длины волны: нельзя нарисовать персидскую миниатюру малярной кистью! Но используя все более длинные волны, наш физик испортит оценку положения каждой точки и вскоре достигнет той стадии, когда каждая оценка будет содержать погрешность, или неопределенность, величина которой сравнима с размерами всей его лаборатории и превышает их. Тем самым наш наблюдатель будет вынужден в конце концов пойти на компромисс между большим числом наблюдаемых точек и неопределенностью в оценке положения каждой точки и не сможет получить точную траекторию — в виде линии в математическом смысле в отличие от своих классических коллег. В лучшем случае квантовый наблюдатель получит весьма широкую размазанную полосу, и если он попытается построить понятие траектории, опираясь на свой опыт, то оно будет сильно отличаться от классического понятия траектории.

Предложенный выше метод построения траектории был оптическим, а теперь мы можем испробовать другую возможность и воспользоваться механическим методом. Для этого наш экспериментатор может построить какой-нибудь миниатюрный механический прибор, например, колокольчики на пружинах, который будет регистрировать прохождение материальных тел, если тело проходит достаточно близко. Большое число таких «колокольчиков» он развешивает в той области пространства, где ожидается прохождение движущегося тела, и «звон колокольчиков» будет указывать траекторию, описываемую телом. В классической физике «колокольчики» можно сделать сколь угодно малыми и чувствительными. В предельном случае бесконечно большого числа бесконечно маленьких колокольчиков понятие траектории и в этом случае может быть построено с любой требуемой точностью. Однако, как и в предыдущем случае, квантовые ограничения на механические системы портят все дело. Если «колокольчики» слишком малы, то величина импульса, которую они смогут забрать у движущегося тела, согласно формуле (3), будет слишком большой и движение окажется сильно возмущенным даже после того, как тело заденет один-единственный колокольчик. Если же колокольчики велики, то неопределенность в положении каждого будет очень большой. В этом случае построенная в результате наблюдения окончательная траектория, как и в предыдущем случае, окажется широкой полосой!

Боюсь, что все эти рассуждения об экспериментаторе, желающем наблюдать траекторию, покажутся вам слишком специальными и вы будете склонны думать, что если используемые средства не позволяют нашему наблюдателю оценить траекторию, то желаемый результат удастся получить с помощью какого-нибудь другого более сложного устройства. Однако я должен вам напомнить, что мы рассматривали не конкретный эксперимент, выполненный в какой-то физической лаборатории, а некую идеализацию самого главного вопроса физического измерения. Поскольку любое существующее в нашем мире действие можно отнести либо к числу действий поля излучения, либо к чисто механическим, любая сколь угодно сложная схема измерения непременно сводится к элементам, описываемых теми двумя методами, о которых я уже упоминал раньше — оптическом и механическом, и в конечном итоге приводит к тому же результату. А поскольку идеальный «измерительный прибор» может вместить весь физический мир, мы в конце концов приходим к выводу, что в мире, где действуют квантовые законы, нет ни точного положения, ни траектории, имеющей строго определенную форму линии.

Но вернемся теперь снова к нашему экспериментатору и попытаемся облечь в математическую форму ограничения, вытекающие из квантовых условий. Мы уже видели, что в обоих методах — оптическом и механическом — всегда существует конфликт между оценкой положения и возмущением скорости движущегося объекта. В оптическом методе столкновение с квантом света (в силу закона сохранения импульса, действующего в классической механике) порождает неопределенность в импульсе частицы, сравнимую с импульсом самого кванта света. Таким образом, используя формулу (2), запишем для неопределенности импульса частицы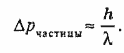

(4)

Памятуя о том, что неопределенность положения частицы определяется длиной волны ((дельта)q = лямбда), получаем

(5)

В механическом методе импульс становится неопределенным на величину, передаваемую «колокольчиком». Используя нашу формулу (3) и помня о том, что в этом случае неопределенность положения определяется размерами колокольчика ((дельта)q = l), мы приходим к той же окончательной формуле, что и в предыдущем случае. Соотношение (5), впервые выведенное немецким физиком Вернером Гейзенбергом, описывает фундаментальную неопределенность, следующую из квантовой теории: чем точнее определено положение, тем неопределеннее скорость, и наоборот.

Так как импульс есть произведение массы движущейся частицы и ее скорости, мы можем записать, что

(6)

Для тел, с которыми нам обычно приходится иметь дело, неопределенность (6) до смешного мала. Так, в случае легкой пылинки с массой 0,0000001 г и положение, и скорость могут быть измерены с точностью 0,00000001 %! Однако в случае электрона (с массой 10^-27 г) произведение (дельта)u * (дельта)q достигает величины порядка 100. Внутри атома скорость электрона необходимо определять по крайней мере в пределах +-10^8 см/с, в противном случае электрон окажется вне атома. Это дает для положения электрона неопределенность 10^8 см, т. е. неопределенность, совпадающую с полными размерами атома. Таким образом, «орбита» электрона в атоме расплывается до такой степени, что «толщина» траектории становится равной ее «радиусу» — электрон оказывается одновременно всюду вокруг ядра.

На протяжении последних двадцати минут я пытался нарисовать вам картину разрушительных последствий нашей критики классических представлений о движении. Изящные и четко определенные классические понятия оказываются вдребезги разбитыми и уступают место тому, что я назвал бы бесформенной размазней. Естественно, вы можете спросить меня, как физики собираются описывать какие-нибудь явления, если квантовый мир буквально захлестывают волны океана неопределенности. Ответ состоит в том, что до сих пор нам удалось лишь разрушить классические понятия, но мы еще не пришли к точной формулировке новых понятий.

Займемся этим теперь. Ясно, что мы не можем, вообще говоря, определить положение материальной частицы с помощью материальной точки, а траекторию ее движения — с помощью математической линии, поскольку в квантовом мире все объекты расплываются. Нам необходимо обратиться к другим методам описания, дающим, так сказать, «плотность размазни» в различных точках пространства. Математически это означает, что мы используем непрерывные функции (такие как, например, в гидромеханике), а физически требует, чтобы при описании квантового мира мы употребляли такие обороты речи, как «этот объект в основном находится здесь, частично там и даже вон там» или «эта монета на 75% находится в моем кармане и на 25% — в вашем». Я понимаю, что такие утверждения кажутся вам дикими, но в нашей повседневной жизни из-за малости квантовой постоянной в них нет надобности. Но если вы вознамеритесь изучать атомную физику, то я настоятельно рекомендую вам предварительно привыкнуть к такого рода выражениям.

Считаю своим долгом предостеречь вас от ошибочного представления о том, будто функция, описывающая «плотность пребывания» объекта в различных точках пространства, обладает физической реальностью в нашем обычном трехмерном пространстве. Действительно, если мы описываем поведение, например, двух частиц, то нам необходимо ответить на вопрос, находится ли одна частица в одном месте и, одновременно, вторая частица в другом месте. Для этого нам необходима функция шести переменных (координат двух частиц), которую невозможно «локализовать» в трехмерном пространстве. Для описания более сложных систем нам понадобились бы функции еще большего числа переменных. В этом смысле «квантово-механическая функция» аналогична «потенциальной функции», или «потенциалу», системы частиц в классической механике или «энтропии» системы в статистической механике: она только описывает движение и позволяет нам предсказывать результат любого конкретного движения при данных условиях. Физическая реальность остается за частицами, движение которых мы описываем.

Функция, которая описывает, какая «доля» частицы или системы частиц присутствует в различных местах пространства, требует специального математического обозначения. Следуя Эрвину Шредингеру, который первым написал уравнение, определяющее поведение такой функции, ее стали обозначать

.

Я не стану сейчас вдаваться в детали математического вывода фундаментального уравнения Шредингера. Хочу лишь обратить ваше внимание на требования, которые привели к его выводу. Самое важное из этих требований весьма необычно: уравнение должно быть записано в таком виде, чтобы функция, описывающая движение материальных частиц, обладала всеми свойствами волны.

На необходимость наделить движение материальных частиц волновыми свойствами впервые указал французский физик Луи де Бройль на основе своих теоретических исследований строения атома. В последующие годы волновые свойства движения материальных частиц были надежно подтверждены многочисленными экспериментами, продемонстрировавшими такие явления, как дифракция пучка электронов при прохождении через малое отверстие и интерференционные явления, происходящие даже с такими сравнительно большими и сложными частицами, как молекулы.

Экспериментально установленные волновые свойства материальных частиц были совершенно непонятны с точки зрения классических представлений о движении, и де Бройль был вынужден принять весьма необычную (чтобы не сказать неестественную) точку зрения: по де Бройлю, все частицы «сопровождаются» определенными волнами, которые, так сказать, «направляют» их движения.

Но как только мы отказываемся от классических понятий и переходим к описанию движения с помощью непрерывных функций, требование о волновом характере становится гораздо более понятным. Оно просто утверждает, что распространение нашей

—функции аналогично (например) нераспространению тепла сквозь стенку, нагреваемую с одной стороны, а распространению сквозь ту же самую стенку механической деформации (звука). Математически это означает, что мы ищем уравнение определенного (а не ограниченного) вида. Это фундаментальное условие вместе с дополнительным требованием, чтобы наши уравнения, если их применять к частицам большой массы, переходили в уравнения классической механики, поскольку квантовые эффекты для таких частиц становятся пренебрежимо слабыми, практически сводят проблему вывода уравнения к чисто математическому упражнению.

Если вас интересует, как выглядит окончательный ответ — фундаментальное уравнение Шредингера, то я могу выписать его. Вот оно: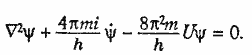

(7)

Здесь U означает потенциал сил, действующих на нашу частицу (с массой m), и порождает определенное решение задачи о движении частицы при любом заданном распределении силы. «Волновое уравнение Шредингера» (так принято называть выведенное Шредингером фундаментальное уравнение) позволило физикам в последующие сорок лет его существования построить наиболее полную и логически непротиворечивую картину явлений, происходящих в мире атомов.

Некоторые из вас, должно быть, удивляются, почему я до сих пор ни разу не употребил слово «матрица», которое часто приходится слышать в связи с квантовой теорией. Должен признаться, что лично я питаю сильную неприязнь к матрицам и предпочитаю обходиться без них. Но чтобы не оставлять вас в абсолютном неведении относительно этого математического аппарата квантовой теории, я скажу о матрицах несколько слов. Как вы уже знаете, движение частицы или сложной механической системы всегда можно описать с помощью некоторых непрерывных волновых функций. Эти функции часто бывают очень сложными и представимы в виде набора из некоторого числа более простых колебаний (так называемых «собственных функций») подобно тому, как сложный звук можно составить из некоторого числа простых гармонических тонов. Сложное движение можно описывать, задавая амплитуды его различных компонент. Поскольку число компонент (обертонов) бесконечно, мы выписываем бесконечную таблицу амплитуд вида

(8)

Над такими таблицами можно производить математические операции по сравнительно простым правилам. Каждая такая таблица и называется «матрицей», и некоторые физики вместо того, чтобы иметь дело непосредственно с волновыми функциями, предпочитают оперировать с матрицами. Такая «матричная механика», как ее иногда называют, представляет собой не более чем математическую модификацию обычной «волновой механики». В наших лекциях, посвященных главным образом принципиальным вопросам, было бы излишне входить в эти проблемы более подробно.

Очень жаль, что недостаток времени не позволяет мне рассказать вам о дальнейшем прогрессе квантовой теории в связи с теорией относительности. Эта глава в развитии квантовой теории, связанная главным образом с работами британского физика Поля Адриена Мориса Дирака, приводит ко многим интереснейшим проблемам и стала основой некоторых чрезвычайно важных экспериментальных открытий. Возможно, когда-нибудь в другой раз я еще вернусь к этим проблемам, а пока я должен остановиться. Надеюсь, что прочитанная мной серия лекций позволила вам составить более ясное представление о современной концепции физического мира и пробудила в вас интерес к дальнейшим научным занятиям.

Глава 8

Квантовые джунгли

На следующее утро мистер Томпкинс еще нежился в постели, как вдруг почувствовал, что в комнате есть еще кто-то. Оглядевшись вокруг, он обнаружил своего старого друга профессора. Тот сидел в кресле, уткнувшись в расстеленную на коленях карту и внимательно изучал ее.

— Так вы со мной? — спросил профессор, поднимая голову.

— А куда это вы собрались? — поинтересовался мистер Томпкинс, размышляя над тем, каким образом профессор оказался у него в комнате.

— Разумеется, для того чтобы полюбоваться на слонов и других обитателей джунглей. Владелец бильярдной, где мы с вами недавно побывали, сообщил мне по секрету, откуда он берет слоновую кость для своих бильярдных шаров. Видите район, который я обвел на карте красным карандашом? Имеются основания полагать, что внутри него все подчинено квантовым законам с очень большой квантовой постоянной. Местные жители считают, что в тех краях поселились дьяволы, и я боюсь, что нам будет очень трудно найти себе проводника. Но если вы хотите отправиться со мной в путь, вам надо поторапливаться. Судно отходит через час, а нам еще нужно по дороге в порт заехать за сэром Ричардом.

— А кто это сэр Ричард? — спросил мистер Томпкинс.

— Как, вы никогда не слыхали о нем? — профессор был явно изумлен. — Сэр Ричард известный охотник на тигров. Он решил отправиться вместе с нами, когда я обещал ему интересную охоту.

На причал участники экспедиции прибыли как раз вовремя для того, чтобы наблюдать за погрузкой на борт судна груза из нескольких длинных ящиков с ружьями сэра Ричарда и специальными пулями, изготовленными из свинца, который профессор получил от управляющего свинцовыми рудниками, расположенными неподалеку от квантовых джунглей. Мистер Томпкинс еще раскладывал вещи в каюте, когда мерная вибрация корпуса судна возвестила ему, что пароход отошел от причала. В морском путешествии всегда есть нечто неотразимо привлекательное, и мистер Томпкинс не заметил, как их судно пришвартовалось в очаровательном восточном городе — ближайшем к таинственным квантовым джунглям населенном пункте.

— Для путешествия по суше нам нужно приобрести слона, — объявил профессор. — Не думаю, что кто-нибудь из местных жителей рискнет отправиться с нами, поэтому управлять слоном придется нам самим. Полагаю, что вы, мистер Томпкинс, прекрасно справитесь с этой задачей. Я буду слишком поглощен научными наблюдениями, а сэр Ричард должен будет управляться со всем охотничьим снаряжением.

На душе у мистера Томпкинса было очень неспокойно, когда придя на слоновый рынок, расположенный на окраине города, он увидел огромных животных, одним из которых ему предстояло управлять. Сэр Ричард, великолепно разбиравшийся в слонах, выбрал красивого крупного слона и спросил у владельца, сколько тот хочет за животное.

— Храп ханвек о хобот хам. Хагори хо, о Хохохохи, — ответил туземец, обнажив в улыбке ослепительно белые зубы.

— Он просит за него уйму денег, — перевел сэр Ричард, — но говорит, что его слон из квантовых джунглей и поэтому стоит дороже. Так как, купим этого слона?

— Непременно, — сказал профессор. — На пароходе мне довелось слышать, что слоны иногда заходят из квантовых территорий и туземцы их ловят. Такие слоны гораздо лучше своих сородичей из других областей, и сейчас нам просто повезло, что мы можем купить животное, которое чувствует себя в квантовых джунглях, как дома.

Мистер Томпкинс осмотрел слона со всех сторон. Что и говорить, это было очень красивое, огромное животное, однако, мистер Томтгкинс не заметил в повадках слона каких-либо отличий по сравнению с теми слонами, которых ему доводилось видеть в зоопарке.

— Вы говорите, что это квантовый слон, а для меня он вполне обычный слон и ведет себя не так занятно, как бильярдные шары, сделанные из бивней некоторых из его сородичей. Например, почему он не расплывается по всем направлениям? — обратился мистер Томпкинс к профессору.

— Вы медленно схватываете суть дела, — заметил профессор. — Слон не расплывается из-за своей очень большой массы. Некоторое время назад я уже объяснял вам, что неопределенность в положении и скорости зависит от массы. Чем больше масса, тем меньше неопределенность. Именно поэтому квантовые законы не наблюдаются в обычном мире даже для таких легких тел, как пылинки, но становятся вполне заметными для электронов, которые в миллиарды миллиардов раз легче пылинок. Но в квантовых джунглях квантовая постоянная гораздо больше, но все же недостаточно велика, чтобы порождать поразительные эффекты в поведении столь тяжелого животного, как слон. Неопределенность в положении квантового слона можно заметить, только если пристально вглядеться в его очертания. Возможно, вы заметили, что поверхность слоновой кожи не вполне определенна и кажется несколько неотчетливо видимой. Со временем эта неопределенность увеличивается очень медленно. Мне кажется, что именно с этим обстоятельством связана местная легенда, будто у старых слонов из квантовых джунглей длинная шерсть. Я полагаю, что на не столь крупных животных, обитающих в квантовых джунглях, замечательные квантовые эффекты будут более заметными.

— Хорошо, что в эту экспедицию мы отправляемся не верхом на лошадях, — подумал мистер Томпкинс. — Ведь если бы мы вздумали отправиться в квантовые джунгли на лошадях, я никогда не мог бы сказать с уверенностью, где моя лошадь — у меня под седлом или в следующей долине.

После того, как профессор и сэр Ричард со своими ружьями взгромоздились в корзину, укрепленную на спине слона, а мистер Томпкинс в новой для себя должности погонщика занял свое место на шее слона, крепко сжимая в руке некое подобие багра — стрекало, которым настоящие погонщики управляют своим подопечным; экспедиция тронулась в путь к таинственным джунглям.

От жителей города наши путешественники узнали, что добраться до джунглей можно примерно за час, и мистер Томпкинс, изо всех сил пытаясь сохранить равновесие между ушами слона, вознамерился с пользой использовать время, чтобы порасспросить у профессора о квантовых явлениях.

— Скажите, пожалуйста, — начал мистер Томпкинс, повернувшись к профессору, — почему тела с малой массой ведут себя столь необычно и как можно истолковать с точки зрения обычного здравого смысла ту квантовую постоянную, о которой вы все время говорите?

— О, — воскликнул профессор, — понять это не так уж трудно. Необычное поведение всех объектов в квантовом мире объясняется просто тем, что вы на них смотрите.

— Они настолько стыдливы? — улыбнулся мистер Томпкинс.

— «Стыдливы» — не то слово, — сурово ответствовал профессор. — Суть дела в том, что всякий раз, производя любое наблюдение, вы непременно возмущаете движение наблюдаемого объекта. Раз вы узнаете что-то о движении какого-то тела, то это означает, что движущееся тело произвело какое-то действие на ваши органы чувств или на прибор, который вы использовали при наблюдении. В силу равенства действия и противодействия мы приходим к заключению, что ваш измерительный прибор также воздействовал на тело и, так сказать, «испортил» его движение, введя неопределенность в положение и скорость тела.

— Если бы я тронул бильярдный шар пальцем, то, конечно, внес бы возмущение в его движение, — недоуменно произнес мистер Томпкинс. — Но я только посмотрел на него. Неужели этого достаточно, чтобы возмутить движение бильярдного шара?

— Разумеется, вполне достаточно! Вы же не можете видеть бильярдный шар в кромешной тьме. А если вы вынесете шар на свет, то лучи света, отражающиеся от шара и делающие его видимым, воздействуют на него (мы говорим о таком воздействии как о «давлении света») и «портят» движение шара.

— А что если я воспользуюсь очень тонкими и очень чувствительными приборами? Разве не смогу я сделать воздействие моих приборов на движущееся тело пренебрежимо малым?

— Именно так мы считали, когда у нас была только классическая физика, до открытия кванта действия. Но в начале XX столетия стало ясно, что действие на любой объект не может быть низведено до уровня ниже определенного предела, называемого квантовой постоянной и обозначаемого символом h. В обычном мире квант действия очень мал; в обычных единицах он выражается числом с двадцатью семью нулями после десятичной запятой. Квант действия становится существенным только для таких легких частиц, как электроны: из-за их очень малой массы на движении таких частиц заметно сказываются и очень слабые воздействия. В квантовых джунглях, к которым мы сейчас приближаемся, квант действия очень велик. Это грубый мир, в котором деликатные действия невозможны. Если кто-нибудь в таком мире попытается погладить котенка, то тот либо вообще не ощутит никакой ласки, либо его шея будет сломана при первом же прикосновении.

— Все это хорошо, — задумчиво проговорил мистер Томпкинс, — но ведут ли тела себя прилично, т.е. так, как обычно принято думать, когда на них никто не смотрит?

— Когда на тела никто не смотрит, — ответил профессор, — никто не может сказать, как они себя ведут. Ваш вопрос не имеет физического смысла.

— Должен признаться, — заметил мистер Томпкинс, — что все это изрядно смахивает на философию, а не на физику.

— Можете называть это философией, — профессор был явно задет, — но, в действительности, речь идет о фундаментальном принципе современной физики — никогда не говорить о том, чего не знаешь. Вся современная физическая теория основана на этом принципе, между тем, как философы обычно упускают его из виду. Например, знаменитый немецкий философ Кант провел немало времени, размышляя о свойствах тел, не таких, какими они «видятся нам», а таких, какие они есть « в себе». Для современного физика имеют смысл только так называемые «наблюдаемые» (т. е. принципиально наблюдаемые свойства), и вся современная физика основана на отношениях между наблюдаемыми свойствами. То, что невозможно наблюдать, хорошо только для праздных размышлений: вы можете придумывать что угодно, и плоды ваших размышлений нельзя ни проверить (т. е. убедиться в их существовании), ни воспользоваться ими. Должен сказать, что…

В этот момент ужасный рев потряс воздух. Слон остановился как вкопанный так внезапно, что мистер Томпкинс чуть не свалился. Огромная стая несколько размазанных тигров напала на слона, выпрыгнув из засады со всех сторон. Сэр Ричард схватил свое ружье и, прицелившись ближайшему тигру между глаз, спустил курок. В следующий момент мистер Томпкинс отчетливо услышал, как сэр Ричард пробурчал себе под нос некое крепкое выражение, принятое среди охотников. Еще бы! Выстрел был метким, но пуля прошла сквозь голову тигра, не причинив тому ни малейшего вреда!

— Стреляй еще! — закричал профессор. — Не цельтесь! Постарайтесь создать вокруг себя как можно большую плотность огня! На нас напал только один тигр, но он распределен вокруг нашего слона, и наш единственный шанс на спасение состоит в том, чтобы поднять гамильтониан.

Профессор схватил другое ружье, и грохот выстрелов смешался с ревом квантового тигра. Мистеру Томпкинсу показалось, что прошла целая вечность прежде, чем весь этот ужасный шум затих. Одна из пуль «попала в цель», и к величайшему удивлению мистера Томтпсинса тигр, внезапно превратившийся в одного-единственного титра, был с силой отброшен назад, и его мертвое тело, описав дугу в воздухе, приземлилось где-то за маячившей в отдалении пальмовой рощей.

— А кто этот Гамильтониан? — спросил мистер Томпкинс, когда все немного успокоилось. — Знаменитый охотник, которого вы хотели поднять из могилы, чтобы он спас нас?

— О, прошу великодушно простить меня! — сказал профессор. — В пылу битвы я перешел на научную терминологию, которую вы не понимаете! Гамильтонианом принято называть математическое выражение, описывающее квантовое взаимодействие между двумя телами. Оно получило свое название в честь ирландского математика Гамильтона, который первым начал использовать эту математическую форму. Я хотел сказать, что, выпуская как можно больше пуль, мы можем увеличить вероятность взаимодействия между пулей и телом тигра. В квантовом мире вы не можете точно прицелиться и быть уверены, что попадете в цель. Из-за расплывания пули и цели всегда существует лишь отличная от нуля вероятность попадания в цель, но эта вероятность никогда не равна единице. В нашем случае мы выпустили по крайней мере тридцать пуль, прежде чем действительно попали в тигра, и тогда действие пули оказалось столь сильным, что тигра отбросило далеко назад. То же самое, только в меньших масштабах, происходит и в нашем привычном мире. Как я уже упоминал, в обычном мире, чтобы заметить нечто подобное, необходимо исследовать поведение таких малых частиц, как электроны. Возможно, вам приходилось слышать о том, что каждый атом состоит из сравнительно тяжелого ядра и нескольких электронов, обращающихся вокруг него. Сначала принято было думать, что движение электронов вокруг ядра совершенно аналогично движению планет вокруг Солнца, но более глубокий анализ показал, что обычные понятия, относящиеся к движению, слишком грубы для такой миниатюрной системы, как атом. Действия, играющие важную роль внутри атома, по порядку величины сравнимы с элементарным квантом действия, и поэтому вся картина в целом сильно расплывается. Движение электрона вокруг атомного ядра во многих отношениях аналогично движению нашего квантового тигра, который в одиночку окружил нашего слона со всех сторон.

— А не стрелял ли кто-нибудь в электрон так, как мы стреляли в тигра? — спросил мистер Томпкинс.

— Стреляли и не раз! Ядро само испускает иногда кванты света высокой энергии, или, что то же, элементарные порции действия света. В электрон можно выстрелить и снаружи атома, освещая атом пучком света. При этом все произойдет так же, как с тигром: многие кванты света пройдут через то место, где находится электрон, не оказав на того ни малейшего действия, пока, наконец, один из квантов света не столкнется с электроном и не выбьет его из атома. На квантовую систему нельзя воздействовать чуть-чуть; она либо вообще не испытывает никакого воздействия, либо претерпевает в результате воздействия сильные изменения.

— Как тот несчастный котенок, которого нельзя приласкать в квантовом мире, не рискуя нанести ему смертельное увечье, — заключил мистер Томпкинс.

— Взгляните вон туда! Газели! Множество газелей! — воскликнул сэр Ричард, поднимая свое ружье. И, действительно, огромное стадо газелей показалось из бамбуковой рощи.

— Дрессированные газели, — подумал мистер Томпкинс. — Бегут строем, как солдаты на параде. Хотел бы я знать, уж не квантовый ли это эффект?

Группа газелей быстро приближалась к слону, на котором восседали наши путешественники, и сэр Ричард изготовился было стрелять, как вдруг профессор остановил его.

— Не тратьте понапрасну ваши охотничьи припасы, — сказал профессор. — Очень мало шансов попасть в животное, когда оно движется в дифракционной картине.

— Почему вы говорите не о животных, а об одном животном, удивленно спросил сэр Ричард. — Здесь по крайней мере несколько дюжин газелей!

— Вы глубоко заблуждаетесь, — возразил профессор. — Здесь перед нами только одна маленькая газель, которая, испугавшись чего-то, мчится сквозь бамбуковую рощу. Дело в том, что «расплывание» всех тел обладает одним свойством, аналогичным свойству обычного света: проходя через правильную систему отверстий («решетку»), например между стволами бамбука в роще, оно порождает явление дифракции, о котором вам, вероятно, приходилось слышать в школе. Поэтому мы говорим о волновом характере материи.

Но ни сэр Ричард, ни мистер Томпкинс не могли вспомнить, что же, собственно говоря, означает загадочное слово «дифракция» и разговор оборвался.

Углубившись в дебри квантовых джунглей, наши путешественники повстречали множество других интереснейших явлений, например, познакомились с квантовыми москитами. Определить местонахождение этих насекомых в пространстве было почти невозможно из-за их малой массы. Очень забавны были квантовые обезьяны.

Но вот впереди показалось что-то напоминающее туземное селение.

— Я не знал, что в этих местах живут люди, — заметил профессор. — Судя по шуму, у них какое-то празднество. Вы только прислушайтесь к неумолкаемому звону колокольчиков.

Различить отдельные фигуры туземцев, исполнявших вокруг большого костра какой-то дикий танец, было очень трудно. Из толпы, куда ни глянь, всюду поднимались темно-коричневые руки с колокольчиками всех размеров. Когда путешественники приблизились, все, включая хижины и окружавшие селение большие деревья, начало расплываться. Звон колокольчиков стал невыносимым для мистера Томпкинса. Он протянул руку, схватил что-то и отбросил в сторону. Будильник разбил стакан с водой, стоявший на ночном столике, и поток холодной воды привел мистера Томпкинса в чувство. Он вскочил и принялся быстро одеваться. Через полчаса ему нужно было быть в банке.

Глава 9

Демон Максвелла

Участвуя на протяжении многих месяцев в невероятных приключениях, в ходе которых профессор не упускал удобного случая посвятить мистера Томпкинса в тайны физики, мистер Томпкинс все более проникался очарованием мисс Мод. Наконец, настал день, когда мистер Томпкинс, заикаясь и краснея от смущения, робко предложил мисс Мод руку и сердце. Предложение было с радостью принято, и вскоре мистер Томпкинс и мисс Мод стали мужем и женой. В новой для себя роли тестя профессор считал своей непременной обязанностью всячески способствовать расширению познаний своего зятя в физике и знакомить его с новейшими достижениями этой увлекательной науки.

Однажды мистер и миссис Томпкинс, с удобством устроившись в креслах, предавались воскресному отдыху в своей уютной квартирке. Миссис Томпкинс с головой погрузилась в изучение журнала мод «Vogue», а ее супруг с увлечением читал статью в журнале «Esquire» [7].

— Подумать только! — внезапно воскликнул мистер Томпкинс. — Оказывается, в азартных играх существуют беспроигрышные стратегии!

— Сирил, неужели ты всерьез думаешь, что такое возможно? — спросила миссис Томпкинс, задумчиво поднимая глаза от приковавших ее внимание страниц модного журнала. — Помнится, папа не раз говорил нам о том, что в азартных играх беспроигрышных стратегий нет и быть и не может.

— Взгляни сама, Мод, — предложил мистер Томпкинс, показывая своей супруге статью, которую он изучал с таким интересом в течение последнего получаса. — Я ничего не знаю о других выигрышных стратегиях, но та, о которой говорится в этой статье, основана на очень простых математических расчетах без всяких обманов и подвохов, и я просто не знаю, где здесь в рассуждения может вкрасться какая-нибудь ошибка. Чтобы выиграть, нужно лишь выписать на листке бумаги числа

и неукоснительно придерживаться простых правил, приводимых в той же статье.

— Попробовать, конечно, можно, — согласилась Мод, начиная проявлять признаки интереса. — А что это за правила?

— Для большей наглядности я буду следовать примеру, приводимому в статье, ведь, как ты знаешь, учиться лучше всего на примерах. В качестве иллюстрации беспроигрышной стратегии автор статьи выбрал игру в рулетку. Как тебе, должно быть, известно, игроки в рулетку делают ставку на красное или на черное, т. е., по существу, как бы заключают между собой пари относительно исхода бросания монеты — выпадет ли монета вверх орлом или решкой. Я начинаю с того, что выписываю на листке бумаги числа

Первое правило состоит в том, что, делая ставку, я должен выложить на стол число фишек, равное сумме первого и последнего и выписанных чисел (а в том случае, если на листке бумаги останется одно-единственное число, ставка должна быть равна одному числу). Следуя этому правилу, я должен выложить на стол четыре (одну плюс три) фишки. Предположим, что я ставлю на красное. По правилам игры, в случае выигрыша мне нужно зачеркнуть первое и последнее из выписанных чисел. В нашем примере это числа 1 и 3, поэтому, делая следующую ставку, я должен выложить на стол две фишки (поскольку после вычеркивания чисел 1 и 3 на листке бумаги останется одно-единственное число 2). В случае проигрыша число фишек в предыдущей (проигранной) ставке необходимо приписать справа к уже выписанным числам, а при определении величины следующей ставки придерживаться прежнего правила, т. е. выставить число фишек, равное сумме первого и последнего из выписанных чисел (либо, если на листке бумаги останется только одно число, то этому числу).

Предположим, что рулетка остановится на черном и крупье специальной лопаткой подвинет к себе выставленные мной четыре фишки. Поскольку я проиграл, новый ряд чисел, выписанных на листке бумаги, выглядит теперь так:

(число выложенных на стол фишек, равное 4, приписано справа). Делая следующую ставку, я должен выложить на стол пять (одну плюс четыре) фишек. В статье говорится, что и во второй раз я снова проигрываю и что, несмотря на повторный проигрыш, мне надлежит придерживаться прежней стратегии, т. е. приписать к уже выписанным числам справа число 5 и выложить на стол шесть (одну плюс пять) фишек.

— На этот раз ты непременно должен выиграть, — воскликнула Мод, все более входя в азарт. — Не можешь же ты все время проигрывать!

— Еще как могу! — заверил супругу мистер Томпкинс. — В детстве я частенько играл с другими мальчишками в орлянку — заключал пари относительно того, какой стороной вверх выпадет брошенная монета и, хочешь верь, хочешь не верь, однажды стал свидетелем того, как монета десять раз подряд выпала вверх орлом. Но предположим, как это делается в статье, что на этот раз я для разнообразия выиграл. В этом случае по правилам игры я должен получить свою удвоенную ставку — двенадцать фишек — и по сравнению со своим первоначальным капиталом стану на три фишки богаче. Следуя рекомендуемой стратегии, я должен вычеркнуть числа 1 и 5, после чего запись на листке бумаги примет следующий вид:

Делая следующую ставку, я должен выложить на стол шесть (две плюс четыре) фишек.

— Здесь в статье написано, что ты снова проиграл, — вздохнула Мод, заглядывая в журнал через плечо мужа. — Значит, теперь ты должен приписать к числам справа шестерку и, делая следующую ставку, выложить на стол восемь фишек. Правильно?

— Ты абсолютно права, но и на этот раз меня подстерегает проигрыш, и запись на листке бумаги выглядит теперь так:

Делая очередную ставку, я должен теперь выложить на стол десять (две плюс восемь) фишек. В статье говорится, что на этот раз я выиграл. Значит, я должен зачеркнуть числа 2 и 8 и, делая следующую ставку, выложить на стол девять (три плюс шесть) фишек. Но тут меня (так говорится в статье) снова подстерегает проигрыш.

— Какой все-таки неудачный пример! — посетовала, надув губки, Мод. — Ты успел проиграть три раза, а выиграл всего лишь один раз!

— Неважно, — успокоил ее мистер Томпкинс со снисходительной уверенностью фокусника. — Все равно в самом конце цикла выигрыш останется за нами. Последний запуск рулетки принес мне (по утверждению автора статьи) проигрыш в девять фишек. Поэтому теперь я должен приписать к уже выписанным числам справа девятку, после чего запись на моем листке будет выглядеть так: 1 (зачеркнуто), 2 (зачеркнуто), 3, 4, 5 (зачеркнуто), 6, 8 (зачеркнуто), 9

На стол мне нужно выложить двенадцать (три плюс девять) фишек. На этот раз выигрыш остается за мной, поэтому я вычеркиваю числа 3 и 9 и, делая новую ставку, выкладываю на стол десять (четыре плюс шесть) фишек. Последующий выигрыш завершает цикл, так как все числа, выписанные на листке бумаги, оказываются зачеркнутыми. Я стал богаче на шесть фишек, хотя выиграл в рулетку только четыре раза, а проиграл пять раз!

— А ты действительно стал на шесть фишек богаче? — недоверчиво спросила Мод.

— В этом не может быть никаких сомнений. Стратегия построена так, что всякий раз по завершении цикла ты, хочешь, не хочешь, непременно выигрываешь шесть фишек. В этом нетрудно убедиться с помощью несложных вычислений, поэтому я называю эту стратегию математической. Как видишь, она беспроигрышна. Если угодно, можешь взять листок бумаги и проверить все выкладки сама.

— Верю тебе на слово, что стратегия действительно беспроигрышна, — задумчиво сказала Мод, — но ведь шесть фищек — не такой уж большой выигрыш.

— Как сказать, — возразил мистер Томпкинс, — ведь выигрыш шести фишек в конце каждого цикла гарантирован. Повторяя процедуру снова и снова (начиная каждый раз с выписывания чисел 1, 2, 3), ты можешь выиграть сколько твоей душе угодно денег, а это совсем неплохо.

— Это просто великолепно! — согласилась Мод. — Теперь ты сможешь оставить службу в банке, мы сможем переехать в более просторную квартиру, а не далее, как вчера, я видела в витрине одного мехового магазина чудесное манто. И стоит оно каких-нибудь…

— Разумеется, мы купим тебе это манто, дорогая, — поспешил заверить жену мистер Томпкинс. — Но сначала нам нужно как можно скорее отправиться в Монте-Карло. Ведь статью, опубликованную в журнале «Esquire», прочитает множество людей, и было бы очень досадно прибыть в Монте-Карло лишь для того, чтобы застать там счастливчика, который опередил нас и довел казино до полного разорения.

— Я сейчас позвоню в аэропорт, — предложила Мод, — и узнаю, когда отправляется ближайший рейс в Монте-Карло.

— Что за спешка? — раздался в прихожей знакомый голос, и в комнату вошел старый профессор. Остановившись в дверях, он с удивлением смотрел на супружескую чету Томпкинсов, несколько разгоряченных внезапно открывшимися перед ними перспективами финансового благополучия.

— Мы намереваемся отправиться ближайшим же рейсом в Монте-Карло и надеемся вернуться основательно разбогатевшими, — пояснил мистер Томпкинс, поднимаясь из кресла навстречу тестю.

— Ах, вот в чем дело! Тогда все понятно, — улыбнулся профессор, с комфортом устраиваясь в старомодном кресле у камина. — У вас есть новая беспроигрышная стратегия?

— Но, папа, эта стратегия действительно беспроигрышная, — с упреком сказала Мод, все еще держа руку на телефонной трубке.

— Мод совершенно права, — подтвердил мистер Томпкинс, протягивая профессору журнал. — Предлагаемая стратегия просто не может не выиграть!

— Так-таки и не может? — иронически переспросил профессор с улыбкой. — Сейчас увидим!

Бегло ознакомившись со статьей, профессор продолжал:

— Отличительная особенность предлагаемой стратегии состоит в том, что правило, регулирующее величину ставок, заставляет вас увеличивать ставку после каждого проигрыша и снижать ставку после каждого выигрыша. Следовательно, если вы будете попеременно выигрывать и проигрывать, причем выигрыши и проигрыши будут чередоваться с абсолютной регулярностью, то ваш капитал будет колебаться, причем каждое увеличение капитала будет чуть больше его уменьшения. В этом случае вы, несомненно, достаточно скоро станете миллионером. Но, как вы понимаете, абсолютная регулярность встречается нечасто. В действительности вероятность появления правильно чередующейся последовательности выигрышей и проигрышей столь же мала, как и вероятность появления одинаковой по длине серии одних только выигрышей. Таким образом, необходимо выяснить, что произойдет, если несколько выигрышей (или несколько проигрышей) следуют подряд друг за другом. Если вам, как говорят игроки, улыбнулась фортуна, то правила беспроигрышной стратегии вынуждают вас либо понижать, либо по крайней мере не повышать ставку после каждого выигрыша, поэтому общий выигрыш окажется не слишком большим. С другой стороны, те же правила заставляют вас после каждого проигрыша повышать ставку, поэтому полоса неудач может иметь для вас катастрофические последствия и даже побудить вас выйти из игры. Кривая колебаний вашего капитала на этот раз состоит из нескольких медленно возрастающих участков, сменяющихся резкими спадами. В начале игры вы с большей вероятностью попадаете на длинную медленно возрастающую часть кривой и в течение какого-то времени наслаждаетесь приятным ощущением того, что ваш капитал медленно, но неуклонно увеличивается. Но если вы продолжаете игру достаточно долго в надежде на получение все большей и большей прибыли, то совершенно неожиданно для вас внезапно наступает резкий спад, который может оказаться достаточно глубоким для того, чтобы вы, сделав очередную ставку, потеряли последний пенни. Можно показать, причем в совершенно общем виде, что в предлагаемой автором статьи стратегии, равно как и в любой другой выигрышной стратегии, вероятность того, что кривая достигнет двойной отметки, равна вероятности достигнуть нулевого значения. Иначе говоря, вы имеете точно такой же шанс на окончательный выигрыш, как если бы поставили все свои деньги на красное или черное и удвоили свой капитал или спустили все, что имели, за один-единственный запуск рулетки. Все «беспроигрышные» стратегии способны лишь продлить игру и тем самым дать вам возможность получить за свои деньги больше удовольствия. Но даже если вы не требуете от игры ничего большего, то и тогда игру не следует так усложнять. Как вы знаете, на ободе колеса рулетки нанесены тридцать шесть чисел. Ничто не мешает поставить по фишке на каждое из чисел, кроме какого-нибудь одного. В этом случае вы имеете тридцать пять шансов из тридцати шести на выигрыш и на то, что банк выплатит вам за одну фишку больше, чем те тридцать пять фишек, которые вы, делая ставку, выложили на стол. Однако в одном из тридцати шести запусков рулеточного колеса шарик остановится на том числе, на которое вы решили не ставить свою фишку, и вы потеряете все свои тридцать пять фишек. Если вы будете придерживаться такой стратегии в достаточно продолжительной игре, то кривая вашего флуктуирующего капитала будет выглядеть точно так же, как кривая, которую вы получили, следуя стратегии, предложенной журналом.

Разумеется, в своих рассуждениях я исходил из предположения о том, что банк не предпринимает никаких мер, чтобы искусственно понизить шансы игрока на выигрыш. В действительности же на каждом рулеточном колесе, которое мне приходилось видеть, был нуль — «зеро», а иногда даже два нуля, что понижает шансы игрока на выигрыш. Таким образом, независимо от выбранной игроком стратегии его денежки мало-помалу перекочевывают из его кармана в карман владельца казино.

— Вы хотите сказать, — удрученно проговорил мистер Томпкинс, — что надежной беспроигрышной стратегии не существует и что выиграть деньги без риска проиграть с вероятностью чуть больше, чем вероятность выигрыша, просто невозможно?

— Именно это я хотел сказать! — подтвердил догадку мистера Томпкинса профессор. — Более того, высказанные мной соображения относятся не только к таким в сущности пустяковым проблемам, как азартные игры, но и ко многим различным физическим явлениям, которые, на первый взгляд, не имеют никакого отношения к вероятностным законам. Поэтому если бы вам удалось изобрести надежную выигрышную стратегию для преодоления законов случая, то для нее нашлось бы немало гораздо более увлекательных применений, чем игра на деньги в казино. Например, такая стратегия позволила бы создавать автомашины, способные совершать пробеги любой протяженности без капли бензина, строить фабрики, работающие без угля, и осуществлять множество других не менее фантастических проектов.

— Я где-то читал о таких фантастических машинах. Кажется, они называются вечными двигателями? — заметил мистер Томпкинс. — Если я правильно помню, вечные двигатели по замыслу их создателей должны были бы работать без топлива. Принято считать, что они невозможны потому, что энергию невозможно производить из ничего. Но как бы то ни было, вечные двигатели не имеют никакого отношения к азартным играм.

— Вы совершенно правы, молодой человек, — согласился профессор, несказанно довольный тем, что его зять начинает понемногу разбираться в физике. — Такие вечные двигатели (их принято называть вечными двигателями первого рода) не могут существовать потому, что их существование противоречило бы закону сохранения энергии. Однако машины, работающие без топлива, которые я имею в виду, совершенно другого типа и их принято называть вечными двигателями второго рода. Их проектируют не для того, чтобы получать энергию из ничего, а для того, чтобы извлекать ее из тепловых резервуаров, скрытых вокруг нас в недрах земли, в море и в воздухе. Вообразите себе пароход, на котором пар в котлах получается не при сжигании угля, а при извлечении тепла из окружающей судно воды. В самом деле, если бы тепло можно было заставить течь от более холодного тела к более теплому, а не в обратном направлении, как обычно, то можно было бы построить систему, которая закачивала бы забортную морскую воду, извлекала бы из нее тепло и сталкивала за борт получающиеся из воды глыбы льда. При превращении в лед одного галлона воды, выделяется столько тепла, что его достаточно для того, чтобы довести до кипения другой галлон холодной воды. Пропуская с помощью насосов несколько галлонов морской воды в минуту, можно легко получить количество теплоты, достаточное для работы двигателя приличных размеров. Для всех практических целей вечные двигатели второго рода ничем не уступали бы вечным двигателям первого рода, предназначенным для получения энергии из ничего. Если бы вечные двигатели второго рода действовали, то все в мире могли бы существовать столь же беззаботно, как человек, обладающий беспроигрышной стратегией для игры в рулетку. К сожалению, ни вечные двигатели второго рода, ни беспроигрышные стратегии существовать не могут, ибо и те, и другие одинаково нарушают законы вероятности.

— Я могу допустить, что пытаться извлекать тепло из морской воды для подогрева судовых котлов — сумасшедшая идея, — сказал мистер Томпкинс. — Однако я не усматриваю никакой связи между этой проблемой и законами случая. Разумеется, если вы не станете предлагать использовать игральные кости или колесо рулетки в качестве движущихся частей машин, работающих без топлива. Но вы же ничего такого, надеюсь, и не предлагаете?

— Разумеется, не предлагаю! — рассмеялся профессор. — Не думаю также, чтобы самые сумасшедшие изобретатели вечных двигателей предлагали нечто подобное. Дело совсем в ином: тепловые процессы сами очень похожи по своей природе на игру в кости, и надеяться на то, что тепло потечет от более холодного тела к более горячему, все равно, что надеяться на то, что монеты из банка казино потекут к вам в карман.

— Вы хотите этим сказать, что банк холодный, а мой карман горячий? — спросил мистер Томпкинс, полностью запутавшийся в объяснениях.

— В каком-то смысле да, — согласился профессор. — Если бы вы не пропустили мою лекцию на прошлой неделе, то знали бы, что тепло представляет собой не что иное, как быстрое беспорядочное движение бесчисленных частиц, известных под названием атомов и молекул, из которых состоят все материальные тела. Чем сильнее это молекулярное движение, тем теплее тело. Поскольку это молекулярное движение совершенно беспорядочно, оно подчиняется законам случая. Нетрудно показать, что наиболее вероятное состояние системы, состоящей из большого числа частиц, соответствует более или менее равномерному распределению всей имеющейся энергии по частицам. Если какая-то часть материального тела нагрета, т. е. если частицы в этой части тела движутся быстрее, то, принимая во внимание огромное число случайных столкновений, можно ожидать, что избыток энергии вскоре равномерно распределится между всеми остальными частицами. Но поскольку столкновения между частицами чисто случайные, существует также вероятность того, что совершенно случайно значительная часть энергии окажется сосредоточенной в какой-то группе частиц в ущерб всем остальным частицам. Такая спонтанная концентрация тепловой энергии в какой-то одной части тела соответствовала бы потоку тепла, направленному против перепада, или градиента, температуры, и в принципе отнюдь не исключается. Но если мы попытаемся вычислить относительную вероятность такой спонтанной концентрации тепла, то получим столь малое числовое значение, что подобное явление с полным основанием можно назвать практически невозможным.

— Теперь мне понятно, — обрадовался мистер Томпкинс. — Вы хотите сказать, что хотя вечные двигатели второго рода могут изредка работать, вероятность такого события столь же мала, как вероятность выпадения семи очков сто раз подряд при игре в кости.

— В действительности шансы встретить действующий вечный двигатель второго рода еще меньше, — сказал профессор. — Вероятности выигрыша в азартной игре против природы столь малы, что трудно найти подходящие слова для их описания. Например, я могу подсчитать вероятность того, что воздух в этой комнате самопроизвольно соберется под столом, оставив повсюду абсолютный вакуум. Число игральных костей, которые вы должны были бы бросать одновременно, эквивалентно числу молекул воздуха в комнате, которое мне было бы необходимо знать. Насколько я помню, один кубический сантиметр воздуха при атмосферном давлении содержит двадцатизначное число молекул, поэтому во всей комнате наберется двадцатисемизначное число молекул воздуха. Пространство под столом составляет примерно около одного процента объема комнаты, и шансы любой данной молекулы оказаться именно под столом, а не где-нибудь еще, составляют поэтому один к ста. Следовательно, вычисляя вероятность того, что все молекулы окажутся под столом, я должен умножить одну сотую на одну сотую, на одну сотую и т. д. столько раз, сколько молекул в комнате. В результате я получу десятичную дробь с пятидесятью четырьмя нулями после запятой.

— Уф! — вздохнул мистер Томпкинс. — Не хотел бы я делать ставку со столь малыми шансами на выигрыш! А не означает ли это, что отклонения от равнораспределения молекул по пространству попросту невозможны?

— Вы совершенно правы, — согласился профессор. — Можно считать твердо установленным фактом, что смерть от удушья из-за того, что весь воздух соберется под столом, нам не угрожает и жидкость в бокале не закипит вдруг сама собой. Но если мы сосредоточим внимание на гораздо меньших областях, содержащих существенно меньшее число наших игральных костей — молекул, то отклонения от статистического распределения станут значительно более вероятными. Например, в этой же самой комнате молекулы воздуха то и дело группируются несколько более плотно в одних точках пространства, чем в других, образуя слабые неоднородности, которые получили название статистических флуктуаций плотности. Когда солнечный свет проходит через земную атмосферу, такие неоднородности приводят к рассеянию голубых лучей спектра и придают небу знакомый всем голубой цвет. Если бы не было этих флуктуаций плотности, то небо всегда было бы совершенно черным и звезды были бы отчетливо видны даже при полном дневном свете. При нагревании жидкости до точки кипения они слегка мутнеют, что также объясняется теми же самыми флуктуациями плотности, возникающими из-за хаотичности движения молекул. Но в больших масштабах флуктуации настолько маловероятны, что мы могли бы напрасно прождать их миллиарды лет и так и не увидеть ни одной флуктуации.

— Тем не менее у нас есть шанс стать свидетелями какого-нибудь необычного события прямо сейчас в этой самой комнате, — настаивал мистер Томпкинс. — Ведь так?

— Разумеется, такой шанс всегда есть, и было бы неразумно утверждать, будто половина содержимого супницы не может выплеснуться на скатерть потому, что половина всех молекул внезапно приобрела тепловые скорости в одном и том же направлении.

— Именно такое событие произошло лишь вчера, — вмешалась в разговор Мод, закончившая просматривать свой журнал и с интересом слушавшая беседу профессора и мистера Томпкинса. — Суп пролился прямо на скатерть, хотя горничная утверждала, что не притрагивалась к столу.

Профессор тихо рассмеялся.

— В этом конкретном случае, — заметил он, — я склонен винить в случившемся все же горничную, а не демона Максвелла.

— Демона Максвелла? — повторил мистер Томпкинс в величайшем изумлении.

— А я-то думал, что ученые менее всего помышляют о всяких там демонах и прочей чертовщине.

— По правде говоря, мы воспринимаем его не слишком серьезно, — пояснил профессор. — Знаменитый физик Джеймс Клерк Максвелл ввел представление о таком статистическом демоне для большей наглядности. Демон понадобился Максвеллу при рассмотрении некоторых явлений, связанных с теплотой. Демон Максвелла — существо весьма проворное и успевает изменять направление движения каждой молекулы в отдельности любым образом, каким вы только пожелаете. Если бы такой демон существовал в действительности, то тепло можно было бы заставить течь против градиента температуры и за фундаментальный закон термодинамики, известный под названием принципа возрастания энтропии, никто бы не дал и ломаного гроша.

— Энтропии? — переспросил мистер Томпкинс. — Мне приходилось слышать это слово и прежде. Один из моих коллег однажды пригласил гостей, и после нескольких тостов присутствовавшие среди приглашенных студенты-химики спели на мотив «Ах, мой милый Августин» куплеты, которые начинались так:

«Возрастает, убывает,

Убывает, возрастает —

Химики того не знают.

Энтропия возрастает?»

Кстати, а что такое энтропия?

— Понять это совсем нетрудно. Энтропия — это просто термин, используемый для описания степени беспорядочности движения молекул в любом физическом теле или в системе тел. Многочисленные случайные столкновения между молекулами всегда способствуют увеличению энтропии, так как полный хаос является наиболее вероятным состоянием любого статистического ансамбля. Но если бы за работу принялся демон Максвелла, то он довольно скоро смог бы навести кое-какой порядок в движении молекул так же, как хорошая сторожевая собака не дает разбежаться и пасет стадо овец, и тогда энтропия системы пошла бы на убыль. Должен сказать вам также, что согласно так называемой Н-теореме, которой мы обязаны Людвигу Больцману…

Явно забыв о том, что он разговаривает с человеком, который практически ничего не понимает в физике, а не читает лекцию студентам-старшекурсникам, профессор с увлечением продолжал свой монолог и без малейших колебаний прибегал даже к таким маловразумительным для непосвященных терминам, как «обобщенные параметры» и «квазиэргодические системы». Ему казалось, что в таком изложении фундаментальные законы термодинамики и их связь со статистической механикой Гиббса становятся кристально ясными. Мистер Томпкинс уже успел привыкнуть к тому, что его тесть изъясняется на несколько недоступном для него уровне, и поэтому с философским спокойствием потягивал виски с содовой, пытаясь придать лицу умное выражение. Но весь блеск и красота статистической физики явно ускользали от Мод, уютно свернувшейся калачиком в своем кресле и с героическими усилиями боровшаяся с дремотой. Дабы окончательно развеять сонливость, она решила встать и пойти посмотреть, как идут приготовления к обеду.

— Мадам что-нибудь желает? — с поклоном спросил ее высокий тщательно одетый дворецкий, едва Мод появилась на пороге столовой.

— Благодарю вас, ничего. Просто решила посмотреть, как идут приготовления к обеду, — ответила она, лихорадочно пытаясь понять, откуда он взялся. Появление метрдотеля было очень странным, поскольку прислуги Томпкинсы не держали, дворецкого у них никогда не было, они и подумать не могли о такой роскоши. Дворецкий был худощав, строен, со смуглой оливковой кожей, длинным крючковатым носом и зеленоватыми глазами, в которых тлел странный огонек. Мурашки пробежали у Мод по спине, когда на лбу у дворецкого она заметила два симметричных выступа, тщательно прикрытых черными, как смоль, волосами.

— Либо я сплю, либо предо мной Мефистофель собственной персоной прямо с оперных подмостков, — подумала она.

— Вас нанял мой муж? — спросила Мод лишь для того, чтобы что-нибудь сказать.

— Не совсем, — ответил необычный дворецкий, завершая великолепную сервировку стола. — Если быть точным, я явился сюда по собственному желанию, дабы показать вашему батюшке, известному своими познаниями, что я не миф, как он думает. Позвольте представиться: я демон Максвелла.

— О! — вымолвила Мод с облегчением. — Тогда вы, должно быть, не злокозненны, как другие демоны, и не имеете намерений причинять вред кому-нибудь.

— Разумеется, — успокоил ее с широкой улыбкой демон, — но я люблю разыгрывать с людьми шутки и хочу подшутить над вашим ученым батюшкой.

— А что вы намереваетесь сделать? — с тревогой спросила Мод, которая никак не могла отделаться от мучивших ее подозрений.

— Просто продемонстрировать ему, что если я захочу, то могу нарушить принцип возрастания энтропии. А чтобы и вы могли убедиться в этом, я был бы очень признателен вам, если бы вы составили мне компанию. Смею уверить вас, что вам не угрожает никакая опасность.

При этих словах Мод почувствовала, как демон крепко взял ее под руку и все предметы вокруг словно сошли с ума. Стол, стулья и вся прочая обстановка столовой вдруг начали с чудовищной скоростью увеличиваться, и на ее глазах спинка кресла, выросшая до гигантских размеров, закрыла горизонт. Когда все вокруг постепенно успокоилось, Мод обнаружила, что плавает в воздухе, поддерживаемая своим необычным спутником. Какие-то туманные шары размером с теннисный мяч со свистом проносились мимо по всем направлениям. Демон Максвелла предусмотрительно предотвращал их от столкновения со всеми мало-мальски опасными предметами. Взглянув вниз, Мод увидела нечто вроде рыбацкой лодки, до самых уключин груженой трепыхающейся, блещущей серебром рыбой. Присмотревшись повнимательнее, Мод увидела, что это были не рыбы, а множество туманных шаров, вроде тех, что то и дело пролетали мимо, со свистом рассекая воздух. Демон, по-прежнему крепко держа ее под руку, влек ее за собой до тех пор, пока они не очутились в море какой-то зернистой жидкости, бесформенной и в то же время подвижной. Шары прямо-таки кипели у самой поверхности моря, а некоторых жидкость засасывала, и они скрывались в пучине. Время от времени некоторые шары всплывали к самой поверхности с такой скоростью, что отрывались от поверхности моря и взмывали в пространство. Другие шары прилетали откуда-то из пространства, врезались в жидкость и исчезали под тысячами других шаров. Вглядевшись в простиравшееся вокруг море, Мод увидела, что туманные шары в действительности были двух различных сортов. Большинство шаров напоминало по внешнему виду теннисные мячи, однако встречались и шары покрупнее. Они были более продолговатыми и по форме напоминали мячи для американского футбола. Все шары были полупрозрачными и имели сложную внутреннюю, структуру, которую Мод никак не удавалось разглядеть.

— Где мы? — произнесла Мод, задыхаясь. — Неужели так выглядит ад?

— Нет, — улыбнулся в ответ демон. — Все гораздо более прозаично. Просто мы с вами видим под очень большим увеличением крохотный участок поверхности жидкости в бокале, с помощью которого ваш муж довольно успешно пытается не уснуть, пока ваш батюшка разглагольствует о квазиэргодических системах. Все эти шары — молекулы. Те, что поменьше, — молекулы воды, те, что побольше, — молекулы спирта. Подсчитав, если угодно, пропорцию между теми и другими, вы сможете определить крепость напитка, который смешал себе ваш муж.

— Очень интересно! — заметила Мод как можно более строгим голосом. — А что это за штуковины плавают там вдали? Они напоминают пару резвящихся китов. Может быть, это какие-нибудь атомные киты?

Демон взглянул в том направлении, куда указывала Мод.

— Нет, это не киты, — заметил он. — Это крохотные кусочки подгоревшего ячменя — того самого ингредиента, который придает виски особый вкус и цвет. Каждый такой кусочек состоит из миллионов и миллионов сложных органических молекул, имеет сравнительно большие размеры и довольно тяжел. То, что они прыгают на поверхности жидкости, объясняется действием тех ударов, которые они получают от молекул воды и спирта, совершающих тепловое движение. Именно изучение таких частиц средних размеров, достаточно малых для того, чтобы ощущать движение молекул, и вместе с тем достаточно больших для того, чтобы их можно было наблюдать в сильный микроскоп, дало ученым первое прямое доказательство правильности основных положений кинетической теории газов. Измеряя интенсивность тарантеллы, исполняемой крохотными частицами, взвешенными в жидкости, — их броуновского движения, как обычно принято называть беспорядочное движение таких частиц, физики научились извлекать непосредственную информацию об энергии движения молекул.

Демон снова повлек за собой Мод. Они неслись по воздуху до тех пор, пока перед ними не возникла гигантская стена, сложенная из бесчисленных молекул воды. Молекулы были подогнаны друг к другу точно и плотно, как кирпичи.

— Какое поразительное зрелище! — вскричала Мод. — Какой прекрасный фон для портрета, который я сейчас рисую! Кстати, а что это за здание?

— Перед вами фрагмент кристалла льда, один из многих кристалликов, образующих кубик льда в стакане вашего мужа, — сказал демон. — А теперь, прошу прощения, самое время начать придуманный мной розыгрыш и подшутить над старым самоуверенным профессором.

С этими словами демон оставил Мод на ребре кристалла льда, наподобие альпиниста, взгромоздившегося на горный хребет, и приступил к работе. Вооружившись инструментом наподобие теннисной ракетки, демон принялся отбивать пролетавшие мимо молекулы. Быстро перемещаясь с места на место, он поспевал вовремя, чтобы отбить упрямую молекулу, упорно продолжавшую двигаться в неправильном направлении. Несмотря на опасность своего положения Мод не могла не восхищаться проворством и ловкостью демона и даже подбадривала его возгласами, когда ему удавалось отбить особенно быструю и трудную молекулу. По сравнению с тем, что вытворял демон, самые знаменитые чемпионы по теннису выглядели жалкими, безнадежно неуклюжими увальнями. Не прошло и нескольких минут, как результаты работы Демона стали заметны. Теперь, хотя часть поверхности жидкости была покрыта очень медленно движущимися спокойными молекулами, другая часть поверхности, расположенная прямо у Мод под ногами, кишела молекулами, яростно сновавшими по всем направлениям. Число молекул, покидавших поверхность в процессе испарения. быстро нарастало. Молекулы покидали жидкость большими группами по тысяче молекул и более, прорываясь сквозь поверхность жидкости в виде больших пузырей. Вскоре облако пара скрыло от Мод все и лишь время от времени она могла различить разящие взмахи ракетки и фалды фрака, в который был облачен демон, среди беснующихся молекул. Наконец, молекулы на том фрагменте льда, на котором она восседала, поддались, и Мод стала падать сквозь тяжелые облака пара, расстилавшиеся под ней…

Когда облака рассеялись, Мод обнаружила, что сидит в том самом кресле, в котором сидела перед тем, как выйти в столовую.

— Святая энтропия! — воскликнул вдруг отец Мод, глядя на высокий бокал, стоявший перед мистером Томпкинсом. — Да ведь жидкость кипит!

Действительно, жидкость в бокале покрылась лопающимися пузырями, и к потолку над бокалом медленно поднималась тонкое облачко пара. Было странно, однако, что напиток в стакане кипел лишь на сравнительно малом участке вокруг кубика льда. Весь остальной напиток был совершенно холодным.

— Нет, вы только подумайте! — продолжал профессор севшим от волнения дрожащим голосом. — Я рассказываю вам о статистических флуктуациях в возрастании энтропии, и, пожалуйста, такая флуктуация перед нами! В результате невероятного стечения обстоятельств впервые с сотворения Земли более быстрые молекулы случайно собрались на одном участке поверхности жидкости, и жидкость сама собой закипела! В ближайшие миллиарды лет мы с вами останемся единственными людьми, которым посчастливилось видеть это необычайное явление.

Профессор не отрывал глаз от напитка, который теперь медленно остывал.

— Какая удача! — вздохнул он с счастливой улыбкой. — Какое необыкновенное везение!

Мод улыбнулась, но ничего не сказала. Зачем ей было спорить с отцом, если на этот раз она точно знала, что истинная причина явления была известна ей лучше, чем ему.

Глава 10

Веселое племя электронов

Через несколько дней, заканчивая обед, мистер Томпкинс вспомнил, что вечером должна состояться лекция профессора о строении атома, которую он обещал посетить. Но маловразумительными объяснениями своего тестя мистер Томпкинс был сыт по горло, и поэтому решил пропустить лекцию и скоротать вечерок дома. Но когда он устраивался поудобнее в своем кресле, мечтая почитать интересную книгу, Мод отрезала этот путь к отступлению: взглянув на часы, она заявила мягко, но тоном, не допускающим возражений, что мистеру Томпкинсу пора отправляться на лекцию. И через каких-нибудь полчаса мистер Томпкинс сидел на жесткой деревянной скамье вместе с толпой гораздо более молодых студентов.

— Леди и джентльмены, — начал профессор, строго глядя на слушателей поверх очков, — на прошлой лекции я обещал вам подробнее рассказать о внутреннем строении атома и объяснить, каким образом те или иные конкретные особенности его строения обуславливают различные физические и химические свойства атома. Вы, конечно, знаете, что атомы не рассматриваются более как элементарные неделимые составные части материи и что эта роль ныне перешла к гораздо меньшим частицам — электронам, протонам и т. д.

Представление об элементарных составляющих материи как о последней ступени в делимости материальных тел восходит к древнегреческому философу Демокриту, жившему в IV веке до н. э. Размышляя о скрытой природе вещей, Демокрит пришел к проблеме строения материи и столкнулся с вопросом о том, может или не может существовать бесконечно малая порция материи. Поскольку в ту далекую эпоху любую проблему имели обыкновение решать лишь одним-единственным способом — с помощью чистого мышления и к тому же вопрос в то время находился далеко за рамками возможностей решения его экспериментальными методами, Демокрит в поисках правильного ответа опустился в глубины собственного разума. Исходя из некоторых довольно смутных философских соображений, он в конце концов пришел к выводу о том, что «немыслимо», чтобы материя безгранично делилась на все более и более мелкие порции, и что поэтому необходимо принять предположение о существовании «наименьших частиц, которые не допускают дальнейшего деления». Такие частицы Демокрит назвал атомами, что, как вы, возможно, знаете, означает по-гречески «неделимые».

Я отнюдь не хочу приуменьшать величие вклада Демокрита в развитие естественных наук, однако справедливости ради хотел бы обратить ваше внимание на то, что наряду с Демокритом и его последователями в древнегреческой философии существовала и другая школа, приверженцы которой считали, что процесс деления неограниченно продолжаем. Поэтому независимо от того, какой ответ на этот вопрос даст в будущем точное естествознание, древнегреческой философии обеспечено почетное место в истории физики. Во времена Демокрита и даже много столетий спустя существование таких неделимых порций материи рассматривалось как чисто философская гипотеза, и только в XIX веке ученые решили, что им, наконец, удалось обнаружить те неделимые кирпичики материи, существование которых было предсказано древнегреческими философами за две тысячи лет до разыгравшихся событий.

В 1808 г. английский химик Джон Дальтон установил так называемый закон кратных отношений. Он показал, что…

Почти с самого начала лекции мистера Томпкинса неудержимо клонило в сон. Ему очень хотелось сомкнуть глаза и, пребывая в приятной дремоте, досидеть до конца лекции, но мешала лишь суровая жесткость университетской скамьи. Но открытый Дальтоном закон кратных отношений оказался последней соломинкой, переломившей спину верблюду, и в притихшей аудитории вскоре можно было отчетливо различить тонкое посвистывание, доносившееся из угла, где сидел мистер Томпкинс.

Когда мистер Томпкинс очнулся от сна, неудобство сидения на жесткой скамье сменилось приятным ощущением парения в воздухе. Открыв глаза, мистер Томпкинс с удивлением обнаружил, что мчится в пространстве с легкомысленно, как ему показалось, большой скоростью. Оглянувшись по сторонам, мистер Томпкинс увидел, что он не одинок в своем фантастическом путешествии. Неподалеку от него несколько расплывчатых смутных существ обращались вокруг большого тяжелого на вид объекта в центре хоровода. Это странные призрачные существа мчались парами, весело гоняясь друг за другом по круговым и эллиптическим траекториям. Внезапно мистер Томпкинс почувствовал себя очень одиноким, осознав, что лишь у него одного нет партнера.

— Почему я не взял с собой Мод? — тоскливо подумал мистер Томпкинс. — Мы бы чудесно провели время в этом хороводе.

Траектория, по которой двигался мистер Томпкинс, пролегала в стороне от траекторий остальных существ, охватывая их снаружи, и хотя мистеру Томпксинсу очень хотелось присоединиться к остальной компании, неприятное чувство постороннего удерживало и мешало ему сделать шаг навстречу веселым путешественникам. Однако когда одному из электронов (к тому времени мистер Томпкинс окончательно понял, что непостижимым и чудесным образом присоединился к сообществу электронов, населявших какой-то атом) случилось пролететь неподалеку от него по сильно вытянутой орбите, мистер Томпкинс решил пожаловаться на свои неудачи.

— Почему у меня нет партнера для игр и забав? — прокричал он вслед электрону.

— Потому, что это нечетный атом, а вы валентный электро-о-н, — донеслось в ответ. С этими словами электрон повернул и устремился в толпу пляшущих электронов.

— Валентные электроны живут в одиночку или находят себе компаньонов в других атомах, — пропищал высоким фальцетом другой электрон, проносясь мимо мистера Томпкинса.

насмешливо пропел третий.

— Вижу, вы здесь новичок, сын мой, и очень одиноки, — раздался над мистером Томпкинсом дружеский голос, и, возведя глаза горе, наш герой увидел плотную фигуру монаха в коричневой сутане.

— Я отец Паулини, — продолжал монах, двигаясь по траектории вместе с мистером Томпкинсом, — и моя миссия в этой жизни состоит в том, чтобы наблюдать за моралью и социальным поведением электронов в атомах и повсюду. Мой долг — следить за тем, чтобы все эти беззаботные и игривые электроны были надлежащим образом распределены по различным квантовым кельям этого прекрасного атомного строения, воздвигнутого нашим великим архитектором Нильсом Бором. Дабы поддерживать порядок и сохранять свойства, я никогда не разрешаю находиться на одной и той же траектории более чем двум электронам. Стоит им собраться втроем, как хлопот не оберешься. Поэтому электроны всегда сгруппированы в пары с противоположным «спином», и если такая пара поселяется в келье, то третьему электрону не разрешается нарушать их покой. Это хорошее правило, и я могу добавить, что до сих пор ни один электрон не нарушил введеного мной распорядка.

— Может быть, это очень хорошее правило, — возразил мистер Томпкинс,

— но в данный момент я терплю из-за него большие неудобства.

— Вижу, сын мой, — улыбнулся монах, — но вам просто не повезло. Угораздило же вас стать валентным электроном в атоме с нечетным атомным номером. Атом натрия, которому вы принадлежите, обязан иметь из-за электрического заряда своего ядра (той большой темной массы, которую вы видите в центре) одиннадцать электронов. К величайшему сожалению для вас, одиннадцать — число нечетное, что само по себе не такая уж редкость, если принять во внимание, что ровно половина всех целых чисел нечетна и только другая половина четна. Так что вам придется как появившемуся последним по крайней мере какое-то время побыть одному.

— Вы хотите сказать, что позднее у меня, возможно, появится шанс обзавестись партнером? — с надеждой спросил мистер Томпкинс. — Например, выбить с орбиты кого-нибудь из электронов-первопоселенцев?

— Это делается не так, — возразил монах, грозя мистеру Томгасинсу коротким толстым пальцем, — но всегда есть шанс, что какой-нибудь из электронов, обращающихся по внутренним орбитам, будет выброшен внешним возмущением и оставит после себя не занятое место, или вакансию. Но на вашем месте я не стал бы на это особенно рассчитывать.

— Электроны сказали мне, что было бы лучше, если бы я проник в атом хлора, — сказал мистер Томпкинс, несколько обескураженный словами отца Паулини. — Можете ли вы посоветовать мне, как это лучше сделать?

— Молодой человек, молодой человек! — с сожалением покачал головой монах. — Ну что вам так не терпится найти компаньона? Почему вы не можете по достоинству оценить прелесть одиночества и насладиться этой ниспосланной небом возможностью созерцать с миром собственную душу? Почему четные электроны так сильно льнут к мирской жизни? Но если вы настаиваете на приобретении компаньона, я помогу вам осуществить ваше желание. Взглянув в том направлении, куда я указываю, вы увидите приближающийся к нам атом хлора, и даже со столь большого расстояния вы можете легко различить свободное место, где вас, несомненно, ожидает самый теплый прием. Это свободное место находится во внешней группе электронов, так называемой М-оболочке, которая состоит из восьми электронов, разбитых на четыре пары. Но, как вы видите, четыре электрона вращаются вокруг своих осей в одном направлении и только три — в другом, поэтому одно место остается вакантным. Внутренние оболочки, называемые К— и Z-оболочками, полностью заполнены, и атом будет рад заполучить вас и заполнить свою внешнюю оболочку. Как только два атома сблизятся, вы должны просто перепрыгнуть с одного атома на другой, как это обычно делают валентные электроны. Да будет мир с вами, сын мой!

С этими словами внушительная фигура электронного пастыря внезапно растворилась в разреженном воздухе.

Ободренный мистер Томпкинс собрался с силами и совершил головоломный прыжок на орбиту пролетавшего мимо атома хлора. К своему удивлению, он приземлился на атоме хлора не без изящества и сразу же оказался в дружеском окружении электронов М-оболочки атома хлора.

— Добро пожаловать! Рады, что вы присоединились к нам! — обратился к нему новый партнер с противоположным спином, изящно скользя вдоль орбиты. — Теперь никто не может сказать, что наше сообщество неполно. Теперь мы можем великолепно повеселиться все вместе!

Мистер Томпкинс не мог не согласиться, что было действительно весело (веселье било через край!), но тут ему в голову закралась одна беспокойная мысль. — А как я объясню все это Мод, когда снова увижу ее?

Впрочем, чувство вины у мистера Томпкинса вскоре рассеялось.

— Мод вряд ли стала бы возражать, — решил он, — ведь в конце концов это лишь электроны.

— Почему покинутый вами атом не улетает прочь? — спросил у мистера Томпкинса с недовольной гримасой его компаньон. — Он все еще надеется на ваше возвращение?

Действительно, потеряв свой валентный электрон, атом натрия накрепко прилепился к атому хлора, как бы в надежде, что мистер Томпкинс передумает и снова вернется на свою орбиту, по которой он мчался в полном одиночестве.

— Нет, как вам это нравится! — сердито пробормотал мистер Томпкинс, хмуро глядя на атом, который поначалу принял его так холодно. — Не атом, а какая-то собака на сене!

— О, они всегда ведут себя так, эти атомы с нечетными номерами, — заметил более опытный член М-оболочки. — Насколько я понимаю, вашего возвращения жаждет не столько сообщество электронов атома натрия, сколько само ядро этого атома. Между центральным ядром и его электронным эскортом всегда существуют некоторые разногласия. Ядро хочет иметь вокруг себя столько электронов, сколько оно может удержать своим электрическим зарядом, в то время как сами электроны предпочитают быть в таком количестве, которое позволяет им до конца заполнять оболочки. Существует лишь несколько видов атомов, так называемые редкие газы, или, как называют их немецкие физики, благородные газы, в которых жажда власти со стороны атомного ядра и стремления подданных-электронов находятся в полной гармонии. Например, такие атомы, как гелий, неон и аргон очень довольны царящим в них согласием между ядром и электронами и никогда не изгоняют своих электронов и не приглашают новых. Они химически инертны и держатся в стороне от всех остальных атомов. Но во всех остальных атомах электронные сообщества всегда готовы обменяться своими членами. В атоме натрия, вашем прежнем обиталище, свита ядра насчитывает на один электрон больше, чем необходимо для гармонии в оболочках. С другой стороны, в нашем атоме нормальная численность электронного населения недостаточна для полной гармонии, поэтому мы очень рады вашему прибытию, несмотря на то, что ваше присутствие перегружает наше ядро. Но покуда вы остаетесь с нами, наш атом перестает быть нейтральным и получает дополнительный электрический заряд. Поэтому атом натрия, который вы покинули, прилип к нашему атому, удерживаемый силой электрического притяжения. Однажды мне довелось слышать нашего первосвященника отца Паулини, и он сказал, что атомные сообщества с лишними или недостающими электронами называются соответственно отрицательными и положительными ионами. Отец Паулини использовал также термин молекула для обозначения групп из двух или более атомов, удерживаемых вместе электрической силой. В частности, комбинацию из одного атома натрия и одного атома хлора отец Паулини назвал молекулой поваренной соли, хотя я решительно не понимаю, что бы это могло означать.

— Вы хотите сказать, будто не знаете, что такое поваренная соль? — удивленно спросил мистер Томпкинс, забыв о том, с кем он разговаривает. — Это тот самый белый порошок, которым вы за завтраком посыпаете яйцо всмятку.

— А что такое яйцо всмятку и что такое завтрак? — с интересом спросил электрон.

Мистер Томпкинс пробормотал что-то невнятное и тут только со всей ясностью понял всю тщетность любых попыток объяснить своим компаньонам даже самые незамысловатые детали повседневной жизни людей.

— Почему-то мне не удается почерпнуть для себя ничего нового из всех этих разговоров о валентности и заполненных оболочках, — сказал себе мистер Томпкинс, решив наслаждаться своим визитом в фантастический мир атома и не забивать себе голову непонятными вопросами. Но отделаться от разговорчивого электрона было не так-то легко. Собеседник мистера Томтпсинса явно горел желанием передать своему партнеру все познания, накопленные за долгую электронную жизнь.

— Не следует думать, — продолжал электрон, — что связывание атомов в молекулы всегда осуществляется только одним валентным электроном. Существуют атомы, например, атомы кислорода, которым для достраивания их оболочек необходимо два электрона, а другим атомам для заполнения оболочек недостает три и даже более электронов. С другой стороны, в некоторых атомах ядро удерживает два или более лишних, или валентных, электронов. При столкновении таких атомов, многие электроны перепрыгивают с одного атома на другой, и в результате образуются весьма сложные молекулы, состоящие из тысяч атомов. Существуют также так называемые гомополярные молекулы, т. е. молекулы, состоящие из двух одинаковых атомов, но это очень неприятная ситуация.

— Неприятная, но почему? — спросил мистер Томпкинс, у которого вновь пробудился интерес к теме беседы.

— Слишком трудно удерживать их вместе, — пояснил электрон. — Как-то раз мне пришлось заниматься этим неблагодарным делом, и пока я находился в гомополярной молекуле, у меня не было ни секунды покоя. Совсем другое дело в таком атоме, как наш, когда валентный электрон перепрыгнул себе и прочно привязал покинутый им атом к другому атому, испытывавшему электрический голод. Чтобы удерживать вместе два одинаковых атома, несчастному электрону приходится прыгать туда и обратно, с одного атома на другой и назад, снова на первый атом. Честное слово! Чувствуешь себя, как пинт-понговый шарик.

Мистер Томпкинс немало удивился, услышав от электрона, не знавшего, что такое яйцо всмятку, столь непринужденное упоминание о пинг-понговом шарике, но не стал задавать вопросов.

— Ни за что на свете я не согласился бы на такую работу опять! — проворчал ленивый электрон, подавляя в себе волну неприятных воспоминаний. — Здесь же мне вполне удобно и покойно.

— Минутку! — воскликнул он внезапно. — Кажется, я вижу местечко поудобнее. По-ка-а!

И гигантским прыжком электрон отправился куда-то в глубь атома.

Бросив взгляд в том направлении, в котором исчез его собеседник, мистер Томпкинс понял, что произошло. Один из находившихся на внутренней оболочке электронов был вырван из атома каким-то чужим электроном, неожиданно проникшим извне в оболочку с высокой скоростью, и в К-оболочке образовалось уютное свободное местечко. Ругая себя за упущенную возможность присоединиться к электронам внутренней оболочки, мистер Томпкинс с огромным интересом наблюдал за полетом электрона, с которым только что беседовал. Счастливый электрон все глубже и глубже внедрялся внутрь атома, и яркие лучи света сопровождали его триумфальный полет. Лишь когда электрон достиг внутренней оболочки, это почти нестерпимое сияние прекратилось.

— Что это было? — спросил мистер Томпкинс, ослепленный неожиданно открывшимся ему зрелищем нового, неизвестного ранее явления. — Откуда весь этот блеск?

— О, это всего лишь испускание гамма-излучения, связанное с переходом с одной орбиты на другую, — пояснил партнер по орбите, улыбаясь при виде растерянности мистера Томпкинса. — Всякий раз, когда один из нас проникает глубже внутрь атома, лишняя энергия непременно испускается в виде излучения. Этот счастливчик совершил гигантский прыжок и испустил при этом огромную энергию. Гораздо чаще нам приходится довольствоваться меньшими прыжками на окраине атома, и испускаемое нами излучение называется «видимым светом». По крайней мере так называет его отец Паулини.

— Но гамма-излучение, или как там вы его называете, также видимо, — возразил мистер Томпкинс. — Мне кажется, что ваша терминология способна лишь вводить в заблуждение.

— Видите ли, мы электроны и чувствительны ко всякого рода излучению. Но отец Паулини рассказывал нам о том, что существуют гигантские существа, или как он их называл, люди, которые могут видеть излучение только в узком интервале энергий, или как любит говорить отец Паулини, интервале длин волн. В одной из своих проповедей отец Паулини упомянул о том, что великий человек по имени, кажется, Рентген открыл гамма-излучение, или рентгеновское излучение, и теперь оно широко используется в чем-то, что люди называют медициной.

— Я довольно хорошо осведомлен об этом, — заметил мистер Томпкинс, ощущая гордость при мысли, что и ему есть что поведать другому. — Хотите, я расскажу вам немало интересного об этой самой медицине?

— Нет, благодарю вас, — ответил электрон, широко зевая. — Мне как-то все равно. Разве вы не можете быть счастливы, если не будете говорить о медицине? Догоняйте меня!

Довольно долго мистер Томпкинс наслаждался приятным ощущением свободы, совершая вместе с другими электронами удивительнейшие перелеты в пространстве, словно искусный акробат, перелетающий с трапеции на трапецию. Внезапно он ощутил, что его волосы поднялись дыбом. Подобное ощущение ему приходилось испытывать и раньше во время грозы в горах. Мистеру Томпкинсу стало ясно, что к их атому приближается какое-то сильное электрическое возмущение, нарушающее гармонию движения электронов и заставляющее электроны существенно отклоняться от их обычных орбит. С точки зрения физика-человека возмущение представляло собой волну ультрафиолетового света, проходившую через то место, где находился атом, но с точки зрения крохотных электронов это была сильнейшая электрическая гроза.

— Держитесь покрепче, — прокричал мистеру Томпкинсу один из его компаньонов, — иначе вас оторвут силы фотоэффекта!

Но было слишком поздно. Мистера Томпкинса оторвало от партнера и, закрутив, с чудовищной скоростью бросило в пространство. Ощущение было такое, словно его схватили чьи-то сильные пальцы. Бездыханный, он уносился все дальше и дальше в пространство, пролетая сквозь всякого рода различные атомы так быстро, что едва успевал разглядеть отдельные электроны. Внезапно прямо перед ним показался большой атом, и мистер Томпкинс понял, что столкновение неизбежно.

— Прошу извинить, но меня зафотоэффектило и я не могу… — вежливо начал мистер Томпкинс, но остаток фразы потонул в оглушительном треске, с которым мистер Томпкинс врезался в один из внешних электронов. Оба участника столкновения кувырком полетели в разные стороны. Однако мистер Томпкинс потерял при столкновении значительную часть своей скорости и теперь мог более детально обследовать свое новое окружение. Громоздившиеся вокруг атомы были гораздо больше тех, которые ему приходилось видеть прежде, и в каждом из атомов мистер Томпкинс насчитал по двадцать девять электронов. Если бы Томпкинс лучше разбирался в физике, то он распознал бы в них атомы меди, но со столь близкого расстояния атомы совсем не походили на медь. Они были расположены вплотную друг к другу и образовывали правильный узор, простиравшийся до самого горизонта. Но более всего мистера Томпкинса удивило то, что эти атомы, по-видимому, не особенно стремились удерживать при себе свою долю электронов, в особенности внешних электронов. Внешние орбиты почти всех атомов были пусты, а толпы кочующих электронов лениво бродили по всему пространству, время от времени останавливаясь, но нигде не задерживаясь подолгу, на окраине то одного, то другого атома. Утомленный головокружительным полетом через пространство мистер Томпкинс попытался сначала немного отдохнуть на стационарной, т. е. не подверженной каким-либо временным изменениям, орбите одного из атомов меди, но вскоре поддался бродяжническим настроениям толпы и присоединился к остальным электронам в их бесцельных блужданиях.

— Порядок здесь оставляет желать лучшего, — прокомментировал про себя мистер Томпкинс. — Слишком много электронов шатаются без дела. Я считаю, что отцу Паулини следовало бы навести порядок.

— Почему вы думаете, что я должен вмешаться? — раздался знакомый голос монаха, который внезапно материализовался из ничего. — Все эти электроны отнюдь не нарушают моих предписаний и к тому же делают очень полезное дело. Может быть, вам будет небезынтересно узнать, что если бы все атомы стремились удержать при себе свои электроны, как это делают некоторые из них, то не было бы такого явления, как проводимость. У вас в доме не было бы электрического дверного звонка, не говоря уже об электрическом освещении и телефоне.

— Вы хотите сказать, что бродячие электроны переносят электричество? — спросил мистер Томпкинс, цепляясь за надежду, что разговор пойдет о более или менее знакомом предмете. — Но что-то я не вижу, чтобы они двигались в каком-то определенном направлении.

— Прежде всего, друг мой, — сурово промолвил монах, — не говорите «они», «мы» звучит гораздо лучше. Должно быть, вы забыли, что вы сами также принадлежите к племени электронов и что стоит кому-нибудь нажать кнопку звонка, с которым соединена эта медная проволока, как электрическое напряжение заставит вас вместе с другими электронами проводимости опрометью броситься, чтобы вызвать горничную или выполнить какую-нибудь другую службу.

— Но я не хочу делать этого! — твердо заявил мистер Томпкинс не без раздражения в голосе. — И вообще я устал быть электроном и не вижу в этом более ничего привлекательного. Что за жизнь вечно выполнять все эти электронные обязанности!

— Не обязательно вечно, — возразил отец Паулини, которому явно не понравилось непослушание со стороны простых электронов. — У вас всегда есть шанс быть уничтоженным и прекратить существование.

— Б-б-быть уничтоженным? — повторил мистер Томпкинс, чувствуя, как по спине у него ползут мурашки. — Но я всегда думал, что электроны вечны!

— Физики тоже так думали вплоть до недавнего времени, — согласился отец Паулини, явно забавляясь эффектом, произведенным его словами, — но подобная точка зрения оказалась не вполне верной. Электроны могут рождаться и умирать, как люди. Разумеется, электрон не может умереть от старости, она наступает при столкновениях.

— Но я пережил столкновение лишь недавно, и, должен вам сказать, претяжелое это было столкновение, — сказал мистер Томпкинс, вновь обретая некоторую уверенность. — Если и такое столкновение не вывело меня из строя, то каким же оно должно быть, чтобы уничтожить меня?

— Вопрос не в том, как сильно вы сталкиваетесь, — поправил мистера Томпкинса отец Паулини, — а в том, с кем вы сталкиваетесь. В своем недавнем столкновении вы, вероятно, наскочили на другой отрицательно заряженный электрон, очень похожий на вас. Такие столкновения не таят в себе никакой опасности. Вы, электроны, можете сталкиваться друг с другом сколько угодно, как два барана, это не причинит никому из вас ни малейшего вреда. Но существует другая разновидность электронов — положительные электроны, лишь сравнительно недавно открытые физиками. Эти положительно заряженные электроны, или позитроны, выглядят в точности так же, как вы, с тем лишь отличием, что их электрический заряд положителен, тогда как ваш отрицателен. При виде приближающегося к вам позитрона вы полагаете, что перед вами один из невинных ваших соплеменников и устремляетесь навстречу, чтобы приветствовать его. Но тут вы внезапно ощущаете, что встречный электрон не отталкивает вас слегка, чтобы избежать столкновения, как это сделал бы любой нормальный электрон, а притягивает вас к себе и тогда сделать что-нибудь поздно.

— Ужасно! — воскликнул мистер Томпкинс. — И сколько несчастных обычных электронов может поглотить один позитрон?

— К счастью, только одного, поскольку уничтожая отрицательно заряженный электрон, позитрон гибнет и сам. Позитроны можно описать как членов клуба самоубийц, ищущих партнеров по взаимоуничтожению. Они не причиняют вреда друг другу, но стоит лишь какому-нибудь отрицательно заряженному электрону встретиться им на пути, как шансов уцелеть у него очень мало.

— К счастью, до сих пор мне не попадались эти чудовища, — произнес мистер Томпкинс, на которого слова отца Паулини произвели сильное впечатление. — Надеюсь, они не слишком многочисленны?

— Не слишком. По той простой причине, что всегда ищут себе неприятностей и погибают вскоре после рождения. Впрочем, подождите минуточку, я, кажется, смогу показать вам один позитрон, — продолжал отец Паулини после короткой паузы. — Если вы внимательно вглядитесь вон в то ядро, то увидите, как рождается один из позитронов.

Атом, на который указывал отец Паулини, претерпевал сильное электромагнитное возмущение из-за упавшего на него извне сильного излучения. Возмущение было гораздо более сильным, чем то, которое выбило мистера Томпкинса из атома хлора, и семейство атомных электронов, окружавших ядро, было рассеяно и унесено прочь, как сухие листья ураганом.

— Вглядитесь внимательно в ядро, — сказал отец Паулини, и, сосредоточив все свое внимание, мистер Томпкинс увидел необычное явление, происходившее в глубинах разрушенного атома. Вблизи ядра, в глубине внутренней электронной оболочки, две смутные тени постепенно обретали все более отчетливые очертания, и секундой позже мистер Томпкинс увидел два блестящих, новеньких с иголочки электрона, с огромной скоростью разлетающихся от места своего рождения.

— Но я вижу две частицы, а не одну, — сказал мистер Томпкинс, захваченный открывшимся ему зрелищем.

— Совершенно верно, — согласился отец Паулини. — Электроны всегда рождаются парами, иначе рождение электронов противоречило бы закону сохранения электрического заряда. Одна из этих двух частиц, родившихся под действием сильного гамма-излучения на ядро, — обычный электрон с отрицательным зарядом, другая частица — электрон с положительным зарядом, или позитрон-убийца. Теперь он рыщет по пространству в поисках жертвы.

— Ну что ж, — задумчиво произнес мистер Томпкинс, — если рождение каждого позитрона, которому на роду написано стать убийцей электрона, сопровождается рождением одного обычного электрона, то дела обстоят не так уж плохо. По крайней мере не приходится опасаться за исчезновение электронного племени, и я…

— Осторожно! — прервал мистера Томпкинса отец Паулини, отталкивая своего собеседника в сторону, в то время как новорожденный позитрон со свистом пронесся в каком-нибудь дюйме от них. — Нужно все время быть начеку, когда эти убийственные частицы находятся где-то поблизости. Но, простите, я слишком задержался, беседуя с вами, и меня ждут другие дела. Мне необходимо навестить милых моему сердцу нейтрино…

И отец Паулини исчез, оставив мистера Томпкинса в неведении относительно того, что такое нейтрино и следует ли их опасаться. Лишившись духовного отца, мистер Томпкинс почувствовал себя еще более одиноким, чем прежде, и всякий раз, когда на его долгом пути через пространство; к нему приближался тот или иной соплеменник-электрон, в сердце мистера Томпкинса начинала теплиться надежда на то, что под невинной внешностью может скрываться сердце убийцы. Время тянулось нестерпимо медленно (мистеру Томпкинсу казалось, что прошло несколько столетий), а его надеждам и чаяниям все никак не суждено было сбыться, и мистеру Томпкинсу не оставалось ничего другого, как исполнять скучные обязанности электрона проводимости.

Все произошло совершенно неожиданно, когда мистер Томпкинс менее всего рассчитывал встретить позитрон. Ощущая острую потребность побеседовать с кем-нибудь, даже с каким-нибудь глупым электроном проводимости, он приблизился к частице, медленно пролетавшей мимо и явно бывшей новичком в данной части медной проволоки. Но даже на расстоянии мистер Томпкинс понял, что ошибся в выборе собеседника и что неодолимая сила притяжения увлекает его, не давая отступить ни на шаг. Какой-то миг он пытался бороться и вырываться, но расстояние между ним и другой частицей все сокращалось, и мистеру Томпкинсу показалось, что он уже видит торжествующую улыбку на лице своего противника.

— Пустите меня! Пустите меня немедленно! — закричал мистер Томпкинс во весь голос, изо всех сил отбиваясь руками и ногами. — Я не хочу аннигилировать! Я хочу вечно проводить электрический ток!

Но все было тщетно, и окружающее пространство внезапно озарилось ослепительной вспышкой сильнейшего излучения.

— Итак, меня больше нет, — подумал мистер Томпкинс, — но как же в таком случае я могу мыслить? Может быть аннигилировало только мое тело, а душа моя улетела на квантовые небеса?

Тут он ощутил новую силу, на этот раз действовавшую мягче, которая твердо и решительно трясла его. Открыв глаза, мистер Томпкинс увидел перед собой университетского служителя.

— Простите, сэр, — сказал тот, — но лекция уже давно закончилась и нам нужно закрыть аудиторию.

Мистер Томпкинс с трудом подавлял зевоту и чувствовал себя весьма неловко.

— Спокойной ночи, сэр, — пожелал ему служитель с сочувственной улыбкой.

Глава 10 1/2

Часть предыдущей лекции, которую проспал мистер Томпкинс

В 1908 г. английский физик Джон Дальтон открыл закон кратных отношений. Он показал, что относительные пропорции различных химических элементов, необходимых для образования более сложных химических веществ, всегда могут быть выражены как отношения целых чисел и объяснил свой закон тем, что все сложные химические вещества состоят из различного числа частиц, соответствующих простым химическим элементам. Безуспешные попытки средневековой алхимии превратить один химический элемент в другой служат еще одним доказательством кажущейся неделимости мельчайших частиц вещества, которые без особых колебаний были названы своим древнегреческим именем — атомы. Данное единожды, это название закрепилось, и хотя теперь твердо установлено, что атомы Дальтона отнюдь не неделимы и в действительности состоят из большого числа более мелких, субатомных частиц, обычно мы предпочитаем закрывать глаза на филологическую непоследовательность этого названия.

Итак, то, что в современной физике принято называть атомами, отнюдь не является элементарными и неделимыми составными частями материи, о которых говорил в своих умозрительных построениях Демокрит, и термин «атом» был бы более обоснован применительно к более мелким субатомным частицам, таким как электроны и протоны, из которых состоят атомы Дальтона. Но такое изменение терминологии породило бы слишком большую путаницу, и ни один физик не заботится особенно о филологической непоследовательности существующей ныне терминологии. Поэтому мы употребляем старое название «атомы» в том же смысле, в каком его употреблял Дальтон, а электроны, протоны и другие субатомные единицы материи называем элементарными частицами.

Это название свидетельствует о том, что в настоящее время мы считаем эти субатомные частицы действительно элементарными и неделимыми в смысле Демокрита, и вы, естественно, можете спросить у меня, не повторится ли история и не выяснится ли в ходе дальнейшего развития современной физики, что так называемые элементарные частицы в действительности обладают весьма сложной внутренней структурой. Мой ответ состоит в том, что хотя нет абсолютной гарантии, что ничего такого не произойдет, имеются достаточно веские основания полагать, что на этот раз мы не ошиблись. Действительно, существуют девяносто две разновидности атомов (соответствующие девяносто двум различным химическим элементам), и каждый такой атом обладает весьма сложными характерными свойствами. В подобной ситуации само собой напрашивается упрощение — стремление свести сложную картину к более простой. С другой стороны, в современной физике известны лишь несколько различных типов элементарных частиц: электроны (отрицательно и положительно заряженные легкие частицы), нуклоны (заряженные или нейтральные тяжелые частицы, известные под названием протонов и нейтронов) и, возможно, так называемые нейтрино, природа которых полностью не выяснена.

Свойства этих элементарных частиц чрезвычайно просты, и дальнейшее деление материи не приведет к сколько-нибудь существенному упрощению. Кроме того, как вы понимаете, всегда необходимо иметь несколько элементарных понятий, с которыми можно было бы играть, если вы хотите построить нечто более сложное. Два или три таких элементарных понятия — отнюдь не много. Я считаю, что вы можете спокойно поставить последний доллар, держа пари, что элементарные частицы современной физики останутся достойными своего названия.

Но вернемся к вопросу о том, каким образом атомы Дальтона построены из элементарных частиц. Первый правильный ответ на этот вопрос был дан в 1911 г. знаменитым британским физиком Эрнестом Резерфордом (впоследствии Резерфорд лорд Нельсон). Резерфорд исследовал строение атома, бомбардируя различные атомы быстро движущимися крохотными снарядами, известными под названием альфа-частицы, испускаемыми при распаде радиоактивных элементов. Наблюдая за отклонениями (рассеянием) снарядов после прохождения кусочка материи (листочка фольги), Резерфорд пришел к выводу, что все атомы должны обладать очень плотной положительно заряженной сердцевиной (атомным ядром), окруженной гораздо более разреженным отрицательно заряженным облаком (атомной атмосферой). Ныне мы знаем, что атомное ядро состоит из определенного числа протонов и нейтронов, известных под собирательным названием нуклонов. Нуклоны тесно связаны между собой сильными силами сцепления. Атомная атмосфера состоит из различного числа отрицательно заряженных электронов, которые роем окружают атомное ядро под действием электростатического притяжения его положительного заряда. Число электронов, образующих атомную атмосферу, определяет все физические и химические свойства атома и изменяется вдоль естественной последовательности химических элементов от одного электрона (для водорода) до девяносто двух электронов (для самого тяжелого из известных элементов урана).

Несмотря на кажущуюся простоту атомной модели Резерфорда, ее детальный анализ оказался далеко не простым. Действительно, согласно одному из наиболее глубоко укоренившихся представлений классической физики, отрицательно заряженные электроны, обращаясь вокруг атомного ядра, должны терять свою энергию в виде испускаемого ими излучения (света). Как показывают вычисления, из-за постоянных потерь энергии все электроны, образующие атомную атмосферу, должны были бы за ничтожно малую долю секунды упасть на ядро. Это, казалось бы, вполне здравое рассуждение классической теории находится в резком противоречии с тем эмпирическим фактом, что атомные атмосферы очень стабильны и атомные электроны не падают на ядро, а бесконечно долго кружатся роем вокруг центрального тела. Таким образом, между основными представлениями классической механики и эмпирическими данными относительно механического поведения крохотных составных частей мира атомов возникает глубокое противоречие. Размышления над этим противоречием привели известного датского физика Нильса Бора к заключению, что классическая механика, на протяжении столетий претендовавшая на особое незыблемое положение в системе естественных наук, должна отныне рассматриваться как ограниченная теория, применимая к макроскопическому миру повседневного опыта, но утрачивающая силу при попытке применить ее к гораздо более тонким типам движения происходящего внутри различных атомов. В качестве пробного фундамента новой обобщенной механики, применимой и к движению крохотных подвижных частей атомного механизма, Бор предложил гипотезу о том, что из всего бесконечного разнообразия типов движения, рассматриваемых в классической механике, в природе реализуется только несколько специально выбранных типов. Эти разрешенные типы движения (называемые также разрешенными траекториями, или орбитами) отбираются в соответствии с определенными математическими условиями, известными под названием условий квантования в теории Бора. Я не стану входить здесь в подробное обсуждение этих условий квантования, но хочу лишь упомянуть об одном обстоятельстве: все эти условия выбраны таким образом, что налагаемые ими ограничения не имеют практического значения в тех случаях, когда масса движущейся частицы во много раз больше масс, с которыми мы встречаемся в структуре атома. Следовательно, применительно к макроскопическим телам новая микромеханика приводит к тем же результатам, что и старая классическая теория (принцип соответствия) и только при переходе к микроскопическим атомным механизмам разногласия между старой и новой теориями становятся существенными. Не вдаваясь в детали, я хочу удовлетворить ваше любопытство и продемонстрировать строение атома с точки зрения теории Бора, а именно схему расположения квантовых орбит в атоме по Бору (первый слайд, пожалуйста!). Вы видите (см. рис. на с. 163), разумеется, в сильно увеличенном масштабе, систему круговых и эллиптических орбит. Они представляют единственно «разрешенные» условиями квантования Бора типы движений для электронов, образующих атомную атмосферу. В то время как классическая механика разрешает электрону двигаться на любом расстоянии от ядра и не накладывает ограничений на эксцентриситет (т. е. на удлинение, или вытянутость) орбиты, разрешенные орбиты в теории Бора образуют дискретное множество с вполне определенными характерными размерами. Числа и латинские буквы, стоящие у каждой орбиты, указывают название соответствующей орбиты в общей классификации. Вы можете, например, заметить, что большие числа соответствуют орбитам с большими диаметрами.

Хотя предложенная Бором теория строения атома оказалась необычайно плодотворной для объяснения различных свойств атомов и молекул, основное понятие — дискретная квантовая орбита — оставалось весьма неясным, и чем глубже физики пытались вникнуть в анализ столь необычного ограничения классической теории, тем более неясной становилась общая картина.

Наконец, физики осознали, в чем именно заключается слабая сторона теории Бора: вместо основательной перестройки классической механики теория Бора просто наложила ограничения на ее результаты, введя дополнительные условия, в принципе чуждые всей структуре классической теории. Правильное решение всей проблемы было получено лишь тринадцать лет спустя в виде так называемой волновой механики, изменившей самые основы классической механики в соответствии с новым квантовым принципом. Несмотря на то, что на первый взгляд система волновой механики может показаться еще более «сумасшедшей», чем теория Бора, эта новая микромеханика представляет собой одну из наиболее последовательных и признанных частей современной теоретической физики. Поскольку фундаментальный принцип новой механики и, в частности, понятия «неопределенность» и «расплывание траекторий» были рассмотрены мной в одной из предыдущих лекций, я обращаюсь теперь к вашей памяти или к вашим конспектам и хотел бы вернуться к проблеме строения атома. На схеме, которую вы сейчас увидите (следующий слайд, пожалуйста!) (см. рис. внизу), изображено движение атомных электронов, рассматриваемое с позиций волновой механики, или с точки зрения «расплывания орбит». Вы видите здесь те же самые типы движения, которые в рамках классической теории были представлены на предыдущем слайде (единственное различие состоит лишь в том, что по чисто техническим причинам каждый тип движения теперь изображен отдельно), но вместо четких линий, изображающих траектории в теории Бора, теперь перед нами расплывчатые пятна в полном согласии с фундаментальным принципом неопределенности. Различные состояния движения имеют такие же обозначения, как на предыдущем слайде, и сравнивая оба слайда, вы заметите, если слегка напряжете воображение, что расплывчатые облака на втором слайде очень точно передают общие характерные особенности старых орбит Бора.

Оба слайда отчетливо показывают, что происходит с добрыми старомодными траекториями классической механики, когда в игру вступает квант, и хотя человеку непосвященному все это может показаться фантастическим сном, ученые, работающие в микрокосмосе атомов, не испытывают особых трудностей в восприятии такой картины.

Завершив на этом краткий обзор возможных состояний движения в электронной атмосфере атома, мы обращаемся теперь к важной проблеме, касающейся распределения различных атомных электронов по различным допустимым состояниям движения. Здесь мы сталкиваемся с новым принципом, совершенно незнакомым в макроскопическом мире. Этот принцип впервые был сформулирован моим молодым другом Вольфгангом Паули. Он утверждает, что в сообществе электронов данного атома никакие два электрона не обладают движением одного и того же типа. Это ограничение не имело бы особого значения, если бы число возможных движений было бесконечно велико, как в классической механике. Но поскольку правила квантования существенно уменьшают число «разрешенных» состояний движения, принцип Паули играет очень важную роль в атомном мире: он обеспечивает более или менее равномерное распределение электронов вокруг атомного ядра и мешает электронам скапливаться в каком-то одном месте.

Но из приведенной выше формулировки нового принципа не следует делать вывода о том, что расплывчатые квантовые состояния движения, изображенные на втором слайде, могут быть «заняты» только одним электроном. Действительно, помимо движения по орбите каждый электрон обладает спином, т.е. вращается вокруг собственной оси, и доктора Паули отнюдь не разочарует, если два электрона окажутся на одной орбите, если их спины будут направлены в противоположные стороны. Исследование спина электронов показывает, что скорость вращения электронов вокруг собственной оси всегда одна и та же и что направление спина всегда должно быть перпендикулярно плоскости орбит. Это означает, что возможны только два различных направления спина, которые соответственно можно считать происходящими «по часовой стрелке» и «против часовой стрелки».

Таким образом, применительно к квантовым состояниям принцип Паули может быть сформулирован следующим образом: в каждом квантовом состоянии движения могут находиться не более двух электронов, спины которых должны быть направлены в противоположные стороны. Проходя всю естественную последовательность элементов к атомам со все большим и большим числом электронов, мы обнаружим, что различные квантовые состояния движения постепенно заполняются электронами и диаметр атома монотонно возрастает. В этой связи нельзя не упомянуть о том, что с точки зрения силы связи различные квантовые состояния атомных электронов могут быть объединены в отдельные группы (или оболочки) с приблизительно равной силой связи. По мере продвижения вдоль естественной последовательности элементов, мы видим, что одна группа заполняется за другой и в результате последовательного заполнения электронных оболочек свойства атомов периодически изменяются. Это объясняет хорошо известную периодичность свойств элементов, открытую эмпирически знаменитым русским химиком Дмитрием Ивановичем Менделеевым.

Глава 12

Внутри ядра

Следующая лекция, которую посетил мистер Томпкинс, была посвящена внутреннему строению ядра как центра, вокруг которого вращаются атомные электроны.

— Леди и джентльмены, — начал профессор. — Все более углубляясь в строение материи, мы попытаемся теперь проникнуть нашим мысленным взором внутрь ядра, в загадочную область, занимающую лишь одну тысячную от миллиардной доли общего объема атома. И все же, несмотря на столь невероятно малые размеры новой области наших иссследований, мы обнаружили в ней самую оживленную деятельность. Ведь атомное ядро — сердце атома, и именно в нем, несмотря на сравнительно малые размеры, сосредоточено 99,97% всей массы атома.

Вступая в область атомного ядра после сравнительно бедно населенной электронной атмосферы атома, мы сразу же будем поражены ее необычной перенаселенностью. Если электроны атомной атмосферы движутся в среднем на расстояниях, превышающих их собственный диаметр примерно в несколько тысяч раз, то частицы, живущие внутри ядра, буквально теснились бы плечом к плечу, будь у них плечи. В этом смысле картина, которая открывается нам внутри ядра, очень напоминает картину обыкновенной жидкости с тем лишь различием, что внутри ядра мы вместо молекул встречаем гораздо более мелкие и гораздо более элементарные частицы, известные под названием протоны и нейтроны. Уместно заметить, что, несмотря на различные имена, протоны и нейтроны можно рассматривать просто как два различных зарядовых состояния одной и той же тяжелой элементарной частицы, известной под названием нуклон. Протон представляет собой положительно заряженный нуклон, нейтрон — электрически нейтральный нуклон. Не исключена возможность, что существуют также отрицательно заряженные нуклоны, хотя их пока никто не наблюдал. Что касается их геометрических размеров, нуклоны не слишком отличаются от электронов: диаметр нуклона составляет около 0,000 000 000 0001 см. Однако нуклоны гораздо тяжелее: на чашках весов протон или нейтрон можно уравновесить 1840 электронами. Как я уже говорил, частицы, образующие атомное ядро, упакованы очень плотно и это объясняется действием особых ядерных сил сцепления, аналогичных силам, действующим между молекулами в жидкости. Так же как в жидкости силы ядерного сцепления не дают нуклонам полностью отделиться друг от друга, но не мешают относительным перемещениям нуклонов. Таким образом, ядерная материя в какой-то степени обладает текучестью и, не будучи возмущаема внешними силами, принимает форму сферической капли, как обычная капля жидкости. На схеме, которую я вам сейчас покажу, условно изображены различные типы атомных ядер, образованных из протонов и нейтронов. Простейшее ядро водорода состоит всего лишь из одного протона, в то время как самое сложное ядро урана состоит из 92 протонов и 142 нейтронов. Разумеется, разглядывая эти картинки, не следует упускать из виду, что перед вами лишь весьма условные изображения реальных ядер, поскольку в силу фундаментального принципа неопределенности квантовой теории положение каждого нуклона в действительности «размазано» по всему объему ядра.

Как я уже упоминал, частицы, образующие атомное ядро, удерживаются вместе мощными силами сцепления, но помимо этих сил притяжения существуют также силы другого рода, действующие в противоположном направлении. Действительно, протоны, на долю которых приходится примерно половина нуклонного населения, несут положительный заряд. Следовательно, между ними действуют силы отталкивания — так называемые кулоновские силы. Для легких ядер, электрический заряд которых сравнительно мал, это кулоновское отталкивание не имеет особого значения, но в более тяжелых ядрах с большим электрическим зарядом кулоновские силы начинают составлять серьезную конкуренцию силам ядерного сцепления. Как только это произойдет, ядро утрачивает стабильность и может испустить какие-нибудь из составляющих его частиц. Именно так ведут себя некоторые элементы, расположенные в самом конце Периодической системы и известные под названием радиоактивные элементы.

Из приведенных выше общих соображений вы можете заключить, что такие тяжелые нестабильные ядра должны испускать протоны, так как нейтроны не несут никакого электрического заряда, и поэтому на них не действуют силы кулоновского отталкивания. Однако, как показывают эксперименты, некоторые радиоактивные ядра испускают так называемые альфа-частицы (ядра гелия), т. е. сложные образования, каждое из которых состоит из двух протонов и двух нейтронов. Объясняется это особой группировкой частиц, образующих атомное ядро. Дело в том, что комбинация двух протонов и двух нейтронов, образующая альфу-частицу, отличается повышенной стабильностью, и поэтому легче оторвать такую группу целиком, чем разделить ее на отдельные протоны и нейтроны.

Как вы, вероятно, знаете, явление радиоактивного распада было впервые открыто французским физиком Анри Беккерелем, а знаменитый британский физик лорд Резерфорд, чье имя я уже упоминал в другой связи, которому наука столь многим обязана за его важные открытия в физике атомного ядра, предложил объяснение радиоактивного распада как спонтанного, т. е. самопроизвольного, распада атомного ядра на части.

Одна из наиболее замечательных особенностей альфа-распада состоит в иногда необычайно долгих периодах времени, необходимых альфа-частицам, чтобы «выбраться» из атомного ядра на свободу. Для урана и тория этот период составляет, по оценкам, миллиарды лет, для радия — около шестнадцати столетий, и хотя существуют элементы, для которых альфа-распад происходит в доли секунды, продолжительность их жизни можно также считать очень долгой по сравнению с быстротой их внутриядерного движения.

Что же заставляет альфа-частицу оставаться внутри ядра на протяжении иногда многих миллиардов лет? И если альфа-частица так долго находится внутри ядра, то что заставляет ее все же покинуть его?

Для ответа на эти вопросы нам необходимо предварительно узнать немного больше о сравнительной интенсивности сил внутриядерного сцепления и электростатических сил отталкивания, действующих на частицу, которая покидает атомное ядро. Тщательное экспериментальное изучение этих сил было проведено Резерфордом, который воспользовался методом так называемой атомной бомбардировки. В своих знаменитых экспериментах, выполненных в Кавендишской лаборатории, Резерфорд направлял пучок быстро движущихся альфа-частиц, испускаемых каким-нибудь радиоактивным веществом, на мишень и наблюдал отклонения (рассеяние) этих атомных снарядов при столкновении их с ядрами бомбардируемого вещества. Эксперименты Резерфорда убедительно показали, что на больших расстояниях от атомного ядра альфа-частицы испытывали сильное отталкивание электрическими силами заряда ядра, но отталкивание сменялось сильным притяжением в тех случаях, когда альфа-частицы пролетали вплотную от внешних границ ядерной области. Вы можете сказать, что атомное ядро в какой-то мере аналогично крепости, окруженной со всех сторон высокими крутыми стенами, не позволяющими частицам ни попасть внутрь, ни бежать наружу. Но самый поразительный результат экспериментов Резерфорда состоял в установлении следующего факта: альфа-частицы, вылетающие из ядра при радиоактивном распаде или проникающие внутрь ядра при бомбардировке извне, обладают меньшей энергией, чем требовалось бы для преодоления высоты стен крепости, или потенциального барьера, как мы обычно говорим. Это открытие Резерфорда полностью противоречило всем фундаментальным представлениям классической механики. В самом деле, как можно ожидать, что мяч перекатится через вершину холма, если вы бросили его с энергией, недостаточной для подъема на вершину холма? Классическая физика могла лишь широко раскрыть глаза от удивления и высказать предположение о том, что в эксперименты Резерфорда где-то вкралась какая-то ошибка.

Но в действительности никакой ошибки не было, и если кто-нибудь и ошибался, то не лорд Резерфорд, а… классическая механика! Ситуацию прояснили одновременно мой добрый друг доктор Гамов и доктора Рональд Герней и Э. У. Лондон. Они обратили внимание на то, что никаких трудностей не возникает, если подойти к проблеме с точки зрения современной квантовой теории. Действительно, как мы знаем, современная квантовая физика отвергает четко определенные траектории-линии классической теории и заменяет их расплывчатыми призрачными следами. Подобно тому, как доброе старомодное привидение могло без труда проходить сквозь толстые каменные стены старинного замка, так призрачные траектории могут проникать сквозь потенциальные барьеры, которые с классической точки зрения казались совершенно непроницаемыми.

Не думайте, пожалуйста, будто я шучу: проницаемость потенциальных барьеров для частиц с недостаточной энергией является прямым математическим следствием из фундаментальных уравнений новой квантовой механики и служит весьма убедительной иллюстрацией одного из наиболее существенных различий между старыми и новыми представлениями о движении. Но хотя новая механика допускает столь необычные эффекты, она делает это только при весьма сильных ограничениях: в большинстве случаев вероятность пересечения барьера чрезвычайно мала, и попавшей в темницу ядра частице придется невероятно большое число раз бросаться на стены, прежде чем ее попытки выбраться на свободу увенчаются успехом. Квантовая теория дает нам точные правила для вычисления вероятности такого побега. Было показано, что наблюдаемые периоды альфа-распада находятся в полном соответствии с предсказаниями теории. В случае альфа-частиц, бомбардирующих атомное ядро извне, результаты квантово-механических расчетов находятся в великолепном соответствии с экспериментом.

Прежде чем я продолжу свою лекцию, мне хотелось бы показать вам некоторые фотографии процессов распада различных ядер, бомбардируемых атомными снарядами высокой энергии (первый слайд, пожалуйста!).

На этом слайде (см. рис. на с. 174) вы видите два различных распада, сфотографированных в пузырьковой камере, о которой я говорил в своей предыдущей лекции. На снимке (А) вы видите столкновение ядра азота с быстрой альфа-частицей. Это первый из когда-либо сделанных снимков искусственной трансмутации (превращения) элементов. Этим снимком мы обязаны ученику лорда Резерфорда Патрику Блэккету. Отчетливо видно большое число треков альфа-частиц, испускаемых мощным источником альфа-частиц. Большинство альфа-частиц пролетают все поле зрения, не претерпевая ни одного серьезного столкновения. Трек альфа-частиц останавливается вот здесь, и вы видите, как из точки столкновения выходят два других трека. Длинный тонкий трек принадлежит протону, выбитому из ядра азота, в то время как короткий толстый трек соответствует отдаче самого ядра. Но это более уже не ядро азота, поскольку, потеряв протон и поглотив налетевшую альфа-частицу, ядро азота превратилось в ядро кислорода. Таким образом, мы становимся свидетелями алхимического превращения азота в кислород с водородом в качестве побочного продукта.

На снимках (Б), (В) вы видите распад ядра при столкновении с искусственно ускоренным протоном. Пучок быстрых протонов создается специальной машиной, работающей под высоким напряжением и известной публике под названием «атомная дробилка», и поступает в камеру через длинную трубку, конец которой виден на снимках. Мишень, в данном случае тонкий слой бора, помещается у открытого конца трубки с таким расчетом, чтобы осколки ядра, возникшие при столкновении, должны были пролетать сквозь воздух в камере, образуя туманные треки. Как вы видите на снимке (В), ядро бора при столкновении с протоном, распадается на три части, и, с учетом сохранения электрического заряда, мы приходим к заключению, что каждый из осколков деления представляет собой альфа-частицу, т. е. ядро гелия. Эти два ядерных превращения представляют весьма типичные примеры нескольких сотен других ядерных превращений, исследованных современной экспериментальной физикой. Во всех превращениях такого рода, известных под названием ядерные реакции замещения, налетающая частица (протон, нейтрон или альфа-частица) проникает в ядро, выбивает какую-то другую частицу и остается на ее месте. Существует замещение протона альфа-частицей, альфа-частицы протоном, протона нейтроном и т.д. Во всех таких превращениях новый элемент, образовавшийся в результате реакции, является близким соседом бомбардируемого элемента в Периодической системе.

Но лишь сравнительно недавно, перед второй мировой войной, два немецких химика О. Ган и Ф. Штрассман открыли совершенно новый тип ядерного превращения, в котором тяжелое ядро распадается на две равные половины с высвобождением огромного количества энергии. На следующем слайде (следующий слайд, пожалуйста!) вы видите (см. с. 175) на снимке (Б) два осколка ядра урана, разлетающихся в разные стороны от тонкой урановой проволочки. Это явление, получившее название расщепление ядра, впервые наблюдалось при бомбардировке урана пучком нейтронов, но вскоре физики обнаружили, что и другие элементы, расположенные в конце Периодической системы, обладают аналогичными свойствами. Эти тяжелые ядра уже находятся у порога своей стабильности и малейшее возмущение, вызываемое столкновением с нейтроном, достаточно, чтобы они распались на два осколка, как распадается на части чрезмерно крупная капля ртути. Нестабильность тяжелых ядер проливает свет на вопрос о том, почему в природе существует только 92 элемента. Любое ядро тяжелее урана не может существовать сколько-нибудь продолжительное время и немедленно распадается на более мелкие осколки. Явление расщепления ядра представляет немалый интерес и с практической точки зрения, так как открывает определенные возможности для использования ядерной энергии. Дело в том, что при распаде ядра на две половинки из ядра вылетает несколько нейтронов, которые могут вызвать расщепление соседних ядер. Дальнейшее распространение такого процесса может привести к взрывной реакции, при которой вся энергия, запасенная в ядрах, высвобождается за малую долю секунды. Если вспомнить, что ядерная энергия, хранящаяся в одном фунте урана, эквивалентна энергетическому содержанию десяти тонн угля, то станет ясно, что возможность высвобождения ядерной энергии могла бы вызвать глубокие перемены в нашей экономике.

Однако все эти ядерные реакции могут быть осуществлены лишь в очень малом масштабе, и, хотя они позволяют нам получить богатейшую информацию о внутреннем строении ядра, вплоть до сравнительно недавнего времени не было ни малейшей надежды на то, что удастся высвободить огромное количество ядерной энергии. И лишь в 1939 г. немецкие химики О. Ган и Ф. Штрассман открыли совершенно новый тип ядерного превращения: тяжелое ядро урана при столкновении с одним-единственным нейтроном распадается на две примерно равные части с высвобождением огромного количества энергии и вылетом двух или трех нейтронов, которые в свою очередь могут столкнуться с ядрами урана и расщепить каждое из них на две части с высвобождением новой энергии и новых нейтронов. Цепной процесс, деления ядер урана может приводить к взрывам или, если сделать его управляемым, стать почти неисчерпаемым источником энергии. Счастлив сообщить вам, что доктор Таллеркин, принимавший участие в работах по созданию атомной бомбы и известный также как отец водородной бомбы, любезно согласился прибыть к нам, несмотря на свою чрезвычайную занятость, и выступить с коротким сообщением о принципах устройства ядерных бомб. Мы ожидаем его прибытия с минуты на минуту.

Едва профессор успел произнести эти слова, как дверь отворилась и в аудиторию вошел человек весьма внушительного вида с горящими глазами и нависшими кустистыми бровями. Обменявшись с профессором рукопожатиями, человек обратился к аудитории:

— Hoolgyeim es Uraim, — начал он. — Roviden kell beszelnem, mert nagyon sok a dolglom. Ma reggel tubb megbeszelesem volt a Pentagonban es a Feher Hazban. Delutan… О, прошу прощения! — воскликнул незнакомец. — Иногда я путаю языки. Позвольте мне начать еще раз.

Леди и джентльмены! Я буду краток, поскольку очень занят. Сегодня утром я присутствовал на нескольких совещаниях в Пентагоне и в Белом доме, а днем мне необходимо быть в Френч Флэте, штат Невада, где предстоит провести подземный взрыв. Вечером я должен произнести речь на банкете, который состоится на базе ВВС США Ванденберг в Калифорнии.

Теперь о главном. Дело в том, что в атомных ядрах поддерживается равновесие между силами двоякого рода — ядерными силами притяжения, которые стремятся удержать ядро в целости, и электрическими силами отталкивания между протонами. В тяжелых ядрах, таких как ядра урана или плутония, силы отталкивания преобладают, и ядра при малейшем возмущении готовы распасться на два осколка — продукты деления. Таким возмущением может быть один-единственный нейтрон, сталкивающийся с ядром.

Обернувшись к доске, гость продолжал:

— Вот делящееся ядро, а вот сталкивающийся с ним нейтрон. Два осколка деления разлетаются в стороны, и каждый из них уносит около одного миллиона электрон-вольт энергии. Кроме того, распадаясь, ядро выстрелило несколькими новыми нейтронами деления (обычно их бывает два в случае легкого изотопа урана и три в случае плутония). Реакция — бац, бац! — продолжается, как я изобразил здесь на доске. Если кусок делящегося материала мал, то большая часть нейтронов деления вырывается из его поверхности прежде, чем они имеют шанс столкнуться с другим делящимся ядром, и цепная реакция так и не начинается. Но если кусок делящегося материала имеет достаточно большие размеры (мы называем такой кусок критической массой), дюйма три-четыре в диаметре, то большинство нейтронов оказываются захваченными, и вся эта штука взрывается. Такое устройство мы называем бомбой деления (в печати ее довольно часто неправильно называют атомной бомбой).

Гораздо лучших результатов можно достичь, если обратиться к другому концу Периодической системы элементов, где ядерные силы превосходят электрическое отталкивание. Когда два легких ядра приходят в соприкосновение, они сливаются, как две капельки ртути на блюдечке. Такое слияние может произойти только при очень высокой температуре, так как электрическое отталкивание — мешает легким ядрам сблизиться и прийти в соприкосновение. Но когда температура достигает десятков миллионов градусов, электрическое отталкивание уже не в силах помешать сближению атомов и процесс слияния, или термоядерного синтеза, начинается. Наиболее подходящими ядрами для термоядерного синтеза являются дейтроны, т. е. ядра атомов тяжелого водорода. Справа на доске я изобразил простую схему термоядерной реакции в дейтерии. Когда мы впервые придумали водородную бомбу, нам казалось, что она станет благословением для всего мира, так как при ее взрыве не образуются радиоактивные продукты деления, которые потом разносятся по всей земной атмосфере. Но нам не удалось создать «чистую» водородную бомбу, потому что дейтерий, лучшее ядерное топливо, которое легко извлекается из морской воды, недостаточно хорошо горит сам по себе. Нам пришлось окружить дейтериевую сердцевину урановой оболочкой. Такие оболочки порождают множество осколков деления, и люди прозвали нашу конструкцию «грязной» водородной бомбой. Аналогичные трудности возникли и при проектировании управляемой термоядерной реакции с дейтерием и, несмотря на все усилия, нам так и не удалось осуществить ее. Но я уверен, что рано или поздно проблема управляемого термоядерного синтеза будет решена.

— Доктор Таллеркин, — спросил кто-то из аудитории, — могут ли осколки деления ядер при испытаниях грязной водородной бомбы вызвать опасные для здоровья человека мутации у населения всего земного шара?

— Не все мутации вредны, — улыбнулся доктор Таллеркин. — Некоторые мутации способствуют улучшению наследственности. Если бы в живых организмах не происходили мутации, то и вы, и я все еще были бы амебами. Разве вы не знаете, что эволюция жизни на Земле происходит исключительно благодаря мутациям и выживанию наиболее приспособленных мутантов?

— Уж не хотите ли вы сказать, — истерически закричала какая-то женщина в аудитории, — что мы должны рожать детей дюжинами и, отобрав наилучших, умервщлять остальных?

— Видите ли… — начал доктор Таллеркин, но в этот момент дверь отворилась и в аудиторию вошел человек в летной форме.

— Поторапливайтесь, сэр! — скороговоркой доложил он. — Ваш вертолет припаркован у входа и, если мы не вылетим сейчас же, вы не сможете вовремя прибыть в аэропорт, где вас ожидает специальный реактивный самолет!

— Прошу меня извинить, — обратился доктор Таллеркин к аудитории, — но мне пора идти. Isten veluk!

И они оба, доктор Таллеркин и пилот, поспешили из аудитории.

Глава 13

Резчик по дереву

Дверь была большая и массивная. Посредине на ней красовалась надпись, сделанная крупными буквами: «Осторожно! Высокое напряжение!». Но первое впечатление негостеприимства несколько смягчалось крупной надписью «Добро пожаловать!» на коврике у двери, и после минутного колебания мистер Томпкинс нажал на кнопку дверного звонка. Дверь открыл молодой ассистент, и мистер Томпкинс оказался в огромном помещении, добрую половину которого занимала замысловатая машина самого фантастического вида.

— Это наш циклотрон, или «атомная дробилка», как его называют в газетах, — пояснил ассистент, любовно поглаживая витки одной из катушек гигантского электромагнита, составляющего основную часть весьма внушительно выглядевшего орудия современной физики.

— Он позволяет получать частицы с энергией до десяти миллионов электрон-вольт, — с гордостью продолжал ассистент, — и немного найдется ядер, которые способны выдержать столкновение с частицей, движущейся с такой невообразимой энергией!

— Потрясающе интересно! — отозвался мистер Томпкинс. — Эти ядра, должно быть, очень прочны! Трудно поверить, что этакая махина была построена только для того, чтобы раскололось крохотное ядро крохотного атома. А как работает эта машина?

— Вы были когда-нибудь в цирке? — спросил мистера Томпкинса его тесть, внезапно возникая откуда-то из-за гигантского циклотрона.

— Разумеется, был, — ответил мистер Томпкинс, несколько удивленный неожиданным вопросом. — Вы хотите предложить мне пойти с вами сегодня в цирк на вечернее представление?

— Не совсем, — улыбнулся профессор. — Просто, если вам случалось бывать в цирке, это поможет вам понять, как работает циклотрон. Взгляните между полюсов этого огромного магнита и вы увидите круглый медный кожух. Он служит кольцом, в котором ускоряются различные заряженные частицы, используемые в экспериментах по бомбардировке ядер. В центре кожуха расположен источник, испускающий все эти заряженные частицы, или ионы. Вылетая из источника, ионы движутся с очень маленькими скоростями, и сильное поле, создаваемое магнитом, изгибает их траектории в небольшие окружности вокруг центра. Затем мы начинаем погонять частицы и разгоняем их до все больших и больших скоростей.

— Я понимаю, как погонять лошадь, — заметил мистер Томпкинс, — но как вам удается погонять крохотные заряженные частицы, выше моего разумения.

— А между тем это очень просто. Если частица движется по кругу, то все, что необходимо делать, это сообщать ей ряд последовательных электрических толчков всякий раз, когда частица будет проходить через определенную точку своей траектории, подобно тому, как в цирке тренер хлыстом подгоняет лошадь всякий раз, когда та, описывая по арене круг за кругом, пробегает мимо него.

— Но тренер видит лошадь, — возразил мистер Томпкинс. — А разве вы видите частицу, описывающую круг за кругом в той медной коробке, чтобы подтолкнуть ее в нужный момент?

— Разумеется, не вижу, — согласился профессор, — но это и необязательно. Вся хитрость устройства циклотрона состоит в том, что, хотя ускоряемая частица движется все быстрее и быстрее, она всегда совершает полный оборот за одно и то же время. Дело в том, что по мере увеличения скорости частицы радиус, а следовательно, и длина ее круговой траектории также соответственно увеличиваются. В результате ускоряемая частица движется по раскручивающейся спирали и всегда приходит в одно и то же место «кольца» через одинаковые промежутки времени. Все, что необходимо сделать, это поместить в данном месте какое-нибудь электрическое устройство, которое подталкивало бы частицу через одинаковые промежутки времени. Мы делаем это с помощью колебательного электрического контура, очень похожего на те схемы, которые вы можете видеть на любой радиостанции. Каждый электрический толчок не очень силен, но кумулятивный эффект многих толчков позволяет разгонять частицу до очень больших скоростей. В этом огромное преимущество циклотрона: он позволяет достигать такого же эффекта, как напряжение во многие миллионы вольт, хотя нигде в циклотроне вы не найдете высоких напряжений.

— Очень остроумно, — задумчиво произнес мистер Томпкинс, — А чье это изобретение?

— Первый циклотрон был построен несколько лет назад ныне покойным Эрнестом Орландо Лоуренсом в Калифорнийском университете, — ответил профессор. — С тех пор циклотроны значительно выросли в своих размерах и распространились по физическим лабораториям со скоростью слухов. Они оказались удобнее, чем старые ускорители с целым каскадом трансформаторов или другие ускорители, работавшие как электростатические машины.

— А нельзя ли разбить атомное ядро вдребезги, не прибегая ко всем этим сложным машинам? — спросил мистер Томпкинс, твердо убежденный сторонник простоты, с недоверием относившийся к любым устройствам сложнее молотка.

— Разумеется, можно. Когда Резерфорд проводил свои первые эксперименты по искусственному превращению элементов, он как раз использовал обычные альфа-частицы, испускаемые естественными радиоактивными источниками. Но это было более двадцати лет назад, и, как вы можете убедиться, с тех пор методы деления атома существенно усовершенствовались.

— А не можете ли вы показать мне, как разбивают атом? — попросил мистер Томпкинс, всегда предпочитавший увидеть своими глазами вместо того, чтобы выслушивать длинные объяснения.

— С удовольствием, — ответил профессор. — Мы как раз приступаем к эксперименту по дальнейшему исследованию деления ядра бора при столкновении с быстрыми протонами. Когда ядро бора сталкивается с протоном и это столкновение достаточно сильно для того, чтобы бомбардирующая частица проникла сквозь потенциальный барьер и оказалась внутри ядра, оно распадается на три примерно равных осколка, которые разлетаются во все стороны. Весь процесс можно наблюдать непосредственно в так называемой пузырьковой камере, делающей видимыми траектории всех частиц, участвующих в столкновении. Такая камера с небольшим кусочком бора в середине установлена у выхода ускорительной системы, и как только циклотрон заработает, вы увидите деление ядра собственными глазами.

— Включите, пожалуйста, ток, — обратился профессор к своему ассистенту,

— а я пока займусь регулировкой магнитного поля.

Чтобы запустить циклотрон, понадобилось некоторое время, и предоставленный самому себе мистер Томпкинс праздно бродил по лаборатории. Его внимание привлекла сложная система усилительных ламп, тлевших слабым голубоватым светом. Не зная в точности, какие электрические напряжения используются в циклотроне (напряжение может быть мало для того, чтобы расщепить атомное ядро, но вполне достаточно, чтобы свалить быка!), мистер Томпкинс осторожно наклонился над лампами.

Последовал резкий щелчок, словно укротитель львов взмахнул своим хлыстом, и мистер Томпкинс почувствовал ужасную боль, пронзившую все его тело. В тот же миг тьма окутала все, и он потерял сознание.

Когда мистер Томпкинс, наконец, открыл глаза, он обнаружил, что лежит на полу в том самом месте, где его сразил электрический разряд. Помещение вроде бы оставалось прежним, но было обставлено совершенно по-другому. Вместо возвышавшегося наподобие башни циклотронного магнита, сияющих медных контактов и десятков сложных электрических устройств, торчавших тут и там, мистер Томпкинс увидел деревянный стол, на котором были разбросаны плотницкие инструменты. На старомодных полках, висевших по стенам, мистер Томпкинс заметил множество вырезанных из дерева фигур странных и необычных форм. За столом сидел приветливый старичок. Приглядевшись к его чертам, мистер Томпкинс был поражен сильным сходством со стариком Джепетто из фильма «Пиноккио» Уолта Диснея и с портретом покойного Резерфорда лорда Нельсона, висевшим в лаборатории у профессора.

— Прошу прощения за невольное вторжение, — сказал мистер Томпкинс, поднимаясь с пола. — Видите ли, я был на экскурсии в ядерной лаборатории и там со мной приключилось что-то странное.

— А, так вы интересуетесь атомным ядром? — оживился старичок, откладывая в сторону деревянную фигурку, которую он вырезал. Тогда вы попали как раз туда, куда надо! Я изготовляю всевозможные ядра и буду рад показать вам свою мастерскую.

— Я не ослышался? — переспросил мистер Томпкинс с озадаченным видом. — Вы сказали, что занимаетесь изготовлением ядер?

— Да, вы не ослышались. Правда, это требует известной сноровки, в особенности изготовление радиоактивных ядер. Ведь не успеешь их выкрасить, как они могут распасться.

— Выкрасить?

— Да, положительно заряженные частицы я обычно окрашиваю в красный цвет, а отрицательно заряженные — в зеленый. Вы, должно быть, знаете, что красный и зеленый цвета принадлежат к числу так называемых дополнительных цветов и при смешивании уничтожают друг друга [8]. Дополнительные цвета соответствуют положительным и отрицательным электрическим зарядам, которые нейтрализуют друг друга. Если атомное ядро состоит из одинакового числа положительных и отрицательных зарядов, быстро двигающихся в одну и в другую сторону, то такое ядро будет электрически нейтральным и покажется вам белым. Если же положительных или отрицательных частиц будет больше, то вся система будет окрашена в красный или в зеленый цвет. Не правда ли, просто?

— Здесь, — продолжал старичок, показывая мистеру Томпкинсу два больших деревянных ящика, стоявших возле стола, — я храню материалы, из которых можно изготовить различные ядра. В первом ящике у меня хранятся протоны — видите эти красные шары? Они очень стабильны и сохраняют свой красный цвет, даже если вы вздумаете поскоблить их ножом или чем-нибудь поцарапать. С нейтронами во втором ящике хлопот гораздо больше. Обычно они белые, или электрически нейтральные, но обнаруживают сильную тенденцию превращаться в красные протоны. Пока ящик плотно закрыт, все в порядке, но стоит лишь вынуть один нейтрон из ящика, как происходит следующее. Вот, полюбуйтесь сами.

Открыв ящик, старый резчик по дереву извлек из него один из белых шаров и положил его на стол. Какое-то время ничего не происходило, но как раз в тот момент, когда мистер Томпкинс начал терять терпение, шар внезапно ожил. На его поверхности появились красноватые и зеленоватые полосы, и вскоре некогда белый шар выглядел, как один из тех пестрых мраморных шариков, в которые так любят играть дети. Зеленый цвет начал концентрироваться на одной стороне шара, которая начала выпячиваться и затем полностью отделилась от шара, образовав блестящую зеленую каплю, которая упала на пол. Шар после этого стал красным и по внешнему виду ничем не отличался от красных шаров-протонов в первом ящике.

— Видите, что происходит, — сказал резчик, поднимая с пола зеленую каплю, ставшую твердой и круглой. — Белый цвет нейтрона превратился в зеленый и красный, а сам нейтрон распался на две отдельные частицы — протон и отрицательно заряженный электрон.

— Да, да, — добавил старичок, видя изумленное выражение на лице мистера Томпкинса, — эта частица цвета нефрита — не что иное, как обыкновенный электрон, ничем не отличающийся от других электронов в любом атоме и в чем угодно.

— Подумать только! — воскликнул мистер Томпкинс. — Это действительно превосходит все фокусы с разноцветными носовыми платками, какие только мне приходилось видеть. А можете ли вы вернуть шарам их исходную окраску?

— Да, я вотру зеленую краску в поверхность красного шара, от чего шар снова станет белым. Разумеется, для этого придется затратить определенное количество энергии. Другой способ состоит в том, чтобы соскрести с шара красную краску, но и он требует затрат энергии. Соскобленная с поверхности протона красная краска образует красную каплю, т. е. положительно заряженный электрон, о котором вам, должно быть, приходилось слышать.

— О да, когда я был электроном, — начал было мистер Томпкинс, но во время спохватился, — т. е. я хочу сказать, что слышал, будто положительные и отрицательные электроны при столкновении аннигилируют, т. е. взаимно уничтожаются. Не могли бы вы проделать этот трюк для меня?

— С удовольствием, — ответил старый мастер. — Делается это очень просто. Я не стану соскребать краску с этого протона. У меня и так осталась парочка-другая протонов от утренней работы.

Открыв один из ящиков, он извлек из него небольшой ярко-красный шар и, крепко держа его между указательным и большим пальцами, прижал к зеленому шару, лежавшему на столе. Последовал громкий треск, словно взорвалась хлопушка, и оба шара одновременно исчезли.

— Видели? — спросил резчик, дуя на слегка обожженные пальцы. — Поэтому из электронов и нельзя строить ядра. Однажды я попытался, но потом бросил эту затею и теперь строю ядра только из протонов и нейтронов.

— Но ведь нейтроны тоже нестабильны, если я не ошибаюсь? — спросил мистер Томпкинс, вспоминая превращения белого шара.

— Если брать нейтроны поодиночке, то они действительно нестабильны. Но когда они плотно упакованы в ядре и окружены другими частицами, то становятся стабильными. Если же нейтронов или протонов становится слишком много, то они могут претерпевать превращения и испускать из ядра лишнюю краску в виде положительно или отрицательно заряженных электронов. Такие события мы называем бета-распадом.

— Используете ли вы при изготовлении ядер клей? — поинтересовался мистер Томпкинс.

— Нет, никакой клей мне не нужен, — ответил старый мастер. — Эти частицы, извольте видеть, сами слипаются, стоит лишь поднести их друг к другу. Попробуйте сами, если хотите.

Последовав этому любезному приглашению, мистер Томпкинс взял в одну руку протон, в другую нейтрон и осторожно начал их сближать. Он сразу же почувствовал сильное притяжение и, взглянув на частицы, заметил чрезвычайно странное явление: частицы начали обмениваться окраской, становясь попеременно то красными, то белыми. Казалось, будто красная краска «перепрыгивает» с шара в правой руке на шар в левой руке, а затем с шара в левой руке снова на шар в правой руке. «Перекраска» шаров происходила так быстро, что казалось, будто между шарами протянулась розоватая лента, по которой то в одну, то в другую сторону перетекала краска.

— Мои друзья-теоретики называют это обменным взаимодействием, — заметил старый мастер, посмеиваясь над удивлением мистера Томпкинса. — Если угодно, можно сказать, что оба шара хотят быть красными, но поскольку они не могут быть красными одновременно, шары как бы попеременно перетягивают красную окраску к себе. Ни один из шаров не желает уступать другому, и поэтому шары вынуждены прилипнуть друг к другу и сосуществовать, покуда вы не разделите их насильно. А теперь я хочу показать вам, как просто изготовить любое ядро, какое вы только пожелаете. Какое ядро вам нравится больше других?

— Золото, — ответил мистер Томпкинс, помня об амбициях средневековых алхимиков.

— Золото? Сейчас посмотрим, — пробормотал себе под нос старый мастер, оборачиваясь к огромной таблице, висевшей на стене. — Ядро золота весит 197 единиц и несет 79 положительных электрических зарядов. Значит, для изготовления ядра золота я должен взять 79 протонов и 118 нейтронов — тогда масса ядра получится правильной.

Отсчитав нужное количество шаров каждого сорта, мастер поместил их в высокий цилиндрический сосуд и вставил в него тяжелый деревянный поршень. Затем изо всех сил он налег на поршень, пытаясь сдвинуть его вниз.

— Это необходимо для того, — пояснил он мистеру Томпкинсу, — чтобы преодолеть сильное электрическое отталкивание между положительно заряженными протонами. Лишь после того, как сжатие поршнем преодолеет отталкивание протонов, протоны и нейтроны слипнутся под действием обменных сил и образуют ядро золота.

С силой опустив поршень до отказа вниз, мастер вынул его и быстро перевернул цилиндрический сосуд. Блестящий розоватый шар выкатился из сосуда на стол, и, присмотревшись повнимательнее, мистер Томпкинс понял, что розоватый цвет возникал из-за смешения красных и белых вспышек, то и дело проскакивавших между быстро движущимися частицами.

— Как красиво! — воскликнул мистер Томпкинс. — Так вот он какой, атом золота!

— Еще не атом, а только атомное ядро, — поправил его старый мастер. — Чтобы завершить построение атома, необходимо добавить надлежащее количество электронов. Они нейтрализуют положительный заряд ядра и создадут вокруг него обычную электронную оболочку. Впрочем, сделать это не составляет особого труда, так как ядро само захватывает свои электроны, как только те окажутся поблизости.

— Интересно, — заметил мистер Томпкинс. — Мой тесть никогда не упоминал о том, что изготовить золото так просто.

— Ваш тесть и все эти так называемые физики-ядерщики! — воскликнул старый мастер с нотками раздражения в голосе. — Очень уж они важничают, хотя делать умеют очень мало. Они утверждают, будто протоны нельзя сжать в составное ядро, так как для этого потребовалось бы слишком большое давление. Один из них даже подсчитал, что для сближения протонов понадобилось бы приложить силу, равную весу Луны. Так почему бы не достать с неба Луну, если им больше нечего делать?

— Но они все же научились осуществлять некоторые ядерные превращения,

— мягко заметил мистер Томпкинс.

— Да, но с каким трудом даются им эти реакции! А новые элементы они получают в таких ничтожных количествах, что сами же едва могут их рассмотреть! Я сейчас продемонстрирую вам, как они это делают.

И схватив протон, старый мастер что было сил запустил им в ядро атома золота, лежавшее на столе. У самого ядра протон чуть замедлил свое движение, поколебался какой-то момент и затем нырнул внутрь ядра. Поглотив протон, ядро затряслось, словно от озноба, а затем от него с треском откололась небольшая часть.

— Видите, — сказал мастер, подбирая осколок. — Это то, что называется альфа-частицей! Если присмотреться повнимательнее, то видно, что она состоит из двух протонов и двух нейтронов. Такие частицы обычно испускаются тяжелыми ядрами так называемых радиоактивных элементов, но альфа-частицу можно выбить и из обычных стабильных ядер, если стукнуть по ним достаточно сильно. Хочу обратить ваше внимание на то, что оставшийся лежать на столе более крупный осколок уже не является ядром атома золота. Он утратил один положительный заряд, и теперь перед нами ядро атома платины, предыдущего элемента в периодической таблице. Однако в некоторых случаях протон, проникнув в ядро, не приводит к распаду ядра на два осколка. В этом случае вы получите ядро элемента, следующего за золотом в периодической таблице, т. е. ядро ртути. Комбинируя эти и аналогичные процессы, можно превращать любой элемент в любой другой.

— Теперь я понимаю, почему в ядерной физике используют пучки быстрых протонов, разогнанных до высоких энергий на циклотроне, — задумчиво произнес мистер Томпкинс. — А почему вы считаете, что этот метод нехорош?

— Потому что эффективность его очень низка. Прежде всего физики-ядерщики не умеют так точно попадать в ядро, как я: у них с ядром сталкивается лишь одна частица из тысячи. Во-вторых, даже в том случае, если частица попала в ядро, она с большой вероятностью не проникает внутрь ядра, а отскакивает от него. Вы, должно быть, заметили, что когда я запустил протоном в ядро атома золота, протон немного помедлил, прежде чем войти внутрь ядра и я уже было подумал, что протон отскочит назад.

— А что мешает частицам проникать в ядра? — поинтересовался мистер Томпкинс.

— Об этом вы могли бы догадаться и сами, — сказал старый мастер. — Если вы помните, и ядра, и бомбардирующие их протоны несут положительные заряды. Силы отталкивания, действующие между этими зарядами, образуют своего рода барьер, преодолеть который не так-то легко. Если бомбардирующие протоны все же проникают в ядерную крепость, то происходит это только потому, что они используют прием, напоминающий Троянского коня: проходят сквозь ядерные стены, как волны, а не как частицы.

— Боюсь, что это выше моего разумения, — печально заметил мистер Томгасинс. — Из ваших объяснений я не понял ни слова.

— Боюсь, что это так, — сказал резчик с улыбкой. — Сказать вам по правде, я и сам не очень разбираюсь во всем этом. Ведь я мастер. Я могу делать все эти вещи руками, но в теоретической абракадабре я не слишком силен. Главное здесь в том, что поскольку все эти ядерные частицы сделаны из квантового материала, они легко проходят, или просачиваются, сквозь препятствия, которые обычно считаются непроницаемыми.

— О, я кажется понимаю, что вы имеете в виду! — воскликнул мистер Томпкинс. — Помнится, однажды, еще до того, как я встретил Мод, мне довелось побывать в одном странном месте, где бильярдные шары вели себя в точности так, как вы сейчас сказали. — Бильярдные шары? Вы имеете в виду бильярдные шары из слоновой кости? — повторил с горечью старый мастер.

— Да, насколько я знаю, шары были выточены из бивней квантовых слонов,

— ответил мистер Томпкинс.

— Ничего не поделаешь, такова жизнь, — печально сказал старый мастер. — Подумать только, кто-то вырезает какие-то дурацкие шары, расходуя столь драгоценный материал для чьей-то забавы, а мне приходится вырезать протоны и нейтроны, фундаментальнейшие частицы Вселенной, из простого квантового дуба!

— Впрочем, — продолжал он бодрым тоном, чтобы скрыть разочарование, — мои несчастные деревянные игрушки ничуть не уступают всем этим дорогим финтифлюшкам из слоновой кости. Как я сейчас покажу вам, они легко проходят сквозь любой барьер. Взобравшись на стул, мастер достал с верхней полки резную фигурку необычного вида, напоминавшую модель вулкана.

— Вот, не угодно ли взглянуть, — продолжал мастер, осторожно смахивая пыль. — Перед вами модель барьера сил отталкивания, который окружает любое атомное ядро. Внешние склоны соответствуют отталкиванию электрических зарядов, а кратер — силам сцепления, удерживающим частицы внутри ядра. Если толкнуть шарик вверх по склону, но не слишком сильно, чтобы он не достиг края кратера, то вы, естественно, ожидаете, что шарик скатится назад. А вот что происходит на самом деле.

Мастер слегка подтолкнул шарик вверх по склону.

— Не вижу ничего необычного, — заметил мистер Томпкинс, когда шарик, поднявшись примерно до середины склона, скатился назад.

— Не торопитесь, — спокойно сказал мастер. — Не все и не всегда получается с первого раза.

Он еще раз толкнул шарик вверх по склону, и шарик снова скатился вниз. И лишь с третьей попытки шарик, поднявшись примерно до середины склона, внезапно исчез.

— Как вы думаете, где теперь шарик? — торжествующе спросил старый мастер с чувством фокусника, удачно выполнившего трудный трюк.

— Наверное, в кратере? — высказал предположение мистер Томпкинс.

— Вы совершенно правы, именно в кратере, — подтвердил его догадку старый мастер, вынимая шарик из углубления двумя пальцами.

— А теперь попробуем запустить его в обратном направлении, — предложил он мистеру Томпкинсу, — и посмотрим, сможет ли шарик выбраться из кратера, не перекатываясь через край.

В течение какого-то времени ничего не происходило, и мистер Томпкинс мог только слышать погромыхивание шарика, катавшегося то в одну, то в другую сторону внутри кратера. Затем, как по мановению волшебной палочки, шарик вдруг появился на середине склона и тихо скатился на стол.

— То, что вы сейчас видели, может служить хорошей иллюстрацией того, что происходит при радиоактивном альфа-распаде, — сказал резчик, ставя модель на полку, — только там вместо барьера из обычного квантового дуба существует барьер сил отталкивания электрических зарядов. В принципе никакой разницы между моделью и настоящим альфа-распадом нет. Иногда эти электрические барьеры в атомах становятся настолько «прозрачными», что частицы покидают ядра за ничтожную долю секунды. В других случаях ядерные барьеры настолько «непрозрачные», что переход из ядра наружу затягивается на многие миллиарды лет, как например в ядре урана.

— Но почему не все ядра радиоактивны? — поинтересовался мистер Томтпсинс.

— Потому что у большинства ядер дно кратера расположено ниже уровня подошвы вулкана, и только у самых тяжелых из известных ядер дно кратера поднято достаточно высоко для того, чтобы «побег» частицы мог состояться.

Трудно сказать, сколько часов провел мистер Томтпсинс в мастерской у милого старого мастера, с готовностью делившегося с ним своими познаниями на любую тему, которую они затрагивали в беседе. Мастер показал мистеру Томпкинсу множество необычных вещей, в том числе тщательно закрытую, но, по-видимому, пустую шкатулку с надписью «НЕЙТРИНО. Обращаться с осторожностью».

— Там внутри что-нибудь есть? — с любопытством спросил мистер Томпкинс, встряхивая шкатулку у самого уха.

— Не знаю, — признался старый мастер. — Одни говорят, что есть, другие, что нет. Но внутри шкатулки вы все равно ничего не увидите. Эту занятную шкатулку подарил мне один приятель, физик-теоретик, и, по правде говоря, я не знаю, что с ней делать. Лучше всего пока оставить ее в покое.

Продолжая осматривать мастерскую, мистер Томпкинс увидел на верстаке покрытую пылью старинную скрипку. Она казалась такой старой, словно ее изготовил дедушка Страдивари.

— Вы играете на скрипке? — повернулся к резчику мистер Томпкинс.

— Только гамма-мелодии, — ответил старый мастер. — Это квантовая скрипка, и ничего другого на ней исполнить нельзя. Когда-то у меня была квантовая виолончель. На ней можно было исполнять мелодии в оптическом диапазоне, но кто-то попросил ее у меня поиграть, да так и не удосужился вернуть.

— Сыграйте мне, пожалуйста, какую-нибудь гамма-мелодию, — попросил мистер Томпкинс. — Мне не приходилось слышать такие мелодии прежде.

— Я сыграю вам «Нуклеат в тональности Th С диез», — сказал старый мастер, беря скрипку, — но приготовьтесь, это очень печальная мелодия.

Музыка, действительно, звучала очень странно. Ничего похожего мистеру Томпкинсу слышать не приходилось. Мелодия напоминала неумолчный шум морских волн, накатывающихся на песчаный берег. Время от времени шум прибоя прерывал резкий звук, напоминавший свист пролетевшей мимо пули. Мистер Томпкинс не был завзятым меломаном, но исполняемая мастером мелодия зачаровала и сковала его. Он потянулся, устроился поудобнее в старом кресле и закрыл глаза…

Глава 14

Дыры в пустоте

Леди и джентльмены!

Сегодня я прошу вас быть особенно внимательными, поскольку проблемы, о которых пойдет речь в моей лекции, столь же трудны, сколь и увлекательны. Я намереваюсь рассказать вам о новых частицах, известных под названием позитроны и обладающих более чем необычными свойствами. Весьма поучительно, что существование этой новой разновидности частиц было предсказано на основе чисто теоретических соображений за несколько лет до того, как они были обнаружены экспериментально, открытию позитронов в значительной мере способствовало теоретическое предсказание их основных свойств.

Честь сделать эти предсказания принадлежит британскому физику Полю Дираку, о котором вам уже приходилось слышать. К своим заключениям Дирак пришел на основе теоретических соображений, столь необычных и фантастических, что большинство физиков долгое время отказывалось верить в них. Основную идею теории Дирака можно сформулировать в следующих простых словах: «В пустом пространстве должны быть дыры». Я вижу, вы удивлены. Не менее вас были удивлены и физики, когда Дирак впервые произнес эти слова. Как могут быть дыры в пустом пространстве? Есть ли в подобном утверждении какой-нибудь смысл? Оказывается, есть, если вспомнить, что так называемое пустое пространство в действительности не так пусто, как нам кажется. В самом деле, основным исходным пунктом теории Дирака служит предположение о том, что так называемое пустое пространство, или вакуум, в действительности плотно заполнено бесконечно многими электронами (обычными отрицательно заряженными электронами), упакованными весьма правильно и равномерно. Нет необходимости говорить о том, что эта старая гипотеза пришла Дираку в голову не просто как игра фантазии. К принятию ее Дирака вынудил целый ряд соображений, связанных с теорией обычных отрицательно заряженных электронов. Эта теория приводит к неизбежному заключению о том, что помимо квантовых состояний движения в атоме существует также бесконечно много особых отрицательных квантовых состояний, принадлежащих чистому вакууму и что электроны, если ничто не мешает им переходить в эти «более удобные» состояния движения, покинут свои атомы и, так сказать, растворятся в пустом пространстве. Более того, поскольку существует только один способ воспрепятствовать электрону переходить, куда ему заблагорассудится, а именно занять то состояние, в которое собирается переходить электрон, другим электроном (вспомните принцип Паули!), все состояния в вакууме должны быть заполнены бесконечно многими электронами, равномерно распределенными по всему пространству.

Боюсь, что мои слова звучат для вас, как своего рода научная абракадабра и что голова у вас от всего этого вдет кругом. Должен заметить, что предмет моей лекции сегодня особенно труден, но я надеюсь, что если вы будете внимательно слушать меня, то в конце концов вам удастся составить определенное представление о характере теории Дирака.

Но вернемся к теме лекции. Так или иначе Дирак пришел к заключению о том, что пустое пространство до отказа заполнено электронами, распределенными равномерно, но с бесконечно большой плотностью. Как могло случиться, что мы вообще не замечаем столь густого скопления электронов и рассматриваем вакуум как абсолютное пространство?

Вы сможете лучше понять ответ на эти вопросы, если вообразите себя глубоководной рыбой, находящейся в толще вод. Понимает ли рыба, разумеется, если она наделена достаточно развитым интеллектом для того, чтобы задать себе вопрос, что она окружена водой?

Эти слова вывели мистера Томпкинса из дремоты, в которую он погрузился в начале лекции. Он был заядлым рыбаком и даже почувствовал на своем лице свежее дыхание морского ветра и воочию увидел плавно катящиеся волны. Но хотя мистер Томпкинс неплохо плавал, почему-то на этот раз ему было трудно удержаться на поверхности и он начал медленно идти ко дну, опускаясь все глубже и глубже. Как ни странно, но он не ощущал нехватки воздуха и чувствовал себя вполне комфортно.

— Может быть, — подумал он, — со мной произошла какая-нибудь особая рецессивная мутация?

По данным палеонтологов, жизнь зародилась в океане и первыми, кто выбрался из воды на сушу, были так называемые двоякодышащие рыбы, ходившие на плавниках. По мнению биологов, эти первые двоякодышащие рыбы, которых называют по-разному (в Австралии рогозубами, в Африке протоптерами, в Южной Америке чешуйчатниками или лепидосиренами), постепенно превратились в сухопутных животных, таких как мыши и кошки, и в людей. Некоторые из животных, например, киты и дельфины, ознакомившись со всеми трудностями жизни на суше, вернулись в океан. Но и после возвращения в воду они сохранили качества, приобретенные во время борьбы за существование на суше, например, остались млекопитающими, их самки вынашивают потомство внутри своего тела, а не откладывают икру, которую затем оплодотворяют самцы. Разве знаменитый венгерский ученый Лео Сцилард [9] не сказал как-то, что дельфины обладают более развитым интеллектом, чем люди?

Тут размышления мистера Томпкинса были прерваны разговором, происходившим где-то глубоко под поверхностью океана между дельфином и типичным гомо сапиенсом, в котором Томпкинс (по некогда виденной фотографии) сразу узнал физика из Кембриджского университета Поля Адриена Мориса Дирака.

— Послушай, Поль, — говорил дельфин, — ты считаешь, что мы находимся не в вакууме, а в материальной среде, состоящей из частиц с отрицательной массой. Я лично считаю, что вода ничем не отличается от пустого пространства. Она совершенно однородна, и смогу свободно двигаться в ней по всем направлениям. Однако от своего далекого предка — пра-пра-пра-пра-прадедушки — я слышал легенду о том, что на суше все иначе. Там есть горы и ущелья, преодолеть которые стоит немалых усилий. Здесь, в воде, я могу двигаться в любую сторону, куда захочу.

— Если говорить о морской воде, то вы правы, друг мой, — отвечал П.A.M.

— Вода создает трение о поверхность вашего тела, и если вы не будете двигать хвостом и плавниками, то не сможете двигаться вообще. Кроме того, поскольку давление воды изменяется с глубиной, вы можете всплывать или погружаться, расширяя или сжимая свое тело. Но если бы вода не была вязкой и не создавала трения о поверхность вашего тела и если бы не было градиента давления, то вы были бы столь же беспомощны, как астронавт, у которого иссякло ракетное топливо. Мой океан, состоящий из электронов с отрицательными массами, абсолютно лишен вязкости и поэтому ненаблюдаем. Физические приборы позволяют наблюдать только отсутствие одного из электронов, так как отсутствие отрицательного электрического заряда эквивалентно присутствию положительного электрического заряда, поэтому даже Кулон мог бы заметить, что одного электрона не хватает.

Однако при сравнении моего океана электронов с обычным океаном следует иметь в виду одно важное отличие, чтобы эта аналогия не завела нас слишком далеко. Дело в том, что электроны, образующие мой океан, подчиняются принципу Паули. Ни одного электрона невозможно добавить к океану, если все возможные квантовые состояния заполнены. Такой «лишний» электрон вынужден был бы остаться над поверхностью моего океана и легко мог бы быть обнаружен экспериментаторами. Электроны были впервые открыты сэром Дж. Дж. Томсоном. Электроны, которые вращаются вокруг атомных ядер или летят в вакуумных трубках, как раз и принадлежат к числу таких «лишних» электронов. До того как я опубликовал свою первую работу в 1930 г., остальное пространство считалось пустым. По общему мнению, физической реальностью обладали тогда только случайные всплески, вздымающиеся над поверхностью энергии.

— Но если ваш океан ненаблюдаем, — заметил дельфин, — из-за своей непрерывности и отсутствия трения, то какой смысл толковать о нем?

— Смысл есть, да еще какой! — возразил П.А.М. — Предположим, что какая-то внешняя сила подняла один из электронов с отрицательной массой из глубин океана над его поверхностью. Число наблюдаемых электронов при этом увеличилось на единицу, что можно рассматривать как нарушение закона сохранения энергии. Но и пустая дырка в океане, образовавшаяся в том месте, откуда был извлечен электрон, также будет наблюдаема, поскольку отсутствие отрицательного заряда в равномерном распределении воспринимается, как присутствие равного по величине положительного заряда. Эта положительно заряженная частица будет к тому же обладать положительной массой, и направление ее движения будет совладать с направлением силы тяжести.

— Вы хотите сказать, что дырка, или положительно заряженная частица, будет всплывать, а не тонуть? — с удивлением спросил дельфин.

— Совершенно верно. Не сомневаюсь, что вам приходилось неоднократно видеть, как различные предметы опускаются на дно, увлекаемые силой тяжести, иногда это были предметы, брошенные за борт с судна, иногда сами суда.

— Но послушайте, — прервал самого себя П.А.М. — Видите эти крохотные серебристые предметы, поднимающиеся к поверхности? Их движение также обусловлено действием силы тяжести, но движутся они в противоположную сторону.

— Но ведь это же пузырьки, — заметил дельфин. — Они, должно быть, оторвались от чего-то, что содержало воздух, когда оно перевернулось или разбилось, ударившись о каменистое дно.

— Вы совершенно правы, это действительно пузырьки, но ведь вам не приходилось видеть, чтобы пузырьки всплывали в вакууме? Следовательно, мой океан не пуст.

— Что и говорить, теория очень остроумна, — согласился дельфин, — только верна ли она?

— Когда я предложил ее в 1930 г., — ответил П.А.М., — никто в нее не поверил. В значительной мере в этом недоверии был виноват я сам, поскольку первоначально предполагал, что положительно заряженные частицы представляют собой не что иное, как хорошо известные экспериментаторам протоны. Вы, конечно, знаете, что протон в 1840 раз тяжелее электрона, но я тогда питал надежду на то, что с помощью одного математического трюка мне удастся объяснить возросшее сопротивление ускорению под действием данной силы и получить число 1840 теоретически. Но из моей затеи ничего не вышло, и материальная масса пузырьков в моем океане оказалась в точности равной массе обычного электрона. Мой коллега Паули, которому я не могу отказать в чувстве юмора, носился с идеей того, что он называл «Вторым Принципом Паули». По его вычислениям выходило, что если обычный электрон приблизится к дырке, образовавшейся при извлечении одного электрона из моего океана, то за ничтожно малое время он заполнит собой дырку. Следовательно, если протон атома водорода действительно был бы «дыркой», то обращающийся вокруг него электрон мгновенно заполнил бы эту дырку, и обе частицы аннигилировали бы со вспышкой света, или, лучше сказать, со вспышкой гамма-излучения. То же самое произошло бы и с атомами всех других элементов. Второй Принцип Паули требовал также, чтобы любая выдвинутая физиком теория была применима и к материи, из которой состоит тело самого физика, поэтому я аннигилировал бы прежде, чем успел бы поведать свою идею кому-нибудь еще. Вот так!

И с этими словами П.А.М. исчез, испустив яркую вспышку света.

— Сэр, — послышался над ухом мистера Томпкинса чей-то раздраженный голос, — вы можете сколько угодно спать на лекции, если вам так нравится, но не храпите так громко! Я не могу расслышать ни слова из того, что говорит профессор.

Открыв глаза, мистер Томпкинс увидел снова переполненную лекционную аудиторию и старого профессора, который продолжал:

— Посмотрим, что произойдет, когда странствующая дырка встречает на своем пути лишний электрон, занятый поиском местечка поудобнее в океане Дирака. Ясно, что в результате такой встречи лишний электрон неизбежно свалится в дырку, заполнит ее и удивленный физик, наблюдая этот процесс, отметит явление взаимной аннигиляции положительного и отрицательного электронов. Высвободившаяся при падении электрона в дырку энергия испускается в виде коротковолнового излучения и представляет собой лишь остаток от двух электронов, поглотивших друг друга, как два волка из известной детской сказки.

Но можно представить себе и обратный процесс, в котором пара частиц, состоящая из отрицательного и положительного электронов, рождается из ничего под действием мощного внешнего излучения. С точки зрения теории Дирака, рождение пары представляет собой просто выбивание электрона из непрерывного распределения, и рассматривать его следовало бы не как рождение, а как разделение двух противоположных по знаку электрических зарядов. На рисунке, который я сейчас покажу вам (с. 205), эти два процесса рождения и уничтожения электронов изображены весьма условно и схематично, но, как вы видите, ничего загадочного в них нет. Должен заметить, что хотя процесс рождения пары, строго говоря, должен происходить в абсолютном вакууме, вероятность его очень мала. Можно сказать, что распределение электронов в вакууме слишком гладко, чтобы распасться. С другой стороны, в присутствии тяжелых материальных частиц, служащих точкой шоры для гамма-излучения, внедряющегося в распределение электронов, вероятность рождения пары сильно возрастает, и процесс становится наблюдаемым.

Ясно, что позитроны, рожденные описанным выше образом, не могут существовать очень долго и вскоре аннигилируют при встрече с одним из отрицательных электронов, обладающих в нашем уголке Вселенной большим численным преимуществом. Именно этим объясняется сравнительно позднее открытие таких замечательных частиц, как позитроны: первое сообщение о положительно заряженных электронах было сделано лишь в августе 1932 г. (теория Дирака была опубликована в 1930 г.) калифорнийским физиком Карлом Андерсоном, который, занимаясь исследованием космического излучения, обнаружил частицы, во всех отношениях напоминавших обычные электроны, но имевших одно важное отличие: вместо отрицательного заряда эти частицы несли положительный заряд. Вскоре после открытия Андерсона мы научились очень просто получать электрон-позитронные пары в лабораторных условиях, пропуская сквозь какое-нибудь вещество мощный поток высокочастотного излучения (радиоактивного гамма-излучения).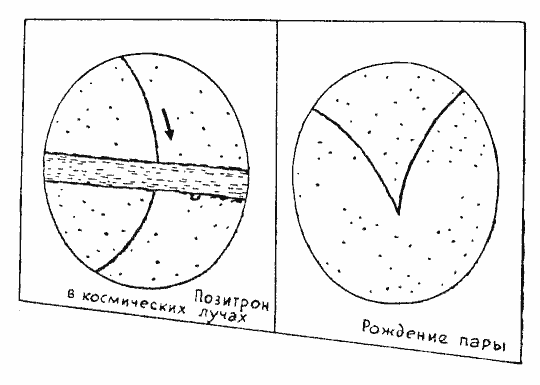

На следующем слайде, который я хочу показать вам, вы увидите снимки позитронов, обнаруженных в космическом излучении с помощью камеры Вильсона, и самого процесса рождения пары. Камера Вильсона — один из самых полезных приборов современной экспериментальной физики. Действие ее основано на том, что любая частица с ненулевым электрическим зарядом, пролетая через газ, образует вдоль своего трека множество ионов. Если газ насыщен водяными парами, то крохотные капельки воды конденсируются на этих ионах, образуя тонкий слой тумана, тянущийся вдоль всего трека. Освещая эту полоску тумана сильным пучком света на темном фоне, мы получаем великолепные картины, на которых отчетливо различимы все детали движения.

На первой из двух картинок, спроецированных на экран, вы видите оригинал снимка позитрона, обнаруженного Андерсоном в космическом излучении. Замечу, что это самый первый из когда-либо сделанных снимков позитрона. Широкая горизонтальная полоса, идущая через весь снимок, — след толстой свинцовой пластины, положенной поперек камеры Вильсона, а трек позитрона выглядит, как тонкая искривленная царапина, идущая через снимок. Трек искривлен потому, что во время эксперимента камера Вильсона была помещена в сильное магнитное поле, влиявшее на движение позитрона. Свинцовая пластина и магнитное поле понадобились Андерсону для того, чтобы определить знак электрического заряда, переносимого частицей. Сделать это можно на основе следующих соображений. Известно, что производимое магнитным полем изгибание траектории зависит от знака заряда движущейся частицы. В эксперименте Андерсона магнит расположен так, что отрицательно заряженные электроны отклоняются от первоначального направления движения влево, а положительно заряженные электроны — вправо. Следовательно, если частица на снимке двигалась вверх, то она должна была нести отрицательный заряд. Но как узнать, в какую сторону двигалась частица? Для этого и понадобилась Андерсону свинцовая пластина. Пройдя сквозь свинцовую пластину, частица неизбежно теряет некую часть своей первоначальной энергии, и поэтому изгибающее действие магнитного поля усиливается. На снимке, который вы видите на слайде, трек изогнут сильнее под свинцовой пластиной (различие в изгибах не слишком видно на глаз, но отчетливо заметно при измерении). Следовательно, частица двигалась сверху вниз и несла положительный заряд.

На правом снимке (с. 206), полученном Джеймсом Чедвиком из Кембриджского университета, вы видите рождение пары в камере Вильсона. Сильное гамма-излучение поступает в камеру снизу и, не оставляя на снимке видимых следов, порождает в центре камеры пару частиц, которые разлетаются в сильном магнитном поле в разные стороны. Глядя на этот снимок, вы можете гадать, почему позитрон (на снимке он слева) не аннигилирует на своем пути через газ. Ответ на этот вопрос также дает теория Дирака, и этот ответ понятен каждому, кто играет в гольф. Если, поставив шар на травяное поле, вы ударите по нему слишком сильно, то шар не попадет в лунку, даже если вы точно прицелились. Произойдет нечто иное: быстро движущийся шар просто перепрыгнет через лунку и покатится дальше. Точно так же быстро движущийся позитрон не попадет в дырку Дирака, покуда его скорость существенно не уменьшится. Поэтому позитрон имеет большую вероятность аннигилировать в конце траектории, когда столкновения с другими частицами по дороге основательно замедлят его. И, как показывают тщательные наблюдения, излучение, сопровождающее любой процесс аннигиляции, действительно обнаруживается в конце траектории позитрона. В этом — еще одно подтверждение теории Дирака.

Нам остается еще обсудить два общих вопроса. До сих пор я рассматривал отрицательно заряженные электроны как лишние брызги переполненного океана Дирака, а позитроны — как дырки в нем. Но вполне допустима и противоположная точка зрения, согласно которой обычные электроны надлежит рассматривать как дырки, а позитроны — как выброшенные частицы. Для этого нам необходимо лишь предположить, что океан Дирака не переполняется, а, наоборот, всегда испытывает недостаток частиц. В этом случае распределение Дирака можно наглядно представить как нечто напоминающее кусок швейцарского сыра с множеством дыр в нем. Из-за общей нехватки частиц дырки будут существовать всегда, и даже если какая-нибудь частица окажется выброшенной из распределения, она вскоре снова упадет в одну из дырок. Следует сказать, однако, что как с физической, так и с математической точки зрения обе картины абсолютно эквивалентны, и поэтому совершенно безразлично, какой из картин мы отдадим предпочтение.

Второе замечание можно сформулировать в виде следующего вопроса: «Если в той части Вселенной, где мы обитаем, существует явное численное преобладание отрицательно заряженных электронов, то можно ли предположить, что где-то в другой части Вселенной численное преимущество наблюдается за положительно заряженными электронами?» Иначе говоря, компенсируется ли переполнение океана Дирака в нашей окрестности недостатком отрицательно заряженных электронов где-то в другом месте?

Ответить на этот чрезвычайно интересный вопрос очень трудно. Действительно, так как атомы, состоящие из положительно заряженных электронов, которые обращаются вокруг отрицательно заряженного ядра, давали бы такие же оптические картины, как и обычные атомы, не существует способа ответить на этот вопрос с помощью спектроскопических наблюдений. Судя по всему, что мы знаем, вполне возможно, что образование вещества где-нибудь в Туманности Андромеды происходит «наоборот» по отношению к привычной для нас схеме, но единственный способ подтвердить или опровергнуть подобную догадку состоит в том, чтобы раздобыть кусочек того вещества и проверить, не аннигилирует ли оно при соприкосновении с земным веществом. Разумеется, в случае аннигиляции последует ужасный взрыв! В последнее время стали поговаривать о том, что некоторые метеориты, взорвавшиеся при вхождении в земную атмосферу, возможно, состояли из такого «перевернутого» вещества, но я не думаю, чтобы подобные разговоры следовало принимать всерьез. Не исключено, что вопрос о переполнении океана Дирака в одних частях Вселенной и нехватке частиц в других ее частях навсегда останется без ответа.

Глава 15

Мистер Томпкинс знакомится с японской кухней

Однажды Мод отправилась на выходной навестить тетушку в Йоркшире, и мистер Томпкинс пригласил профессора отобедать с ним в знаменитом японском ресторане. Расположившись на мягких подушках за низким столиком, они пробовали деликатесы японской кухни и потягивали из чашечек сакэ.

— Скажите, пожалуйста, — обратился к профессору мистер Томпкинс, — доктор Таллеркин упомянул в своей лекции, что протоны и нейтроны удерживаются в ядре особыми силами сцепления. Это те самые силы, которые удерживают электроны в атоме?

— О, нет! — возразил профессор. — Ядерные силы представляют собой нечто совершенно другое. Атомные электроны притягиваются к ядру обычными электростатическими силами, впервые подробно исследованными французским физиком Шарлем Опостеном де Кулоном в конце XVIII века. Это сравнительно слабые силы, убывающие обратно пропорционально квадрату расстояния от центра. Ядерные силы имеют совершенно иную природу. Когда протон и нейтрон сближаются вплотную, но не соприкасаются, то между ними ядерные силы практически не действуют. Но как только частицы входят в прямой контакт, между ними возникает необычайно мощная сила, которая удерживает их вместе. В этом смысле протон и нейтрон напоминают два кусочка липкой ленты, которые не притягивают друг друга даже на малых расстояниях, но становятся неразлучными, как братья, стоит лишь им соприкоснуться. Физики назвали силы, удерживающие протоны и нейтроны в ядре, сильным взаимодействием. Эти силы не зависят от электрического заряда двух частиц и с одинаковой интенсивностью действуют и между двумя нейтронами, и между протоном и нейтроном, и между двумя протонами.

— Существуют ли какие-нибудь теории, объясняющие сильное взаимодействие? — спросил мистер Томпкинс.

— Существуют. В начале 30-х годов японский физик Хидеки Юкава высказал гипотезу о том, что сильное взаимодействие обусловлено обменом какой-то неизвестной частицей между двумя нуклонами (нуклон — это собирательное название протона и нейтрона). Когда два нуклона сближаются, между ними туда и обратно начинают прыгать какие-то загадочные частицы, что и приводит к возникновению сильной связи, удерживающей нуклоны вместе. Юкаве удалось теоретически оценить массу гипотетических частиц. Оказалось, что она примерно в 200 раз больше массы электрона, или примерно в 10 раз меньше массы протона или нейтрона. Такие частицы получили название мезатронов. Но отец Вернера Гейзенберга, бывший профессором классических языков, возразил против столь грубого нарушения древнегреческого языка. Дело в том, что название электрон происходит от греческого

Действительно, на сцене появились шесть гейш, которые начали играть в бильбоке: в каждой руке у гейш было по чашке и они ловко перебрасывали шарик из одной чашки в другую и обратно. Между тем на заднем плане появился мужчина и запел:

— А почему выступают три пары гейш? — спросил мистер Томпкинс.

— Они изображают три возможных варианта обмена мезонами, — пояснил профессор. — Мезоны бывают трех типов: положительно заряженные, отрицательно заряженные и электрически нейтральные. Возможно, что ядерные силы порождены мезонами всех трех типов.

— Итак, ныне существуют восемь элементарных частиц, — подвел итог своим размышлениям мистер Томпкинс и принялся считать на пальцах, — нейтроны, протоны (положительно и отрицательно заряженные), положительно и отрицательно заряженные электроны и мезоны трех сортов.

— Нет! — воскликнул профессор. — Элементарных частиц сейчас известно не восемь, а ближе к восьмидесяти. Сначала выяснилось, что существуют две разновидности мезонов, тяжелые и легкие. Тяжелые мезоны физики обозначили греческой буквой пи и назвали пионами, а легкие — греческой буквой мю и назвали мюонами. Пионы рождаются на границе атмосферы при столкновении протонов очень высокой энергии с ядрами газов, образующих воздух. Но пионы очень нестабильны и распадаются, прежде чем достигнут поверхности Земли, на мюоны и нейтрино (самые загадочные из всех частиц), которые не обладают ни массой, ни зарядом, а только переносят энергию. Мюоны живут несколько дольше, около нескольких микросекунд, поэтому они успевают достигнуть поверхности Земли и распадаются на наших глазах на обычный электрон и два нейтрино. Существуют также частицы, обозначаемые греческой буквой ка и называемые каонами.

— А какие из частиц используют эти гейши в своей игре? — поинтересовался мистер Томпкинс.

— По-видимому, пионы, скорее всего нейтральные (они играют наиболее важную роль), но я не вполне уверен. Большинство новых частиц, открываемых ныне почти каждый месяц, настолько короткоживущие, даже если они движутся со скоростью света, что распадаются на расстоянии нескольких сантиметров от места рождения, и поэтому даже чувствительные приборы, запускаемые в атмосферу на шарах, «не замечают» их.

Но теперь у нас есть мощные ускорители частиц, способные разгонять протоны до столь же высоких энергий, какие те достигают в космическом излучении, т. е. до многих тысяч миллионов электрон-вольт. Одна из этих машин под названием лоуренстрон расположена здесь неподалеку, ближе к вершине холма, и я буду рад показать ее вам.

После непродолжительной поездки на автомашине профессор и мистер Томпкинс подъехали к огромному зданию, внутри которого находился ускоритель. Войдя в здание, мистер Томпкинс был потрясен сложностью гигантского сооружения. Но по заверению профессора, ускоритель в принципе был не более сложен, чем праща, из которой Давид убил Голиафа. Заряженные частицы инжектировались (поступали) в центре гигантского барабана и, двигаясь по раскручивающимся спиралям, ускорялись переменными электрическими импульсами. Движением частиц управляет сильное магнитное поле.

— Мне кажется, я уже видел нечто подобное, — сказал мистер Томпкинс, — когда несколько лет назад посетил циклотрон, который назывался «атомной дробилкой».

— Вы совершенно правы, — подтвердил профессор. — Циклотрон, который вы тогда видели, был изобретен доктором Лоуренсом. Ускоритель, который вы видите здесь, основан на том же принципе, но он может разгонять частицы уже не до нескольких миллионов электрон-вольт, а до многих тысяч миллионов электрон-вольт. Два таких ускорителя были недавно сооружены в Соединенных Штатах. Один из них находится в Беркли (штат Калифорния) и называется бэватрон, поскольку разгоняет частицы до энергий в миллиарды электрон-вольт. Это чисто американское название, так как только в Америке тысячу миллионов принято называть биллионом. В Великобритании биллионом называется миллион миллионов, и никто в доброй старой Англии еще не пытался достичь столь высоких энергий. Другой американский ускоритель частиц находится в Брукхейвене, Лонг-Айленд, и называется космотрон. Это название несколько претенциозно, так как энергии, достижимые в космическом излучении, часто намного превышают те, до которых разгоняет частицы космотрон. В Европе, в Европейском центре ядерных исследований (ЦЕРН) близ Женевы, построены ускорители, сравнимые с двумя американскими ускорителями. В России, недалеко от Москвы, построен еще один ускоритель такого же типа, общеизвестный под названием хрущевтрон. Возможно, что теперь он будет переименован в брежневтрон.

Оглядевшись по сторонам, мистер Томпкинс обратил внимание на дверь, на которой красовалась надпись:

ЖИДКИЙ ВОДОРОД АЛЬВАРЕСА

ВАННОЕ ОТДЕЛЕНИЕ

— А что за этой дверью? — спросил он.

— О! — ответил профессор. — Видите ли, лоуренстрон производит все больше и больше различных элементарных частиц все большей и большей энергии. Их приходится анализировать, наблюдая траектории и вычисляя массы, времена жизни, взаимодействия и многие другие свойства, такие как странность, четность и т. д. В давние времена для наблюдения траекторий использовалась так называемая камера Вильсона, за создание которой Ч. Т. Р. Вильсон в 1927 г. получил Нобелевскую премию. В то время быстрые электрически заряженные частицы с энергией в несколько миллионов электрон-вольт, исследуемые физиками, пропускались через камеру со стеклянной крышкой, наполненную воздухом, почти до предела насыщенным водяными парами. Когда дно камеры резко опускалось, воздух вследствие расширения охлаждался и водяной пар становился перенасыщенным. В результате некоторая доля пара конденсировалась в крохотные водяные капельки. Вильсон обнаружил, что такая конденсация паров в воду происходит гораздо быстрее вокруг ионов, т. е. электрически заряженных частиц газа. Но вдоль траекторий электрически заряженных частиц, пролетающих сквозь камеру, газ ионизируется. В результате непрозрачные полоски тумана, освещаемые источником света, расположенным на стенке камеры, становятся видимыми на выкрашенном в черный цвет дне камеры. Вспомните снимки, которые я показывал вам на прошлой лекции.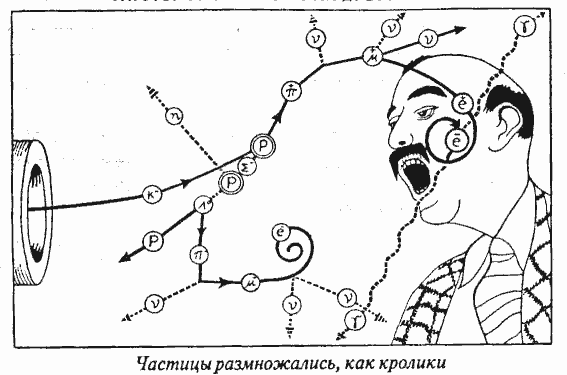

В случае частиц из космических лучей с энергиями, тысячекратно превосходящими энергии частиц, которые мы изучали до сих пор, ситуация иная потому, что треки частиц становятся очень длинными и камеры Вильсона, заполненные воздухом, слишком малы для того, чтобы можно было проследить весь трек частицы от начала до конца, поэтому наблюдению доступна лишь небольшая часть траектории.

Большой шаг вперед был недавно сделан американским физиком Дональдом А. Глезером, которому в 1960 г. была присуждена за это Нобелевская премия. Как рассказывает сам Глезер, однажды он сидел в баре и угрюмо наблюдал за пузырьками, поднимавшимися в стоявшем перед ним бокале пива. Внезапно ему пришла в голову идея: «Если Ч. Т. Р. Вильсон мог изучать капельки жидкости в газе, то почему бы мне не заняться изучением пузырьков газа в жидкости?»

— Не стану вдаваться в технические детали, — продолжал профессор, — и касаться трудностей, возникших на пути к техническому воплощению идеи Глезера. Вам все равно они были бы непонятны. Скажу только, что для надлежащего функционирования пузырьковой камеры (такое название получило изобретение Глезера) наиболее подходящей жидкостью оказался жидкий водород, температура которого составляет около двухсот пятидесяти градусов по Фаренгейту ниже температуры замерзания воды. В соседней комнате стоит большой контейнер; построенный Луисом Альваресом и заполненный жидким водородом. Обычно его называют «ванной Альвареса».

— Бр-р-р! — поежился мистер Томпкинс. — Для меня холодновато!

— Вам вовсе не нужно лезть в ванну. Вполне достаточно наблюдать за траекториями частиц сквозь прозрачные стенки.

Ванная функционировала как всегда, и камеры со вспышкой, расположенные вокруг нее, непрерывно делали снимок за снимком. Сама ванна была помещена внутри большого электромагнита, изгибавшего траектории частиц, чтобы затем по изгибу экспериментаторы могли оценивать скорость их движения.

— Производство одного снимка занимает несколько минут, — пояснил Альварес. — В день получается до нескольких сотен снимков, если установка не выходит из строя и не требует какого-нибудь ремонта. Каждый снимок подвергается тщательному изучению, все треки анализируются, а их кривизна тщательно измеряется. Анализ и измерения занимают от нескольких минут до часа в зависимости от того, насколько интересен снимок и насколько быстро справляется с работой девушка.

— Почему вы сказали «девушка»? — прервал его мистер Томпкинс. — Разве это чисто женское занятие?

— Разумеется, нет, — ответил Альварес. — Многие из наших девушек в действительности мальчики. Но когда мы говорим о тех, кто занимается обработкой снимков, то называем их девушками независимо от пола. Термин «девушка» означает единицу эффективности и точности. Когда вы говорите «машинистка» или «секретарь», то обычно представляете себе женщину, а не мужчину. Так вот, для анализа всех снимков, получаемых в нашей лаборатории, нам понадобились бы сотни девушек, что превратилось бы в нелегкую проблему. Поэтому мы рассылаем множество наших снимков в другие университеты, не имеющие достаточно средств, чтобы построить лоуренстроны и пузырьковые камеры, но располагающие суммами денег, которых вполне хватает на покупку приборов для анализа наших снимков.

— Такого рода снимки получаете только вы или кто-нибудь еще? — поинтересовался мистер Томпкинс.

— Аналогичные ускорители имеются в Брукхейвенской Национальной Лаборатории на Лонг-Айленде в Нью-Йорке, в ЦЕРНе (Европейском центре ядерных исследований) близ Женевы и в Лаборатории «Щелкунчик» неподалеку от Москвы в России. Все эти лаборатории заняты поиском иголки в стоге сена и, что самое удивительное, время от времени им все же удается найти иголку!

— А для чего ведется эта кропотливая работа? — спросил в удивлении мистер Томпкинс.

— Чтобы искать и находить новые элементарные частицы (найти которые, кстати сказать, гораздо труднее, чем иголку в стоге сена!) и исследовать взаимодействие между ними. Здесь на стене таблица известных элементарных частиц и она уже сейчас содержит больше частиц, чем элементов в Периодической системе Менделеева.

— А почему столь чудовищные усилия предпринимаются лишь для того, чтобы найти новые частицы? — продолжал удивляться мистер Томпкинс.

— Такова наука, — ответил профессор, — попытка человеческого разума понять все, что нас окружает, будь то гигантские звездные галактики, микроскопические бактерии или элементарные частицы. Познавать окружающий мир захватывающе интересно, и поэтому мы занимаемся этим.

— А не способствует ли развитие науки достижению практических целей, увеличивая благосостояние людей и делая их жизнь более удобной?

— Разумеется, способствует, но это лишь второстепенная цель. Не думаете же вы, что основное назначение музыки состоит в том, чтобы учить горнистов будить по утрам солдат, сзывать их на завтраки, обеды и ужины или призывать их на битву? Говорят: «Любопытство сгубило кошку». Я говорю: «Любознательность рождает ученого».

С этими словами профессор пожелал мистеру Томпкинсу спокойной ночи.

* * *

Замечательный физик-теоретик Георгий Антонович (Джордж) Гамов (1904-1968) не был узким специалистом. Он оставил заметный след в квантовой механике, атомной и ядерной физике, астрофизике, космологии и биологии. Его идеи, яркие и оригинальные, не раз прокладывали новые направления научных исследований. Ему принадлежат пионерские работы по квантовой теории альфа-распада и туннельному эффекту, уровням энергии в ядре, моделям звезд с термоядерными источниками энергии, роли нейтрино при вспышках сверхновых и новых, образованию химических элементов путем захвата нейтронов, реликтовому излучению и генетическому коду.

Не менее обширно, оригинально и ярко литературное наследие Г. А. Гамова. Его перу принадлежит увлекательная автобиография «Моя мировая линия» и целая россыпь замечательных научно-популярных книг, таких, как «Мистер Томпкинс в Стране Чудес», «Мистер Томпкинс исследует атом», «Раз, два, три… бесконечность», «Тридцать лет, которые потрясли физику», «Сотворение Вселенной», «Биография физики», «Звезда под названием Солнце», «Биография Земли», «Планета под названием Земля».

Предлагаемая вниманию читателя книга — первая публикация произведений Г. А. Гамова на русском языке.

1

Инициалы мистера Томпкинса (в английском оригинале) C. G. H. Tompkins обязаны своим происхождением трем фундаментальным физическим константам: скорости света с, гравитационной постоянной G и квантовой постоянной Планка h. Чтобы эти константы стали заметны человеку с улицы, их необходимо во много раз увеличить.

2

Ньютон И. Математические начала натуральной философии. — Пер. с латинского и комментарии А.Н. Крылова. Предисловие Л.С.Полака. — М.: Наука, 1989. — С. 30. (Прим. пер.)

3

Название «Цирк Хукхэма» восходит к мистеру Джону Хукхэму, работавшему художником-иллюстратором в издательстве Кембриджского университета. Незадолго до выхода в отставку мистер Хукхэм создал многие из рисунков, украсивших эту книгу.

4

Канал, или Английский Канал, — английское название пролива Ла-Манш. (Прим. пер)

5

Идя навстречу пожеланиям меломанов, предпочитающих слушать оперу в подлиннике, и ценителей стилистических красот английского текста, мы приводим все оперные арии на языке оригинала, а для тех, кто интересуется содержанием, приводим перевод, не искаженный погоней за рифмами. (Прим. пер.)

6

Недели за две до выхода в свет первого издания этой книги появилась статья Фреда Хойла «Последние достижения в космологии» (Nature, October 9, 1965, p. Ill), в которой говорилось следующее: «Хойл и его сотрудники занимались подсчетом радиоисточников… Результаты подсчета радиоисточников указывают на то, что Вселенная в прошлом имела большую плотность, чем в настоящее время». Однако автор настоящей книги, поразмыслив, решил не вносить какие-либо изменения в текст арий «Космической оперы», памятуя о том, что оперы, единожды написанные, становятся классическими: например, даже сегодня Дездемона поет прекрасную арию перед тем, как умереть от рук Отелло.

7

Если быть точным, то следует сказать, что внимание мистера Томпкинса привлекла статья в январском номере этого журнала за 1940 г.

8

Читатель должен иметь в виду, что, говоря о смешивании цветов, мы имеем в виду только лучи света соответствующей окраски, а не сами цвета. Если смешать красную и зеленую краски, то получится некий грязный цвет. Если же половину верхней стороны волчка выкрасить в красный цвет, а другую половину — в зеленый, то, закрутив волчок, мы увидим, что он белый.

9

Автор имеет в виду научно-фантастическую новеллу Лео Сциларда «Голос дельфинов».