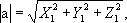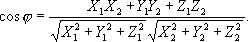|
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ВЕ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ВЕ) - Чтение (стр. 7)
7.1739, близ Штутгарта, - 24.2. 1792, Ансбах), немецкий публицист и сатирик. В своих журналах «Кронологен» («Chronologen», 1779-81) и «Грауэ унгеойер» («Das graue Ungeheuer», 1784-1787) В. освещал социально-политические условия немецкой жизни, вёл борьбу против феодального гнёта и церковного обскурантизма; осуждал междоусобные войны. В. - автор сатирического путевого дневника «Бешеный Ансельм, путешествие по верхней Германии» (1778). От надежд на просвещённый абсолютизм В. перешёл к приятию Великой французской революции. В 1792 В. был арестован по подозрению в связи с якобинцами.
Соч.: Auswahl, hrsg. von F. W. Ebeling, B., 1869 (mit Biographic). Лит.:Рейман П., Основные течения в немецкой литературе 1750-1848, пер. с нем., М., 1959, гл. 9: Bцhm G., Ludwig Wekhrlin..., Mьnch., 1895. М. Л. Тройская. Векса Ве'кса,Вёкса, название нескольких рек в СССР: 1) река в Костромской области РСФСР, левый приток р. Кострома, вытекает из Галичского озера. Длина 84 км,площадь бассейна 2880 км 2.У устья - г. Буй. 2) Река в Костромской области, сток Чухломского озера в р. Кострома. Длина 43 км,площадь бассейна 1360 км 2.Сплавная. 3) Река в Вологодской области, левый приток р. Вологда (бассейн Северной Двины). Длина 9 км. Вексель Ве'ксель(нем. Wechsel), вид ценной бумаги,представляет собой денежное обязательство строго установленной законом формы. Является безусловным и бесспорным долговым документом. В международной торговле, а также во внутреннем обороте капиталистических стран В. используется в качестве одного из важных средств оформления кредитно-расчётных отношений, выполняет различные по характеру функции и применяется, например, как платёжный документ, передаваемый в установленном порядке одним лицом другому взамен денежного платежа, выступает в качестве орудия кредита, а также используется для инкассирования (получения) долга. Различают 2 вида В.: простой и переводный (тратта). Простой В. - ничем не обусловленное обязательство лица, его выдавшего, об уплате означенной суммы денег по требованию или в определенный срок поименованному в В. лицу или его приказу (то есть другому, указанному им лицу). По переводному В. плательщиком обычно является не векселедатель, а третье лицо - акцептант, который при помощи акцепта принимает на себя безусловное обязательство платежа. Таким образом, переводный В. по своей форме представляет собой документ, содержащий ничем не обусловленный приказ векселедателя плательщику (акцептанту) произвести платёж определённой денежной суммы лицу, указанному в В., или его приказу - по предъявлении В. или в определенный срок. Поскольку В. выступает в качестве орудия обращения взамен наличных денег, в процессе вексельного обращения к векселедателю и акцептанту могут присоединиться и др. лица: индоссанты, передающие В. по индоссаменту,авалисты, гарантирующие платёж по В. за какое-либо другое, ответственное по В., лицо. В практике международных расчётов распространён, так называемый, учёт векселей,заключающийся в том, что держатель В. может до наступления срока платежа предъявить его в банк и получить указанную в нём сумму (за вычетом учётного процента). По наступлении срока платежа банк сам предъявляет В. к оплате. Отношения участников вексельного оборота имеют характер гражданско-правовых отношений, регулируемых специальными нормами вексельного законодательства. В большинстве стран это законодательство основано либо на Женевских вексельных конвенциях 1930, либо на английском вексельном законе. СССР присоединился к Женевским вексельным конвенциям в 1936, постановление ЦИК и СНК СССР от 7 августа 1937 на территории СССР было введено в действие основанное на этих конвенциях Положение о переводном и простом В. Вексель широко используется в расчётных и кредитных отношениях, возникающих в сфере экономического сотрудничества СССР с капиталистическими странами. Во внутреннем обороте СССР вексельное обращение ликвидировано в 1930 в связи с переходом к системе прямого целевого банковского кредитования. Лит.:Валютные отношения во внешней торговле СССР, М., 1968, с. 185-248, с. 326-48. А. Б. Альтшуллер. Вексельный кредит Ве'ксельный креди'т,см. Кредит вексельный. Вексельный курс Ве'ксельный курс,см. в ст. Валютный курс. Векслер Владимир Иосифович Ве'кслерВладимир Иосифович [19.2(4.3).1907, Житомир, - 22.9.1966, Москва], советский физик, академик АН СССР (1958; член-корреспондент 1946). Академик-секретарь Отделения ядерной физики АН СССР (1963-66). Член КПСС с 1937. Окончил Московский энергетический институт (1931). С 1936 работал в Физическом институте АН СССР, одновременно с 1949 начал работать в Дубне, где с 1954 возглавлял организованную им лабораторию высоких энергий. Основные работы В. - по физическим принципам ускорения заряженных частиц, физике высоких энергий, космическим лучам. В. разработал новые методы ускорения заряженных частиц. В 1944 В. предложил принцип автофазировки,который позволил поднять предел достижимых энергий частиц в тысячи раз. В 1956-66 разработал основы, так называемого, коллективного метода ускорения. В. руководил созданием первого в СССР синхротрона (1947) и синхрофазотрона в Дубне (1957). Главный редактор организованного (1965) по его инициативе журнала «Ядерная физика». Создал школу специалистов в области ускорительной физики и техники. Ленинская премия (1959) и Государственная премия СССР; международная премия «Атом для мира» (1963). Награжден 3 орденами Ленина, орденом Трудового Красного Знамени и медалями. Соч.: Экспериментальные методы ядерной физики, М. - Л., 1940 (совм. с Л. Грошевым и Н. Добротиным); Ионизационные методы исследования излучений, 2 изд., М. - Л., 1950 (совм. с Л. Грошевым и В. Исаевым); Новый метод ускорения релятивистских частиц, «Докл. АН СССР», 1944, т. 43, № 8; т. 44, № 9; Когерентный принцип ускорения заряженных частиц, «Атомная энергия», 1957, т. 2, №5, с. 427. Лит.:Рабинович М. С., Памяти В. И. Векслера, «Успехи физических наук», 1967, т. 91, в. 1. М. С. Рабинович. 
В. И. Векслер. Вектор Ве'ктор(от лат. vector, буквально - несущий, перевозящий), в геометрическом смысле - направленный отрезок, то есть отрезок, у которого указаны начало (называемое также точкой приложения В.) и конец. Для обозначения В. используются либо жирные латинские буквы а , b ,либо буквы обычного алфавита с чёрточками или стрелками наверху:
В., имеющий начало в точке
Аи конец в точке
В,обозначается
Понятие В. возникло в связи с изучением величин, характеризуемых численным значением и направленностью (например, перемещение, скорость и ускорение движущейся материальной точки, действующая на неё сила и т.п.). В механике и физике рассматривают свободные, скользящие и связанные В. Вектор называется свободным, если его значение не меняется при произвольном параллельном переносе. Свободным В. является, например, скорость движения материальной точки. В. называется скользящим, если его значение не меняется при любом параллельном переносе вдоль линии его действия. Примером скользящего В. может служить сила, действующая на абсолютно твёрдое тело (две равные и расположенные на одной прямой силы оказывают на абсолютно твёрдое тело одинаковое воздействие). В. называется связанным, если фиксировано его начало. Например, сила, приложенная к некоторой точке упругого тела, представляет собой связанный В. Свойства свободных В. изучаются средствами векторной алгебры (см. Векторное исчисление ) .Общее понятие В. как элемента, так называемого, векторного пространства определяется аксиоматически. Лит.:Ильин В. А., Позняк Э. Г., Аналитическая геометрия, М., 1968. Э. Г. Позняк. Вектор состояния Ве'ктор состоя'ния,величина, играющая в квантовой теории поля такую же роль, как волновая функция в квантовой механике.Квадрат абсолютного значения (модуля) В. с. указывает вероятность состояния. Векторкардиография Векторкардиогра'фия(от вектор,греч. kardнa - сердце и ...графия ), метод пространственного (объёмного) исследования электрического поля сердца; один из видов электрокардиографии.В. предложена в 1913 голландским учёным В. Эйнтховеном. Векторметр Векторме'тр,электрический прибор для измерений среднего значения силы и фазы переменного тока или электрического напряжения. При отсутствии в измеряемой величине чётных гармоник В. позволяет измерять мгновенные значения силы тока и напряжения и строить кривые их изменения во времени. На рис. приведена схема, поясняющая принцип действия В.: исследуемое переменное напряжение U xподаётся на зажимы магнитоэлектрического вольтметра Vчерез прерыватель К,который работает под воздействием электромагнита, включенного на вспомогательное управляющее напряжение U K.При совпадении по фазе напряжения U xс напряжением U Kконтакты Кзамыкаются и остаются в таком положении на протяжении положительного полупериода изменения U x,в этом случае вольтметр покажет половину среднего значения напряжения U x.При изменении фазы напряжения U xпо отношению к фазе напряжения U Kна вольтметр будет подаваться в течение некоторой части периода отрицательное напряжение второго полупериода, и показание прибора уменьшится. При сдвиге фазU Kи U xна 90° вольтметр покажет 0. Источник управляющего напряжения снабжается устройством (со шкалой) для отсчёта фазы U K.Изменяя фазу U Kдо получения максимального показания вольтметра, то есть до совпадения по фазе напряжений U Kи U x,находят по шкале источника управляющего напряжения фазу U x.Промышленность СССР изготовляет В. такого типа с синхронным микродвигателем в качестве прерывателя К.Эти приборы, предназначенные для измерений в цепях переменного тока с частотой 50 гц,имеют пределы измерений по напряжению от 0,15 до 300 в,по силе тока от 0,003 до 5 аи по фазе от 0 до 360°. Пределы измерений могут быть изменены при дополнительном включении наружных шунтов, отдельных добавочных сопротивлений и измерительных трансформаторов. В. применяют при лабораторных исследованиях сложных электрических схем и устройств, а также при испытании магнитных свойств электротехнических сталей. Н. Г. Вострокнутов. 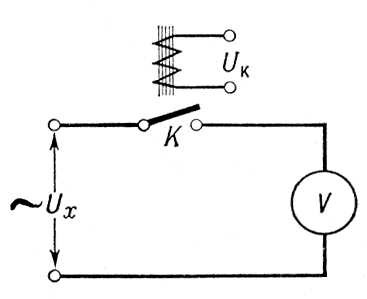
Схема действия векторметра. Векторная диаграмма Ве'кторная диагра'мма,графическое изображение значений периодически изменяющихся величин и соотношений между ними при помощи направленных отрезков - векторов. В. д. широко применяются в электротехнике, акустике, оптике и т. п. Простые гармонические функции одного периода, например a 1= B 1sinwt, f 2= B 2sin(a+ wt), f 3= B 3sin(b+ wt), могут быть представлены графически ( рис .) в виде проекции на ось О у векторов
Сумма или разность двух и более колебаний на В. д. обозначается как геометрическая сумма или разность векторов составляющих колебаний, полученная по правилу параллелограмма, а мгновенное значение искомой величины определяется проекцией вектора суммы на ось Оу.
Например, требуется найти сумму
Fколебаний
f
1с амплитудой

Рис. к ст. Векторная диаграмма. Векторное исчисление Ве'кторное исчисле'ние,математическая дисциплина, в которой изучают свойства операций над векторами евклидова пространства. При этом понятие вектора представляет собой математическую абстракцию величин, характеризующихся не только численным значением, но и направленностью (например, сила, ускорение, скорость). Возникновение и развитие В. и.Возникновение В. и. тесно связано с потребностями механики и физики. До 19 в. для задания векторов использовался лишь координатный способ, и операции над векторами сводились к операциям над их координатами. Лишь в середине 19 в. усилиями ряда учёных было создано В. и., в котором операции проводились непосредственно над векторами, без обращения к координатному способу задания. Основы В. и. были заложены исследованиями английского математика У. Гамильтона и немецкого математика Г. Грасмана по гиперкомплексным числам (1844-50). Их идеи были использованы английским физиком Дж. К. Максвеллом в его работах по электричеству и магнетизму. Современный вид В. и. придал американский физик Дж. Гиббс. Значительный вклад в развитие В. и. внесли русские учёные. В первую очередь следует отметить работы М. В. Остроградского. Им была доказана основная теорема векторного анализа (см. Остроградского формула ) .Исследования казанского математика А. П. Котельникова по развитию винтового исчисления имели важное значение для механики и геометрии. Эти исследования были продолжены советскими математиками Д. Н. Зейлигером и П. А. Широковым. Большое влияние на развитие В. и. имела книга «Векторный анализ», написанная в 1907 русским математиком П. О. Сомовым. Векторная алгебра.Вектором называют направленный отрезок ( рис. 1 ), то есть отрезок, у которого указаны начало (называется также точкой приложения вектора) и конец. Длина направленного отрезка, изображающего вектор, называется длиной, или модулем, вектора. Длина вектора a обозначается | a | .Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и одинаково направлены. Все нулевые векторы считаются равными. Изображенные на рис. 1 векторы а и b коллинеарны и равны. В В. и. рассматриваются свободные векторы. В векторной алгебре важную роль играют линейные операции над векторами: операция сложения векторов и умножения вектора на действительное число. Суммой а + b векторов а и b называют вектор, идущий из начала вектора а в конец вектора b при условии, что начало вектора b приложено к концу вектора а ( рис. 2 ). Происхождение этого правила связано с правилом параллелограмма сложения векторов ( рис. 3 ), источником которого является экспериментальный факт сложения сил (векторных величин) по этому правилу. Построение суммы нескольких векторов ясно из рис. 4 . Произведением a авектора ана число aназывается вектор, коллинеарный вектору а,имеющий длину, равную l al . l a l, и направление, совпадающее с направлением а при a> 0 и противоположное а при a< 0. Вектор -1 · а называется противоположным вектору а и обозначается - а.Операции сложения векторов и умножения вектора на число обладают следующими свойствами: 1) а + b = b + a, 2) ( a + b ) + c = a + ( b + c ) , 3) а + 0 = а, 4) a + ( -a ) = 0, 5) 1 · a= a, 6) a( b a) = ( ab) a, 7) a( a + b ) = a а+ a b, 8) ( a+ b) a = a a+ b a. В векторной алгебре часто используется понятие линейно зависимых и линейно независимых векторов. Векторы a 1, a 2,..., a nназываются линейно зависимыми, если найдутся такие числа a 1, a 2,..., a nиз которых хотя бы одно отлично от нуля, что линейная комбинация ( a 1 a 1+ ...+ a n a n) этих векторов равна нулю. Векторы a 1, a 2,..., a n, не являющиеся линейно зависимыми, называются линейно независимыми. Отметим, что любые три ненулевых вектора, не лежащие в одной плоскости, являются линейно независимыми. Векторы евклидова пространства обладают следующим свойством: существуют три линейно независимых вектора, любые же четыре вектора линейно зависимы. Это свойство характеризует трехмерность рассматриваемого множества векторов. В сочетании с перечисленными выше свойствами указанное свойство означает, что совокупность всех векторов евклидова пространства образует, так называемое, векторное пространство.Линейно независимые векторы e 2, e 2, e 3 , образуют базис. Любой вектор аможет быть единственным образом разложен по базису: а = X e 2+ Y e 2+ Z e 3; коэффициенты X, Y, Zназываются координатами (компонентами) вектора а в данном базисе. Если вектор аимеет координаты X, Y, Z, то это записывают так: а = н X, Y, Zэ .Три взаимно ортогональных (перпендикулярных) вектора, длины которых равны единице и которые обычно обозначают так : i, j, k,образуют, так называемый ортонормированный базис. Если эти векторы поместить началами в одну точку О, то они образуют в пространстве декартову прямоугольную систему координат. Координаты X, Y, Zлюбой точки Мв этой системе определяются как координаты вектора ОМ( рис. 5 ). Указанным выше линейным операциям над векторами отвечают аналогичные операции над их координатами: если координаты векторов а и b равны соответственно н X 1, Y 1, Z 1э и н X 2, Y 2, Z 2э ,то координаты суммы а + b этих векторов равны нX 1+ X 2, Y 1+ Y 2, Z 1+ Z 2э, координаты вектора l aравны н lX 1+ lY 1+ lZ 1э . Развитие и применение векторной алгебры тесно связано с различными типами векторных произведений: скалярного, векторного и смешанного. Понятие скалярного произведения векторов возникает, например, при рассмотрении работы силы F на заданном пути S : работа равна | F || S | cosj,где j- угол между векторами F и S.Математически скалярное произведение векторов а и b определяется как число, обозначаемое ( а, b) и равное произведению длин этих векторов на косинус угла между ними: ( a, b) = | a || b | cosj. Величина | b | cosjназывается проекцией вектора b на ось, определяемую вектором а,и обозначается пр ab. Поэтому ( a, b ) = | a | пр ab. В частности, если a - единичный вектор (| a | = 1) ,то ( а, b ) = пр ab. Очевидны следующие свойства скалярного произведения: ( а, b) = ( b, а), ( l а, b) = l( а, b) , ( а + b, с) = ( а, с) + ( b, с), ( a, а) ³ 0, причём равенство нулю имеет место лишь при a = 0 . Если в ортонормированном базисе i, j, k векторы а и b имеют соответственно координаты н X 1, Y 1, Z 1э и н Х 2, Y 2, Z 2э, то ( a, b) = X 1X 2+ Y 1Y 2+ Z 1Z 2,
Для определения векторного произведения векторов нужно понятие левой и правой упорядоченной тройки векторов. Упорядоченная тройка векторов а, b, с ( а -первый вектор, b-второй , с- третий), приведённых к общему началу и не лежащих в одной плоскости, называется правой (левой), если они располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки. На рис. 6 изображены справа - правая, а слева - левая тройки векторов. Векторным произведением векторов a и b называют вектор, обозначаемый [ a, b ] и удовлетворяющий следующим требованиям: 1) длина вектора [ a, b ] равна произведению длин векторов a и b на синус угла jмежду ними (таким образом, если a и b коллинеарны, то [ a, b ] = 0); 2) если a и b неколлинеарны, то [ a, b ] перпендикулярен каждому из векторов a и b и направлен так, что тройка векторов a, b,[ a, b ] является правой. Векторное произведение обладает следующими свойствами: [ a, b] = -[ b, а] ,[( l a) , b] = l[ a, b] , [ с,( a + b )] = [ с, a] + [ с, b] ,[ a,[ b, с]] = b ( a, с) - с( a, b) , ([ a, b] ,[ с, d]) = ( a, c)( b, d) -( a, d)( b, c) . Если в ортонормированном базисе
i, j, k,образующем правую тройку, векторы
a
и
b
имеют соответственно координаты н
X
1, Y
1, Z
1э и н
X
2, Y
2, Z
2э
,то [
a, b
]
= н
Y
1Z
2- Y
2Z
1,
Z
1X
2- Z
2X
1, X
1Y
2- X
2Y
1э. Понятие векторного произведения связано с различными вопросами механики и физики. Например, скорость
v точки
Мтела, вращающегося с угловой скоростью со вокруг оси
l,равна [
w, r
]
,где
Смешанным произведением векторов a, bи cназывается скалярное произведение вектора [ a, b ] на вектор с:([ a, b ] , с) .Обозначается смешанное произведение символом abc.Смешанное произведение не параллельных одной плоскости векторов a, bи с численно равно объёму параллелепипеда, построенного на приведённых к общему началу векторах a, bи с , взятому со знаком плюс, если тройка a, bи с правая, и со знаком минус, если тройка левая. Если же векторы a, bи с параллельны одной плоскости, то abc = 0. Справедливо также следующее свойство abc = bca = cab . Если координаты векторов a, bи с в ортонормированном базисе i, j, k,образующем правую тройку, соответственно равны н X 1, Y 1, Z 1э ,н X 2, Y 2, Z 2э и н Х 3, Y 3, Z 3э, то 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76 |
|||||||
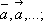
 .Прямая, на которой расположен В., называется линией действия данного В.
.Прямая, на которой расположен В., называется линией действия данного В.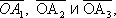 вращающихся с постоянной угловой скоростью
w, причём
вращающихся с постоянной угловой скоростью
w, причём
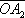 и
и
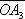 повёрнуты относительно
повёрнуты относительно
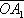 на углы
aи
b. Длина векторов соответствует амплитудам колебаний:
на углы
aи
b. Длина векторов соответствует амплитудам колебаний: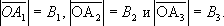
 и
f
2амплитудой
и
f
2амплитудой
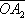 . При геометрическом сложении векторов
. При геометрическом сложении векторов
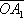 и
и
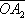 по В. д. находим, что амплитуда суммарного колебания
Fравна длине вектора
по В. д. находим, что амплитуда суммарного колебания
Fравна длине вектора
 и опережает по фазе колебание
f
1на угол
j.
и опережает по фазе колебание
f
1на угол
j.