 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (ТВ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ТВ) - Чтение (стр. 3)
В кристаллах состояние электрона в зоне благодаря периодичности сил, действующих на него, определяется квазиимпульсом р,а энергия электрона E— периодическая функция квазиимпульса: 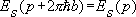 . [ . [
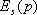 — закон дисперсии,
s— номер зоны]. В аморфных телах, хотя состояние электрона не определяется квазиимпульсом (квазиимпульс ввести нельзя), зонный характер электронного энергетического спектра сохраняется. Строго запрещенных зон энергии в аморфных телах, по-видимому, нет, однако есть квазизапрещённые области, где плотность состояний меньше, чем в разрешенных зонах. Движение электрона с энергией из квазизапрещённой области локализовано, из разрешенной зоны — делокализовано (как в кристалле). — закон дисперсии,
s— номер зоны]. В аморфных телах, хотя состояние электрона не определяется квазиимпульсом (квазиимпульс ввести нельзя), зонный характер электронного энергетического спектра сохраняется. Строго запрещенных зон энергии в аморфных телах, по-видимому, нет, однако есть квазизапрещённые области, где плотность состояний меньше, чем в разрешенных зонах. Движение электрона с энергией из квазизапрещённой области локализовано, из разрешенной зоны — делокализовано (как в кристалле).В соответствии с в каждом энергетическом состоянии может находиться не более двух электронов. Поэтому в каждой энергетической зоне кристалла может поместиться не более 2Nэлектронов, где N —число уровней в зоне, равное числу элементарных ячеек кристалла. При Т® 0 К все электроны занимают наиболее низкие энергетические состояния. Существование Т. т. с различными электрическими свойствами связано с характером заполнения электронами энергетических зон при Т= 0 К. Если все зоны либо полностью заполнены электронами, либо пусты, то такие Т. т. не проводят электрического тока, то есть являются ( рис. 2 , а). Т. т., имеющие зоны, частично заполненные электронами, — проводники электрического тока — ( рис. 2 , б) .Полупроводники представляют собой диэлектрики (нет частично заполненных зон при Т= 0 К) со сравнительно малой шириной запрещенной зоны между последней заполненной (валентной) зоной и первой (свободной — зоной проводимости, ( рис. 2 , в). Наличие дефектов и примесей в кристалле приводит к возникновению дополнительных (примесных) энергетических уровней, располагающихся в запрещенной зоне. У полупроводников эти уровни часто расположены очень близко либо от валентной зоны ( рис. 2 , д), либо от зоны проводимости ( рис. 2 , г). Т. т. с аномально малым перекрытием валентной зоны и зоны проводимости называется (например, у Bi ширина перекрытия ~ 10 -5ширины зоны). Существуют бесщелевые полупроводники, у которых зона проводимости примыкает к валентной (например, сплавы Bi — Sb, Hg — Те с определённым соотношением компонент). Энергия, отделяющая занятые состояния от свободных, называется .Если она расположена в разрешенной зоне, то ей соответствует изоэнергетическая ,выделяющая область занятых электронных состояний в пространстве квазиимпульсов. У полупроводников энергия Ферми расположена в запрещенной зоне и носит несколько формальный характер. У бесщелевых полупроводников она совпадает с границей, отделяющей валентную зону от зоны проводимости. Энергетическая зона, в которой не заняты состояния с энергиями, близкими к максимальной, проявляет себя как зона, содержащая положительно заряженные частицы — дырки. В зависимости от расположения поверхность Ферми бывает электронной и дырочной. Если число электронов n э (число занятых состояний вблизи минимума энергии в зоне) равно числу дырок n д, проводник называется скомпенсированным (например, Bi, у которого n э= n д» 10 -5на атом). У бесщелевых полупроводников поверхность Ферми вырождается в точку либо в линию. Элементарное возбуждение электронной системы кристалла заключается в приобретении электроном энергии, благодаря чему он оказывается в области р-пространства, где в основном состоянии электрона не было; одновременно возникает свободное место (дырка) в области р-пространства, занятой электронами в основном состоянии. Так как электрон и дырка движутся независимо, то их следует считать различными квазичастицами. Другими словами, элементарное возбуждение электронной системы заключается в рождении пары квазичастиц — электрона проводимости и дырки. Электроны и дырки подчиняются статистике Ферми — Дирака. В диэлектриках и полупроводниках возбуждённые состояния отделены от основного состояния энергетической щелью, в металлах (а также в полуметаллах и бесщелевых полупроводниках) — непосредственно примыкают к основному состоянию ( рис. 2 ). Электронная система Т. т. порождает и более сложные возбуждения: в полупроводниках — экситоны Ванье — Мотта и Френкеля и ;в сверхпроводящих металлах — куперовские пары (см. ниже). Кроме того, по электронной системе Т. т. могут распространяться волны — плазменные колебания (соответствующие им квазичастицы — называются ). Металлы. В металлах при низких температурах электроны частично заполненных зон (электроны проводимости) играют важную роль в тепловых свойствах. Линейная зависимость теплоёмкости и коэффициента теплового расширения от температуры (при Т® 0 К) объясняется тем, что электроны, подчиняющиеся статистике Ферми — Дирака, сильно вырождены. Вырождение сохраняется практически при всех температурах, так как температура вырождения T F= E F/kдля хороших металлов ³ 10 4К. Этим объясняется тот факт, что теплоёмкость металлов при высоких температурах неотличима от теплоёмкости диэлектриков. Благодаря вырождению в металлах во многих процессах участвуют только электроны, энергия которых E» E F,то есть электроны, расположенные вблизи поверхности Ферми. Поверхности Ферми, как правило, имеют сложную форму. Разнообразие формы поверхностей Ферми у различных металлов обычно выявляется в их поведении в достаточно сильном магнитном поле Н,когда размеры орбиты электрона (~ 1/ Н) значительно меньше длины его свободного пробега. Проекция траектории электрона на плоскость, перпендикулярную Н,подобна плоскому сечению поверхности Ферми, и, если между двумя актами рассеяния электрон многократно опишет свою траекторию, то форма поверхности Ферми проявится в его свойствах. Осцилляции магнитной восприимчивости и электросопротивления в магнитном поле позволяют измерить экстремальные площади сечений поверхности Ферми (см. , ) .По поглощению ультразвука в магнитном поле можно измерить экстремальные диаметры поверхности Ферми; дают возможность установить общие контуры поверхности Ферми. — метод определения частоты обращения электрона в магнитном поле Н,которая зависит от его эффективной массы m*,связанной с законом дисперсии электронов. Перечисленные эксперименты производятся при низкой температуре на монокристаллических сверхчистых образцах и дают возможность исследовать электронный энергетический спектр. Одной из важнейших характеристик металла является его удельная электропроводность ( ,которую для изотропного металла можно записать в виде 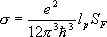 , где
S
F— площадь поверхности Ферми, а
l
p— длина свободного пробега электронов, учитывающая рассеяние электронов с изменением квазиимпульса. Температурная зависимость s и удельного сопротивления r = 1/s (
рис. 3
) определяется температурной зависимостью длины свободного пробега
l
p.При
Т³ q механизм рассеяния обусловлен столкновениями с фононами , где
S
F— площадь поверхности Ферми, а
l
p— длина свободного пробега электронов, учитывающая рассеяние электронов с изменением квазиимпульса. Температурная зависимость s и удельного сопротивления r = 1/s (
рис. 3
) определяется температурной зависимостью длины свободного пробега
l
p.При
Т³ q механизм рассеяния обусловлен столкновениями с фононами
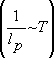 ; при
Т<< q из-за уменьшения числа фононов «проявляются» др. механизмы: столкновения со статическими дефектами кристалла, в частности с поверхностью образца, электрон-электронные столкновения и др. (
рис. 4
). В металлах большая часть теплоты переносится электронами проводимости. В широком диапазоне температур существует простое соотношение между электропроводностью s и электронной частью теплопроводности c
c(
)
: ; при
Т<< q из-за уменьшения числа фононов «проявляются» др. механизмы: столкновения со статическими дефектами кристалла, в частности с поверхностью образца, электрон-электронные столкновения и др. (
рис. 4
). В металлах большая часть теплоты переносится электронами проводимости. В широком диапазоне температур существует простое соотношение между электропроводностью s и электронной частью теплопроводности c
c(
)
: ', ',где  — число Лоренца. Наблюдающиеся при
ТЈ q отклонения от закона Видемана — Франца отражают особенности взаимодействия электронов проводимости с фононами (при
Т< q длина свободного пробега, входящая в выражение для c и учитывающая изменение потока энергии электронов за счёт столкновений, не равна
l
p)
.
(
,
и др.) также являются следствием участия электронов в переносе тепла. Магнитное поле изменяет электропроводность и теплопроводность и служит причиной гальваномагнитных и термомагнитных явлений (см.
,
). — число Лоренца. Наблюдающиеся при
ТЈ q отклонения от закона Видемана — Франца отражают особенности взаимодействия электронов проводимости с фононами (при
Т< q длина свободного пробега, входящая в выражение для c и учитывающая изменение потока энергии электронов за счёт столкновений, не равна
l
p)
.
(
,
и др.) также являются следствием участия электронов в переносе тепла. Магнитное поле изменяет электропроводность и теплопроводность и служит причиной гальваномагнитных и термомагнитных явлений (см.
,
).Коэффициент отражения электромагнитных волн металлом близок к 1. Электромагнитная волна благодаря практически не проникает в металл; глубина d проникновения в радиодиапазоне равна 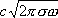 (w — частота волны). В оптическом диапазоне d =
с/w
0х»
10
-5
см, с— скорость света; w
0» 1015
сек
–1— плазменная, или ленгмюровская, частота электронов металла ( (w — частота волны). В оптическом диапазоне d =
с/w
0х»
10
-5
см, с— скорость света; w
0» 1015
сек
–1— плазменная, или ленгмюровская, частота электронов металла (
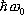 — энергия
)
.При низких температурах взаимодействие металла с электромагнитной волной обладает особенностями, связанными с аномальным характером скин-эффекта (d Ј
l, см.
)
.На характер распространения электромагнитных волн в металле влияет магнитное поле
Н:в некоторых металлах при
Н¹ 0 и при низких температурах могут распространяться слабозатухающие электромагнитные волны (магнитоплазменные волны, см.
). — энергия
)
.При низких температурах взаимодействие металла с электромагнитной волной обладает особенностями, связанными с аномальным характером скин-эффекта (d Ј
l, см.
)
.На характер распространения электромагнитных волн в металле влияет магнитное поле
Н:в некоторых металлах при
Н¹ 0 и при низких температурах могут распространяться слабозатухающие электромагнитные волны (магнитоплазменные волны, см.
).Сверхпроводимость. У многих металлов и сплавов при охлаждении ниже некоторой температуры T cнаблюдается полная потеря электросопротивления — металл переходит в сверхпроводящее состояние. Такой переход — фазовый переход 2-го рода, если Н= 0, и 1-го рода, если Н¹ 0. T cзависит от Н.В достаточно больших магнитных полях [ Н > Нкр(Т)] сверхпроводящего состояния не существует. Сверхпроводники обладают аномальными магнитными свойствами, по которым делятся на два класса — сверхпроводники 1-го и 2-го родов. В толще сверхпроводника 1-го рода при Н < Нкрмагнитное поле равно 0 ( ) .В сверхпроводник 2-го рода магнитное поле может проникать в виде сложной вихревой структуры. Явление сверхпроводимости объясняется притяжением между электронами, обусловленным обменом фононами. При этом образуются электронные (куперовские) пары, возникает «конденсат», способный двигаться без сопротивления. Устойчивость сверхпроводящего состояния обеспечена наличием энергии связи электронов в паре, благодаря чему зона энергий элементарных возбуждений отделена энергетической щелью от энергии основного состояния (см. , ). Сверхпроводники 2-го рода находят техническое применение как материал для обмотки источников сильного магнитного поля — сверхпроводящих соленоидов. С ними связывают надежды на создание генераторов, транспортных средств на магнитной подушке и линий передач электрической энергии без потерь. Обнаружение или синтез сверхпроводников с высокой критической температурой и внедрение их в технику имели бы последствия, возможно, соизмеримые с освоением пара, электричества и т. п. Полупроводники. В полупроводниках при Т> 0 часть электронов из валентной зоны и примесных уровней переходит в возбуждённое состояние: появляются электроны в зоне проводимости и дырки в валентной зоне. Благодаря этому при комнатной температуре полупроводник обладает заметной электропроводностью ( рис. 5 ). Основным параметром, определяющим число электронов и дырок в полупроводнике при тепловом возбуждении, служит ширина запрещенной зоны — минимальное расстояние D Eмежду валентной зоной и зоной проводимости (у Ge D E= 0,746 эв, а у Si D E= 1,165 эв). Возбуждение полупроводника может быть произведено и др. путём, например освещением. Электроны, поглощая кванты света, переходят в зону проводимости и освобождают места в валентной зоне. Особенность полупроводников: их свойства легко изменяются при сравнительно слабых внешних воздействиях (темп-рой, давлением, освещением, введением примесей и т. п.). На этом основаны многочисленные применения полупроводников (см. ) .Многие свойства полупроводников обусловлены электронами и дырками с энергиями, близкими к «дну» зоны проводимости и «потолку» валентной зоны. Законы дисперсии электронов и дырок определены для большого числа полупроводников. Электропроводность полупроводников определяется числом n i и подвижностью u i носителей заряда (электронов и дырок): 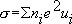 . Экспоненциальная зависимость
аот температуры — следствие экспоненциальной зависимости от
Тчисла носителей
n
i.Измерения проводимости, константы Холла, термоэлектрических и термомагнитных характеристик позволили выяснить зависимость от температуры величин
n
i, u
iи понять основные механизмы торможения электронов и дырок. . Экспоненциальная зависимость
аот температуры — следствие экспоненциальной зависимости от
Тчисла носителей
n
i.Измерения проводимости, константы Холла, термоэлектрических и термомагнитных характеристик позволили выяснить зависимость от температуры величин
n
i, u
iи понять основные механизмы торможения электронов и дырок.В некоторых полупроводниках (например, в Те), легированных большим числом примесей, при низких температурах наступает вырождение газа носителей, что сближает их с металлами (число носителей перестаёт зависеть от температуры, наблюдаются эффекты Шубникова — Де Хааза, Де Хааза — ван Альфена и др.). У ряда полупроводников обнаружена сверхпроводимость. Электроны и дырки, притягиваясь друг к другу, способны образовать систему, подобную ,называемую экситоном Ванье — Мотта. Он обнаруживается по серии водородоподобных линий поглощения света, соответствующих уровням энергии, расположенным в запрещенной зоне полупроводника. В полупроводниках обнаружено большое число явлений, характерных для плазмы (см. ). Сильное магнитное поле изменяет свойства полупроводников при низких температурах. Здесь область квантовых эффектов 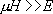 ,где
E— средняя энергия электрона (дырки), значительно доступнее, чем в металлах (в полупроводниках
,где
E— средняя энергия электрона (дырки), значительно доступнее, чем в металлах (в полупроводниках
 ,а в металлах
,а в металлах
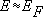 ). ).Электронные свойства аморфных тел зависят от того, в какой области (разрешенной или квазизапрещённой) расположен уровень Ферми. Существование в аморфных телах зонной структуры объясняет их деление на металлы, диэлектрики и полупроводники. Наиболее детально изучены аморфные полупроводники (например, халькогенидные стекла). Существование квазизапрещённой зоны обнаруживается оптическими исследованиями, которые подтверждают «заполнение» запрещенной зоны квазилокальными уровнями («хвосты» поглощения). Специфическая особенность аморфных полупроводников — «прыжковая» проводимость — объясняет экспоненциальную зависимость подвижности носителей от температуры: 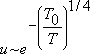 (закон Мотта,
T
0~ 10
6—10
8K) в условиях, когда вероятность теплового возбуждения мала (при низкой температуре). Электрон «выбирает» себе место для «прыжка», так чтобы достигался максимум вероятности перехода из одного состояния в другое. (закон Мотта,
T
0~ 10
6—10
8K) в условиях, когда вероятность теплового возбуждения мала (при низкой температуре). Электрон «выбирает» себе место для «прыжка», так чтобы достигался максимум вероятности перехода из одного состояния в другое.Диэлектрики. Кристаллы, имеющие только заполненные и пустые электронные энергетические зоны, ведут себя в электрическом поле как изоляторы. Первый возбуждённый уровень находится на конечном расстоянии от основного, причём ширина запрещенной зоны D Eпорядка нескольких эв. Делокализация электронов в таких Т. т. не играет роли даже при описании электронных свойств, диэлектрики можно считать состоящими из разделённых в пространстве атомов, молекул или ионов. Электрическое поле E,сдвигая заряды, поляризует диэлектрики. Характеристикой поляризации может служить электрический дипольный момент единицы объёма Р,электрическая индукция D= Е+ 4p Рили a ,связывающая поляризацию Ри внешнее электрическое поле Е: Р= a Е.Отсюда e = 1 + 4pa, где e — диэлектрическая проницаемость. В природе отсутствуют вещества с поляризацией Р,направленной против поля Е,и a <0 (аналоги диамагнетиков). Поэтому всегда e > 1. У обычных диэлектриков дипольный момент появляется лишь во внешнем электрическом поле. При этом e близка к 1 и слабо зависит от температуры. У некоторых диэлектриков частицы обладают спонтанными дипольными моментами, а электрическое поле их ориентирует (ориентационная поляризация), в этом случае при высоких температурах e ~ 1/ Т. При низких температурах дипольные моменты спонтанно ориентируются и вещество переходит в пироэлектрическое состояние (см. ) .Появление спонтанной поляризации сопровождается изменением симметрии кристалла и перестройкой кристаллической структуры (или ею вызвано) и является фазовым переходом. Если этот переход 2-го рода, то называется сегнетоэлектрическим. В точке сегнетоэлектрического перехода e имеет максимум (см. ) .Особый класс диэлектриков составляют пьезоэлектрики, у которых упругие напряжения вызывают поляризацию, пропорциональную им. Только кристаллы, не обладающие центром симметрии, могут быть пьезоэлектриками (см. ). Диэлектрическая проницаемость меняется с частотой w внешнего электрического поля. Эта зависимость (дисперсия) проявляется как зависимость от частоты w фазовой и групповой скоростей распространения света в диэлектрике. Взаимодействие переменного электрического поля с Т. т. сопровождается переходом энергии этого поля в тепло ( ) и описывается мнимой частью e. Частотная и температурная зависимости e — следствие диссипативных и релаксационных процессов в Т. т. Поглощение света диэлектриком можно трактовать как электронное возбуждение фотоном структурной частицы кристалла. Однако возбуждённое состояние не локализуется на определённых атомах или молекулах, а благодаря резонансному взаимодействию соседних частиц движется по кристаллу, за счёт чего уровень энергии расширяется в зону (экситон Френкеля). Магнитные свойства Т. т.При достаточно высоких температурах Т. т. либо диамагнитны (см. ) ,либо парамагнитны (см. ) .В первом случае вектор намагниченности направлен против магнитного поля и его происхождение — результат общей прецессии всех электронов Т. т. с угловой частотой w L= еН/2mc(см. ) .Диамагнитная восприимчивость c пропорциональна среднему квадрату расстояния электронов от ядра и поэтому может служить источником информации о структуре Т. т. Электроны проводимости металлов и полупроводников делокализованы, однако благодаря квантованию их движения в плоскости, перпендикулярной магнитному полю, они вносят вклад в c ,причём у металлов этот вклад того же порядка, что и c ионного остова (диамагнетизм Ландау). Диамагнетизм (общее свойство атомов и молекул) слабо зависит от агрегатного состояния вещества и от температуры. Он проявляется только в том случае, если не перекрывается парамагнетизмом. Парамагнетизм — следствие ориентации магнитных моментов атомов и электронов проводимости (в металле и полупроводнике) магнитным полем. При высоких температурах парамагнитная восприимчивость убывает обратно пропорционально температуре ( ) ;для типичных парамагнетиков при 300 К она » 10 -5Исключение составляют непереходные металлы. Их парамагнитная восприимчивость аномально мала (~ 10 -6) и слабо зависит от температуры. Это — результат вырождения электронов проводимости (парамагнетизм Паули). Наличие собственных магнитных моментов у атомов, ионов, электронов и связанное с этим расщепление электронных уровней энергии в магнитном поле (см. ) приводят к существованию резонансного поглощения энергии переменного магнитного поля (см. ) .Структура магнитных уровней очень чувствительна к сравнительно слабым взаимодействиям (например, к окружению частиц). Поэтому парамагнетизм (в частности, электронный парамагнитный резонанс) служит одним из важнейших источников сведений о состоянии атомных частиц в Т. т. (о положении в ячейке кристалла, химической связи и т. п.). При понижении температуры парамагнетики (диэлектрики и переходные металлы) переходят в ферро-, в антиферро- или ферримагнитное состояния (см. , , ) ,для которых характерно упорядоченное расположение собственных магнитных атомов. Непереходные металлы, как правило, остаются парамагнитными вплоть до Т=0 К (Li, Na и т. д.). Однако нельзя утверждать, что упорядоченное магнитное состояние — следствие локализации атомных магнитных моментов. Существуют ферромагнитные сплавы (например, типа ZrZn 2), в которых ферромагнетизм, по-видимому, полностью обусловлен зонными (делокализованными) электронами. Переходы парамагнитное — ферромагнитное и парамагнитное — антиферромагнитное состояния в большинстве случаев — фазовые переходы 2-го рода. температура, при которой происходит переход в ферромагнитное состояние, называется температурой Кюри T c,а в антиферромагнитное — температурой Нееля T N.При Т = T cили Т = T Nнаблюдаются скачок теплоёмкости, рост магнитной восприимчивости и т. п. температуры T cи T N,для различных Т. т. сильно различаются (например, для Fe T c=1043 К, для Gd T c=289 К, а для FeCI T N=23,5 К). Силы, упорядочивающие магнитные моменты при температуре Т < T cили Т < T N,имеют квантовое происхождение, хотя обусловлены электростатическими кулоновскими взаимодействиями между атомарными электронами (см. ) .Релятивистские (магнитные, спинорбитальные и т. п.) взаимодействия ответственны за анизотропию магнитных свойств (см. ) . Вблизи Т =0 К отклонения от магнитного порядка малы и не локализуются в определённых участках, а в виде волн распространяются по кристаллу. Это — ;соответствующие им квазичастицы — магноны проявляют себя в тепловых и магнитных свойствах. Так, тепловое возбуждение спиновых волн увеличивает теплоёмкость магнетиков (по сравнению с немагнитными телами) и приводит к характерной зависимости теплоёмкости от температуры (например, при T<< q 2 /T cу ферромагнитных диэлектриков С~ Т 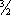 Ядерные явления в Т. т.Роль атомных ядер в свойствах Т. т. не ограничивается тем. что в них сосредоточены масса тела и его положительный заряд. Если ядра обладают магнитными моментами, то при достаточно низкой температуре их вклад в парамагнитную восприимчивость и теплоёмкость становится ощутимым. Особенно отчётливо это проявляется при измерении резонансного поглощения энергии переменного магнитного поля. Зеемановское расщепление ядерных уровней энергии является причиной ,одного из широко распространённых методов изучения Т. т., так как структура ядерных магнитных уровней существенно зависит от свойств электронной оболочки атома. Многие процессы (ядерные, электронные) в Т. т. приобретают специфические черты, позволяющие использовать их для изучения свойств Т. т.; например, изучение электронно-позитронной аннигиляции позволяет исследовать свойства электронной системы Т. т.; резонансное поглощение g-квантов ядрами является распространённым методом исследования энергетического спектра Т. т., локальных магнитных полей (см. ) и т. п.; частота ядерного магнитного резонанса изменяется при переходе из нормального в сверхпроводящее состояние. Исследование взаимодействия быстрых заряженных частиц с Т. т. показало, что упорядоченное расположение атомов накладывает существенный отпечаток на передачу энергии от быстрой частицы атомам Т. т. Например, имеется резкая зависимость длины пробега быстрой частицы от направления относительно кристаллографических осей (см. , ) . Заключение.Электрические, магнитные и оптические свойства Т. т. широко используются в радиотехнике и электротехнике, в приборостроении и т. п. Полупроводниковые приборы заменили электронные лампы; сверхпроводящие соленоиды заменяют электромагниты; создаются высокочастотные устройства и измерительные приборы, использующие сверхпроводники; основой квантовых генераторов являются кристаллы. Современная техника широко использует квантовые свойства Т. т. Расширяются экспериментальные методы исследования Т. т., они включают низкие температуры, сильные магнитные и электрические поля, высокие давления, практически весь диапазон электромагнитных волн (от радиоволн до жёстких g-квантов), разнообразные «проникающие» частицы (нейтроны, протоны больших энергии) и т. д. Некоторые исследования Т. т. стали возможны только после появления сверхчистых кристаллов. Важная особенность физики Т. т. — возможность синтезировать Т. т. с необходимыми свойствами. Техническое использование сверхпроводимости основано на создании сплавов (Nb 3Sn и др.), совмещающих сверхпроводящие свойства (при высоких Ткри Нкр) с пластичностью. Физика Т. т. — непрерывно действующий источник новых материалов. Новые физические идеи, рождающиеся в физике Т. т., проникают в , ,в физику ,в , и др. Лит.:Ландау Л. Д., Лифшиц Е. М., Механика сплошных сред, 2 изд., М., 1953 (Теоретическая физика); их же, Статистическая физика, 2 изд., М., 1964 (Теоретическая физика, т. 5); их же, Электродинамика сплошных сред, М., 1959 (Теоретическая физика); Киттель Ч., Введение в физику твердого тела, пер. с англ., 2 изд., М., 1962; 3аиман Д ж., Электроны и фотоны, пер. с англ., М., 1962; Пайерлс Р., Квантовая теория твердых тел, пер. с англ., М., 1956; Физика твердого тела. Атомная структура твердых тел. Электронные свойства твердых тел, пер. с англ., М., 1972 (Над чем думают физики, в. 7—8). см. также лит. при статьях , , , . И. М. Лифшиц, М. И. Каганов.     
Твёрдость
|
|||||||