 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (ТВ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ТВ) - Чтение (стр. 2)
8) В большинстве случаев при определённой температуре все степени свободы атомных частиц в Т. т. можно разделить на 2 категории. Для одних kTвелико по сравнению с характерной энергией их взаимодействия Uвз,для др. степеней свободы kTмало по сравнению с Uвз.Степени свободы, для которых kT³ Uвз,могут быть описаны в терминах «газа частиц» (например, «газ магнитных стрелок» при Т³ Тс) ;степени свободы, для которых kTЈ Uвз,находятся на низком уровне возбуждения, благодаря чему соответствующие им движения могут быть описаны путём введения квазичастиц, слабо взаимодействующих друг с другом. Т. о., в большинстве случаев свойства Т. т. могут быть «сведены» к свойствам газов — либо частиц, либо квазичастиц. Сильное взаимодействие при этом не «выпадает», оно определяет структуру Т. т. (например, его кристаллической решётки) и свойства отдельной квазичастицы. Квазичастицы существуют не в свободном пространстве (как частицы в реальных газах), а в кристаллической решётке, структура которой отражается в свойствах квазичастиц. Вблизи точек фазового перехода 2-го рода такое «сведёние» невозможно, так как движение атомных частиц Т. т. в этих условиях скоррелировано (на «языке» квазичастиц это (означает, что нельзя пренебречь их взаимодействием). Корреляция носит особый (не силовой) характер: вероятность коллективных движений частиц и квазичастиц столь же велика, сколь и их индивидуальных движений. Возрастание роли корреляции в движении частиц приводит к наблюдаемым эффектам: возрастают теплоёмкость, магнитная восприимчивость и т. п. Вблизи фазового перехода 2-го рода Т. т. ведёт себя как система тсильно взаимодействующих частиц (или квазичастиц), принципиально не сводимая к газу. Вблизи фазового перехода 2-го рода Т. т. может служить моделью значительно более сложных систем (например, ядерной материи, элементарных частиц в процессе их взаимодействия). Знание атомно-молекулярной структуры Т. т., характера движения составляющих его частиц объясняет наблюдаемые явления и позволяет предсказывать ещё не открытые свойства Т. т., а также целенаправленно изменять структуру Т. т. и синтезировать Т. т. с уникальным, набором свойств. Физика Т. т. разделилась на ряд областей, обособление которых происходит путём выделения либо объекта исследования (физика металлов, физика полупроводников, физика магнетиков и др.), либо метода исследования ( , Т. т. и т. п.), либо определённых свойств Т. т. (механических, тепловых и т. д.). Возможность обособления — следствие относительной независимости атомных движений в Т. т. Атомно-кристаллическая структура Т. т.зависит от сил, действующих между атомными частицами. Изменяя среднее расстояние между атомами с помощью внешнего давления, можно существенно изменить вклад межатомных сил различной природы и благодаря этому — кристаллическую структуру Т. т. Обнаружено большое число различных существующих при больших давлениях кристаллических модификаций, многие из которых отличаются по физическим свойствам. Например, Bi под давлением образует 3 сверхпроводящие модификации: при 25 300 атм < р <27 000 атмBi llI ( Tc= 3,93 К); при 27 000 атм < р <80 000 атмBi III ( Tc =6,9 К); при 80 000 атм < рBi IV ( Tc= 7 К). Многие полупроводники под давлением переходят в металлическое состояние (Ge при р» 120 000 атмстановится металлом), a Yb (металл) под давлением превращается в полупроводник. Есть основания считать, что молекулярный водород под давлением в 2—3 106 атмпревращается в металл. При чрезвычайно большом давлении (или плотности), когда объём, приходящийся на один атом, становится меньше обычного атомного размера, атомы теряют свою индивидуальность и вещество превращается в сильно сжатую электронноядерную плазму. Исследование такого состояния вещества важно, в частности, для понимания структуры . Атомная структура кристаллов экспериментально определяется методами рентгено-структурного анализа, магнитная структура и (ориентация магнитных моментов атомов) — методами .Полное знание атомной структуры предполагает знание размеров элементарной ячейки кристалла и положения всех атомов внутри неё. Однако во многих случаях достаточно знать лишь элементы симметрии данного кристалла. При макроскопическом описании Т. т. (механических, электрических, тепловых, оптических свойств) кристаллы можно рассматривать как сплошную анизотропную среду, в которой симметричное расположение атомов приводит к эквивалентности направлений. Основу симметрии бесконечной кристаллической решётки составляет её пространственная периодичность — способность совмещаться с собой при параллельных переносах ( ) на определённые расстояния в определённых направлениях. Эквивалентные узлы кристаллической решётки, которые могут быть совмещены друг с другом путём трансляции, образуют .Их существует 14 типов. По симметрии Браве решётки делятся на 7 кристаллических сингоний. Кроме того, кристаллическая решётка может обладать осями и плоскостями симметрии, зеркально-поворотными и винтовыми осями и плоскостями зеркального скольжения. Совокупность осей и плоскостей симметрии, определяющая симметрию физических свойств кристаллов, называется кристаллическим классом; их 32. Совокупность всех элементов симметрии кристаллической решётки называется её пространственной группой. Всего возможно 230 различных пространственных групп. Если учесть магнитные свойства атомов, составляющих кристаллическую решётку, то число возможных магнитных пространственных групп увеличится до 1651 (см. ) . Структура реального кристалла. Хотя большого размера в природе встречаются редко, они всё чаще используются в технике. Выращивают их искусственно (см. ) .Применяемые на практике конструкционные материалы, как правило, — ,состоящие из огромного числа мелких монокристаллов (кристаллических зёрен). Многие свойства Т. т. (например, пластичность, прочность) зависят от величины зёрен. При хаотической ориентации кристаллических зёрен поликристалл можно считать изотропным телом, хотя каждый кристалл в отдельности анизотропен. В некоторых поликристаллах возникает анизотропия, связанная с условиями их и обработки (ориентированный рост, прокатка, ковка); она называется . Границы зёрен нарушают строгую периодичность в расположении атомов в кристалле. Однако это — не единственные .Дефектами являются микроскопические включения (в частности, зародыши др. кристаллической модификации, пустоты и т. п.), сама поверхность образца, чужеродные примесные атомы, ,атомы в междоузлиях, и т. д. Наличие или отсутствие тех или др. дефектов во многих случаях определяет так называемые структурночувствительные свойства Т. т.: механические (прочность, пластичность), электропроводность, оптические и др. (см. ниже). Межатомные связи. По типам связей Т. т. делят на 5 классов, каждый из которых характеризуется своеобразным пространств. распределением электронов (табл. 1). 1) В (NaCI, KCl и др.) основные силы, действующие между ионами, — силы электростатического притяжения. Распределение электронного заряда вблизи каждого иона близко к сферическому и слегка нарушается в области соприкосновения соседних ионов. 2) В кристаллах с валентные электроны обобществлены соседними атомами. Табл. 1. — Классификация кристаллов по типам связей Тип кристалла Пример Энергия связи*, ккал/моль Характерные свойства Ионный …………. Атомный (с ковалентной связью) Металлический… Молекулярный…. С водородными связями..………… NaCI С (алмаз), Ge, Si Cu, Al Ar, СН 4Н 2О (лёд) H 2F 180—220 170—283 26—96 1,8 3—10 Отражение и поглощение света в инфракрасной области; малая электропроводность при низких температурах; хорошая ионная проводимость при высоких температурах Высокая твёрдость (у чистых образцов), слабая проводимость при низких температурах Высокая электропроводность Низкие точки плавления и кипения, сильная сжимаемость Тенденция к полимеризации; энергия связи между молекулами больше, чем у аналогичных молекул без водородных связей * Для кристаллов первых двух типов энергия связи определена при 300 К; для молекулярных кристаллов и кристаллов с водородными связями — в точке плавления. Иногда мерой энергии связи служит энергия (на одну частицу), которую надо затратить, чтобы, нагревая Т. т. от 0 К, расщепить его на невзаимодействующие атомы или ионы. Кристалл по существу представляет собой огромную молекулу. Этот тип характеризуется высокой электронной плотностью между ионами и резкой направленностью связей. Примеры кристаллов с ковалентной связью: алмаз, Ge, Si. 3) У большинства металлов (например, щелочных) энергию связи обусловливают электроны проводимости; металл можно представлять как решётку из положительных ионов, погруженную в электронную жидкость (металлическая связь). У некоторых металлов (например, переходных) важна также ковалентная связь, осуществляемая электронами незаполненных внутренних оболочек. 4) В молекулярных кристаллах (например, в отвердевших инертных газах) молекулы связаны слабыми электростатическими силами (силы Ван-дер Ваальса), обусловленными взаимной поляризацией молекул. Для всех молекулярных кристаллов характерна слабая связь; они имеют низкую точку плавления и заметно сублимируют. В большинстве органических кристаллов молекулы связаны силами Ван-дер Ваальса (см. ) .5) В кристаллах с водородными связями каждый атом водорода связан силами притяжения одновременно с двумя др. атомами. Водородная связь — основная форма взаимодействия между молекулами воды. Водородная связь вместе с электростатическим притяжением дипольных моментов молекул H 2O определяет свойства воды и льда. Следует отметить, что классификация Т. т. по типам связи условна. Во многих веществах наблюдаются комбинации различных типов связи. Природа сил связи в Т. т. получила объяснение только после привлечения квантовой механики, хотя источником сил, действующих между атомными частицами, в Т. т. служат электростатическое притяжение и отталкивание. Образование из атомов и молекул устойчивых Т. т. показывает, что силы притяжения на расстояниях ~ 10 -8 смуравновешиваются силами отталкивания, быстро спадающими с расстоянием. Это даёт возможность в ряде случаев рассматривать атомные частицы как твёрдые шары и характеризовать их кристаллохимическими радиусами (см. ). Для описания энергии UТ. т. как функции среднего расстояния rмежду частицами часто пользуются формулой Ленарда — Джонса:  , ,в которой первое слагаемое описывает энергию притяжения, а второе — отталкивания; здесь а— среднее межатомное расстояние в нормальных условиях, nзависит от типа связи, например в ионных кристаллах n =1, а в молекулярных n= 6; m ~9—11. Энергия имеет минимум, равный Uoпри r= а.Выражая rчерез удельный объём V( r ~ V  )
,получаем уравнение состояния Т. т. — зависимость давления )
,получаем уравнение состояния Т. т. — зависимость давления
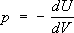 от удельного объёма. Такой подход связывает экспериментально измеряемые величины (энергию связи, и др.) друг с другом и с величинами, 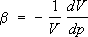 входящими в выражение для силы, действующей между частицами. Теоретические методы позволяют, исходя из «первых принципов», рассчитать кристаллическую структуру, уравнение состояния, тепловые свойства Т. т. в широком интервале температур. Теоретические данные хорошо согласуются с экспериментом для ионных и молекулярных кристаллов. Для ковалентных кристаллов и металлов необходим учёт непарного характера сил, действующих между частицами. Механические свойства Т. т.(реакции на внешние механические воздействия — сжатие, растяжение, изгиб, удар и т. д.) определяются силами связи между его структурными частицами. Многообразие этих сил приводит к разнообразию механических свойств: одни Т. т. пластичны, другие хрупки. Обычно металлы, в которых силы связи определяются коллективным действием электронов проводимости, более пластичны, чем диэлектрики; например, деформация Cu при комнатной температуре в момент разрыва достигает нескольких десятков %, а NaCI разрушается почти без деформации (хрупкость). Механические характеристики изменяются с температурой, например с повышением температуры пластичность обычно увеличивается. У большинства Т. т. реакция на внешнее механическое воздействие зависит от его темпа: хрупкое при ударе Т. т. может выдержать значительно большую статическую нагрузку. При небольших статических нагрузках у всех Т. т. наблюдается линейное соотношение между напряжением и деформацией ( ) .Такая деформация называется упругой. Упругая деформация обратима: при снятии напряжения она исчезает. Для идеального монокристалла (без дефектов) область обратимой деформации наблюдалась бы вплоть до разрушения, причём предел прочности должен был бы соответствовать силам связи между атомами. При больших нагрузках реакция реального Т. т. существенно зависит от дефектности образца (от наличия или отсутствия дислокаций, от размеров кристаллических зёрен и т. п.) — разрушение начинается в самых слабых местах. Дислокация — наиболее подвижный дефект кристалла, поэтому именно дислокации в большинстве случаев определяют его пластичность. Появление (рождение) и перемещение дислокации — элементарные акты пластичности. Механические свойства Т. т. зависят от его обработки, вносящей или устраняющей дефекты ( , , ,гидроэкструзия и т. п.). Например, предел прочности при растяжении специально обработанной стали 300—500 кгс/мм 2 ,а обычной стали того же химического состава — не более 40—50 кгс/мм 2(табл. 2). Табл. 2. — Механические характеристики идеальных и реальных металлических кристаллов Идеальный кристалл.........………. Реальные кристаллы.........………. Специально термомеханически обработанные или нитевидные кристаллы..………………………… Предел прочности, кгс/мм 2 Упругая деформация, % Пластическая деформация, % (1,5—2) Ч10 30,1—1 (0,5—1,4) Ч10 3 1—5 10 -20,5—2 0 От десятков до сотен % 1 Упругие свойства изотропных Т. т. (в частности, поликристаллов) описываются модулем Юнга Е(отношение напряжения к относительному удлинению) и коэффициентом Пуассона v(отношение изменения поперечных и продольных размеров), характеризующими реакцию на растяжение (сжатие) образца в виде однородного стержня (см. ) .Для стали и ковкого железа Е =2,1Ч10 6 кгс/см2.Из условия устойчивости недеформированного состояния следует, что Е >0, а—1 < n <  . Однако в природе тела с отрицательным коэффициентом Пуассона не обнаружены. Модуль Юнга и коэффициент Пуассона определяют скорость распространения звуковых волн в изотропном Т. т. . Однако в природе тела с отрицательным коэффициентом Пуассона не обнаружены. Модуль Юнга и коэффициент Пуассона определяют скорость распространения звуковых волн в изотропном Т. т.В анизотропном кристалле упругие свойства описываются 4-го ранга, число независимых компонент которого обусловлено симметрией кристалла. Поглощение звука (и вообще упругих волн) в Т. т. обусловлено: неодинаковостью температуры в разных участках Т. т. при прохождении по нему волны и возникновением в результате этого необратимых тепловых потоков (теплопроводность); конечностью скорости движения частиц Т. т. Необратимые процессы рассеяния, связанные с конечностью скорости движения, называются ,или .В идеальных кристаллах и вязкость определяются столкновениями квазичастиц друг с другом, в реальных кристаллах к этим процессам добавляется рассеяние звуковых волн на дефектах кристаллической решётки, важную роль играет также диффузия. Исследование поглощения звука — метод изучения динамических свойств Т. т., в частности свойств квазичастиц. Механические свойства Т. т. — основа их инженерного применения как конструкционных материалов. В частности, знание связи деформаций и напряжений позволяет решать конкретные практические задачи о распределении напряжений и деформаций в Т. т. различной формы (балки, пластины, оболочки и т. п.) при разнообразных нагрузках — изгибе, кручении (см. ). Движение частиц в Т. т.Фононы. Исследование теплового движения частиц в конденсированных средах приводит к понятию фононов. Если N— число ячеек кристалла, а n — число атомов (ионов) в элементарной ячейке, то 3 Nn — полное атомов кристалла, совершающих колебательное движение вблизи положений равновесия. Колебательный характер их движения сохраняется вплоть до температуры плавления Т пл. При Т= Т плсредняя амплитуда колебания атома меньше межатомного расстояния. Плавление обусловлено тем, что термодинамический потенциал жидкости при Т> Т плменьше термодинамического потенциала Т. т. В первом (гармония.) приближении систему с 3 Nn колебательными степенями свободы можно рассматривать как совокупность 3 Nn независимых осцилляторов, каждый из которых соответствует отдельному нормальному колебанию. В кристалле с нарушениями периодичности (дефектами) среди нормальных колебаний имеются особые, в которых участвуют не все атомы кристалла, а только локализованные вблизи дефекта (например, чужеродного атома). Такие колебания называются локальными. Хотя их число невелико, они в ряде случаев определяют некоторые физические свойства (оптические свойства, особенности и др.). Вблизи поверхности в Т. т. могут распространяться локальные поверхностные волны, амплитуда которых экспоненциально уменьшается при удалении от поверхности (Рэлея волны). Подобные волны могут распространяться также и внутри кристалла вдоль плоских дефектов (например, границ кристаллических зёрен) и вдоль дислокаций. Нормальное колебание — волна смещений атомов из положения равновесия. Существует 3n типов нормальных колебаний (для простых решёток n = 1). Каждая волна характеризуется волновым вектором kи частотой w. Разным типам нормальных колебаний соответствуют различные зависимости: w s ( k)( s= 1, 2,..., 3n), называемые законом дисперсии. Периодичность в расположении атомов приводит к тому, что все величины, зависящие от k,в кристалле оказываются также периодическими функциями. Например, w s( k+ 2p b) = w s( k), где b —произвольный вектор обратной решётки. Зная силы взаимодействия между структурными частицами кристалла, можно рассчитать законы дисперсии. Существуют и экспериментальные методы их определения. Наиболее результативный из них — неупругое рассеяние в кристаллах. Некоторые выводы о законе дисперсии можно сделать, исходя из общих положений: среди нормальных колебаний должны быть такие, которые при больших длинах волн (по сравнению с межатомными расстояниями) соответствуют обычным звуковым волнам в кристалле. Таких волн три (для упругоизотропного тела — две волны поперечные и одна продольная), причём для всех трёх частота w — однородная функция 1-го порядка от компонент вектора k,обращающаяся в нуль при k= 0, то есть для трёх из 3n типов нормальных колебаний закон дисперсии при малых значениях волнового вектора имеет вид: w s = c sk (s = 1, 2, 3), где c s— скорость звука в кристалле, зависящая от направления распространения звука. Эти три типа нормальных колебаний называются акустическими, при их возбуждении атомы одной ячейки колеблются как целое. Остальные 3n — 3 типов колебаний называются оптическими (впервые наблюдались по резонансному поглощению света). Частота w оптического колебания при k® 0 стремится к конечному пределу. При этом атомы элементарной ячейки колеблются друг относительно друга, а центр тяжести ячейки покоится. Колебание каждого типа имеет макс. частоту w sмакс; это значит. что существует максимальная частота колебаний атомов в кристалле w макс» с/а» 10 12—10 13 сек –1 .Знание закона дисперсии позволяет определить плотность состояний n(w). Число колебательных состояний в интервале частот (w, w + Dw) равно n(w) Dw. При w ® 0 n(w) ~ w 2, а при w ® w максn(w) » 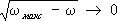 . Плотность состояний играет определяющую роль в термодинамических равновесных свойствах Т. т. . Плотность состояний играет определяющую роль в термодинамических равновесных свойствах Т. т.Каждой волне с волновым вектором kи частотой со можно сопоставить квазичастицу с квазиимпульсом 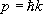 и энергией и энергией
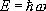 (см.
)
.Квазичастица, соответствующая волне нормальных колебаний, называется фононом. Квазиимпульс фонона во многом схож с импульсом свободной частицы. Скорость фонона u
ф— групповая скорость волны: (см.
)
.Квазичастица, соответствующая волне нормальных колебаний, называется фононом. Квазиимпульс фонона во многом схож с импульсом свободной частицы. Скорость фонона u
ф— групповая скорость волны: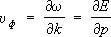 . .Распределение фононов по энергиям в состоянии термодинамического равновесия описывается функцией Планка: 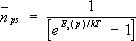 , ,где 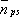 ,— среднее число фононов сорта
s(
s= 1, 2..., 3n) с квазиимпульсом
р.
Функцию Планка можно рассматривать как функцию распределения
фононов, подчиняющихся статистике Бозе — Эйнштейна (см.
)
.Химический потенциал фононов равен нулю, что указывает на зависимость числа фононов от температуры. При высоких температурах число фононов растет с температурой линейно, а при низких — пропорционально
T
3
,что отражает уменьшение амплитуды тепловых колебаний атомов с уменьшением температуры. В действительности газ фононов не является идеальным, так как фононы взаимодействуют друг с другом (ангарионизм колебаний); чем выше температура, тем это взаимодействие существеннее. Взаимодействие фононов описывается в теории введением для них длины свободного пробега, которая возрастает при понижении температуры. Фононы взаимодействуют не только друг с другом, но и с др. квазичастицами, а также со всеми дефектами кристалла (в частности, рассеиваются границами Т. т.).
,— среднее число фононов сорта
s(
s= 1, 2..., 3n) с квазиимпульсом
р.
Функцию Планка можно рассматривать как функцию распределения
фононов, подчиняющихся статистике Бозе — Эйнштейна (см.
)
.Химический потенциал фононов равен нулю, что указывает на зависимость числа фононов от температуры. При высоких температурах число фононов растет с температурой линейно, а при низких — пропорционально
T
3
,что отражает уменьшение амплитуды тепловых колебаний атомов с уменьшением температуры. В действительности газ фононов не является идеальным, так как фононы взаимодействуют друг с другом (ангарионизм колебаний); чем выше температура, тем это взаимодействие существеннее. Взаимодействие фононов описывается в теории введением для них длины свободного пробега, которая возрастает при понижении температуры. Фононы взаимодействуют не только друг с другом, но и с др. квазичастицами, а также со всеми дефектами кристалла (в частности, рассеиваются границами Т. т.).В аморфных телах тепловое движение частиц также носит колебательный характер. Однако фононы удаётся ввести только для низкочастотных акустических колебаний, когда на длине волны расположено много атомов, колеблющихся синфазно, и их взаимное расположение не слишком существенно. Максимальные частоты колебаний в аморфных телах мало отличаются от максимальных частот в кристаллах, так как определяются силами взаимодействия между ближайшими атомами. В результате этого, а также наличия ближнего порядка в аморфных телах плотность колебательных состояний близка к плотности колебательных состояний кристаллов. Диффузия атомов. В процессе колебания кинетическая энергия частицы в результате флуктуаций может превысить глубину ,в которой она движется. Это означает, что частица способна «оторваться» от своего положения равновесия. Обычно вероятность Wтакого процесса при комнатной температуре мала:  . .Здесь W 0~ W макс» 10 12—10 13 сек –1 ,а величина u порядка энергии связи, рассчитанной на одну частицу. Поэтому все процессы в Т. т., сопровождающиеся переносом вещества (диффузия, и т. д.), идут сравнительно медленно. Только вблизи температуры плавления скорость этих процессов возрастает. Коэффициент диффузии, определяющий поток частиц по известному градиенту их концентрации, пропорционален Wи существенно зависит от состояния кристаллической решётки. Пластическая деформация обычно «разрыхляет» кристалл, снижает потенциальные барьеры, разделяющие равновесные положения атомов, и поэтому увеличивает вероятность их «перескоков». В исключительных случаях, например в твёрдом Не, возможно туннельное «просачивание» атомов из одного положения равновесия в другое (см. ) .Эта «квантовая» диффузия приводит к тому, что коэффициент диффузии ¹ 0 при Т® 0 К. Делокализация атомов, связанная с туннельными переходами, превращает примесные атомы и вакансии в своеобразные квазичастицы (примесоны, вакансионы). Они определяют свойства квантовых кристаллов. Тепловые свойства Т. т.У большинства Т. т. Спри комнатных температурах приближённо подчиняется : С =3 R кал/моль( R — ) .Закон Дюлонга и Пти — следствие того, что за тепловые свойства Т. т. при высоких температурах ответственны колебательные движения атомов, подчиняющиеся закону равнораспределения (средняя энергия, приходящаяся на одну колебательную степень свободы, равна kT) .Наблюдаемые при высоких температурах отклонения от закона Дюлонга и Пти объясняются повышением роли ангармонизма колебаний. Понижение температуры приводит к уменьшению теплоёмкости; благодаря квантовому «замораживанию» средняя энергия колебания Ek, определяемая выражением: 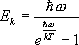 , меньше
kT.При самых низких температурах часть теплоёмкости, обусловленная колебаниями решётки, С ~
T
3
.Колебательная часть теплоёмкости Т. т. может быть представлена как теплоёмкость газа фононов. , меньше
kT.При самых низких температурах часть теплоёмкости, обусловленная колебаниями решётки, С ~
T
3
.Колебательная часть теплоёмкости Т. т. может быть представлена как теплоёмкость газа фононов.Переход от классического значения теплоёмкости С = 3Rк квантовому С ~ T 3наблюдается при характерной для каждого Т. т. температуре q, называемой ,физический смысл которой определяется соотношением: 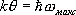 . Отсюда следует, что при
Т <.q в Т. т. есть колебания, к которым необходимо применять квантовые законы. Для большинства Т. т. q колеблется в пределах 10
2—10
3K. У молекулярных кристаллов q аномально низка (» 10 К). . Отсюда следует, что при
Т <.q в Т. т. есть колебания, к которым необходимо применять квантовые законы. Для большинства Т. т. q колеблется в пределах 10
2—10
3K. У молекулярных кристаллов q аномально низка (» 10 К).Температурная зависимость колебательной части теплоёмкости при Т<< q, как и её значение при Т>> q, одинакова для всех Т. т. ( рис. 1 ), в частности и аморфных. В промежуточной области температур теплоёмкость зависит от детальных свойств n(w), то есть от конкретного распределения частот по спектру Т. т. Вблизи Т= 0 К из-за уменьшения колебательной части теплоёмкости Т. т. проявляются другие (неколебательные), низко расположенные уровни энергии Т. т. Так, в металлах при 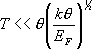 (
E
F— энергия Ферми, см. ниже) основной вклад в теплоёмкость вносят электроны проводимости (электронная часть теплоёмкости ~
Т), а в ферритах при
ТЈ q
2/
Т
с(
T
c— температура Кюри) — спиновые волны (магнонная часть теплоёмкости ~
T (
E
F— энергия Ферми, см. ниже) основной вклад в теплоёмкость вносят электроны проводимости (электронная часть теплоёмкости ~
Т), а в ферритах при
ТЈ q
2/
Т
с(
T
c— температура Кюри) — спиновые волны (магнонная часть теплоёмкости ~
T
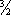 Важной характеристикой тепловых свойств Т. т. служит коэффициент теплового расширения  (
V- объем Т. т.,
р —давление). Отношение a/
Сне зависит от температуры (закон Грюнайзена). Хотя закон Грюнайзена выполняется приближённо, он качественно правильно передаёт температурный ход a
.Тепловое расширение — следствие ангармоничности колебаний (при гармонических колебаниях среднее расстояние между частицами не зависит от температуры). (
V- объем Т. т.,
р —давление). Отношение a/
Сне зависит от температуры (закон Грюнайзена). Хотя закон Грюнайзена выполняется приближённо, он качественно правильно передаёт температурный ход a
.Тепловое расширение — следствие ангармоничности колебаний (при гармонических колебаниях среднее расстояние между частицами не зависит от температуры).Теплопроводность зависит от типа Т. т. Металлы обладают значительно большей теплопроводностью, чем диэлектрики, что связано с участием электронов проводимости в переносе тепла (см. ниже). Теплопроводность — структурно чувствительное свойство. Коэффициент теплопроводности зависит от кристаллического состояния (моно- или поликристалл), наличия или отсутствия дефектов и т. п. Явление теплопроводности удобно описывать, используя концепцию квазичастиц. Все квазичастицы (прежде всего фононы) переносят тепло, причём, согласно кинетической теории газов, вклад каждого из газов квазичастиц в коэффициент теплопроводности можно записать в виде: 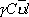 ,где g — численный множитель,
С— теплоёмкость,
,где g — численный множитель,
С— теплоёмкость,
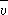 — средняя тепловая скорость,
l— длина свободного пробега квазичастиц. Величина
lопределяется рассеянием квазичастиц, которое в случае фонон-фононных столкновений — следствие ангармоничности колебаний. — средняя тепловая скорость,
l— длина свободного пробега квазичастиц. Величина
lопределяется рассеянием квазичастиц, которое в случае фонон-фононных столкновений — следствие ангармоничности колебаний.Из-за участия в тепловых свойствах разнообразных движений, присущих Т. т., температурная зависимость большинства характеристик Т. т. очень сложна. Она дополнительно осложняется фазовыми переходами, которые сопровождаются резким изменением многих величин (например, теплоёмкости) при приближении к точке фазового перехода. Электроны в Т. т. Зонная теория.Сближение атомов в Т. т. на расстоянии порядка размеров самих атомов приводит к тому, что внешние (валентные) электроны теряют связь с определённым атомом — они движутся по всему Т. 1, 2, 3, 4, 5 |
|||||||