 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (РА)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (РА) - Чтение (стр. 58)
Разработка философских вопросов математики занимает большое место в его работах. Открытый Р. один из теории множеств (т. н. парадокс Р.) привёл его к построению оригинального варианта (см. также ) и к последующей попытке сведения математики к логике. В написанном в соавторстве с А. Уайтхедом трёхтомном труде «Principia Mathematica» (1910-13) Р. систематизировал и развил дедуктивно-аксиоматическое построение логики в целях логического обоснования математики (см. ). Р. принадлежит также оригинальная теория . По социологическим взглядам был близок к психологизму: в основе исторического процесса и поведения людей, по Р., лежат инстинкты, страсти. Р. утверждал, что из совокупности факторов, определяющих историческое изменения, невозможно выделить главный и установить объективные исторические законы. В этике и политике Р. придерживался позиции буржуазного либерализма, выступая против теории, проповедующих поглощение личности обществом и государством. Он отрицательно относился к христианству и в особенности к ханжеству религиозной морали, противопоставляя ей мораль «науки свободного разума». Особенностью этической и общественно-политической позиции Р. являлась активная борьба против фашизма, антиимпериалистическая направленность, непримиримость к войне, насильственным, агрессивным методам в международной политике. Р. - один из инициаторов Пагуошского движения; он выступал на стороне прогрессивных общественных сил за запрещение ядерного оружия, за мирное сосуществование. Нобелевская премия по литературе (1950). Соч.: Scientific method in philosophy, Oxf., 1914; Our knowledge of the external world..., Chi. - L., 1915; Principles of social reconstruction, L., 1916; The problems of philosophy, L., [1920]; The analysis of mind, N. Y. - L., 1924; Religion and science, N. Y., 1935; Power: a new social analysis, N. Y., [1938]; Philosophy and politics, L., 1947; Introduction to mathematical philosophy, L., 1953; The analysis of matter, N. Y. - L., [1954]: Logic and knowledge, L., 1956; Mysticism and logic, N. Y., 1957; My philosophical development, N. Y., 1959; Fact and fiction, L., 1961; An inquiry into meaning and truth, L., [1967]; The autobiography of Bertrand Russell, v. 1-3, L., 1967-69; в рус. пер. - Германская социал-демократия, СПБ, 1906; Проблемы философии, СПБ, 1914; Воздействие науки на общество, М., 1952; Человеческое познание. Его сфера и границы, М., 1957; Почему я не христианин, М., 1958; История западной философии, М., 1959. Лит.:История философии, т. 5, М., 1961, гл. 13; Нарский И. С., Философия Б. Рассела, М., 1962; Быховский Б, Э., Мееровский Б. В., Атеизм Бертрана Рассела, в книге: От Эразма Роттердамского до Бертрана Рассела, М., 1969; Нарский И. С., Помогаев а Е. Ф., Бертран Рассел - философ и гуманист, «Вопросы философии», 1972, № 6; Богомолов А. С., Английская буржуазная философия XX века, М., 1973, гл. 5; The philosophy of Bertrand Russell, ed. by P. A. Schilpp, L., 1952; Bertrand Russell, philosopher of the century. Essays in his honour, ed. by R. Schoenman, L., 1967. И. С. Нарский. 
Б. Рассел. Рассел Джон Ра'ссел(Russel) Джон (18.8.1792, Лондон, - 28.5.1878, Пемброк-Лодж, Суррей), английский государственный деятель, лидер .С 1813 член парламента. Занимал важные государственные посты: министра внутренних дел (1835-39), министра по делам колоний (1839-41), премьер-министра (1846-52 и 1865-66), министра иностранных дел (1852-53 и 1859-65). В 1861 получил титул графа. Выразитель интересов аристократической олигархии, Р. в своей практической деятельности придерживался гибкой политической линии, предусматривавшей определённые уступки промышленной буржуазии и проведение умеренных реформ. Способствовал сговору английского правительства с буржуазной верхушкой ирландского национального движения ( ), применяя в то же время репрессии по отношению к его революционному крылу (Исключительный закон для Ирландии 1847, подавление ирландского восстания 1848); был вдохновителем полицейских мер против чартистов в 1848. Р. стремился к усилению колониальной экспансии. Отстаивал агрессивные цели в восточном конфликте, приведшем к .Во время Гражданской войны в США 1861-65 оказывал под флагом нейтралитета всемерную поддержку рабовладельцам Юга. Р. - автор нескольких исторических и биографических работ. Лит.:Маркс К. и Энгельс Ф., Соч., 2 изд., т. 8-15, 21 (см. Указат. имен); Tilby A. W., Lord J. Russel, L., 1930. Л. И. Гольман. Расселение животных Расселе'ние живо'тных,постепенное увеличение области обитания - тех или иных видов. Обычно связано с изменением абиотических и биотических условий окружающей среды и численности животных. Состояние данного вида, увеличение её численности, обусловливающее возрастание , стимулирует Р. ж. (например, в 20 в. в Евразии в связи с общим потеплением климата сев. граница распространения ряда видов животных продвинулась на С.). Различают Р. ж. активное (бег, плавание, полёт) и пассивное (перенос реками, морскими течениями, на плавающих в море предметах, ветром); последнее имеет значение главным образом для мелких (морские планктонные организмы, насекомые и т.п.), а иногда н более крупных животных (например, стая белых цапель была перенесена бурей из Африки в Америку и заселила её; с плавающими стволами деревьев расселяются мелкие пресмыкающиеся - змеи, гекконы). Некоторых мелких животных расселяют более крупные (так, птицы, кроме паразитов, переносят иногда моллюсков, яйца пресноводных животных и т.п.). Лит.:Гептнер В. Г., Общая зоогеография, М. -Л., 1936. В. Г. Гептнер. Расселение растений Расселе'ние расте'ний,расширение области распространения - тех или иных видов посредством рассеивания их зачатков (семян, спор) и на новых местах. Р. р. зависит от количества производимых растением жизнеспособных зачатков, средств расселения, возможностей закрепления в местах, куда они переносятся. Р. р. бывает постепенным и скачкообразным (сразу на большое расстояние); в естественных условиях преобладает первый тип. Основные факторы расселения: воздушные течения - ветры, восходящие токи воздуха ( ), воды суши ( ), морские течения, животные ( ), различные формы деятельности человека ( ). Р. р. ограничивается следующими факторами: географическими (моря и проливы, горы, «непроходимые» для растений данного вида), экологическими (несоответствие климатических и др. абиотических и биотических условий природе вида) и биологическими (конкуренция др. видов). Сочетание действия средств расселения и преград определяет возможный темп Р. р. Лит.:Толмачев А, И., Введение в географию растений, Л., 1974. А. И. Толмачев. «Рассерженные молодые люди» «Рассе'рженные молоды'е лю'ди»,или «Сердитые молодые люди» («Angry young men»), принятое в критике название группы английских писателей, выступивших в 50-е гг. 20 в. Термин восходит к автобиографической книге Л. А. Пола «Рассерженный молодой человек» (1951); широко распространился после постановки в Лондоне в 1956 пьесы Дж. «Оглянись во гневе» - в страстных мизантропических монологах её героя дана концентрация настроений «Р. м. л.». Наиболее типичные «Р. м. л.» - романисты Дж. Уэйн, К. Эмис, Дж. Брейн и драматург Осборн, которые, однако, не образовали литературной школы. «Р. м. л.» объединяет недовольство английской буржуазной действительностью и, в частности, положением молодёжи в обществе, протест против социального неравенства, сословного чванства, лжи и лицемерия. Их герой - обычно молодой человек, получивший университетское образование; он разочарован в жизни, недоволен своей работой, обществом, в котором ему нет места. Бунт против принятых норм поведения и морали он проявляет в экстравагантных и шутовских выходках, в скандальном адюльтере, в демонстративном уходе в ряды рабочего класса. «Р. м. л.» не выдвинули положительной программы, их критика носила индивидуалистический характер. К концу 50-х гг. они отошли от прежних тем и героев. Лит.:Ивашева В. В., Английская литература XX века, М., 1967; Гозенпуд А. А., Пути и перепутья, Л., 1967; Шестаков Д., Современная английская драма (Осборновцы), М., 1968; Maschler Т. (ed.), Declaration, by С. Wilson [and others], L., 1957; Allsop K., The angry decade, L., 1958; Gindin J., Postwar British fiction, Berk., 1962. Рассеяние микрочастиц Рассея'ние микрочасти'ц,теория рассеяния, процесс столкновения частиц, в результате которого меняются импульсы частиц (упругое рассеяние) или наряду с изменением импульсов меняются также их внутреннего состояния либо образуются др. частицы (неупругое рассеяние). Одна из основных количественных характеристик как упругого рассеяния, так и неупругих процессов, - процесса (называемое обычно просто сечением) - величина, пропорциональная вероятности процесса и имеющая размерность площади ( см 2). Измерение сечений процессов позволяет изучать законы взаимодействия частиц, исследовать структуру частиц. Например, классическими опытами Э. по рассеянию a-частиц атомами было установлено существование атомных ядер (см. ); из опытов по рассеянию электронов большой энергии на протонах и нейтронах (нуклонах) получают информацию о структуре нуклонов; эксперименты по упругому рассеянию нейтронов и протонов протонами позволяют детально исследовать ядерные силы и т.д. (О столкновениях атомов и ядер см. , .) Классическая теория рассеяния.Согласно законам классической (нерелятивистской) механики, задачу рассеяния двух частиц с массами m 1и m 2можно свести переходом к системе сталкивающихся частиц (системе, в которой покоится центр инерции частиц, т. е. суммарный импульс частиц равен нулю) к задаче рассеяния одной частицы с приведённой массой m = m 1 m 2/( m 1+ m 2) на неподвижном силовом центре. В силовом поле (с центром О) траектория частицы искривляется - происходит рассеяние. Угол между начальным ( р нач) и конечным ( р кон) импульсами рассеиваемой частицы называется углом рассеяния. Угол рассеяния J зависит от взаимодействия между частицами и от т. н. прицельного параметра r - расстояния, на котором частица пролетела бы от силового центра, если бы взаимодействие отсутствовало ( рис. 1 ). Классическая механика устанавливает следующую связь между прицельным параметром и углом рассеяния:
где U( r) -потенциальная энергия взаимодействия, r -расстояние до силового центра ( r мин- минимальное расстояние), Е= р 2 нач/2m - энергия частицы. На опыте обычно не измеряют рассеяние индивидуальной частицы, а направляют на мишень из исследуемого вещества пучок одинаковых частиц, имеющих одинаковую энергию, и измеряют количество частиц, рассеянных под данным углом. Число частиц dN, рассеянных в единицу времени на углы, лежащие в интервале J, J + dJ, равно числу частиц, проходящих в единицу времени через кольцо 2pr drЧ n.Если n -плотность потока падающих частиц (число частиц, проходящих в единицу времени через единичную площадку, перпендикулярную направлению движения частиц в пучке), то dN= 2pr drЧ n,а сечение упругого рассеяния ds определяется как отношение dN /nи равно
(т. е., как уже отмечалось, сечение имеет размерность площади). Сечение рассеяния на все углы - полное сечение рассеяния - получается интегрированием (2) по всем прицельным параметрам. Если а -минимальный прицельный параметр, при котором J = 0 (т. е. частица проходит без отклонения), то полное сечение рассеяния s = p a 2 . Квантовая теория рассеяния.В квантовой теории процессы упругого рассеяния и неупругие процессы описываются амплитудами рассеяния - комплексными величинами, квадрат модуля которых пропорционален сечениям соответствующих процессов. В 1943 В. для описания процессов рассеяния ввёл т. н. S-матрицу, или .Её матричные элементы определяют амплитуды различных процессов. Через матричные элементы S-матрицы выражаются физические величины, непосредственно измеряемые на опыте: сечение, поляризация частиц (среднее значение оператора спина), асимметрия, возникающая при рассеянии на поляризованной мишени и др. С др. стороны, матричные элементы S-матрицы могут быть вычислены при определённых предположениях о виде взаимодействия. Сравнение результатов опыта с предсказаниями теории позволяет проверить теорию. Общие принципы инвариантности (инвариантность относительно вращений, из которой вытекает сохранение момента количества движения, отражений - сохранение чёткости, и др.) существенно ограничивают возможный вид матричных элементов S-матрицы и позволяют получить проверяемые на опыте соотношения. Например, из закона сохранения чётности следует, что поляризация конечной частицы при столкновении неполяризованных частиц направлена по нормали к плоскости рассеяния (плоскости, проходящей через начальный и конечный импульсы частицы). Измеряя направление вектора поляризации, можно выяснить, сохраняется ли чётность во взаимодействии, обусловливающем процесс. сильных взаимодействий приводит к соотношениям между сечениями различных процессов, а также к запрету некоторых процессов. В частности, из изотопической инвариантности следует, что при столкновении двух дейтронов не могут образоваться a-частица и p°-мезон. Исследование этого процесса на опыте подтвердило справедливость изотопической инвариантности. Условие унитарности S-матрицы, являющееся следствием сохранения полной вероятности (суммарная вероятность рассеяния по всем возможным каналам реакции должна равняться 1), также накладывает ограничения на матричные элементы процессов. Одно из важных соотношений, вытекающих из этого условия, - , связывающая амплитуду упругого рассеяния на угол 0° с полным сечением (суммой сечений упругого рассеяния и сечений всех возможных неупругих процессов). Из общих принципов квантовой теории ( , и др.) следует, что матричные элементы S-матрицы являются в некоторых областях комплексных переменных. Аналитические свойства матричных элементов S-матрицы позволяют получить ряд соотношений между определяемыми из опыта величинами - т. н. дисперсионные соотношения (см. ), и др. В случае упругого рассеяния бесспиновых частиц асимптотика волновой функции Y( r), являющейся решением ,имеет вид:
Здесь
r- расстояние между частицами,
k=
p/
Для амплитуды рассеяния имеет место следующее разложение по парциальным волнам (волнам с определённым орбитальным моментом l):
Здесь P l(cosJ) - , S l -коэффициенты разложения, которые зависят от характера взаимодействия и являются матричными элементами S-матрицы (в представлении, в котором она диагональна по энергии, моменту количества движения и проекции момента). Если число падающих на центр частиц с моментом lравно числу идущих от центра частиц с тем же моментом (случай упругого рассеяния), то I S ll = 1. В общем случае l S ll Ј 1. Эти условия являются следствием условия унитарности S-матрицы. Если возможно только упругое рассеяние, то S lможет быть представлено в виде: S l= e 2i d l ,где d l- вещественные величины, называемые фазами рассеяния. Если d l= 0 при некотором l, то рассеяние в состояние с орбитальным моментом lотсутствует. Полное сечение упругого рассеяния равно:
где
при этом d
l= p/2 (резонанс в рассеянии). Т. о., при резонансе сечение процесса определяется де-бройлевской длиной волны
Поведение сечения рассеяния вблизи резонанса определяется формулой Брейта - Вигнера:
где
E
0
-энергия, при которой сечение достигает максимума (положение резонанса), а Г- ширина резонанса. При
Е=
E
0±
1/
2G сечение s
lравно
1/
2
Условие унитарности ограничивает величину парциального сечения для неупругих процессов:
Для короткодействующих потенциалов взаимодействия основную роль играют фазы рассеяния с lЈ b/ k,где b- радиус действия сил. Это условие можно переписать следующим образом: l/ kЈ b; величина l/ kопределяет минимальное расстояние, на которое может приблизиться к центру сил свободная частица с моментом l(прицельный параметр в квантовой теории). При bk<<
и сечение рассеяния не зависит от угла (рассеяние сферически симметрично). При малых энергиях имеет место разложение:
Параметры аи r 0называются соответственно длиной рассеяния и эффективным радиусом рассеяния. Эти величины определяются из опыта и являются важными характеристиками сил, действующих между частицами. Длина рассеяния равна по величине и противоположна по знаку амплитуде рассеяния при k= 0. Полное сечение рассеяния в точке k= 0 равно s 0= 4p a 2. Если у частиц имеется с малой энергией связи, то рассеяние таких частиц при kb<< 1 носит резонансный характер (типичный пример - рассеяние нейтронов протонами в состоянии с полным спином J = 1; в этом состоянии у системы нейтрон - протон имеется уровень, соответствующий связанному состоянию - дейтрону). Сечение рассеяния в этом случае зависит только от энергии связи.Если параметр kbневелик, фазы рассеяния могут быть найдены из измеренных на опыте значений сечения и др. величин. Эта процедура называется фазовым анализом. Найденные путём фазового анализа фазы рассеяния сравниваются с предсказаниями теории и позволяют, т. о., получить важную информацию о характере взаимодействия. Один из основных приближённых методов теории рассеяния - теория возмущений (метод решения, основанный на разложении в ряд по малому параметру). Если падающая плоская волна, описывающая начальные частицы, слабо возмущается потенциалом взаимодействия, то применимо т. н. борновское приближение (первый член ряда теории возмущений). Амплитуда упругого рассеяния в борновском приближении равна:
где q= 2 ksin (J/2), V( r) - потенциал взаимодействия, m = m 1 m 2/( m 1 + m 2) -приведённая масса ( m 1и m 2 -массы частиц). Для описания процессов рассеяния при высоких энергиях используются методы .Например, упругое рассеяние электронов (е) протонами (р) в низшем порядке теории возмущений (применимость теории возмущений в данном случае основывается на малости постоянной тонкой структуры a » 1/ 137, характеризующей «силу» электромагнитного взаимодействия) обусловлено обменом фотоном между электроном и протоном ( , рис. 2 ). В выражение для сечения этого процесса входят зарядовый (электрический) и магнитный протона - величины, характеризующие распределение электрического заряда и магнитного момента протона (электромагнитную структуру протона). Информация об этих важнейших характеристиках протона может быть получена, следовательно, непосредственно из измеренных на опыте значений сечения упругого рассеяния электронов протонами. При достаточно высоких энергиях наряду с упругим ер-рассеянием становятся возможными неупругие процессы образования частиц. Если на опыте регистрируются только электроны, то тем самым измеряется сумма сечений всех возможных процессов. Лит.:Ландау Л. Д., Лифшиц Е. М., Квантовая механика, 3 изд., М., 1974 (Теоретическая физика, т. 3); Давыдов А. С., Квантовая механика, 2 изд., М., 1973; Гольдбергер М., Ватсон К., Теория столкновений, пер. с англ., М., 1967; Мотт Н., Месс и Г., Теория атомных столкновений, пер. с англ., М., 1951; Ситенко А. Г., Лекции по теории рассеяния, К., 1971. С. М. Биленький. 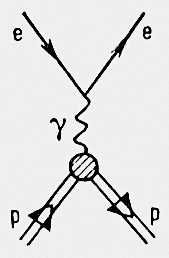
Рис. 2. к ст. Рассеяние микрочастиц. 
Рис. 1. к ст. Рассеяние микрочастиц. Рассеяние света Рассе'яние све'та,изменение характеристик потока (света) при его взаимодействии с веществом. Этими характеристиками могут быть пространственное распределение интенсивности, частотный спектр, .Часто Р. с. называется только обусловленное пространственной неоднородностью среды изменение направления распространения света, воспринимаемое как несобственное свечение среды. Последовательное описание Р. с. возможно в рамках квантовой теории взаимодействия излучения с веществом, основанной на
и квантовых представлениях о строении вещества. В этой теории единичный акт Р. с. рассматривается как поглощение частицей вещества падающего
с энергией
Во многих случаях оказывается достаточным описание Р. с. в рамках волновой теории излучения (см. , ). С точки зрения этой теории (называемой классической), падающая световая волна возбуждает в частицах среды электрических зарядов («токи»), которые становятся источниками вторичных световых волн. При этом определяющую роль играет между падающей и вторичными волнами (см. ниже). Количественной характеристикой Р. с. и при классическом, и при квантовом описании является дифференциальное сечение рассеяния ds ,определяемое как отношение dl,рассеянного в малый элемент телесного угла dW, к величине падающего потока l 0: ds = dl/ l 0 .Полное сечение рассеяния s есть сумма ds по всем dW (сечение измеряют обычно в см 2) .При упругом рассеянии можно считать, что s -размер площадки, «не пропускающей свет» в направлении его первоначального распространения (см. ). При классическом описании Р. с. часто пользуются матрицей рассеяния, связывающей амплитуды падающей и рассеянных по всевозможным направлениям световых волн и позволяющей учесть изменение состояния поляризации рассеянного света. Неполной, но наглядной характеристикой Р. с. служит рассеяния - кривая, графически отображающая различие в интенсивностях света, рассеянного в разных направлениях. Вследствие обилия и разнообразия факторов, определяющих Р. с., весьма трудно развить одновременно единый и детальный способ его описания для различных случаев. Поэтому рассматривают Идеализированные ситуации с разной степенью адекватности самому явлению. Р. с. отдельным электроном с большой точностью является упругим процессом. Его сечение не зависит от частоты (т. н. томсоновское Р. с.) и равно s = (8p/3) r 2 0= 6,65Ч10 -25 см 2( r 0= e 2/ mc 2- т. н. классический радиус электрона, много меньший длины волны света; еи m -заряд и масса электрона; с - в вакууме). Индикатриса рассеяния неполяризованного света в этом случае такова, что вперёд или назад (под углами 0° и 180°) рассеивается вдвое больше света, чем под углом 90°. Р. с. отдельными электронами - процесс, обычный в астрофизической ; в частности, оно ответственно за многие явления в и коронах др. звёзд. Основная особенность Р. с. отдельным атомом - сильная зависимость сечения рассеяния от частоты. Если частота w падающего света мала по сравнению с частотой w 0собственных колебаний атомных электронов (атомной линии поглощения), то s ~ w 4, или l -4 (l -длина волны света). Эта зависимость, найденная на основе представления об атоме как об электрическом , колеблющемся в поле световой волны, называется .Вблизи атомных линий (w » w 0) сечения резко возрастают, достигая в резонансе (w = w 0) очень больших значений s » l 2~ 10 -10 см 2 .Вследствие ряда особенностей резонансного Р. с. оно носит специальное название резонансной флуоресценции. Индикатриса рассеяния неполяризованного света атомами аналогична описанной для свободных электронов. Р. с. отдельными атомами наблюдается в разреженных газах. При Р. с. молекулами наряду с рэлеевскими (несмещенными) линиями в спектре рассеяния появляются, в отличие от случая атомарного Р. с., линии неупругого Р. с. (смещенные по частоте). Относит. смещения чw - w'ъ/w ~ 10 -3-10 -5, а интенсивность смещенных линий составляет лишь 10 -3-10 -6интенсивности рэлеевской. О неупругом Р. с. молекулами см. . Р. с. мелкими частицами обусловливает широкий класс явлений, которые можно описать на основе теории на диэлектрических частицах. Многие характерные особенности Р. с. частицами удаётся проследить в рамках строгой теории, разработанной для сферических частиц английским учёным А. Лявом (1889) и немецким учёным Г. Ми (1908, теория Ми). Когда радиус шара rмного меньше длины волны света l n в его веществе, Р. с. на нём аналогично нерезонансному Р. с. атомом. Сечение (и интенсивность) Р. с. в этом случае сильно зависит от rи от разности e и e 0вещества шара и окружающей среды: s ~ l n -4 r 6(e - e 0)(Рэлей, 1871). С увеличением rдо r ~l n и более (при условии e > 1) в индикатрисе рассеяния появляются резкие максимумы и минимумы - вблизи т. н. резонансов Ми (2 r= ml n, m= 1, 2, 3,...) сечения сильно возрастают и становятся равными 6p r 2,рассеяние вперёд усиливается, назад - ослабевает; зависимость поляризации света от угла рассеяния значительно усложняется. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69 |
|||||||
 ,
, (2)
(2) (3)
(3) -волновой вектор,
р- импульс в системе центра инерции (с. ц. и.) сталкивающихся частиц,
-волновой вектор,
р- импульс в системе центра инерции (с. ц. и.) сталкивающихся частиц,
 - постоянная Планка, J
-угол рассеяния,
f(J)
-амплитуда рассеяния, зависящая от угла рассеяния и энергии сталкивающихся частиц. Первый член в этом выражении описывает свободные частицы с импульсом
р=
- постоянная Планка, J
-угол рассеяния,
f(J)
-амплитуда рассеяния, зависящая от угла рассеяния и энергии сталкивающихся частиц. Первый член в этом выражении описывает свободные частицы с импульсом
р=
 k(падающая волна), второй - частицы, идущие от центра (рассеянная волна). Дифференциальное сечение рассеяния определяется как отношение числа частиц, рассеянных за единицу времени в элемент телесного угла
dW, к плотности потока падающих частиц. Сечение рассеяния на угол J (в с. ц. и.) в единичный телесный угол равно:
k(падающая волна), второй - частицы, идущие от центра (рассеянная волна). Дифференциальное сечение рассеяния определяется как отношение числа частиц, рассеянных за единицу времени в элемент телесного угла
dW, к плотности потока падающих частиц. Сечение рассеяния на угол J (в с. ц. и.) в единичный телесный угол равно: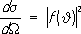 (4)
(4) (5)
(5) (6)
(6)
 ; - парциальное сечение упругого рассеяния частиц с орбитальным моментом
l,
; - парциальное сечение упругого рассеяния частиц с орбитальным моментом
l,
 = 1/
k -длина
частицы. При Sl = -1
= 1/
k -длина
частицы. При Sl = -1
 достигает максимума и равно:
достигает максимума и равно: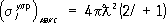 (7)
(7)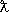 и для медленных частиц, для которых
и для медленных частиц, для которых
 >>
R
0
,где
R
0
-радиус действия сил, намного превосходит величину p
R
0
2(классическое сечение рассеяния). Этот факт (непонятный с точки зрения классической теории рассеяния) является следствием волновой природы микрочастиц.
>>
R
0
,где
R
0
-радиус действия сил, намного превосходит величину p
R
0
2(классическое сечение рассеяния). Этот факт (непонятный с точки зрения классической теории рассеяния) является следствием волновой природы микрочастиц.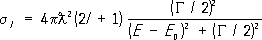 , (8)
, (8)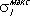 . Полное сечение всех неупругих процессов равно:
. Полное сечение всех неупругих процессов равно: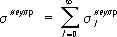 (9)
(9)
 . (10)
. (10) (11)
(11)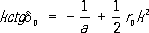 (12)
(12)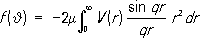 (13)
(13)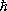 w, импульсом (
)
w, импульсом (
)
 kи поляризацией m, а затем испускание фотона с энергией
kи поляризацией m, а затем испускание фотона с энергией
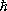 w, импульсом
w, импульсом
 k'и поляризацией m
'.Здесь
k'и поляризацией m
'.Здесь
 - Планка постоянная, w и w' - частоты фотонов, каждая из величин
kи
k' -
.Если энергия испущенного фотона равна энергии поглощённого (w
= w'), Р. с. называется рэлеевским, или упругим. При w ¹ w
'Р. с. сопровождается перераспределением энергии между излучением и веществом и его называют неупругим.
- Планка постоянная, w и w' - частоты фотонов, каждая из величин
kи
k' -
.Если энергия испущенного фотона равна энергии поглощённого (w
= w'), Р. с. называется рэлеевским, или упругим. При w ¹ w
'Р. с. сопровождается перераспределением энергии между излучением и веществом и его называют неупругим.