 |
|
Популярные авторы:: Горький Максим :: Борхес Хорхе Луис :: Раззаков Федор :: Азимов Айзек :: Грин Александр :: Толстой Лев Николаевич :: Лесков Николай Семёнович :: Сименон Жорж :: Чехов Антон Павлович :: Лондон Джек Популярные книги:: The Boarding House :: Долгожданное возвращение :: Опасайтесь лысых и усатых :: Эсперанса :: Упражнения по стилистике русского языка :: Старик-годовик :: Дюна (Книги 1-3) :: Зайти с короля :: Эволюция человеческой науки :: Алиби (Том 2) |
Большая Советская Энциклопедия (ПО)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ПО) - Чтение (стр. 2)
Основной формой выражения наследственного П. являются врождённые инстинкты (см.
Инстинктивное поведение
)
,тогда как функциональные схемы П. включают в себя элемент субъективной оценки ситуации (у высших животных существенную роль здесь играют элементы рассудочной деятельности, в частности способность экстраполировать прежний опыт на новые ситуации). Поскольку рефлекторная теория не даёт объяснения активного характера П., предпринимаются различные попытки построить такое объяснение (например, в физиологии активности это делается за счёт развития схемы рефлекторной дуги в схему рефлекторного кольца, включающую в себя некоторые дополнительные звенья, в частности т. н. модели потребного будущего); однако предложенные схемы не получили пока достаточного экспериментального подтверждения.
Одна из важных линий биологического анализа П. - изучение надорганизменных уровней П. (П. в популяциях и сообществах, видоспецифические аспекты П.). Главную роль здесь играют наследственные структуры группового П., весьма разнообразные по направленности (от агрессивности до альтруизма) и существенно влияющие на характер и прочность связей в сообществах животных. Изучение этого круга проблем позволило установить, что само П. является объектом и вместе с тем участником биологической эволюции, оказывающим заметное воздействие на её темп и результаты. В современной науке в изучении П. животных интенсивно накапливается огромный эмпирический материал и выдвинут ряд теоретических обобщений, однако единая общепринятая теория пока не построена. В психологии П. выступает как одна из основных категорий этой науки. Бихевиоризм вообще сводил исследование психики к изучению П. по схеме «стимул - реакция», пренебрегая теми звеньями системы П., которые лежат между стимулом и реакцией и формируют П. Это вело к игнорированию специфики П. человека по сравнению с П. животных, определяемой социальной природой человека. В современной психологии в качестве центральной принято рассматривать категорию не П., а деятельности.П. при этом выступает как внешний компонент предметной деятельности. Понятие деятельности, охватывая психику в единстве её аффективного (эмотивного) и познавательного аспектов, акцентирует структурную устойчивость, целесоооразную организацию системы психических действий, т. е. познавательный аспект, логику замысла и его реализации, а также объективно-социальную детерминацию этой системы действий. Понятие П. фиксирует такие формы самовыражения психики, которые менее жестко связаны с интеллектом, но зато более непосредственно зависят от эмоционально-волевой и ценностной сфер сознания; поэтому акты П. в системе деятельности занимают место отдельных звеньев, моментов, форм. Их важная роль определяется тем, что они аккумулируют в себе внутреннее отношение субъекта к самой деятельности и благодаря этому существенно влияют на её общую оценку. Это различие П. и деятельности ещё более резко выступает в социологии и социальной психологии. Если деятельность выступает прежде всего как социально-философская категория (в частности, в марксизме она является одним из основных понятий при объяснении процесса общественного развития), то понятие П. используется при характеристике не всегда осознаваемых форм и стереотипов самовыражения индивида в социальном окружении, усваиваемых им в процессе социализации,воспитания. В конкретных социальных исследованиях наиболее адекватным для выражения активности индивида оказывается понятие социального действия, которое в известном смысле соединяет содержание понятий П. и деятельности. В технических системах понятие П. выражает способность системы к таким действиям, которые связаны не только с реализацией некоторой совокупности функций, но и с необходимостью осуществлять выбор оптимальных решений в альтернативных ситуациях. Лит.:Леонтьев А. Н., Очерк развития психики, в его кн.: Проблемы развития психики, 3 изд., М., 1972; Рубинштейн С. Л., Махизм и кризис психологии. Проблема сознания и поведения в истории зарубежной психологии, в его кн.: Принципы и пути развития психологии, М., 1959; Миллер Дж., Галантер Е., Прибрам К., Планы и структура поведения, пер. с англ., М., 1965; Тинберген Н., Поведение животных, пер. с англ., М., 1969; Крушинский Л. В., Роль элементарной рассудочной деятельности в эволюции групповых отношений животных, «Вопросы философии», 1973, № 11; Хайнд P., Поведение животных, пер. с англ., М., 1974; Marler P. R. and Hamilton W. J., Mechanisms of animal behavior, N. Y., 1968; Tembrock G., Grundriss der Verhaltenswissenschaften, Jena, 1968. Э. Г. Юдин. Повеллит Повелли'т(от имени американского геолога Дж. Поуэлла ) ,минерал, молибдат кальция Ca [MoO 4]. Химический состав 28,48% CaO, 71,52% MoO 3; некоторые П. содержат до 10,3% WO 3. Кристаллизуется в тетрагональной системе. Редко встречается в виде мелких кристаллов пластинчатого или дипирамидального облика. Наиболее часто П. образует скрытокристаллические агрегаты - продукты изменения молибденита (иногда сохраняя при этом свойственную последнему листоватую форму выделений). Окраска от белой до тёмно-зелёной и бурой. Твердость по минералогической шкале 3,5; плотность 4250-4520 кг/м 3. В ультрафиолетовых лучах обычно обнаруживает жёлтое свечение. П. - характерный минерал зоны окисления руд молибденовых месторождений. См. Молибдаты природные, Молибденовые руды. Повенец Повене'ц,посёлок городского типа в Медвежьегорском районе Карельской АССР. Расположен на берегу Онежского озера, в 26 кмот ж.-д. станции Медвежья Гора. Начальный пункт Беломорско-Балтийского канала. Известен с 15 в. как селение Вяжицкого Новгородского монастыря. В конце 17 в. назван «рядком» (торгом). В 1703 Петр I основал в П. чугунолитейный завод (закрыт в 1736). С 1782 П. - уездный город Олонецкого наместничества, в 1796-1801 - Архангельской, с 1802 - Олонецкой губернии. Поверенный Пове'ренный,по сов. гражданскому праву сторона в договоре поручения.В обязанности П. входит совершение от имени и за счёт другой стороны-доверителя определённых юридических действий (например, купля-продажа,управление имуществом). П. может быть дееспособный гражданин или юридическое лицо (если это допускается его уставом или положением). Выполняемые П. действия порождают, изменяют или прекращают права и обязанности непосредственно для доверителя. П. обязан: исполнить поручение в точном соответствии с указаниями доверителя; выполнить поручение лично, хотя в случаях, предусмотренных законом (например, ГК РСФСР, ст. 68), он может передать исполнение поручения другому лицу; сообщать доверителю по его требованию о ходе исполнения поручения; по исполнении поручения представить отчёт, передать доверителю имущество, полученное в связи с исполнением поручения. Поверенный в делах Пове'ренный в дела'х,см. в ст. Дипломатические ранги. Поверка Пове'ркасредств измерений, определение погрешностей средств измерений и установление их пригодности к применению. П. производится органами метрологической службы при помощи эталонов и образцовых средств измерений.Обязательной государственной П. подлежат средства измерений, применяемые для учёта материальных ценностей, государственных испытаний, экспертиз, регистрации национальных и международных рекордов в спорте, а также для П. исходных образцовых средств измерений. Ведомственной П. подлежат все остальные средства измерений. Существуют следующие виды П.: первичная ,производимая при выпуске средств измерений в обращение из производства или ремонта; периодическая, выполняемая во время эксплуатации и хранения средств измерений; внеочередная, обусловленная необходимостью немедленного подтверждения исправности средств измерений; инспекционная, производимая при метрологических ревизиях на предприятиях, базах снабжения, складах и в торговых организациях. П. может осуществляться: непосредственным сличением поверяемого средства измерений с образцовым того же вида (т. е. меры с мерой или одного измерительного прибора с другим); сличением средств измерений одного и того же вида при помощи компаратора (например, гирь на весах); прямым измерением поверяемым прибором величины, воспроизводимой образцовой мерой (см. Измерение ) ;прямым измерением образцовым прибором величины, воспроизводимой подлежащей поверке мерой; косвенным измерением величины, измеряемой подлежащим поверке средством измерений. Возможна также независимая П., т. е. П. средств измерений относительных (безразмерных) величин, не требующая передачи размеров единиц от эталонов. Описание методов и технических приёмов П. конкретных средств измерений содержится в соответствующих государственных стандартах или методических указаниях. Нередко методы П. и соответствующие компарирующие приборы указываются в поверочных схемах, устанавливающих порядок и точность передачи единиц от эталонов образцовым, а от них - рабочим средствам измерений. При положительных результатах П. на средство измерений налагается поверительное клеймо и в необходимых случаях выдаётся свидетельство о П. Лит.:Бурдун Г. Д., Марков Б. Н., Основы метрологии, М., 1972; Тюрин Н. И., Введение в метрологию, М., 1973. К. П. Широков. Поверка вечерняя Пове'рка вече'рняя, ежедневная поверка рядового и сержантского состава в подразделениях Советских Вооруженных Сил. При П. в. дежурный по роте выстраивает роту без оружия и старшина роты или лицо, его замещающее, поверяет личный состав поименному списку. Первыми называют фамилии военнослужащих, зачисленных приказами министра обороны СССР за совершенные ими подвиги в списки роты навечно или почётными солдатами. По окончании П. в. старшина роты объявляет приказы, отдельные приказания и наряд на следующий день. Периодически производятся общие батальонные или полковые П. в., на которых присутствуют и все офицеры батальона (полка); поверку личного состава проводят командиры рот и докладывают командиру батальона, который при полковой поверке докладывает командиру полка. Поверочная линейка Пове'рочная лине'йкав машиностроении, линейка, предназначенная для определения непрямолинейности (неплоскостности и непараллельности) поверхности, т. е. наибольшего расстояния от точек её реального профиля до прилегающей прямой (ребра линейки). Различают П. л. лекальные (с двусторонним скосом, трёхгранные и четырёхгранные) и с широкой рабочей поверхностью (прямоугольного, двутаврового сечения и в виде мостиков). Лекальные П. л. служат для определения непрямолинейности поверхности на просвет приложением ребра линейки к контролируемой поверхности. Так может быть определён просвет в 1-5 мкм.П. л. с широко и рабочей поверхностью используют для определения непрямолинейности по методу измерения линейных отклонений от поверхности контролируемой детали до поверхности линейки, установленной на опорах, или при проверке неплоскостности деталей по т. н. методу пятен «на краску». Угловыми П. л. пользуются только при проверке «на краску». П. л. лекального типа изготовляют длиной 80-500 мм,линейки с широкой рабочей поверхностью - 200-4000 мм,угловые - 630 и 1000 ммс углами 45, 55 и 60°. В зависимости от длины и класса точности рабочие поверхности лекальных линеек имеют отклонения от прямолинейности 0,6-4 мкм;П. л. с широкой поверхностью имеют отклонения от плоскостности 2,5-100 мкм. С Н. Н. Марков. Поверхностей теория Пове'рхностей тео'рия, раздел дифференциальной геометрии, в котором изучаются свойства поверхностей (см. Дифференциальная геометрия, Поверхность) .В классической П. т. рассматриваются свойства поверхностей, неизменные при движениях. Одна из основных задач классической П. т. - задача измерений на поверхности. Совокупность фактов, получаемых при помощи измерений на поверхности, составляет внутреннюю геометрию поверхности. К внутренней геометрии поверхности относятся такие понятия, как длина линии, угол между двумя направлениями, площадь области, а также геодезические линии,геодезическая кривизна линии и др. Внутреннюю геометрию определяет первая основная квадратичная форма поверхности ds 2= Edu 2+ 2 Fdudu+ Gdu 2, (1) [здесь Е= r 2 u, F= r ur u, G= r 2 u , r= r( u, u) -радиус-вектор переменной точки поверхности, u, u -её криволинейные координаты], выражающая квадрат дифференциала дуги линии на поверхности. Именно, если известны функции Е= E( u, u) , F = F( u, u) , G = G( u, u) ,то, зная внутренние уравнения линии u= u( t) ,u = u( t) и интегрируя ds,можно определить длину этой линии; кроме того, существуют формулы, которые при данных Е, F, Gвыражают угол между двумя линиями и площадь области по внутренним уравнениям этих линий и по внутреннему уравнению контура области. Изучение пространственного строения окрестности точки на поверхности производится при помощи второй основной квадратичной формы поверхности 2 h = Ldu 2+ 2 Mdudu + Ndu 2, (2) здесь L = r u иn, М = r u u n, N = r uu n,
-единичный вектор нормали к поверхности. Величина h сточностью до малых более высокого порядка относительно du, duравна расстоянию от точки М’поверхности с координатами u+ du, u+ duдо касательной плоскости g в точке Мс координатами u, u,причём расстояние берётся со знаком + или - в зависимости от того, с какой стороны от у расположена точка М'.Если форма (2) знакоопределённая, то поверхность в достаточно малой окрестности точки Мрасполагается по одну сторону от касательной плоскости g, и в этом случае точка Мповерхности называется эллиптической ( рис. 1 ). Если форма (2) знакопеременная, то поверхность в окрестности точки Мрасполагается по разные стороны от плоскости g, и точка Мтогда называется гиперболической ( рис. 2 ). Если форма (2) знакоопределённая, но принимает нулевые значения (при не равных одновременно нулю duи du) ,то точка Мназывается параболической (на рис. 3 показан один из примеров строения поверхности в окрестности параболической точки). Более точная характеристика пространственной формы поверхности может быть получена с помощью исследования геометрических свойств линий на поверхности. Пусть
М -некоторая точка поверхности S и
n- единичный вектор нормали к поверхности в
М.Линия (
L) пересечения S с плоскостью, проходящей через
nв направлении
Нормальная кривизна поверхности в данной точке
Мв данном направлении
где k n-кривизна нормального сечения Lв точке Мв направлении касательной к Г, а q - угол между главными нормалями к Ги Lв этой точке (см. Мёнье теорема ) . Поверхности, между точками которых можно установить такое взаимно однозначное соответствие, что длины соответствующих линий равны, называются изометричными. Изометричные поверхности имеют одинаковую внутреннюю геометрию, но их пространственное строение может быть различным и главные кривизны в соответствующих точках у них могут быть также различными (например, окрестность точки на плоскости изометрична некоторой окрестности точки на цилиндре, но имеет иную пространственную структуру). Однако произведение Кглавных кривизн 1/ R 1и 1/ R 2в точке Мне меняется при изометричных преобразованиях поверхности (теорема Гаусса, 1826) и может служить внутренней мерой искривлённости поверхности в данной точке. Величина Кназывается полной (или гауссовой) кривизной поверхности в точке Ми выражается соотношением:
которое называется формулой Гаусса (полная кривизна в соответствии с теоремой Гаусса может быть выражена только через коэффициенты первой квадратичной формы и их производные). Приведённая выше классификация точек регулярной поверхности может быть сопоставлена со значениями полной кривизны: в эллиптической точке кривизна положительна, в гиперболической - отрицательна и в параболической - равна нулю. Во многих вопросах П. т. рассматривается другая характеристика искривлённости поверхности - т. н. средняя кривизна, равная полусумме главных кривизн поверхности. Так, например, одним из объектов исследований П. т. являются минимальные поверхности,средняя кривизна которых в каждой точке равна нулю. Важное значение в П. т. имеет вопрос о возможности изгибания поверхности: можно ли утверждать, что данная поверхность будет изгибаемой? Математически этот вопрос формулируется следующим образом: возможно ли включить данную регулярную поверхность в однопараметрическое семейство изометричных неконгруэнтных регулярных поверхностей (конгруэнтные поверхности - поверхности, совмещаемые движением). Достаточно малые куски поверхностей положительной и отрицательной кривизны допускают непрерывные изгибания. Существуют поверхности с точкой уплощения (т. е. точкой, где все нормальные кривизны равны нулю), сколь угодно малая окрестность которой не допускает изгибания. Последний результат установлен советским геометром Н. В. Ефимовым. Кроме самой возможности изгибания, рассматриваются и изгибания специальных типов. Задача изгибания поверхностей тесно связана с задачей определения поверхности по заданным основным квадратичным формам, получившей полное решение в работах немецкого математика К. Гаусса, русского математика К. М. Петерсона, итальянских математиков Г. Майнарди и Д. Кодацци и французского математика О. Бонне. Поскольку значение полной кривизны Кповерхности может быть выражено через коэффициенты первой квадратичной формы, то уравнение (3) является одним из соотношений, связывающих коэффициенты первой (1) и второй (2) форм. Другие два соотношения
(здесь
К числу наиболее важных проблем П. т. относится проблема разыскания признаков, которые позволяют по заданным двум основным квадратичным формам поверхности (в произвольных координатах) установить, относится ли поверхность к данному классу поверхностей или нет. Для решения этой общей проблемы, как и многих других проблем П. т., используются методы тензорного исчисления. С начала 20 в. в П. т. появляется новое направление, в котором исследуется поверхность «в целом» по данным свойствам окрестностей её точек. Например, Л. Г. Шнирельманом и Л. А. Люстерником было доказано существование трёх замкнутых геодезических на регулярных замкнутых поверхностях, гомеоморфных сфере. Продолжение гладких поверхностей иногда приводит к появлению на них особенностей. Например, всякая развёртывающаяся поверхность, не являющаяся цилиндрической, при продолжении доходит до ребра (или острия в случае конуса). Рассмотрение поверхностей во всём их протяжении и с особенностями (т. е. отказ от требований дифференцируемости) потребовало изобретения принципиально новых методов исследования поверхностей и привлечения методов из других разделов математики. Развитие П. т. в этом направлении привело к созданию содержательных разделов геометрии. Так, например, глубокие и принципиально новые результаты были получены А. Д. Александровым и А. В. Погореловым в теории выпуклых поверхностей. Александровым был предложен новый метод исследования выпуклых поверхностей, основанный на приближении выпуклых поверхностей выпуклыми многогранниками. Рассмотренные свойства поверхностей не меняются при любых изометрических преобразованиях всего пространства, т. е. они относятся к т. н. метрической П. т. Изучают также свойства поверхностей, инвариантные по отношению к какой-либо другой группе преобразований пространства, например группе аффинных или проективных преобразований. Аффинная П. т. рассматривает свойства поверхностей, неизменные при эквиаффинных преобразованиях (аффинных преобразованиях, сохраняющих объём). Проективная П. т. рассматривает проективно-инвариантные свойства поверхностей. Лит.:Рашевский П. К., Курс дифференциальной геометрии, 4 изд., М., 1956; Норден А. П., Теория поверхностей, М., 1956; Погорелов А. В., Дифференциальная геометрия, 5 изд., М., 1969; Каган В. Ф., Основы теории поверхностей в тензорном изложении, ч. 1-2, М. - Л., 1947-48; Бляшке В., Дифференциальная геометрия и геометрические основы теории относительности Эйнштейна, пер. с нем., т. 1, М. - Л., 1935; Александров А. Д., Внутренняя геометрия выпуклых поверхностей, М. - Л., 1948; Погорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969; Фиников С. П., Проективно-дифференциальная геометрия, М. - Л., 1937; Широков П. А., Широков А. П., Аффинная дифференциальная геометрия, М., 1959; Blaschke W., Vorlesungen Ьber Differentialgeometrie, Bd 2, В., 1923; Biarichi L., Lezioni di geometria differenziale, 3 йd., t. 1-2, Bologna, 1937; Darboux G., Leзons sur la thйorie gйnйrale des surfaces, 2 йd., t. 1-4, P., 1924-25. Э. Г. Позняк. 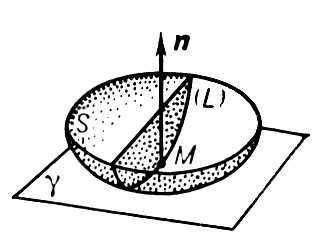
Рис. 1 к ст. Поверхностей теория. 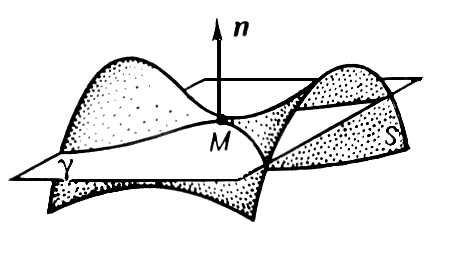
Рис. 2 к ст. Поверхностей теория. 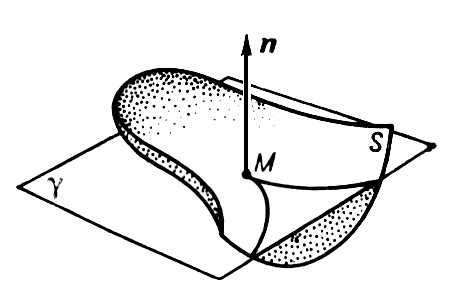
Рис. 3 к ст. Поверхностей теория. Поверхности вращения Пове'рхности враще'ния, поверхности, образуемые вращением плоской кривой вокруг прямой (оси П. в.), расположенной в плоскости этой линии. Примером П. в. может служить сфера (которую можно рассматривать как поверхность, образованную вращением полуокружности вокруг её диаметра). Линии пересечения П. в. с плоскостями, проходящими через её ось, называется меридианами; линии пересечения П. в. с плоскостями, перпендикулярными оси, - параллелями. Если по оси П. в. направить ось Ozпрямоугольной системы координат Oxyz,то параметрическое уравнения П. в. можно записать следующим образом: x = f( u) cosu, y = f( u) sinu, z = u. [здесь f( u) - функция, определяющая форму меридиана, а u - угол поворота плоскости меридиана]. Поверхности второго порядка Пове'рхности второ'го поря'дка, поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2-й степени: a 11 x 2+ a 22 y 2+ a 33 z 2+ 2 a 12 xy+ 2 a 23 yz+ 2 a 13 xz+ 2 a 14 x+ 2 a 24 y+ 2 a 34 z+ a 44= 0 (*) Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую П. в. п. В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из 17 приведённых ниже канонических видов, каждому из которых соответствует определённый класс П. в. п. Среди них выделяют пять основных типов поверхностей. Именно, 1) эллипсоиды
2) гиперболоиды:
3) параболоиды ( p> 0, q> 0):
4) конусы второго порядка:
5) цилиндры второго порядка:
Перечисленные П. в. п. относятся к т. н. нераспадающимся П. в. п.; распадающиеся П. в. п.:
х 2= а 2- пары параллельных плоскостей, х 2= -а 2- пары мнимых параллельных плоскостей, х 2= 0 - пары совпадающих плоскостей. При исследовании общего уравнения П. в. п. важное значение имеют т. н. основные инварианты - выражения, составленные из коэффициентов уравнения (*) и не меняющиеся при параллельном переносе и повороте системы координат. Например, если
то уравнение (*) определяет вырожденные П. в. п.: конусы и цилиндры второго порядка и распадающиеся П. в. п.; если определитель
то поверхность имеет единственный центр симметрии (центр П. в. п.) и называется центральной поверхностью. Если d = 0, то поверхность либо не имеет центра, либо имеет бесконечно много центров. Для П. в. п. установлена аффинная и проективная классификация. Две П. в. п. считают принадлежащими одному аффинному классу, если они могут быть переведены друг в друга некоторым аффинным преобразованием (аналогично определяются проективные классы П. в. п.). Каждому аффинному классу соответствует один из 17 канонических видов уравнения П. в. п. Проективные преобразования позволяют установить связь между различными аффинными классами П. в. п. Это объясняется тем, что при этих преобразованиях исчезает особая роль бесконечно удалённых элементов пространства. Например, эллипсоиды и двуполостные гиперболоиды, различные с аффинной точки зрения, принадлежат одному проективному классу П. в. п. Лит.:Александров П. С., Лекции по аналитической геометрии..., М., 1968; Ильин В. А., Позняк Э. Г., Аналитическая геометрия, 2 изд., М., 1971; Ефимов Н. В., Квадратичные формы и матрицы, 5 изд., М., 1972. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127 |
|||||||
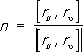
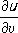 называется нормальным сечением в этом направлении, а ее кривизна - нормальной кривизной 1/
R,которая вычисляется по формуле:
называется нормальным сечением в этом направлении, а ее кривизна - нормальной кривизной 1/
R,которая вычисляется по формуле: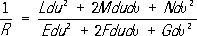 .
.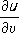 может рассматриваться как мера искривлённости поверхности в
Мв направлении
может рассматриваться как мера искривлённости поверхности в
Мв направлении
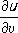 . Экстремальные значения нормальной кривизны в данной точке называется главными кривизнами, а соответствующие направления на поверхности - главными направлениями. Кривизна произвольного нормального сечения в данной точке связана простым соотношением с главными кривизнами (см.
Эйлера формулы
)
.Если главная кривизны в точке
Мразличны, то в этой точке существуют два различных главных направления. Линии, направления которых в каждой точке являются главными, называются линиями кривизны. Направления, в которых нормальная кривизна равна нулю, называются асимптотическими, а линии, имеющие в каждой точке асимптотическое направление, - асимптотическими линиями. Поверхность, состоящая из эллиптических точек (например, сфера), не имеет асимптотических линий. Поверхность, состоящая из гиперболических точек, имеет два семейства асимптотических линий (например, две системы прямолинейных образующих однополостного гиперболоида). Поверхность, состоящая из параболических точек, имеет одну систему асимптотических линий - систему прямолинейных образующих. Дальнейшее изучение свойств произвольных линий на поверхности (в первую очередь кривизн линий) тесно связано с кривизнами нормальных сечений. Кривизна
kв данной точке
Мпроизвольной линии
Гможет быть вычислена по формуле:
. Экстремальные значения нормальной кривизны в данной точке называется главными кривизнами, а соответствующие направления на поверхности - главными направлениями. Кривизна произвольного нормального сечения в данной точке связана простым соотношением с главными кривизнами (см.
Эйлера формулы
)
.Если главная кривизны в точке
Мразличны, то в этой точке существуют два различных главных направления. Линии, направления которых в каждой точке являются главными, называются линиями кривизны. Направления, в которых нормальная кривизна равна нулю, называются асимптотическими, а линии, имеющие в каждой точке асимптотическое направление, - асимптотическими линиями. Поверхность, состоящая из эллиптических точек (например, сфера), не имеет асимптотических линий. Поверхность, состоящая из гиперболических точек, имеет два семейства асимптотических линий (например, две системы прямолинейных образующих однополостного гиперболоида). Поверхность, состоящая из параболических точек, имеет одну систему асимптотических линий - систему прямолинейных образующих. Дальнейшее изучение свойств произвольных линий на поверхности (в первую очередь кривизн линий) тесно связано с кривизнами нормальных сечений. Кривизна
kв данной точке
Мпроизвольной линии
Гможет быть вычислена по формуле: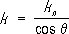 ,
,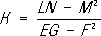 , (2)
, (2)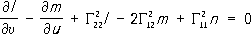 (4)
(4)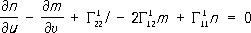
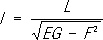 ;
;
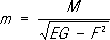 ;
;
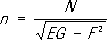 ;
;
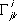 -
Кристоффеля символы
второго рода) были установлены в 1853 К. М.
Петерсоном.Справедливо и обратное утверждение - если коэффициенты двух форм, одна из которых положительно-определённая, удовлетворяют уравнениям (3) и (4), то существует определённая с точностью до движения и зеркального отражения поверхность, для которой указанные формы будут первой и второй квадратичными формами.
-
Кристоффеля символы
второго рода) были установлены в 1853 К. М.
Петерсоном.Справедливо и обратное утверждение - если коэффициенты двух форм, одна из которых положительно-определённая, удовлетворяют уравнениям (3) и (4), то существует определённая с точностью до движения и зеркального отражения поверхность, для которой указанные формы будут первой и второй квадратичными формами.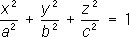 - эллипсоиды,
- эллипсоиды,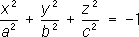 - мнимые эллипсоиды;
- мнимые эллипсоиды;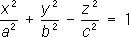 - однополостные гиперболоиды,
- однополостные гиперболоиды,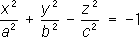 - двуполостные гиперболоиды;
- двуполостные гиперболоиды;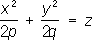 - эллиптические параболоиды,
- эллиптические параболоиды,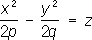 - гиперболические параболоиды;
- гиперболические параболоиды;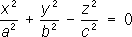 - конусы,
- конусы,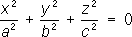 - мнимые конусы;
- мнимые конусы;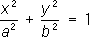 - эллиптические цилиндры,
- эллиптические цилиндры,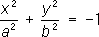 - мнимые эллиптические цилиндры,
- мнимые эллиптические цилиндры,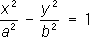 - гиперболические цилиндры,
- гиперболические цилиндры,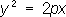 - параболические цилиндры.
- параболические цилиндры.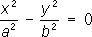 - пары пересекающихся плоскостей,
- пары пересекающихся плоскостей,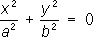 -пары мнимых пересекающихся плоскостей,
-пары мнимых пересекающихся плоскостей, (
a
ij = a
jii),
(
a
ij = a
jii), ,
,