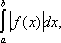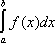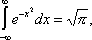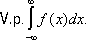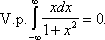|
|
���������� ������:: ������ ����� ���� :: ������ ����� :: ���� ��������� :: ��� :: �������� ����� :: ����� ����� �������� :: ������� ������ :: ������� ��� ���������� :: ������� ���� :: ������ ���� ���������� �����:: ���� (����� 2) :: The Boarding House :: Everything and Nothing :: ������ ����� :: ������� ���������� �������� :: ��������� ���������� :: ������������� ��������� :: ����� ���� (��� 1) :: ���������� �� ������� Windows XP :: ����� ������� |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 73)
Несменяемость судей Несменя'емость суде'й,в буржуазных государствах один из принципов судоустройства, согласно которому судья может быть уволен с должности только в связи с достижением предельного возраста, вследствие наступившей физической непригодности, по приговору суда либо по собственному желанию. Принцип Н. с. сложился в период абсолютизма, например, в Испании и Франции в начале 15 в. в процессе укрепления королевской власти, затем государственные должности (в том числе и судейские) продавались королём. Великая французская революция ликвидировала во Франции право передачи судейских должностей по наследству и провозгласила принцип выборности судей (существовал очень недолго), но при этом сохранялась Н. с. Позже был восстановлен, как правило, порядок назначения судей. Чтобы обеспечить деятельность судов в желаемом для господствующего класса направлении, судьи назначаются пожизненно или устанавливается предельный срок (очень высокий) их пребывания в должности. Например, в Великобритании право возбуждать вопрос об увольнении судей предоставлено только парламенту; для членов судов графств предельный возраст пребывания в должности установлен в 72 года. В США судьи федеральных судов назначаются пожизненно президентом с согласия сената. Предельного возраста для пребывания этих судей в должности не установлено, поэтому реально существует только один путь для отстранения их от должности - проведение по постановлению конгресса специальной процедуры - импичмента (судебное разбирательство парламентом дел о грубых должностных преступлениях, совершенных высшими государственными должностными лицами). Во Франции все судьи (кроме персонала коммерческих судов) назначаются президентом по представлению Высшего совета магистратуры, предельный возраст для исполнения судейских функций установлен в 65 лет (в кассационном суде - 70 лет). В Бельгии, Дании, Нидерландах, Норвегии, Швеции судьи назначаются королевской властью пожизненно. В Японии судьи не могут быть отстранены от должности без публичного разбирательства в порядке импичмента. буржуазии утверждают, что Н. с. обеспечивает им независимость при разрешении судебных дел. По существу Н. с. в сочетании с принципом назначаемости судей свидетельствует о недемократическом характере буржуазного суда. Выдвинут первоначально принцип Н. с. в борьбе с феодализмом, буржуазия использует его для сохранения на судейских должностях представителей своего класса. Несмещённая оценка Несмещённая оце'нка,оценка параметра распределения вероятностей по наблюдённым значениям, лишённая систематической ошибки. Более точно: если оцениваемое распределение зависит от параметров q 1, q 2,..., q s, то функция q i* ( x 1 , x 2 ,..., x n) от результатов наблюдения x 1 , x 2 ,..., x nназываемых Н. о. для параметра q i , если при любых допустимых значениях параметров q 1, q 2,..., q sматематическое ожидание Еq i*( x 1 , x 2 ,..., x n) = q i ,. Например, если. x 1, x 2 ,..., x nсуть результаты nнезависимых наблюдений случайной величины, имеющей нормальное распределение
с неизвестными а(математическое ожидание) и s 2(дисперсия), то среднее арифметическое
будет Н. о. для а.Часто используемая для оценки эмпирической дисперсии
не является несмещенной оценкой. Н. о. для s 2служит
величина Н. о. квадратичного отклонения s имеет более сложное выражение
Оценка (1) для математического ожидания и оценка (2) для дисперсии являются Н. о. и при распределениях, отличных от нормального; оценка (3) для квадратичного отклонения, вообще говоря (при распределениях, отличных от нормального), может быть смещенной. Использование Н. о. необходимо при оценке неизвестного параметра по большому числу серий наблюдений, каждая из которых состоит из небольшого числа наблюдений. Пусть, например, имеется kсерий x i 1, x i 2,ЧЧЧ, x i n( i= 1, 2, ЧЧЧ , k) по nнаблюдений в каждой и пусть s i-несмещенная оценка s 2для s 2, составленная по i-й серии наблюдений. Тогда при большом kв силу закона больших чисел
даже когда nневелико. Н. о. играют важную роль в статистическом контроле массовой продукции. Лит.:Крамер Г., Математические методы статистики, пер. с англ., М., 1948; Колмогоров А. Н., Несмещенные оценки, «Изв. А. Н. СССР. Серия математическая», 1950, № 4: Гнеденко Б. В., Беляев Ю. К.. Соловьев А. Д., Математические методы в теории надежности, М., 1965. Ю. В. Прохоров. Несмеянов Александр Николаевич Несмея'новАлександр Николаевич [р. 28.8(9.9).1899, Москва], советский химик-органик, академик АН СССР (1943; член-корреспондент 1939), общественный деятель, Герой Социалистического Труда (1969). Член КПСС с 1944. После окончания МГУ (1922) работает там же (с 1935 профессор, с 1944 заведующий кафедрой органической химии, в 1944-48 декан химического факультета, в 1948-51 ректор, руководил организацией строительства МГУ на Ленинских горах). Одновременно работал в институте удобрений и инсектофунгицидов (1930-34), в АН СССР: в институте органической химии (с 1934, в 1939-54 директор), академик-секретарь Химического отделения (1946-51). Президент АН СССР (1951-61), директор института элементоорганических соединений (с 1954), академик-секретарь Отделения общей и органической химии (с 1961). В 1947-1961 председатель Комитета по Ленинским и Государственным премиям в области науки и техники. Принимал деятельное участие в работе Всемирного Совета Мира и Советского комитета защиты мира. Основная область исследований - химия металлоорганических соединений. В 1929 предложил диазометод синтеза ртутьорганических соединений, который в дальнейшем им и его сотрудниками распространён на синтез металлоорганических соединений Sn, Pb, Tl, Sb, Bi (см. Несмеянова реакция ). Н. изучил разнообразные пути взаимных превращений металлоорганических соединений, разработал простые и удобные методы синтеза металлоорганических соединений Mg, Zn, Cd, Al, Tl, Sn, Pb, Sb, Bi из ртутьорганического соединения. Доказал (совместно с Р. Х. Фрейдлиной ), что продукты присоединения солей тяжёлых металлов к непредельным соединениям (название Н. «квазикомплексные соединения») имеют строение ковалентных металлоорганических соединений. Исследованиями металлических производных оксо-енольных систем и альфа-меркурированных оксосоединений Н. с сотрудниками внёс ясность в сложный вопрос о связи строения и двойственной реакционной способности металлических производных таутомерных систем, развил представление о сопряжении простых связей, о реакциях с переносом реакционного центра и др.; выяснил (совместно с О. А. Реутовым ) механизм электрофильного замещения у насыщенного атома углерода. Впервые синтезировал хлорониевые, бромониевые и триарилоксониевые соединения; открыл явление металлотропии. С 1952 широко разработал область производных ферроцена и др. «сандвичевых» соединений переходных металлов. По инициативе Н. и под его редакцией (совместно с К. А. Кочешковым ) вышла серия монографий «Синтетические методы в области металлоорганических соединений» и издаётся серия «Методы элементоорганической химии». Н. с сотрудниками выполнено также много работ в области химии хлорвинилкетонов (совместно с Н. К. Кочетковым ) и по синтезу алифатических соединений при помощи реакции теломеризации. Н. - член ряда зарубежных академий. Делегат 19-го и 20-го съездов КПСС. Депутат Верховного Совета СССР 3-5-го созывов. Государственная премия СССР (1943), Ленинская премия (1966). Награжден 6 орденами Ленина, орденом Трудового Красного Знамени, а также медалями. Соч.: Избр. труды, т. 1-4, М., 1959: Химия ферроцена, М., 1969; Элементоорганическая химия, М., 1970; Исследования в области органической химии, М., 1971; Начала органической химии, кн. 1-2, М., 1969-70 (совм. с Н. А. Несмеяновым). Лит.:Александр Николаевич Несмеянов, М., 1951 (АН СССР. Материалы к биобиблиографии учёных СССР. Сер. химических наук, в. 15); Фрейдлина Р. Х., Кабачник М. И., Коршак В. В., Новый вклад в развитие элементоорганической и органической химии, «Успехи химии», 1969, т. 38, в. 9. М. И. Кабачник.

А. Н. Несмеянов. Несмеянов Андрей Николаевич Несмея'новАндрей Николаевич [р. 15(28).1.1911, Москва], советский радиохимик, член-корреспондент АН СССР (1972). Брат Ал. Н. Несмеянова.Окончил МГУ (1934). В 1934-47 работал в Московском авиационном институте, затем в МГУ (с 1960 заведующий кафедрой радиохимии). Основные работы посвящены химии атомов, образующихся в результате ядерных превращений, методам получения радиоактивных изотопов и меченых соединений, а также применению радиоактивных изотопов для исследования технически важных материалов. Н. с сотрудниками изучены реакции «горячих» атомов с различными химическими соединениями. Н. разработал метод изотопного обмена и ряд др. методов применения изотопов для измерения давления пара труднолетучих веществ. Соч.: Получение радиоактивных изотопов, М., 1954 (совм. с А. В. Лапицким и Н. П. Руденко); Давление пара химических элементов, М., 1961; Руководство к практическим занятиям по радиохимии, М., 1968 (совм. с др.); Руководство к практическим занятиям по физическим основам радиохимии, М., 1971 (совм, с др.); Радиохимия, М., 1972. Несмеянова реакция Несмея'нова реа'кция,синтез металлоорганических соединений ароматического ряда разложением металлическими порошками двойных солей арилдиазонийгалогенидов с галогенидами тяжёлых металлов, например: [ArN 2] + HgX 3- + Cu ® ArHgX + N 2+ CuX 2, где Ar - ароматический радикал, Х - атом галогена. Реакция использована для синтеза металлоорганических соединений Hg, Sb, As, Bi, Sn и др. Вместо солей диазония могут быть использованы соли галогенониев [Аr 2Наl] +X -(Hal = хлор, бром, йод) и сульфония [Ar 3S] +X -. На их основе получены арильные производные не только непереходных, но и переходных металлов (Fe, Mo, W). Метод имеет важное препаративное значение: открыт Ал. Н. Несмеяновым в 1929. Лит.:Несмеянов А. Н., Избр. труды, т. 1-2, М., 1959; его же, Элементо-органическая химия, М., 1970. М. И. Рыбинская. Несмит Джеймс Не'смит(Nasmyth) Джеймс (19.8.1808, Эдинбург, - 7.5.1890, Лондон), английский машиностроитель. Получил классическое школьное образование, в 1829-31 учился у Г. Модсли.Организатор и владелец машиностроительного предприятия в Манчестере (с 1834). В 1839 сконструировал паровой молот и в 1842 получил на него патент. Создал поперечно-строгальный и фрезерный станки для обработки граней гаек, конструировал др. машины. В 1843 приезжал в Петербург, затем поставлял в Россию паровые молоты и станки. Опубликовал труд, в котором обобщил опыт конструирования станков (1841). Несмита система рефлектора Не'смита систе'ма рефле'ктора,разновидность Кассегрена системы рефлектора,в которой в сходящемся к фокусу пучке лучей установлено дополнительное плоское зеркало. Оно отражает лучи к стенке трубы телескопа, где размещается светоприёмная аппаратура. Предложена Дж. Несмитом в середине 19 в. Использована в 2,6- мрефлекторе Крымской астрофизической обсерватории и в ряде др. крупных телескопов. Несобственные интегралы Несо'бственные интегра'лы,обобщение классического понятия интеграла на случай неограниченных функций и функций, заданных на бесконечном промежутке интегрирования (см. Интеграл ). Определённый интеграл как предел интегральных сумм Римана может существовать (иметь определённое конечное значение) лишь для ограниченных функций, заданных на конечном интервале. Поэтому, если интервал интегрирования или подынтегральная функция не ограничены, для определения интеграла требуется ещё один предельный переход: получающиеся при этом интегралы называются несобственными интегралами. Если функция f( x) интегрируема на любом конечном отрезке [ a, N] и если существует
то его называют Н. п. функции f(x) на интервале [ а, Ґ] и обозначают
В этом случае говорят, что Н. и. сходится. Когда этот предел, а значит и Н. и., не существует, то иногда говорят, что Н. и. расходится. Например,
сходится при g > 1 и расходится при g Ј 1. Аналогично определяют Н. и. на интервалах [-Ґ, b] и [-Ґ, Ґ]. Если функция f( x) ,заданная на отрезке [ a, b], не ограничена в окрестности точки a, но интегрируема на любом отрезке [ а+ e, b], 0 < e < b - aи если существует
то его называют Н. и. функции f(x) на [ а, b] и записывают обычным образом:
Аналогично поступают, если f( x) не ограничена в окрестности точки b. Если существует Н. и.
или
то говорят, что Н. и.
или
абсолютно сходится: если же последние интегралы сходятся (но первые расходятся), то Н. и.
или
называются условно сходящимися. Задачи, приводящие к Н. и., рассматривались в геометрической форме Э. Торричелли и П. Ферма в 1644. Точные определения Н. и. даны О. Коши в 1823. Различие условно и абсолютно сходящихся Н. и. установлено Дж. Стоксом и П. Г. Л. Дирихле (1854). Ряд работ математиков 19 в. посвящен вычислению Н. и. в случаях, когда соответствующая первообразная не выражается через элементарные функции. Основными приемами вычисления Н. и. являются дифференцирование и интегрирование по параметру, разложение в ряды, применение теории вычетов. Значения многих Н. и. приводятся в различных таблицах. Н. и. имеют важное значение во многих областях математического анализа и его приложений. В теории специальных функций (цилиндрических функций, ортогональных многочленов и др.) одним из основных способов изучения является изображение функций в виде Н. и., зависящих от параметра, например
(см. Гамма-функция ) .К Н. и. относится и Фурье интеграл,а также интегралы, встречающиеся при др. интегральных преобразованиях. Решения краевых задач математической физики записываются кратными Н. и. с неограниченной подинтегральной функцией. В теории вероятностей важное значение имеет Н. и.
в теории диффракции света - Н. и.
В ряде случаев расходящимся Н. и. можно приписать определённое значение (см. Суммирование ) .В частности, если интеграл
расходится, но существует
то Аназывается главным значением Н. и. и обозначают
Так,
Аналогично вводится главное значение Н. и. от неограниченных функций. В работах Н. И. Мусхелишвили и его учеников построена теория интегральных уравнений, содержащих Н. и., понимаемые в смысле главного значения. Лит.:Смирнов В. И., Курс высшей математики, 20 изд., т. 2, М. - Л., 1967; Фихтенгольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд. т. 2, М., 1969; Кудрявцев Л. Д., Математический анализ, т. 1, М., 1970. Несобственные элементы Несо'бственные элеме'нтыв геометрии, элементы (точки, прямые, плоскости), которыми пополняется евклидова плоскость (или пространство) при изучении вопросов, относящихся к проективной геометрии. См. Бесконечно удалённые элементы. Несовершенной конкуренции теория Несоверше'нной конкуре'нции тео'рия,мелкобуржуазная теория рынка, признающая господство на нём монополий и их всесилие в формировании цени в эксплуатации мелких собственников. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91 |
|||||||