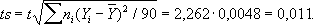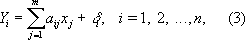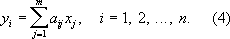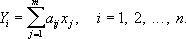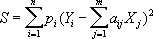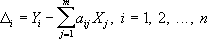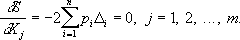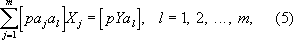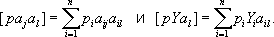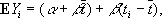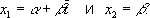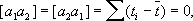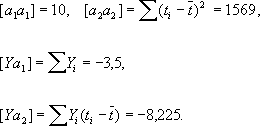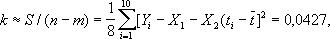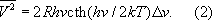|
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Раззаков Федор :: Азимов Айзек :: Чехов Антон Павлович :: Грин Александр :: Борхес Хорхе Луис :: Горький Максим :: Андреев Леонид Николаевич :: Сименон Жорж Популярные книги:: Ожерелье Иомалы :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: О «Двух душах» М. Горького :: Магия луны (Том 1) :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер :: Вторая книга Царств |
Большая Советская Энциклопедия (НА)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (НА) - Чтение (стр. 12)
(здесь n i- число случаев, в которых наблюдался вес Y i, причём n= S n i, = 10). Так как все взвешивания равноточные, то следует положить p i= n iи в качестве оценки для неизвестного веса m, выбрать величину
Задавая, например, I 9= 0,95, по таблицам распределения Стьюдента с девятью степенями свободы можно найти, что t= 2,262, и поэтому в качестве предельной абсолютной погрешности приближённого равенства m » 18,431 следует принять величину
Т. о. 18,420 < m < 18,442. Случай нескольких неизвестных (линейные связи). Пусть nрезультатов измерений Y 1, Y 2,..., Y nсвязаны с mнеизвестными величинами x 1, x 2,..., х m( m< n) независимыми линейными отношениями
где a ij- известные коэффициенты, а d i - независимые случайные ошибки измерений. Требуется оценить неизвестные величины x j(эту задачу можно рассматривать как обобщение предыдущей, в которой m = x 1и m= a i1= 1; i= 1,2,..., n). Так как Еd i = 0, то средние значения результатов измерений y i, = E y i. связаны с неизвестными величинами x 1, x 2,..., х mлинейными уравнениями (линейные связи):
Следовательно, искомые величины x jпредставляют собой решение системы (4), уравнения которой предполагаются совместными. Точные значения измеряемых величин y iи случайные ошибки d i обычно неизвестны, поэтому вместо систем (3) и (4) принято записывать так называемые условные уравнения
Согласно Н. к. м., качестве оценок для неизвестных x jприменяют такие величины X j, для которых сумма квадратов отклонений
будет наименьшей (как и в предыдущем случае, p i- вес измерения Y i, - величина, обратно пропорциональная дисперсии случайной ошибки d i ). Условные уравнения, как правило, несовместны, т. е. при любых значениях X jразности
не могут, вообще говоря, все обратиться в нуль, и в этом случае
также не может обратиться в нуль. Н. к. м. предписывает в качестве оценок выбрать такие значения X j, которые минимизируют сумму S. В тех исключительных случаях, когда условные уравнения совместны и, значит, обладают решением, это решение совпадает с оценками, полученными согласно Н. к. м. Сумма квадратов Sпредставляет собой квадратичный многочлен относительно переменных X j; этот многочлен достигает минимума при таких значениях X 1, X 2,..., Х m, при которых обращаются в нуль все первые частные производные:
Отсюда следует, что оценки X j, полученные согласно Н. к. м., должны удовлетворять системе так называемых нормальных уравнений, которая в обозначениях, предложенных Гауссом, имеет вид:
где
Оценки X j, получающиеся в результате решения системы нормальных уравнений, лишены систематических ошибок ( E x j= x j); дисперсии D x j; величин X jравны kd jj/d, где d- определитель системы (5), а d jj- минор, соответствующий диагональному элементу [ ра ja j] (иными словами, d jj/d- вес оценки X j). Если множитель пропорциональности k( kназывается дисперсией на единицу веса) заранее неизвестен, то для его оценки, а также для оценки дисперсии D x jслужат формулы: k» S/( n- m) и D x j» s 2 j= Sd jj/d( n- m) ( S- минимальное значение исходной суммы квадратов). При некоторых общих предположениях можно показать, что если количество наблюдений nдостаточно велико, то абсолютная погрешность приближённого равенства x i» X jменьше ts jс вероятностью, близкой к значению интеграла (1). Если случайные ошибки наблюдений d i подчиняются нормальному распределению, то все отношения ( X j- x j)/ s jраспределены по закону Стьюдента с n- mстепенями свободы [точная оценка абсолютной погрешности приближённого равенства производится здесь с помощью интеграла (2) так же, как в случае одного неизвестного]. Кроме того, минимальное значение суммы Sв вероятностном смысле не зависит от X 1, X 2,..., X mи поэтому приближённые значения дисперсий оценок D x j» s 2 jне зависят от самих оценок X j. Один из наиболее типичных случаев применения Н. к. м. - «выравнивание» таких результатов наблюдений Y i, для которых в уравнениях (3) a ij= a j( t i), где a j( t) - известные функции некоторого параметра t(если t- время, то t 1, t 2,... - те моменты времени, в которые производились наблюдения). Особенно часто встречается в приложениях случай так называемой параболической интерполяции, когда a j( t) - многочлены [например, a 1( t) = 1, a 2( t) = t, a 3( t) = t 2,... и т.д.]; если t 2- t 1= t 3- t 2=... = t n- t n -1, a наблюдения равноточные, то для вычисления оценок X jможно воспользоваться таблицами ортогональных многочленов, имеющимися во многих руководствах по современной вычислительной математике. Другой важный для приложения случай - так называемая гармоническая интерполяция, когда в качестве a j( t) выбирают тригонометрические функции [например, a j( t) = cos ( j- 1) t, j= 1, 2,..., m]. Пример. Для оценки точности одного из методов химического анализа этим методом определялась концентрация CaO в десяти эталонных пробах заранее известного состава. Результаты равноточных наблюдений указаны в таблице ( i- номер эксперимента, t i- истинная концентрация CaO, T i- концентрация CaO. определённая в результате химического анализа, Y i= T i- t i- ошибка химического анализа):
Если результаты химического анализа не имеют систематических ошибок, то E y i= 0. Если же такие ошибки имеются, то в первом приближении их можно представить в виде: E y i= a + b t i(a называется постоянной ошибкой, а b t i- методической ошибкой) или, что то же самое,
где
Для отыскания оценок a и b достаточно оценить коэффициенты
Условные уравнения в данном случае имеют вид:
поэтому a i1= 1, a i2= t i- t(согласно предположению о равноточности наблюдений, все p i= 1). Так как
то система нормальных уравнений записывается особенно просто: [ a 1a 1] X 1= [ Ya 1]; [ a 2a 2] X 2= [ Ya 2], где
Дисперсии компонент решения этой системы суть
где k- неизвестная дисперсия на единицу веса (в данном случае k- дисперсия любой из величин Y i). Так как в этом примере компоненты решения принимают значения X 1= -0,35 и X 2= -0,00524, то
D x 1» s 1 2= 0,00427, D x 2» s 2 2= 0,0000272, s 1= 0,065, s 2= 0,00522. Если случайные ошибки наблюдений подчиняются нормальному распределению, то отношения | X j– x jl/ s j( j= 1, 2) распределены по закону Стьюдента. В частности, если результаты наблюдений лишены систематических ошибок, то x 1= x 2= 0 и, значит, закону Стьюдента должны подчиняться отношения | X 1|/ s 1и | X 2|/ s 2. С помощью таблиц распределения Стьюдента с n– m= 8 степенями свободы можно убедиться, что если действительно x 1= x 2= 0, то с вероятностью 0,999 каждое из этих отношений не должно превосходить 5,04 и с вероятностью 0,95 не должно превосходить 2,31. В данном случае | X 1|/ s 1= 5,38 > 5,04, поэтому гипотезу отсутствия систематических ошибок целесообразно отвергнуть; в то же время следует признать, что гипотеза об отсутствии методической ошибки ( x 2= 0) не противоречит результатам наблюдений, так как | X 2|/ s 2= 1,004 < 2,31. Т. о., можно заключить, что для определения tпо результату наблюдения Тцелесообразно пользоваться приближённой формулой t= Т+ 0,35. Во многих практически важных случаях (и в частности, при оценке сложных нелинейных связей) количество неизвестных параметров бывает весьма большим и поэтому реализация Н. к. м. оказывается эффективной лишь при использовании современной вычислительной техники. Лит.:Марков А. А., Исчисление вероятностей, 4 изд., М., 1924; Колмогоров А. Н., К обоснованию метода наименьших квадратов, «Успехи математических наук», 1946, т. 1, в. 1; Линник Ю. В., Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений, 2 изд., М., 1962; Helmert F. R., Die Ausgieichungsrechnung nach der Methode der kleinsten Quadrate..., 2 Aufl., Lpz., 1907. Л. Н. Большев. Наин-Синга На'ин-Си'нга,горный хребет на Ю.-З. Тибетского нагорья, в Китае; см. Алинг-Гангри . Наири Наи'ри,название стран, расположенных к С. от Ассирии, в бассейнах Урмийского и Ванского озера. Упоминается в ассирийских надписях начиная со времени царя Тукультининурты I (около 13 в. до н. э.) до Саргона II (722-705). Значительной части Н. соответствует территория государства Урарту. Лит.:Пиотровский Б. Б., Ванское царство (Урарту), М., 1959. Най Най,нэй, духовой музыкальный инструмент: 1) арабо-иранская продольная флейта с 6-8 игровыми отверстиями. 2) Узбекская и таджикская поперечная флейта с 6 игровыми отверстиями. Звукоряд диатонический; с помощью особой аппликатуры и частичного прикрывания отверстий получают и хроматически измененные звуки. В зависимости от материала называется агач-Н. (деревянный), гарау-Н. (бамбуковый), мис-Н. (жестяной), бриндгжи-Н. (латунный). 3) Молдавская и румынская продольная многоствольная флейта. Состоит из 8-24 трубок разной длины (от неё зависит высота звука), укрепленных в дугообразной кожаной обойме. Звукоряд диатонический. Найдёнов Сергей Александрович Найдёнов(псевдоним; настоящая фамилия Алексеев) Сергей Александрович [14(26).9.1868, Казань, - 5.12.1922, Ялта], русский драматург. Родился в купеческой семье. Окончил московское Музыкально-драматическое училище филармонического общества (1889); несколько лет играл на провинциальной сцене. Первая и лучшая пьеса Н. - «Дети Ванюшина» (1901, постановка петербургского Театра литературно-художественного общества, московского Театра Корша). В 1902 сблизился с М. Горьким и начал печататься в издательстве «Знание» . Автор пьес: «Номер тринадцатый» (1903), «Блудный сын» (1903), «Авдотьина жизнь» (1904, постановка Театра В. Ф. Комиссаржевской), «Стены» (1907), «Роман тёти Ани» (1912), «Работница» (1915) и др. В основе реалистического творчества Н. - обличение пороков капиталистического общества, душевной разобщённости людей. После Октябрьской революции 1917 Н. опубликовал пьесу-хронику «Москва» (1921), посвященную Революции 1905-1907, и историко-революционную драму «Неугасимый свет» (1922). Соч.: Пьесы, т. 1-2, СПБ. 1904-11; Дети Ванюшина. [Послесл. В. Сергеева], М. 1955. Лит.:Боровский В. В., Раскол в «темном царстве», в его кн.: Литературно-критические статьи, М., 1956; «Дети Ванюшина» на сцене, М., 1940; История русской литературы конца XIX - нач. XX века. Библиографический указатель, М. - Л., 1963. И. И. Подольская. Найдёновы Найдёновы,представители крупной российской буржуазии, выходцы из крепостных крестьян Владимирской губернии. В 1764 (или 1765) посессионный крестьянин Егор Иванович Н. (1745-1821) определён в Москву в красильную мастерскую, в 1816 записался в московское купечество, имея собственную красильную мастерскую. Его сын Александр Егорович Н. (1789-1864) владел землями, домами и красильными мастерскими в Москве. До конца 19 в. Н. занимались хлопчато-бумажным и шерстяным производством и торговлей. В 70-х гг. сыновья Александра Егоровича - Николай Александрович Н. и Виктор Александрович Н. занялись банкирской деятельностью. Н. участвовали в учреждении Московского торгового банка и неизменно возглавляли его. Николай Александрович был до 1905 председателем Биржевого комитета, где группа Н., впоследствии Крестовникова - Н., располагая большинством, выступала от имени всей крупной московской буржуазии в качестве её ультраконсервативного лидера. После 1905 эта группа стала опорой октябристов . Лит.:Найдёнов Н. А., Воспоминания о виденном, слышанном и испытанном, кн. 1, 2, М., 1903-05; Черменский Е. Д., Буржуазия и царизм в первой русской революции, 2 изд., М., 1970. Найджел На'йджел,Нигел (Nigel), город на В. ЮАР, в провинции Трансвааль. 33,8 тыс. жителей (1970). Один из центров золотопромышленного района Витватерсранд. Веткой соединён с ж.-д. магистралью ЮАР. Основан в 1909. Найквиста критерий На'йквиста крите'рий(по имени американского физика Х. Найквиста, Н. Nyquist; р. 1889), частотный критерий устойчивости линейных систем автоматического регулирования с постоянными параметрами; может применяться и для систем с запаздыванием. См. Устойчивость систем автоматического управления. Найквиста формула На'йквиста фо'рмула,теорема Найквиста, соотношение, определяющее величину тепловых флуктуаций тока или напряжения в электрической цепи. Получена американским физиком Х. Найквистом (Н. Nyquist) в 1928. Согласно Н. ф., обусловленное тепловыми флуктуациями среднее значение квадрата напряжения на концах проводника с сопротивлением R, находящегося в состоянии теплового равновесия при абсолютной температуре Т, равно:
где k- Больцмана постоянная , Dn - полоса частот, внутри которой измеряются флуктуации напряжения. При низких температурах и достаточно высоких частотах, когда h³ kT(n - частота, h- Планка постоянная ), вместо формулы (1), следует пользоваться более общим выражением:
Н. ф. широко используется при расчёте тепловых шумов в измерительных и радиотехнических устройствах. Лит.:Киттель Ч., Элементарная статистическая физика, пер. с англ., М., 1960; Мак-Доналд Д., Введение в физику шумов и флуктуаций, пер. с англ., М., 1964. Э. М. Эпштейн. Найлон На'йлон(англ. nylon), широко распространённое за рубежом торговое название полиамидных волокон . Найман Найма'н,посёлок городского типа в Наукатском районе Ошской области Киргизской ССР. Расположен в 30 кмк С.-В. от ж.-д. станции Кызыл-Кия. Добыча ртутных руд. Наймиты Найми'ты,внесословная категория населения феодальной Руси 12-17 вв. Термин «Н.» встречается впервые в Русской правде . Н. обычно становились разорившиеся сельские и городские общинники, беглые крестьяне и холопы, вынужденные заключать договор о найме с феодалами, горожанами и др. нанимателями. При заключении договоров Н. формально выступали как свободные люди, однако хозяин получал право не только на труд Н., но и на его личность. С 15-16 вв., в связи с ростом числа Н. и использования их труда, закон (Псковская судная грамота, Судебник 1497 и Судебник 1550 , Уложение Алексея Михайловича 1649 и др.) начинает отделять право на пользование трудом Н. от права на его личность, хотя и в 16-17 вв. Н. заключали неравноправные договоры. Лит.:Панкратова А. М., Наймиты на Руси в XVII в., в сборнике: Академику Б. Д. Грекову ко дню 70-летия. Сб. ст., М., 1952. М. Я. Волков. Найрамдал Найрамда'л,Хыйтун, самая высокая вершина в горном массиве Табын-Богдо-Ола на Алтае. Высота 4356 м. Найроби болезнь Найроби болезнь,острая вирусная трансмиссивная болезнь овец и коз характеризующаяся лихорадкой и геморрагическим гастроэнтеритом. Распространена в Кении, Уганде, некоторых районах ЮАР и др. Источник возбудителя инфекции - больное животное; переносчики - клещи. Резервуаром вируса в природе могут быть голубой гну, крысы. Н. б. начинается с повышения температуры до 41-41,6°C, которая держится 2-3 сут, затем понижается до нормальной. Животные угнетены, пульс частый, нитевидный, дыхание учащённое, затруднённое, из носа слизисто-гнойное выделение, иногда с примесью крови, непроизвольное выделение водянистых каловых масс, нередко с кровью. У беременных животных часты аборты. У переболевших образуется напряжённый и длительный иммунитет. Лечение не разработано. Профилактика - защита животных от нападения клещей. Лит.:Малоизвестные заразные болезни животных, 2 изд., М., 1973, с. 115-22. Найроби (нац. парк в Кении) Найро'би(Nairobi), национальный парк в Кении, в 5 кмот г. Найроби. Площадь 11,4 тыс. га. Создана 1946. Саванна с преобладанием зарослей колючих кустарников и ряда видов акации. Обитают лев, леопард, буйвол, зебра, антилопы (импала, канна, гну, газели Томпсона и Гранта, водяной козёл), жирафа, немногочислен чёрный носорог, из птиц - страус, дрофа-кори, птица-секретарь и др. Найроби (столица Кении) Найро'би(Nairobi), столица Кении. Расположена на плато, на высоте 1,7 тыс. м. Климат экваториальный, муссонный, средняя температура июля 15°C, марта 18,7°C. Осадков 932 ммв год. Около 550 тыс. жителей (1973, с пригородами; 267 тыс. в 1962). Н. образует столичный округ, приравненный в административном отношении к провинции. Управление осуществляет выборный Совет (часть членов Совета назначается комиссаром Н.). Н. основан в 1899 при прокладке железной дороги Момбаса - Кисуму; позднее стал административным центром английской колонии Кения. Английская военная база в Н. использовалась в 20-40-х гг. 20 в. британскими колонизаторами для подавления национально-освободительного движения в Восточной Африке. Н. был одним из центров борьбы народов Кении против английского господства. С 12 декабря 1963 - столица независимой Кении (с 12 декабря 1964 - Республика Кения). Н. - узел железных и шоссейных дорог; в 16 кмк Ю.-В. от города аэропорт международного значения Эмбакаси. Главный торгово-промышленный центр Кении. Пищевая, кожевенно-обувная, текстильная, металлообрабатывающая, цементная промышленность. Электроэнергию Н. получает от ГЭС Оуэн-Фолс (Уганда). В 5 кмот Н. - национальный парк Найроби . С 1920 город имеет прямоугольную планировку. Застроен зданиями европейского типа. Среди сооружений 1950-70-х гг. - парламент (1950-е гг.), Национальный театр (открыт в 1952) с примыкающим к нему Культурным центром (открыт в 1960), Национальный университет (1956), конференц-центр Кениаты (начало 1970-х гг.), госпиталь Агахана, отели «Нью-Стэнли»-, «Найроби-Хилтон». В восточной части - район лачуг Пум-вани. В Н. находятся также Мемориальная библиотека Макмиллана, Национальный музей. С 1948 существует английский театр (руководитель Д. Маул). В помещении Национального театра выступают любительские коллективы. В 1968 создана Школа драмы, из её воспитанников в 1970 сформирована Национальная театральная труппа. Лит.:Smart J., A jubilee history of Nairobi, [Nairobi, 1950]. 
Здание парламента. 
Общий вид города. Справа - конференц-центр Кениаты (нач. 1970-х гг.). 
Канцелярия президента. 
Памятник кенийцам, погибшим в двух мировых войнах. 
Отель «Найроби-Хилтон». 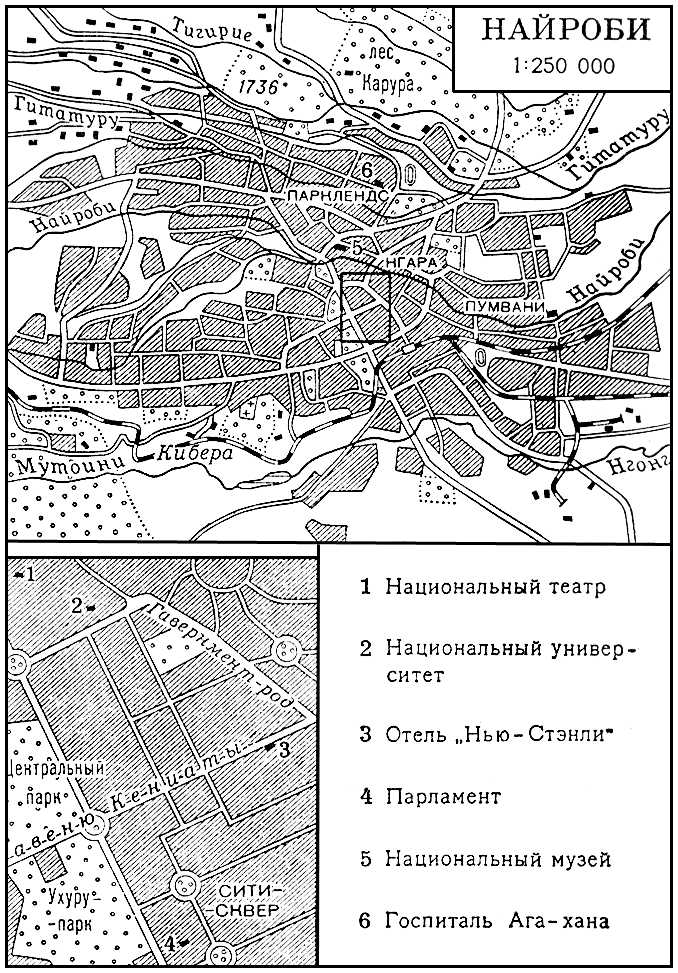
Найроби. План города. Найстенъярви Найстенъя'рви,посёлок городского типа в Суоярвском районе Карельской АССР. Расположен на р. Ирста (бассейн Онежского озера). Ж.-д. станция. Лесозавод, производство стройматериалов. Найт Фрэнк Хайнеман Найт(Knight) Фрэнк Хайнеман (р. 7.11.1885, округ Маклин, Иллинойс), американский экономист. Образование получил в университетах штата Теннесси и Корнеллском. С 1919 преподавал в университете штата Айова, с 1928 до ухода в отставку - в Чикагском университете. Экономическая теория рассматривается Н. как наука, которая, используя анализ экономического поведения производителей и потребителей, должна дать обобщённое представление о принципах функционирования экономической системы. По мнению Н., обмен является определяющим по отношению к производству. Откровенный апологет капитализма, Н. считает, что предприниматель играет важную динамическую роль в производстве, требования же рабочих о повышении зарплаты объявляет неоправданным вмешательством в безупречно действующий рыночный механизм. Соч.: The ethics of competition, L., [1935]; The economic organization, N. Y., 1951; On the history and method of economics, [Chi., 1956]; Risk, uncertainty and profit, N. Y., 1957; Intelligence and democratic action, Camb. (Mass.), 1960. Найтингейл Флоренс На'йтингейл(Nightingale) Флоренс (12.5.1820, Флоренция, - 13.8.1910, Лондон), английская сестра милосердия и общественный деятель. Изучала организацию помощи больным в больницах Германии и Франции. Во время Крымской войны 1853-56 с 38 помощницами наладила полевое обслуживание раненых в английской армии, что резко сократило смертность в лазаретах. В 1860 организовала первую в мире школу медсестёр в госпитале Сент-Томас (Лондон). До 1872 эксперт английской армии по вопросам медицинского обслуживания больных и раненых. Автор работ о системе ухода за больными и ранеными (в рус. пер. - «Как нужно ухаживать за больными», «Домашний и госпитальный уход за больными»). В 1912 Лига Международного Красного Креста учредила медаль им. Н. как высшую награду медсестрам, отличившимся при уходе за больными и ранеными. К 1974 эта медаль присуждена 712 чел., среди которых 19 советских медсестёр и санинструкторов, в том числе Герои Советского Союза З. М. Туснолобова-Марченко, М. С. Шкарлетова, И. Н. Левченко, В. С. Кащеева. Лит.:Рейтенбарг Д., Флоренция Найтингейл, «Медицинская сестра», 1960, № 7-8; Horndasch М., Die Lady mit der Lampe, Bonn, 1948; Bishop W., Goldle S., A biobibliography of Florence Nightingale, L., 1962. Л. А. Станкевич. Найтовский сдвиг На'йтовский сдвиг,смещение Найта, сдвиг резонансных частот ядерного магнитного резонанса в металлах и сплавах из-за релаксации, обусловленной взаимодействием электронов проводимости с магнитными моментами атомных ядер. Обнаружен и объяснён американским физиком У. Д. Найтом (W. D. Knight) в 1949. Накадзато Кисё Накадза'тоКисё (р. 13.3.1936, Нагасаки), японский писатель. Член правления Союза демократической литературы Японии. Литературное творчество совмещает с работой на судостроительном заводе, где окончил техническое училище. Первый рассказ «Вор» опубликован в 1959 под псевдонимом Хата Сацуки. Автор романов: «На распутье» (1963), «Старая шахта» (1966), «Недолгий сон» (т. 1-2, 1967-68), «Вернись к поэзии» (1970-1973). В романе «Недолгий сон» автор противопоставил силы реакции и сторонников демократических преобразований после 2-й мировой войны 1939-45, попытался дать художественное воплощение ведущей роли Коммунистической партии Японии в деле защиты интересов народных масс, поднял проблему создания единого демократического фронта. Лит.:Накано К., Мир Накадзато К., «Минею бунгаку», 1970, № 54, с. 136-50. О. В. Морошкина. Наказ Екатерины II Нака'з Екатери'ны II,философско-юридический трактат, руководство для депутатов «Комиссии об уложении» 1767, издан в 1767 на русском, французском, немецком и латинском языках. Состоял из 22 глав, 655 статей государственного, уголовного и гражданского права и процесса, вступления, заключения и 2 дополнений. Фразеология просветительских теорий (более 400 статей почти дословно заимствовано из Монтескьё, Беккариа и др.) сочеталась в Н. Е. II с обоснованием необходимости самодержавия в России, с рекомендацией барщины и т.п. Наказ неоднократно исправлялся, особенно его 11-я глава о крестьянах, откуда были изъяты упоминания об ограничении крепостного права и др., но даже и в таком виде его не рассылали в местные канцелярии. Практического применения не имел. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||