 |
|
Популярные авторы:: Чехов Антон Павлович :: Горький Максим :: Азимов Айзек :: БСЭ :: Раззаков Федор :: Толстой Лев Николаевич :: Борхес Хорхе Луис :: Лондон Джек :: Коллектив Рубоард :: Кларк Артур Чарльз Популярные книги:: Справочник по реестру Windows XP :: На страже :: Лунный нетопырь :: Брат мой... :: Сон Педро Энрикеса Уреньи :: Чужое :: Патруль :: Бурый волк :: Посланники хаоса-1: Проверка на прочность :: Не тяни леопарда за хвост |
Большая Советская Энциклопедия (МН)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (МН) - Чтение (стр. 2)
Изоэдры и изогоны. Изоэдром (изогоном) называется такой выпуклый М., что группа его поворотов (первого и второго, т. е. с отражениями, родов) вокруг центра тяжести переводит любую его грань (вершину) в любую другую его грань (вершину). Каждому изоэдру (изогону) соответствует дуальный изогон (изоэдр). Если М. одновременно и изогон и изоэдр, то он правильный М. Комбинаторно различных изоэдров (изогонов) имеется 13 специальных типов и две бесконечные серии (призмы и антипризмы). Оказывается, что каждый из этих изоэдров может быть реализован так, что все его грани суть правильные многоугольники. Полученные так М. называются полуправильными многогранниками (телами Архимеда).
Параллелоэдры (выпуклые; найдены рус. учёным Е. С. Федоровым в 1881) - М., рассматриваемые как тела, параллельным перенесением которых можно заполнить всё бесконечное пространство так, чтобы они не входили друг в друга и не оставляли пустот между собой, т. е. образовать разбиение пространства. Таковы, например, куб или правильная 6-угольная призма. Топологически различных сеток рёбер параллелоэдров пять. Число их граней - 6, 8, 12, 12, 14. Для того чтобы М. был параллелоэдром, необходимо и достаточно, чтобы он был выпуклым М. одного из пяти указанных топологических типов и чтобы все грани его имели центры симметрии. Если параллелоэдры разбиения смежны целыми гранями, разбиение называется нормальным. Центры параллелоэдров такого разбиения образуют решётку, т. е. совокупность всех точек с целыми координатами относительно какой-то, вообще говоря, не прямоугольной декартовой системы координат. Множество точек пространства, из которых каждая отстоит от некоторой данной точки Орассматриваемой решётки L не дальше, чем от всякой другой точки этой решётки, называется областью Дирихле (или областью Вороного) D oL точки Ов решётке L. Область D oL является выпуклым М. с центром в точке О. Совокупность областей Дирихле всех точек произвольной решётки образует нормальное разбиение пространства. Существует замечательная теорема: произвольное (даже n-мерное) нормальное разбиение на параллелоэдры, в каждой из вершин которого сходится n+ 1 параллелоэдр, может быть аффинным преобразованием превращено в разбиение Дирихле для некоторой решётки. Всякое движение, переводящее в себя решётку L и оставляющее на месте её точку О, преобразует в себя область D oL и обратно. Группу всех таких движений называют голоэдрией решётки. Их всего семь: кубическая, ромбоэдрическая, квадратная (или тетрагональная), ортогональная (или ромбическая), моноклинная, триклинная и гексагональная. Кристаллографические многогранники. Каждая из семи рассмотренных групп имеет подгруппы, всех различных таких групп и их подгрупп 32; их называют кристаллографическими классами. Пусть какой-нибудь кристаллографический класс есть подгруппа некоторой голоэдрии, тогда говорят, что он принадлежит этой голоэдрии (или входит в состав её сингонии), если этот класс не является подгруппой никакой голоэдрии, содержащейся в данной. Если взять плоскость, не проходящую через точку О, и подвергнуть её всем поворотам какого-нибудь кристаллографического класса, то полученные плоскости ограничивают либо некоторый изоэдр с центром в точке, либо бесконечное выпуклое призматическое тело, либо многогранный угол. Полученные тела называются простыми формами кристаллов, в первом случае замкнутыми, во втором и третьем - открытыми. Две простые формы считают одинаковыми, если они имеют один и тот же комбинаторный тип, порождены одним и тем же кристаллографическим классом и повороты этого класса одинаковым образом связаны с формой. Существует 30 различных в этом смысле замкнутых форм и 17 открытых, каждая из них имеет вполне определённое название (см. ) . Основываясь на первом (указанном в начале статьи) определении М., можно указать ещё четыре правильных невыпуклых многогранника (т. н. тела Пуансо), впервые найденных французским математиком Л. Пуансо в 1809. Доказательство несуществования других невыпуклых правильных М. дал французский математик О. Коши в 1811. В этих М. либо грани пересекают друг друга, либо сами грани - самопересекающиеся многоугольники. Для изучения вопросов, связанных с площадями поверхностей и объёмами таких М., удобно пользоваться именно первым определением М. Если у М. можно так ориентировать грани, чтобы каждое ребро в тех двух гранях, которые смежны по этому ребру, имело бы обратные направления, то его называют ориентируемым, в противном случае - неориентируемым. Для ориентируемого М. (даже если он самопересекающийся и его грани - самопересекающиеся многоугольники) можно ввести понятия площади поверхности и величины объёма. Площадью ориентируемого М. называют просто сумму площадей его граней (об определении площади самопересекающегося многоугольника см. ) .Для определения объёма надо заметить, что совокупность внутренних кусков граней М. разрезает пространство на определённое число связных кусков, из которых один по отношению к М. бесконечный (внешний), а остальные конечные (внутренние). Если из внешней по отношению к М. точки провести отрезок в какую-либо внутреннюю точку внутреннего куска, то сумму «коэффициентов» тех внутренних кусков граней М., которые пересечёт этот отрезок, называют коэффициентом рассматриваемого внутреннего куска М. (она не зависит от выбора внешней точки О); такой коэффициент есть целое положительное, отрицательное число или нуль. Сумму обычных объёмов всех внутренних кусков М., умноженных на эти их коэффициенты, называют объёмом М. Можно рассматривать и n-мерные М. Некоторые из указанных определений и теорем имеют n-мерное обобщение. В частности, найдены все выпуклые правильные М.; при n= 4 их оказалось 6, а при всех больших nвсего три: обобщение тетраэдра, куба и октаэдра. В то же время, например, неизвестны все четырёхмерные изоэдры и изогоны. Примеры нерешенных задач теории многогранников. 1) Немецкий математик Э. Штейниц дал примеры того, что не для всякого топологического типа сетки рёбер выпуклого М. существует М., который можно описать вокруг шара; в общем виде задача не решена. 2) Параллелоэдры суть выпуклые основные области групп параллельных переносов, но до сих пор не определены основные типы стереоэдров, т. е. выпуклых основных областей произвольных (федоровских) дискретных групп движений. 3) Определение всех типов четырёхмерных изоэдров. Лит.:Фёдоров Е. С., Начала учения о фигурах, СПБ, 1885; Александров А. Д., Выпуклые многогранники, М. - Л., 1950; Вороной Г. Ф., Собр. соч., т. 2, К., 1952; Brьckner М., Vielecke und Vielflache. Theorie und Geschichte, Lpz., 1900; Steinitz E., Vorlesungen liber die Theorie der Polyeder unter Einschiuss der Elemente der Topologie..., B., 1934; Coxeter H. S. М., Regular polytopes, 2 ed., L. - N. Y., 1963. Б. Н. Делоне. 
Правильные невыпуклые многогранники (тела Пуансо). 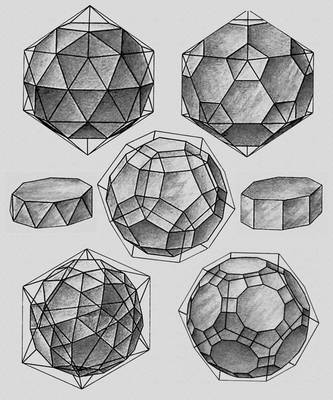
Полуправильные многогранники (тела Архимеда). 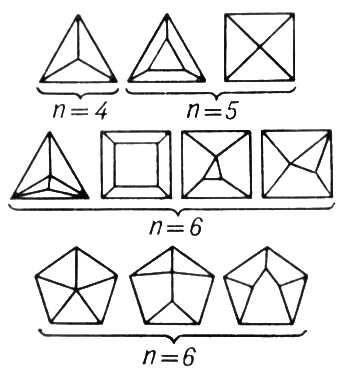
Рис. к ст. Многогранник. 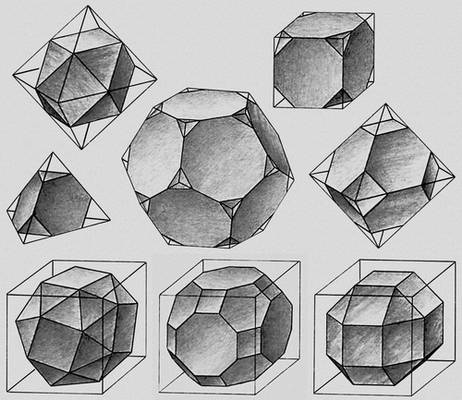
Полуправильные многогранники (тела Архимеда). 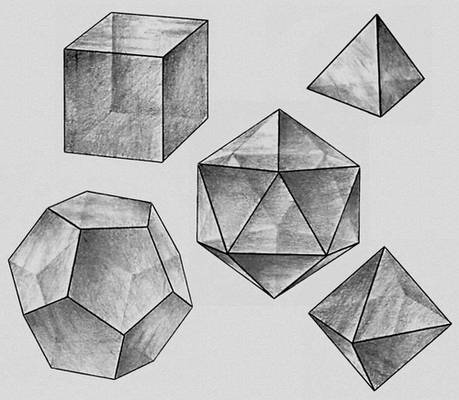
Правильные выпуклые многогранники (тела Платона). 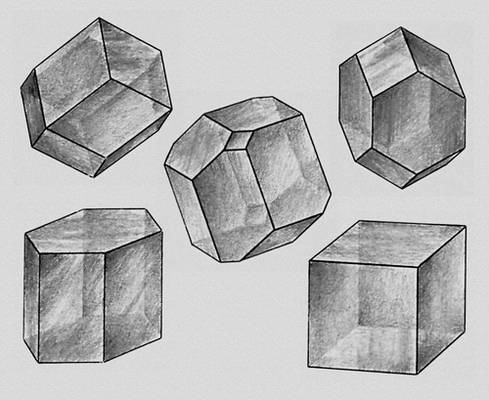
Выпуклые параллелоэдры (тела Фёдорова). Многогранный угол Многогра'нный у'гол,часть пространства, ограниченная одной полостью многогранной конической поверхности, направляющая которой - плоский многоугольник без самопересечений. Грани этой поверхности называются гранями М. у., вершину - вершиной М. у. М. у. называют правильным, если равны все его линейные углы и все его двугранные углы. Мерой М. у. является площадь, ограниченная сферическим многоугольником полученным пересечением граней М. у., сферой с радиусом, равным единице, и с центром в вершине М. у. См. также . 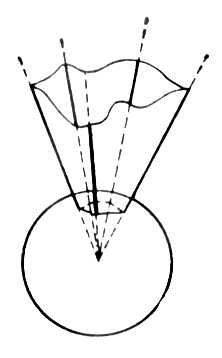
Рис. к ст. Многогранный угол. Многогрешный Демьян Игнатович Многогре'шныйДемьян Игнатович (умер не ранее 1696), гетман Левобережной Украины в 1668-72. Выходец из народа. Активный участник Освободительной войны украинского народа 1648-54. В 1649 в чине генерального есаула подписал .Став гетманом, М. проводил политику, угодную зажиточному казачеству. В 1670 участвовал в подавлении восстания казацкой и крестьянской бедноты под руководством И. Дзиковского. В 1672 был обвинён в тайных связях с Турцией, арестован и сослан в Иркутск вместе с женой и детьми. В 1688 освобожден. В 1696 постригся в монахи. Многодвигательный электропривод Многодви'гательный электроприво'д,группа электродвигателей, объединённых общей системой управления и приводящих в движение отдельные рабочие органы машины или установки (например, прокатных станов, бумагоделательных машин, комбинированных металлообрабатывающих станков, шагающих экскаваторов и т. и.). См. . Многодетные матери Многоде'тные ма'тери,в трудовом законодательстве СССР - матери, имеющие 3 и более детей, для которых установлены определённые льготы. Женщинам, имеющим 2 детей, выплачивается единовременное пособие при рождении 3-го и каждого следующего ребёнка и ежемесячное пособие при рождении 4-го и каждого следующего ребёнка, начиная с достижения ребёнком одного года и до того времени, когда ему исполнится 5 лет. При назначении пособия учитываются как родные дети, так и усыновленные, а также дети мужа и усыновленные им дети, находящиеся на воспитании М. м. не позже чем с 12 лет (с учётом требований, установленных законом). М. м. предоставляются льготы по оплате содержания детей в детских садах и яслях (плата снижается на 25-50 %, с учётом количества детей и общего заработка родителей). Для М. м. установлены также льготы в области пенсионного обеспечения. Так, женщины, родившие 5 и более детей и воспитавшие их до 8-летнего возраста, имеют право на пенсию по старости по достижении 50 лет и при стаже работы не менее 15 лет, если они не имеют права на пенсию по старости в более раннем возрасте. Для М. м. учреждены специальные ордена и медали: «Мать-героиня», «Материнская слава», «Медаль материнства». Женщинам, родившим и воспитавшим 10 детей, присваивается почётное звание «Мать-героиня» с вручением ордена «Мать-героиня» и грамоты Верховного Совета СССР. См. также , , . Многодомные растения Многодо'мные расте'ния,многобрачные, полигамные, цветковые растения, которые наряду с обоеполыми цветками имеют и однополые. На одном и том же растении могут быть обоеполые и мужские цветки (андромонэция, например у чемерицы); обоеполые и женские цветки (ганомонэция, например у смолевки и многих растений семейства сложноцветных); как обоеполые, так и мужские и женские цветки (тримонэция, например у конского каштана). На одних экземплярах М. р. бывают обоеполые цветки, на других - мужские (андродиэция - у куропаточьей травы и др.) или женские (гинодиэция - у незабудок, многих растений семейства губоцветных). Наконец, обоеполые, мужские и женские цветки могут быть на разных растениях (триэция - у ясеня, винограда). Между указанными типами имеются переходы. Многодомность у растений способствует перекрёстному опылению. Многожёнство Многожёнство,см. и . Многозабойное бурение Многозабо'йное буре'ние,сооружение буровых скважин, имеющих ответвления в виде резко искривленных дополнительных стволов от основного ствола скважины в пределах продуктивного пласта (нефти, газа и т. п.). М. б. применяется для добычи нефти и газа, а также при разведке твёрдых полезных ископаемых. М. б. целесообразно в сравнительно устойчивых продуктивных пластах мощностью 20 ми более, например в монолитных или с прослоями глин и сланцев нефтеносных песчаниках, известняках и доломитах, при глубинах 1500-2500 ми при отсутствии газовой шапки и аномально высоких пластовых давлений. М. б. сокращает число обычных скважин путём увеличения дренирующей поверхности эксплуатационной скважины ( рис. 1 ). Для проведения таких скважин в СССР созданы мощные искривленные и ,способы и средства для принудительного продвижения геофизических приборов, разработаны технологические приёмы и инструменты для забуривания и крепления ответвлений. Впервые М. б. осуществлено в США в штате Техас (1930). Ответвления бурились специально спроектированными для этой цели шарнирными и в виде гибкого шланга бурильными трубами, которые приводились во вращение с земной поверхности. Недостаточная прочность таких труб и сложность технологии ограничили длину дополнительных стволов до 30 м.Новый принцип - использование забойных двигателей (турбобуров, электробуров) был впервые реализован в СССР по предложению А. М. Григоряна, В. А. Брагина и К. А. Царевича в 1948, когда этим методом были пробурены первые многозабойные скважины. Это позволило применить обычные высокопрочные бурильные трубы и увеличить длину дополнитеельных стволов до нескольких сотен метров. В нефтедобывающих районах СССР эксплуатируются скважины с 5-10 ответвляющимися стволами длиной по 150-300 мкаждый. Благодаря этому приток нефти в несколько раз больше, чем в обычных скважинах (стоимость сооружения скважин возросла всего на 30-80 %). Важное преимущество таких скважин перед обычными в возможности более полного извлечения нефти из залежей. Так, три многозабойные скважины с горизонтальными стволами, пробурённые в 1957 вблизи г. Борислава, давали в сутки по 28-15 тнефти на истощённой залежи, которая эксплуатировалась с 1914 и на которой суточные дебиты обычных скважин не превышали 0,1-2 т.Применяя методы М. б., можно бурить скважины строго заданного направления, что используется при ликвидации открытого газонефтяного фонтана (проведение специальных скважин для соединения со стволом фонтанирующей скважины). Достижение в области М. б. - проведение разведочной скважины на Марковском нефтяном месторождении (Иркутская обл.) в 1968 с протяжённостью горизонтального ствола 630 м,при глубине по вертикали 2250 м.Скважина бурилась с такой же скоростью, как и обычная вертикальная, и была дороже всего на 23 %. Большая длина горизонтальных участков при М. б. дала возможность проводить скважины-гиганты ( рис. 2 ) с охватом большой площади залежи и с высокими дебитами нефти (это особенно важно для разработки труднодоступных залежей, например, при разработке шельфов, в заболоченных районах, в черте городов и т. п.). В СССР (1974) М. б. успешно проведено несколько десятков скважин на нефть, разрабатывается и испытывается скоростное М. б. глубоких горизонтальных скважин большой протяжённости (несколько км) .
Лит.:Григорян А. М., Вскрытие пластов многозабойными и горизонтальными скважинами, М., 1969. А. М. Григорян. 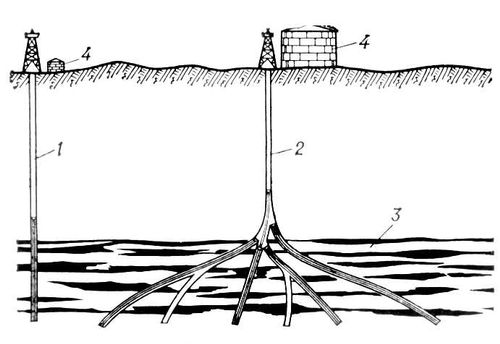
Рис. 1. Способы вскрытия пласта: 1 - обычная скважина; 2 - многозабойная скважина; 3 - продуктивный пласт нефти; 4 - резервуар для нефти. 
Рис. 2. Многозабойно-горизонтальная скважина-гигант: 1 - плавучая буровая установка; 2 - трубы; 3 - устье скважины; 4 - основной ствол; 5 - ответвления; 6 - нефтеносный пласт. Многозначная логика Многозна'чная ло'гика,раздел ,изучающий математические модели .Эти модели отражают две основные черты последней - множественность значений истинности высказываний и возможность построения новых, более сложных высказываний из заданных при помощи логических операций, которые позволяют также по значениям истинности исходных высказываний устанавливать значение истинности сложного высказывания. Примерами многозначных высказываний являются суждения с модальным исходом («да», «нет», «может быть») и суждения вероятностного характера, а примерами логических операций - логической связки типа «и», «или», «если..., то». В общем случае модели М. л. представляют собой обобщения .Важно отметить, что в алгебре логики высказывания принимают только два значения истинности («да», «нет»), в связи с чем она в общем случае не может отразить всего многообразия логических построений, встречающихся на практике. При достаточно широком толковании М. л. в неё иногда включают также логические . Исторически первыми моделями М. л. явились двузначная логика Дж. (называемая также алгеброй логики), трёхзначная логика Я. (1920) и m-значная логика Э. (1921). Изучение этих моделей составило важный этап в создании теории М. л. М. л. обладает определённой спецификой, состоящей в рассмотрении задач и подходов, возникающих при исследовании М. л. с позиций математической логики, теоретической и .Так, с позиций теоретической кибернетики, модели М. л. рассматриваются как языки, описывающие функционирование сложных управляющих систем, компоненты которых могут находиться в некотором числе различных состояний; а с точки зрения алгебры, модели М. л. представляют собой алгебраические системы, имеющие наряду с прикладным и чисто теоретический интерес. Построение моделей М. л. осуществляется по аналогии с построением двузначной логики. Так, индивид, высказывания логики, разбитые на классы с одним и тем же значением истинности, приводят к понятию множества Е- констант модели, которые фактически отождествляют все индивидуальные высказывания, заменяя их соответствующими значениями истинности; переменные высказывания - к переменным величинам x 1 , x 2, ..., которые в качестве значений принимают элементы из множества Е; логической связки - к множеству Мэлементарных функций (операций), которые, как и их аргументы, принимают значения из Е. Сложные высказывания, построенные из индивидуальных и переменных высказываний, а также логических связок, приводят к множеству < М> формул над М. Значение истинности из Есложного высказывания является функцией от соответствующих значений истинности высказываний, входящих в данное сложное высказывание. В модели эта функция приписывается формуле, соответствующей данному сложному высказыванию; говорят также, что формула реализуют эту функцию. Множество формул < М> приводит к множеству [ М] функций, реализуемых формулами из < М> и называемых суперпозициями над М. Множество [ М] называется замыканием множества М. Задание конкретной модели М. л. считается эквивалентным указанию множеств Е, М, < М> и [ М]; при этом говорят, что модель порождается множеством М. Эта модель называется формульной моделью, а также m-значной логикой, где mобозначает мощность множества Е. Своеобразие подхода математической кибернетики к М. л. состоит в рассмотрении моделей М. л. как управляющих систем. Элементарные функции при этом являются элементами, производящими определённые операции, а формулы интерпретируются как схемы, построенные из элементов и также осуществляющие переработку входной информации в выходную. Такого рода управляющие системы, известные в кибернетике как схемы из функциональных элементов, широко используются в теоретических и практических вопросах кибернетики. Вместе с тем существует ряд задач логики и кибернетики, который связан с изучением соответствий между множествами Ми [ М] и при котором роль множества < М> несколько затушёвывается, сводясь к способу определения второго множества по первому. В этом случае приходят к другой модели М. л., которая представляет собой алгебру, элементами которой являются функции, принимающие в качестве значений, как и их аргументы, элементы из Е. В качестве операций в этих алгебрах обычно используется специальный набор операций, эквивалентный в смысле соответствий Ми [ М] множеству формул, построенных из функций множества М, т. е. получению сложных функций из заданных путём подстановки одних функций вместо аргументов других. К числу задач, характерных для формульной модели М. л., относится задача «об описании», т. е. вопрос об указании для заданного множества М 2Н [ M 1] всех формул из < M 1>, реализующих функции из М 2. Частным случаем такой задачи является важный вопрос математической логики об указании всех формул, реализующих заданную константу, что, например, для исчисления высказываний эквивалентно построению всех тождественно истинных высказываний. Пограничным вопросом между математической логикой и алгеброй, примыкающим к задаче об описании, является задача о тождественных преобразованиях. В ней при заданном множестве Мтребуется выделить в некотором смысле простейшее подмножество пар равных (т. е. реализующих одну и ту же функцию) формул из < М>, позволяющее путём подстановки выделенных равных формул одной вместо другой получить из любой формулы все формулы, равные ей. Аналогичное место занимает один из важнейших вопросов для М. л. - т. н. проблема полноты, состоящая в указании всех таких подмножеств M 1заданного замкнутого, т. е. совпадающего со своим замыканием, множества М, для которых выполнено равенство [ M 1] = М, т. е. имеет место свойство полноты M 1в М. Глобальной задачей для М. л. является описание структуры замкнутых классов данной модели М. л. Характерный для теории управляющих систем вопрос о сложности этих систем естественно возникает и по отношению к формулам и функциям из М. л. Типичной при таком подходе является следующая задача о сложности реализации. На множестве всех элементарных формул некоторым способом вводится числовая мера (сложность формул), которая затем распространяется на множество всех формул, например, путём суммирования мер всех тех элементарных формул, которые участвуют в построении заданной формулы. Требуется для заданной функции указать ту формулу (простейшую), которая реализует эту функцию и имеет наименьшую сложность, а также выяснить, как эта сложность зависит от некоторых свойств рассматриваемой функции. Исследуются различные обобщения этой задачи. Широкий круг вопросов связан с реализацией функций формулами с наперёд заданными свойствами. Сюда относятся задача о реализации функций алгебры логики дизъюнктивными нормальными формами и связанная с этим задача о минимизации; а также задача о реализации функций формулами в некотором смысле ограниченной глубины (т. е. такими формулами, в которых цепочка подставляемых друг в друга формул имеет ограниченную длину, такое ограничение связано с надёжностью и скоростью вычислений). Решения всех перечисленных задач существенно зависят от мощности множества Еи множества М, порождающего заданную модель М. л. К числу наиболее важных примеров М. л. относятся конечнозначные логики (т. е. m-значные логики, для которых mконечно). Среди них наиболее глубоко исследован случай m= 1. Важнейшим результатом здесь является полное описание структуры замкнутых классов и получение для них важной информации по задаче о сложности реализации. Установлено, что при m> 2 у конечнозначных логик возникает ряд особенностей, существенно отличающих их от двузначного случая. Таковы, например, континуальность множества замкнутых классов (при m= 2 их счётное число), особенности решения задачи о сложности реализации и ряд других. Общим результатом для конечнозначных логик является эффективное решение задачи о полноте для замкнутых классов, содержащих все функции со значениями в Е. Решение остальных проблем для конечнозначных логик продвинуто в различной степени. Особая значимость конечнозначных логик связана ещё и с тем, что они позволяют описывать работу самых различных реальных вычислительных устройств и автоматов. Примерами другой М. л. являются счётнозначные и континуум-значные логики (т. е. такие m-значные логики, для которых мощность mявляется, соответственно, счётной или континуальной). Эти модели играют важную роль в математической логике, и в математическом анализе. К М. л. иногда относят и такие алгебры функций, в которых запас операций несколько отличается от указанного. Как правило, это достигается путём сужения описанного запаса или введения в операции некоторых функций рассматриваемой М. л. Лит.:Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б., Функции алгебры логики и классы Поста, М., 1966; Яблонский С. В., Функциональные построения в k-значной логике, «Тр. Матем. института АН СССР», 1958, т. 51, с. 5-142. В. Б. Кудрявцев. Многозначная функция
Многозна'чная фу'нкция,функция, принимающая несколько значений для одного и того же значения аргумента. М. ф. появляются при обращении однозначных функций, повторяющих свои значения. Так, функция
x
2принимает каждое положительное значение дважды (при значениях аргумента, различающихся только знаком); обращение её даёт двузначную функцию
Многозначность слова Многозна'чность сло'ва,полисемия, наличие у слова более чем одного значения, т. е. способность одного слова передавать различную информацию о предметах и явлениях внеязыковой действительности. Например, у слова горло 4 значения: передняя часть шеи; полость позади рта; верхняя суженная часть сосуда; узкий выход из залива, устье. Во многих языках, в том числе в русском, многозначные слова преобладают над однозначными. М. с. принято отграничивать от ,т. к. значения многозначного слова связаны общими семантическими элементами (семантическими признаками) и образуют определённое семантическое единство (семантическую структуру слова). Различаются первичные и вторичные (производные) значения, которые иногда понимаются как прямые и переносные значения. Первичные значения, как правило, наименее контекстно обусловленны. Соотношение между первичными и вторичными значениями с течением времени может меняться. У разных типов слов существуют различные типы М. с., например относительно регулярная и нерегулярная М. с. - слова, обозначающие населённые пункты (город, деревня, село, посёлок и т. д.), могут иметь в русском языке также значение «жители данного населенного пункта», т. е. следуют определённой семантической формуле, в то время как вторичные значения, например обозначения животных (лев, лиса и т. д.) в применении к людям индивидуальны. Особенности объединения значений в пределах одного слова во многом определяют своеобразие словарного состава каждого языка. Многозначными могут быть также грамматические формы слова и синтаксические конструкции. Лит.:Виноградов В. В., Основные типы лексических значений слова, «Вопросы языкознания», 1953, № 5; Ахманова О. С., Очерки по общей и русской лексикологии, М., 1957; Курилович Е., Заметки о значении слова, в его кн.: Очерки по лингвистике, пер. с польск., англ., франц., нем., М., 1962; Ьllmann S., The principles of semantics, 2 ed., Glasgow, 1959. Д. Н. Шмелев. Многозуб Многозу'б(Polyodon spathula), рыба семейства отряда осетрообразных. Многозубые белозубки Многозу'бые белозу'бки(Suncus), род млекопитающих семейства землероек отряда насекомоядных. Длина тела 3-15 см,хвоста - 2,5-10 см.Представитель рода - малая белозубкa (S. etruscus) - самое маленькое млекопитающее. Около 20 видов. Распространены в Африке, Южной Европе, Южной Азии на В. до Филиппин и Новой Гвинеи. Отдельные виды обитают на лугах и в заболоченных местах, иногда селятся в постройках человека. Питаются главным образом насекомыми, нередко мясом, хлебом. Активны ночью. Размножаются круглый год. В помёте 2-5 детёнышей. 1, 2, 3, 4, 5, 6, 7 |
|||||||||||||||||||||||||
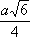
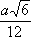
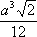
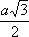
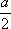
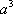
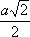
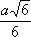
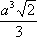
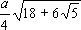
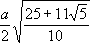
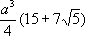
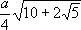
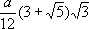
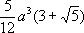
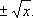 Функция sin
хпринимает каждое своё значение бесконечное множество раз; обращение её даёт бесконечнозначную функцию Arcsin
х. Существенную роль М. ф. играют в теории
комплексного переменного. В комплексной области
Функция sin
хпринимает каждое своё значение бесконечное множество раз; обращение её даёт бесконечнозначную функцию Arcsin
х. Существенную роль М. ф. играют в теории
комплексного переменного. В комплексной области
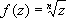 имеет
nзначений при любом
z¹ 0;
f(
z) = Ln
zпри
z¹ 0 - бесконечное число значений.
имеет
nзначений при любом
z¹ 0;
f(
z) = Ln
zпри
z¹ 0 - бесконечное число значений.