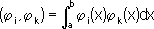Линдблад Бертиль

Ли'ндблад(Lindblad) Бертиль (26.11.1895, Эребру, - 25.6.1965, Стокгольм), шведский астроном. Директор Стокгольмской обсерватории (с 1927). Главные работы по динамике звёздных систем, изучению их структуры и фотометрическим наблюдениям спиральных галактик. Разработал также удобный метод определения светимостей звёзд (абсолютных звёздных величин) по снимкам их спектров. В 1948-1952 председатель Международного астрономического союза.

Линдгрен Астрид Анна Эмилия

Ли'ндгрен(Lindgren) Астрид Анна Эмилия (р. 14.11.1907, Виммербю), шведская писательница. Родилась в крестьянской семье. Первые книги Л. - «Бритт-Мари облегчает сердце» (1944) и 1-я часть повести «Пеппи Длинный чулок» (1945-1952, русский перевод 1968), нарушившей дидактические и сентименталистские традиции детской литературы Швеции. Автор книг для детей: «Мио, мой Мио!» (1954), «Малыш и Карлсон, который живёт на крыше» (1955, русский перевод 1957), «Карлсон, который живёт на крыше, опять прилетел» (1962, русский перевод 1965), «Снова появляется Карлсон, который живёт на крыше» (1968). В книгах «Знаменитый сыщик Калле Блюмквист» (1946, русский перевод 1959), «Расмус-бродяга» (1956, русский перевод 1963) Л. поднимает острые проблемы детской беспризорности. Написала трилогию: «Эмиль из Лённеберги» (1963, русский перевод 1969), «Новые проделки Эмиля из Лённеберги» (1966, русский перевод 1969) и «Жив ещё Эмиль из Лённеберги» (1970, русский перевод 1972). Повесть Л. «Мы на острове Сальткрока» (1964, русский перевод 1971) - о радостях и горестях современных детей. Многие книги Л. экранизированы. Героев книг Л. отличают непосредственность и изобретательность, а озорство в них сочетается с серьёзностью и пытливостью. Сказочное, фантастическое в книгах Л. соседствует с реальными картинами. В 1958 Л. присуждена Международная золотая медаль Х. К. Андерсена за гуманистический характер творчества.

  Соч.: Alla vi barn i Bullerbyn, 13 uppi., Stockh., 1962; Mera om oss barn i Bullerbyn, 3 uppi., Stockh., 1962; Salikons rosor, Stockh., 1967.

  Лит.:Брауде Л., Сказка и действительность в творчестве А. Линдгрен, в сборнике: О литературе для детей, в. 8, Л., 1963; её же, О творчестве Астрид Линдгрен, в кн.: Скандинавский сборник, в. 9, Тал., 1964; её же, Астрид Линдгрен детям и юношеству, в сборнике: Детская литература 1969, М., 1969; Фиш Г., У шведов, М., 1966.

  Л. Ю. Брауде.

Линдгрен Вальдемар

Ли'ндгрен(Lindgren) Вальдемар (14.2.1860, Швеция, - 3.11.1939, Брайтон, Массачусетс, США), американский геолог, исследователь рудных месторождений. В 1883 окончил Фрейбергскую горную академию. В 1883 переехал в Чили, а затем (1884) в США. С 1897 ассистент Станфордского университета, а с 1911 сотрудник Геологической службы США, в которой с 1905 исполнял обязанности главы секции драгоценных и цветных металлов, а с 1908 - начальника отдела металлов. С 1908 читал лекции в Массачусетсском технологическом институте; профессор и заведующий кафедрой экономической геологии (1912). Председатель отделения геологии и географии Национального научного совета США (1927). Л. участвовал в геологических исследованиях, связанных с деятельностью Северной тихоокеанской ж.-д. компании. С 1884 изучал рудные месторождения США, Норвегии, Швеции, Германии, Австрии, Италии, Австралии, Мексики, Чили и Боливии. Большая часть научных трудов Л. посвящена геологии рудных месторождений. Важнейшие труды Л. связаны с разработкой (в 1903) генетической классификации месторождений полезных ископаемых, в основу которой были положены физико-химические параметры (давление, температура), регулировавшие процесс формирования месторождений полезных ископаемых. Л. выделял следующие основные группы месторождений полезных ископаемых, возникшие: 1) на поверхности Земли при механических процессах концентрации минеральной массы в обстановке умеренных давления и температуры; 2) на дне поверхностных водоёмов при умеренной температуре и изменчивом давлении; 3) внутри горных пород при различных условиях температуры и давления. Среди последней группы Л. различал концентрации минеральных веществ, связанные с одновременным формированием горных пород (сингенетические), и залежи, возникшие после образования горных пород (эпигенетические) из магмы, магматических водных растворов и водных растворов, не связанных с магмой.

  Л. был членом Национальной АН США (с 1924 - её президентом), почётным членом академий и научных обществ ряда стран, президентом Международного геологического конгресса в 1933. Удостоен золотой медали Пенроза (1933) Геологического общества США.

  Соч. в рус, пер.: Минеральные месторождения, в. 1-3, М. - Л., 1934-35.

  Лит.: Graton L. С., Life and scientific work of Waldemar Lindgren, в кн.: Ore deposits of Western States. Lindgren volume, N. Y., 1933.

Линде Карл

Ли'нде(Linde) Карл (11.6.1842, Берндорф, - 16.11.1934, Мюнхен), немецкий физик и инженер. Получил степень доктора философии в Гёттингенском университете. В 1868-78 и 1892-1910 профессор Высшего технического училища в Мюнхене. В 1879 основал общество холодильных машин (в Висбадене). В 1895 сконструировал и построил первую промышленную установку для получения жидкого воздуха с использованием Джоуля - Томсона эффекта и усовершенствовал этот процесс введением предварительного охлаждения. В дальнейшем Л. работал над проблемой разделения на составные части смесей различных технически важных газов. В 1902 им создан, а в 1907 существенно усовершенствован непрерывно действующий ректификационный аппарат для разделения воздуха на компоненты.

  Лит.:Клод Ж., Жидкий воздух, пер. с франц., Л., 1930, с. 71-74; Carl von Linde. Zum 90. Geburtstag, B., 1932 (имеется библ. трудов Л.): Техника низких температур, М. - Л., 1964.

Линде (река в Якутской АССР)

Ли'нде, Линдя, река в Якутской АССР, левый приток р. Лена. Длина 804 км,площадь бассейна 20 тыс. км ².Берёт начало на В. Среднесибирского плоскогорья. В верховьях порожистая, далее течёт по Центрально-якутской низменности, очень извилиста. Питание главным образом снеговое и дождевое. Замерзает в начале октября, вскрывается во второй половине мая. Наиболее крупные притоки слева: Себирдёх, Серки, Делингдэ.

Линдеман Эдуард Эдуардович

Ли'ндеманЭдуард Эдуардович [1(13).1.1842, Нижний Новгород, ныне Горький, - 10(22).12.1897, Пулково], русский астроном. С 1868 работал на Пулковской обсерватории. Занимался исследованием блеска звёзд; на основе наблюдений 1870-83 Л. уточнил значение фотометрического коэффициента, т. е. отношение блеска звёзд двух соседних звёздных величин. В 1895 составил первый фотометрический каталог звёздного скопления hПерсея.

  Лит: Сто лет Пулковской обсерватории. Сб. ст., М. - Л., 1945.

Линденау Якоб

Линдена'уЯкоб (Яков Иванович) (около 1700-1795), русский путешественник и учёный, по происхождению швед. Участник 2-й Камчатской экспедиции (1737-46) под руководством Г. Ф. Миллера и И. Фишера; позже занимал административные должности в Сибири. Составил ряд географических и этнографических описаний местностей и народов Сибири (наиболее подробно «Описание якутов»). Все материалы Л. хранятся в рукописях (на немецком языке) в Центральном государственном архиве древних актов (Москва) и архиве Якутского филиала АН СССР.

  Лит.:Токарев С. А., История русской этнографии. М., 1966; Иванов Е. Ф., «Описание якутов» Я. И. Линденау, «Советская этнография», 1971, № 3.

Линдер Макс

Ли'ндер(Linder) Макс (настоящее имя и фамилия - Габриель Лёвьель, Leuvielle) (16. 12.1883, Сен-Лубес, Жиронда, - 30.10.1925, Париж), французский киноактёр. С 1905 снимался в кино. Его короткометражные комедии пользовались громадной популярностью, главным образом в 1910-13 («Макс и хинин», «Макс-тореадор», «Чемпион по боксу», «Макс женится», «Макс-гипнотизёр» и многих др.). Блестящий комедийный актёр, Л. создал образ элегантного, невозмутимого, влюбчивого повесы, часто попадающего в смешные положения. Творчество Л. ознаменовало во французском и мировом кино переход от бездумного комикования к бытовой достоверности, тонкой иронии. С триумфом выступал в США, Германии, Испании, России и др. Участвовал в 1-й мировой войне 1914-18. Последний фильм, имевший успех, - «Три пройдохи» (1922). Потеря популярности усилила нервное заболевание и Л. покончил с собой. В 1963 его дочь выпустила фильм, включавший лучшие работы Л., - «В компании Макса Линдера».

  Лит.:Юткевич С., Макс Линдер. Жизнь - работа - смерть, М. - Л., 1926; Юренев P., Макс Линдер, в сборнике: Комики мирового экрана, М., 1966.

Кадр из фильма «В компании Макса Линдера».

Линдерут Свен Харальд

Ли'ндерут(Linderot) (псевдоним до 1917 - Ларсон, Larsson) Свен Харальд (8.10. 1889, Скедеви, Эстерйётланд, - 7.4.1956, Стокгольм), деятель шведского рабочего движения. По профессии рабочий-стеклодув. В 1908-17 член Социал-демократической партии Швеции, примыкал к её левому крылу. В мае 1917 участвовал в основании Левой социал-демократической партии (в 1921 переименована в компартию Швеции, КПШ). В 1927-29 и с 1951 секретарь ЦК КПШ, в 1929-51 председатель КПШ. В 1938-49 депутат 1-й палаты риксдага и председатель парламентской фракции КПШ. Автор работ по вопросам шведского и международного коммунистического движения, шведской внутренней политики.

  Соч.: Bondefrеgan i Sverge, Stockh., 1943; Svensk arbetarrцrelse i brytningstid, Stockh., 1949.

Линди

Ли'нди(Lindi), город в Танзании, на берегу Индийского океана, в устье р. Лукуледи, в области Мтвара. 13,4 тыс. жителей (1967). Начальный пункт автодороги в глубь континента. Порт (вывоз с.-х. продукции). Торговый центр с.-х. района (акажу, агава, хлопчатник, просо, сорго, арахис). Пищевая промышленность. Рыболовство.

Линдман Соломон Арвид Ахатес

Ли'ндман(Lindman) Соломон Арвид Ахатес (19.9.1862, Упсала, - 9.12.1936, Кройдон), шведский государственный и военный деятель, промышленник, контр-адмирал (с 1907). Депутат 1-й (в 1905-11) и 2-й (с 1912) палат риксдага. В 1905 военно-морской министр, в 1906-11 премьер-министр. В 1907 под давлением общественного мнения провёл избирательную реформу, увеличившую число избирателей, но оставившую ряд существенных ограничений в избирательном праве. По инициативе Л. была начата милитаризация страны. В 1912-36 лидер Правой партии (консервативной). В 1912-23 председатель правления Шведского торгового банка. В 1917 министр иностранных дел, в 1928-30 премьер-министр.

Линдсей Джэк

Ли'ндсей(Lindsay) Джэк (р. 28.10.1900, Мельбурн, Австралия), английский писатель, учёный и общественный деятель. С 1926 живёт в Великобритании. Член компартии Великобритании с 1941. В исторических романах «1649 год» (1938), «Люди сорок восьмого гола» (1948, русский перевод 1959), «Костры в Смитфилде» (1950) и др. Л. на материале английской и мировой истории создал эпическое повествование о революционной борьбе народных масс. Большое место занимают в романах образы героев-мыслителей, участвующих в острейших конфликтах эпохи. Писатель соединяет документальную основу с символикой мифологического плана в традициях народного искусства (система «годового цикла»). В эпопее «Британский путь» - романы «Весна, которую предали» (1953, русский перевод 1955), «Твой дом» (1957, русский перевод 1961), «Маски и лица» (1963, русский перевод 1965) и др. - Л. рисует жизнь различных общественных слоев Великобритании после 1945. Для Л.-учёного характерны широта интересов, стремление (не всегда последовательно реализуемое) по-марксистски освещать проблемы мировой культуры. Он литературовед (книги о Дж. Беньяне, Ч. Диккенсе, Дж. Мередите), историк («Византия и Европа», 1950, «Уот Тайлер», 1964), искусствовед (монографии о Дж. Тёрнере, 1966, П. Сезанне, 1969, Г. Курбе, 1973), историк культуры («Сдвигающиеся скалы», 1965, «Клеопатра», 1971). Л. - активный борец за мир, участник 2-го и 3-го съездов СП СССР. В 1967 награжден орденом «Знак Почёта» за заслуги в пропаганде и переводах советской литературы на английский язык.

  Соч. в рус. пер.: Подземный гром, М., 1970; Письма, «Волга», 1969, № 9.

  Лит.:Ванчура З., Двадцать лет английского романа, М., 1968; Miller Е. М., Australian literature. A bibliography, Sydney - L., 1956.

  В. С. Вахрушев.

Линдси

Ли'ндси(Lindsey), административная часть графства Линкольншир в Великобритании. Площадь 3,9 тыс. км ²,население 470,5 тыс. человек (1971). Административный центр - Линкольн.

Лине Велта Мартыновна

Ли'неВелта Мартыновна (р. 28.8.1923, Рига), латышская советская актриса, народная артитска СССР (1973). Член КПСС с 1953. В 1946 окончила студию при Театре драмы Латвийской ССР; в труппе театра с 1945. Роли: Лиена («Земля зелёная» Упита), Кайва («Глина и фарфор» Григулиса), Лариса («Бесприданница» А. Н. Островского), Дездемона, Офелия («Отелло», «Гамлет» Шекспира), Зента («Сын рыбака» Лациса), Маргарита («Дама с камелиями» Дюма-сына), Анна («Анна Каренина» по Л. Н. Толстому), Таня («Таня» Арбузова) и др. Снималась в кино. Кандидат в члены ЦК КП Латвии с 1975. Депутат Верховного Совета СССР 9-го созыва, Верховного Совета Латвийской СССР 3-го и 4-го созывов. Государственная премия СССР (1948, 1951). Награждена орденом «Знак Почёта».

  Лит.:Балюнас В., Войткевич Н., Вельта Лине, М., 1955; Dzene L., Musu paaudzes aktieri portreti, Rїga, 1963.

Линеамент

Линеаме'нт(от лат. lineamentum - линия, контур), 1) выдержанные по направлению прямолинейные элементы рельефа и ландшафта, обычно связанные с трещинами и разломами земной коры. 2) Крупнейшие, глобального значения, зоны разломов, мегалинеаменты (по Е. Хиллсу, 1967). См. Глубинные разломы.

Линеаризация

Линеариза'ция(от лат. linearis - линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной. Методы Л. имеют ограниченный характер, т. е. эквивалентность исходной нелинейной системы и её линейного приближения сохраняется лишь при определённом «режиме» работы системы, а если система переходит с одного режима работы на другой, то следует изменить и её линеаризированную модель. Применяя Л., можно выяснить многие качественные и особенно количественные свойства нелинейной системы.

  Лит.:Попов Е. П., Пальтов И. П., Приближённые методы исследования нелинейных автоматических систем, М., 1960; Первозванский А. А., Случайные процессы в нелинейных автоматических системах, М., 1962; Основы автоматического управления, под ред. В. С. Пугачева, М., 1963.

Линеаризм

Линеари'зм(от лат. linearis - линейный), в многоголосной музыке - господство мелодической линии (см. Линеарность ) над гармонией. Представляет собой гипертрофию полифонического принципа, предусматривающего самостоятельность и относительное равноправие всех голосов. В сочинениях, позволяющих говорить о Л., самостоятельность каждого из голосов, автономия их мелодических линий приобретают главенствующее значение, тогда как ясность образуемых их сочетанием гармоний, логика гармонического развития, отчасти и объединение голосов единством метра, ритмических акцентов отступают на второй план. Л. обычно связан с абстрактным и односторонним пониманием мелодии как звуковысотной линии, воспринимаемой не столько слухом, сколько зрительно в нотной записи. Он выступает по преимуществу в творчестве представителей музыкального экспрессионизма,часто сочетается с додекафонией.

Линеарность

Линеа'рность, последование звуков различной высоты, образующее мелодическую линию. Понятие «Л.» акцентирует звуковысотную сторону мелодии, проявляющуюся в определённой ритмической организации. Абстрактное понимание мелодической линии ведёт к линеаризму.

Линёва Евгения Эдуардовна

Линёва(урожденная Паприц) Евгения Эдуардовна [28.12.1853 (9.1.1854), Брест-Литовск, ныне Брест, - 24.1.1919, Москва], русская фельклористка, певица (контральто), хоровой дирижёр. Пению училась в Вене у М. Маркези. Пела за рубежом и на сцене Большого театра в Москве. С 1870 участвовала в революционном движении, переписывалась с Ф. Энгельсом. Находясь в эмиграции (до 1896), организовывала хоры, пропагандировала русскую народную и классическую музыку. В 1897-1914 предприняла ряд фольклорных экспедиций (Поволжье, районы Центральной России, Украина, Кавказ), ввела в практику собирания русских и украинских песен звукозапись (фонограф), была пионером нотной расшифровки звукозаписей.

  Соч.: Великорусские песни в народной гармонизации, в. 1-2, М., 1904-09.

  Лит.:Канн-Новикова Е., Собирательница русских народных песен Евгения Линёва, М., 1952.

Линевич Николай Петрович

Лине'вич(Леневич) Николай Петрович [24.12.1838 (5.1.1839) - 10(23).4.1908, Петербург], русский военный деятель, генерал от инфантерии (1903), генерал-адъютант (1905). В 1855 поступил юнкером на военную службу. Участвовал в русско-турецкой войне 1877-78. С 1895 командующий войсками Южно-Уссурийского отдела. С 1900 командир корпуса. Во время подавления Ихэтуаньского восстания 1899-1901 возглавлял (в 1900-01) союзные войска империалистических государств и штурмом взял Пекин. С 1903 командующий войсками Приамурского военного округа и генерал-губернатор Приамурья. В начале русско-японской войны 1904-05 (до середины марта) временно командовал Маньчжурской армией, а с октября 1904 по март 1905 - 1-й Маньчжурской армией; с 3 марта 1905 главнокомандующий вооруженными силами на Дальнем Востоке. В февраля 1906 за недостаточно активную борьбу с революционным движением снят с должности. Оставил мемуары («Русско-японская война. Из дневников А. Н. Куропаткина и Н. П. Линевича», 1925).

Линёво

Линёво, посёлок городского типа в Жирновском районе Волгоградской области РСФСР. Расположен на левом берегу р. Медведица (приток р. Дон), в 14 кмк С.-В. от ж.-д. станции Медведица (на линии Балашов - Камышин). Консервный завод.

Линейка

Лине'йка, применяется для геометрических построений, линейных измерений и вычислений. На Л., как правило, нанесена шкала (или шкалы) с ценой деления, зависящей от назначения Л. На некоторых Л. для удобства пользования имеются различные справочные данные (значения единиц физических величин, таблица умножения и др.), а также специального приспособления, например на Л., применяемой в картографии, - перемещающиеся вдоль неё лупы. Для геометрических построений и измерений служат Л.: прямые, треугольные (см. Угольник ) ,фигурные (например, офицерская, штурманская, трафаретная и др.), а также лекала.Кроме того, в промышленности применяют Л. для измерения линейных размеров в определённых единицах (например, пункты в полиграфии). Л. используются для измерений в различных технологических целях. Например, с помощью усадочной линейки сравнивают нормативный и действительные размеры (в литейном, текстильном и др. производствах), поверочная линейка служит для проверки прямолинейности образующих и плоскостности поверхностей обработанных изделий и т. д. Для измерения больших длин и диаметров пользуются рулеткой. При необходимости переводить размеры из одного масштаба в другой применяют масштабную линейку. Для математических вычислений служит логарифмическая линейка.

  Г. Ю. Филановский.

Линейная алгебра

Лине'йная а'лгебра, наиболее важная в приложениях часть алгебры.Первым по времени возникновения вопросом, относящимся к Л. а., была теория линейных уравнений.Развитие последней привело к созданию теории определителей,а затем теории матриц и связанной с ней теории векторных пространств и линейных преобразований в них. В Л. а. входит также теория форм,в частности квадратичных форм,и частично теория инвариантов и тензорное исчисление.Некоторые разделы функционального анализа представляют собой дальнейшее развитие соответствующих вопросов Л. а., связанное с переходом от n-мерных векторных пространств к бесконечномерным линейным пространствам.

  Лит.:Александров П. С., Лекции по аналитической геометрии..., М., 1968; Курош А. Г., Курс высшей алгебры, 9 изд., М., 1968; Мальцев А. И., Основы линейной алгебры, 3 изд., М., 1970; Фаддеев Д. К., Фаддеева В. Н., Вычислительные методы линейной алгебры, 2 изд., М. - Л., 1963.

Линейная вектор-функция

Лине'йная ве'ктор-фу'нкция, функция f( x) векторного переменного х, обладающая следующими свойствами: 1) f( x + у) = f( x) + f( y) ,2) f(l x) =l f( x) (l - число). Л. в.-ф. в n-мерном пространстве вполне определяется значениями, принимаемыми ею для n линейно независимых векторов. Скалярную (принимающую числовые значения) Л. в.-ф. называют также линейным функционалом;в n-mepном пространстве она выражается линейной формой, f( x) = a ₁x ₁+ a ₂x ₂+... + a _nx _nот координат x ₁, x ₂,..., x _nвектора х. Примером скалярной Л. в.-ф. является скалярное произведение вектора х и некоторого постоянного вектора а:

  f( x) =( а, х) ,

  в пространстве, в котором определено скалярное произведение, всякая скалярная Л. в.-ф. имеет такой вид. Векторная (принимающая векторные значения) Л. в.-ф. определяет линейное или аффинное преобразование пространства и называется также линейным оператором,или аффинором. Векторная Л. в.-ф. у = f( x) в n-мерном пространстве выражается в координатах формулами:

  y ₁= a ₁₁x ₁+ a ₁₂x ₂+ ... + a _1nx _n,

  y ₂= a ₂₁x ₁+ a ₂₂x ₂+ ... + a _2nx _n,

  ...

  y _n= a _n1x ₁+ a _n2x ₂+ ... + a _nnx _n.

 Здесь числа a _ij( i, j = 1, 2,..., n) составляют матрицу векторной Л. в.-ф. Если определить сумму векторных Л. в.-ф. f( x) и g( x) как Л. в.-ф. f( x) + g( x) ,а произведение тех же функций, как Л. в.-ф. g{f( x) },то сумме и произведению векторных Л. в.-ф. будут соответствовать сумма и произведение соответствующих матриц. Примером векторной Л. в.-ф. является Л. в.-ф. вида:

  f( x) =( A ₁, х) a ₁+( А ₂, х) a ₂+... +( A _n, х) a _n,

 где A ₁, A ₂, ..., A _n, a ₁, a ₂, ... a _n- постоянные векторы; в n-мерном пространстве, в котором определено скалярное произведение, всякая векторная Л. в.-ф. может быть представлена в таком виде.

  Функцию нескольких векторных переменных, являющуюся Л. в.-ф. относительно каждого своего аргумента, называют полилинейной (билинейной, трилинейной и т. д.) вектор-функцией. Скалярное и векторное произведения двух переменных векторов могут служить примерами, соответственно скалярной и векторной билинейных вектор-функций. Полилинейные вектор-функции приводят к понятию тензора.О Л. в.-ф. (линейных функционалах и операторах) в бесконечномерном пространстве см. Функциональный анализ.

Линейная зависимость

Лине'йная зави'симость(матем.), соотношение вида

  C ₁₁u ₁+ C ₂u ₂+ ... + C _nu _n= 0, (*)

  где С ₁, C ₂, ..., C _n- числа, из которых хотя бы одно отлично от нуля, а u ₁, u ₂, ..., u _n- те или иные матем. объекты, для которых определены операции сложения и умножения на число. В соотношение (*) объекты u ₁, u ₂, ..., u _nвходят в 1-й степени, т. е. линейно; поэтому описываемая этим соотношением зависимость между ними называется линейной. Знак равенства в формуле (*) может иметь различный смысл и в каждом конкретном случае должен быть разъяснён. Понятие Л. з. употребляется во многих разделах математики. Так, можно говорить о Л. з. между векторами, между функциями от одного или нескольких переменных, между элементами линейного пространства и т. д. Если между объектами u ₁, u ₂, ..., u _nимеется Л. з., то говорят, что эти объекты линейно зависимы; в противном случае их называется линейно независимыми. Если объекты u ₁, u ₂, ..., u _nлинейно зависимы, то хотя бы один из них является линейной комбинацией остальных, т. е.

  u ₁=a ₁u ₁+ ... +a _i-1u _i-1+a _i+1u _i+1+ ... +a _nu _n.

 Непрерывные функции от одного переменного

  u ₁=j ₁ ( х) , u ₂=j ₂ ( х) , ..., u _n=j _n ( x) называются линейно зависимыми, если между ними имеется соотношение вида (*), в котором знак равенства понимается как тождество относительно х. Для того чтобы функции j ₁ ( x) ,j ₂ ( x) , ...,j _n ( x) ,заданные на некотором отрезке а Ј х Ј b, были линейно зависимы, необходимо и достаточно, чтобы обращался в нуль их определитель Грама

  где

  i, k= 1,2, ..., n.

  Если же функции j ₁(x), j ₂(x), ..., j _n(x) являются решениями линейного дифференциального уравнения,то для существования Л. з. между ними необходимо и достаточно, чтобы вронскиан обращался в нуль хотя бы в одной точке.

   Линейные формы от m переменных

  u ₁= a _i1x ₁+ a _i2x ₂+ ... + a _imx _m

 ( i= 1, 2, ..., n)

  называются линейно зависимыми, если существует соотношение вида (*), в котором знак равенства понимается как тождество относительно всех переменных x ₁, x ₂, ..., x _m. Для того чтобы n линейных форм от n переменных были линейно зависимы, необходимо и достаточно, чтобы обращался в нуль определитель

D=   

Линейная подстановка

Лине'йная подстано'вка, замена переменных x ₁, x ₂,..., x _mпеременными y ₁, y ₂, ..., y _nпо формулам

  x ₁= a _i1y ₁+ a _i2y ₂+ ... + a _iny _n,

  i= 1,2, ..., m,