 |
|
Популярные авторы:: Азимов Айзек :: Борхес Хорхе Луис :: Толстой Лев Николаевич :: Горький Максим :: Грин Александр :: Раззаков Федор :: Сименон Жорж :: Картленд Барбара :: Чехов Антон Павлович :: Лесков Николай Семёнович Популярные книги:: Справочник по реестру Windows XP :: Чтобы мы не помнили :: Дюна (Книги 1-3) :: О дубляже :: Памятные встречи :: The Boarding House :: Индийские рассказы :: О культе книг :: Сашка :: Жизнь, Вселенная и все остальное |
Большая Советская Энциклопедия (ГР)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ГР) - Чтение (стр. 21)
Тепловыделяющие элементы
размещают в цилиндрических каналах графитовой кладки. Активная зона заключена в прочный корпус, стальной или из предварительно напряжённого железобетона, несущий давление теплоносителя. Иногда активная зона вместе с парогенераторами и газодувками заключается в единый корпус из железобетона. Защита от нейтронного излучения, которой окружена активная зона, предохраняет парогенераторы и газодувки от активации, так что они доступны для ремонта при остановленном реакторе. Внутренняя поверхность бетонного корпуса для защиты его от перегрева покрывается теплоизоляцией. Кроме того, применяют специальные системы охлаждения.
Г.-г. р. являются основные типом реакторов в ядерной энергетике Великобритании и Франции. АЭС с такими реакторами построены также в Италии, Японии. В США введена в строй АЭС с Г.-г. р., в котором в качестве теплоносителя применяется гелий. Лит.:см. при ст. Ядерный реактор . Ю. И. Корякин. Графитопласты Графитопла'сты,пластмассы, в которых наполнителями служат природный или искусственный графит или карбонизованные продукты (коксы, термоантрацит и др.). Связующими в Г. могут быть феноло-альдегидные смолы , полиамиды , фторопласты , эпоксидные смолы и др. Г. применяют для изготовления различных фильтров, поршневых колец и др. уплотнителей, электродов в электрофильтрах, литьевых форм, вкладышей подшипников скольжения, шестерней и др. Г. получают в виде пресс-порошков (например, антегмит ), гранул и заливочных компаундов (например, эпоксилит). Изделия из пресспорошков изготовляют горячим прессованием. Гранулированные Г. хорошо перерабатываются в изделия литьём под давлением . Свойства Г. разнообразны и зависят от вида наполнителя и связующего. Антегмит стоек к тепловым ударам, но обладает низкой механической прочностью и хрупкостью. Изделия из антегмита хорошо обрабатываются режущими и абразивными инструментами. Заливочные компаунды обладают высокой адгезией ко многим материалам и хорошей износостойкостью. Однако по теплопроводности они уступают антегмиту. Гранулированные Г., получаемые на основе полиамидов и фторопласта-4, обладают высокой износостойкостью, а также масло-, бензо- и щелочестойкостью. К недостаткам этих Г. относят низкую теплопроводность и теплостойкость, а также значительное водопоглощение. Графическая идентификация Графи'ческая идентифика'цияв криминалистике, отождествление личности по письму (почерку), т. е. установление исполнителя (автора) путём сравнительного исследования признаков почерка, отобразившихся в документе, исполнитель которого неизвестен, и признаков почерка, имеющихся в образцах, написанных подозреваемыми. Объектами Г. и. являются документы, имеющие значение вещественных доказательств по уголовному делу. Основой Г. и. является то, что всякое письмо имеет две стороны: смысловую (содержание, стиль, манера изложения, лексика и др. особенности письменной речи) и графическую (почерк как система выработанных двигательных актов, необходимых для автоматизированного скорописного исполнения букв, слов, цифр, знаков препинания). В основе процесса формирования почерка (письма) лежат навыки (технической, графической, письменной речи), относящиеся к сложным механизмам высшей нервной деятельности человека. Закономерности формирования т. н. динамического стереотипаупишущего лица обусловливают индивидуальность и относительную устойчивость выработанных признаков почерка, которые запечатлеваются в рукописных текстах, подписях и в которых проявляется индивидуальная совокупность графических навыков, присущих данному лицу. Идентификационные признаки письма (почерка) в целях Г. и. классифицируются: на признаки письменной речи - особенности грамматические (в т. ч. ошибки в словах, в построении предложений и расстановке знаков препинания), лексические [запас слов и особенности словарного состава, например архаизмы, неологизмы, варваризмы (иностранные слова), диалектизмы (слова из местного говора), профессионализмы (характерные для данной профессии), жаргон (условный язык, например «блатная музыка» профессиональных преступников)]; на признаки почерка - топографические (привычные особенности размещения на бумаге текста и его частей - поля, абзацы, интервалы между словами, строками, подписи, даты и т. п.), общие признаки, характеризующие письменно-двигательный навык всей системы письменных движений (выработанность почерка, его размер, наклон, связность, нажим), частные признаки, которые характеризуют индивидуально-устойчивые письменные навыки при автоматизированном исполнении отдельных письменных знаков и их деталей. При проведении Г. и. учитывается неразрывность смысловой и двигательной стороны письма. Г. и. составляет основу графической экспертизы (см. Экспертиза судебная ), которая осуществляется в криминалистических экспертных учреждениях (научно-исследовательских институтах и лабораториях судебной экспертизы) по постановлениям следственно-прокурорских органов или по определению суда. См. также Почерковедение судебное .
Лит.:Буринский Е. Ф., Судебная экспертиза документов, производство ее и пользование ею, СПБ, 1903; Манцветова А. И., Мельникова Э. Б., Орлова В. Ф., Теория и практика криминалистической экспертизы. Экспертиза почерка, М., 1961; Ланцман Р. М., Кибернетика и криминалистическая экспертиза почерка, М., 1968. А. И. Винберг. Графическая статика Графи'ческая ста'тика,графостатика, учение о графических методах решения задач статики . Методами Г. с. путём соответствующих геометрических построений могут определяться искомые силы, изгибающие моменты, центры тяжести и моменты инерции плоских фигур и др. С использованием Д'Аламбера принципа методы Г. с. могут применяться к решению задач динамики . Г. с. пользуются в строительной механике при расчётах балок, ферм и др. конструкций, а также при расчётах усилий в различных деталях механизмов и машин. По точности расчётов методы Г. с. значительно уступают аналитическим (численным) методам и с появлением ЭВМ утратили былое значение. С. М. Тарг. Графические вычисления Графи'ческие вычисле'ния,методы получения численных решений различных задач путём графических построений. Г. в. (графическое умножение, графическое решение уравнений, графическое интегрирование и т. д.) представляют систему построений, повторяющих или заменяющих с известным приближением соответствующие аналитические операции. Графическое выполнение этих операций требует каждый раз последовательности построений, приводящих в результате к графическому определению искомой величины. При Г. в. используются графики функций. Г. в. находят применение в приложениях математики. Достоинства Г. в. - простота их выполнения и наглядность. Недостаток - малая точность получаемых ответов. Однако в большом числе задач, особенно в инженерной практике, точность Г. в. вполне достаточна. Графические методы с успехом могут быть использованы для получения первых приближении, уточняемых затем аналитически. Иногда Г. в. называются вычисления, производимые при помощи номограмм. Это не совсем правильно, т. к. номограммы являются геометрическими изображениями функциональных зависимостей и не требуют для нахождения численных значений функции каких-либо построений (см. Номография ). Вычисление алгебраических выражений. Числа при Г. в. обычно изображаются направленными отрезками на прямой. Для этого выбирают единичный отрезок (длина его называется масштабом построения). Одно из направлений на прямой принимают за положительное. В этом направлении откладывают отрезки, изображающие положительные числа; отрицательные числа изображаются отрезками, имеющими противоположное направление. На рис. 1 показаны отрезки M 0M, A 0Aи B 0B, соответствующие числам 1, 3 и -4 (положительное направление здесь слева направо). Для нахождения суммы чисел соответствующие им отрезки откладывают на прямой один за другим так, чтобы начало следующего совпадало с концом предыдущего. Отрезок, началом которого является начало первого отрезка и концом - конец последнего, будет изображать сумму. Разность чисел находят, строя сумму отрезка, изображающего первое число, и отрезка, изображающего число, противоположное второму. Умножение и деление осуществляют построением пропорциональных отрезков, которые отсекают на сторонах угла параллельные прямые ( MAи BCна рис. 2 ). Так построены отрезки 1, а, би с, длины которых удовлетворяют соотношению а: 1 = с: b, откуда с= аbили b= с/а; следовательно, зная два из трёх отрезков a, bи с, всегда можно найти третий, т. е. можно построить произведение или частное двух чисел. При этом построении единичные отрезки на прямых OBи OCмогут быть различными. Комбинируя действия умножения и сложения, графически вычисляют суммы произведений вида a 1 x 1+ a 2 x 2+ ... + a n x n и взвешенное среднее ( a 1 x 1+ ... + a n x n)/( a 1+ ... + а 2). Графическое возведение в целую степень заключается в последовательном повторении умножения. Построение значений многочлена f( x) = a 0 x n+ a 1 x n-1+ ... + a n-1 x+ a n основано на представлении его в виде f( x) = {[( a 0 x+ a 1) х+ а 2] х+ ...} х+ а n и последовательном графическом выполнении действий, начиная с выражения, заключённого во внутренние скобки. Графическое решение уравнения f( x) = 0 заключается в вычерчивании графика функции у= f( x) и нахождении абсцисс точек пересечения кривой с осью Ox, которые и дают значения корней уравнения. Иногда решение можно значительно упростить, если представить уравнение в виде j 1( x) = j 2( x) и вычертить кривые y= j 1( x) и y= j 2( x). Корнями уравнения будут значения абсцисс точек пересечения этих кривых (на рис. 3 показано нахождение корня x 0). Так, для решения уравнения третьей степени
z
3+
az
2+
bz+
c= 0 его приводят к виду
x
3+
px+
q= 0 заменой
z=
х - а/3, затем уравнение представляют в виде
x
3= -
px - qи вычерчивают кривую
у=
х
3и прямую
у=-
px - q. Точки их пересечения определяют корни
x
1,
x
2,
x
3уравнения. Построение удобно тем, что кубическая парабола
у=
х
3
остаётся одной и той же для всех уравнений третьей степени. На
рис. 4
решено уравнение
x
3- 2,67
x- 1 = 0. Его корни
x
1= -1,40,
x
2=
-0,40,
x
3= 1,80. Аналогично решается уравнение четвёртой степени
z
4+
az
3+
bz
2+
cz+
d= 0. Подстановкой
z=
x - a/4 его приводят к виду
x
4+
px
3+
qx+
s= 0
и затем переходят к системе уравнений:
у=
х
2, (
х – х
0)
2+ (
у - у
0)
2=
r
2, вводя переменное
y. Здесь
x
0=
-q/2,
у
0= (1 –
р)/2 и
Графическое интегрирование.Вычисление определенного интеграла
Графическое дифференцирование. График производной можно строить по значениям тангенса угла наклона касательной к графику данной функции в различных его точках. Точность такого построения мала из-за больших погрешностей при определении направлений касательных. График производной строят также по секущим, повторяя в обратном порядке процесс графического интегрирования, изображенный на
рис. 7
. Для этого график функции (
рис. 8
) разбивают на части прямыми, параллельными оси
Оуи проведёнными через равные расстояния D
x.Через точки деления
A
1,
A
2, ... проводят отрезки
AB
1,
A
2
B
2, …, параллельные оси
Ox. Отрезки
B
1
A
1,
B
2
A
2, ...
равны соответствующим приращениям функции. Их откладывают от оси
Ox. По полученным точкам
Графическое интегрирование дифференциальных уравнений.Дифференциальное уравнение первого порядка dy/ dx= f( x, у) определяет на плоскости поле направлений. Задача интегрирования уравнения заключается в проведении кривых, касательные к которым имеют направления поля. Различные приёмы графического интегрирования состоят в последовательном построении интегральных кривых по касательным, направления которых заданы, и в известной мере повторяют численные методы интегрирования (см. Приближённое решение дифференциальных уравнений). Лит.:Головинин Д. Н., Графическая математика, М. - Л., 1931; Рунге К., Графические методы математических вычислений, пер. с нем., М. - Л., 1932. М. В. Пентковский. 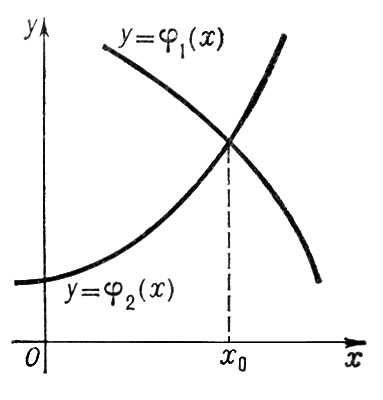
Графическое решение уравнения j 1( x) = j 2( x). 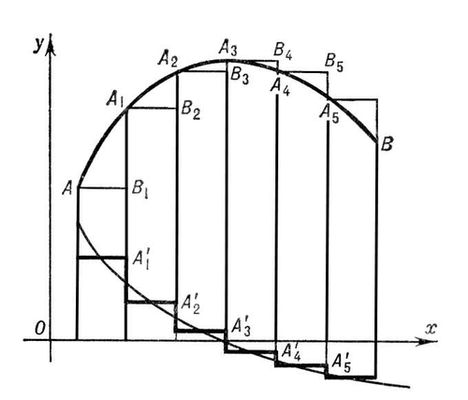
Рис. 8. Графическое дифференцирование. 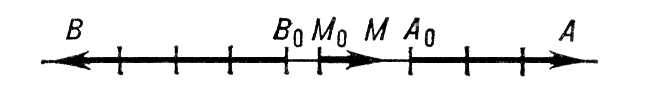
Рис. 1. Изображение чисел 1, 3 и -4 направленными отрезками на прямой. 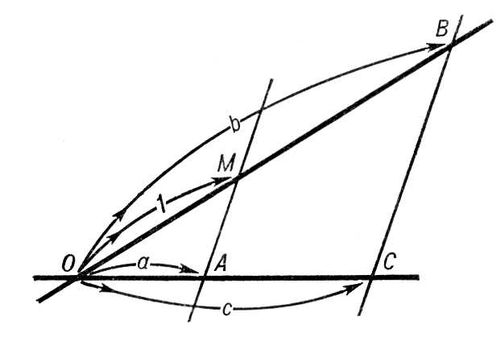
Рис. 2. Графическое умножение и деление: с= аb, b= с/ а. 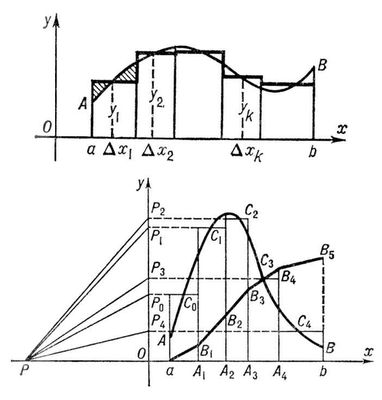
Рис. 6-7. Графическое интегрирование. 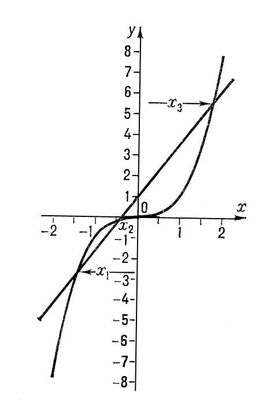
Рис. 4. Графическое решение кубического уравнения x 3- 2,67 х- 1 = 0. 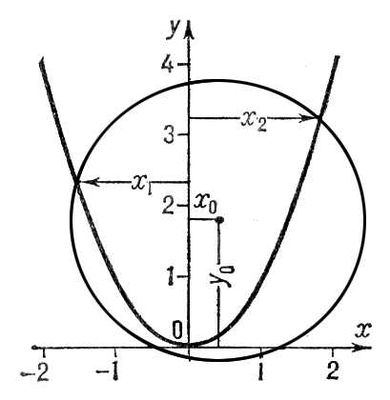
Рис. 5. Графическое решение уравнения 4-йстепени: x 4- 2,6 x 2- 0,8 x- 0,6 = 0. Графические методы Графи'ческие ме'тодыв управлении производством, совокупность способов условного (графического) изображения какого-либо организационного или управленческого явления на производстве. Впервые применены американскими инженерами ф. У. Тейлором и Г. Л. Гантом в начале 20 в. в качестве одного из методов организации руководства производством. В СССР Г. м. в управлении производством начали применять в 20-х гг. С помощью Г. м. решаются задачи моделирования процессов управления, выявляются и рационализируются взаимосвязи между различными факторами, определяются расчётные показатели и нормативы, выполняются контроль и учёт, группировка и классификация хозяйственных операций, информация представляется в наглядном виде. В управлении производством используются графики иллюстративно-информационные, оперативные, аналитические и расчётные. Иллюстративно-информационные содержат строго подобранные и предварительно проанализированные данные, отражающие фактическое состояние управляемых процессов ( рис. 1 , 2 и 8, А); оперативные графики служат для быстрого принятия решений и содержат для этого всю сумму информации на определенный момент ( рис. 8 , Б); аналитические графики содержат сведения, полученные после логической и математической обработки данных ( рис. 3 ); расчётные графики (например, номограммы ) несут информацию, позволяющую получать функцию, зависящую от большого числа переменных. В Г. м. различаются объекты графирования (например, динамика брака) и форма передачи идеи (диаграмма точечная, столбиковая, ломаная кривая и др.). По этим признакам графики, применяемые в управлении производством, можно разделить на следующие группы. 1) Графики, отражающие состав объекта и взаимосвязи его частей. К ним относятся классификационные и структурные схемы ( рис. 1 , 2 ), табличные оргасхемы, схемы потоков информации ( рис. 3 ) и схемы рабочих процессов ( рис. 8 , В). Эта группа графиков используется для анализа различных показателей производства: затрат рабочего времени, производств, брака по причинам и виновникам, документооборота и др. 2) Графики изменения управляемого процесса во времени и пространстве. Эта группа включает гармонограммы, учётно-контрольные и плановые графики ( рис. 4 , 5 ), планы объектов на местности, планировки оборудования и рабочих мест ( рис. 6 ), циклограммы ( рис. 8 , В). Основное назначение графиков этой группы - оперативно-календарное планирование, учёт и организация движения производства. 3) Графики функциональных зависимостей между отдельными параметрами (графики сравнения структур и параметров, рис. 7). Такого рода графики используются, в основном, для разработки нормативов, в статистическом учёте и анализе хода производства в планируемом периоде (квартал, полугодие, год). 4) Расчётные графики (номограммы и шкалограммы) служат для упрощения расчётов трудовых, материальных и календарно-плановых нормативов, а также различных математических расчётов: перевода абсолютных величин в проценты, расчёта размера партий и т.п. 5) Смешанные графики - балансовые ( рис. 8 ) и сетевые графики используют для анализа хода производства одновременно по нескольким параметрам, для контроля «узких» мест и оптимизации планирования. По форме передачи идеи графики могут иметь разнообразный вид: точечные ( рис. 5 ), столбиковые ( рис. 8 , Б), прямые, ломаные и кривые линии, круговые диаграммы ( рис. 2 ) и др. Графики, применяемые в управлении производством, отличаются усложнённой и комбинированной формой. Лит.:Герчук Я. П., Графические методы в статистике, М.. 1968; его же. Графические методы планирования и учета производства, М., 1935; его же. Графические методы управления производством, в кн.: Оргатехника в управлении и планировании производства, М., 1949, с. 102-203; Дейнеко О. А., Графические методы в управлении производством, в кн.: Научные основы управления производством, М., 1966; Организация производства на промышленных предприятиях США. [Справочник], т. 2, пер. с англ., М., 1961 (раздел: Графики Гантта); Шмид К. Ф., Руководство по графическим изображениям, пер. с англ., под ред. Я. П. Герчука, М., 1960; Кнеппель Ч.Э., Графические методы управления предприятием, 2 изд., пер. с англ., Л. - М., 1931; Вызов Л. А., Методы графических изображении. Курс лекций, М. - Л., 1930. В. П. Беспалов. 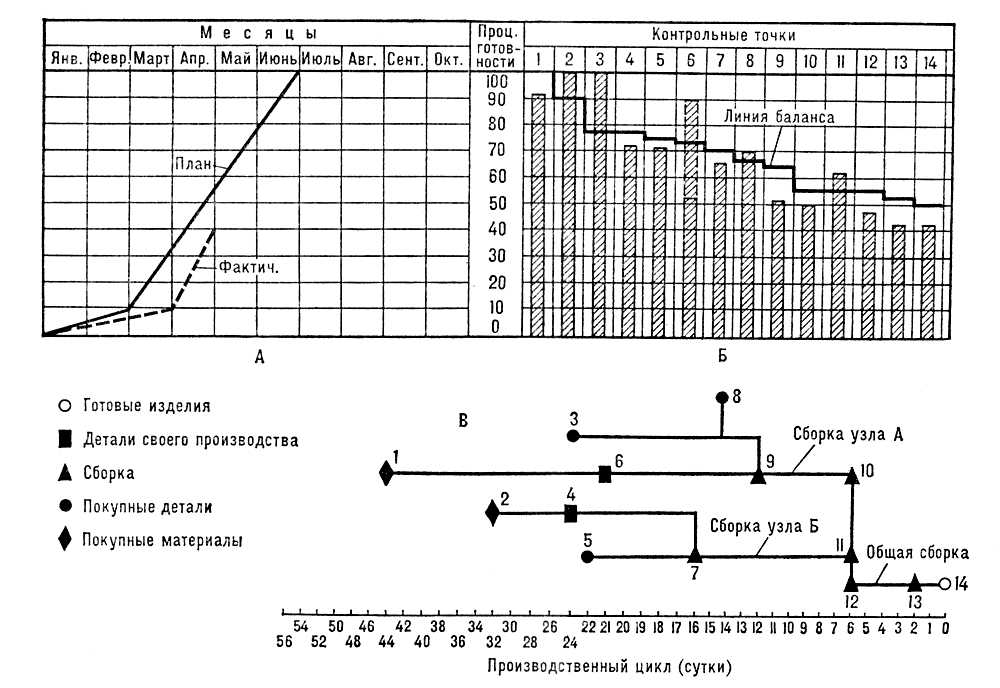
Рис. 8. Балансовый график контроля выполнения плана предприятия. А - учётно-плановый график. Б - собственно балансовый график, В - циклограмма. Балансовый график (Б) показывает степень готовности изделия на начало мая месяца. Плановый процент готовности указан столбиками в контрольных точках циклограммы. Так, на конец апреля для узла Б должно быть изготовлено 72% деталей собственного производства (см. точку 4 на графиках Б и В), а фактически уровень производства достиг 77% Выполнение плана (график А) в целом по изделию оказалось ниже нормы (40% против 56% по плану). 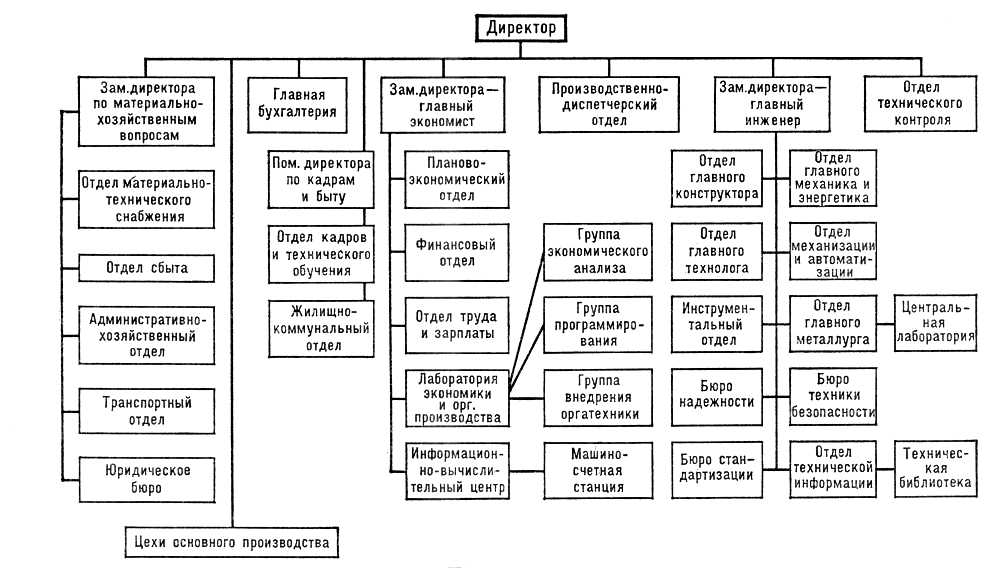
Рис. 1. Структурная схема функциональной организации управления предприятием. Показывает состав подразделений и их взаимосвязи в процессе управления предприятием. 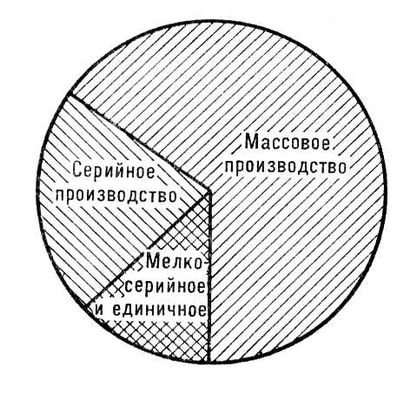
Рис. 2. Удельный вес продукции по типам производства на станкостроительном заводе. 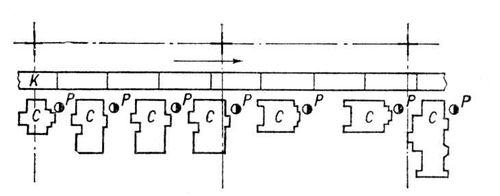
Рис. 6. Схема планировки конвейерной поточной линии: К - конвейер, С - станки, Р - рабочие. 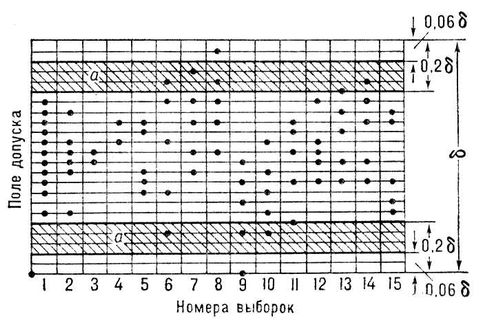
Рис. 5. Карта статистического контроля размера деталей по методу индивидуальных значений; d - поле допуска; а - предупредительные зоны верхней и нижней границ поля допуска. Карта - оперативный документ, с помощью которого прогнозируются отклонения от нормального хода производства (отклонения фактических размеров детали от границ поля допуска). 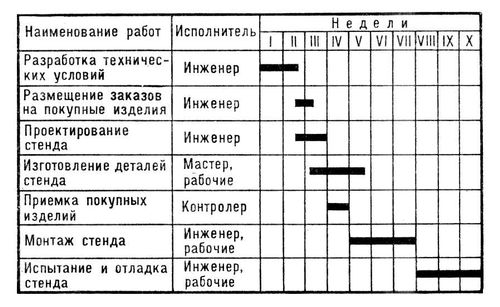
Рис. 4. Плановый график подготовки производства и изготовления испытательного стенда. Служит основанием для определения исполнителей и сроков выполнения всей номенклатуры работ. 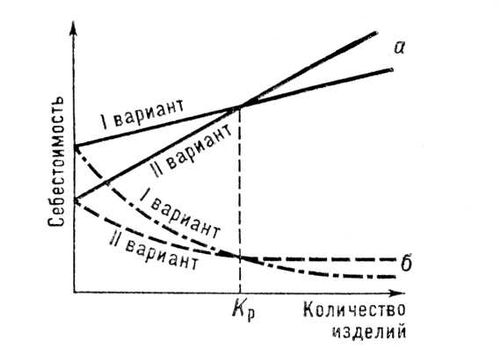
Рис. 7. График зависимости себестоимости продукции от годового выпуска: а - себестоимость годового выпуска, б - одного изделия, при разных вариантах технологического процесса; К р- критическое количество изделий, при котором оба технологических варианта равноценны. С помощью этого графика устанавливаются условия, при которых каждый из вариантов технологического процесса наиболее экономичен. При плане выпуска, меньшем К, II вариант процесса потребует меньше затрат и даст более низкую себестоимость изделий. 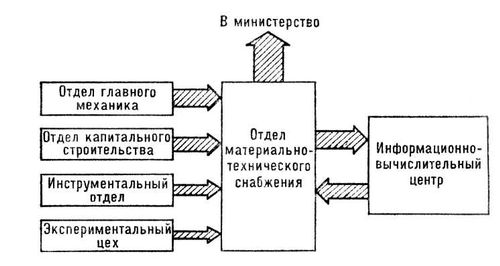
Рис. 3. Схема потока информации по материально-техническому снабжению предприятия. ...графия ...гра'фия(от греч. grapho - пишу, черчу, рисую), часть сложных слов, означающих: 1) название науки, изучающей, описывающей предмет, указанный в первой части слова (например, география, историография). 2) Название графического способа воспроизведения чего-либо при помощи записи, чертежа, рисунка, печатания (например, каллиграфия, стенография, литография), а также предприятия, в котором применяются подобные способы (например, типография). 3) Тематический характер научного произведения, посвященного определенной проблеме (монография). Графо... Графо...(от греч. grapho - пишу, черчу, рисую), составная часть сложных слов, означающая: относящийся к письму, почерку, черчению, рисованию (например, графология). Графов теория Гра'фов тео'рия,раздел конечной математики , особенностью которого является геометрический подход к изучению объектов. Основное понятие теории - граф. Граф задаётся множеством вершин (точек) и множеством рёбер (связей), соединяющих некоторые (а может быть, и все) пары вершин. При этом пары вершин могут соединяться несколькими ребрами. Примеры графов: множество городов (вершины графа), например Московской области, и соединяющие их дороги (ребра графа); элементы электрической схемы и провода, соединяющие их. На рис. 1 изображен граф, вершинами которого являются станции городского метрополитена, а ребрами - пути, соединяющие соседние станции (одна из задач: указать какой-либо маршрут от станции Ак станции В). Граф называется ориентированным, если на ребрах задана ориентация, т. е. указан порядок прохождения вершин. Наконец, в Г. т. изучаются графы, у которых ребрам приписаны какие-либо веса (или символы), а также графы, в которых выделены особые вершины, называются полюсами. Примеры: диаграмма состояний автомата, сеть ж.-д. путей с указанием на дугах их длин или пропускных способностей. На рис. 2 приведена схема автомобильных дорог между Москвой и Таллином; надо, например, выбрать маршрут минимальной общей длины пути из Москвы в Таллин (эти два города - полюсы сети); сравнение двух маршрутов Москва - Ленинград - Таллин и Москва - Витебск - Рига - Таллин показывает, что путь через Ленинград короче (1049 км). Одной из первых работ по Г. т. можно считать работу Л. Эйлера (1736), относящуюся к решению головоломок и математических развлекательных задач. Первые глубокие результаты были получены в 1-й половине 20 в. в связи с решением задач построения электрических цепей и подсчёта химических веществ с различными типами молекулярных соединений. Однако широкое развитие Г. т. получила лишь с 50-х гг. в связи со становлением кибернетики и развитием вычислительной техники, когда Г. т. существенно обогатилась и новым материалом, и новыми подходами и когда началось систематическое изучение графов с разных точек зрения (структурной, информационной и т. д.). Именно в это время формулировались проблематика и методы Г. т. Г. т. находит применение в теории программирования и при построении вычислительных машин, в изучении физических, химических и технологических процессов, в решении задач планирования, в лингвистических и социологических исследованиях и т. д. Г. т. имеет тесные связи как с классическими, так и с новыми разделами математики; это - топология, алгебра, комбинаторный анализ, теория чисел, теория минимизации булевских функций. Г. т. включает большое число разнообразных задач. Одни из них группируются в отдельные направления, другие стоят более изолированно. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67 |
|||||||
 Первое уравнение даёт на плоскости параболу, одну и ту же для всех уравнений четвёртой степени, второе - окружность радиуса
г, координаты центра
x
0,
y
0которой легко подсчитать по коэффициенту данного уравнения. На
рис. 5
решено уравнение
x
4
-2,6
x
2- 0,8
х- 0,6 = 0 (для него
x
0= 0,4;
y
0= 1,8,
r= 2). Его корни
x
1=
-1,55,
x
2= 1,80. Как видно из
рис.
, уравнение др. действительных корней не имеет.
Первое уравнение даёт на плоскости параболу, одну и ту же для всех уравнений четвёртой степени, второе - окружность радиуса
г, координаты центра
x
0,
y
0которой легко подсчитать по коэффициенту данного уравнения. На
рис. 5
решено уравнение
x
4
-2,6
x
2- 0,8
х- 0,6 = 0 (для него
x
0= 0,4;
y
0= 1,8,
r= 2). Его корни
x
1=
-1,55,
x
2= 1,80. Как видно из
рис.
, уравнение др. действительных корней не имеет.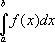 основано на замене графика подинтегральной функции
y=
f(
x) ступенчатой ломаной. На
рис. 6
изображена криволинейная трапеция
aABb, площадь которой численно равна вычисляемому интегралу. Для построения ломаной криволинейную трапецию разрезают прямыми, параллельными оси
Оу, на ряд полос - элементарных криволинейных трапеций. В каждой из них отрезок кривой заменяют отрезком, параллельным оси
Ox, так, чтобы получающиеся прямоугольники имели примерно ту же площадь, что и соответствующие элементарные криволинейные трапеции (ломаная изображена на
рис. 6
жирной линией). Площадь, ограниченная ломаной, равна сумме площадей построенных прямоугольников, т. е.
основано на замене графика подинтегральной функции
y=
f(
x) ступенчатой ломаной. На
рис. 6
изображена криволинейная трапеция
aABb, площадь которой численно равна вычисляемому интегралу. Для построения ломаной криволинейную трапецию разрезают прямыми, параллельными оси
Оу, на ряд полос - элементарных криволинейных трапеций. В каждой из них отрезок кривой заменяют отрезком, параллельным оси
Ox, так, чтобы получающиеся прямоугольники имели примерно ту же площадь, что и соответствующие элементарные криволинейные трапеции (ломаная изображена на
рис. 6
жирной линией). Площадь, ограниченная ломаной, равна сумме площадей построенных прямоугольников, т. е.
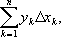 D
x
k- длина основания
k-гo прямоугольника,
y
k
-одно из значений функции
у=
f(
x) на отрезке D
x
k, равное высоте прямоугольника. Это выражение принимают за приближённое значение интеграла
D
x
k- длина основания
k-гo прямоугольника,
y
k
-одно из значений функции
у=
f(
x) на отрезке D
x
k, равное высоте прямоугольника. Это выражение принимают за приближённое значение интеграла
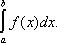 Сумму
Сумму
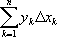 вычисляют графически так, как уже было указано. На
рис. 7
выполнены все построения, необходимые для вычисления интеграла
вычисляют графически так, как уже было указано. На
рис. 7
выполнены все построения, необходимые для вычисления интеграла
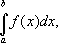 где функция
y=
f(
x) задана графиком
AC
0...
C
4
B.
После разбиения криволинейной трапеции на части прямыми, проходящими через точки
A
1, ...,
A
4, построены прямоугольники. Высоты их, ординаты точек
C
0, ...,
C
4, снесены на ось
Оу. Полученные точки
P
0,
...,
P
4соединены с точкой
Р(
OP= 1). Затем, начиная от точки
а,
построена ломаная
aB
1...
B
5, звенья которой параллельны соответствующим отрезкам
PP
0,
PP
1, ...,
PP
4. Величина интеграла численно равна ординате точки
B
5. Для построения графика первообразной функции
y=
f(
x), т. е.
где функция
y=
f(
x) задана графиком
AC
0...
C
4
B.
После разбиения криволинейной трапеции на части прямыми, проходящими через точки
A
1, ...,
A
4, построены прямоугольники. Высоты их, ординаты точек
C
0, ...,
C
4, снесены на ось
Оу. Полученные точки
P
0,
...,
P
4соединены с точкой
Р(
OP= 1). Затем, начиная от точки
а,
построена ломаная
aB
1...
B
5, звенья которой параллельны соответствующим отрезкам
PP
0,
PP
1, ...,
PP
4. Величина интеграла численно равна ординате точки
B
5. Для построения графика первообразной функции
y=
f(
x), т. е.
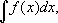 достаточно соединить плавной кривой вершины ломаной, получаемой при вычислении
достаточно соединить плавной кривой вершины ломаной, получаемой при вычислении
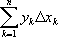 (на
рис. 7
точки
B
0,
B
1, ...,
B
5).
(на
рис. 7
точки
B
0,
B
1, ...,
B
5).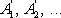 строят ступенчатую ломаную. Затем проводят кривую, следя за тем, чтобы криволинейные треугольники в пределах одной ступени ломаной имели равные площади. Эта кривая и является графиком производной.
строят ступенчатую ломаную. Затем проводят кривую, следя за тем, чтобы криволинейные треугольники в пределах одной ступени ломаной имели равные площади. Эта кривая и является графиком производной.