 |
|
���������� ������:: ��� :: ������� ��� ���������� :: �������� ����� :: ������ ����� :: ����� ����� �������� :: ���� ��������� :: ������ ����� ���� :: ������� ������ :: ������� ������ ���������� :: ������� ���� ���������� �����:: �������� ������ :: ������ � ������ ��� ����� (��������� ��. ����������� � �������� ������ ������) :: �������� ���� :: � ����� ������ �. �������� :: ����� ���� (��� 1) :: ���� (����� 2) :: ������� ����� :: ������ � �� ����� :: ��� �� ������ �� ������� ������ :: ������ ����� ������ |
������� ��������� ������������ (��)ModernLib.Net / ������������ / ��� / ������� ��������� ������������ (��) - ������ (���. 48)
В 1911-16 профессор Брауншвейгской высшей технической школы с 1916 работал в институте физической химии и электрохимии в Берлине. В 1933 переехал в Великобританию, затем в США, где был профессором университета в штате Миннесота. Основные труды
по проблемам коагуляции и устойчивости коллоидных растворов. Ф. исследовал важное в научном и практическом отношении явление тиксотропного гелеобразования, названное им «тиксотропией», разработал ряд коллоидно-химических проблем, связанных с биологией и медициной.
Соч. в рус. пер.: Химия каучука, М. - Л., 1938; Тиксотропия, М. - Л., 1939. Лит.:Donnan F. H., Freundlich, 1880-1941, «Journal of the Chemical Society», 1942, p. 645-54. Фрейр Фрейр,в скандинавской мифологии бог плодородия, богатства, мира. Брат (и муж) Фрейи , муж Герд (по-видимому, богини земли). Атрибуты Ф. - чудесный корабль Скидбладнир и вепрь Гуллинбурсти. Культ Ф. (или Ингви, откуда название шведского королевского рода Инглингов) был распространен по всей Скандинавии (особенно в Швеции). Фрейсине Шарль Луи де Сольс Фрейсине'(Freycinet) Шарль Луи де Сольс. (Saulces) (14.11.1828, Фуа, - 15.5.1923, Париж), французский государственный деятель, член Французской академии (1891). Выдвинулся во время Франко-прусской войны 1870-71; возглавил штаб обороны в Туре (октябрь 1870), принимал деятельное участие в формировании новых войск для продолжения воины, в 1876-1920 сенатор. Занимал посты министра общественных работ (1877-1879), министра иностранных дел (1879-80, 1882, 1885, 1886) и военного министра (1888-93, 1898-99); неоднократно был главой кабинетов (1879-80, 1882, 1886, 1890-92). Умеренный буржуазный республиканец, Ф. в начале своей деятельности поддерживал антиклерикальные законы о просвещении (1880). Провёл амнистию коммунаров (1880), закон об изгнании претендентов на французский престол (1886). В 1891 выступил в защиту конкордата с католической церковью, был противником пересмотра дела Дрейфуса (см. Дрейфуса дело ). Ф. содействовал росту военной мощи Франции, провёл закон о 3-летней службе в армии (1889). При участии Ф. были подготовлены соглашение 1891 и военная конвенция 1892 с Россией. Фрейсине Эжен Фрейсине'(Freyssinet) Эжен (13.7.1879 Обжа, департамент Коррез, - 8.6.1962, Сен-Мартен-Везюби, департамент Приморские Альпы), французский инженер и учёный, специалист в области железобетонных конструкций, один из создателей предварительно напряжённого железобетона, Окончил Национальную школу мостов и дорог (1904). В период 1905-28 по проектам Ф. и под его руководством построено много железобетонных мостов и др. инженерных сооружений оригинальной конструкции, среди них - арочные мосты в г. Сен-Пьер-дю-Вовре (пролёт 130 м) и Плугастеле (3 пролёта по 186,4 м), тонкостенное пространственное покрытие ангара в г. Орли. В этот же период Ф. впервые выполнил исследования ползучести бетона и её влияния на потери предварительного напряжения. С 1928 начал разработку и исследование предварительно напряжённых железобетонных конструкций и методов их изготовления на основе бетона и стали высокой прочности. Организовал (1932) первое промышленное производство предварительно напряженных изделий - мачт, свай, шпал. Предложил и осуществил ряд новых конструктивных решений мостов, гидротехнических сооружений, покрытий больших пролётов из предварительно напряжённого железобетона, получивших распространение во многих странах. Фрейтаг Густав Фре'йтаг(Freytag) Густав (13.7.1816, Крёйцбург, Силезия, - 30.4.1895, Висбаден), немецкий писатель. В 1835-38 изучал германистику в Бреславльском и Берлинском университетах. От симпатий к «Молодой Германии» постепенно перешёл к сочувствию национал-либеральным идеям предымпериалистической поры. В комедии «Журналисты» (1854, рус. пер. 1896) разоблачил коррупцию и беспринципность периодической печати. Программу развития сельского хозяйства Германии по капиталистическому пути и упрочения отечественной коммерции развернул в нравоописательном и историческом романе «Приход и расход» (1855, рус. пер. 1858), отмеченном филистерской моралью и националистической тенденциозностью. Итог обширных культурно-исторических занятий Ф. - «Картины из немецкого прошлого» (1859) и серия исторических романов «Предки» (1872-80) о судьбах многих поколений одного немецкого рода. Соч.: Gesammelte Werke, 2 Aufl., Bd 1-22, Lpz., 1896-98; в рус. пер. - Картины средневековой жизни, М., 1868; Картины из прошлого Германии, СПБ, 1913. Лит.:История немецкой литературы, т. 4, М., 1968; Меринт Ф., Литературно-критические статьи, М. - Л., 1934. Фрейя Фре'йяв скандинавской мифологии богиня плодородия, любви, красоты. Сестра (и жена) Фрейра , жена Ода которого она ищет по Земле, оплакивая золотыми слезами. По-видимому, Ф. - более позднее имя богини Фригг . Френ Христиан Данилович ФренХристиан Данилович (23.5.1782, Росток, - 16.8.1851, Петербург), русский востоковед-историк и нумизмат, академик Петербургской АН (1817). В 1803 окончил университет в Ростоке. В 1807-17 профессор восточных языков Казанского университета. Основатель и первый директор (1818-42) Азиатского музея . Нумизматические работы Ф. заложили основы восточной нумизматики в России и Европе. Эпоху в науке составили труды Ф. по использованию арабских источников для изучения истории Древней Руси. Лит.:Крачковский И. Ю., Очерки по истории русской арабистики Избр. соч., т. 5, М. - Л., 1958 (см. Указатель); Ливотова О. Э., Португаль В. Б., Востоковедение в изданиях Академии наук, 1726-1917. Библиография, М., 1966, № 1513-1597. Френе формулы Френе' фо'рмулы,формулы, дающие разложение производных (по дуге) единичных векторов касательной t, нормали nи бинормали bпроизвольной кривой Lпо векторам t, n, b. Если kи s - кривизна и кручение L, то Ф. ф. имеют вид
С помощью Ф. ф. исследуются дифференциально-геометрические свойства кривых линий, в кинематике - движение материальной точки по криволинейной траектории. Ф. ф. опубликованы в 1852 французским математиком Ф. Френе (F. Frenet), но были известны ему ещё в 1847; впервые же они были опубликованы в 1851 французским математиком Ж. Серре (J. Serret), почему их иногда называют формулами Серре - Френе. Френель Огюстен Жан Френе'ль(Fresnel) Огюстен Жан (10.5.1788, Брольи, - 14.7.1827, Виль-д'Авре, близ Парижа), французский физик, один из основателей волновой оптики, член Парижской АН (с 1823). Родился в семье архитектора. Окончил Политехническую школу (1806) и Школу дорог и мостов (1809) в Париже. Работал инженером по ремонту дорог. В период 100 дней за участие в военных действиях против Наполеона был отстранен от работы. К этому периоду относятся первые серьезные работы Ф. по оптике. В конце 1815 он был восстановлен в должности и по ходатайству Д. Ф. Араго и П. С. Лапласа в 1818 переведён в Париж, где занимался реорганизацией маяков, предложил принципиально новый способ маячного освещения (см. Френеля линза ). В 1815-23 Ф. выполнил классические исследования дифракции и поляризации света. Ф. создал теорию дифракции (независимо от Т. Юнга), положив в основу принцип Гюйгенса и дополнив его фундаментальной идеей об интерференции элементарных волн (см. Гюйгенса - Френеля принцип ). Он объяснил на основе этого принципа законы геометрической. оптики, в частности - прямолинейный характер распространения света. Им создан приближённый метод расчёта дифракционной картины, основанный на разбиении волнового фронта на зоны ( зоны Френеля ), и впервые рассмотрена дифракция от края экрана и круглого отверстия. Ф. - автор опытов с бизеркалами (1816) и бипризмами (1819), ставшими классическими методами демонстрации интерференционных явлений (см Френеля зеркала ). Он впервые объяснил поляризационные явления, приняв в качестве основной гипотезу о поперечности световых волн (1818, независимо от Юнга), и установил количественные законы явления поляризации света при его отражении и преломлении ( Френеля формулы , 1823). Высказанные Ф. идеи о неподвижном эфире и коэффициенте увлечения световых волн легли в основу электродинамики движущихся сред Х. А. Лоренца . Член Лондонского королевского общества (с 1825). Соч.: CEuvres complиtes..., t. 1-3, P., 1866-70; в рус. пер. - Избр. труды по оптике, М., 1955. Лит.:Boutry G. A., Augustin Fresnel: his time, life and work, L.,[1949]; Кудрявцев П. С., История физики, [2 изд.], т.1, М., 1956; Льоцци М., История физики, пер. с итал., М., 1970. Я. М. Гельфер. 
О. Ж. Френель. Френеля дифракция Френе'ля дифра'кция,дифракция сферической световой волны на неоднородности (например, отверстии), размер которой сравним с диаметром одной из зон Френеля . Название дано в честь изучившего этот вид дифракции О. Ж. Френеля . Подробнее см. в ст. Дифракция света . Френеля зеркала Френе'ля зеркала',бизеркала Френеля, оптическое устройство, предложенное в 1816 О. Ж. Френелем для наблюдения явления интерференции когерентных световых пучков. Устройство состоит из двух плоских зеркал Iи II, образующих двугранный угол, отличающийся от 180° всего на несколько угловых мин(см. рис. 1 в ст. Интерференция света ). При освещении зеркал от источника Sотражённые от зеркал пучки лучей можно рассматривать как исходящие из когерентных источников S 1и S 2, являющихся мнимыми изображениями S. В пространстве, где пучки перекрываются, возникает интерференция. Если источник Sлинеен (щель) и параллелен ребру Ф. з., то при освещении монохроматическим светом интерференционная картина в виде параллельных щели равностоящих тёмных и светлых полос наблюдается на экране М, который может быть установлен в любом месте в области перекрытия пучков. По расстоянию между полосами можно определить длину волны света. Опыты, проведённые с Ф. з., явились одним из решающих доказательств волновой природы света. Лит.:Захарьевский А. Н., Интерферометры, М., 1952; Нагибина И. М., Интерференция и дифракция света, Л., 1974. Френеля интегралы Френе'ля интегра'лы,интегралы вида
и
введённые О. Ж. Френелем при решении задач дифракции света . Несобственные Ф. и. равны S(Ґ) = С(Ґ) = 1/ 2. Таблицы Ф. и. приводятся во многих справочниках (например, Янке Е., Эмде Ф., Лёш Ф., Специальные функции, перевод с немецкого, 2 изд., 1968). Френеля линза Френе'ля ли'нза,сложная составная линза, применяемая в маячных и сигнальных фонарях. Предложена О. Ж. Френелем . Состоит не из цельного шлифованного куска стекла со сферическими или иными поверхностями, как обычные линзы, а из отдельных примыкающих друг к другу концентрических колец небольшой толщины, которые в сечении имеют форму призм специального профиля ( рис. ). Эта конструкция обеспечивает малость толщины (а следовательно, и массы) Ф. л. даже при большом угле охвата. Сечения колец таковы, что сферическая аберрация Ф. л. невелика, и лучи света от точечного источника S, помещенного в фокусе Ф. л., после преломления в кольцах выходят практически параллельным пучком (в кольцевых Ф. л.). Ф. л. бывают кольцевыми и поясными. Первые представляют собой систему, получаемую вращением изображенного на рис . профиля вокруг оптической оси SO; они направляют световой поток в каком-либо одном направлении. Поясные Ф. л. получают вращением этого же профиля вокруг оси ASA', перпендикулярной SO; они посылают свет от источника по всем горизонтальным направлениям. Диаметр Ф. л. - от 10-20 смдо нескольких м. 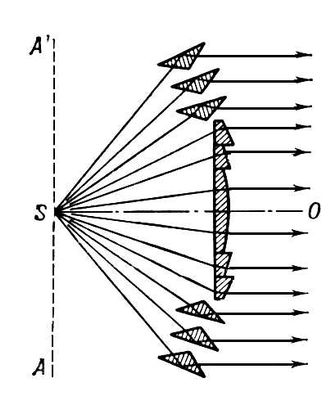
Сечение кольцевой линзы Френеля. В центе линзы - кольца, наружные поверхности к-рых являются частями тороидальных поверхностей. По краям линзы - кольца, где, помимо преломления, происходит полное внутреннее отражение. Френеля формулы Френе'ля фо'рмулыопределяют отношения амплитуды, фазы и состояния поляризации отражённой и преломленной световых волн, возникающих при прохождении света через неподвижную границу раздела двух прозрачных диэлектриков, к соответствующим характеристикам падающей волны. Установлены О. Ж. Френелем в 1823 на основе представлений об упругих поперечных колебаниях эфира . Однако те же самые соотношения - Ф. ф. следуют в результате строгого вывода из электромагнитной теории света при решении Максвелла уравнений и отождествлении световых колебаний с колебаниями вектора напряжённости электрического поля в световой волне, с которыми связано большинство эффектов волновой оптики. Пусть плоская световая волна падает на границу раздела двух сред с преломления показателями n 1и n 2. Углы j, j'' и j"' есть соответственно углы падения, отражения и преломления, причём всегда n 1sinj = n 2sinj"' (закон преломления) и ½j½ = ½j'½ (закон отражения). Электрический вектор падающей волны разложим на составляющую с амплитудой А р, параллельную плоскости падения, и составляющую с амплитудой A s, перпендикулярную плоскости падения. Аналогично разложим амплитуды отражённой волны на составляющие R pи R s, а преломленной волны - на D pи D s. Ф. ф. для этих амплитуд имеют вид:
Из (1) следует, что при любом значении углов j и j"' знаки A pи D p, а также знаки A sи D sсовпадают. Это означает, что совпадают и фазы, т. е. во всех случаях преломленная волна сохраняет фазу падающей. Для компонент отражённой волны ( R pи R s) фазовые соотношения зависят от j, n 1и n 2. Так, если j = 0, то при n 2> n 1фаза отражённой волны сдвигается на p. В экспериментах обычно измеряют не амплитуду световой волны, а её интенсивность, т. е. переносимый ею поток энергии, пропорциональный квадрату амплитуды (см. Пойнтинга вектор ). Отношения средних за период потоков энергии в отражённой и преломленной волнах к среднему потоку энергии в падающей волне называется коэффициентом отражения rи коэффициентом прохождения d. Из (1) получим Ф. ф., определяющие коэффициент отражения и прохождения для S- и р-составляющих падающей волны:
При отсутствии поглощения света r s+ d s= 1 и r p+ d p= 1, в соответствии с законом сохранения энергии. Если на границу раздела падает естественный свет (см. Поляризация света ), т. е. все направления колебаний электрического вектора равновероятны, то половина энергии волны приходится на р-колебания, а вторая половина - на S-колебания; полный коэффициент отражения в этом случае:
Если j' + j"' = 90° и tg (j' + j"') ® Ґ, r p= 0, т. е. свет, поляризованный так, что его электрический вектор лежит в плоскости падения, в этих условиях совсем не отражается от поверхности раздела. Отражённый же свет (при падении естественного света под таким углом) будет полностью поляризован. Угол падения, при котором это происходит, называется углом полной поляризации или углом Брюстера (см. Брюстера закон ). Для угла Брюстера справедливо соотношение tg j Б= n 2/n 1. При нормальном падении света на границу раздела двух сред (j = 0) Ф. ф. для амплитуд отражённой и преломленной волн могут быть приведены к виду
При этом исчезает различие между составляющими sи p, т.к. понятие плоскости падения теряет смысл. В этом случае, в частности, получаем
Из (4) следует, что отражение света на границе раздела тем больше, чем больше абсолютная величина разности n 2- n 1; коэффициенты rи dне зависят от того, с какой стороны границы раздела приходит падающая световая волна. Условие применимости Ф. ф. - независимость показателя преломления среды от амплитуды вектора электрической напряжённости световой волны. Это условие, тривиальное в классической (линейной) оптике, не выполняется для световых потоков большой мощности, например излучаемых лазерами . В этих случаях Ф. ф. не дают удовлетворительного описания наблюдаемых явлений и необходимо использовать методы и понятия нелинейной оптики . См. также Отражение света . Оптика тонких слоев , Преломление света . 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61 |
|||||||
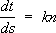 ,
,
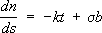 ,
,
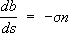 .
.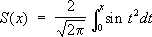
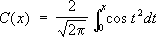
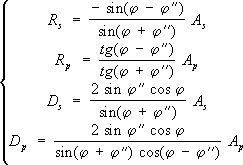 (1)
(1)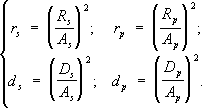 (2)
(2)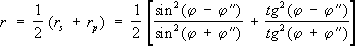 .
.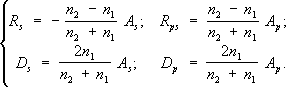 (3)
(3)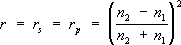 ;
;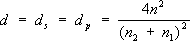 . (4)
. (4)