 |
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ЭЛ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ЭЛ) - Чтение (стр. 38)

Эллинистическая культура. «Дионис на пантере». Мозаика дворца в Пелле. 4 в. до н. э. Музей Пелла. 
Эллинистическая культура. «Танцующий пигмей». Бронза. 2-1 вв до н. э. Национальный музей Бардо. Тунис. 
Эллинистическая культура. Голова Диониса из Хатры. Бронза. 1 в. до н. э. Иракский музей. Багдад. 
Эллинистическая культура. Руины храма Зевса Олимпийского в Афинах. Вид с востока. 1-я пол. 2 в. до н. э. Перестройки римского времени. 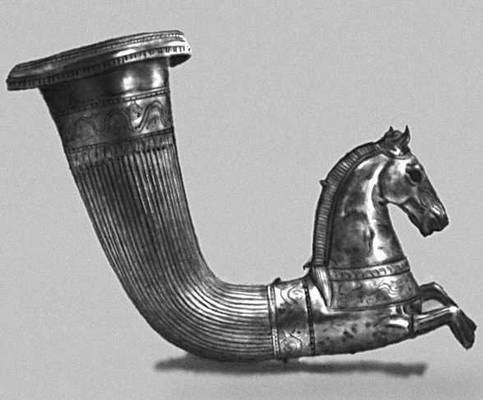
Эллинистическая культура. Ритон. Серебро, позолота. 1 в. до н. э. - 1 в. н. э. Эрмитаж, Ленинград. 
Эллинистическая культура. Фасад святилища Афины Никефоры в Пергаме. 4-3 вв. до н. э. 
Эллинистическая культура. Символические сцены и «гигантомахия» фриза храма Гекаты в Лагине. Мрамор. Кон. 2 - нач. 1 вв. до н. э. Археологический музей. Стамбул. 
Аллегория Нила. Т. н. Тарелка Фарнезе. Сардоникс. Национальный музей. Неаполь. 
Эллинистическая культура. Голова статуи Антиоха IV из Шами. Бронза. 2 в. до н. э. Археологический музей. Тегеран. 
Эллинистическая культура. «Раненый галл». Мрамор. Римская копия с греческого оригинала. Ок. 230 до н. э. Капитолийские музеи. Рим. 
Эллинистическая культура. Дойдалс из Вифинии. «Коленопреклонённая Афродита». Мрамор. Ок. сер. 3 в. до н. э. Национальный римский музей, Рим. 
Эллинистическая культура. Голова философа. Бронза. Кон. 3 - нач. 2 вв. до н. э. Национальный археологический музей. Афины. 
Эллинистическая культура. Капитель «Малых пропилей» святилища Деметры в Элевсине. Ок. 40 до н. э. 
Эллинистическая культура. «Александр Македонский». Фрагмент мозаики с изображением битвы греков и персов. Национальный музей, Неаполь. 
Эллинистическая культура. Руины дворца в Пелле. 4 в. до н. э. 
Эллинистическая культура. Диоскурид из Самоса. «Уличные музыканты». Мозаика. Кон. 2 в. до н. э. Национальный музей, Неаполь. 
Эллинистическая культура. «Саркофаг Александра» из Сидона. Мрамор. Роспись. 325-310 до н. э. Археологический музей. Стамбул. 
Эллинистическая культура. «Хирон, воспитывающий Ахилла». Фреска из Геркуланума. По оригиналу последней трети 4 в. до н. э. Национальный музей. Неаполь. 
Эллинистическая культура.«Девушка из Анцио». Мрамор. 1-я пол. 3 в. до н. э. Национальный римский музей, Рим. 
Эллинистическая культура. Чаша с двойными стенками. Стекло. Орнамент из тонких листов золота между стенками. 2-1 вв. до н. э. Эрмитаж, Ленинград. Эллины Э'ллины(греч. Hellenes), самоназвание .Впервые термин «Э.» для обозначения всех греков встречается у поэта Архилоха (7 в. до н. э.). Эллипс (геометрич.) Э'ллипс,линия пересечения круглого конуса с плоскостью, встречающей одну его полость ( рис. 1 ). Э. может быть также определён как геометрическое место точек Мплоскости, для которых сумма расстояний до двух определенных точек F 1и F 2(фокусов Э.) этой плоскости есть величина постоянная. Если выбрать систему координат xOyтак, как указано на рис. 2 ( OF 1 =OF 2 =с), то уравнение Э. примет вид:
(2
a = F
1
M + F
2
M,
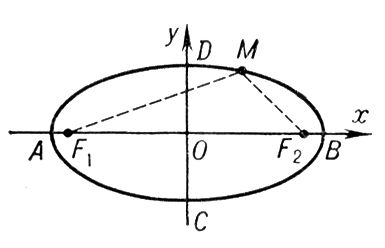
Рис. 2. к ст. Эллипс. 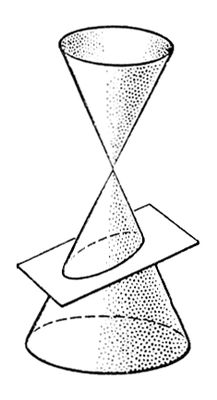
Рис. 1. к ст. Эллипс. Эллипс инерции Э'ллипс ине'рциив сопротивлении материалов, графическое изображение, используемое для вычисления осевых и центробежных плоской фигуры (например, поперечного сечения стержня) относительно осей, проходящих через её центр тяжести. При построении Э. и. его полуоси, численно равные главным фигуры, совмещаются с её главными центральными осями. Эллипс (пропуск в речи) Э'ллипс(от греч. elleipsis - нехватка, опущение, выпадение), пропуск в речи (тексте) подразумеваемой языковой единицы: звука или звукосочетания (обычно в разговорной речи: «када» - когда, «мож-быть» - может быть), слова (словосочетания), названного в контексте («У отца был большой письменный стол, а у сына маленький»), составляющего часть фразеологического оборота («Ты в любом случае выйдешь сухим» [из воды]), предсказываемого значением и (или) формой др. слов («Ты на работу?» [идёшь]; [Я] «сижу за решёткой в темнице сырой...» - Пушкин), ясного из ситуации («Мне чёрный» [кофе, хлеб...]). Э. синтаксического члена, не восстанавливаемого однозначно, носит экспрессивный, эмоциональный характер и используется как («Я за свечку, свечка - в печку», К. Чуковский). Эллипсоид Эллипсо'ид(от и греч. eidos - вид), замкнутая центральная .Э. имеет центр симметрии О (см. рис. ) и три оси симметрии, которые называются осями Э. Точки пересечения координатных осей с Э. называются его вершинами. Сечения Э. плоскостями являются эллипсами (в частности, всегда можно указать круговые сечения Э.). В надлежащей системе координат уравнение Э. имеет вид: x 2/ a 2+ y 2/ b 2+ z 2/ c 2= 1. 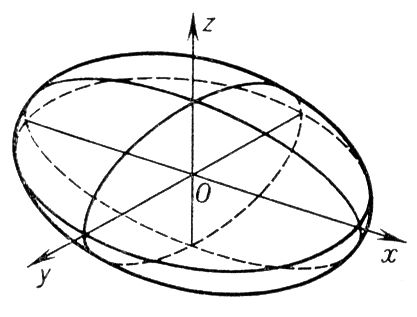
Рис. к ст. Элипсоид. Эллиптическая геометрия Эллипти'ческая геоме'трия,то же, что . Эллиптическая точка Эллипти'ческая то'чкаповерхности, точка, в которой поверхности положительна. В окрестности Э. т. поверхность расположена по одну сторону от своей касательной плоскости. Эллиптические галактики Эллипти'ческие гала'ктики,гигантские звёздные системы, имеющие форму эллипсоида. Э. г., как правило, не содержат космической пыли. См. . Эллиптические интегралы Эллипти'ческие интегра'лы,интегралы вида
где
R(
x, у) - рациональная функция
хи
Под Э. и. первого рода понимают интеграл
под Э. и. второго рода - интеграл
где k -модуль Э. и., 0 < k <1 ( х= sin j, t= sin a. Интегралы в левых частях равенств (1) и (2) называются Э. и. в нормальной форме Якоби, интегралы в правых частях - Э. и. в нормальной форме Лежандра. При х= 1 или j = p/2 Э. и называются полными и обозначаются, соответственно, через
и
Своё назв. Э. и. получили в связи с задачей вычисления длины дуги эллипса и = a sina , v = b cosa( a < b) .Длина дуги эллипса выражается формулой
где
Эллиптические координаты Эллипти'ческие координа'ты,координаты, связанные с семейством софокусных эллипсов и гипербол (см. ) .Э. к. точки Ми её декартовы координаты х, усвязаны соотношениями х = сch ucos v, у = сsh usin v. Эллиптические траектории
Эллипти'ческие траекто'рии,
,которые может описывать материальная точка (или центр масс тела) при движении под действием силы ньютонианского
.В поле тяготения Земли, если пренебречь сопротивлением среды, Э. т. будет в 1-м приближении траектория центра масс тела, которому вблизи поверхности Земли сообщена начальная скорость
Эллиптические функции Эллипти'ческие фу'нкции,функции, связанные с обращением .Э. ф. применяются во многих разделах математики и механики как при теоретических исследованиях, так и для численных расчётов. Подобно тому как тригонометрическая функция u = sinxявляется обратной по отношению к интегралу
так обращение нормальных эллиптических интегралов 1-го рода
где z = sinjw, k -модуль эллиптического интеграла, порождает функции: j = am z -амплитуда z(эта функция не является Э. ф.) и w = sn z =sin (am z) -синус амплитуды. Функции cn -косинус амплитуды и dn z- дельта амплитуды определяются формулами
Функции sn z,cn z,dn zназывают Э. ф. Якоби. Они связаны соотношением sn 2 z+ cn 2z =k 2sn 2 z+ dn 2 z= 1. На рис. представлен вид графиков Э. ф. Якоби. Они связаны соотношением sn 2 z + cn 2z = k 2sn 2 z+ dn 2 z= 1 На рис. представлен вид графиков Э. ф. Якоби для действительного x и 0 < k < 1; а
- полный нормальный эллиптический интеграл 1-го рода и 4 K -основной период Э. ф. sn z.В отличие от однопериодической функции sin х,функция sn z -двоякопериодическая. Её второй основной период равен 2 iK,где
и
Э. ф. Вейерштрасса Г( х) может быть определена как обратная нормальному эллиптическому интегралу Вейерштрасса 1-го рода
где параметры g 2и g 2- называются инвариантами Г( x) .При этом предполагается, что нули e 1, e 2и e 3многочлена 4 t 3- g 2 t - g 3 различны между собой (в противном случае интеграл (*) выражался бы через элементарные функции). Э. ф. Вейерштрасса Г( х) связана с Э. ф. Якоби следующими соотношениями:
Любая мероморфная двоякопериодическая функция
f(
z) с периодами w
1и w
2, отношение которых мнимо, т. е.
f(
z+
mw
1+
пw
2) =
f(
z) при
m,
n =0
, ±1, ±2,... и
Изучению Э. ф. предшествовало накопление знаний об эллиптических интегралах, систематическое изложение теории которых дал А. .Основоположниками теории Э. ф. являются Н. (1827) и К. (1829). Последний дал развёрнутое изложение теории Э. ф., названное его именем. В 1847 Ж. опубликовал изложение основ общей теории Э. ф., рассматриваемых как мероморфные двоякопериодические функции. Представление Э. ф. через Г-функцию, а также z-, s-функции дано К. в 40-х гг. 19 в. (две последние не являются Э. ф.). Лит.:Маркушевич А. И., Теория аналитических функций, 2 изд., т. 2, М., 1968; Гурвиц А., Курант Р., Теория функций, пер. с нем., М., 1968; Уиттекер Э, Т., Ватсон Дж. Н., Курс современного анализа, пер. с англ., 2 изд., ч. 2, М., 1963; Бейтмен Г., Эрдейи А., Высшие трансцендентные функции. Эллиптические и автоморфные функции. Функции Ламе и Матье, пер. с англ., М., 1967. 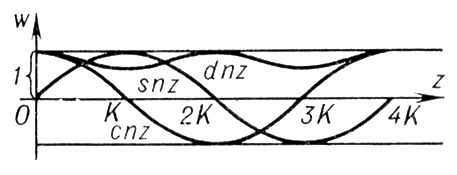
Рис. к ст. Эллиптические функции. Эллиптический параболоид Эллипти'ческий параболо'ид,один из двух видов . Эллиптический цилиндр Эллипти'ческий цили'ндр,линейчатая цилиндрическая поверхность, уравнение которой может быть приведено к виду x 2/ a 2 + y 2 b 2= 1. См. . Эллис (атоллы) Э'ллис(Ellice) (с 1975 - Тувалу; Tuvalu), группа атоллов на З. Тихого океана, в Полинезии. Владение Великобритании. Площадь 24 км 2 .Население 5,8 тыс. человек (1973). Состоит из 9 низменных коралловых атоллов, вытянутых на 600 км.Плантации кокосовой пальмы, бананов. Экспорт копры. Административный центр - г. Фунафути. Эллис Фред Э'ллис(Ellis) Фред (5.6. 1886, Чикаго, - 10. 6. 1965, Нью-Йорк), американский график-карикатурист. С 1924 член компартии США. Учился в художественной школе в Чикаго (1905), с 1927 главный художник «Дейли уоркер», в 1930-36 работал в СССР для газет «Правда» и «Труд». В ясных, широких и живописных по манере рисунках Э. нашли страстное и лаконичное выражение темы обличения капитализма, призыв к борьбе рабочего класса, гневное осуждение фашизма. Лит.:Дурус А., Фред Эллис, М. - Л., 1937; Выгодская Т., Фред Эллис, «Искусство», 1964, № 11. 
Ф. Эллис. «Не беспокойтесь, здесь только коммунисты». Рисунок. 1934. Эллора Элло'ра,Эллур, Элура, деревня в Индии, в 15 кмот Аурангабада (штат Махараштра), близ которой - группа из 34 высеченных в скале буддийских, брахманских и джайнских храмов (все - между 6-13 вв.), в том числе монолитный храм Кайласанатха, одной из трёх частей которого опоясан изваяниями слонов в натуральную величину. Элляй Элля'й(литературное имя; настоящее имя и фамилия Серафим Романович Кулачиков) [16(29). 11. 1904, Нижнеамгинский наслег Ботурусского улуса, ныне Алексеевского района Якутской АССР, - 14. 12. 1976, Якутск], якутский советский поэт. Народный поэт Якутской АССР (1964). Член КПСС с 1946. В 1928 окончил Московский институт журналистики. Участник Великой Отечественной войны 1941-45. Автор сборников стихов и поэм «Красные песни» (1925), «Счастливая жизнь» (1938), «Песни победы» (1950), «Негаснущий огонь» (1969), «Сердце друга» (1973) и др. Новизна формы, самобытность, гражданский пафос стихов Э. обусловили влияние его творчества на развитие якутской поэзии. Перевёл произведения А. С. Пушкина, Т. Г. Шевченко, В. В. Маяковского и др. Награжден орденом Октябрьской Революции, 2 другими орденами, а также медалями. Соч.: Талыллыбыт айымньылар, т. 1-2, Якутскай, 1964-65; Талыллыбыт айымньылар, т. 1-2, Якутскай, 1974; в рус. пер. - Мой хомус, М., 1974. Лит.:Очерк истории якутской советской литературы, М., 1970. Элмайра Элма'йра(Elmira), город на С.-В. США, в штате Нью-Йорк, на р. Шеманг (приток Саскуэханны). 36 тыс. жителей (1975), с пригородами 100 тыс. жителей Металлообрабатывающая и машиностроительная (производство пишущих и счётных машин, конторского и радиоэлектронного оборудования, противопожарной техники), химическая промышленность. Основан в 1788. Элодея Элоде'я, водяная зараза, водяная чума (Elodea), род многолетних трав семейства водокрасовых. Стебли погружены в воду. Листья в мутовках. Около 10 видов, родом из Америки. Э. канадская (Е. canadensis) как заносное растение встречается во многих районах земного шара, в СССР - в Европейской части и Западной Сибири, в стоячих и медленно текущих водах. Известны только пестичные (женские) растения, очень быстро размножающиеся вегетативно. Обширные скопления Э. препятствуют судоходству, рыболовству и т. п. (отсюда название «водяная зараза» или «водяная чума»). Зелёная масса Э. используется как корм и на удобрение. Несколько видов разводят в аквариумах. 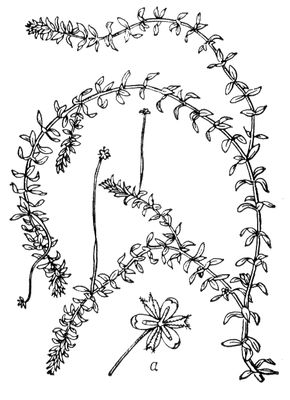
Элодея канадская: часть растения с пестичными цветками; а - пестичный цветок. Элой Бланко Андрее Эло'й Бла'нко(Eloy Blanco) Андрее (6. 8. 1897, Кумана, - 21. 5. 1955, Мехико), венесуэльский поэт, политический деятель. Окончил юридический факультет Центрального университета (1920). Участвовал в антидиктаторском движении, за что подвергался репрессиям; много лет провёл в эмиграции. После смерти в 1935 Х. В. -председатель муниципалитета Каракаса, председатель Национального собрания и министр иностранных дел в правительстве Р. .В стихах воспел природу и народ Венесуэлы, любовь и семейную жизнь, выразил мечту о всеобщем братстве народов. Внёс в поэзию Венесуэлы темы и формы латиноамериканского фольклора. Автор сборников стихов «Песни моей земли» (1921), «Время стрижки деревьев» (1934), «Каменный корабль» (1937), «Лунацвет» (1955), «Хуанбимбада» (опубликовано 1960), сборников рассказов «Аэроплан-наседка» (1935) и «Возвращение Мальвина» (1937), драмы «Аби-гайль» (1937), эссе «Варгас - душеприказчик скорби» (1947). Соч.: Obras, v. 1-10, [Caracas, 1960]; в рус. пер. - Зеркало в чёрной раме, М., 1974; [Стихи], в сборнике: Поэзия Латинской Америки, М., 1975. Лит.:Художественное своеобразие литератур Латинской Америки, М., 1976 (см. указатель); Homenaje е Andres Eloy Blanco, Caracas, 1958. Элонгация звезды Элонга'ция звезды'(позднелат. elongatio, от elongo - удаляюсь), положение звезды в её видимом суточном движении по небесной сфере, при котором она максимально отклонена по азимуту от точки юга. Элонгация наблюдается только у звёзд, имеющих верхнюю кульминацию на участке небесного меридиана между полюсом мира и зенитом места наблюдений. Различают западную и восточную Э. з. Элонгация планеты Элонга'ция плане'ты,положение нижней планеты (Венеры или Меркурия) в момент, когда её долгота максимально отличается от долготы Солнца. Различают восточную и западную Э. п. В момент элонгации Венера находится на угловом расстоянии 48° от Солнца. Угловое расстояние Меркурия от Солнца в момент элонгации, вследствие большего эксцентриситета его орбиты, изменяется в пределах от 18 до 28°. Во время элонгации планеты движутся по лучу зрения к Земле или от Земли. См: в астрономии. Элпидин Михаил Константинович Элпи'динМихаил Константинович (1835, с. Никольское Лаишевского у. Казанской губернии, - 1908, Женева, Швейцария), русский революционер-шестидесятник, деятель .Сын дьякона. Окончил Чистопольское духовное училище, служил в Казанском уездном суде. С 1860 - вольнослушатель Казанского университета. Во время находился в с. Бездна, был арестован и вскоре освобожден за недостатком улик. За участие в студенческих выступлениях 1861 выслан на родину. Член казанского революционного кружка (с 1862 - отделение общества ) .В 1863 арестован по делу о ,приговорён к 5 годам каторги, 6 июля 1865 бежал из Казанского тюремного замка, эмигрировал, примкнул к .В 1866 организовал в Женеве русскую типографию, в 1881 - книжную лавку. Вместе с Н. Я. издавал журнал «Подпольное слово» (1866, № 1-2); в типографии Э. печатались журналы «Современность» (1868, № 1-7) и (1868, № 1-2), газета ,одним из издателей которой он был. За 40 лет Э. выпустил около 200 книг, в том числе первое отдельное издание романа «Что делать?» (1867) и сборник сочинений Н. Г. Чернышевского (т. 1-4, 1868-70), запрещенные цензурой произведения М. Е. Салтыкова-Щедрина, Л. Н. Толстого и др., а также каталоги своего книжного магазина (последний в 1906). Соч.: Библиографический каталог. Профили редакторов и сотрудников, [Geneve, 1906]. Лит.:Козьмин Б. П., Казанский заговор 1863 г., М., 1929; его же, Революционное подполье в эпоху «белого террора», [М.], 1929; Пинаев М., М. К. Элпидин в 80- 90-е гг. (Из истории русской эмиграции), «Русская литература», 1966, № 2; его же, «Вольные» русские издания М. Элпидина, в кн.: Вопросы русской и зарубежной литературы, Волгоград, 1970; Сводный каталог русской нелегальной и запрещенной печати XIX в., ч. 8, М., 1971 Ю. Н. Коротков. Элсмир Э'лсмир(Ellesmere), остров на С.-В. Канадского Арктического архипелага. Площадь около 250 тыс. км 2 .Высота до 2604 м.Многочисленные фьорды разделяют остров на несколько обособленных частей - земель (Гранта, Гриннелла, Свердрупа, Элсмир). Около 1/ 3поверхности покрыто ледниками. Растительность арктических пустынь и тундр. Элсуорт (горы) Э'лсуорт(Ellsworth Mountains), горы в южной части Земли Элсуорта (Западная Антарктида). Простираются на 300 кмот 77° до 80° ю. ш. Наиболее крупные хребты - Сентинел и Херитидж. Массив Винсон в горах Сентинел (5140 м) -высочайшая вершина Антарктиды. Открыты в 1935 американским лётчиком Л. . Элсуорт Линкольн Э'лсуорт(Ellsworth) Линкольн (12. 5. 1880, Чикаго, - 26. 5. 1951, Нью-Йорк), американский полярный исследователь, лётчик. В 1925 был штурманом одного из двух самолётов в экспедиции Р. к Северному полюсу. В 1926 участвовал в экспедиции Амундсена на дирижабле «Норвегия» (по маршруту Шпицберген - Северный полюс - Аляска). В 1931 участник полёта на дирижабле «Граф Цеппелин» на Землю Франца-Иосифа. В ноябре-декабре 1935 вместе с лётчиком Г. Холлик-Кеньоном совершил первый трансантарктический перелёт (от Антарктического полуострова до Литл-Америка). В полёте были открыты горная цепь Этернити, хребет Сентинел, Земля и горы Э., названные им в честь своего отца Дж. Элсуорта. В 1938-39 совершил полёты во внутренние области Антарктиды. В честь Э. названы мыс на о. Янг (о-ва Баллени), горная вершина в хребте Куин-Мод и антарктическая станция. Соч.: Beyond horizons, N. Y., 1938. Лит.:Трешников А. Ф., История открытия и исследования Антарктиды, М., 1963. Элсуорт (полярная станция) Э'лсуорт(Ellsworth), научная станция на шельфовом леднике Фильхнера (77° 43' ю. ш., 41° 07' з. д.). Открыта США 11 февраля 1957; в 1959 передана Аргентине. В 1957-62 на станции проводились метеорологические, актинометрические, геофизические и гляциологические наблюдения. Служила базой для маршрутных исследований прилегающих районов. Названа в честь американского лётчика Л. . Элсуорта Земля Э'лсуорта Земля'(Ellsworth Land), часть территории Западной Антарктиды к Ю.-З. от Антарктического полуострова, между 62° и 102° з. д. На 3. в Э. 3. вдаётся шельфовый ледник Фильхнера. Высота ледникового покрова 2000 м;мощность льда 1000-3000 м.В центре над ледниковой поверхностью возвышаются горы Элсуорт (высота до 5140 м -высшая точка Антарктиды). Открыта в 1935 Л. . Элсхот Биллем Э'лсхот(Elsschot) Биллем (псевдоним; настоящее имя - Альфонс Де Риддер, De Ridder) (7.5.1882, Антверпен, - 31.5. 1960, там же), бельгийский писатель. Писал на фламандском языке. Получил коммерческое образование. Выступил как поэт: сборник «Ранние стихотворения» (1934). В романе «Вилла роз» (1913) разоблачен нравственный мир мещанства. Повесть «Избавление» (1921) рассказывает о деревенской жизни. Трагической судьбе «маленького человека» в буржуазном обществе посвящен роман «Разочарование» (1921). Автор сатирического романа «Силки» (1924) и повестей. Психологическая проза Э. - значительная веха в развитии критического реализма в бельгийской литературе 20 в. Соч.: Verzameld werk, Arnst., 1957; в рус. пер. - Вилла роз. Силки. Сыр. Танкер. Блуждающий огонек. Предисл. И. Шкунаевой, М., 1972. Лит.:Smits F., W. Elsschot, Brussel, 1952; Stuiveling G., W. Elsschot, Brussel, 1960; Carmiggelt S., Notities over Willem Elsschot, Arnst., 1976. В. В. Данчев. Элуру Элу'ру, город в Индии, в штате Андхра-Прадеш. 127 тыс. жителей (1971). Расположен на судоходном канале, соединяющем реки Годавари и Кришна. Хлопкоочистка, производство кожаных, табачных изделий, электротоваров. Кустарные промыслы. Эль Греко Доменико Эль Гре'ко(El Greco; собств. Теотокопули, Teotocopuli) Доменико (1541, о. Крит, - 7.4.1614, Толедо), испанский живописец. По происхождению грек. Первоначально учился, по-видимому, на о. Крит у иконописцев, что во многом предопределило своеобразие его творчества. После 1560 уехал в Венецию, где, возможно, учился у .С 1570 работал в Риме. Испытал воздействия , ,а также венецианских мастеров Позднего Возрождения (Тициана, Я. , Тинторетто) . Расцвет таланта Э. Г. наступил в Испании, куда он переехал около 1577 (не получив признания при дворе в Мадриде, художник поселился в Толедо). В зрелом творчестве Э. Г., родственном религиозной поэзии испанских мистиков 16 в. (Хуан де ла Крус и др.), в иллюзорно-беспредельном живописном пространстве стираются грани между землёй и небом; резкие ракурсы и неестественно вытянутые пропорции создают эффект стремительного изменения масштабов фигур и предметов, то внезапно вырастающих, то исчезающих в глубине («Мученичество св. Маврикия», 1580-1582, Эскориал; «Погребение графа Оргаса», 1586-88, церковь Санто-Томе, Толедо; «Святое Семейство», около 1590-95, Музей искусств, Кливленд). Но ведущее значение в этих произведений получает колорит, основанный на обилии неожиданных рефлексов, беспокойной игре контрастирующих цветов, то ярко вспыхивающих, то гаснущих в призрачном мерцании. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41 |
|||||||||||||||||||||
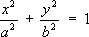 (*)
(*)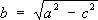 ). Э. -
;она симметрична относительно осей
ABи
CD;точка
О- центр Э. - является его центром симметрии; отрезки
AB= 2
aи
CD= 2
bназываются соответственно большой и малой осями Э.; число
е = с/а<1 - эксцентриситет Э. (при
е= 0, то есть при
а = b,Э. есть окружность). Прямые, уравнения которых
x = -а/еи
х = а/е,называются директрисами Э.; отношение расстояния точки Э. до ближайшего фокуса к расстоянию до ближайшей директрисы постоянно и равно эксцентриситету. Точки
А, В, С, Dпересечения Э. с осями
Oxи
Оуназываются его вершинами. См. также
.
). Э. -
;она симметрична относительно осей
ABи
CD;точка
О- центр Э. - является его центром симметрии; отрезки
AB= 2
aи
CD= 2
bназываются соответственно большой и малой осями Э.; число
е = с/а<1 - эксцентриситет Э. (при
е= 0, то есть при
а = b,Э. есть окружность). Прямые, уравнения которых
x = -а/еи
х = а/е,называются директрисами Э.; отношение расстояния точки Э. до ближайшего фокуса к расстоянию до ближайшей директрисы постоянно и равно эксцентриситету. Точки
А, В, С, Dпересечения Э. с осями
Oxи
Оуназываются его вершинами. См. также
.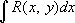 ,
,
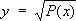 , а
Р(
х)
-многочлен 3-й или 4-й степени без кратных корней.
, а
Р(
х)
-многочлен 3-й или 4-й степени без кратных корней.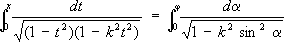 (1)
(1)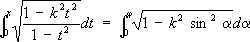
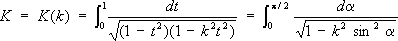
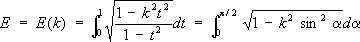
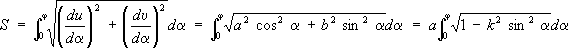
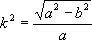 - эксцентриситет эллипса. Длина дуги четверти эллипса равна
E(
k)
.Функции, обратные Э. и., называются
.
- эксцентриситет эллипса. Длина дуги четверти эллипса равна
E(
k)
.Функции, обратные Э. и., называются
.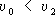 ,где
,где
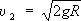 » 11,2
км/сек -вторая космическая скорость (
R -радиус Земли,
g -ускорение силы тяжести).
» 11,2
км/сек -вторая космическая скорость (
R -радиус Земли,
g -ускорение силы тяжести).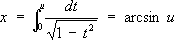
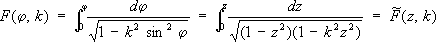
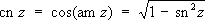
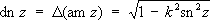
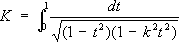
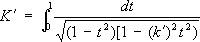
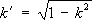 -дополнительный модуль. Периоды, нули и полюсы Э
.ф. Якоби приведены в таблице, где
mи
n -любые целые числа.
-дополнительный модуль. Периоды, нули и полюсы Э
.ф. Якоби приведены в таблице, где
mи
n -любые целые числа.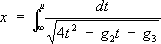
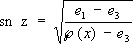 ,
,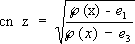 ,
,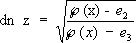 .
.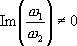 , является Э. ф. Для построения Э. ф., а также численных расчётов применяют
и
.
, является Э. ф. Для построения Э. ф., а также численных расчётов применяют
и
.