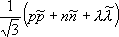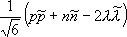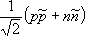|
|
Популярные авторы:: БСЭ :: Толстой Лев Николаевич :: Азимов Айзек :: Раззаков Федор :: Чехов Антон Павлович :: Грин Александр :: Горький Максим :: Борхес Хорхе Луис :: Сименон Жорж :: Андреев Леонид Николаевич Популярные книги:: Ожерелье Иомалы :: Магия луны (Том 1) :: Истина — страна без дорог (Заявление Дж. Кришнамурти о роспуске Ордена Звезды) :: Огненная река :: Ночной орёл :: О «Двух душах» М. Горького :: Русь (Часть 2) :: Роковые кости :: Звезды в их руках :: Лет за триста до братьев Люмьер |
Большая Советская Энциклопедия (ЭЛ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ЭЛ) - Чтение (стр. 33)
png">
|
|

497,7(1) |
|
|
|

|
| * |
|
|
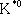
|

|
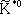
892,2(5) |
1 |
э |
50(1) |
* |
|

|
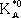
|

|
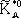
1242(10) |
1 |
|
| 127(25) |
* |
|

|
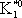
|
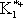
|

1421(3) |
2 |
|
| 100(10) |
* |
|
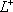
|
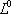
|

|
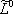
1765(10) |
? |
ш |
140(50) |
* |
|
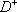
|
|
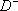
| 1868,4(9) |
0
- |
ц |
½,-S,1 |
? |
|
|
|

|
|

1863,3(9) |
0
- |
э |
? |
* |
|

|
|
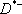
| 2009(1) |
1
- |
|
| ? |
* |
|
|
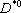
|
|
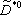
2006(1,5) |
1
- |
ш |
? |
Барионы (пВч=1) |
| p |
| p |
|
|
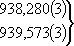
½
+ |
ц |
½,1,0 |
стабильны |
|
| n |
| n |
|
|
| 918(14) |
* |
|

|

|
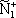
|
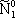
1470 |
½
+ |
|
| ~200 |
* |
|
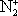
|
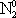
|

|
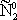
1520 |
3
2
- |
э |
~125 |
* |
|
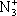
|
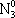
|

|
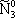
1688 |
5
2
+ |
|
| ~140 |
* |
|

|
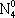
|
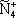
|

2190 |
7
2
- |
|
| ~250 |
* |
|

|
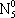
|

|

2220 |
9
2
+ |
ш |
~300 |
* |
|
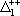
|

|
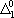
|
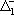
|
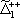
|

|

|
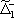
1232 |
3
2
+ |
ц |
3
2,1,0 |
~110 |
* |
|
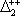
|
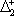
|

|

|
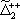
|
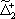
|
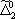
|
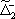
1650 |
½
- |
э |
~140 |
* |
|

|

|

|
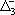
|
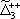
|
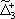
|
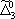
|
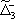
1890 |
5
2
+ |
|
| ~250 |
* |
|
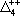
|
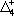
|
|

|

|
|
|
1950 |
7
2
+ |
ш |
~220 |
* |
L |
L |
1115,60(5) |
½
+ |
0,0,0 |
2,58(2)Ч10
-
10 |
* |
L
1 |
L
1 |
1405(5) |
½
- |
40(10) |
* |
L
2 |
L
2 |
1518(2) |
3
2
- |
16(2) |
* |
L
3 |
L
3 |
1820(5) |
5
2
+ |
85 |
* |
L
4 |
L
4 |
2100 |
7
2
- |
250 |
| S
+ |
|
| S
+ |
|
|
|

| ц |
1,0,0 |
0,800(6)Ч10
-
10 |
|
| S
0 |
|
| S
0 |
| ½
+ |
|
| <1Ч10
-
14 |
|
|
| S
- |
|
| S
- |
|
|
| 1,482(17) 10
-
10 |
* |
S*
+ |
S*
0 |
S*
- |
S*
+ |
S*
0 |
S*
- |
1383(1) |
3
2
+ |
э |
35(2) |
* |
|

|

|

|

|
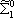
|
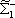
1670(10) |
3
2
- |
|
| ~50 |
* |
|
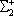
|
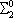
|
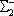
|
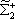
|

|

1765(5) |
5
2
- |
|
| ~120 |
* |
|
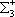
|
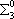
|

|
|

|
2030 |
7
2
+ |
ш |
~180 |
| X
0 |
| X
0 |
|
|
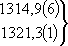
| ц |
½,-1,0 |
2,96(12) 10
-
10 |
|
| X
- |
| X
- |
½
+ |
|
| 1,65(2) 10
-
10 |
* |
X*
0 |
X*
- |
X*
0 |
X*
- |
1531,8(3) |
3
2
+ |
э |
9,1(5) |
* |
|
|
|
 X X
|
1820 |
? |
ш |
~60 |
W
- |
W
- |
1672,2(4) |
3
2
+ |
0,-2,0 |
1,3(2) 10
-
10 |
|
|
2260(10) |
½? |
0,-
2
3,1 |
<75? |
|
|

2450 |
½? |
1,-
2
3,1 |
? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| В табл. 1 приведены наиболее хорошо изученные Э. ч. из групп лептонов и адронов и их квантовые числа. В специальную группу выделен фотон. Раздельно даны частицы и античастицы (изменение Р у антибарионов не указано). Абсолютно нейтральные частицы помещены посередине первой колонки. Слева значком * помечены резонансы, для которых вместо т приведена более удобная величина - ширина резонанса
Как следует из табл. 1, лептоны представлены сравнительно небольшим числом частиц: электроном, мюоном, t-лептоном и соответствующими им нейтрино. Массы v eи v mочень малы, но равны ли они в точности нулю, предстоит решить будущим экспериментам; информация о массе v tпока ограничена. Основную часть Э. ч. составляют адроны. Увеличение числа Э. ч. в 60-70-х гг. происходило исключительно за счёт расширения данной группы. Адроны в своём большинстве представлены резонансами; наблюдается тенденция к росту спина по мере роста массы резонансов, которая хорошо прослеживается на различных группах мезонов и барионов с заданными Jи Yи Ch.Следует также отметить, что странные частицы (особенно квазистабильные) несколько тяжелее обычных (нестранных) частиц, а очарованные частицы тяжелее странных. Классификация элементарных частиц. Унитарная симметрия.Классификация лептонов пока не представляет проблем, большое же число адронов, известных уже в начале 50-х гг., явилось основанием для поиска закономерностей в распределении масс и квантовых чисел барионов и мезонов, которые могли бы составить основу их классификации. Выделение изотопических мультиплетов адронов было первым шагом на этом пути. С математической точки зрения группировка адронов в изотопические мультиплеты отражает наличие у них симметрии, связанной с группой вращения (см. ) ,более формально, с группой SU(2) - группой унитарных преобразований в комплексном двумерном пространстве. Предполагается, что эти преобразования действуют в некотором специфическом внутреннем пространстве - «изотопическом пространстве», отличном от обычного. Существование изотопического пространства проявляется только в наблюдаемых свойствах симметрии. На математическом языке изотопические мультиплеты суть неприводимые представления группы симметрии SU(2). Концепция симметрии как фактора, определяющего существование различных групп и семейств Э. ч., в современной теории является доминирующей при классификации адронов и других Э. ч. Предполагается, что внутренние квантовые числа Э. ч., позволяющие выделять те или иные группы частиц, связаны со специальными типами симметрий, возникающими за счёт свободы преобразований в особых «внутренних» пространствах. Отсюда и происходит название «внутренние квантовые числа». Внимательное рассмотрение показывает, что странные и обычные адроны в совокупности образуют более широкие объединения частиц с близкими свойствами, чем изотопические мультиплеты. Они называются супермультиплетами. Число частиц, входящих в наблюдаемые супермультиплеты, равно 8 и 10. С точки зрения симметрий возникновение супермультиплетов истолковывается как проявление существования у адронов группы симметрии более широкой, чем группа SU(2), а именно: SU(3) - группы унитарных преобразований в трёхмерном комплексном пространстве (М. Гелл-Ман и независимо Ю. Нееман, 1961). Соответствующая симметрия получила назв. унитарной симметрии. Группа SU(3) имеет, в частности, неприводимые представления с числом компонент 8 и 10, отвечающие наблюдаемым супермультиплетам: октету и декуплету. Примерами могут служить следующие группы частиц с одинаковыми значениями J P:
Общими для всех частиц в супермультиплете являются значения двух величин, которые по математической природе близки к изотопическому спину и поэтому часто называются унитарным спином. Для октета значения связанных с этими величинами квантовых чисел равны (1, 1), для декуплета - (3, 0). Унитарная симметрия менее точная, чем изотопическая симметрия. В соответствии с этим различие в массах частиц, входящих в октеты и декуплеты, довольно значительно. По этой же причине разбиение адронов на супермультиплеты сравнительно просто осуществляется для Э. ч. не очень высоких масс. При больших массах, когда имеется много различных частиц с близкими массами, это разбиение осуществляется менее надёжно. Однако в свойствах Э. ч. имеется много разнообразных проявлений унитарной симметрии. Включение в систематику Э. ч. очарованных адронов позволяет говорить о сверхсупермультиплетах и о существовании ещё более широкой симметрии, связанной с унитарной группой SU(4). Примеры до конца заполненных сверхсупермультиплетов пока отсутствуют. SU(4)-симметрия нарушена ещё сильнее, чем SU(3)-симметрия, и её проявления выражены слабее. Обнаружение у адронов свойств симметрии, связанных с унитарными группами, и закономерностей разбиения на мультиплеты, отвечающих строго определённым представлениям указанных групп, явилось основой для вывода о существовании у адронов особых структурных элементов - кварков.
Кварковая модель адронов.Развитие работ по классификации адронов с первых своих шагов сопровождалось попытками выделить среди них частицы более фундаментальные, чем остальные, которые могли бы стать основой для построения всех адронов. Начало этой линии исследования было положено Э.
и Ян Чжэнь-нином (1949), которые предположили, что такими фундаментальными частицами являются нуклон (N) и антинуклон (
В первоначальном варианте в основу модели было положено предположение, что все известные адроны построены из трёх типов частиц спина 1/ 2, названных р-, n-,l-кварками, не принадлежащих к числу наблюдавшихся адронов и обладающих весьма необычными свойствами. Название «кварки» заимствовано из романа Дж. Джойса (см. ) .Современный вариант модели предполагает существование как минимум четырёх типов кварков. Четвёртый кварк необходим для описания очарованных адронов. Идея кварков подсказана унитарной симметрией. Математическая структура унитарных групп открывает возможность описания всех представлений группы
SU(
n) (и, следовательно, всех мультиплетов адронов) на основе самого простого представления группы, содержащего
nкомпонент. В случае группы
SU(3)
таких компонент три. Необходимо только допустить наличие частиц, связанных с этим простейшим представлением. Эти частицы и есть кварки. Кварковый состав мезонов и барионов был выведен из того факта, что супермультиплеты мезонов содержат, как правило, 8 частиц, а барионов - 8 и 10 частиц. Эта закономерность легко воспроизводится, если предположить, что мезоны составлены из кварка
qи антикварка
Добавление к схеме четвёртого кварка (и, если окажется необходимым, новых дополнительных кварков) осуществляется при сохранении основного предположения кварковой модели о строении адронов:
В =( qqq). Все экспериментальные данные хорошо соответствуют приведённому кварковому составу адронов. Имеются, видимо, лишь небольшие отклонения от этой структуры, которые не влияют существенным образом на свойства адронов. Указанная структура адронов и математические свойства кварков, как объектов, связанных с определённым (простейшим) представлением группы SU(4), приводят к след. квантовым числам кварков (табл. 2). Обращают внимание необычные - дробные - значения электрического заряда Q, а также В, Sи Y, не встречающиеся ни у одной из наблюдавшихся Э. ч. С индексом a у каждого типа кварка q i( i =1, 2, 3, 4) связана особая характеристика кварков - «цвет», которой нет у изученных адронов. Индекс a принимает значения 1, 2, 3, т, е. каждый тип кварка q iпредставлен тремя разновидностями q i a(Н. Н. с сотрудниками, 1965; американские физики И. Намбу и М. Хан, 1965; японский физик И. Миямото, 1965). Квантовые числа каждого типа кварка не меняются при изменении «цвета» и поэтому табл. 2 относится к кваркам любого «цвета». Табл. 2. - Характеристики кварков
Необходимость введения «цвета» вытекает из требования антисимметрии волновой функции системы кварков, образующих барионы. Кварки, как частицы со спином 1/ 2, должны подчиняться статистике Ферми - Дирака. Между тем имеются барионы, составленные из трёх одинаковых кварков, с одинаковой ориентацией спинов: D ++( p р р ), W +(l l l ), которые явно симметричны относительно перестановок кварков, если последние не обладают дополнительной степенью свободы. Такой дополнительной степенью свободы и является «цвет». С учётом «цвета» требуемая антисимметрия легко восстанавливается. Уточнённые формулы структурного состава мезонов и барионов выглядят при этом следующим образом:
где e
a
b
g- полностью антисимметричный
(
В табл. 2 не приведены массы кварков. Это связано с тем, что кварки пока выступают лишь как составные части адронов, - в свободном состоянии они не наблюдались, поэтому прямых данных о массах кварков нет. На основании величин масс различных связанных состояний кварков (обычные, странные, очарованные адроны) можно только заключить, что mp ~ m n< m l<< m c.
Всё многообразие адронов возникает за счёт различных сочетаний
р-,
п-,g- и
с-кварков, образующих связанные состояния. Обычным адронам соответствуют связанные состояния, построенные только из
р-и
n-кварков [для мезонов с возможным участием комбинаций
Поскольку спин кварков равен 1/ 2, приведённая выше кварковая структура адронов имеет своим следствием целочисленный спин у мезонов и полуцелый - у барионов, в полном соответствии с экспериментом. При этом в состояниях, отвечающих орбитальному моменту l= 0, в частности в основных состояниях, значения спина мезонов должны равняться 0 или 1 (для антипараллельной Їи параллельной ориентации спинов кварков), а спина барионов - 1/ 2или 3/ 2(для спиновых конфигураций Ї и ). С учётом того, что внутренняя чётность системы кварк-антикварк отрицательна, значения J Pдля мезонов при l= 0 равны 0 -и 1 -, для барионов - 1/ 2 +и 3/ 2 +. Именно эти значения J Pнаблюдаются у адронов, имеющих наименьшую массу при заданных значениях Iи Y(см. табл. 1). Поскольку индексы i, k, lв структурных формулах пробегают значения 1, 2, 3, 4, число мезонов M ikс заданным спином должно быть равно 16. Для барионов B iklмаксимально возможное число состояний при заданном спине (64) не реализуется, т. к. в силу принципа Паули при данном полном спине разрешены только такие трёхкварковые состояния, которые обладают вполне определённой симметрией относительно перестановок индексов i, k, 1,а именно: полностью симметричные для спина 3/ 2и смешанной симметрии для спина 1/ 2. Это условие при l =0 отбирает 20 барионных состояний для спина 3/ 2и 20 - для спина 1/ 2. Более подробное рассмотрение показывает, что значение кваркового состава и свойств симметрии кварковой системы даёт возможность определить все основные квантовые числа адрона ( J, Р, В, Q, I, Y, Ch) ,за исключением массы; определение массы требует знания динамики взаимодействия кварков и массы кварков, которое пока отсутствует. Табл. 3. - Кварковый состав мезонов с J P = 0 -(Ї)
Табл. 4. - Кварковый состав мезонов с J P = 1 -()
В качестве иллюстрации в табл. 3 и 4, 5 и 6 приведён вытекающий из описанных представлений кварковый состав мезонов 0 -и 1 -и барионов 1/ 2 +и 3/ 2 +и его соответствие известным частицам (символы наблюдавшихся частиц подчёркнуты). 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 . Члены одного изотопического мультиплета расположены в одной строке, иногда с небольшим смещением (в тех случаях, когда даются характеристики каждого члена мультиплета).
. Члены одного изотопического мультиплета расположены в одной строке, иногда с небольшим смещением (в тех случаях, когда даются характеристики каждого члена мультиплета).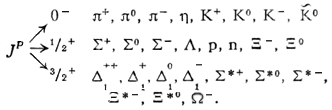
 ), a p-мезоны есть их связанные состояния (
), a p-мезоны есть их связанные состояния (
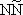 ). При дальнейшем развитии этой идеи в число фундаментальных частиц были включены также странные барионы (М. А.
,1955; японский физик С. Саката, 1956; Л. Б.
,1957). Модели, построенные на этой основе, хорошо описывали мезонные мультиплеты, но не давали правильного описания мультиплетов барионов. Важнейший элемент данных моделей - использование для «построения» адронов небольшого числа фермионов - органически вошёл в модель, которая наиболее успешно решает задачу описания всех адронов, - кварковую модель (австрийский физик Г. Цвейг и независимо М. Гелл-Ман, 1964).
). При дальнейшем развитии этой идеи в число фундаментальных частиц были включены также странные барионы (М. А.
,1955; японский физик С. Саката, 1956; Л. Б.
,1957). Модели, построенные на этой основе, хорошо описывали мезонные мультиплеты, но не давали правильного описания мультиплетов барионов. Важнейший элемент данных моделей - использование для «построения» адронов небольшого числа фермионов - органически вошёл в модель, которая наиболее успешно решает задачу описания всех адронов, - кварковую модель (австрийский физик Г. Цвейг и независимо М. Гелл-Ман, 1964). - символически:
- символически:
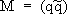 , а барионы из трёх кварков - символически:
В= (
qqq). В силу свойств группы
SU(3) 9 мезонов разбиваются на супермультиплеты из 1 и 8 частиц, а 27 барионов - на супермультиплеты, содержащие 1, 10 и дважды по 8 частиц, что и объясняет наблюдаемую выделенность октетов и декуплетов.
, а барионы из трёх кварков - символически:
В= (
qqq). В силу свойств группы
SU(3) 9 мезонов разбиваются на супермультиплеты из 1 и 8 частиц, а 27 барионов - на супермультиплеты, содержащие 1, 10 и дважды по 8 частиц, что и объясняет наблюдаемую выделенность октетов и декуплетов.
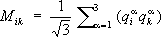 ,
,
 ,
,
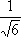 - нормировочные множители). Важно отметить, что ни мезоны, ни барионы не несут цветовых индексов (лишены цвета) и являются, как иногда говорят, «белыми» частицами.
- нормировочные множители). Важно отметить, что ни мезоны, ни барионы не несут цветовых индексов (лишены цвета) и являются, как иногда говорят, «белыми» частицами. и
и
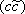 ]. Наличие в связанном состоянии наряду с
р- и
n-кварками одного g- или
с-кварка означает, что соответствующий адрон странный (
S= -1) или очарованный (
Ch =+ 1). В состав бариона может входить два и три g -кварка (соответственно
с-кварка), т. е. возможны дважды и трижды странные (очарованные) барионы. Допустимы также сочетания различного числа g- и
с-кварков (особенно в барионах), которые соответствуют «гибридным» формам адронов («странно-очарованным»). Очевидно, что чем больше g- или
с-кварков содержит адрон, тем он тяжелее. Если сравнивать основные (не возбуждённые) состояния адронов, именно такая картина и наблюдается (см. табл. 1, а также табл. 3 и 5).
]. Наличие в связанном состоянии наряду с
р- и
n-кварками одного g- или
с-кварка означает, что соответствующий адрон странный (
S= -1) или очарованный (
Ch =+ 1). В состав бариона может входить два и три g -кварка (соответственно
с-кварка), т. е. возможны дважды и трижды странные (очарованные) барионы. Допустимы также сочетания различного числа g- и
с-кварков (особенно в барионах), которые соответствуют «гибридным» формам адронов («странно-очарованным»). Очевидно, что чем больше g- или
с-кварков содержит адрон, тем он тяжелее. Если сравнивать основные (не возбуждённые) состояния адронов, именно такая картина и наблюдается (см. табл. 1, а также табл. 3 и 5).