 |
|
Популярные авторы:: Joyce James :: БСЭ :: Толстой Лев Николаевич :: Чехов Антон Павлович :: Нортон Андрэ :: Громов Дмитрий :: Грин Александр :: Раззаков Федор :: Борхес Хорхе Луис :: Сименон Жорж Популярные книги:: The Boarding House :: Уроки любви :: Справочник по реестру Windows XP :: Путь на Грумант :: Гусев :: Повесть о Воронихине :: Амнезия творца :: Том 3. Село Степанчиково и его обитатели. Записки из Мертвого дома. :: Gump & Company :: Приказы не обсуждаются |
Большая Советская Энциклопедия (ЭЛ)ModernLib.Net / Энциклопедии / БСЭ / Большая Советская Энциклопедия (ЭЛ) - Чтение (стр. 13)
,зарядовая чётность и
.С хорошей степенью точности установлено, что Э. в. инвариантно по отношению к
.Э. в. адронов нарушает присущие сильному взаимодействию законы сохранения
и G-чётности, при этом изотопический спин адронов может измениться при испускании или поглощении фотона не более чем на 1 (см., например,
)
.Унитарная симметрия адронов (SU (3)-симметрия; см.
) приводит к определённым соотношениям между электромагнитными характеристиками (например, магнитными моментами) частиц, принадлежащих к одному и тому же унитарному мультиплету.
Законы сохранения и свойства фотонов в значит, степени определяют специфические черты Э. в. Так, равенство нулю массы покоя фотона обусловливает дальнодействующий характер Э. в. между заряженными частицами, а его отрицательная зарядовая чётность - возможность радиационного распада абсолютно нейтральных частиц или связанных систем частиц [т. е. частиц (систем), тождественных своим ] ,обладающих положит. зарядовой чётностью, - p 0-мезона, парапозитрония (см. ) лишь на чётное число фотонов. Возможность описания (в соответствующем пределе) Э. в. в рамках классической (а не только квантовой) физики и его макроскопические проявления обусловлены дальнодействующим характером Э. в. и тем, что фотоны подчиняются .Малая величина се определяет малость сечений электромагнитных процессов с участием адронов по сравнению с сечениями аналогичных процессов, протекающих за счёт сильных взаимодействий; например, сечение рассеяния фотона с энергией 320 Мэвна протоне составляет около 2Ч10 -30 см 2 ,что примерно в 10 5раз меньше сечения рассеяния p +-мезона на протоне при соответствующей полной энергии сталкивающихся частиц в системе их центра масс. Тот факт, что электрический заряд определяет «силу» взаимодействия и в то же время является сохраняющейся величиной - уникальное свойство Э. в.; вследствие этого Э. в. зависят только от электрического заряда частиц и не зависят от типа частиц или электромагнитных процессов. При описании электромагнитного поля 4-мерным вектором-потенциалом Аm(m=®0,1,2,3) [ А(j, А) , А -векторный, j - скалярный потенциалы] плотность лагранжиана LЭ. в. поля с зарядом записывается в виде скалярного произведения:
где: j m- 4-мерный вектор плотности электрического тока: j =( cr , j) , j -плотность тока, r - плотность заряда. При градиентном преобразовании вектор-потенциала, которое называется также калибровочным преобразованием (2-го рода): А® А +grad f( х, t) ,
где j m ( x, t) -произвольная функция координат хи времени t,наблюдаемые физические величины (напряжённости полей, вероятности электромагнитных процессов и т. п.) остаются неизменными. Это свойство, специфическое для Э. в., получило название принципа калибровочной инвариантности - одного из принципов симметрии в природе (см. в физике), выражающего в наиболее общей форме факт существования электромагнитного поля (фотона) и Э. в. Обобщение калибровочной инвариантности на слабые взаимодействия позволило сформулировать единую теорию слабых и электромагнитных взаимодействий (см. ) . Эффекты квантовой электродинамики. К ним относятся рассеяние фотонов на электронах ( ) , ,фоторождение пар е +е -или m +m -на кулоновском поле ядер, энергии атомов из-за поляризации электрон-позитронного вакуума (см. физический) и другие эффекты, в которых можно пренебречь структурой заряда (его отличием от точечности) при взаимодействии с ним электромагнитного поля. Развитая для описания атомных явлений квантовая электродинамика оказалась справедливой для значительно меньших, чем атомные, расстояний. Изучение рассеяния электронов друг на друге и аннигиляции е ++е -® m ++m -при больших энергиях сталкивающихся частиц (до ~ 6 Гэвв системе центра масс), фоторождения пар е ++е -, m ++m -с большими относительными импульсами, а также прецизионные измерения уровней энергии электронов в атомах и аномальных магнитных моментов электрона и мюона установили справедливость квантовой электродинамики вплоть до очень малых расстояний: ~ 10 -15 см.Её предсказания с высокой степенью точности согласуются с экспериментальными данными. Так, не найдено расхождения между теоретическим и экспериментальным значениями магнитного момента мюона на уровне 10 -7%. Характерной чертой электродинамических процессов при высоких энергиях Е( Е>> mc2,где m -масса электрона или мюона) является острая направленность вперёд угловых распределений частиц (g, е ±, m ±) -продуктов процессов: бо'льшая их часть вылетает в пределах угла J Ј mc 2 /Eотносительно направления налетающих частиц. Основной вычислительный метод квантовой электродинамики - теория возмущений: благодаря слабости Э. в. процессов с участием электромагнитного поля можно разложить в ряд по степеням малого параметра a и при вычислениях ограничиться рассмотрением небольшого числа первых членов этого ряда (обычно не более четырёх). В диаграммной технике теории возмущений (см. ) простейший процесс квантовой электродинамики - взаимодействие фотона с бесструктурной (точечной) заряженной частицей входит как составной элемент в любой электродинамический процесс. Из-за малости a процессы с участием большого числа таких взаимодействий менее вероятны. Однако они доступны наблюдению и проявляются в т. н. ,в эффектах поляризации электрон-позитронного вакуума, в .В частности, поляризация вакуума приводит к рассеянию света на свете ( рис. 1 , а) -эффекту, который отсутствует в классической электродинамике; этот эффект наблюдается при рассеянии фотонов на кулоновском поле тяжёлого ядра ( рис. 1 , б) . В характере Э. в. для электронов (позитронов) и для мюонов не обнаружено отличия несмотря на значит, разницу в их массах; это легло в основу т. н. m-е-универсальности, пока не получившей теоретического объяснения. Э. в. адронов и атомных ядер.В электромагнитных процессах с участием адронов (фоторождении мезонов, рассеянии электронов и мюонов на протонах и ядрах, аннигиляции пары е +е -в адроны и др.) один из объектов взаимодействия - электромагнитное поле - хорошо изучен. Это делает Э. в. исключительно эффективным инструментом исследования строения адронов и природы сильных взаимодействий. Сильные взаимодействия, как уже упоминалось, играют важную роль в электромагнитных процессах с участием адронов. Так, резонансные состояния адронов (
) могут возбуждаться фотонами и ярко проявляются, например, в полных сечениях поглощения фотонов протонами с образованием адронов (
рис. 2
). Электромагнитные свойства и электромагнитная структура адронов (магнитные моменты, поляризуемости, распределения зарядов и токов) обусловлены «облаком» виртуальных частиц (преимущественно p-мезонов), испускаемых адронами. Например, среднеквадратичный радиус распределения заряда в протоне определяется размерами этого «облака» и составляет ~0,8Ч10
-13
см(см.
)
.Вместе со слабыми взаимодействиями Э. в. ответственны за различие масс заряженных и нейтральных частиц в изотопических мультиплетах (например, n и р, p
0и p
±). Короткодействующий характер сильных взаимодействий определяет при энергиях
Это сходство легло в основу модели векторной доминантности, согласно которой фотон взаимодействует с адронами, предварительно перейдя в адронное состояние - векторные мезоны r 0, w, j и др. Возможность такого перехода ярко иллюстрируется резонансной зависимостью от энергии сечения процесса е ++ е -® К ++ К -, обусловленной превращением виртуального фотона промежуточного состояния в векторный j-мезон и его последующим распадом на пару К- ( рис. 3 , б) .Виртуальный фотон характеризуется отличным от 0 значением квадрата 4-мерного импульса q 2 = E 2 /c 2 - p 2¹ 0, где Е, р -энергия и трёхмерный импульс фотона (для реального фотона q 2 =0). Например, для виртуального фотона, которым обмениваются электрон и протон при рассеянии, q 2 =-(4 EE'/ c 2) sin 2(J/2), где Е, E' -энергии электрона до и после рассеяния (для случая Е, E'>> mc2) ,J - угол рассеяния в лабораторной системе отсчёта. Эксперимент показал удовлетворит. применимость модели векторной доминантности для описания электромагнитных явлений с участием реальных фотонов и виртуальных фотонов с |q 2|< 2 ( Гэв/с) 2 .В частности, в сечении аннигиляции е ++ е -® m ++ m -при энергии в системе центра масс 1019,5 Мэвнаблюдаются отклонения от предсказаний квантовой электродинамики, которые вытекают из данной модели (обусловлены образованием К-мезона в промежуточном состоянии; см. рис. 3, а). (Согласно квантовой электродинамике, этот процесс происходит посредством превращения пары е +е -в виртуальный фотон g, а g - в пару m +m -. Однако модель векторной доминантности не описывает Э. в. адронов при больших | q 2|[ |q 2 | > 2( Гэв/с 2] .Так, измеренное сечение упругого рассеяния электронов на протонах, которое зависит от пространственного распределения электрических зарядов и токов внутри нуклона, спадает с ростом |q 2 |значительно быстрее, чем предсказывается моделью. Напротив, сечение глубоко неупругого рассеяния электронов (процесса е -+ р ® е -+ адроны при больших передачах энергии и импульса адронной системе) падает медленнее; при этом с увеличением полной энергии Wадронов в конечном состоянии характер рассеяния приближается к характеру рассеяния на точечной частице. Последнее обстоятельство привело к формулировке т. н. партонной модели адронов; согласно этой модели адроны состоят из частей (партонов), которые при взаимодействии с фотонами проявляют себя как бесструктурные точечные частицы. Отождествление партонов с оказалось плодотворным для понимания глубоко неупругого рассеяния. Несмотря на то, что Э. в. - наиболее полно изученный тип фундаментального взаимодействия, его продолжают интенсивно исследовать во многих научных центрах. Это обусловлено как исключительным многообразием микроскопических и макроскопических проявлений Э. в., имеющих прикладное значение, так и уникальной ролью электромагнитного поля (как хорошо изученного объекта) в исследовании строения вещества на предельно малых расстояниях, в получении сведений о других типах взаимодействий, в выявлении новых законов и принципов симметрии в природе. Эти фундаментальные исследования ведутся с использованием прецизионных методов атомной и ядерной спектроскопии, с помощью полученных на ускорителях интенсивных пучков фотонов, электронов, мюонов высокой энергии, в . Лит.:Электромагнитные взаимодействия и структура элементарных частиц, пер. с англ., М., 1969; Ахиезер А. И., Берестецкий В. Б., Квантовая электродинамика, 3 изд., М., 1969; Фельд Б., Модели элементарных частиц, пер. с англ., М., 1971; Фейнман Р., Взаимодействие фотонов с адронами, пер. с англ., М., 1975; Вайнберг С., Свет как фундаментальная частица, пер. с англ., «Успехи физических наук», 1976, т. 120, в. 4. А. И. Лебедев.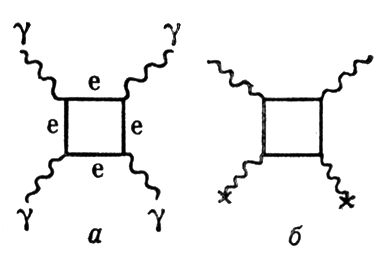 
Рис. 1. Диаграмма Фейнмана для рассеяния света на свете: ? + ? ?? + ?(а) в квантовой электродинамике; волнистые линии изображают фотоны, прямые - электроны и позитроны вакуума. Этот процесс наблюдался (б) при рассеянии фотонов на кулоновском поле ядра (помечено крестиками), т. е. на виртуальных фотонах.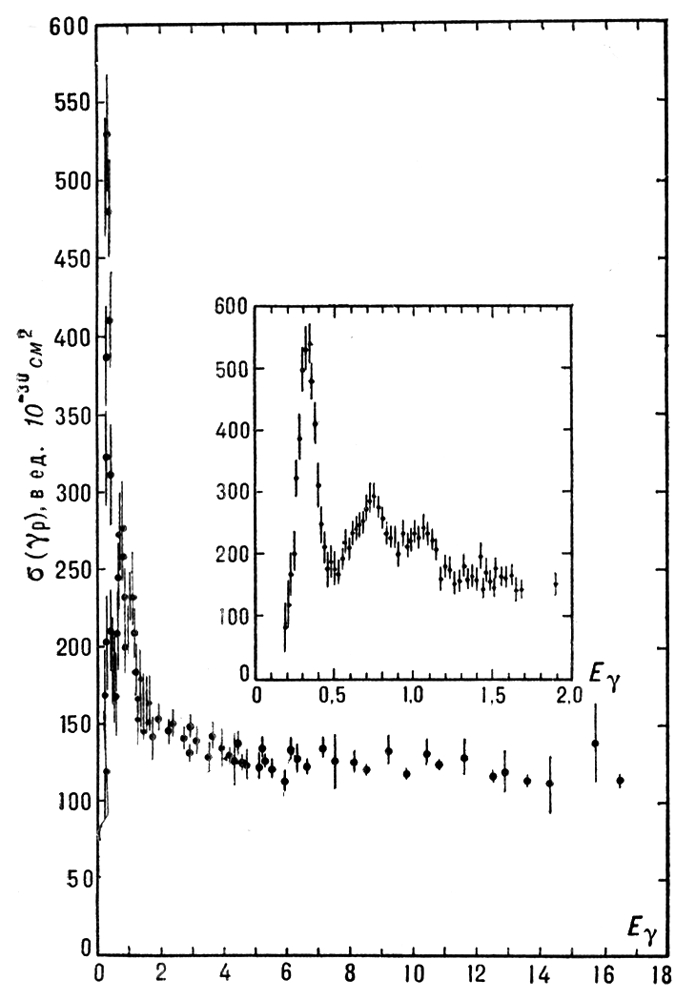 
Рис. 2. Зависимость от энергии фотона Е? в лабораторной системе полного сечения ? (?p) поглощения фотонов протонами, приводящего к образованию адронов. Максимумы соответствуют возбуждению фотонами нуклонных резонансов.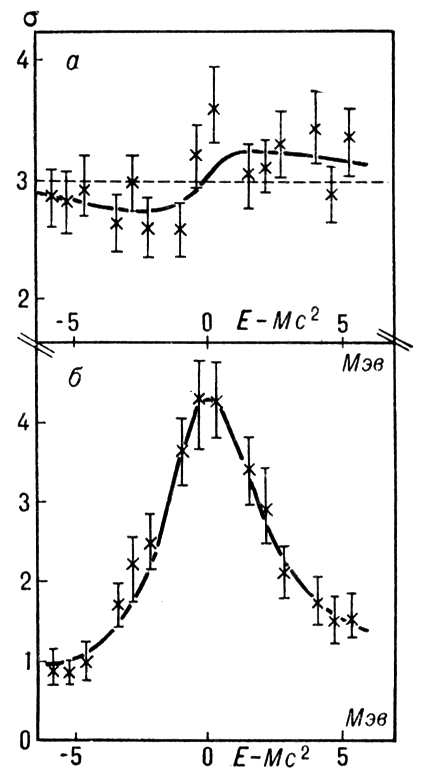 
Рис. 3. Поведение сечений s (в произвольных единицах) процессов е ++ е -® m ++ m -(а) и е ++ е -® К ++ К -(б) в окрестности порога рождения j-мезона. По оси абсцисс отложена разность Е - Мс 2, где Е- полная энергия в системе центра масс, М- масса покоя j-мезона ( Мс 2= 1019,5 Мэв). Пунктирная кривая на рис. а - предсказание квантовой электродинамики. Сплошные кривые - результаты расчётов с учётом превращения виртуального фотона в j-мезон и его последующего распада на пару m +m -через виртуальный фотон или на К ++ К -. Экспериментальные точки получены на установке со встречными пучками е +е -. Электромагнитные волны Электромагни'тные во'лны, ,распространяющиеся в пространстве с конечной скоростью. Существование Э. в. было предсказано М. в 1832. Дж. в 1865 теоретически показал, что электромагнитные колебания не остаются локализованными в пространстве, а распространяются в вакууме со сво все стороны от источника. Из того обстоятельства, что скорость распространения Э. в. в вакууме равна скорости света, Максвелл сделал вывод, что свет представляет собой Э. в. В 1888 максвелловская теория Э. в. получила подтверждение в опытах Г. ,что сыграло решающую роль для её утверждения. Теория Максвелла позволила единым образом подойти к описанию ,света, и .Оказалось, что это не излучения различной природы, а Э. в. с различной длиной волны. Частота w колебаний электрического Еи магнитного Нполей связана с длиной волны l соотношением: l =2p с/w .Радиоволны, рентгеновские лучи и g-излучение находят своё место в единой шкале Э. в. ( рис. ), причём между соседними диапазонами шкалы Э. в. нет резкой границы. Особенности Э. в., законы их возбуждения и распространения описываются .Если в какой-то области пространства существуют электрические заряды еи токи I,то изменение их со временем tприводит к Э. в. На скорость распространения Э. в. существенно влияет среда, в которой они распространяются. Э. в. могут испытывать преломление, в реальных средах имеет место волн, вблизи неоднородностей наблюдаются волн, волн (прямой и отражённой), полное внутреннее отражение и другие явления, свойственные любой природы. Пространств, распределение электромагнитных полей, временные зависимости E( t) и H( t) ,определяющие тип волн (плоские, сферические и др.), вид поляризации (см. ) и другие особенности Э. в. задаются, с одной стороны, характером источника излучения, и с другой - свойствами среды, в которой они распространяются. В случае однородной и изотропной среды, вдали от зарядов и токов, создающих электромагнитное поле, уравнения Максвелла, приводят к волновым уравнениям:
описывающим распространение плоских монохроматических Э. в.: Е = E 0cos ( kr -w t+ j) Н = H 0cos ( kr -w t+ j). Здесь e - ,mС - магнитная проницаемость среды, E 0и H 0 -амплитуды колебаний электрических и магнитных полей, w -частота этих колебаний, j - произвольный сдвиг фазы, k -волновой вектор, r -радиус-вектор точки; С 2- . Если среда неоднородна или содержит поверхности, на которых изменяются её электрические либо магнитные свойства, или если в пространстве имеются проводники, то тип возбуждаемых и распространяющихся Э. в. может существенно отличаться от плоской линейно-поляризованной волны. Э. в. могут распространяться вдоль направляющих поверхностей (поверхностные волны), в передающих линиях и в полостях, образованных хорошо проводящими стенками (см. , , ) . Характер изменения во времени Еи Нопределяется законом изменения тока Iи зарядов e, возбуждающих Э. в. Однако форма волны в общем случае не следует I( t) или e( t) .Она в точности повторяет форму тока только в случае, если и Э. в. распространяются в линейной среде (электрические и магнитные свойства которой не зависят от Еи Н) .Простейший случай -возбуждение и распространение Э. в. в однородном изотропном пространстве с помощью диполя Герца (отрезка провода длиной l <<l ,по которому протекает ток I = I 0sin w t). На расстоянии от диполя много большем l образуется волновая зона (зона излучения), где распространяются сферические Э. в. Они поперечные и линейно поляризованы. В случае анизотропии среды могут возникнуть изменения поляризации (см. ) .
В изотропном пространстве скорость распространения гармонических Э. в., т. e. фазовая скорость
Появление квантовых генераторов, в частности ,позволило достичь напряжённости электрического поля в Э. в., сравнимых с внутриатомными полями. Это привело к развитию нелинейной теории Э. в. При распространении Э. в. в нелинейной среде (e и m зависят от Еи Н) её форма изменяется. Если дисперсия мала, то по мере распространения Э. в. они обогащаются т. н. высшими гармониками и их форма постепенно искажается. Например, после прохождения синусоидальной Э. в. характерного пути (величина которого определяется степенью нелинейности среды) может сформироваться ,характеризующаяся резкими изменениями Еи Н(разрывы) с их последующим плавным возвращением к первоначальным величинам. Ударная Э. в. далее распространяется без существ, изменений формы; сглаживание резких изменений обусловлено главным образом затуханием. Большинство нелинейных сред, в которых Э. в. распространяются без сильного поглощения, обладает значительной дисперсией, препятствующей образованию ударных Э. в. Поэтому образование ударных волн возможно лишь в диапазоне l от нескольких смдо .При наличии дисперсии в нелинейной среде возникающие высшие гармоники распространяются с различной скоростью и существенного искажения формы исходной волны не происходит. Образование интенсивных гармоник и взаимодействие их с исходной волной может иметь место лишь при специально подобранных законах дисперсии (см. , ) . Э. в. различных диапазонов l характеризуются различными способами возбуждения и регистрации, по-разному взаимодействуют с веществом и т. п. Процессы излучения и поглощения Э. в. от самых длинных волн до достаточно полно описываются соотношениями .На более высоких частотах доминируют процессы, имеющие существенно квантовую природу, а в оптическом диапазоне и тем более в диапазонах рентгеновских и g-лучей излучение и поглощение Э. в. могут быть описаны только на основе представлений о дискретности этих процессов.
внесла существенные дополнения и в само представление об Э. в. Во многих случаях электромагнитное излучение ведёт себя не как набор монохроматических Э. в. с частотой w и волновым вектором
k,а как поток квазичастиц -
с энергией
Лит.:Тамм И. Е., Основы теории электричества, 9 изд., М., 1976; Ландау Л. Д., Лифшиц Е. М., Теория поля, 6 изд., М., 1973 (Теоретическая физика, т. 2); их же, Электродинамика сплошных сред, М., 1959; Ландсберг Г. С., Оптика, 5 изд., М., 1976. В. В. Мигулин.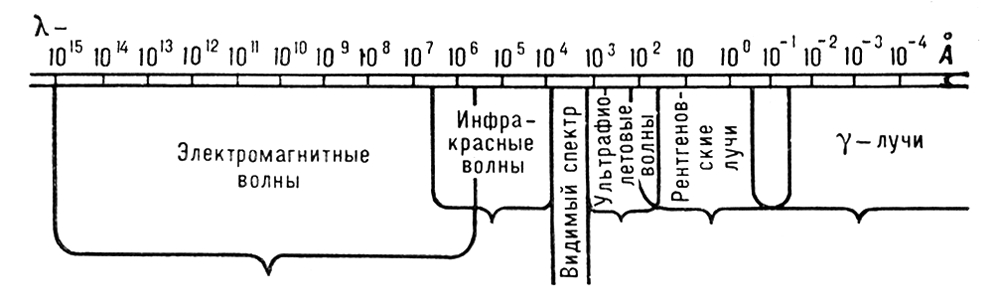 
Шкала электромагнитных волн. Электромагнитные колебания Электромагни'тные колеба'ния,взаимосвязанные колебания электрического ( Е) и магнитного ( Н) полей, составляющих единое .Распространение Э. к. происходит в виде ,скорость которых в вакууме равна скорости света с,а длина волны l связана с периодом Ти частотой w соотношением: l = cT = 2p с/w .По своей природе Э. к. представляют собой совокупность фотонов, и только при большом числе фотонов их можно рассматривать как непрерывный процесс. Различают вынужденные Э. к., поддерживаемые внешними источниками, и собственные Э. к., существующие и без них. В неограниченном пространстве или в системах с потерями энергии (диссипативных) возможны собственные Э. к. с непрерывным спектром частот. Пространственно ограниченные консервативные (без потерь энергии) системы имеют дискретный спектр собственных частот, причём каждой частоте соответствует одно или несколько независимых колебаний ( ) . Например, между двумя отражающими плоскостями, отстоящими друг от друга на расстояние l, возможны только синусоидальные Э. к. с частотами w n= пp с/l,где п -целое число. Собственно моды имеют вид синусоидальных ,в которых колебания векторов Еи Нсдвинуты во времени на T/4, а пространственные распределения их амплитуд смещены на l/4, так что максимумы (пучности) Есовпадают с нулями (узлами) Ни наоборот. В таких Э. к. энергия в среднем не переносится в пространстве, но внутри каждого четвертьволнового участка между узлами полей происходит независимая периодическая перекачка электрической энергии в магнитную и обратно. Представление Э. к. в виде суперпозиции мод с дискретным или непрерывным спектром допустимо для любой сложной системы проводников и диэлектриков (см. , , ) ,если поля, токи, заряды в них связаны между собой линейными соотношениями. В квазистационарных системах, размеры которых значительно меньше длины волны, области, где преобладают электрические или магнитные поля, могут быть пространственно разделены и сосредоточены в отдельных элементах: Е -в ёмкостях С, Н -в индуктивностях L.Типичный пример такой системы с сосредоточенными параметрами - ,где происходят колебания зарядов на обкладках конденсаторов и токов в катушках самоиндукции. Э. к. в системах с распределёнными параметрами Lи С, имеющие дискретный спектр собственных частот, могут быть представлены как Э. к. в связанных колебательных контурах (электромагнитных осцилляторах), число которых равно числу мод. В средах Э. к. взаимодействуют со свободными и связанными заряженными частицами (электронами, ионами), создавая индуцированные токи. Токи проводимости обусловливают потери энергии и затухание Э. к.; токи, обусловленные поляризацией и намагниченностью среды, определяют значения её и ,а также скорость распространения в ней электромагнитных волн и спектр собственных частот Э. к. Если индуцированные токи зависят от Еи Ннелинейно, то период, форма и другие характеристики Э. к. зависят от их амплитуд (см. ) ;при этом принцип суперпозиции недействителен, и может происходить перекачка энергии Э. к. от одних частот к другим. На этом основаны принципы работы большинства генераторов, усилителей и преобразователей частоты Э. к. (см. , ) .Возбуждение Э. к. в устройствах с сосредоточенными параметрами, как правило, осуществляется путем прямого подключения к ним генераторов, в высокочастотных устройствах с распределёнными параметрами - путём возбуждения Э. к. при помощи различных элементов связи (вибраторов, петель связи, рамок, отверстий и др.), в оптических устройствах - с применением линз, призм, отражающих полупрозрачных зеркал и т. д. Лит.:Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Андронов А. А, Витт А. А., Хайкин С. Э., Теория колебаний, 2 изд., М., 1959; Парселл Э., Электричество и магнетизм, пер. с англ., 2 изд., М., 1975 (Берклеевский курс физики, т. 2); Крауфорд Ф., Волны, пер. с англ., 2 изд., М., 1976 (Берклеевский курс физики, т. 3). М. А. Миллер, Л. А. Островский. Электромагнитный выключатель Электромагни'тный выключа'тель, ,служащий для отключения высоковольтных цепей под нагрузкой в нормальных и вынужденных режимах работы; принципиально отличается от выключателей других систем тем, что гашение электрической дуги, возникающей между расходящимися в процессе отключения цепи контактами выключателя, осуществляется непосредственно в воздушной среде т. н. электромагнитным дутьём в .Дуга затягивается в камеру дугогасительного устройства мощным магнитным полем, создаваемым электромагнитами, в обмотках которых протекает отключаемый ток. Обмотки электромагнитов имеют такую полярность, при которой создаваемое магнитное поле затягивает дугу в дугогасительную камеру (камеры), где дуга растягивается и охлаждается, её сопротивление резко увеличивается и она гаснет. Дугогасительные камеры выполняются из жаростойких материалов, обладающих высокой диэлектрической прочностью, теплопроводностью и теплоёмкостью. В Э. в. переменного тока для повышения надёжности работы обычно предусматривается воздушный поддув, который ускоряет перемещение дуги в камеру. Э. в. применяют обычно в сетях на напряжение 6-10 кв.
Лит.:Вабиков М. А., Электрические аппараты, ч. 3, М. - Л., 1963; Бронштейн А. М., Курицын В. П., Улиссова И. Н., Электромагнитные выключатели и опыт их эксплуатации, «Электричество», 1971, № 4; Быков Е. И., Колузаев А. М., Электромагнитные выключатели ВЭМ-6 и ВЭМ-10, М., 1973. Р. Р. Мамошин. Электромагнитный насос Электромагни'тный насо'с, 1) насос поршневого типа или диафрагмовый насос, у которого поступательно-возвратное движение рабочего органа осуществляется стальным сердечником, вставленным в соленоид, подключенный к источнику электроэнергии. 2) То же, что . Электромагнитный прибор Электромагни'тный прибо'р, ,принцип действия которого основан на взаимодействии магнитного поля, пропорционального измеряемой величине, с сердечником, выполненным из ферромагнитного материала. Основные элементы Э. п.: измерительная схема, преобразующая измеряемую величину в постоянный или переменный ток, и измерит, механизм электромагнитной системы ( рис. ). Электрический ток в катушке электромагнитной системы создаёт электромагнитное поле, втягивающее сердечник в катушку, что приводит к возникновению на оси вращающего момента, пропорционального квадрату силы тока, протекающего по катушке. В результате действия на ось пружины создаётся момент, противодействующий вращающему моменту и пропорциональный углу поворота оси. При взаимодействии моментов ось и связанная с ней стрелка поворачиваются на угол, пропорциональный квадрату измеряемой величины. При равенстве моментов стрелка останавливается. Выпускаются электромагнитные и для измерений главным образом в цепях переменного тока частотой 50 гц.В электромагнитном амперметре катушка измерительного механизма включается последовательно в цепь измеряемого тока, в вольтметре параллельно. Электромагнитные измерит, механизмы применяют также в .Наиболее распространены щитовые приборы классов точности 1,5 и 2,5, хотя существуют приборы классов 0,5 и даже 0,1 с рабочей частотой до 800 гц. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41 |
|||||||
,
,
(
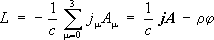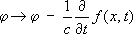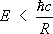R -размер адронной системы) участие в реакциях лишь низших мультипольных моментов фотона и, как следствие этого, плавную зависимость дифференциальных сечений от углов. При высоких энергиях (
Е>2 Гэв) угловые и энергетические зависимости характеристик (сечений, поляризаций и др.) процессов Э. в. адронов и чисто адронных процессов схожи [на рис. 2 s (g p) при Е>2 Гэв слабо зависит от энергии, что характерно для полных сечений взаимодействия адронов].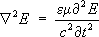
;
,
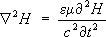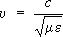. При наличии дисперсии скорость переноса энергии
с(
) может отличаться от
v.Плотность потока энергии S, переносимой Э. в., определяется
: S =(с/4p) [
ЕН]
.Т
.к. в изотропной среде векторы
Е и Н иволновой вектор образуют правовинтовую систему, то
Sсовпадает с направлением распространения Э. в. В анизотропной среде (в том числе вблизи проводящих поверхностей)
Sможет не совпадать с направлением распространения Э. в.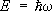
и импульсом
(
-
)
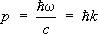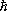.Волновые свойства проявляются, например, в явлениях дифракции и интерференции, корпускулярные - в
и
.