Лаплас

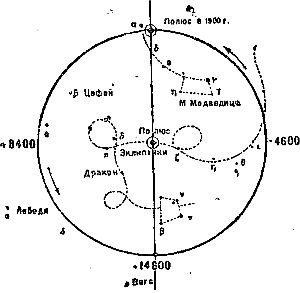
Так же изменяется ускорение и в движении одной и той же планеты, когда при движении по эллипсу меняется ее расстояние от Солнца. Пользуясь сформулированными им понятиями массы и силы, Ньютон доказал, что сила взаимного тяготения между планетой и Солнцем пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними.
      Ньютон доказал также – и это чрезвычайно важно, – что если между двумя телами действует сила тяготения, то тело с меньшей массой должно двигаться около тела с большей массой именно по законам Кеплера, а не как-либо иначе. Мало того, выведенные им законы движения под действием тяготения получили очень общий характер: те законы, которые открыл сам Кеплер, оказались лишь частным случаем этих, более общих законов.
      Таким образом, Ньютон установил законы:
      1. Всякое тело под действием тяготения к другому (большей массы) должно описывать около него одно из конических сечений (рис. 2). Коническими сечениями являются кривые, получаемые от – пересечения поверхности конуса с плоскостью. В число их входят: круг, эллипс, парабола и гипербола (рис. 2), из которых две последние кривые не замкнуты.
      2. Закон, устанавливающий, что площади, описываемые радиусом-вектором, пропорциональны времени, оказался справедливым при движении по любой из перечисленных кривых.
      3. Выражение третьего закона Кеплера, связывающее размеры орбит и периоды обращения, должно быть более сложным, в него должны войти массы Солнца и планет. Вследствие того, что масса Солнца гораздо больше массы всех планет, вместе взятых, различие между выражением третьего закона, установленным Кеплером, и выражением того же закона, найденным Ньютоном, очень незначительно. Однако именно это различие позволяет на основании наблюдаемого движения тел вычислить их массу.
      Ньютон развил также способы вычислить орбиту планеты по наблюденным положениям ее на небе среди звезд, т. е. способы определения элементов орбиты. Зная элементы орбиты, можно наперед вычислить, в какой точке неба планета будет видна с Земли в тот или другой момент.
      Далее, Ньютон сделал еще одно замечательное открытие: он доказал, что тяготение Луны к Земле имеет ту же природу, что и тяготение к ней обычных предметов, находящихся у ее поверхности. Другими словами, он доказал, что сила тяготения – та же сила, которую до тех пор называли тяжестью и наблюдали ее проявление в падении предметов на Землю. Так, большинство движений, наблюдаемых на Земле, связывалось воедино с разнообразнейшими движениями всех тел солнечной системы и находило себе общую причину: свойство взаимного притяжения, действующее во всех случаях по одному и тому же закону.
      Обнаружилось, что движение спутников вокруг своих планет происходит в согласии с тем же законом тяготения. Во второй половине XIX века было строго доказано, что и за пределами солнечной системы, в движении далеких двойных звезд друг около друга, закон тяготения действует так же, как на Земле. Недаром поэтому закон тяготения получил название всемирного. Рассматриваемый как причина, он об'яснил не только качественно, но и количественно все основные движения планет и их спутников в солнечной системе. С этих пор картина мироздания получила законченную ясность. В науке не осталось больше места для астрологии – лжеучения о мнимом влиянии небесных светил на судьбу людей и народов и о возможности, якобы, предсказать эту судьбу на основе астрономических данных.
      Тем же законом тяготения Ньютон удачно об'яснил основные черты двух явлений, стоящих на первый взгляд совсем особняком.
      Периодическое возникновение приливов и отливов в земных океанах оказалось естественным следствием различия в величине силы, с которой Луна притягивает к себе ближайшие и далекие части Земли и ее океанов.
      С давних пор было известно открытое еще Гиппархом (II в. до нашей эры) систематическое перемещение среди звезд полюса мира – точки, вокруг которой кажется происходящим суточное вращение небосвода, обусловливающее восход и заход светил (рис. 4). Благодаря этому явлению, с течением времени некоторые созвездия перестают быть видимыми в данной местности, и на смену им появляются другие. Так, рассчитано, что через несколько тысячелетий в Европе станет видимо созвездие Южного Креста, которым сейчас могут любоваться только жители Южного полушария Земли и жители тропических стран.
 

 
       Рис. 4.
 
      Вместе с перемещением полюса мира перемещается перпендикулярная к ней плоскость небесного экватора и точка ее пересечения с небесной эклиптикой – линией кажущегося годичного перемещения Солнца среди созвездий. Эта точка, называемая точкой весеннего равноденствия, медленно и равномерно смещается по направлению к западу. Солнце, перемещаясь по эклиптике, попадает каждый год в эту точку раньше, и весна на Земле ежегодно наступает раньше, чем через один полный оборот Земли вокруг Солнца. Поэтому описанное явление назвали предварением равноденствий (21 марта день равен ночи на всей Земле) или прецессией.
 

 
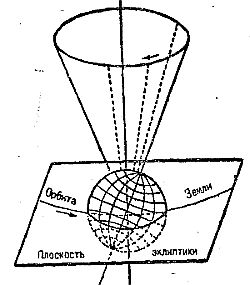
       Рис. 5.
 
      Коперник, создав свою систему мира, правильно об'яснил явление прецессии тем, что ось вращения Земли медленно поворачивается в пространстве. Она описывает при этом конус (рис. 5) с периодом в 26 тысяч лет. Каждые 26 тысяч лет весна начинается в тот момент, когда Земля находится в одной и той же точке пространства. Причина прецессии, т. е. движения земной оси по конусу, однако, оставалась загадочной. Ньютон, применив свои законы механики к вращающейся Земле, пришел к убеждению, что вследствие развивающейся при вращении центробежной силы Земля должна быть сплющена у полюсов, имея вдоль своего экватора как бы выступ.
      Между прочим, это теоретическое заключение Ньютона горячо оспаривалось французскими учеными, определявшими в 1718 году размеры и форму Земли.
      Впоследствии оказалось, что результат французских ученых был вызван неточностью их измерений. Новые измерения, произведенные в середине XVIII века, подтвердили правильность вывода Ньютона.
      Ньютон, решившись раскрыть тайну прецессии, доказал, что прецессия вызвана этой сплюснутостью Земли. Луна и Солнце, находясь обычно не в плоскости земного экватора и действуя на избыток массы, расположенной вдоль него (благодаря упомянутому сжатию), стремятся повернуть ось Земли. Но Земля вращается вокруг своей оси, и, сопротивляясь этому насилию со стороны Луны и Солнца, земная ось, в согласии с законами механики, описывает при этом конус. Общеизвестно, что Землю можно сравнить с вращающимся волчком. Если надавить на ось волчка, она станет описывать в пространстве конус, подобный тому, какой описывает ось Земли.
      Открыв закон тяготения и об'яснив им количественно почти все движения, известные астрономам, Ньютон не стремился выяснить природу этого тяготения и глубже проникнуть в его сущность. Вскоре стало принято считать, что тяготение может молниеносно передаваться через пустоту, действовать на огромных расстояниях без посредства какой-либо вещественной среды. Сам Ньютон сказал знаменитую фразу о природе тяготения: «Гипотез я не строю, ибо все то, что не может быть выведено из явлений, должно быть названо гипотезой».
      Понять закон тяготения современникам Ньютона было не легко, особенно тем из них, которые находились под влиянием философии Декарта. Многие крупнейшие ученые, даже позднейшей эпохи, не могли понять тяготения и признать его существование. Например, Лейбниц, соперник Ньютона в области изобретения дифференциального и интегрального исчислений, писал Гюйгенсу: «Я не понимаю, как Ньютон представляет себе тяжесть или притяжение. По его мнению, повидимому, это не что иное, как некое необ'яснимое нематериальное качество». Гюйгенс, тогда уже широко известный своими работами по математике, физике и астрономии, отвечал Лейбницу: «Что касается причины приливов, которую дает Ньютон, то она меня не удовлетворяет нисколько, как и все другие его теории, которые он строит на своем принципе притяжения, который мне кажется нелепым».
      Еще в 1730 году Иоганн Бернулли получил премию от парижской Академии наук за попытку выяснить причину эллиптичности орбит планет, совершенно игнорируя закон тяготения. Оппозиция, с которой теория Ньютона была принята на континенте, стала ослабевать, когда расширенная парижская Академия приняла в свой состав много молодежи, более восприимчивой к новым идеям.
      В 1727 году молодой Вольтер, вернувшись из Англии на континент, со свойственным ему остроумным сарказмом так описал антагонизм научных взглядов, разделивших передовые страны его времени на два лагеря. «Если француз приедет в Лондон, он найдет здесь большое различие в философии, а также во многих других вопросах. В Париже он оставил мир, полным вещества, здесь он находит его пустым. В Париже вселенная наполнена эфирными вихрями, тогда как тут в том же пространстве действуют невидимые силы. В Париже давление Луны на море вызывает отлив и прилив, – в Англии же, наоборот, море тяготеет к Луне. У картезианцев все достигается давлением, что, по правде говоря, не вполне ясно, у ньютонианцев все об'ясняется притяжением, что, однако, немногим яснее. Наконец, в Париже Землю считают вытянутой у полюсов, как яйцо, а в Лондоне она сжата, как тыква…»

Успехи ньютонианства

      Ньютон вполне строго разрешил проблему двух тел, т. е. вопрос о том, каково должно быть относительное движение двух тел под действием взаимного тяготения. Такой случай является идеализацией условий, имеющихся в солнечной системе. Какая-нибудь планета притягивается в действительности не только Солнцем, но и остальными планетами. В реальном мире мы имеем проблему не двух, а большего числа тел. Наиболее простым будет случай проблемы трех тел, но и эта проблема настолько сложна, что Ньютон не мог ее решить даже в самом общем виде. Однако все, сделанное им, было так грандиозно, потребовало такой затраты времени и сил, что ждать большего было невозможно. Вскоре выяснилось, что определение условия движения нескольких тел под действием взаимного тяготения требует несравненно более совершенного математического аппарата, чем тот, которым располагал Ньютон.
      Основную задачу небесной механики – изучение движения нескольких тел – можно разделить на две: одну, имеющую самый общий характер, и другую – непосредственно относящуюся к частному случаю солнечной системы. Первая значительно труднее, чем вторая. В солнечной системе масса Солнца в 770 раз больше массы всех планет вместе взятых, и потому движение их происходит в первом приближении, как говорят, в соответствии с решением проблемы двух тел, т. е. по законам Кеплера. Притяжение данной планеты остальными лишь немного расстраивает это движение. Движение немного отклоняется от законов Кеплера; например, орбита оказывается не эллипсом, а более сложной кривой, притом не лежащей строго в одной плоскости. Точно также скорость движения планеты по своей орбите в сравнении с требованиями второго закона Кеплера бывает то больше, то меньше. Эти отклонения от кеплеровского движения называются возмущениями. Они невелики и потому не помешали Кеплеру и Ньютону открыть свои законы. Тем не менее, накапливаясь с течением времени, действие возмущений заметным образом меняет элементы орбиты планеты. Если возмущения не учитывать теоретически заранее, то вычисленные наперед положения светил на небе разойдутся с наблюдениями, и астрономическая теория не ответит тем требованиям, которые пред'являют к ней техника и астрономы-наблюдатели.
      Было бы долго перечислять все области науки, техники и промышленности, которые так или иначе связаны с теорией движения небесных тел, т. е. с небесной механикой. Например, мореплавание, аэронавигация, картография и нахождение залежей подземных ископаемых нуждаются в точном теоретическом предвычислении положений небесных светил. Стоит вспомнить, например, как широко пользовались астрономическими методами ориентировки летчики Герои Советского Союза при организации плавучей полярной станции, при перелете через Северный полюс, при перелетах вдоль всего СССР и т. п. Кроме того, необходимо доказать, что если взаимное притяжение планет и расстраивает их движение по сравнению с элементарной теорией движения двух тел, то теория тяготения все же способна предусмотреть их количественно. При этом результат подсчета должен в точности совпадать с фактическими данными. Без подобного доказательства абсолютная истинность теории тяготения все же может быть подвергнута сомнению.
      Ньютон вполне отдавал себе отчет в существовании всех этих осложнений, он отметил их, но успел коснуться их математически лишь вскользь, хотя главнейшие неправильности в движении Луны, установленные наблюдателями еще до изобретения телескопа, он смог об'яснить.
      На долю последователей Ньютона – Эйлера, Клеро, Даламбера, Лагранжа и Лапласа выпало завершить! грандиозное здание, заложенное Ньютоном, и довести его до полного совершенства. Лаплас застал Эйлера и Даламбера еще в расцвете их творческих способностей. Воинствующим оплотом защитников Ньютона явилась не Англия, а Франция, так долго вначале не принимавшая ньютонианства. Лаплас был младшим в этой плеяде великих умов, и он в значительной степени закончил то, что не вполне удалось его предшественникам и старшим товарищам.
      После Ньютона Эйлер и Клеро первыми принялись за разработку небесной механики. В 1747 году Эйлер закончил работу о возмущениях в движении планет Юпитера и Сатурна. Следующие работы Эйлер посвятил исследованию движения Луны. Огромные услуги дальнейшему развитию небесной механики принесла разработка Эйлером методов дифференциального и в особенности интегрального исчислений, которые в его руках (по сравнению с тем, чем располагал Ньютон) выросли необычайно. Недаром Лаплас часто говаривал постоянно окружавшей его молодежи: «Читайте, читайте Эйлера, он наш общий учитель».
      Так же велики были и заслуги Даламбера, которого можно считать воспреемником Лапласа во французской Академии наук. В один день с Клеро он представил в Академию попытку решения проблемы трех тел и ее применения к теории движения Луны. Стало уже выясняться, что решение общей задачи о трех телах вообще не может быть получено вполне точно. Можно написать уравнения, соответствующие этой проблеме, но затем встает задача их интегрирования. Она оказалась столь трудной, по крайней мере при тогдашнем состоянии математики, что Клеро махнул на эти уравнения рукой, сказав: «Пусть интегрирует, кто сможет».
      Однако оказалось возможным найти решение поставленной задачи приближенно или для частных случаев. Тогда дело свелось к нахождению наиболее точных и практически наиболее удобных способов приближенного решения, и лучшие представители небесной механики начали соревнование в этой области.
      Даламбер решил свою задачу, пожалуй, удачнее, чем Клеро, но, как часто бывало с ним, не приложил своих формул к определенным конкретным случаям, известным в природе. Он ограничился – составлением небольших таблиц движения Луны.
      Зато Даламбер, как упоминалось, составил к 1743 году знаменитый трактат по механике – «Аналитическую механику», связавший воедино и обычную земную механику и небесную. Развитие науки о небе обогатило и прикладные знания, призванные двигать «самую земную», «самую практическую» технику.
      В 1749 году Даламбер разработал строгую теорию прецессии или предварения равноденствий, которую Ньютон мог рассмотреть лишь в общих чертах. При этом он об'яснил также и явление нутации – небольших колебаний земной оси, осложняющих явление прецессии и заставляющих земную ось как бы колебаться около того направления, – куда ее влечет действие прецессии. Оказалось, что сила, с которой Луна действует на экваториальную выпуклость Земли, меняется, ибо положение лунной орбиты в отношении Земли непрерывно и быстро меняется. Это создает изменение сил, вызывающих прецессию, – осложняет явления прецессии, т. е. создает то, что было названо нутацией (нутация была открыта уже после Ньютона – в 1721 году). Алексис Клеро в еще большей степени, чем его конкуренты – Эйлер и Даламбер, способствовал торжеству ньюотонианских идей. Еще двенадцатилетним мальчиком он сделал доклад французской Академии наук об изученных им кривых линиях. В дальнейшем его плодовитость немногим уступала эйлеровской.
      Кроме теории Луны, Клеро занимался вопросом о фигуре Земли, и его теория не только далеко продвинула вперед дело Ньютона, но до сих пор сохранила большое значение даже в ряде чисто практических вопросов.
      Однако наибольшей известностью пользуется предсказанное Клеро появление кометы Галлея. Галлей, ученик Ньютона, установил, что комета, наблюдавшаяся им в 1682 году, тождественна с рядом комет, наблюдавшихся ранее и нередко наводивших ужас на невежественное население Европы. Он нашел, что комета периодически возвращается к Солнцу, когда мы ее и видим, т. е., что эта комета обращается по орбите подобно планетам, но только эллипс ее вытянут гораздо сильнее. Время ее обращения он мог определить лишь приблизительно – семьдесят пять, семьдесять шесть лет. Это была первая периодическая комета, открытая человечеством. Галлей решился даже предсказать следующее появление своей кометы в 1758 году, когда сам он не будет в живых. Клеро предпринял грандиозную работу по точному предвычислению следующего появления кометы. Отметив значение теории тяготения, он писал: «Истинные любители науки ожидали комету с нетерпением, потому что она должна была своим появлением подтвердить законы Ньютона; другие же надеялись увидеть философов осмеянными, а их теории поколебленными, и утверждали, что она не вернется, а открытия Ньютона и его последователей не подтвердятся. Многие из них уже ликовали и смотрели на год задержки в появлении кометы, как на доказательство несостоятельности теории. Я хочу показать… что эта задержка не может повредить системе „всемирного тяготения“, а, наоборот, составляет необходимое следствие ее, и что комета опоздает более, чем на один год».
      Действительно, удалившись от Солнца, комета должна была сблизиться с Юпитером, и его притяжение должно было задержать возвращение кометы.
      Клеро, разработав теорию вопроса, спешно принялся за необходимые огромные вычисления. В этом ему помогал астроном Лаланд, известный своим атеизмом, и одна из первых ученых женщин – Гортензия Лепот, жена парижского часовщика. (В честь этой женщины Гортензией впоследствии назвали известный цветок, вывезенный из Индии). Перед самым появлением кометы Клеро опубликовал свой огромный труд, к которому Вольтер написал эпиграф:

      «Кометы, которых боятся, словно ударов грома, Полно вам пугать народы, населяющие землю; Двигайтесь по гигантским эллиптическим путям; Приближайтесь к светилу дня, удаляйтесь от: него; Распускайте ваши пламенные хвосты, Мчитесь в пространство, все время возвращаясь…»

      В результате вычислений комета Галлея должна была пройти ближе всего от Солнца 4 апреля 1759 года. В действительности же это произошло всего лишь на двадцать два дня раньше срока. Комета была замечена впервые немецким крестьянином Паличем еще в декабре 1758 года.
      Последнее появление яркой кометы Галлея состоялось в 1910 году, когда ее видели, вероятно, многие из наших читателей.
      Все эти исследования заканчивают эпоху, предшествующую появлению Лапласа на научной арене.

«НЕБЕСНАЯ МЕХАНИКА» ЛАПЛАСА

Теория возмущений

      Научные работы Лапласа трудно рассматривать в хронологическом порядке. К основным темам своих исследований он возвращался неоднократно на протяжении нескольких десятилетий, уточняя, проверяя и обобщая полученные им результаты. Некоторые его ранние исследования опубликованы лишь в его поздней капитальной работе «Небесная механика», печатавшейся в продолжение четверти века.
      Первая крупная работа Лапласа, напечатанная в 1773 году (ее автору было только двадцать четыре года), касается труднейшего, вопроса, перед которым опустили руки его предшественники: Эйлер, Клеро и молодой Лагранж. Дело шло о примирении теории тяготения Ньютона с неправильностями в движении двух самых крупных планет солнечной системы – Юпитера и Сатурна. Эти неправильности обнаруживались уже давно, но никто не мог дать им точного об'яснения, ввести в рамки известных законов природы.
      Далее, ряд работ Лапласа затрагивает другие важные вопросы небесной механики; с ними в основном он справился уже к 1784 году, когда ему исполнилось всего тридцать пять лет и он только-что был «причислен к лику» пенсионеров-академиков. В последующие годы Лаплас обобщал и подытоживал свои выводы, тщательно укладывая их, как кирпичи, в общее стройное здание астрономии. В это же время много внимания уделял он другим вопросам, в особенности теории вероятностей.
      Издание томов «Небесной механики» началось в эпоху Консульства и закончилось при Реставрации.
      Как указывалось, главной целью научной работы Лапласа было, доказать, что законом тяготения можно об'яснить все движения небесных тел как те, из изучения которых он был выведен, так и те, которые на первых порах казались ему противоречащими. «Потомство, – говорит Лаплас, – вероятно, с благодарностью увидит, что новейшие геометры не передали ему ни – одного астрономического явления, не определив его законов и причины». «Лучшим» – из геометров, о которых говорит Лаплас, был, конечно, он сам, и его успех породил в нем глубокую уверенность в абсолютной правильности закона тяготения.
      «Когда я выяснил эти неравенства (в движении Юпитера и Сатурна) – и определил с большим вниманием, чем это делалось до-сих пор, те, которые были уже вычислены, я убедился, что все наблюдения, древние и современные, представлены моей теорией во всей их точности. Прежде они казались необ'яснимыми при помощи закона всемирного тяготения; теперь же они служат одним из наиболее ярких его подтверждений. Такова судьба этого блестящего открытия: всякое затруднение, которое возникало тут, превращалось в его торжество, и это является вернейшим признаком его соответствия истинной системе природы».
      Многие из уклонений в движении планет, интересовавшие Лапласа, можно обнаружить только после громадных промежутков времени. Таких же периодов, часто превышающих возраст телескопической астрономии, требовала проверка некоторых теорий Лапласа на практике. Поэтому Лаплас живо интересовался развитием практической астрономии и для своих работ заказывал специальные переводы с греческого, индусского и даже китайского языков, если находил в сочинениях древних авторов наблюдения, которые могли принести ему пользу, Несмотря на грубость и неточность, ценность этих наблюдений была велика, именно благодаря древности, – астрономия своими корнями глубоко уходит в седую древность, а ветви ее тянутся к далекому будущему…
      При исследовании отклонений в движении планет от законов Кеплера Лапласу приходилось учитывать взаимодействие не двух тел, а трех или даже больше.
      Например, Луна движется вокруг Земли, а притяжение Солнца возмущает это движение. Сатурн движется около Солнца, но его движение нарушается притяжением других планет, главным образом, Юпитера. Лаплас интересовался как возможностью теоретически предсказать на ближайшее время положение планет, т. е. составить их эфемериды или таблицы непосредственно для практиков, так и возможностью предсказать наиболее отдаленное будущее и солнечной системы в целом и ее членов. В XVIII столетии еще не возникла идея эволюции, выдвинутая впервые самим Лапласом в результате его занятий небесной механикой. Среди многих ученых господствовало еще представление об изначальной неизменности вселенной, вытекающей из религиозных догматов. Лучшие умы того времени, например, Эйлер, убеждаясь в изменчивости природы и сталкиваясь с трудностью предсказать ее законы, становились втупик и впадали в мистицизм.
      Как же мог, однако, Лаплас об'яснить непокорные движения многочисленных детей солнечной семьи, непрестанно тревожащих друг друга? Ведь проблема трех, а тем более многих тел, практически не разрешена в общем виде и до сих пор.
      К счастью, в солнечной системе существует ряд особенностей, значительно упрощающих в применении к ней проблему многих тел.
      Эти особенности привлекли внимание Лапласа и позволили ему впоследствии создать свою знаменитую космогоническую гипотезу.
      Бездны пространства, отделяющие планеты и Солнце друг от друга, позволяют при математической трактовке движения рассматривать эти тела как материальные точки, массы которых сосредоточены в их. центрах.
      Масса Солнца гораздо больше массы всех планет вместе взятых и потому взаимодействие планет лишь понемногу отклоняет их движение от движения около Солнца по законам Кеплера. Орбиты планет имеют малые эксцентриситеты и близки к кругам, поэтому не только столкновения их, но и близкие встречи в настоящее время невозможны. Плоскости движения всех планет почти совпадают с плоскостью земной эклиптики (наклонения орбит невелики).
      При таких условиях проблема движения многих тел солнечной системы может быть разрешена приближенными методами. Необходимо, однако, найти эти приближенные методы и доказать, что точность, которую дает их применение, все время находится под контролем исследователя. Лаплас совместно с Лагранжем создал так называемые классические методы небесной механики, вдохновлявшие и вдохновляющие до сих пор многие поколения механиков неба.
      Возмущения в движении планет были представлены в классической небесной механике формулами, содержащими бесконечные ряды очень сложных членов. Простейшим приемом бесконечного ряда членов является известная из алгебры бесконечно убывающая геометрическая прогрессия.
      Нельзя думать, что метод, применяющий бесконечные ряды, – единственный и других быть не может. Это только следствие несовершенного состояния математического анализа, но хорошо уже то, что при всей громоздкости метода рядов Лаплас сумел извлечь из него поразительные результаты.
      В рядах, какими пользовался Лаплас, числовая величина членов постепенно убывает, быстро или медленно. Если можно доказать, например, для убывающей геометрической прогрессии, что сумма членов ряда конечна, и если ее нельзя вычислить точно, то можно ограничиться суммированием первых, самых больших, членов ряда, пренебрегая остальными. В небесной механике каждый член ряда выражается сложной формулой, поэтому, не всегда можно строго доказать законность подобного приближения. В некоторых случаях может быть, что где-нибудь далеко от начала, в особенности при некоторых особых условиях, член такого ряда окажется настолько большим, что пренебречь им – значит получить совсем неверный результат. Рядам можно придавать различную форму, и от неудачного выражения ряда может зависеть результат. Бывали случаи, когда до Лапласа разные ученые приходили к разным результатам из-за одного лишь различия в виде формул, которыми они пользовались. Кроме совершенствования чисто математической стороны дела, известным средством для правильности использованного приема может служить практика, даже современная созданию теории. Лаплас говорит: «Чрезвычайная трудность задач, относящихся к системе мира, принудила геометров прибегнуть к приближениям, при которых всегда можно опасаться, как бы отбрасываемые величины не оказали заметного влияния. Когда наблюдения указывали им на такое влияние, они снова обращались к их анализу; при проверке они всегда находили причину замеченных отклонений; они определяли их закон, открывая неравенства, которые еще не были указаны наблюдениями. Таким образом, можно сказать, что сама природа содействовала аналитическому совершенствованию теорий, основанных на принципе всемирного тяготения».
      В работе, названной «О принципе всемирного тяготения и о вековых неравенствах планет, которые от него зависят» (1773), Лаплас рассматривает замеченное до него явление «беспорядка» в движении гигантских планет.
      Из сравнения древнейших наблюдений с современными выяснилось, что Сатурн Двигался С явным замедлением, а Юпитер испытывал ускорение своего движения.
      Лаплас погрузился в изучение вопроса, на котором потерпели поражение и Эйлер и Лагранж, – по крайней мере, их выводы были противоположны.
      Представляя возмущения в движении планет бесконечными рядами членов, создатели небесной механики убедились, что члены таких рядов бывают двух видов. В одних из них время, рассматриваемое как переменная величина, входит множителем в некоторой степени, в других же это время входит под – знак так называемой «периодической функции» (встречаются, впрочем, члены и смешанного вида). Первые из этих членов называются вековыми, вторые – периодическими. Если в формуле, выражающей изменения в величине какого-нибудь элемента, характеризующего определенную орбиту, есть только периодические члены, этот элемент испытывает лишь периодические колебания, не выходя из известных пределов. Например, в этом случае наклон плоскости орбиты планет к плоскости эклиптики то увеличивается, то уменьшается, но никогда не становится очень большим. Если в формуле содержатся вековые члены, то данный элемент с течением времени будет изменяться постоянно в одном и том же направлении. Например, линия узлов планетной орбиты будет непрерывно вертеться около Солнца, все время в одну и ту же сторону!
      В 1773 году Лаплас применил ряды к исследованию движения Юпитера и Сатурна, пользуясь в усовершенствованной форме методом, предложенным Лагранжем (в 1766 г.). При этом Лаплас доказал, что Эйлер и Лагранж, вычисляя свои ряды, отбросили такие члены, которых нельзя было отбрасывать, ибо их величина с течением времени становилась не меньше той, какую давали первые члены рядов. Таким образом, Лаплас получил более точные формулы, и когда он подставил в них соответствующие числа для Юпитера и Сатурна, то оказалось, что, благодаря принятию им во внимание новых членов ряда, вековые ускорения для этих планет пропали. Это доказывало, что ускорения, наблюдаемые в движении Юпитера и Сатурна, являются не вековыми, а периодическими, хотя и имеющими, повидимому, очень длинный период, измеряемый не одним столетием.
      В 1784 году, через десять с лишним лет, Лаплас снова вернулся к этой нерешенной окончательно задаче.