Лаплас

      Лагранж, с которым Лаплас, младший по возрасту, только начинал соперничать, писал непременному секретарю Академии Кондорсе: «Меня несколько удивляет то, что Вы мне пишете о Лапласе: это – недостаток, свойственный главным образом очень молодым людям – кичиться своими первыми успехами. Однако самонадеянность обычно уменьшается по мере того, как увеличиваются знания», но и впоследствии самоуверенность Лапласа отталкивала от него многих.
      Другая характерная черта Лапласа, которая создавала ему много покровителей, но мало друзей, состояла в заискивании перед власть имущими. В своем стремлении угодить Лаплас не стеснялся, что не могло нравиться, в частности, и Даламберу. Устроив его преподавателем в военную школу и впоследствии помогая ему неоднократно, Даламбер отзывался о Лапласе несколько суховато. Впрочем, Лаплас скоро уже начал соперничать с ним самим и не раз уязвлял самолюбие Даламбера.
      Неудача на выборах во французскую Академию наук сильно разочаровала Лапласа, но он твердо решил улучшить свое положение.
      Прусский король Фридрих II прослыл философом и меценатом. Король выписал в свое время в Берлин великого Эйлера и знаменитого Лагранжа. Эйлер, ранее уже живший в России, в 1766 году вторично уехал из Берлина в петербургскую Академию наук, куда его «на любых условиях» настойчиво приглашала Екатерина II. В это время Эйлер был уже слеп, но сила его гения и воображения была такова, что он с прежней энергией продолжал разработку труднейших проблем, диктуя свои статьи сыну и ученикам. Как увидим, многие из работ Лапласа были развитием и усовершенствованием того, что поразительный по плодовитости швейцарец год за годом публиковал в изданиях петербургской Академии наук. После от'езда Эйлера в Петербург Лагранж состоял президентом берлинской Академии наук.
      Немедленно после своей неудачи в Париже Лаплас начал хлопотать о приглашении его «на приличную пенсию» в берлинскую Академию наук и снова обратился за содействием к Даламберу. Несмотря на то, что Лаплас ему не очень нравился как человек, Даламбер взял на себя эту заботу и начал переписку с Лагранжем. Рекомендуя Лапласа, Даламбер отзывался о нем довольно холодно, холоднее, чем этого заслуживал талантливый юноша. Все же он писал: «Этот молодой человек горит желанием заниматься математикой, и я думаю, что у него достаточно таланта, чтобы выделиться в этой области».
      Лагранж не имел оснований противиться переходу Лапласа в Берлин, но искренне не советовал ему это делать. В своем ответе Даламберу Лагранж писал, что условия в берлинской Академии наук совсем не блестящи и недаром больной Эйлер променял покровительство «короля-философа» на туманную столицу России, где крепостничество и самодурство бесконечных царицыных фаворитов находились в своем апогее.
      Действительно «король-философ» платил Эйлеру, светочу своей Академии, мизерное содержание, оставшееся ничтожным даже после того, как Лагранж, гостя в Берлине, выпросил для него у монарха жалкую прибавку. «Чистая математика» мало интересовала Фридриха, и он с открытым подозрением относился к пользе дифференциального исчисления. На что мог рассчитывать при таких условиях молодой француз, еще не получивший никакой известности?
      Пока тянулись эти переговоры, Лаплас и сам вступил в научную переписку со старшим по возрасту Лагранжем, и их научная судьба с этих пор тесно переплелась между собой.
      Лаплас и Лагранж работали в одной области, и у них надолго установилось своего рода соревнование. Работы их часто так тесно связывались, что рассматривать их отдельно почти невозможно. Один из них нередко высказывал идеи, которые затем использовал и расширял другой. То один из них углублял методы и анализ, предложенные другим, то, наоборот, и между ними начиналась научная конкуренция, доходившая иногда и до корректного, но настойчивого спора о приоритете открытия данного явления или метода исследования.
      В 1759 году Лагранж, по рекомендации Эйлера, восхищенного его талантом и работоспособностью, был избран в берлинскую Академию наук, но переехал туда лишь в 1766 году, после от'езда Эйлера в Россию.
      Сделавшись президентом берлинской Академии наук, он получил несколько премий от парижской Академии наук за свои исследования по небесной механике – по теории движения Луны и спутников Юпитера.
      Уже после смерти Фридриха II в 1787 году Лагранж отклонил приглашения, сделанные ему королевствами Неаполя и Сардинии, а также герцогством Тосканским, и переехал в Париж, где и прожил до своей смерти.
      Основной заслугой Лагранжа является созданная им ко времени переезда в Париж «аналитическая механика» удивительная по стройности мысли и красоте изложения. Основные законы равновесия и движения тел Лагранж выразил несколькими знаменитыми уравнениями, носящими теперь его имя.
      Характеры Лагранжа и Лапласа были весьма различны. Спокойный и добродушный Лагранж вызывал самое восторженное восхищение у всех, кто его знал. Завязавшаяся в 70-х годах переписка Лагранжа с Лапласом касается исключительно научной работы и обмена мыслями и выводами. Ни политическая жизнь, ни личные события в них не отражены: оба они с головой были погружены в научную работу, события же, волновавшие всю Европу и заставившие каждого француза определить свое место среди борющихся партий, произошли значительно позднее.
      Переписка двух величайших людей своего века – Лагранжа и Лапласа – не дает ничего для уяснения их личной жизни, хотя чрезвычайно ярко вскрывает мировоззрение Лапласа как ученого. Возникшая, в связи со стремлением Лапласа в Берлин, его переписка с Лагранжем становилась все оживленней.
      Дело приглашения Лапласа в берлинскую Академию наук тянулось несколько месяцев и было, наконец, прекращено, так как уже в следующем после начала хлопот году (1773) двадцатичетырехлетний Лаплас был избран в парижскую Академию наук, правда, не как геометр, чего ему хотелось, а как ад'юнкт-механик. Избранием в Академию полоса небольших затруднений в жизни Лапласа была закончена: молодой ученый получил официальное признание и возможность усиленной научной работы, хотя назначенное ему содержание было все еще очень скудным.

Лестница успехов

      Можно себе представить гордость юноши, когда он впервые отправился на заседание Академии, открытое только для избранных. Аппартаменты Академии помещались в первом этаже Лувра и выходили окнами на широкий внутренний двор. Нужно было подняться по лестнице Генриха II, потом пройти через бывший «Зал правительства», разбитый на мелкие комнатки с коридором между ними, шириной шагов в двенадцать, и отсюда в «Зал Генриха II», в котором происходили заседания Академии. Пройдя через следующий «Зал семи каминов», посетитель доходил до комнат, отведенных для опытов анатомов и механиков. «Зал семи каминов» был разбит тогда на две комнаты, в одной из которых красовались скелеты крупных четвероногих – слонов и верблюдов, большие земные и небесные глобусы и находилась часть библиотеки. В другой комнате помещалась главная часть библиотеки. В 1785 году «его величество милостиво пожаловал» Академии подвал, в котором велел устроить кунсткамеру, доступную для публичного обозрения.
      Знакомство с Бошар де Сароном, состоявшееся при содействии Даламбера, вскоре помогло Лапласу улучшить свое положение и найти в лице Бошара издателя своих трудов, а через одиннадцать лет получить место экзаминатора в королевском корпусе артиллеристов; это место занимал раньше известный математик Безу, и оно давало приличное жалованье. Смерть Безу позволила Лапласу получить сносное материальное обеспечение. Ко времени знакомства с Лапласом Бошар де Сарон прошел длинный путь государственных должностей. Он был сведущим математиком и астрономом и в 1779 году был назначен в Академию наук почетным членом. Им были опубликованы некоторые научные работы (в 1761 и 1769 гг.). Бошар де Сарон принимал участие в вычислениях астрономов и иногда давал им средства на опубликование трудов или на приобретение новых инструментов. Кроме Лапласа, покровительством Бошар де Capoнa пользовались и другие астрономы.
      В начале 1776 года военная школа, куда пять лет назад Даламбер устроил Лапласа, была совершенно реорганизована, и Лаплас должен был оставить свою должность. Однако ему назначили (вероятно, не без хлопот с его стороны) пенсию в размере 600 ливров «за услуги, оказанные в качестве профессора математики».
      В 1785 году Лаплас был назначен пенсионером на место скончавшегося Леруа, т. е. стал полноправным членом Академии наук. Назначение Лапласа пенсионером состоялось в связи с новой реорганизацией Академии. По королевскому указу от 23 апреля 1785 года Академия наук была разбита на восемь разрядов: геометрии, астрономии, механики, физики, анатомии, химии и металлургии, ботаники и агрономии, естественной истории и минералогии. В каждый разряд назначалось по три пенсионера и по три сотрудника. Кроме них, назначались непременный секретарь и казначей, двенадцать почетных академиков и двенадцать нештатных «сотрудников». Восемь мест «сотрудников» было оставлено для иностранцев. В разряд механики были назначены пенсионерами Лаплас и два аббата – Боссю и Рошон. В разряд геометрии, куда первоначально метил Лаплас, среди других назначили Борда и Кузеня. Разряд астрономии составили Лемонье, Лаланд и Лежантиль (пенсионеры), Кассини и Дажеле (сотрудники). Друг Лапласа – астроном Байи попал в разряд физики, а среди химиков близкими ему людьми являлись пенсионер Лавуазье и сотрудник Бертолле. Вскоре Лавуазье был назначен директором Академии.
      Еще в самом начале пребывания в Академии наук Лаплас написал свою основную работу по вопросу об устойчивости солнечной системы; она имела значение не только для астрономии, но дала богатую пищу и для философской дискуссии. Попутно он выполнил ряд ценных работ по чистой математике и физике.
      Работы Лапласа по чистой математике, сравнительно немногочисленные, относятся К двум периодам; к ранней молодости (1771–1777) и к поздним годам (1809). Они касаются преимущественно так называемой теории интегрирования уравнений в частных производных. Некоторые из данных им методов применяются до сих пор и носят имя Лапласа.
      Другие работы Лапласа по математике, о которых речь будет дальше, связаны с теорией тяготения и с теорией вероятностей. Они касались теории определителей, теории алгебраических уравнений и теории конечных разностей. Гораздо важнее была развитая Лапласом теория потенциала и открытие шаровых функций, играющих теперь большую роль в естествознании.
      Среди второстепенных работ Лапласа хорошо известны его исследования о теплоте и электричестве, сделанные им совместно с Лавуазье, с которым он в период 1779–1784 годов был очень близок.
      Гениальный родоначальник современной научной химии был богатым человеком, имел большую собственную лабораторию и не жалел средств на производство опытов в таком масштабе и с такой точностью, которые не снились его предшественникам.
      Лавуазье, поддерживаемый Бертолле, Фуркруа и Гиттоном де Морво, вел горячую и упорную борьбу с защитниками старых взглядов, ведущих свое начало от алхимии и мистицизма. До какой степени разгорались страсти в этой борьбе, можно судить по тому, что в Германии был торжественно сожжен портрет Лавуазье, как вредного научного шарлатана. Лаплас не только решительно поддерживал великого химика своими трудами и авторитетом, но и лично оказывал на него огромное влияние.
      Лаплас и Лавуазье занялись вопросом о теплоемкости тел, о так называемой скрытой теплоте плавления, т. е. о том количестве тепла, Которое надо затратить, чтобы твердое тело перевести в жидкое состояние. Они же определяли теплоемкость тел, т. е. количество тепла, которое нужно им сообщить, чтобы единицу их массы нагреть на один градус. Для определения теплоемкости тел они устроили прибор – «ледяной калориметр», до сих пор иногда употребляющийся наряду с более совершенным калориметром Бунзена (предложен лет на восемьдесят позднее). Этим прибором Лаплас и Лавуазье измерили теплоемкость ряда тел и, кажется, это был единственный случай, когда Лаплас соприкоснулся вплотную с наблюдением и экспериментом. Вероятно, лабораторная часть работы лежала практически на Лавуазье и его помощниках. Их данные по расширению твердых тел были первыми, пригодными для практики. Для измерения самого расширения они впервые применили зрительную трубу. Эти опыты долгое время, однако, не обращали на себя внимания ученых.
      В 1783 году Лаплас вместе с Лавуазье принимал участие в опытах по горению водорода в кислороде. Он помогал Лавуазье и в обосновании теории теплоты и в борьбе с устаревшей гипотезой о флогистоне.
      В туманных представлениях химиков старого закала флогистон был «жидкостью», особым тонким веществом, выделяющимся из тел при горении и нагревании. Опыты и теоретические рассуждения Лапласа и Лавуазье положили начало правильному взгляду на процессы горения и окисления тел. В частности, в некоторых высказываниях Лапласа мелькает правильный взгляд на теплоту, как на один из видов движения материи.
      В марте 1780 года Париж посетил Вольта. В связи с исследованием атмосферного электричества он демонстрировал в Академии следующий опыт. Он испарял в сосуде воду и доказал, что водяной пар заряжается положительным, а металлический сосуд отрицательным электричеством. Одновременно с ним эти опыты произвели Лаплас и Лавуазье, и можно считать, что все трое одновременно и совместно явились первыми исследователями происхождения атмосферного электричества. Через шестьдесят три года их опыт был повторен гениальным Фарадеем.
      В эти непосредственно предшествующие революции годы Лаплас уделил некоторое время вопросам, связанным с социальной гигиеной.
      Так, например, в 1785 году Лаплас участвовал в комиссии Академии, которая под руководством Байи обследовала состояние больницы для бедных, известной под названием «Дом милосердия». Комиссия была назначена потому, что городской архитектор Пойе предлагал перевести больницу в другое помещение, но администрация больницы всячески Препятствовала обследованию. Отчет комиссии рисует самую жуткую и омерзительную картину безобразий и издевательств, чинимых над больными. Это был очаг заразы и царство ужасающей смертности. Больных оспой укладывали по шестеро на одну кровать в полтора метра шириной. На такую же кровать помещали вповалку тифозных и беременных, детей и взрослых. Нечистоты валялись тут же, в палатах, и на них лежали те, для кого нехватало постелей. Стоит ли добавлять, что доклад Академии не привел ни к каким переменам, и «Дом милосердия» или, вернее, «Дом истязаний» просуществовал в том же виде еще шестьдесят лет.
      В 1786 году Лаплас в комиссии того же состава обследовал антисанитарное состояние парижских боен. Ряд столетий бойни находились в самом городе, распространяя заразу, грязь, зловоние. Доклад правительству, назначившему эту комиссию, с требованием вынести бойни за город, также остался безрезультатным. Лишь через пятнадцать лет Наполеон освободил столицу от боен.
      Годы, следовавшие за вступлением в Академию наук до самой революции 1789 года, текли для Лапласа тихо и спокойно. За это время им были выполнены и напечатаны его главные работы, в частности – по небесной механике, хотя вторичное опубликование их в виде обобщенной сводки в «Небесной механике» началось лишь после революции и продолжалось много лет.
      В марте 1788 года, в возрасте тридцати девяти лет, Лаплас женился на Шарлотте де Курти, красивой женщине с живым и мягким характером. Она всячески стремилась обеспечить мужу наилучшие условия для работы. Она была гостеприимна, и в доме Лапласа с удовольствием проводили время его многочисленные знакомые и ученики. Через год после женитьбы Шарлотта Лаплас родила сына, которому дали имя Шарль Эмиль Пьер Жозеф.

ВСЕМИРНОЕ ТЯГОТЕНИЕ

Новая астрономия

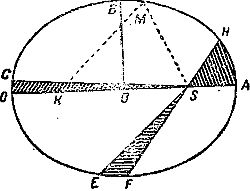
      За два столетия до Лапласа скромный Николай Коперник произвел революцию в мировоззрении человечества и в астрономии. Он сдвинул Землю с того центрального и неподвижного места, которое в течение тысячелетий она занимала в глазах человечества.
      Смелостью своей мысли Коперник низвел Землю с роли божьей фаворитки в разряд планет, свершающих свой круговой бег около лучезарного Солнца. В этом ряду он назначил Земле третье место по ее расстоянию от Солнца и, допустив ее вращение вокруг наклонной оси, об'яснил все основные небесные явления, известные человечеству в ту пору. Кажущийся путь Солнца среди созвездий в течение года по линии, называемой эклиптикой, смена времен года, восход и заход звезд, Солнца и Луны – все стало естественным следствием движений Земли. Замысловатое петлеобразное движение планет среди созвездий Коперник об'яснил сочетанием движения Земли и планет. Мы видим эти планеты с движущейся Земли и потому смотрим на них, тоже не остающихся в покое, все время из разных мест пространства. Звезды, несравненно более далекие и лежащие в безднах, простирающихся за пределами солнечной системы, являются тем фоном, на котором планеты кажутся перемещающимися.
      Коперник не мог все же отрешиться еще от мистической идеи о «совершенстве» небес. Он допустил для планет лишь «совершенное» круговое движение и комбинацией таких круговых движений приблизительно согласовал данные наблюдений со своей теорией. В этом вопросе Коперник не отошел от традиционной точки зрения, утвержденной авторитетом Птолемея, которого, несмотря на его «языческое вероисповедание», через тысячу лет после смерти канонизировала в области науки католическая церковь.
      Новым идеям Коперника церковь об'явила войну не на жизнь, а на смерть, и его последователи, обвиненные в ереси, шли на костры, пытки, в тюрьму. Несмотря на все гонения, мировоззрение Коперника, поддержанное философией Бруно, телескопическими открытиями и публицистикой Галилея, одержало верх в этой жестокой борьбе, и к середине XVII века число людей, уверовавших в эту истину, число коперниканцев, стало значительным. Клерикальные силы уже не могли остановить победоносного шествия науки, и волна критического изучения природы и места человека в ней начала разливаться по Европе. Это уже не была схоластическая мудрость средневековья. Критерий человеческой практики, введенный Галилеем в науку, все больше стал входить в обиход исследователей.
      Современник Галилея Кеплер в начале XVII века решил согласовать теорию Коперника с богатейшими рядами наблюдений, оставленными ему в наследство его учителем, искуснейшим наблюдателем предыдущих веков – Тихо де Браге.
      Теория Коперника в том виде, как она вышла из рук своего творца, не вполне согласовалась с наблюдениями. Предполагавшая в своей первоначальной форме круговое движение планет, она не являлась надежным средством к предвычислению видимого положения планет на небе. Растущие потребности мореплавания и картографии требовали улучшения таких предвычислений. Быстрый рост морских путей сообщения понуждал моряков определять свое местоположение в необозримых просторах океана, и яркие светила-планеты, видимые для глаза как яркие звезды, были очень удобны для этой цели. Между тем, ни отмирающая теория Птолемея, ни новая теория Коперника не давали нужной точности.
      В поисках причины этого разногласия между теорией и наблюдениями Кеплер открыл свои знаменитые законы, установившие истинную закономерность движения планет. Он убедился в том. что движение планет происходит вокруг Солнца не по кругам, а по эллипсам, что Солнце находится в так называемом фокусе этих эллипсов. Напомним, что фокусами эллипса называются две такие точки (S и К на рис. 1), сумма расстояний которых от любой точки эллипса есть величина постоянная. Вместе с тем Кеплер убедился, что движение планет, в том числе и Земли, происходит по этим путям (орбитам) не равномерно, а так, что радиус, проведенный от Солнца к планете (радиус-вектор), своим движением описывает площадь, пропорциональную времени. Это означает, что, находясь ближе всего к Солнцу (в перигелии), планета движется быстрее, а находясь от него дальше всего (в афелии), движется медленнее.
      Эти два закона вполне определили истинный характер движения планет и, устранив из небесного пространства «совершенное» круговое движение, сделали мировоззрение Коперника ближе отвечающим как об'ективной истине, так и здравому смыслу и практическим запросам жизни.
      В поисках правильных числовых соотношений между размерами орбит, по которым несутся в пространстве планеты, и временами (периодами) их обращения около Солнца Кеплер открыл свой третий закон; квадраты времен обращения планет около Солнца относятся как кубы их средних расстояний от Солнца. Этим законом была окончательно установлена истинная закономерность движений планет. Вместе с тем, третий закон Кеплера позволяет, определив из наблюдений период обращения планеты около. Солнца, сразу высчитать ее расстояние от него. Заметим, что средним расстоянием планеты от Солнца является большая полуось описываемой ею эллиптической орбиты (ОА на рис. 1).
 

       Рис. 1.
 
      Для полной характеристики орбиты данной планеты потребовалось ввести понятие о шести величинах, так называемых элементах орбиты. Одним из них является большая полуось орбиты, выражаемая в единицах большой полуоси земной орбиты. Последнюю поэтому называют «астрономической единицей» Второй элемент определяет степень вытянутости эллипса и измеряется величиной его эксцентриситета.
 

 
       Рис. 2. Конические сечения.
 
      Для круговой орбиты эксцентриситет равен нулю и растет с увеличением вытянутости эллипса. При эксцентриситете, равном единице, эллипс становится бесконечно вытянутым, так что если один из его фокусов остается на месте, то другой отодвигается в бесконечность, и две ветви этого эллипса в пределе становятся параллельными друг другу: они никогда больше фактически не соединяются. Такая, уже разомкнутая кривая называется параболой и изображена на рис. 2. Третий элемент определяет угол i, под которым плоскость планетного эллипса наклонена к плоскости земной орбиты (плоскость эклиптики), и называется наклонением.
      Четвертый элемент определяет положение в пространстве той линии, по которой пересекаются плоскости планетной и земной орбит. Он измеряется углом ?, который отсчитывают от некоторого неизменного направления, идущего от Солнца в мировое пространство. Этот элемент называют долготой восходящего узла.
      Пятый элемент указывает угол ? который с упомянутой линией пересечения плоскостей, называемой линией узлов, образует направление от Солнца на перигелий планетной орбиты. Этот элемент называют расстоянием перигелия от узла и выражают его в градусах.
 

 
       Рис. 3. Элементы планетных орбит.
 
      Шестой элемент представляет один из моментов времени, когда планета при своем движении проходит через точку перигелия.
      Зная шесть элементов орбиты, которые вначале считали совершенно постоянными, легко представить себе мысленно, как расположена орбита данной планеты по отношению к Солнцу и к орбите Земли. Знание шести элементов орбиты позволяет, как доказал сам Кеплер, всегда строго рассчитать, в какой точке своего пути находится планета в любой момент будущего или прошедшего времени. Зная, где в то же время находится на своей орбите Земля, легко рассчитать, как должна быть видна планета с нее в этот момент, в каком созвездии и на каком расстоянии от Земли. Когда впоследствии были открыты спутники, обращающиеся вокруг своих планет подобно тому, как Луна обращается вокруг Земли, то оказалось, что их движение также подчиняется законам Кеплера, если только в них слово Солнце заменить словами «своя планета». Например, системы девяти спутников Юпитера и девяти спутников Сатурна являются как бы уменьшенными копиями системы Солнца и планет. Луна тоже движется по законам Кеплера, и в фокусе ее эллиптической орбиты находится Земля. Когда в почти бесконечной дали от солнечной системы были открыты двойные звезды, из которых меньшая обращается около большей, то и тут оказались в силе законы Кеплера. Очевидно, движения небесных тел, происходящие везде по законам Кеплера, всеобщи и обусловлены одной причиной.

От Кеплера до Ньютона

      Кеплер открыл законы движения планет, но он еще не об'яснил их причины. Почему, например, именно Солнце находится в фокусе всех планетных орбит? Кеплер сравнивал Солнце с магнитом по его Действию на планеты и полагал, что вращающееся Солнце своими лучами увлекает планеты в движение по орбитам. Правда, он понимал, что тут кроется какая-то иная причина, но не мог даже выразиться ясно о ней – четкое понятие силы и взаимодействия было лишь позднее введено Ньютоном. Кеплер писал: «Физики, навострите ваши уши, ведь здесь предпринимается замысел насчет вторжения в вашу область». Но вторгнуться в эту область никто не мог, потому что из всех понятий механики были сколько-нибудь разработаны только простейшие понятия статики (учения о равновесии) и кинематики (науки о движении). Понятия динамики – учения о силах и их взаимодействии, четкие понятия массы и ускорения создал лишь гений Ньютона.
      В таких условиях большое впечатление произвела на современников теория вихрей, выдвинутая во Франции Декартом в 1644 году.
      По мнению Декарта, к которому нам придется еще не раз возвращаться, мировое пространство заполнено особым, легко подвижным веществом, образующим гигантские вихри. В центральной части каждого такого вихря сгущается светоносное вещество, образующее небесные светила. Вихри Декарта, которые он называет небесами, окружают все небесные тела, причем каждое из них окружено одним таким вихрем. Эти вихревые потоки увлекают и приводят в движение все тела, попадающие в сферу вихря. Так, солнечный вихрь увлекает в своем движении все планеты с их спутниками, а вихрь, окружающий Землю, увлекает круговым движением около Земли ее спутника Луну. Так же двигаются вокруг своих планет и другие спутники, причем в каждом вихре тело, находящееся ближе к центру, вращается вокруг него быстрее, чем более далекое – точно так же, как речные водовороты крутят соломинки, захваченные течением воды. Этим Декарт об'яснил в глазах своих современников тот поражавший их факт, что, чем ближе планеты к Солнцу, тем короче периоды их обращения – всего 88 дней для Меркурия, 225 дней для Венеры, год для Земли и т. д. вплоть до долгих тридцати лет, в течение которых Сатурн только один раз завершает свой путь вокруг центрального светила.
      Конечно, такие взгляды являлись огромным шагом вперед по сравнению с средневековыми воззрениями, так выпукло обрисованными в строфах «Божественной Комедии» Данте и позднее в поэме Торквато Тассо «Освобожденный Иерусалим».
 
«… Планеты ниже стройные вертятся,
Что ангелами в ход приведены.
Так что в пути не могут заблуждаться…»
 
      Эллиптическое движение планет по известным уже тогда законам Кеплера Декарт мог об'яснить лишь очень неясно, говоря, что под действием давления соседних вихрей и от других причин вихри могут принимать сплюснутую или эллиптическую форму. Проще говоря, теория вихрей Декарта совершенно не могла об'яснить движения планет по законам Кеплера.
      Система философских и научных взглядов Декарта получила название картезианства: Декарт подписывал свои сочинения фамилией Картезиус. Картезианское мировоззрение быстро получило широкое распространение, особенно во Франции, и еще в первой половине XVIII века, непосредственно перед выступлением Лапласа на научной арене, картезианство имело там своих ярых последователей.
      В идеях Декарта не допускается мысль о дальнодействии, и само пространство, по его понятиям, является материальным в физическом смысле этого слова. Взаимодействие тел, в частности приведение их в состояние движения, может произойти только при непосредственном их соприкосновении. Такое соприкосновение может осуществляться и посредством промежуточной среды, роль которой у Декарта выполняли вихри. Дальнодействие – действие на расстоянии в пустоте, отвергалось его философией и всей его физической теорией мироздания. Таким образом, еще примитивная материалистическая точка зрения на взаимодействие небесных тел выражена в мировоззрении Декарта наиболее четко.
      Французская Академия наук во второй половине XVII века и даже в начале XVIII века являлась оплотом картезианских идей.

Всемирное тяготение

      В Англии, где идеи француза Декарта не оставили столь же сильных следов, как на родине философа, развитие научного мышления шло более самостоятельным путем и увенчалось гениальными работами Ньютона. В 1687 году появилось его сочинение «Математические начала натуральной философии», которое с небывалой дотоле ясностью и четкостью определило новое научное мировоззрение. Здесь давалось исчерпывающее, на первый взгляд, об'яснение величайшего множества явлений природы, исходя из немногих четких принципов. Кроме того, тут же давался и новый метод научного исследования природы, метод индукции. Этой работой Ньютона были предопределены, как известно, основные линии дальнейшего развития всей астрономии и физики вплоть до начала XX века и отчасти даже позднее. Понятие причинности всех явлений природы стало после этого на твердую почву и вдохновило исследователей на дальнейшее углубление полученных результатов. Успехи Ньютона в значительной мере определялись тем что ему, независимо от Лейбница и почти одновременно с ним, удалось изобрести могущественное средство математического анализа – исчисление бесконечно малых. Другими словами, Ньютон изобрел высшую математику – основы дифференциального и интегрального исчислений. Только при посредстве этого метода Ньютон мог шагнуть гораздо дальше, чем его предшественники. С тех пор дифференциальное и интегральное исчисления являются незаменимым способом математической трактовки различных явлений природы.
      Анализируя законы, найденные Кеплером непосредственно из наблюдений, как говорят, эмпирически, учитывая эллиптичность планетных орбит, Ньютон доказал, что планеты испытывают ускорение, всегда направленное к Солнцу и изменяющееся обратно пропорционально квадрату расстояния планет от Солнца.