Артиллерия

На наблюдательном пункте уже установили связь с командиром стрелковой роты, который потребовал подавить пулеметы противника у окраины деревни Заозерье. Командир роты настаивал на немедленном открытии огня.

Командиру батареи доложили, что батарея готова, но еще не могли определить сколько-нибудь точно, где она стоит; среди кустов, где расположены орудия, не так-то просто ориентироваться.

Командир батареи решил все же начать стрельбу, не теряя времени на уточнение положения батареи и на вычисления.

Он знал, что стрелять надо на запад, то-есть приблизительно по буссоли 45-00.

Кроме того, он знал, что батарея находится примерно в километре позади его наблюдательного пункта; расстояние же от своего наблюдательного пункта до деревни Заозерье он определил на-глаз километра в два. Значит, от батареи до цели – километра три.

Важно было не попасть в случае ошибки в свою пехоту, поэтому командир батареи на всякий случай прибавил к результату своего подсчета еще 200 метров.

На все эти расчеты опытному командиру батареи понадобилось всего секунд 5, после чего раздались команды:

«По пулеметам.

Гранатой.

Взрыватель осколочный.

Заряд третий.

Буссоль 45-00.

Уровень 30-00.

Прицел 64.

Первому один снаряд.

Огонь!»

Телефонист быстро передавал на огневую позицию команду за командой; принимавший громко повторял ее, и тогда телефонист громко отвечал «да», чтобы и принимающий и командир батареи были уверены, что команда принята правильно.

Не прошло и минуты, как с огневой позиции передали: «Выстрел», и мягко зашуршала где-то в вышине гаубичная граната.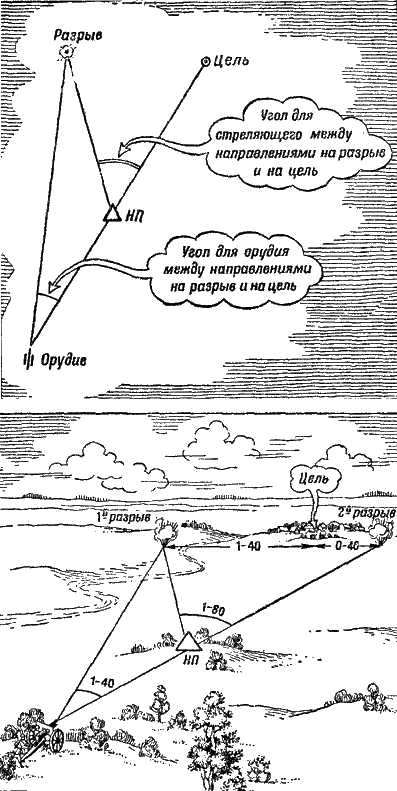

Рис. 253. Угол отклонения разрыва от цели не одинаков для командира и для батареи, поэтому снаряд и не послушался команды – второй разрыв оказался правее цели на 0-40

Вот и разрыв. Он оказался далеко в стороне от цели.

«Влево 1-40», – доложил разведчик.

Не удивляйтесь, что первый разрыв получился так далеко от цели: ведь орудия цели не видят, а никаких точных расчетов командир батареи не производил, так как он должен был возможно скорее открыть огонь.

«Правее 1-40.

Огонь!» – раздалась команда.

Но и второй разрыв оказался не против цели: на этот раз снаряд ушел уже вправо на 40 делений угломера.

«Вправо 40», – доложил разведчик.

Вы в недоумении: почему снаряд не послушался команды?

Если вдумаетесь, увидите, что дело, однако, очень просто: стреляющий на этот раз находился не около орудия.

Если батарея стояла бы там же, где находился наблюдательный пункт, то угол отклонения снаряда от цели был бы, конечно, одинаков и для командира батареи и для орудия. Но орудие находилось далеко позади наблюдательного пункта, поэтому угол «разрыв – наблюдательный пункт – цель» оказался больше, чем угол «разрыв – орудие – цель». Рисунок 253 показывает наглядно эту разницу. Первые два выстрела показали командиру батареи, что поправка, равная отклонению разрыва, велика. Нужно учесть «коэффициент удаления». Он быстро сделал в уме новый расчет; артиллеристы знают наизусть несложные формулы для таких случаев. Получилось, что на этот раз, при отклонении в 0-40, надо брать поправку в 0-30. Вы слышите команду:

«Левее 0-30.

Огонь!»

Выстрел – и разрыв оказался против цели – недолет.

Вы сами стреляли и знаете, как поступить в этом случае: надо сделать скачок, равный срединной ошибке для данного способа измерения дальности. Но при дальностях стрельбы от трех до шести километров эта ошибка составляет уже не 200 метров, как было при вашей стрельбе, а в среднем около 400 метров, или 8 делений прицела.

Теперь вам понятна следующая команда командира батареи:

«Прицел 72.

Огонь!»

И несколько секунд спустя за целью – в деревне – взметнулся кверху большой темный куст: это был разрыв.

«Прицел 68.

Огонь!» – скомандовал командир батареи.

Получив на этот раз недолет, он продолжал сужать вилку.

Рис. 254. Параллельный веер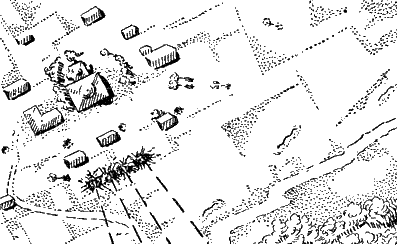

Рис. 255. Веер по ширине цели

Как это делается, вы уже знаете из своего опыта. Но для того чтобы ускорить пристрелку, получить сразу обеспеченный предел вилки, командир скомандовал:

«Прицел 70.

Батареею огонь!»

Четыре выстрела раздались один за другим, с промежутками около одной секунды, и вслед за последним из них услышали вы доклад телефониста:

«Очередь!»

Это означает, что выпущены все назначенные последней командой снаряды.

Разрывы появились опять за целью и легли на широком фронте; орудия на огневой позиции направлены были параллельно друг другу; расстояние по фронту между разрывами равно было расстоянию между орудиями. Это был так называемый «параллельный веер» батареи (рис. 254).

А цель была значительно более узкой по фронту, чем веер разрывов.

Требовалось сузить веер, чтобы снаряды не ложились без пользы по сторонам от цели. И так как ближе всех к цели лег разрыв второго орудия, командир скомандовал:

«Соединить огонь ко второму в 0-06. Прицел 68.

Огонь!»

Теперь уж разрывы приблизились друг к другу: «веер разрывов» стал равен фронту цели (рис. 255).

Дым окутал цель сплошной тучей, и вражеские пулеметы замолкли: если даже они и не погибли, то, ничего не видя, метко стрелять они все равно уже не могли.

Как принято говорить на военном языке, пулеметы были «подавлены».

Пока командир батареи решал эту первую огневую задачу, на батарее продолжалась работа: вычислители «привязывали» огневую позицию и наблюдательный пункт к точкам на местности, положение которых на карте известно.

Работая со своими приборами, вычислители точно определили, где находятся огневая позиция и наблюдательный пункт, и нанесли их на карту.

Когда после решения первой огневой задачи наступил небольшой перерыв в стрельбе, командир батареи мог уже приготовиться к стрельбе по карте.

Для этого он подготовил данные по ориентирам и записал их.

Вот как он это сделал.

Прочертив на карте прямые линии, соединяющие каждый из ориентиров с батареей, он измерил линейкой дальности до каждого ориентира (рис. 256); прикладывая затем к карте целлулоидный круг так, чтобы ноль был направлен в соответствующий ориентир, он читал, какое деление круга приходится против направления на север, и записывал буссоль этого ориентира (рис. 257).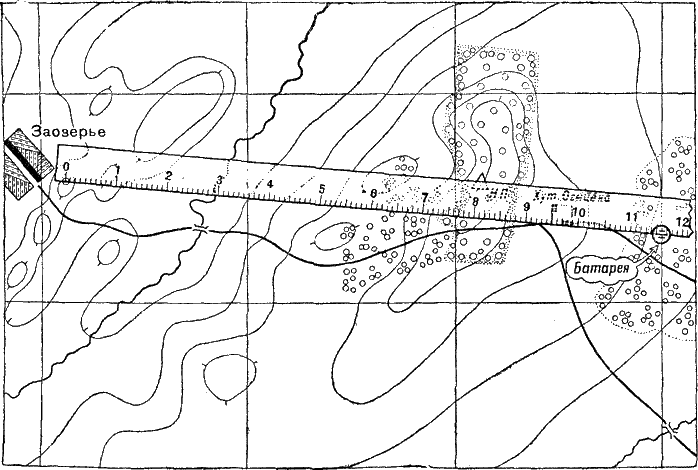

Рис. 256. Измерение дальности по карте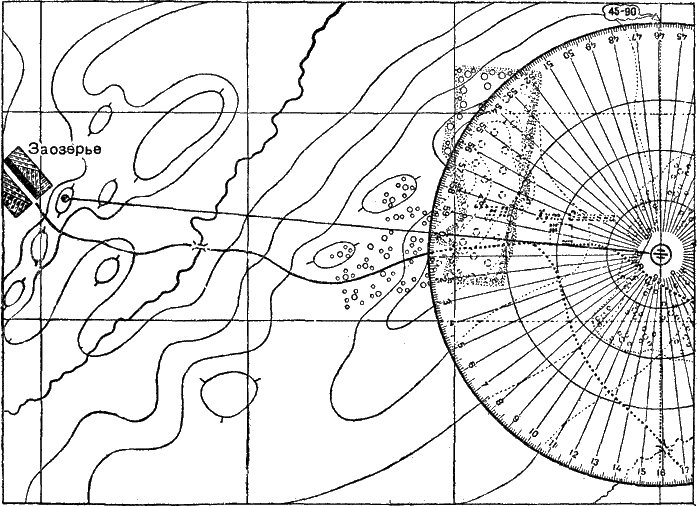

Рис. 257. Так определяют по карте буссоль цели

Теперь уже не нужно будет больше тратить так много снарядов на пристрелку: исходные данные подсчитаны гораздо точнее, чем раньше.

Кроме того, по карте можно определить, насколько тот или иной ориентир расположен выше или ниже орудий батареи. Это позволит заранее учесть уровнем угол места цели (рис. 258).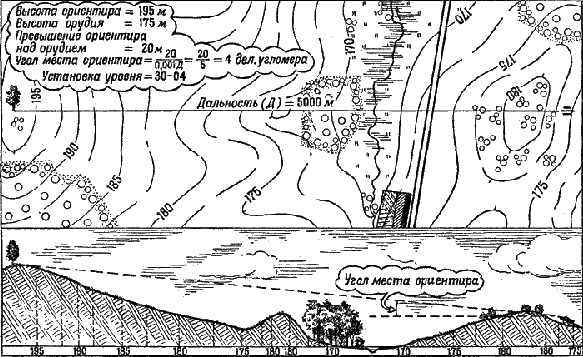

Рис. 258. Так подсчитывают по карте исходную установку уровня

Минут через семь в руках у командира батареи была готовая схема (рис. 259). Такая схема помогает командиру открывать огонь не только быстрее, но и точнее.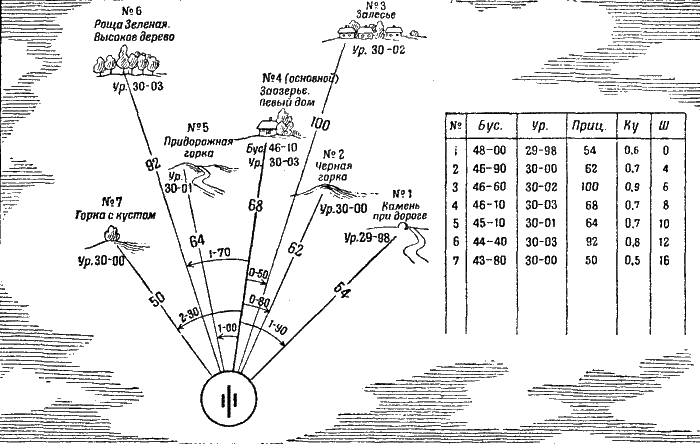

Рис. 259. Схема переносов огня

Как раз в это время появилась новая цель: один из разведчиков доложил, что он ясно видит пулеметную батарею, открывшую огонь из кустов, влево от придорожной горки.

Быстро проверил командир батареи доклад разведчика, приложился сам к стереотрубе и тотчас увидел цель.

Вот она: от придорожной горки влево 40 – маленькие кустики, метров на 500 подальше этой горки. Четыре легких струйки беловатого дыма дрожат на опушке этих кустиков, и, перебивая друг друга, «строчат» четыре пулемета.

Если вглядеться внимательнее, можно увидеть, что возле струек дыма чуть виднеются какие-то темные точки, а иногда что-то шевелится.

Это – действительно пулеметная батарея противника. Так как наша батарея не была занята выполнением приказаний командира дивизиона и командиров пехоты, то командир тут же решил подавить эту цель, потому что пулеметный огонь задерживал нашу пехоту и наносил ей потери.

Взгляд на карту, чтобы проверить удаление кустиков от придорожной горки, и одновременно – команды:

«По пулеметной батарее.

Гранатой.

Взрыватель осколочный.

Заряд третий».

Быстро мелькает ряд чисел в уме командира батареи – и расчеты готовы. Он командует:

«Буссоль 44-70.

Уровень 30-01.

Прицел 74.

Первому один снаряд. Огонь!»

Подготовленная схема помогла быстро направить огонь батареи на новую цель. Можно было воспользоваться также результатами первой проведенной стрельбы: это тоже помогло бы быстро и достаточно точно перенести огонь на новую цель.

Теперь, когда исходные данные подготовлены по карте, снаряды уже не блуждают по полю: первый же разрыв оказывается против левого края цели; виден недолет.

Ошибки определения дальности при работе по карте не так велики, как при работе на-глаз: срединная ошибка составляет всего лишь 4% дальности. Первый скачок прицелом достаточно сделать в 4 деления – так учат «Правила стрельбы».

Командир батареи быстро считает в уме и командует:

«Правее 0-08.

Прицел 78.

Огонь!»

Опытный командир-артиллерист тратит на такие расчеты всего лишь 15-20 секунд. Снова шуршит в воздухе граната. Перелет!

А на прицеле 76 в батарейной очереди получаются уже и перелеты, и недолеты.

Это значит, что средняя точка падений где-то недалеко от цели. «Два снаряда беглый огонь!»

В следующие 3-4 минуты пулеметная батарея противника была подавлена и прекратила огонь.

Математика в артиллерии

Вы уже убедились в том, что артиллеристу на поле боя приходится решать ряд математических задач. Вероятно, эти задачи показались вам очень простыми, и вам кажется странным, почему в артиллерии придают такое большое значение математике, почему принято говорить, что хорошими командирами-артиллеристами могут стать только хорошие математики.

Не удивляйтесь – до сих пор мы выбирали для примера только простейшие случаи, умышленно не затрудняли вас расчетами и вычислениями, чтобы понятнее была суть описанных приемов стрельбы.

Но если вас интересует «артиллерийская математика» и вы ее не боитесь, посмотрите, как выполняются расчеты и как решаются некоторые более сложные задачи.

Вы наверное, помните, как командир опытом, то-есть стрельбой, установил так называемый «коэффициент удаления». Всегда ли необходимо проделывать этот опыт и, следовательно, тратить лишний снаряд и лишнее время?

Оказывается, далеко не всегда и даже наоборот – очень редко. Обычно командир батареи вычисляет коэффициент удаления заранее, в промежуток времени между подачей первой команды и первым выстрелом. Для решения этой задачи надо знать всего лишь два расстояния: командир – цель (его обозначают сокращенно буквами Дк – дальность командира или Дн – дальность наблюдения) и батарея (орудие) – цель (Дб – дальность батареи или До – дальность орудия).

Отношение Дк/Дб и называют коэффициентом удаления, обозначая его буквами Ку. Таким образом, первая формула, которой пользуется каждый артиллерист, имеет следующий вид: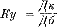

Простой расчет для нашего примера покажет, что формула эта дает правильное решение задачи. Предположим, что у нас Дк = =2 500 метров. Дб мы знаем – оно равно 3 200 метров (вспомните, что командир скомандовал прицел 64).

Значит,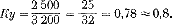

И, знай командир величину Ку, он вместо угла 1-40 (рис. 253) должен был бы скомандовать 1-40 • 0,8 = 1-12 = 1-10.

Тот же вывод дал и опыт: сначала батарея была повернута вправо на 1-40, а затем влево на 0-30, то-есть всего вправо на 1-40 – 0-30 = 1-10.

При этом командир, не зная своего удаления от цели, определил коэффициент удаления по отношению полученных углов – для батареи это было 1-40, а для командира 1-80 (рис. 253):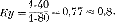

Коэффициент удаления избавляет от лишних расчетов, помогает артиллеристам экономить снаряды и время. Но коэффициент удаления можно применять, когда командир не очень далеко ушел в сторону от батареи (угол при цели не более 3-00).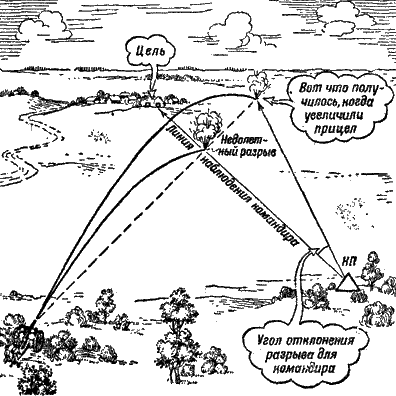

Рис. 260. Прицел увеличили – разрыв ушел с линии наблюдения командира

Теперь посмотрите на рисунок 260. В начале стрельбы командир добился того, что разрыв оказался точно против цели. Но едва лишь он изменил установку прицела, как разрыв снова ушел в сторону от цели.

Рисунок поможет вам понять причину этого нового отклонения разрыва: вспомните, что командир батареи не находится возле своих орудий; он ушел не только вперед, но и в сторону.

Когда командир находится в стороне от батареи, разрывы сходят с его «линии наблюдения» при изменении установки прицела. Их надо удерживать на линии наблюдения, исправляя направление одновременно с изменением установки прицела.

Поправка направления, с помощью которой при изменении установки прицела удерживают разрыв на линии наблюдения, называется «шагом угломера» (рис. 261). Этот «шаг угломера» можно тоже заранее рассчитать по формуле, известной каждому артиллеристу: ширину вилки (сокращенно б), выраженную в делениях прицела, надо умножить на «угол при цели» или на так называемую «поправку на смещение» (ПС) и разделить на прицел от батареи до цели (П), то-есть шаг угломера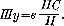

Проще всего вычислить шаг угломера тогда, когда мы готовим данные по карте: «угол при цели» нетрудно измерить с помощью целлулоидного круга.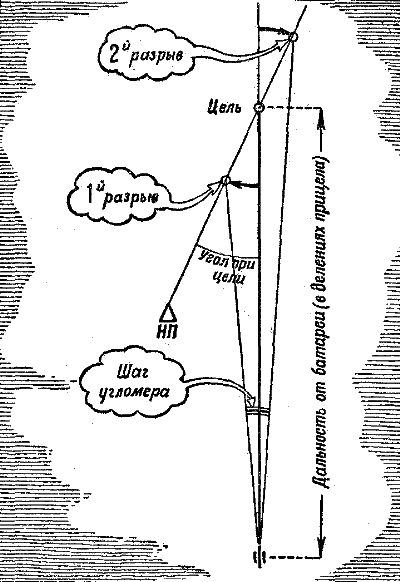

Рис. 261. «Шаг угломера»

И в других случаях нам тоже поможет математика. Мы можем, например, заменить карту несложным чертежом, который даст ответ на интересующий нас вопрос.

Кстати, этот же чертеж поможет нам сделать первый выстрел не наугад.

Возьмите листок бумаги и поставьте где угодно точку – это ваш наблюдательный пункт, или, короче, НП (рис. 262). Проведите прямую линию вверх. На ней отложите в масштабе, которым вы задались, расстояние до цели, положим, 2 километра. Здесь на чертеже окажется цель. Теперь подойдите к буссоли и направьте ее нолем в цель.

Но цель находится далеко и видна плохо. На помощь вам приходит монокуляр буссоли с шестикратным увеличением: оптическая ось монокуляра направлена всегда параллельно диаметру 30-0 буссоли (рис. 245).

Отпустите теперь магнитную стрелку и прочтите, против какого деления она остановилась. Пусть вы прочли 46-20. Это – азимут, или «буссоль цели». Закрепите в этом положении угломерный круг и, освободив визирную трубку, направьте ее в сторону батареи. Против указателя визира прочтите «отметку по батарее».

Теперь наложите на ваш чертеж (рис. 262) целлулоидный круг: центром – на точку, которую вы приняли за наблюдательный пункт, нолем – в сторону цели. Прочертите на чертеже направление на батарею. Узнайте расстояние от вас до батареи (его можно промерить шагами, определить на-глаз или установить другим способом). Отложите это расстояние, например 1 500 метров, в том масштабе, какой вы приняли для чертежа, и вы получите на чертеже точку – место батареи.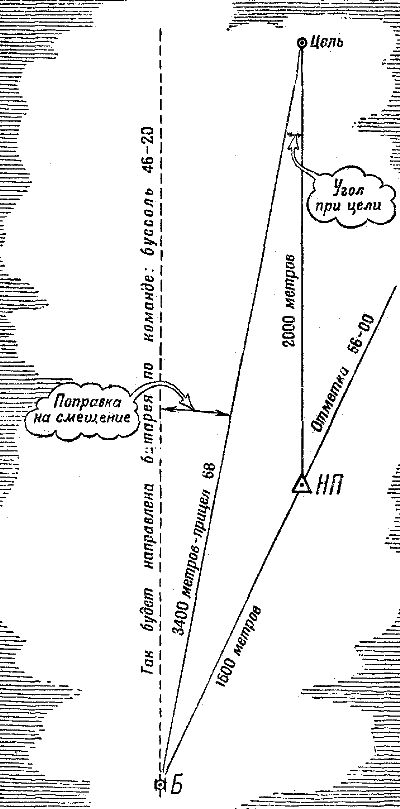

Рис. 262. Графический способ подготовки данных для стрельбы

Соедините на чертеже точки «батарея» и «цель» прямой линией и, приложив линейку, измерьте дальность от батареи до цели.

Вы проделали не что иное, как решение геометрической задачи на построение треугольника по двум сторонам и углу между ними.

Несколько сложнее решить задачу-какую следует скомандовать буссоль, чтобы направить батарею в цель. Если вы скомандуете ту буссоль, какая получилась у вас на наблюдательном пункте, батарея, очевидно, будет направлена параллельно линии «наблюдательный пункт – цель» (рис. 262).

Надо довернуть батарею в сторону наблюдательного пункта на угол, который отчетливо виден на рисунке; этот угол и называется «поправкой на смещение».

Каждому, кто знаком с геометрией, ясно, что поправка на смещение равна «углу при цели».

Значит, на чертеже незачем рисовать линию, параллельную линии «наблюдательный пункт – цель»: достаточно измерить целлулоидным кругом «угол при цели».

На этот угол и надо довернуть батарею в сторону наблюдательного пункта.

В примере на рисунке 262 батарею надо повернуть правее на величину угла при цели, равного 1-80. Чтобы повернуть батарею правее, установку угломера или буссоли надо увеличить. Вот почему надо командовать буссоль не 46-20, а 46-20+1-80, то-есть 48-00.

Понятно, что, имея такой чертеж, можно легко подсчитать и коэффициент удаления, и шаг угломера.

А можно обойтись и без чертежа: та же математика дает артиллеристам все формулы, нужные для расчетов.

Представьте себе взаимное расположение батареи, наблюдательного пункта и цели такое, как показано на рисунке 263.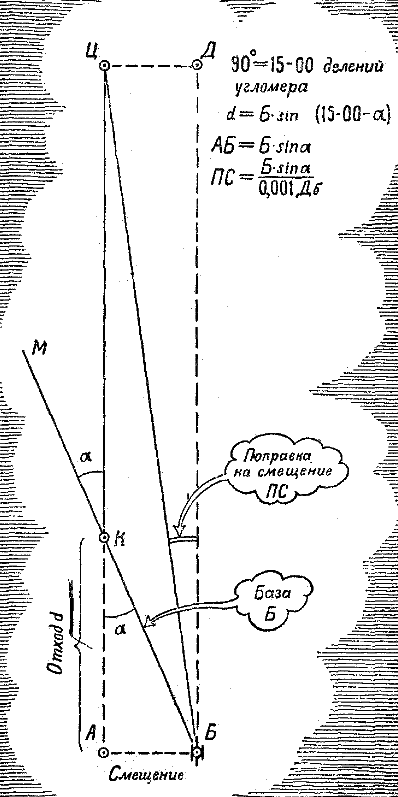

Рис. 263. Как можно рассчитать «поправку на смещение»

Для того чтобы сделать расчеты, надо знать те же три величины, что и для решения задачи чертежом: во-первых, Дк во-вторых, расстояние от батареи до наблюдательного пункта (его принято называть «базой» и обозначать буквой Б); в-третьих, угол, составленный направлениями «наблюдательный пункт – цель» и «наблюдательный пункт – батарея». Этот угол, приведенный к первой четверти, то-есть к острому углу, обозначают греческой буквой альфа (а).

Опустите из точки Б (батарея) перпендикуляр на продолжение линии КЦ (командир – цель). В прямоугольном треугольнике АБК вам известна гипотенуза КБ и угол АКБ, который, как вертикальный, равен измеренному вами с помощью буссоли углу ЦКМ.

Зная эти две величины и тригонометрию, нетрудно найти катет АК (в артиллерии его называют «отход» и обозначают латинской буквой d: он равен базе КБ, умноженной на косинус угла АКБ или же на синус угла (90°-АКБ). Это дает нам такую формулу: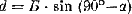

или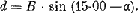

А расстояние от батареи до цели без значительной ошибки можно принять в нашем случае равным КЦ + АК, то-есть расстоянию от командира до цели плюс отход: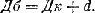

Таким образом, вы знаете теперь, какой надо назначить прицел.

Нетрудно подсчитать и «поправку на смещение».

Для этого достаточно изучить чертеж и формулы, приведенные на рисунке 263.

Теперь вы можете не только направить батарею в цель безо всяких чертежей, но и сосчитать коэффициент удаления и шаг угломера.

Однако нетрудно сообразить, что способ этот не отличается особой точностью: во-первых, составляя формулы, принимают, что БЦ=АЦ, а это неверно; ошибка составляет тут нередко 100—200 метров; во-вторых, и это самое главное, расстояние Дк и базу Б чаще всего при этом способе определяют на-глаз. Все это приводит к ошибкам, которые в среднем составляют 0-40 по направлению и 10% в дальности.

Этот способ подготовки исходных данных для стрельбы артиллеристы применяют лишь тогда, когда важнее всего простота и скорость решения задачи, точностью, же можно и поступиться: в бою это бывает нередко.

Ну, а как же быть, если нужна высокая точность подготовки данных для стрельбы?

Топография и математика и тут приходят на выручку: артиллеристы делают так называемый аналитический расчет дальности и угломера по гораздо более точным и сложным формулам. Тригонометрия и таблицы логарифмов позволяют с очень большой точностью рассчитать установку угломера и дальность до цели.

Всем этим далеко не ограничиваются случаи применения математики в артиллерии. Артиллеристу она нужна буквально на каждом шагу. Даже из приведенных здесь примеров ясно, что артиллерист должен отлично знать и арифметику, и геометрию, и тригонометрию, и алгебру, и, отчасти, аналитическую геометрию. Этими науками артиллеристу надо овладеть так хорошо, чтобы даже в бою, под огнем неприятеля, он не ошибался в расчетах, уверенно и спокойно применяя нужные формулы.

Для полного же понимания теории стрельбы и науки о полете снаряда – баллистики – надо знать всю высшую математику.

Быть хорошим артиллеристом – это значит обязательно быть хорошим математиком.

Батарея «устраивается» на позиции

Вы знаете уже, как использовал командир батареи свободные от стрельбы минуты: он точнее подготовил данные для стрельбы, лучше изучил местность.

И на огневой позиции тоже никто не терял попусту свободное время.

В стороне от батареи орудийные номера нарубили больших веток; несколько больших кустов они срубили целиком; подтащили все это к своим орудиям и тотчас же принялись маскировать их, чтобы неприятельский летчик-наблюдатель не обнаружил, где стоит батарея.

Конечно, нетрудно замаскироваться, когда батарея стоит в кустах или в лесу: тут достаточно забросать ветками орудия и снаряды.

Труднее справиться с этим делом, если батарея расположена в открытом поле или на лугу: маскировка ветками тут уж не поможет, она только повредит. Неприятельский летчик-наблюдатель увидит батарею в виде четырех кустов, расположенных на одной прямой линии и приблизительно на равных расстояниях друг от друга. Такие фальшивые кусты обычно резко выделяются на фоне окружающей местности и сразу привлекают внимание воздушного наблюдателя.

Лучше будет в этом случае применить технические средства маскировки.

Каждая батарея имеет комплект маскировочных сетей – по числу орудий. Имеются сети и для наблюдательных пунктов. Каждая такая сеть напоминает большой невод. С помощью специального каркаса натягивают маскировочную сеть над орудием, вплетают в нее траву, солому или другой материал, который не отличается по цвету от окружающей местности. Важно, чтобы замаскированное орудие не выделялось в виде пятна, а при наблюдении издали сливалось с окружающими предметами, – иначе маскировка только поможет врагу обнаружить батарею.

Но все же недостаточно только спрятать орудия. Ведь противник услышит их выстрелы, когда они начнут стрелять, увидит разрывы их снарядов, ощутит на себе их действие. Он станет искать батарею – и не одним, так другим способом найдет ее в конце концов, даже и в том случае, если она замаскирована безукоризненно.

Чтобы этого не случилось, надо не только хорошо спрятать батарею, но еще и обмануть неприятеля: надо отвести его глаза от огневой позиции. Это удастся, если мы сумеем построить «ложную батарею».

Был во время империалистической войны такой случай.

Одна из русских батарей расположилась на позиции между двумя перелесками, на поляне. Когда-то стоял на этой поляне кирпичный завод; остались от него развалины навесов, под которыми сушили кирпич; остались ямы, кучи битого кирпича и глины. Вот здесь-то, среди ям и развалин, и расставили артиллеристы свои орудия. Перелесок укрывал их от наземного наблюдателя; заметить их с самолета было тоже нелегко – в глазах летчика рябило от разбросанных по поляне развалин, куч и ям.

Но раньше или позже германский летчик все же обнаружил бы батарею на поляне, если бы русские артиллеристы не приняли заранее особых мер. Вот в чем состояли эти меры.

На опушке леса, в стороне от своей позиции, метров за двести, выбрали русские артиллеристы удобное место и из чурбанов, досок, старых, негодных колес и жердей смастерили что-то похожее на орудия (рис. 264).

Рис. 264. Ложная батарея

Потом они притащили несколько небольших мешочков пороху и стали поджидать самолет.

Едва лишь загудел вдали мотор, как артиллеристы начали поджигать мешочки с порохом возле самых орудий.

Получились вспышки, словно при настоящей стрельбе. Не было, правда, звука стрельбы. Но звука выстрела летчику все равно не услыхать за шумом мотора.

Немецкий летчик, как видно, заметил блеск «выстрелов»: самолет стал приближаться. Тогда артиллеристы нарочно засуетились на ложной позиции, словно они только что заметили самолет: бросились накрывать деревянные «пушки» палатками, ветками, а потом разбежались по кустам.

Летчик-наблюдатель попался на эту удочку: вскоре с немецкой стороны раздались выстрелы. Снаряды ложились все ближе к ложной позиции. А русские артиллеристы уходили тем временем по кустам подальше от обстреливаемого места.

Немцы выпустили по ложной батарее несколько сотен снарядов.

С тех пор всякий раз, когда начинала? стрелять действительная русская батарея, немцы отвечали ей, обстреливая ложную батарею.

Иногда немцы высылали самолет – проверить, стоит ли на прежнем месте русская батарея. Тогда русские артиллеристы повторяли возню у ложных орудий. Временами перетаскивали они ложные орудия на какое-нибудь другое место, неподалеку от старого, и на этом новом месте проделывали все с начала.

Германский летчик доносил о том, что русская батарея переменила позицию, и направлял огонь своей артиллерии на новую ложную батарею.

Так продолжалось целых три месяца: настоящая батарея, умело обманывая врага, спокойно вела свою боевую работу.

В наши дни пороховые вспышки не годятся уже для обмана врага: – звуковая разведка неприятеля, засекая звуки настоящих выстрелов, легко обнаружит подобный обман. Вот почему теперь ставят обычно на ложную позицию минут на десять одно настоящее орудие. Орудие это ведет огонь настоящими снарядами, а затем возможно быстрее уходит, чтобы самому не попасть под обстрел. Время от времени оно, однако, возвращается на то же место, чтобы выпустить снова несколько снарядов: враг должен видеть и слышать, что позиция не оставлена и батарея продолжает еще вести с нее огонь.

Нередко устраивают несколько таких ложных позиций; орудия, предназначенные для стрельбы с них, переходят поочередно с одной такой позиции на другую и с каждой ведут огонь. Это так называемые «кочующие орудия».

Если искусно применять их, неприятеля можно так запутать, что ему не под силу будет разобраться, где же стоят настоящие, а где – ложные батареи, если даже он сумеет обнаружить и те и другие с помощью самолетов и звуковой разведки.

Но как бы искусно мы ни обманывали врага, он может все же раскрыть обман и обстрелять нашу огневую позицию: никакая маскировка не дает гарантии, что батарея не будет обнаружена.

Вот почему орудийный расчет, покончив с маскировкой, начинает сразу же рыть окопы – сперва для людей, а потом и для орудий. Нелегко попасть целым снарядом в небольшой окоп, который, к тому же, замаскирован и не виден ни с земли, ни с воздуха. А от осколков и пуль уберечься в окопе нетрудно. Окоп дает возможность бойцам успешно выполнять свою боевую работу даже под сильным обстрелом и нести при этом самые незначительные потери.

Вот яркий пример.

Одна из республиканских батарей под Мадридом наносила фашистам особенно большие потери. Фашистским летчикам удалось отыскать позицию этой батареи; как видно, решено было уничтожить батарею во что бы то ни стало. С аэродрома поднялось восемь фашистских самолетов; они сбросили на республиканскую батарею несколько десятков бомб. Вслед за первым отрядом прилетел второй, потом – третий. У республиканцев тогда не было еще здесь ни авиации, ни зенитной артиллерии, чтобы помешать фашистам. Самолеты фашистов возвращались на свой аэродром, брали новый запас бомб и прилетали снова, чтобы сбросить их на республиканскую батарею.

И так продолжалось много часов подряд.

Почти весь день рвались на батарее авиационные бомбы, свистели их осколки, позиция батареи вся была окутана дымом. Ни один кустик не уцелел – все они были срезаны осколками. Казалось, ни одному артиллеристу не уйти живым с этой позиции, почти сплошь изрытой воронками. Лишь к вечеру прекратили фашисты свои налеты. Республиканские артиллеристы подсчитали свои потери: на батарее оказался всего лишь один легко раненый, все остальные были живы и здоровы: ни одна из фашистских бомб не попала прямо в орудийный окоп, а осколки их не могли достать людей, которые весь день не покидали своих окопов.

Так хорошие окопы спасли испанскую батарею от разгрома. Не раз выручали они артиллеристов и в других боях и в других войнах. Поэтому артиллеристы при первой к тому возможности всегда берутся за лопаты, чтобы как можно лучше оборудовать свою позицию.

Почему снаряд летит ночью не на ту же дальность, что и днем?

В то время, пока на огневой позиции маскировали орудия и рыли окопы, вычислители, окончив привязку огневой позиции и наблюдательного пункта, приступили уже к работе другого рода: взяв книжку «Таблиц стрельбы», они начали выписывать ряды цифр, складывать, вычитать, выводить итоги, производя подсчет «поправок».

Что это за поправки и зачем они нужны?

Пример пояснит этот вопрос.

Во время мировой империалистической войны был такой случай. Батарея стреляла по проволочным заграждениям противника. Пристрелялась хорошо: снаряды ложились прямо в проволоку.

Подошел вечер. Батарея получила задачу: ночью продолжать огонь, чтобы не дать противнику исправить разрушения. А утром пехота должна была итти в атаку.

Всю ночь батарея стреляла.

А на утро смотрят – все проволочные заграждения исправлены; проходов, проделанных вчера, нет и в помине.

В чем дело? Где же следы ночной стрельбы?

Приглядевшись получше, разведчики заметили, что в 100—150 метрах перед проволочными заграждениями видны воронки от разрывов снарядов. Вчера этих воронок не было. Значит, это – результаты ночной стрельбы. Кто же ночью отводил снаряды от цели? Почему они падали не туда, же, куда и днем, хотя установок орудий артиллеристы не меняли?