Термин «информационная безопасность» в последнее десятилетие стал довольно широко употребляться к месту и не к месту. При этом, мало кто из его употребляющих прямо говорит, как и какие процессы в жизни общества и в техносфере, он связывает с этим термином. Т.е. в большинстве случаев его смысл при употреблении не определён.
      При взгляде с позиций достаточно общей теории управления:
      Информационная безопасность (а точнее - информационно-алгоритмическая безопасность) это - устойчивое течение процесса управления объектом (самоуправления объекта), в пределах допустимых отклонений от идеального предписанного режима, в условиях ЦЕЛЕНАПРАВЛЕННЫХ сторонних или внутренних попыток вывести управляемый объект из предписанного режима: от помех до перехвата управления им либо попыток уничтожения.
      Таким образом термин «информационно-алгоритмическая» («информационная безопасность») всегда связан с конкретным объектом управления, находящимся в определённых условиях (среде). И соответственно он относится к полной функции управления, представляющей собой совокупность разнокачественных действий, осуществляемых в процессе управления, начиная от выявления факторов, требующих управленческого вмешательства и формирования целей управления, и кончая ликвидацией управленческих структур, выполнивших своё предназначение.
      Это общее в явлении, именуемом «информационная безопасность» по отношению к информационно-алгоритмической безопасности как самого мелкого и незначительного дела, так и по отношению к информационно-алгоритмической безопасности человечества в целомв глобальном историческом процессе.
      Разные схемы управления и разные концепции управления обеспечивают разный уровень информационно-алгоритмической безопасности.
      При этом программная схема управления обладает парадоксальными характеристиками обеспечения информационно-алгоритмической безопасности вследствие своей полной неспособности воспринимать информацию извне:
      · так артиллерийский снаряд, летящий по баллистической траектории, запрограммированной параметрами наведения орудия и энергообеспеченностью выстрела, по помехозащищённости процесса попадания в цель превосходит любую самонаводящуюся ракету.
      · в других ситуациях программная схема управления, реализованная в отношении каких-то иных объектов (процессов), оказывается полностью неработоспособной, если в конфликте управлений противник навязывает ситуацию, в которой программа, заложенная в систему, становится неадекватной. Пример тому - разгром войском под руководством Александра Невского немецких рыцарей на льду Чудского озера.
      Программно-адаптивная схема менее парадоксальна, но абсолютной помехоустойчивостью тоже не обладает: примерами тому всевозможные успешные хитрости военных на тему о том, как самонаводящиеся средства поражения (ракеты, торпеды, мины) увести на ложные цели, заставить сработать их взрыватели ложно, либо вообще заставить не сработать в тех ситуациях, когда их программы обязывают их срабатывать.
      Наиболее высокий уровень информационно-алгоритмической безопасности обеспечивает организация процессов обработки информации в интеллектуальной модификации схемы управления предиктор-корректор, показанная в разделе 4 объединённого текста лекций 6 и 7 как схема 3.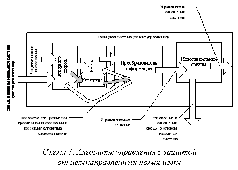
 
 
      В ней информация, поступающая из внешней среды, достоверность которой сомнительна, алгоритмом-сторожем загружается в «буферную память» временного хранения(на схеме она обозначена надписью «Карантин»). Некий алгоритм-ревизор в «Преобразователе информации», выполняя в данном варианте роль защитника мировоззрения и миропонимания от внедрения в них недостоверной информации,анализирует информацию в буферной памяти «Карантина» и присваивает ей значения: «ложь» - «истина» - «требует дополнительной проверки» и т.п. Только после этого определения и снабжения информационного модуля соответствующим маркером («ложь» - «истина» и т.п.) алгоритм-ревизор перегружает информацию из «Карантина» в долговременную память, информационная база которой обладает более высокой значимостью для алгоритма выработки управленческого решения, чем входные потоки информации. Также «Преобразователь информации» осуществляет совершенствование алгоритма-сторожа, распределяющего входной поток информации между «Карантином» и остальной памятью.
      Управленческое решение строится в процессе сопоставления информации, уже наличествующей в долговременной памяти, с информацией входных потоков. При этом информация, помещённая в «Карантин», не может стать основой выработки управленческих решений, по крайней мере, - особо значимых решений, неосуществимость которых неприемлема.
 

 
      Метод динамического программирования - один из формально-алгоритмических методов оптимизации управления и решения иного рода задач, интерпретируемых в качестве задач управления. В изложении существа метода динамического программирования мы опираемся на книгу «Курс теории автоматического управления» (автор Палю де Ла Барьер: французское издание 1966 г., русское издание - «Машиностроение», 1973 г.), хотя и не повторяем его изложения. Отдельные положения взяты из курса «Исследование операций» Ю.П. Зайченко (Киев, «Вища школа», 1979 г.).
      Метод динамического программирования работоспособен, если формальная интерпретация реальной задачи позволяет выполнить следующие условия:
      1. Рассматриваемая задача может быть представлена как N-шаговый процесс, описываемый соотношением:
       X n + 1= f(X n,U n, n), где n- номер одного из множества возможных состояний системы, в которое она переходит по завершении n-ного шага; X n- вектор состояния системы, принадлежащий упомянутому n-ному множеству; U n- управление, выработанное на шаге n(шаговое управление), переводящее систему из возможного её состояния в n-ном множестве в одно из состояний ( n + 1)-го множества. Чтобы это представить наглядно, следует обратиться к рис. 1, о котором речь пойдёт далее.
      2. Структура задачи не должна изменяться при изменении расчётного количества шагов N.
      3. Размерность пространства параметров, которыми описывается состояние системы, не должна изменяться в зависимости от количества шагов N.
      4. Выбор управления на любом из шагов не должен отрицать выбора управления на предыдущих шагах. Иными словами, оптимальный выбор управления в любом из возможных состояний должен определяться параметрами рассматриваемого состояния, а не параметрами процесса, в ходе которого система пришла в рассматриваемое состояние.
      Чисто формально, если одному состоянию соответствуют разные предыстории его возникновения, влияющие на последующий выбор оптимального управления, то метод позволяет включить описания предысторий в вектор состояния, что ведёт к увеличению размерности вектора состояния системы. После этой операции то, что до неё описывалось как одно состояние, становится множеством состояний, отличающихся одно от других компонентами вектора состояния, описывающими предысторию процесса.
      5. Критерий оптимального выбора последовательности шаговых управлений U nи соответствующей траектории в пространстве формальных параметров имеет вид:
       V = V 0(X 0, U 0) + V 1(X 1, U 1) +… + V N - 1(X N- 1, U N - 1) + V N(X N).
      Критерий Vпринято называть полным выигрышем,а входящие в него слагаемые - шаговыми выигрышами. В задаче требуется найти последовательность шаговых управлений U nи траекторию, которым соответствует максимальный из возможных полных выигрышей. По своему существу полный выигрыш V- мера качества управления процессом в целом. Шаговые выигрыши, хотя и входят в меру качества управления процессом в целом, но в общем случаене являются мерами качества управления на соответствующих им шагах, поскольку метод предназначен для оптимизации процесса управления в целом, а эффектные шаговые управленияс большим шаговым выигрышем, но лежащие вне оптимальной траектории,интереса не представляют. Структура метода не запрещает при необходимости на каждом шаге употреблять критерий определения шагового выигрыша V n,отличный от критериев, принятых на других шагах. Кроме того, критерий оптимальности может быть построен и как произведение шаговых выигрышей, которые однако в этом случае не должны принимать отрицательных значений.
      С индексом n- указателем-определителем множеств возможных векторов состояния - в реальных задачах может быть связан некий изменяющийся параметр, например: время, пройденный путь, уровень мощности, мера расходования некоего ресурсаи т.п. То есть метод применим не только для оптимизации управления процессами, длящимися во времени, но и к задачам оптимизации многовариантного одномоментного или нечувствительного ко временирешения, если такого рода «безвременные», «непроцессные» задачи допускают их многошаговую интерпретацию.
      Теперь обратимся к рис. 1 - рис. 3, повторяющим взаимно связанные рис. 40, 41, 42 из курса теории автоматического управления П. де Ла Барьера, хотя в нём они иначе озаглавлены.
      На рис. 1 (приведён ниже по тексту) показаны начальное состояние системы - «0» и множества её возможных последующих состояний - «1», «2», «3», а также возможные переходы из каждого возможного состояния в другие возможные состояния. Всё это вместе похоже на карту настольной детской игры, по которой перемещаются фишки: каждому переходу-шагу соответствует свой шаговый выигрыш, а в завершающем процесс третьем множестве - каждому из состояний системы придана его оценка, помещенная в прямоугольнике. Принципиальное отличие от игры в том, что гадание о выборе пути, употребляемое в детской игре, на основе бросания костей либо вращения волчка и т.п., в реальном управлении недопустимо, поскольку это - передача целесообразного управления тем силам, которые способны управлять выпадением костей, вращением волчка и т.п., т.е. тем, для кого избранный в игре «генератор случайностей» - достаточно эффективно (по отношению к их целям) управляемое устройство.
 
 
       Рис. 1. К существу метода динамического программирования. Матрица возможностей.
 
      Если выбирать оптимальное управление на первом шаге, то необходимо предвидеть все его последствия на последующих шагах. Поэтому описание алгоритма метода динамического программирования часто начинают с описания выбора управления на последнем шаге, ведущем в одно из завершающих процесс состояний. При этом ссылаются на «педагогическую практику», которая свидетельствует, что аргументация при описании алгоритма от завершающего состояния к начальному состоянию легче воспринимается, поскольку опирается на как бы уже сложившиесяк началу рассматриваемого шага условия, в то время как возможные завершения процесса также определены.
      В соответствии с этим на рис. 2 анализируются возможные переходы в завершающее множество состояний «3» из каждого возможного состояния в ему предшествующем множестве состояний «2», будто бы весь предшествующий путь уже пройден и осталось последним выбором оптимального шагового управления завершить весь процесс. При этом для каждого из состояний во множестве «2» определяются все полные выигрыши как сумма = «оценка перехода» + «оценка завершающего состояния».Во множестве «2» из полученных для каждого из состояний, в нём возможных полных выигрышей, определяется и запоминаетсямаксимальный полный выигрыш и соответствующий ему переход (фрагмент траектории). Максимальный полный выигрыш для каждого из состояний во множестве «2» взят в прямоугольную рамку, а соответствующий ему переход отмечен стрелкой. Таких оптимальных переходов из одного состояния в другие, которым соответствует одно и то же значение полного выигрыша, в принципе может оказаться и несколько. В этом случае все они в методе неразличимы и эквивалентны один другому в смысле построенного критерия оптимальности выбора траектории в пространстве параметров, которыми описывается система.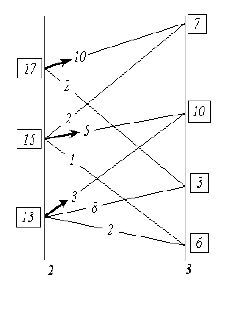
 
 
       Рис. 2. К существу метода динамического программирования. Анализ переходов.
 
      После этого множество «2», предшествовавшее завершающему процесс множеству «3», можно рассматривать в качестве завершающего, поскольку известны оценки каждого из его возможных состояний (максимальные полные выигрыши) и дальнейшая оптимизация последовательности шаговых управлений и выбор оптимальной траектории могут быть проведены только на ещё не рассмотренных множествах, предшествующих множеству «2» в оптимизируемом процессе (т.е. на множествах «0» и «1»).
      Таким образом, процедура, иллюстрируемая рис. 2, работоспособна на каждом алгоритмическом шаге метода при переходах из n-го в (n - 1)-е множество, начиная с завершающего N-ного множества до начального состояния системы.
      В результате последовательного попарного перебора множеств, при прохождении всего их набора, определяется оптимальная последовательность преемственных шаговых управлений, максимально возможный полный выигрыш и соответствующая им траектория. На рис. 3 утолщённой линией показана оптимальная траектория для рассматривавшегося примера.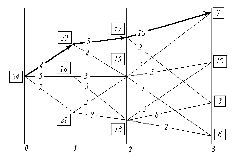
 
 
       Рис. 3. К существу метода динамического программирования. Оптимальная траектория.
 
      В рассмотренном примере критерий оптимальности - сумма шаговых выигрышей. Но как было отмечено ранее, критерий оптимальности может быть построен и как произведение обязательно неотрицательныхсомножителей.
      Поскольку результат (сумма или произведение) не изменяется при изменении порядка операций со слагаемыми или сомножителями, то алгоритм работоспособен и при переборе множеств возможных состояний в порядке, обратном рассмотренному: т.е. от исходного к завершающему множеству возможных состояний.
      Если множества возможных состояний упорядочены в хронологической последовательности, то это означает, что расчётная схема может быть построена как из реального настоящего в прогнозируемое определённоебудущее, так и из прогнозируемого определённогобудущего в реальное настоящее. Это обстоятельство говорит о двух неформальных соотношениях реальной жизни, лежащих вне алгоритма метода:
      1. Метод динамического программирования формально алгоритмически нечувствителен к характеру причинно-следственных обусловленностей (в частности, он не различает причин и следствий). По этой причине каждая конкретная интерпретация метода в прикладных задачах должна строиться на неформальном учёте реальных обусловленностей следствий причинами.
      2. Если прогностика в согласии с иерархически наивысшим всеобъемлющим управлением, а частное управление, вложенное во всеобъемлющее управление, осуществляется квалифицировано, в силу чего процесс частного управления протекает в ладу с иерархически наивысшим всеобъемлющим управлением, то НЕ СУЩЕСТВУЕТ УПРАВЛЕНЧЕСКИ ЗНАЧИМОЙ РАЗНИЦЫ МЕЖДУ РЕАЛЬНЫМ НАСТОЯЩИМ И ИЗБРАННЫМ БУДУЩИМ.
      Процесс целостен, по какой причине ещё не свершившееся, но уже нравственно избранное и объективно не запрещённое Свыше будущее, в свершившемся настоящем защищает тех, кто его творит на всех уровнях: начиная от защиты психики от наваждений до защиты от целенаправленной «физической» агрессии. То есть, если матрица возможных состояний (она же матрица возможных переходов) избрана в ладу с иерархически высшим объемлющим управлением, то она сама - защита и оружие, средство управления, на которое замкнуты все шесть приоритетов средств обобщённого оружия и управления.
      Объективное существование матриц возможных состояний и переходовпроявляется в том, что в слепоте можно «забрести» в некие матрицы перехода и прочувствовать на себе их объективные свойства. Последнее оценивается субъективно, в зависимости от отношения к этим свойствам, как полоса редкостного везения либо как нудное «возвращение на круги своя» или полоса жестокого невезения.
      Но для пользования методом динамического программирования и сопутствующими его освоению неформализованными в алгоритме жизненными проявлениями матриц перехода, необходимо СОБЛЮДЕНИЕ ГЛАВНОГО из условий:
      В задачах оптимизации процессов управления метод динамического программирования ‹реального будущего: - по умолчанию› работоспособен только, если определён вектор целей управления, т.е. должно быть избрано завершающее процесс определённое состояние.
      В реальности это завершающее определённое состояние должно быть заведомо устойчивым и приемлемым процессом, объемлющим и несущим оптимизируемый методом частный процесс. Но выбор и определение определённых характеристик процесса, в который должна войти управляемая система по завершении алгоритма метода, лежит вне этого метода - в области «мистики» или в области методов, развитых в нематематических по своему существу науках и ремёслах.
       «Каково бы ни было состояние системы перед очередным шагом, надо выбирать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным»,- Е.С. Вентцель, «Исследование операций. Задачи, принципы, методология». (Москва, «Наука», 1988 г., стр. 109).
      Неспособность определить вектор целей управления (достижением которого должен завершиться оптимизируемый в методе процесс) и (или) неспособность выявить исходное состояние объекта управления не позволяет последовать этой рекомендации, что объективно закрываетвозможности к использованию метода динамического программирования, поскольку начало и конец процесса должны быть определены в пространстве параметров, на которых построена математическая (или иная) модель метода (она должна быть метрологически состоятельной, что является основой её соотнесения с реальностью). Причём определённость завершенияоптимизируемого процесса имеет управленчески большее значение, чем ошибки и некоторые неопределённости в идентификации (выявлении) начального состояния объекта управления.
      Это тем более справедливо для последовательных многовариантных шаговых переходов, если матрица возможных состояний вписывается в пословицу «Все дороги ведут в “Рим”», а которые не ведут в “Рим”, - ведут в небытие . Для такого рода процессов, если избрана устойчивая во временицель и к ней ведут множество траекторий, то при устойчивом пошаговом управлении «расстояние»

      

        
между оптимальными траекториями, идущими к одной и той же цели из различных исходных состояний, от шага к шагу сокращается, вплоть до полного совпадения оптимальных траекторий, начиная с некоторого шага. Это утверждение тем более справедливо, чем более определённо положение завершающего процесс вектора целей в пространстве параметров. По аналогии с математикой это можно назвать асимптотическим множеством траекторий: асимптотичность множества траекторий выражается в том, что «все дороги ведут в “Рим”…»
      И в более общем мировоззренческом случае, рекомендации Нового Завета и Корана утверждают возможность обретения благодати, милости Вседержителя вне зависимости от начального состояния (греховности человека) в тот момент, когда он очнулся и увидел свои дела такими, каковы они есть.
      Другое замечание относится уже к практике - к вхождению в матрицу перехода. Если начальное состояние системы определено с погрешностью, большей, чем необходима для вхождения в матрицу перехода из реального начального состояния в избранное конечное, то управление на основе самого по себе безошибочного алгоритма метода динамического программирования приведёт к совсем иным результатам, а не расчётному оптимальному состоянию системы. Грубо говоря, не следует принимать за выход из помещения на высоком этаже открытое в нём окно.
      То есть метод динамического программирования, необходимостью как определённости в выборе конечного состояния-процесса, так и выявления истинного начального состояния, сам собойзащищён от применения его для наукообразной имитации оптимизации управления при отсутствии такового.
      Однако главная полезность в ДОТУ метода динамического программирования не в его возможностях и особенностях, о которых было сказано выше. ВАЖНО ОБРАТИТЬ ВНИМАНИЕ И ПОНЯТЬ:Если в математике видеть науку об объективной общевселенской мере (через “ять”), а в её понятийном, терминологическом аппарате и символике видеть одно из предоставленных людям средств описания объективных частных процессов, выделяемых ими из некоторых объемлющих процессов, то всякое описание метода динамического программирования есть краткое изложение всейранее изложенной достаточно общей теории управления, включая и её мистико-религиозные аспекты; но - на языке математики и формальной логики.
      Чтобы пояснить это, обратимся к рис. 4 (помещён ниже по тексту), памятуя о сделанном ранее замечании об определённости начального состояния с достаточной для вхождения в матрицы перехода точностью.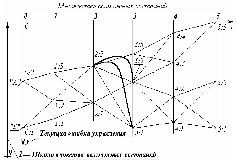
 
 
       Рис. 4. Динамическое программирование, его символизм и вхождение в управление
 
      На нём показаны два объекта управления «А» и «Б» в начальном состоянии; три объективно возможных завершающих состояния (множество «5»); множества («1» - «4») промежуточных возможных состояний; и пути объективно возможных переходов из каждого состояния в иные.
      Рис. 4 можно уподобить некоторому фрагменту общевселенской меры развития (многовариантного предопределения бытия) - одной из составляющих в триединстве материя-информация-мера.
      Если принять такое уподобление рис. 4, то объективно возможен переход из любого начального состояния «0:1» или «0:2» в любое из завершающих состояний «5:1», «5:2», «5:3». Но эта объективная возможность может быть ограничена субъективными качествами управленцев, намеревающихся перевести объекты «А» и «Б» из начального состояния в одно из завершающих состояний.
      Если дано Свыше Различение, то управленец «А» (или «Б») снимет с объективной меры «кальку»

      

        
, на которой будет виден хотя бы один из множества возможных путей перевода объекта из начального состояния во множество завершающих. Если Различение не дано, утрачено или отвергнуто в погоне за вожделениями, или бездумной верой в какую-либо традицию, но не Богу по совести, то на «кальке» будут отсутствовать какие-то пути и состояния, но могут «появиться» объективно невозможные пути и состояния, объективно не существующие в истинной Богом данной мере - Предопределении бытия. Кроме того, по субъективному произволу управленца выбирается и желанное определённое завершающее состояние из их множества. Соответственно следование отсебятине или ошибка в выборе предпочтительного завершающего состояния может завершиться катастрофой с необратимыми последствиями.
      Но матрица возможных состояний, показанная на рис. 4, вероятностно предопределяеттолько частный процесс в некой взаимной вложенности процессов. По этой причине каждое из начальных состояний «0:1», «0:2» может принадлежать либо одному и тому же, либо различным объемлющим процессам, в управленческом смысле иерархически высшим по отношению к рассматриваемому; то же касается и каждого из завершающих состояний «5:1», «5:2», «5:3» в паре «исходное - завершающее» состояния. Каждый из объемлющих процессов обладает их собственными характеристиками и направленностью течения событий в нём.
      Может оказаться, что цель «5:1» очень привлекательна, если смотреть на неё из множества начальных неудовлетворительных состояний. Но не исключено, что объемлющий процесс, к которому завершающее состояние «5:1» принадлежит, как промежуточное состояние, в силу взаимной вложенности процессов, на одном из последующих шагов завершается полной и необратимой катастрофой. Например, цель «5:1» - не опоздать на «Титаник», выходящий в свой первый рейс,… ставший трагическим и последним. Чтобы не выбирать такую цель из множества объективно возможных, необходимо быть в ладу с иерархически наивысшимвсеобъемлющим управлением, которое удержит частное ладное с ним управление от выбора такой цели, принадлежащей к обречённому на исчезновение процессу.
      Но если рис. 4 - «калька» с объективной меры, то может статься, что какое-то завершающее состояние, являющееся вектором целей - отсебятина, выражающая желание «сесть на два поезда сразу». Иными словами, разные компоненты вектора целей принадлежат к двум или более взаимно исключающим друг друга иерархически высшим объемлющим процессам протекающим одновременно.