ОТ РЕДАКЦИИ

Предлагаемое издание “Занимательной физики” Я.И. Перельмана повторяет четыре предыдущих. Автор в течение многих лет работал над книгой, совершенствуя текст и дополняя его, и в последний раз при жизни автора книга вышла в 1936 г. (тринадцатое издание). Выпуская последующие издания, редакция не ставила своей целью коренную переработку текста или существенные дополнения: автор так подобрал основное содержание “Занимательной физики”, что оно, иллюстрируя, и углубляя основные сведения из физики, не устарело до сих пор. Кроме того, времени после 1936г. прошло уже так много, что желание отразить новейшие достижения физики привело бы и к значительному увеличению книги, и к изменению ее “лица”. Например, авторский текст о принципах космических полетов не устарел, а фактического материала в этой области уже так много, что можно только адресовать читателя к другим книгам, специально посвященным этой теме.

Четырнадцатое и пятнадцатое издания (1947 и 1949 гг.) вышли под редакцией проф. А. Б. Млодзеевского. В подготовке шестнадцатого издания (1959 — 1960 гг.) принял участие доц. В.А.Угаров. При редактировании всех изданий, вышедших без автора, лишь заменены устаревшие цифры, изъяты не оправдавшие себя проекты, сделаны отдельные дополнения и примечания.

ИЗ ПРЕДИСЛОВИЯ АВТОРА К ТРИНАДЦАТОМУ ИЗДАНИЮ

В этой книге автор стремится не столько сообщить читателю новые знания, сколько помочь ему “узнать то, что он знает”, т. е. углубить и оживить уже имеющиеся у него основные сведения из физики, научить сознательно ими распоряжаться и побудить к разностороннему их применению. Достигается это рассмотрением пестрого ряда головоломок, замысловатых вопросов, занимательных рассказов, забавных задач, парадоксов и неожиданных сопоставлений из области физики, относящихся к кругу повседневных явлений или черпаемых из общеизвестных произведений научно-фантастической беллетристики. Материалом последнего рода составитель пользовался особенно широко, считая его наиболее соответствующим целям сборника: приведены отрывки из романов и рассказов Жюля Верна, Уэллса, Марка Твена и др. Описываемые в них фантастические опыты, помимо их заманчивости, могут и при преподавании играть немаловажную роль в качестве живых иллюстраций.

Составитель старался, насколько мог, придавать изложению внешне интересную форму, сообщать привлекательность предмету. Он руководился той психологической аксиомой, что интерес к предмету повышает внимание, облегчает понимание и, следовательно, способствует более сознательному и прочному усвоению.

Вопреки обычаю, установившемуся для подобного рода сборников, в “Занимательной физике” весьма мало места отводится описанию забавных и эффектных физических опытов. Эта книга имеет иное назначение, нежели сборники, предлагающие материал для экспериментирования. Главная цель “Занимательной физики” — возбудить деятельность научного воображения, приучить читателя мыслить в духе физической науки и создать в его памяти многочисленные ассоциации физических знаний с самыми разнородными явлениями жизни, со всем тем, с чем он обычно входит в соприкосновение. Установка, которой составитель старался придерживаться при переработке книги, была дана В. И. Лениным в следующих словах: “Популярный писатель подводит читателя к глубокой мысли, к глубокому учению, исходя из самых простых и общеизвестных данных, указывая при помощи несложных рассуждений или удачно выбранных примеров главные выводы из этих данных, наталкивая думающего читателя на дальнейшие и дальнейшие вопросы. Популярный писатель не предполагает не думающего, не желающего или не умеющего думать читателя, — напротив, он предполагает в неразвитом читателе серьезное намерение работать головой и помогает ему делать эту серьезную и трудную работу, ведет его, помогая ему делать первые шаги и уча идти дальше самостоятельно” [В. И. Ленин. Собр. соч., изд. 4, т. 5, стр. 285.].

Ввиду интереса, проявляемого читателями к истории этой книги, приводим некоторые библиографические данные о ней.

“Занимательная физика” “родилась” четверть века назад и была первенцем в многочисленной книжной семье ее автора, насчитывающей сейчас несколько десятков членов.

“Занимательной физике” посчастливилось проникнуть — как свидетельствуют письма читателей — в самые глухие уголки Союза.

Значительное распространение книги, свидетельствующее о живом интересе широких кругов к физическим знаниям, налагает на автора серьезную ответственность за качество ее материала. Сознанием этой ответственности объясняются многочисленные изменения и дополнения в тексте “Занимательной физики” при повторных изданиях. Книга, можно сказать, писалась в течение всех 25 лет ее существования. В последнем издании от текста первого сохранена едва половина, а от иллюстраций — почти ни одной.

К автору поступали от иных читателей просьбы воздерживаться от переработки текста, чтобы не вынуждать их “из-за десятка новых страниц приобретать каждое повторное издание”. Едва ли подобные соображения могут освободить автора от обязанности всемерно улучшать свой труд. “Занимательная физика” не художественное произведение, а сочинение научное, хотя и популярное. Ее предмет — физика — даже в начальных своих основаниях непрестанно обогащается свежим материалом, и книга должна периодически включать его в свой текст.

С другой стороны, приходится нередко слышать упреки в том, что “Занимательная физика” не уделяет места таким темам, как новейшие успехи радиотехники, расщепление атомного ядра, современные физические теории и т. п. Упреки такого рода — плод недоразумения. “Занимательная физика” имеет вполне определенную целевую установку; рассмотрение же этих вопросов — задача иных сочинений.

К “Занимательной физике”, помимо второй ее книги, примыкает и несколько других сочинений того же автора. Одно предназначено для сравнительно мало подготовленного читателя, еще не приступавшего к систематическому изучению физики, и озаглавлено “Физика на каждом шагу” (издание “Детиздата”). Два других, напротив, имеют в виду тех, кто уже закончил изучение среднешкольного курса физики. Это — “Занимательная механика” и “Знаете ли вы физику?”. Последняя книга является как бы завершением “Занимательной физики”.

1936 г. Я. Перельман

Глава первая. СКОРОСТЬ. СЛОЖЕНИЕ ДВИЖЕНИЙ.

Спортивную дистанцию 1,5 км хороший бегун пробегает примерно за 3 мин. 50 сек. (мировой рекорд 1958 г. — 3 мин. 36,8 сек.). Для сравнения с обычной скоростью пешехода — 1,5 м в секунду — надо сделать маленькое вычисление; тогда окажется, что спортсмен пробегает в секунду 7 м. Впрочем, скорости эти не вполне сравнимы: пешеход может ходить долго, целые часы, делая по 5 км в час, спортсмен же способен поддерживать значительную скорость своего бега только короткое время. Пехотная воинская часть перемещается бегом втрое медленнее рекордсмена; она делает 2 м в секунду, или 7 с лишком километров в час, но имеет перед спортсменом то преимущество, что может совершать гораздо большие переходы.

Интересно сравнить нормальную поступь человека со скоростью таких — вошедших в пословицу — медлительных животных, как улитка или черепаха. Улитка вполне оправдывает репутацию, приписываемую ей поговоркой: она проходит 1,5 мм в секунду, или 5,4 м в час — ровно в тысячу раз меньше человека! Другое классически медленное животное, черепаха, не намного перегоняет улитку: ее обычная скорость — 70 м в час.

Проворный рядом с улиткой и черепахой, человек предстанет перед нами в ином свете, если сопоставить его движение с другими, даже не очень быстрыми движениями в окружающей природе. Правда, он легко перегоняет течение воды в большинстве равнинных рек и не намного отстает от умеренного ветра. Но с мухой, пролетающей 5 м в секунду, человек может успешно состязаться разве только на лыжах. Зайца или охотничью собаку человек не перегонит даже на лошади карьером. Состязаться в скорости с орлом человек может лишь на самолете.

Машины, изобретенные человеком, делают его самым быстрым существом мира.

Сравнительно недавно в СССР был построен пассажирский теплоход с подводными крыльями, развивающий скорость 60 — 70 км/час. На суше человек может двигаться быстрее, чем на воде. На некоторых участках пути скорость движения пассажирских поездов в СССР доходит до 100 км/час. Новая легковая автомашина ЗИЛ-111 (рис. 1) может развивать скорость до 170 км/час, семиместный легковой автомобиль “Чайка” — до 160 км/час.

Рис. 1. Автомобиль ЗИЛ-111.

Эти скорости далеко превзошла современная авиация. На многих линиях Гражданского воздушного флота СССР работают многоместные лайнеры ТУ-104 и ТУ-114 (рис. 2). Средняя скорость их полета составляет около 800 км/час. Еще не так давно перед авиаконструкторами ставилась задача перешагнуть “звуковой барьер”, превысить скорость звука (330 м/сек, т. е. 1200 км/час). Сейчас эта задача решена. Скорости небольших самолетов с мощными реактивными двигателями приближаются к 2000 км/час.

Аппараты, создаваемые человеком, могут достигать еще больших скоростей. Искусственные спутники Земли, летающие вблизи границы плотных слоев атмосферы, движутся со скоростью около 8 км/сек. Космические аппараты, направляющиеся к планетам солнечной системы, получают начальную скорость, превышающую вторую космическую скорость (11,2 км/сек, у поверхности Земли).

Рис. 2. Пассажирский реактивный самолет ТУ-104.

Читатель может просмотреть следующую таблицу скоростей: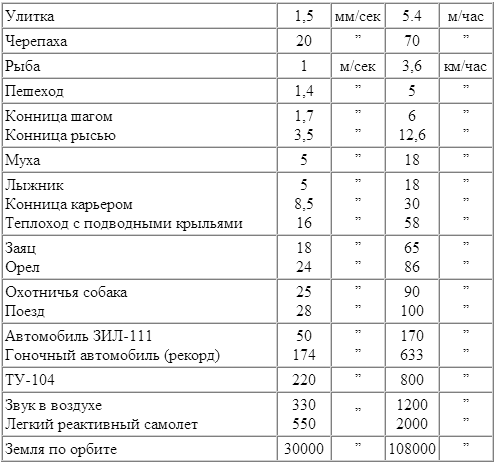

Можно ли в 8 часов утра вылететь из Владивостока и в 8 часов утра того же дня прилететь в Москву? Вопрос этот вовсе не лишен смысла. Да, можно. Чтобы понять этот ответ, нужно только вспомнить, что разница между поясным временем Владивостока и Москвы составляет девять часов. И если самолет сможет пройти расстояние между Владивостоком и Москвой за это время, то он прибудет в Москву в час своего вылета из Владивостока.

Расстояние Владивосток — Москва составляет примерно 9000 км. Значит, скорость самолета должна быть равна 9000: 9 = 1000 км/час. Это вполне достижимая в современных условиях скорость.

Чтобы “перегнать Солнце” (или, точнее, Землю) в полярных широтах, нужна значительно меньшая скорость. На 77-й параллели (Новая Земля) самолет, обладающий скоростью около 450 км/час, пролетает столько же, сколько успевает за тот же промежуток времени пройти точка земной поверхности при вращении Земли вокруг оси. Для пассажира такого самолета Солнце остановится и будет неподвижно висеть на небе, не приближаясь к закату (при этом, конечно, самолет должен двигаться в подходящем направлении).

Еще легче “перегнать Луну” в ее собственном обращении вокруг Земли. Луна движется вокруг Земли в 29 раз медленнее, чем Земля вокруг своей оси (сравниваются, конечно, так называемые “угловые”, а не линейные скорости). Поэтому обыкновенный пароход, делающий 25 — 30 км в час, может уже в средних широтах “перегнать Луну”.

О таком явлении упоминает Марк Твен в своих очерках “Простаки за границей”. Во время переезда по Атлантическому океану от Нью-Йорка к Азорским островам “стояла прекрасная летняя погода, а ночи были даже лучше дней. Мы наблюдали странное явление: Луну, появляющуюся каждый вечер в тот же час в той же точке неба. Причина этого оригинального поведения Луны сначала оставалась для нас загадочной, но потом мы сообразили, в чем дело: мы подвигались каждый час на 20 минут долготы к востоку, т. е. именно с такой скоростью, чтобы не отставать от Луны!”.

Для нас, привыкших мерить время на свою человеческую мерку, тысячная доля секунды равнозначна нулю. Такие промежутки времени лишь недавно стали встречаться в нашей практике. Когда время определяли по высоте Солнца или длине тени, то не могло быть речи о точности даже до минуты (рис. 3); люди считали минуту слишком ничтожной величиной, чтобы стоило ее измерять. Древний человек жил такой неторопливой жизнью, что на его часах — солнечных, водяных, песочных — не было особых делений для минут (рис. 4, 5). Только с начала XVIII века стала появляться на циферблате минутная стрелка. А с начала XIX века появилась и секундная стрелка.

Рис. 3. Определение времени дня по положению Солнца на небе (слева) и по длине тени (справа).

Рис. 4. Водяные часы. употреблявшиеся в древнем мире.

Рис. 5. Старинные карманные часы.

Что же может совершиться в тысячную долю секунды? Очень многое! Поезд, правда, может переместиться за этот промежуток времени всего сантиметра на три, звук — уже на 33 см, самолет — примерно на полметра; земной шар пройдет в своем движении вокруг Солнца в такую долю секунды 30 м, а свет — 300 км.

Мелкие существа, окружающие нас, если бы они умели рассуждать, вероятно, не считали бы тысячную долю секунды за ничтожный промежуток времени. Для насекомых, например, величина эта вполне ощутима. Комар в течение одной секунды делает 500 — 600 полных взмахов крылышками; значит, в тысячную долю секунды он успевает поднять их или опустить.

Человек неспособен перемещать свои члены так быстро, как насекомое. Самое быстрое наше движение — мигание глаз, “мгновение ока”, или “миг”, в первоначальном смысле этих слов. Оно совершается так быстро, что мы не замечаем даже временного затмения поля нашего зрения. Немногие, однако, знают, что это движение — синоним невообразимой быстроты — протекает в сущности довольно медленно, если измерять его тысячными долями секунды. Полное “мгновение ока” длится, как обнаружили точные измерения, в среднем 2/5 секунды, т. е. 400 тысячных долей ее. Оно распадается на следующие фазы: опускание века (75 — 90 тысячных секунды), состояние неподвижности опущенного века (130 — 170 тысячных) и поднятие его (около 170 тысячных). Как видите, один “миг” в буквальном смысле этого слова — промежуток довольно значительный, в течение которого глазное веко успевает даже немного отдохнуть. И если бы мы могли раздельно воспринимать впечатления, длящиеся тысячную долю секунды, мы уловили бы “в один миг” два плавных движения глазного века, разделенных промежутком покоя.

При таком устройстве нашей нервной системы мы увидели бы окружающий нас мир преображенным до неузнаваемости. Описание тех странных картин, какие представились бы тогда нашим глазам, дал английский писатель Уэллс в рассказе “Новейший ускоритель”. Герои рассказа выпили фантастическую микстуру, которая действует на нервную систему так, что делает органы чувств восприимчивыми к раздельному восприятию быстрых явлений.

Вот несколько примеров из рассказа:

“ — Видали ли вы до сих пор, чтобы занавеска прикреплялась к окну этаким манером?

Я посмотрел на занавеску и увидел, что она словно застыла и что угол у нее как загнулся от ветра, так и остался.

— Не видал никогда, — сказал я. — Что за странность!

— А это? — сказал он и растопырил пальцы, державшие стакан.

Я ожидал, что стакан разобьется, но он даже не шевельнулся: он повис в воздухе неподвижно.

— Вы, конечно, знаете, — сказал Гибберн, — что падающий предмет опускается в первую секунду на 5 м. И стакан пробегает теперь эти 5 м, — но, вы понимаете, не прошло еще и сотой доли секунды. [Надо иметь в виду, к тому же, что в первую сотую долю первой секунды своего падения тело проходит не сотую часть от 5 м, а 10000-ю (по формуле S = gt2/2), т.е. полмиллиметра, а в первую тысячную долю секунды — всего 1/200 мм.] Это может вам дать понятие о силе моего “ускорителя”.

Стакан медленно опускался. Гибберн провел рукой вокруг стакана, над ним и под ним…

Я глянул в окно. Какой-то велосипедист, застывший на одном месте, с застывшим облаком пыли позади, догонял какую-то бричку, которая также не двигалась ни на один дюйм.

… Наше внимание было привлечено омнибусом, совершенно окаменевшим. Верхушка колес, лошадиные ноги, конец кнута и нижняя челюсть кучера (он только что начал зевать) — все это, хотя и медленно, но двигалось; остальное же в этом неуклюжем экипаже совершенно застыло. Сидящие там люди были как статуи.

…Какой-то человек застыл как раз в тот момент, когда он делал нечеловеческие усилия сложить на ветру газету. Но для нас этого ветра не существовало.

…Все, что было сказано, подумано, сделано мной с той поры, как “ускоритель” проник в мой организм, было лишь мгновением ока для всех прочих людей и для всей вселенной”.

Вероятно, читателям интересно будет узнать, каков наименьший промежуток времени, измеримый средствами современной науки? Еще в начале этого века он равнялся 10000-й доле секунды; теперь же физик в своей лаборатории способен измерить 100000000000-ю долю секунды. Этот промежуток примерно во столько же раз меньше целой секунды, во сколько раз секунда меньше 3000 лет!

Когда Уэллс писал свой “Новейший ускоритель”, он едва ли думал, что нечто подобное когда-нибудь осуществится в действительности. Ему довелось, однако, дожить до этого: он мог собственными глазами увидеть — правда, только на экране — те картины, которые создало некогда его воображение. Так называемая “лупа времени” показывает нам на экране в замедленном темпе многие явления, протекающие обычно очень быстро.

“Лупа времени” — это кинематографический фотоаппарат, делающий в секунду не 24 снимка, как обычные киноаппараты, а во много раз больше. Если заснятое так явление проектировать на экран, пуская ленту с обычной скоростью 24 кадра в секунду, то зрители увидят явление растянутым — совершающимся в соответствующее число раз медленнее нормального. Читателю случалось, вероятно, видеть на экране такие неестественно плавные прыжки и другие замедленные явления. С помощью более сложных аппаратов того же рода достигается замедление еще более значительное, почти воспроизводящее то, что описано в рассказе Уэллса.

В парижских газетах появилось однажды объявление, обещавшее каждому за 25 сантимов указать способ путешествовать дешево и притом без малейшего утомления. Нашлись легковерные, которые прислали требуемые 25 сантимов. В ответ каждый из них получил по почте письмо следующего содержания:

“Оставайтесь, гражданин, спокойно в своей кровати и помните, что Земля наша вертится. На параллели Парижа — 49-й — вы пробегаете каждые сутки более 25 000 км. А если вы любите живописные виды, откиньте оконную занавеску и восхищайтесь картиной звездного неба”.

Привлеченный к суду за мошенничество, виновник этой затеи выслушал приговор, уплатил наложенный на него штраф и, говорят, став а театральную позу, торжественно повторил знаменитое восклицание Галилея:

— А все-таки она вертится!

В известном смысле обвиняемый был прав, потому что каждый обитатель земного шара не только “путешествует”, вращаясь вокруг земной оси, но с еще большей скоростью переносится Землей в ее обращении вокруг Солнца. Ежесекундно планета наша со всеми своими обитателями перемещается в пространстве на 30 км, вращаясь одновременно и вокруг оси.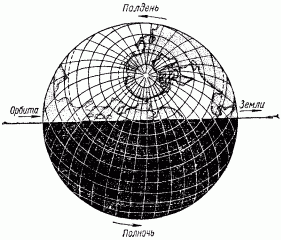

Рис. 6. На ночной половине земного шара люди движутся вокруг Солнца быстрее, чем на дневной.

По этому поводу можно задать интересный вопрос: когда мы движемся вокруг Солнца быстрее — днем или ночью?

Вопрос способен вызвать недоумение: ведь всегда на одной стороне Земли день, на другой — ночь; какой же смысл имеет наш вопрос? По-видимому, никакого. Однако это не так. Спрашивается ведь не о том, когда вся Земля перемещается скорее, а о том, когда мы, ее обитатели, движемся скорее среди звезд. А это уже вовсе не бессмысленный вопрос. В солнечной системе мы совершаем два движения: вращаемся вокруг Солнца и в то же время обращаемся вокруг земной оси. Оба движения складываются, но результат получается различный, смотря по тому, находимся ли мы на дневной или ночной половине Земли. Взгляните на рис. 6, и вы поймете, что в полночь скорость вращения прибавляется к поступательной скорости Земли, а в полдень, наоборот, отнимается от нее. Значит, в полночь мы движемся в солнечной системе быстрее, нежели в полдень.

Так как точки экватора пробегают в секунду около полукилометра, то для экваториальной полосы разница между полуденной и полуночной скоростью достигает целого километра в секунду. Знакомые с геометрией легко могут вычислить, что для Ленинграда (который находится на 60-й параллели) эта разница вдвое меньше: в полночь ленинградцы каждую секунду пробегают в солнечной системе на полкилометра больше, нежели в полдень.

Прикрепите сбоку к ободу тележного колеса (или к шине велосипедного) цветную бумажку и наблюдайте за ней во время движения телеги (или велосипеда). Вы заметите странное явление: пока бумажка находится в нижней части катящегося колеса, она видна довольно отчетливо; в верхней же части она мелькает так быстро, что вы не успеваете ее разглядеть.

Выходит как будто, что верхняя часть колеса движется быстрее, чем нижняя. То же наблюдение можно сделать, если сравнить между собой верхние и нижние спицы катящегося колеса какого-нибудь экипажа. Будет заметно, что верхние спицы сливаются в одно сплошное целое, нижние же видимы раздельно. Дело опять-таки происходит так, словно верхняя часть колеса быстрее движется, чем нижняя.

В чем же разгадка этого странного явления? Да просто в том, что верхняя часть катящегося колеса действительно движется быстрее, чем нижняя. Факт представляется с первого взгляда невероятным, а между тем простое рассуждение убедит нас в этом. Ведь каждая точка катящегося колеса совершает сразу два движения: обращается вокруг оси и в то же время подвигается вперед вместе с этой осью. Происходит — как в случае земного шара — сложение двух движений, и результат для верхней и нижней частей колеса получается разный. Вверху вращательное движение колеса прибавляется к поступательному, так как оба движения направлены в одну и ту же сторону. Внизу же вращательное движение направлено в обратную сторону и, следовательно, отнимается от поступательного. Вот почему верхние части колеса перемещаются относительно неподвижного наблюдателя быстрее, чем нижние.

То, что это действительно так, легко понять на простом опыте, который следует проделать при удобном случае. Воткните в землю палку рядом с колесом стоящей телеги так, чтобы палка приходилась против оси. На ободе колеса, в самой верхней и в самой нижней его частях, сделайте пометки мелом или углем; пометки придутся, следовательно, как раз против палки. Теперь откатите телегу немного вправо (рис.7), чтобы ось отошла от палки сантиметров на 20 — 30, и заметьте, как переместились ваши пометки. Окажется, что верхняя пометка A переместилась заметно больше, нежели нижняя В, которая только едва отступила от палки.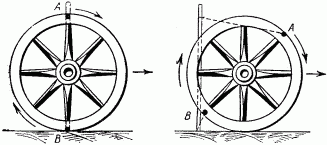

Рис. 7. Как убедиться, что верхняя часть колеса движется быстрее нижней Сравните расстояния точек А и В откатившегося колеса (правый чертеж) от неподвижной палки.

Итак, не все точки движущегося колеса телеги перемещаются одинаково быстро. Какая же часть катящегося колеса движется всего медленнее?

Нетрудно сообразить, что медленнее всех движутся те точки колеса, которые в данный момент соприкасаются с землей. Строго говоря, в момент соприкосновения с почвой эти точки колеса совершенно неподвижны.

Все сказанное справедливо только для колеса катящегося, а не для такого, которое вращается на неподвижной оси. В маховом колесе, например, верхние н нижние точки обода движутся с одинаковой скоростью.

Вот еще одна не менее любопытная задача: в поезде, идущем, скажем, из Ленинграда в Москву, существуют ли точки, которые по отношению к полотну дороги движутся обратно — от Москвы к Ленинграду?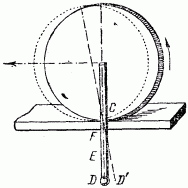

Рис. 8. Опыт с кружком и спичкой. Когда колесо откатывается налево, точки F, Е, D выступающей части спички подвигаются в обратную сторону.

Рис. 9. Когда железнодорожное колесо катится налево, нижние части его выступающего края движутся направо, т. е. в обратную сторону.

Оказывается, что в каждый момент на каждом колесе существуют такие точки. Где же они находятся?

Вы знаете, конечно, что железнодорожные колеса имеют на ободе выступающий край (реборду). И вот оказывается, что нижние точки этого края при движении поезда перемещаются вовсе не вперед, а назад.

В этом легко удостовериться, проделав такой опыт. К небольшому кружочку, например к монете или пуговице, прилепите воском спичку так, чтобы она прилегала к кружку по радиусу и далеко выступала за край. Если теперь упереть кружок (рис. 8) в край линейки в точке С и начать катить его справа налево, то точки F, Е и D выступающей части отодвинутся не вперед, а назад. Чем дальше точка от края кружка, тем заметнее подастся она назад при качении кружка (точка D перейдет в D').

Точки реборды железнодорожного колеса движутся так же, как и выступающая часть спички в нашем опыте.

Вас не должно удивлять теперь, что в поезде существуют точки, которые движутся не вперед, а назад.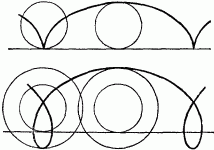

Рис. 10. Вверху изображена та кривая линия (“циклоида”), которую описывает каждая точка обода катящегося колеса телеги. Внизу — кривая линия, описываемая каждой точкой выступающего края железнодорожного колеса.

Правда, это движение длится лишь ничтожную долю секунды; но, как бы то ни было, обратное перемещение в движущемся поезде все же существует наперекор нашим обычным представлениям. Сказанное поясняется рисунками 9 и 10.

Вообразите, что весельная лодка плывет по озеру, и пусть стрелка а на нашем рис. 11 изображает направление и скорость ее движения. Наперерез идет парусная лодка; стрелка b изображает ее направление и скорость. Если вас, читатель, спросят, откуда эта лодка отчалила, вы, конечно, сразу укажете пункт м на берегу. Но если с тем же вопросом обратиться к пассажирам весельной лодки, они указали бы совершенно другую точку. Почему?

Рис. 11. Парусная лодка идет наперерез весельной. Стрелки а и b — скорости. Что увидят гребцы?

Происходит это оттого, что пассажиры видят лодку движущейся вовсе не под прямым углом к пути своей лодки. Они ведь не чувствуют собственного движения: им кажется, что сами они стоят на месте, а все кругом движется с их собственной скоростью, но в обратном направлении. Поэтому для них парусная лодка движется не только по направлению стрелки b, но и по направлению пунктирной линии а, обратно движению весельной лодки (см. рис. 12). Оба движения парусной лодки — действительное и кажущееся — складываются по правилу параллелограмма. В результате пассажирам шлюпки кажется, будто парусная лодка движется по диагонали параллелограмма, построенного на b и а. Вот почему пассажирам представляется, что парусная лодка отчалила от берега вовсе не в точке М, а в некоторой точке N, далеко впереди по движению весельной шлюпки (рис. 12).

Двигаясь вместе с Землей по ее орбите и встречая лучи звезд, мы судим о положении источников этих лучей так же неправильно, как пассажиры весельной лодки ошибочно определяют место отплытия парусной. Поэтому звезды представляются нам немного смещенными вперед по пути движения Земли. Конечно, скорость движения Земли ничтожна по сравнению со скоростью света (в 10000 раз меньше); поэтому кажущееся смещение звезд незначительно. Но оно может быть обнаружено с помощью астрономических приборов. Явление это носит название аберрации света.

Если подобные вопросы заинтересовали вас, попробуйте, не изменяя условий нашей задачи о лодке, сказать:

1) по какому направлению движется весельная лодка для пассажиров парусной?

2) куда направляется весельная лодка, по мнению пассажиров парусной?

Чтобы ответить на эти вопросы, вам нужно на линии а (рис. 12) построить параллелограмм скоростей; диагональ его покажет, что пассажирам парусной лодки весельная кажется плывущей в косом направлении, словно собираясь причалить к берегу.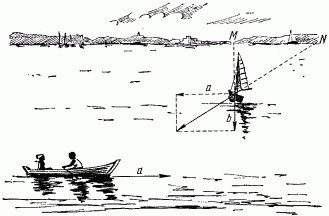

Рис. 12. Гребцам кажется, что парусная лодка идет не наперерез им, а косо — от точки N, а не от М.

Глава вторая. ТЯЖЕСТЬ И ВЕС. РЫЧАГ. ДАВЛЕНИЕ

Если я скажу вам: “Сейчас вы сядете на стул так, что не сможете встать, хотя и не будете привязаны”, вы примете это, конечно, за шутку.

Хорошо. Сядьте же так, как сидит человек, изображенный на рис. 13, т. е. держа туловище отвесно и не пододвигая ног под сиденье стула. А теперь попробуйте встать, не меняя положения ног и не нагибая корпуса вперед.

Рис. 13. В таком положении невозможно подняться со стула.

Что, не удается? Никаким усилием мускулов не удастся вам встать со стула, пока вы не пододвинете ног под сиденье или не подадитесь корпусом вперед.

Чтобы понять, почему это так, нам придется побеседовать немного о равновесии тел вообще и человеческого в частности. Стоящий предмет не опрокидывается только тогда, когда отвесная линия, проведенная из центра тяжести, проходит внутри основания вещи. Поэтому наклонный цилиндр (рис, 14) должен непременно опрокинуться; но если бы он был настолько широк, что отвесная линия, проведенная из его центра тяжести, проходила бы в пределах его основания, цилиндр не опрокинулся бы. Так называемые “падающие башни” — в Пизе, в Болонье или хотя бы “падающая колокольня” в Архангельске (рис. 15) не падают, несмотря на свой наклон, также потому, что отвесная линия из их центра тяжести не выходит за пределы основания (другая, второстепенная, причина та, что они углублены в землю своими фундаментами).

Рис. 14. Такой цилиндр должен опрокинуться, потому что отвесная линия, проведенная из центра тяжести, проходит вне основания.

Рис. 15. “Падающая” колокольня в Архангельске (со старинной фотографии).

Стоящий человек не падает только до тех пор, пока отвесная линия из центра тяжести находится внутри площадки, ограниченной краями его ступней (рис. 16). Поэтому так трудно стоять на одной ноге; еще труднее стоять на канате: основание очень мало и отвесная линия легко может выйти за его пределы. Заметили ли вы, какой странной походкой отличаются старые “морские волки”? Проводя всю жизнь на качающемся судне, где отвесная линия из центра тяжести их тела ежесекундно может выйти за пределы пространства, занятого ступнями, моряки вырабатывают привычку ступать так, чтобы основание их тела (т. е. широко расставленные ноги) захватывало возможно большее пространство. Это придает морякам необходимую устойчивость на колеблющейся палубе; естественно, что та же привычка сохраняется при ходьбе по твердой земле. Можно привести и обратный пример, когда необходимость поддерживать равновесие обусловливает красоту позы. Обращали вы внимание на то, какой стройный вид имеет человек, несущий на голове груз? Всем известны изящные изваяния женских фигур с кувшином на голове. Неся на голове груз, по необходимости приходится держать голову и туловище прямо: малейшее уклонение грозит вывести центр тяжести (приподнятый в таких случаях выше обычного положения) из контура основания, и тогда равновесие фигуры будет нарушено. Теперь вернемся к опыту с вставанием сидящего человека. Центр тяжести туловища сидящего человека находится внутри тела, близ позвоночника, сантиметров на 20 выше уровня пупка. Проведите отвесную линию из этой точки вниз: она пройдет под стулом, позади ступней. А чтобы человек мог стоять, линия эта должна проходить между ступнями.

Рис. 16. Когда человек стоит, отвесная линия, проведенная из центра тяжести, проходит внутри площадки, ограниченной ступнями.

Значит, вставая, мы должны либо податься грудью вперед, перемещая этим центр тяжести, либо же пододвинуть ноги назад, чтобы подвести опору под центр тяжести. Обычно мы так и делаем,.когда встаем со стула. Но если нам не разрешают делать ни того, ни другого, то встать мудрено, как вы и убеждаетесь на описанном опыте.

То, что вы делаете десятки тысяч раз в день в течение всей жизни, должно быть вам прекрасно известно. Так принято думать, но это далеко не всегда верно. Лучший пример — ходьба и бег. Есть ли что-нибудь более нам знакомое, чем эти движения? А много ли найдется людей, которые ясно представляют себе, как, собственно, передвигаем мы свое тело при ходьбе и беге и в чем разнятся эти два рода движений? Послушаем же, что говорит о ходьбе и беге физиология [Текст отрывка заимствован из “Лекций по зоологии” проф. Поля Бера; иллюстрации прибавлены составителем.]. Для большинства, я уверен, это описание будет совершенно ново.

“Предположим, что человек стоит на одной ноге, например, на правой. Вообразим себе, что он приподнимает пятку, наклоняя в то же время туловище вперед [При этом идущий человек, отталкиваясь от опоры, оказывает на нее добавочное к весу давление — около 20 кг. Отсюда, между прочим, следует, что идущий человек сильнее давит на землю, чем стоящий. Я. П.].

Рис. 17. Как человек ходит. Последовательные положения тела при ходьбе.

При таком положении перпендикуляр из центра тяжести, понятно, выйдет из площади основания опоры, и человек должен упасть вперед. Но едва начинается это падение, как левая нога его, оставшаяся в воздухе, быстро подвигается вперед и становится на землю впереди перпендикуляра из центра тяжести, так что последний, т. е. перпендикуляр, попадает в площадь, образуемую линиями, которыми соединяются точки опоры обеих ног. Равновесие таким образом восстанавливается; человек ступил, сделал шаг.

Рис. 18. Графическое изображение движений ног при ходьбе. Верхняя линия (А) относится к одной ноге, нижняя (В) — к другой. Прямые линии отвечают моментам опоры о землю, дуги — моментам движения ног без опоры. Из графика видно, что в течение промежутка времени а обе ноги опираются о землю; в течение b — нога А в воздухе, В продолжает опираться; в течение с — вновь обе ноги опираются о землю. Чем быстрее ходьба, тем короче становятся промежутки а, с (ср. с графиком бега, рис. 20).

Он может и остановиться в этом довольно утомительном положении. Но если хочет идти дальше, то наклоняет свое тело еще более вперед, переносит перпендикуляр из центра тяжести за пределы площади опоры и в момент угрозы падения снова выдвигает вперед ногу, но уже не левую, а правую — новый шаг, и т. д. Ходьба поэтому есть не что иное, как ряд падений вперед, предупреждаемых вовремя поставленной опорой ноги, остававшейся до того позади.

Рис. 19. Как человек бежит. Последовательные положения тела при беге (есть моменты, когда обе ноги находятся без опоры.

Рассмотрим дело несколько ближе. Предположим, что первый шаг сделан. В этот момент правая нога еще касается земли, а левая уже ступает на землю.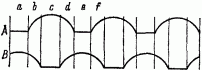

Рис. 20. Графическое изображение движения ног в беге (ср. с рис. 18).

Из графика видно, что для бегущего человека существуют моменты (b, d, f), когда обе ноги витают в воздухе. Этим и отличается бег от ходьбы.

Но если только шаг не очень короток, правая пятка должна была приподняться, так как именно это-то приподнимание пятки и позволяет телу наклониться вперед и нарушить равновесие. Левая нога ступает на землю прежде всего пяткой. Когда вслед за тем вся подошва ее становится на землю, правая нога поднимается совершенно на воздух. В то же время левая нога, несколько согнутая в колене, выпрямляется сокращением трехглавой бедренной мышцы и становится на мгновение вертикальной. Это позволяет полусогнутой правой ноге продвинуться вперед, не касаясь земли, и, следуя за движением тела, поставить на землю свою пятку как раз вовремя для следующего шага.

Подобный же ряд движений начинается затем для левой ноги, которая в это время опирается на землю только пальцами и вскоре должна подняться на воздух.

Бег отличается от ходьбы тем, что нога, стоящая на земле, внезапным сокращением ее мышц энергично вытягивается и отбрасывает тело вперед, так что последнее на одно мгновение совсем отделяется от земли. Затем оно снова падает на землю на другую ногу, которая, пока тело было на воздухе, быстро передвинулась вперед. Таким образом, бег состоит из ряда скачков с одной ноги на другую”.

Что касается энергии, затрачиваемой человеком при ходьбе по горизонтальной дороге, то она не равна кулю, как иные думают: центр тяжести тела пешехода при каждом шаге поднимается на несколько сантиметров. Можно рассчитать, что работа при ходьбе по горизонтальному пути составляет около одной пятнадцатой доли работы поднятия тела пешехода на высоту, равную пройденному пути [Расчет можно найти в брошюре проф. В. П. Горячкина “Работа живых двигателей”, 1914.].

Задав кому-нибудь этот вопрос, вы, конечно, получите ответ: “Вперед, по движению, согласно закону инерции”. Попросите, однако, объяснить подробнее, причем тут закон инерции. Можно предсказать, что при этом произойдет: ваш собеседник начнет уверенно доказывать свою мысль; но если не перебивать его, он скоро сам остановится в недоумении: выйдет, что именно вследствие инерции надо прыгать как раз наоборот — назад, против движения!

И в самом деле, закон инерции играет здесь роль второстепенную, — главная причина совсем другая. И если эту главную причину забыть, то мы действительно придем к выводу, что надо прыгать назад, а никак не вперед.

Пусть вам необходимо выпрыгнуть на ходу. Что произойдет при этом?

Когда мы прыгаем из двигающегося вагона, то тело наше, отделившись от вагона, обладает скоростью вагона (оно движется по инерции) и стремится двигаться вперед. Делая прыжок вперед, мы, конечно, не только не уничтожаем этой скорости, но, наоборот, еще увеличиваем ее.

Отсюда следует, что надо было бы прыгать назад, а вовсе не вперед, по направлению движения вагона. Ведь при прыжке назад скорость, сообщаемая прыжком, отнимается от скорости, с которой наше тело движется по инерции; вследствие этого, коснувшись земли, тело наше с меньшей силой будет стремиться опрокинуться.

Однако если уж и приходится прыгать из движущегося экипажа, то все прыгают вперед, по движению. Это действительно лучший способ и настолько проверенный, что мы настойчиво предостерегаем читателей от попыток проверить неудобство прыганья назад с движущегося экипажа.

Так в чем же дело?

В неверности объяснения, в его недоговоренности. Будем ли прыгать вперед, будем ли прыгать назад, — в том и другом случае нам грозит опасность упасть, так как верхняя часть туловища будет еще двигаться, когда ноги, коснувшись земли, остановятся [Можно объяснить падение в этом случае также и с иной точки зрения (см. об этом “Занимательную механику”, гл. III, статью: “Когда горизонтальная линия не горизонтальна?”).]. Скорость этого движения при прыжке вперед даже больше, чем при прыжке назад. Но существенно важно то, что вперед падать гораздо безопаснее, чем падать назад. В первом случае мы привычным движением выставляем ногу вперед (а при большой скорости вагона — пробегаем несколько шагов) и тем предупреждаем падение. Это движение привычно, так как мы всю жизнь совершаем его при ходьбе: ведь с точки зрения механики, как мы узнали из предыдущей статьи, ходьба есть не что иное, как ряд падений нашего тела вперед, предупреждаемых выставлением ноги. При падении же назад нет этого спасительного движения ног, и оттого здесь опасность гораздо больше. Наконец, важно и то, что когда мы даже в самом деле упадем вперед, то, выставив руки, расшибемся не так, как при падении на спину.

Итак, причина того, что безопаснее прыгать из вагона вперед, кроется не столько в законе инерции, сколько в нас самих. Ясно, что для предметов неживых правило это неприменимо: бутылка, брошенная из вагона вперед, скорее может разбиться при падении, нежели брошенная в обратном направлении. Поэтому, если вам придется почему-либо прыгать из вагона, выбросив предварительно свой багаж, следует кидать багаж назад, самим же прыгать вперед.

Люди опытные — кондукторы трамвая, контролеры — часто поступают так: прыгают назад, обратившись спиной по направлению прыжка. Этим достигается двоякая выгода: уменьшается скорость, приобретенная нашим телом по инерции, и, кроме того, предупреждается опасность падения на спину, так как прыгающий обращен передней стороной тела по направлению возможного падения.

Во время империалистической войны, как сообщали газеты, с французским летчиком произошел совершенно необыкновенный случай. Летая на высоте двух километров, летчик заметил, что близ его лица движется какой-то мелкий предмет. Думая, что это насекомое, летчик проворно схватил его рукой. Представьте изумление летчика, когда оказалось, что он поймал… германскую боевую пулю!

Не правда ли, это напоминает россказни легендарного барона Мюнхгаузена, будто бы ловившего пушечные ядра руками?

А между тем в сообщении о летчике, поймавшем пулю, нет ничего невозможного.

Пуля ведь не все время движется со своей начальной скоростью 800 — 900 м в секунду. Из-за сопротивления воздуха она постепенно замедляет свой полет и к концу пути — на излете — делает всего метров 40 в секунду. А такую скорость развивает и самолет. Значит, легко может случиться, что пуля и самолет будут иметь одинаковую скорость; тогда по отношению к летчику пуля будет неподвижна или будет двигаться едва заметно. Ничего не будет стоить тогда схватить ее рукой, — особенно в перчатке, потому что пуля, движущаяся в воздухе, сильно разогревается.

Если при известных условиях пуля может стать безвредной, то возможен и обратный случай: “мирное тело”, брошенное с незначительной скоростью, произведет разрушительное действие. Во время автомобильного пробега Ленинград — Тифлис (в 1924 г.) крестьяне кавказских селений приветствовали проносящиеся мимо них автомобили, кидая пассажирам арбузы, дыни, яблоки. Действие этих невинных подарков оказывалось вовсе не приятным: арбузы и дыни вдавливали, сминали и ломали кузов машины, а яблоки, попав в пассажира, причиняли серьезные увечья. Причина понятна: собственная скорость автомобиля складывалась со скоростью брошенного арбуза или яблока и превращала их в опасные, разрушительные снаряды. Нетрудно рассчитать, что пуля в 10 г весом обладает такой же энергией движения, как арбуз в 4 кг, брошенный в автомобиль, который мчится со скоростью 120 км в час, Пробивное действие арбуза при таких условиях не может, однако, сравниться с действием пули, так как арбуз не обладает ее твердостью.

Рис. 21. Арбуз, брошенный навстречу быстро мчащемуся автомобилю, превращается в “снаряд”.

Когда разовьется скоростная авиация в высших слоях атмосферы (в так называемой стратосфере), самолеты будут иметь скорость около 3000 км в час, т. е. скорость пуль, летчикам придется иметь дело с явлениями, напоминающими рассмотренное сейчас. А именно, каждый предмет, попадающийся на пути такого сверхбыстроходного самолета, превратится для него в разрушительный снаряд. Наткнуться на горсть пуль, просто уроненных с другого самолета, даже не летящего навстречу, будет все равно, что подвергаться обстрелу из пулемета: падающие пули ударятся об аэроплан с такой же силой, с какой вонзились бы в эту машину пули из пулемета. Так как относительные скорости в обоих случаях одинаковы (самолет и пуля сближаются со скоростью около 800 м в секунду), то разрушительные последствия столкновений будут одинаковы.

Наоборот, если нуля летит вслед аэроплану, несущемуся с равной скоростью, то для летчика она, как мы уже знаем, безвредна. Тем, что тела, движущиеся с почти одинаковой скоростью в одном направлении, приходят в соприкосновение без удара, искусно воспользовался в 1935 г. машинист Борщев, приняв движущийся состав из 36 вагонов на свой поезд без удара и тем предотвратив железнодорожную катастрофу. Произошло это на Южной дороге, на перегоне Ельников — Ольшанка, при следующих обстоятельствах. Впереди поезда, который вел Борщев, шел другой. За недостатком паров передний поезд остановился; его машинист с паровозом и несколькими вагонами отправился вперед, на станцию, оставив остальные 36 вагонов на пути. Вагоны, под которые не было подложено башмаков, покатились под уклон назад со скоростью 15 км в час, грозя налететь на поезд Борщева. Заметив опасность, находчивый машинист остановил свой поезд и повел его назад, постепенно развив скорость также 15 км в час. Благодаря такому маневру ему удалось весь 36-вагонный состав принять на свой поезд без малейшего повреждения.

Наконец, на том же принципе основан прибор, чрезвычайно облегчающий письмо в движущемся поезде. Писать в вагоне па ходу поезда трудно лишь потому, что толчки на стыках рельсов передаются бумаге и кончику пера не одновременно. Если устроить так, чтобы бумага и перо получали сотрясение в одно и то же время, они друг относительно друга будут в покое и письмо на ходу поезда не составит никакого затруднения.

Это и достигается благодаря прибору, изображенному на рис. 22. Рука с пером пристегивается к дощечке а, могущей передвигаться в пазах по планке b; последняя в свою очередь может перемещаться в пазах дощечки, лежащей на столике в вагоне. Рука, как видим, достаточно подвижна, чтобы писать букву за буквой, строку за строкой; вместе с тем, каждый толчок, получаемый бумагой на дощечке, в тот же самый момент и с такой же силой передается руке, держащей перо. При таких условиях письмо на ходу поезда становится столь же удобным, как и в неподвижном вагоне; мешает лишь то, что взгляд скользит по бумаге рывками, так как голова и рука получают толчки не одновременно.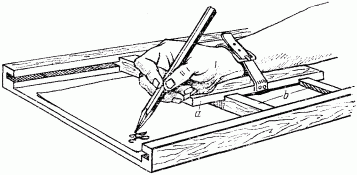

Рис. 22. Приспособление, позволяющее удобно писать в движущемся поезде.

Десятичные весы только в том случае верно показывают вес вашего тела, когда вы стоите на их платформе совершенно неподвижно. Вы нагибаетесь — и весы в момент сгибания показывают уменьшенный вес. Почему? Потому что мускулы, пригибающие верхнюю часть туловища, подтягивают в то же время нижнюю часть тела вверх, уменьшая давление, оказываемое ею на опору. Напротив, в тот момент, когда вы прекращаете нагибание туловища усилием мышц, расталкивающих обе части тела врозь, весы показывают заметно увеличенный вес соответственно усиленному давлению нижней части тела на платформу.

Даже поднятие руки должно вызвать колебание чувствительных весов, соответствующее небольшому увеличению кажущегося веса вашего тела. Мускулы, поднимающие руку вверх, опираются на плечо и, следовательно, отталкивают его вместе с туловищем вниз: давление на платформу возрастает. Останавливая поднимаемую руку, мы приводим в действие противоположные мышцы, которые подтягивают плечо вверх, стремясь сблизить его с концом руки, — и вес тела, его давление на опору, уменьшается.

Наоборот, опуская руку вниз, мы во время этого движения вызываем уменьшение веса своего тела, а в момент остановки руки — увеличение веса. Словом, действием внутренних сил мы можем увеличивать или уменьшать вес нашего тела, разумея под весом давление на опору.

Сила, с какой тела притягиваются земным шаром, убывает по мере возвышения над земной поверхностью. Если бы мы подняли килограммовую гирю на высоту 6400 км, т. е. удалили ее от центра земного шара на два его радиуса, то сила притяжения ослабела бы в 22, т. е. в 4 раза, и гиря на пружинном безмене вытянула бы всего 250 г вместо 1000. Согласно закону тяготения земной шар притягивает внешние тела так, как если бы вся его масса сосредоточена была в центре, а сила этого притяжения убывает обратно квадрату расстояния. В нашем случае расстояние гири от центра Земли удвоилось, и оттого притяжение ослабело в 22, т. е. вчетверо. Удалив гирю на 12800 км от земной поверхности, т. е. на тройное расстояние от центра Земли, мы ослабили бы притяжение в 32, т. е. в 9 раз; 1000— граммовая гиря весила бы тогда всего 111 г, и т. д.

Естественно рождается мысль, что, углубляясь с гирей в недра Земли, т. е. приближая тело к центру нашей планеты, мы должны наблюдать усиление притяжения: гиря в глубине Земли должна весить больше. Эта догадка неверна: с углублением в Землю тела не увеличиваются в весе, а, напротив, уменьшаются.

Рис. 23. Почему с углублением в Землю сила тяжести ослабевает.

Объясняется это тем, что в таком случае притягивающие частицы Земли расположены уже не по одну сторону тела, а по разные его стороны. Взгляните на рис. 23. Вы видите, что гиря, помещенная в глубине Земли, притягивается вниз частицами, расположенными ниже гири, но в то же время притягивается вверх теми частицами, которые лежат выше нее. Можно доказать, что в конечном итоге имеет значение притягивающее действие только шара, радиус которого равен расстоянию от центра Земли до местонахождения тела. поэтому вес тела по мере углубления в Землю должен быстро уменьшаться. Достигнув центра Земли, тело совсем утратит вес, сделается невесомым, так как окружающие частицы влекут его там во все стороны с одинаковой силой.

Итак, всего больше тело весит на самой поверхности Земли; с удалением от нее ввысь или вглубь вес его уменьшается [Так происходило бы, если бы земной шар был вполне однороден по плотности: в действительности плотность Земли возрастает с приближением к центру; поэтому сила тяжести при углублении в Землю сначала, на некотором расстоянии, растет и лишь затем начинает ослабевать.].

Заметили ли вы, какое странное ощущение испытываете вы в тот момент, когда начинаете спускаться на лифте? Ненормальная легкость, вроде той, какую испытывает человек, летящий в пропасть… Это — не что иное, как ощущение невесомости: в первый момент движения, когда пол под вашими ногами уже опускается, а вы сами не успели еще приобрести той же скорости, тело ваше почти не давит на пол и, следовательно, весьма мало весит. Проходит мгновение, и странное ощущение прекращается; ваше тело, стремясь падать быстрее, чем равномерно движущийся лифт, давит на его пол и, значит, снова приобретает свой полный вес.

Привесьте гирю к крючку пружинных весов и следите, куда двинется указатель, если весы с гирей быстро опустить вниз (для удобства поместите кусочек пробки в прорезь весов и заметьте изменение его положения). Вы убедитесь, что во время падения указатель показывает не полный вес гири, а гораздо меньше! Если бы весы падали свободно и вы имели возможность во время падения следить за их указателем, вы заметили бы, что гиря при падении вовсе ничего не весит: указатель находится у нуля.

Самое тяжелое тело становится совершенно невесомым в течение всего того времени, пока оно падает, Легко понять, почему это так. “Весом” тела мы называем силу, с которой тело тянет точку подвеса или давит на свою опору. Но падающее тело не производит никакого натяжения пружины весов, так как пружина опускается вместе с ним. Пока тело падает, оно ничего не натягивает и ни на что не напирает. Следовательно, спрашивать о том, сколько весит тело, когда оно падает, все равно, что спрашивать: сколько тело весит, когда оно не весит?

Еще основатель механики, Галилей, в XVII веке писал [В “Математических доказательствах, касающихся двух отраслей новой науки”. В 1934 г. вышел полный русский перевод этого замечательного сочинения.]: “Мы ощущаем груз на наших плечах, когда стараемся мешать его падению. Но если станем двигаться вниз с такой же скоростью, как и груз, лежащей на нашей спине, то как же может он давить и обременять нас? Это подобно тому, как если бы мы захотели поразить копьем [Не выпуская его из рук.Я.П.] кого-либо, кто бежит впереди нас с такой же скоростью, с какой движемся и мы”.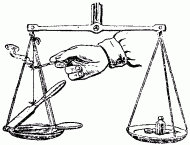

Рис. 24. Опыт, иллюстрирующий невесомость падающего тела.

Следующий легко исполнимый опыт наглядно подтверждает правильность этих рассуждений.

На одну чашку торговых весов положите щипцы для раскалывания орехов так, чтобы одно колено их покоилось на чашке, другое же привяжите за конец ниткой к крючку коромысла (рис. 24). На другую чашку поместите столько груза, чтобы весы были в равновесии. Поднесите к нитке зажженную спичку; нитка перегорит и верхнее колено щипцов упадет на чашку.

Что же произойдет в этот момент с весами? Опустится ли чашка с щипцами в то время, пока колено еще падает, поднимется она или останется в равновесии?

Теперь, когда вы знаете уже, что падающее тело не имеет веса, вы можете заранее дать правильный ответ на этот вопрос: чашка должна подняться на мгновение вверх.

В самом деле: верхнее колено щипцов, падая, хотя и остается в соединении с нижним, все же давит на него меньше, чем в неподвижном состоянии. Вес щипцов на мгновение уменьшается, и чашка, естественно, поднимается вверх.

В 1865 — 1870 гг. появился во Франции фантастический роман Жюля Верна “Из пушки на Луну”, в котором высказана необычайная мысль: послать на Луну исполинский пушечный снаряд-вагон с живыми людьми! Жюль Берн представил свой проект в столь правдоподобном виде, что у большинства читателей, наверное, возникал вопрос: нельзя ли в самом деле осуществить эту мысль? Об этом интересно побеседовать [Теперь, после запуска искусственных спутников Земли и космических ракет, мы можем сказать, что для космических путешествий будут использоваться ракеты, а не снаряды. Однако движение ракеты, после того как сработала ее последняя ступень, подчиняется тем же законам, что и движение артиллерийского снаряда. Поэтому текст автора не устарел. (Прим. ред.)].

Сначала рассмотрим, можно ли — хотя бы теоретически — выстрелить из пушки так, чтобы снаряд никогда не упал назад, на Землю. Теория допускает такую возможность. В самом деле, почему снаряд, горизонтально выброшенный пушкой, в конце концов падает на Землю? Потому что Земля, притягивая снаряд, искривляет его путь: он летит не по прямой линии, а по кривой, направленной к Земле, и поэтому рано или поздно встречается с почвой. Земная поверхность, правда, тоже искривлена, но путь снаряда изгибается гораздо круче. Если же кривизну пути снаряда ослабить и сделать ее одинаковой с искривлением поверхности земного шара, то такой снаряд никогда не сможет упасть на Землю! Он будет двигаться по кривой, концентрической с окружностью земного шара; другими словами, сделается его спутником, как бы второй Луной.

Но как добиться, чтобы снаряд, выброшенный пушкой, шел по пути, менее искривленному, чем земная поверхность? Для этого необходимо только сообщить ему достаточную скорость. Обратите внимание на рис. 25, изображающий разрез части земного шара.

На горе, высотой которой будем пренебрегать, в точке A стоит пушка. Снаряд, горизонтально выброшенный ею, был бы через секунду в точке B, если бы не существовало притяжения Земли. Но притяжение меняет дело, и под действием этой силы снаряд через секунду скажется не в точке B, а на 5 м ниже, в точке C. Пять метров — это путь, проходимый (в пустоте) каждым свободно падающим телом в первую секунду под действием силы тяжести близ поверхности Земли. Если, опустившись на эти 5 м, снаряд наш окажется над уровнем Земли ровно настолько же, насколько был он в точке A, то, значит, он движется по кривой, концентрической с окружностью земного шара.

Рис. 25. Вычисление скорости снаряда, который должен навсегда покинуть Землю.

Остается вычислить отрезок АВ (рис. 25), т. е. тот путь, который проходит снаряд в секунду по горизонтальному направлению; мы узнаем тогда, с какой секундной скоростью нужно для нашей цели выбросить снаряд из жерла пушки. Вычислить это, нетрудно из треугольника АОВ, в котором ОА — радиус земного шара (около 6 370 000 м); ОС = ОА, ВС = 5 м; следовательно, 0В = 6 370 005 м. Отсюда по теореме Пифагора имеем: (AB)2 = (6 370 005)2 — (6 370 000)2.

Сделав вычисление, находим, что путь AB равен примерно 8 км.

Итак, если бы не было воздуха, который сильно мешает быстрому движению, снаряд, выброшенный горизонтально из пушки со скоростью 8 км/сек, никогда не упал бы на Землю, а вечно кружился бы вокруг нее, подобно спутнику.

А если выбросить снаряд из пушки с еще большей скоростью, — куда полетит он? В небесной механике доказывается, что при скорости в 8, 9, даже 10 км/сек снаряд, вылетев из жерла пушки, должен описывать вокруг земного шара эллипс тем более вытянутый, чем больше начальная скорость. При скорости же снаряда 11,2 км/сек он вместо эллипса опишет уже незамкнутую кривую — параболу, навсегда удаляясь от Земли (рис. 26).

Мы видим, следовательно, что теоретически мыслимо полететь на Луну внутри снаряда, выброшенного с достаточно большой скоростью [Тут могут представиться, однако, затруднения совсем особого рода. Подробнее вопрос этот рассматривается во второй книге “Занимательной физики”, а также в другой моей книге — “Межпланетные путешествия”.].

Рис. 26. Судьба пушечного снаряда, выпущенного с начальной скоростью 8 км/сек и более.

(Предыдущее рассуждение имело в виду атмосферу, не препятствующую движению снарядов. В реальных условиях наличие сопротивляющейся атмосферы чрезвычайно затруднило бы получение таких высоких скоростей, а быть может, сделало бы их совершенно недостижимыми.)

Кто читал упомянутый сейчас роман Жюля Верна, тому памятен интересный момент путешествия, когда снаряд пролетел через точку, где притяжение Земли и Луны одинаково. Здесь произошло нечто поистине сказочное: все предметы внутри снаряда утратили свой вес, а сами путешественники, подпрыгнув, повисли в воздухе без опоры.

Описано это совершенно верно, но романист упустил из виду, что то же самое должно было наблюдаться также и до и после перелета через точку равного притяжения. Легко показать, что путешественники и все предметы внутри снаряда должны стать невесомыми с первого же момента свободного полета.

Это кажется невероятным, но, я уверен, вы сейчас будет удивляться тому, что сами не заметили ранее столь крупного упущения.

Возьмем пример из романа Жюля Верна. Без сомнения, вы не забыли, как пассажиры выбросили наружу труп собаки и как они с изумлением заметили, что он вовсе не падает на Землю, а продолжает нестись вперед вместе со снарядом. Романист правильно описал это явление и дал ему верное объяснение. Действительно, в пустоте, как известно, все тела падают с одинаковой скоростью: притяжение Земли сообщает всем телам одинаковое ускорение. В данном случае и снаряд, и труп собаки должны были под действием земного притяжения приобрести одинаковую скорость падения (одинаковое ускорение); вернее, та скорость, которая сообщена была им при вылете из пушки, должна была под действием тяжести уменьшаться одинаково. Следовательно, скорости снаряда и трупа во всех точках пути должны оставаться равными, поэтому труп собаки, выброшенный из снаряда, продолжал следовать за ним, нисколько не отставая.

Но вот о чем не подумал романист: если труп собаки не падает к Земле, находясь вне снаряда, то почему будет он падать, находясь внутри него? Ведь и там и тут действуют одинаковые силы! Тело собаки, помещенное без опоры внутри снаряда, должно оставаться висящим в пространстве, оно имеет совершенно ту же скорость, что и снаряд, и, значит, по отношению к нему остается в покое. Что верно для трупа собаки, то верно и для тел пассажиров и вообще для всех предметов внутри снаряда: в каждой точке пути они имеют такую же скорость, как и сам снаряд, и, следовательно, не должны падать, даже если остаются без опоры. Стул, стоящий на полу летящего снаряда, можно поместить вверх ножками у потолка, и он не упадет “вниз”, потому что будет продолжать нестись вперед вместе с потолком. Пассажир может усесться вниз головой на этот стул и оставаться на нем, не испытывая ни малейшего стремления падать па пол снаряда. Какая сила может заставить его упасть? Ведь если бы он упал, т. е. приблизился к полу, то это значило бы, собственно говоря, что снаряд мчится в пространстве с большей скоростью, чем пассажир (иначе стул не приблизился бы к полу). А между тем это невозможно: мы знаем, что все предметы внутри снаряда имеют то же ускорение, как и сам снаряд.

Этого романист не заметил: он думал, что предметы внутри свободно несущегося снаряда, находящегося под действием одних лишь сил притяжения, будут продолжать давить на свои опоры, как давили тогда, когда снаряд был неподвижен. Жюль Верн упустил из виду, что если и тело, и опора движутся в пространстве с одинаковым ускорением, сообщаемым действием сил притяжения (другие внешние силы — сила тяги, сила сопротивления воздуха — отсутствуют), то давить друг на друга они не могут.

Итак, с того момента путешествия, когда, на снаряд перестали действовать газы, пассажиры не имели никакого веса и могли свободно витать в воздухе внутри снаряда; точно так же и все предметы в нем должны были казаться совершенно невесомыми. По этому признаку пассажиры легко могли определить, мчатся ли они в пространстве или продолжают неподвижно оставаться в пушке. Между тем романист рассказывает, как в первые полчаса своего небесного путешествия пассажиры тщетно ломали голову над вопросом: летят ли они или нет?

“ — Николь, движемся ли мы?

Николь и Ардан переглянулись: они не чувствовали колебании снаряда.

— Действительно! Движемся ли мы? — повторил Ардан.

— Или спокойно лежим на почве Флориды? — спросил Николь.

— Или на дне Мексиканского залива? — прибавил Мишель”.

Такие сомнения возможны у пассажиров парохода, но немыслимы у пассажиров свободно несущегося снаряда: первые сохраняют свой вес, вторые же не могут не заметить, что сделались совершенно невесомыми.

Странное явление должен был представлять собой этот фантастический вагон-снаряд! Крошечный мир, где тела лишены веса, где, выпущенные из рук, они спокойно остаются на месте, где предметы сохраняют равновесие во всяком положении, где вода не выливается из опрокинутой бутылки… Все это упустил из виду автор “Путешествия из Луну”, а между тем какой простор могли бы дать фантазии романиста эти изумительные возможности! [Условия работы и быта в условиях невесомости сейчас хорошо известны из рассказов советских и американских космонавтов, из кинофильмов, заснятых в космосе. Многие читатели наблюдали явления в состоянии невесомости на телевизионных экранах во время прямых передач с борта советских космических кораблей. Специальному рассмотрению проблема невесомости посвящены книги: Хайкин С. Э., Силы инерции и невесомость, Изд-во “Наука”, 1967; Левантовский В. И, Тяжесть, невесомость, перегрузка, Изд-во “Знание”, 1965. (Прим. ред.)].

Что важнее для правильного взвешивания: весы или гири?

Вы ошибаетесь, если думаете, что одинаково важно и то и другое: можно правильно взвесить и не имея верных весов, когда под рукой есть верные гири. Существует несколько способов верно взвешивать на неверных весах. Рассмотрим из них два.

Первый способ предложен нами великим химиком Д. И. Менделеевым. Взвешивание начинают с того, что на одну из чашек кладут какой-нибудь груз, — безразлично какой, лишь бы он был тяжелее тела, подлежащего взвешиванию. Груз этот уравновешивают гирями на другой чашке. После этого на чашку с гирями кладут взвешиваемое тело и снимают с нее столько гирь, сколько требуется, чтобы восстановить нарушенное равновесие. Вес снятых гирь, очевидно, равен весу тела; оно заменяет их теперь на одной и той же чашке и, значит, имеет одинаковый с ними вес.

Этот прием, который называют “способом постоянной нагрузки”, особенно удобен, когда приходится отвешивать одно за другим несколько тел: первоначальная нагрузка остается и ею пользуются для всех отвешиваний.

Другой прием, названный по имени предложившего его ученого “способом Борда”, выполняется так. Поместите предмет, подлежащий взвешиванию, на одну чашку весов, а на другую насыпайте песок или дробь до тех пор, пока весы не придут в равновесие. Затем, сняв с чашки взвешиваемый предмет (песок не трогайте), кладите на нее гири до тех пор, пока весы снова не уравновесятся. Ясно, что теперь вес гирь равен весу замененного ими предмета. Отсюда другое название способа — “взвешивание заменой”.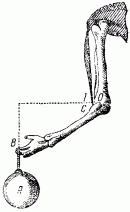

Рис. 27. Предплечье С человека — рычаг второго рода. Действующая сила приложена к точке I; опора рычага находится в точке O сочленения; преодолеваемое же сопротивление (груз R) приложено в точке В. Расстояние ВО больше расстояния IO приблизительно в 8 раз. (Рисунок взят из старинного сочинения Борелли, флорентийского ученого XVII века, “О движении животных”, где законы механики впервые прилагаются к физиология.)

Для пружинных весов, имеющих только одну чашку, также применим этот простой прием, если у вас, кроме того, есть верные гири. Здесь нет надобности запасаться песком или дробью. Положите взвешиваемую вещь на чашку и заметьте, у какого деления остановится указатель. Затем, сняв вещь, поставьте на чашку столько гирь, сколько нужно, чтобы указатель остановился у прежнего деления. Вес этих гирь, очевидно, должен равняться весу замененной ими вещи.

Какой груз вы можете поднять рукой? Положим, что 10 кг. Вы думаете, что эти 10 кг определяет силу мускулов вашей руки? Ошибаетесь: мускулы гораздо сильнее! Проследите за действием, например, так называемой двуглавой мышцы вашей руки (рис. 27). Она прикреплена близ точки опоры рычага, каким является кость предплечья, а груз действует на другой конец этого живого рычага. Расстояние от груза до точки опоры, т. е. до сустава, почти в 8 раз больше, чем расстояние от конца мышцы до опоры. Значит, если груз составляет 10 кг, то мускул тянет с силой, в 8 раз большей. Развивая силу в 8 раз большую, чем наша рука, мускул мог бы непосредственно поднять не 10 кг, а 80 кг.

Мы вправе без преувеличения сказать, что каждый человек гораздо сильнее самого себя, т. е. что наши мускулы развивают силу, значительно большую той, которая проявляется в наших действиях.

Целесообразно ли такое устройство? На первый взгляд как будто нет, — мы видим здесь потерю силы, ничем не вознаграждаемую. Однако вспомним старинное “золотое правило” механики: что теряется в силе, выигрывается в перемещении. Тут и происходит выигрыш в скорости: наши руки движутся в 8 раз быстрее, чем управляющие ими мышцы. Тот способ прикрепления мускулов, который мы видим в теле животных, обеспечивает конечностям проворство движении, более важное в борьбе за существование, нежели сила. Мы были бы крайне медлительными существами, если бы наши руки и ноги не были устроены по этому принципу.

Задумывались ли вы над вопросом: отчего игла так легко пронизывает предмет насквозь? Отчего сукно или картон легко проткнуть тонкой иглой и трудно пробить тупым гвоздем? В обоих случаях действует, казалось бы, одинаковая сила.

Сила одинакова, но давление все же не одинаково. В первом случае вся сила сосредоточивается на острие иглы; во втором — та же сила распределяется на большую площадь конца гвоздя; следовательно, давление иглы гораздо больше, нежели давление тупого стержня при одном и том же усилии наших рук.

Каждый скажет, что борона с 20 зубьями глубже разрыхлит землю, чем борона того же веса, но с 60 зубьями. Почему? Потому что нагрузка на каждый зуб в первом случае больше, чем во втором.

Когда речь идет о давлении, всегда необходимо, кроме силы, принимать во внимание также и площадь, на которую эта сила действует. Когда нам говорят, что кто-либо получает 1000 рублей зарплаты, то мы не знаем еще, много это или мало: нужно знать — в год или в месяц? Точно так же и действие силы зависит от того, распределяется ли она на квадратный сантиметр или сосредоточивается на сотой доле квадратного миллиметра.

Человек на лыжах ходит по рыхлому снегу, а без лыж проваливается. Почему? Потому что в первом случае давление его тела распределяется на гораздо большую поверхность, чем во втором. Если поверхность лыж, например, в 20 раз больше поверхности наших подошв, то на лыжах мы давим на снег в 20 раз слабее, чем стоя на снегу прямо ногами. Рыхлый снег выдерживает первое давление, но не выдерживает второго.

По той же причине лошадям, работающим на болоте, подвязывают особые “башмаки” к копытам, чтобы увеличить площадь опоры ног и тем уменьшить давление на болотистую почву: ноги лошадей при этом не увязают в болоте. Так же поступают и люди в некоторых болотистых местностях.

По тонкому льду люди передвигаются ползком, чтобы распределить вес своего тела на большую площадь.

Наконец, характерная особенность танков и гусеничных тракторов не увязать в рыхлом грунте, несмотря на свой значительный вес, объясняется опять-таки распределением веса на большую поверхность опоры. Гусеничная машина весом 8 и более тонн оказывает на 1 кв. см грунта давление не более 600 г. С этой точки зрения интересен автомобиль на гусеничном ходу для перевозки грузов на болотах. Такой грузовик, везущий 2 тонны груза, оказывает на грунт давление всего 160 г на 1 кв. см; благодаря этому он хорошо ходит на торфяном болоте и по топким или песчаным местностям.

В этом случае большая площадь опоры так же выгодна технически, как малая площадь в случае иглы.

Из сказанного ясно, что острие прокалывает лишь благодаря незначительности площади, по которой распределяется действие силы. Совершенно по той же причине острый нож лучше режет, нежели тупой: сила сосредоточивается на меньшем пространстве.

Итак, заостренные предметы оттого хорошо колют и режут, что на их остриях и лезвиях сосредоточивается большие давление.

Почему на простом табурете сидеть жестко, в то время как на стуле, тоже деревянном, нисколько не жестко? Почему мягко лежать в веревочном гамаке, который сплетен из довольно твердых шнурков? Почему не жестко лежать на проволочной сетке, устраиваемой в кроватях взамен пружинных матрасов?

Нетрудно догадаться. Сидение простого табурета плоско; наше тело соприкасается с ним лишь по небольшой поверхности, на которой и сосредоточивается вся тяжесть туловища. У стула же сиденье вогнутое; оно соприкасается с телом по большей поверхности;

по этой поверхности и распределяется вес туловища: на единицу поверхности приходится меньший груз, меньшее давление.