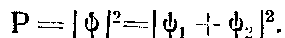Волновая функция есть максимально полное допустимое описание состояния частицы. Она заменяет классическое состояние, которое задается координатами и скоростями.
Волновая функция, описывающая состояние электромагнитного поля, имеет ту же природу; она не есть электромагнитное или какое-либо другое физическое поле, она определяет только вероятность того или иного значения поля в каждой точке.
Применению квантовой механики к полю посвящен конец этой главы.
Предсказания квантовой механики не дают однозначного ответа, они дают лишь вероятность того или иного результата. Как бы точно мы ни определяли состояние до падения на экран, нельзя предсказать, в какой именно точке фотопластинки окажется электрон. Можно указать только распределение вероятности найти его в той или иной точке.
Не означает ли эта неоднозначность нарушения причинности? Классическая физика не знала неопределенности. Успехи небесной механики в XVII и XVIII веках внушили глубокую веру в возможность однозначных предсказаний. Эту гордость неограниченными возможностями науки выразил Пьер Лаплас (1749-1827): «Дайте мне координаты и скорости всех частиц - и я предскажу будущее Вселенной!» Появление электродинамики не изменило этой веры. Хотя начальное состояние в электродинамике задается не только координатами и скоростями частиц, но и распределением полей, - ее предсказания однозначны.
Предсказания классической статистической физики носят вероятностный характер. Она отвечает, например, на вопрос, какова вероятность найти частицу нагретого газа с той или иной энергией, или, иными словами, предсказывает распределение частиц по энергии. Но есть важное отличие от квантовой механики. Вероятность в статистической физике есть результат сложности системы, результат неточного определения начального состояния. Кроме того, механическая система должна обладать важным свойством - она должна быть «размешиваемой». Это означает, что малая неточность начальных условий за короткое время приводит к размешиванию системы по всей области ее возможных состояний. Но за всем этим стоит однозначность механических законов.
В квантовой механике неопределенность принципиальная, она следует из дополнительности квантовомеха-нических свойств и классического описания. И, кроме того, она проявляется уже для самых простых объектов, для индивидуальных наблюдений за одной частицей.
Главное открытие квантовой механики - вероятностный характер законов Вселенной. На некоторые вопросы нельзя однозначно ответить.
Как мы уже знаем, «задать координаты и скорости всех частиц» невозможно. Самое большее, что можно сделать - задать в начальный момент волновую функцию. Квантовая механика позволяет однозначно найти волновую функцию в любой более поздний момент. Вместо восклицания Лапласа можно произнести с такой же гордостью: «Дайте мне волновую функцию всех частиц - и я предскажу будущее!»
Впрочем, невозможность предсказывать будущее в практической жизни не связана с квантовой неопределенностью. Мы имеем дело с такими сложными системами, в которых определить начальную волновую функцию так же невозможно, как координаты и скорости.
Нильс Бор отмечал, что попытка определить волновую функцию живого объекта немедленно приводит к его гибели. Наше будущее зависит от таких сложных, неопределенных систем, как люди! Но вернемся к физическим законам.
Итак, мы не можем проследить траектории отдельных частиц; причинность в лапласовом смысле нарушена, но в более точном смысле она соблюдается. Из максимально полно определенного начального состояния однозначно следует единственно возможное конечное состояние. Изменился только смысл слова «состояние». Что же делать, если выяснилось, что понятие «состояние», принятое в классической физике, принципиально неосуществимо?
Состояние частицы можно изменить, не прикасаясь к ней!
Невозможность однозначно предсказать исход единичного опыта была настолько непривычна, что вызвала много возражений. Является ли квантовомеханическое описание полным, или необходимо создать более точную теорию, где все было бы однозначно? Не надо ли изменить интерпретацию волновой функции?
Эйнштейн писал в 1936 году: «Это мнение логично и не приводит к противоречиям, но оно настолько противоречит моему научному инстинкту, что я не могу отказаться от поисков более полного понимания».
Многолетний спор Бора с Эйнштейном привел к углублению и уточнению теории измерений в квантовой физике. Дальнейшее развитие до сих пор подтверждало позицию Бора о полноте квантовомеханического описания реальности.
Чтобы понять существо затруднений, нужно разобраться в особенностях квантовомеханических наблюдений.
Прежде всего свойства микроскопических объектов нельзя изучать, отвлекаясь от способа наблюдения. В зависимости от него электрон проявляет себя либо как волна, либо как частица, либо как нечто промежуточное. Разумеется, есть также свойства, не зависящие от способа наблюдения: масса, заряд, спин частицы, барионный заряд, магнитный момент… Но всякий раз, когда мы хотим измерить какие-либо величины, не имеющие определенного значения, результат будет зависеть от способа наблюдения. Это свойство квантовых объектов В. А. Фок называл «относительностью к средствам наблюдения». Доквантовая физика знала только относительность, связанную с движением, - относительность скорости, относительность формы: быстро движущееся колесо из-за сокращения Лоренца имеет вид эллипса. В квантовой теории результат зависит от того, как и что измерять в одной и той же системе координат.
Мы уже говорили, что причины этого неустранимы- мы вынуждены описывать квантовые объекты на классическом языке. Но так же, как объективность явлений природы не умаляется, а выявляется теорией относительности, относительность к средствам наблюдения в квантовой теории нисколько не затрудняет определение объективных свойств микрообъектов. История развития Вселенной не делается менее объективной от того, что мы описываем ее на нашем человеческом языке. Язык классической физики, на котором говорят наши средства наблюдения и на котором мы формулируем свои мысли, позволяет полностью охарактеризовать свойства микрообъектов. Мы неминуемо, но без потерь пользуемся субъективными инструментами для описания объективного. Карл Вейцзеккер - немецкий физик, много сделавший в теории ядра, - сказал: «Природа существовала до человека, но человек был до естествознания», И вместе с тем слишком частое упоминание слова «наблюдатель» при описании измерений в квантовой механике оставляет неприятное чувство. Мне кажется, от этого легко избавиться - можно не говорить о наблюдателе и под словом «наблюдение» понимать способ выяснить тот или иной вопрос, сформулированный на классическом языке. Мы как бы узнаем форму предмета, изучая его проекции - рассекая его ножом по разным плоскостям.
Вернемся к нашему измерительному прибору - экрану с дыркой. После прохождения отверстия поперечный импульс делается неопределенным. Это и приводит к дифракционному пятну. А что получится, если уточнить импульс отдачи электрона? Для этого нужно сделать такое устройство, чтобы экран вместе с отверстием мог свободно перемещаться в поперечном направлении. Измеряя изменение импульса экрана, мы по закону сохранения количества движения найдем и поперечный импульс электрона. Если импульс отдачи определен очень точно, то положение экрана будет полностью неопределенным, и дифракционная картина исчезнет - любое зерно на фотопластинке может почернеть с одинаковой вероятностью. Электрон будет такой же плоской волной, как и до экрана, только с новым определенным значением импульса.
Теперь вы видите, как работает относительность к средствам наблюдения! От наблюдения за движением экрана зависит характер почернения пластинки. Допустим, экран и пластинка находятся в разных городах. Измеряя в одном городе, я как будто могу повлиять на результат измерений в другом… Не мистика ли? Нельзя ли использовать такое явление для экстрасенсорной связи? Это так важно, что нужно задуматься. А лучший способ думать - получить то же самое другим способом. Ю. Манин говорит в упомянутой нами книжке: «Думать - значит вычислять, волнуясь».
Сделаем еще один мысленный эксперимент. Просверлим в экране второе отверстие на большом расстоянии от первого. И опять посмотрим, что получается, когда на экран падает пучок света. На втором экране мы увидим хорошо известную в оптике интерференционную картину. Помимо двух светлых пятен, против каждого из отверстий получится система светлых и темных кривых, заполняющих плоскость между пятнами. Светлые места будут там, где волны, идущие от каждого из отверстий, складываются, а темные - где они вычитаются. Это и есть интерференция. Если одно отверстие закрыть, вся эта красивая картина исчезнет.
Разумеется, то же самое будет и с электронами. Как бы редко они ни падали, на фотопластинке в конце концов получится интерференционная картина. Если сделать заслонку, закрывающую одно отверстие, на фотопластинке не будет интерференции - будет лишь одно дифракционное пятно.
Здесь проявляется еще одна важная особенность квантовой механики: волновая функция складывается из волновых функций взаимоисключающих событий. Это свойство называется «принципом суперпозиции». Закроем заслонкой одно из отверстий - тогда электрон идет обязательно через другое, и на его волновую функцию заслонка не влияет. Обозначим эту функцию через \psi_1. Перенесем заслонку на другое отверстие и обозначим
новую функцию через \psi_1. Если оба отверстия открыты, волновая функция \psi равна сумме \psi_1 и \psi_2: \psi=\psi_1+\psi_2. Вероятность найти электрон в какой-либо точке пластинки будет
Если в какой-либо точке Ф1 и ф2 равны, мы получим вероятность Р = 4 abs(\psi_1)^2 = 4P_1, а если они отличаютсд по знаку, то Р = 0 - в эти места электроны не попадают. Если отверстия будут открыты попеременно, будут складываться вероятности, а не волновые функции. Соответствующая вероятность будет
Интерференция исчезнет, величины Р, и Рг-положительные и друг друга не погашают. Эти простые формулы поясняют то, что мы получили и без них.
Мы видим, что любая попытка уточнить траекторию, отбирая случаи, когда электрон проходит через одно отверстие, уничтожает интерференцию. Опять и в этом случае наблюдение, сделанное в Москве, как будто влияет на результаты опытов в Париже.
Кроме того, есть еще одна, не меньшая на первый взгляд, странность: после каждого измерения волновая функция изменяется скачком. В самом деле, после измерения импульса отдачи скачком появилась волна с новым импульсом. В этом состоянии до падения на пластинку электрон можно было с одинаковой вероятностью найти в любом месте; после почернения неопределенность его положения скачком за ничтожное время изменилась, - теперь она задается размерами зерна. Это явление имеет красивое название: «редукция волновой функции», или «редукция волнового пакета».
Именно эта странная возможность изменить волновую функцию частицы без воздействия на нее была главным физическим аргументом знаменитой статьи Эйнштейна, Подольского и Розена «Можно ли считать квантовомеханическое описание физической реальности полным?» (1935). Они писали: «…поскольку эти системы уже не взаимодействуют, то в результате каких бы то ни было операций на первой системе, во второй системе уже не может получиться никаких реальных изменений».
Проследим это явление на совсем простом примере, где оно станет тривиальностью. Допустим, мы знаем импульсы двух частиц до столкновения, а после столкновения одна из них пролетает через лабораторию в
Дубне, а вторая - через измерительные установки Сакле возле Парижа. Если дубненский физик получит определенное значение импульса, он по закону сохранения количества движения рассчитает импульс парижской частицы. Следовательно, волновая функция этой частицы в результате измерения в Дубне определилась - она соответствует определенному импульсу.
Но это не странно, это обычный случай изменения вероятности предсказаний с каждой новой информацией. Мы задаем вопрос: какова вероятность, что парижанин найдет то или иное значение импульса при условии, что в Дубне нашли определенный импульс. Это означает, что нужно взять весь набор многократных измерений импульса в этих двух лабораториях и отобрать из него те случаи, когда в Дубне получался заданный импульс. После такого отбора все парижские измерения окажутся тоже с определенным импульсом. По существу, это просто подтверждение закона сохранения импульса. Могут быть и более сложные ситуации, но всегда влияние измерений в одной из подсистем на результаты измерений в другой нужно понимать именно в смысле отбора случаев, соответствующих определенному условию. Вероятность события при выполнении какого-либо условия называется «условной вероятностью».
Дополнительное условие заставляет нас отбирать другую последовательность событий. Естественно, что при этом вероятности изменяются, а следовательно, изменяется и волновая функция.
Какова вероятность автомобильной аварии, или, иными словами, какая доля автомобилей попадает в аварию? Ответ зависит от многих условий. Так, предсказание изменится скачком, если добавить: «в случае испорченных тормозов» или «с опытным водителем». Какова вероятность высказать неверное суждение в квантовой механике? Она резко увеличится, если добавить: «не подумав». Вот довольно распространенное утверждение: «как бы далеко ни разошлись две подсистемы, они остаются жестко связанными». Это и есть та физическая бессмыслица, против которой правильно возражали Эйнштейн, Подольский и Розен. А разгадка такова: подсистемы на большом расстоянии, разумеется, физически никак не связаны, они независимы. Но условная вероятность для одной из них, разумеется, зависит от того, какое состояние второй подсистемы мы отбираем. И явление это, как мы видим, не специально квантовое, а есть и в классической физике, и даже в повседневной жизни. Предсказание скачком изменяется при изменении условий отбора событий.
«Исправить можно, но будет хуже…» (из разговора с портным)
Нужно ли искать другую интерпретацию квантовой механики? Мне кажется, что главное - вероятностная природа предсказаний - сохранится при любых изменениях теории. Квантовая механика вместе с теорией измерений представляет собой логически замкнутую и необыкновенно красивую теорию. Все попытки ее «усовершенствовать» пока оказывались несостоятельными и в лучшем случае ограничивались вопросом: как менее красиво и более сложно получить уже известные результаты квантовой механики? Мы сейчас увидим, что единственная более или менее последовательная попытка «исправления» противоречит опыту.
В период бурных споров о полноте квантовомехани-ческого описания возникла идея: не объясняется ли
неопределенность в поведении электрона тем, что его состояние зависит не только от импульса, координаты и проекции спина, но еще от каких-то внутренних скрытых параметров? Неопределенность результата, как и в статистической физике, возникает от произвола в значении этих параметров. В принципе, если бы скрытые параметры можно было определить, предсказания сделались бы детерминированными (определенными), как в классической механике.
Конечно, это очень неуклюжий и неприятный способ спасти детерминизм такой дорогой ценой - вводя лишние переменные. Тем более что поначалу удавалось только подтверждать уже известные квантовомеханические соотношения. Некоторое время казалось, что такой подход по своим следствиям неотличим от квантовой механики. Для единичного измерения игрой скрытых параметров удается получить совпадения с квантовой механикой. Однако при повторных измерениях это не всегда возможно.
Первое измерение так ограничивает область возможных значений скрытых параметров, что их свободы ко второму измерению уже недостаточно для согласия с квантовой механикой. Наиболее убедительно это показал Джон Белл в 1966 году. Для доказательства ему достаточно было предположить, что значения скрытых параметров в разделенных подсистемах независимы. Но ведь эти параметры только для того и вводились, чтобы избежать вероятностной «зависимости» разделенных объектов квантовой механики. Иначе говоря, утверждение Белла не вызывает сомнений.
Итак, было указано, при каких экспериментах можно увидеть различие между предсказаниями квантовой механики и теории скрытых переменных. Такой опыт был выполнен в 1972 году Стюартом Фридманом и Джоном Клаузером. Они наблюдали свет, испускаемый возбужденными атомами кальция. В условиях их эксперимента кальций испускал последовательно два кванта видимого света, которые можно было отличать с помощью обычного цветного фильтра. Каждый квант попадал в свой счетчик, проходя через поляриметр, который отбирал определенное направление поляризации. Изучалось число совпадений счетчиков как функция угла между направлениями поляризации двух квантов. Теория скрытых переменных предсказывает провалы на кривой, изображающей эту зависимость. На опыте не
только не оказалось никаких провалов, но вся экспериментальная кривая с поразительной точностью совпала с теоретической кривой, полученной из квантовой механики.
Итак, никаких скрытых параметров нет. Квантовая механика лишний раз подтвердилась. Для микрообъектов нет лапласовского детерминизма.
Как ни удивительно, парапсихологи восприняли этот результат как возможное обоснование экстрасенсорных явлений. Но сначала признание: я впервые услышал о теореме Белла и об опытах Фридмана и Клаузера от американского парапсихолога. Большинство физиков, и я в том числе, были убеждены в справедливости квантовой механики и настолько не доверяли идее скрытых параметров, что перестали следить за событиями в этой области.
Неосторожная фраза «две подсистемы остаются жестко связанными после удаления на большое расстояние» оказалась не такой уж невинной. Если забыть о вероятностной природе волновой функции, то можно подумать, что связь между подсистемами - физическая, тогда как она не материальная, а информативная, в смысле условной вероятности, о чем недавно и шла речь. Физические же системы, жестко связанные на больших расстояниях, - прямой путь к объяснению многих чудесных явлений. Между тем опыт Фридмана и Клаузера только подтвердил квантовую механику, в которой нет никаких нарушений физических принципов, - соблюдается причинность: причина раньше следствия; нельзя осуществить физическое взаимодействие без того, чтобы какое-либо поле не распространилось от передающего объекта к принимающему, и скорость распространения этого поля меньше или равна скорости света.
Еще один физический факт, который некоторые парапсихологи пытаются использовать, в такой же мере не имеет отношения к экстрасенсорным явлениям. Из релятивистской квантовой механики следует - и это наблюдается на опыте, что наряду с частицами существуют античастицы: вместе с электроном - позитрон, с протоном - антипротон. Эти античастицы - такие же физические объекты, как и их более привычные партнеры, и, как и полагается, они движутся вперед по времени. Однако существует очень красивое, но не физическое, а математическое следствие их родства с частицами: античастицу можно рассматривать как частицу, движущуюся в сторону прошлого. Условность этого утверждения видна из того, что можно было бы с тем же успехом двигать вспять по времени частицы.
Если понимать этот математический факт как физическое явление, то может прийти в голову физическая нелепость: раз позитрон - это электрон, пришедший к нам из будущего, нельзя ли с его помощью узнать, что с нами будет? Нельзя ли научно обосновать удачные предсказания гадалок? Или, поскольку позитрон, родившийся рядом, - электрон, который пришел не только из будущего, но и издалека, нельзя ли увидеть удаленные предметы?
Должен разочаровать сторонников чудесного: релятивистская квантовая механика, так же как и нерелятивистская, не дает никаких научных оснований для экстрасенсорных явлений. Будущее и в этой теории вытекает из прошлого и определяется, в согласии с причинностью, событиями, которые происходили до предсказываемого момента. Видеть на расстоянии можно только с помощью чего-то, аналогичного телевизору; должен быть источник какого-либо излучения, которое передает информацию в приемник и распространяется со скоростью, не большей, чем скорость света.
В квантовой физике, так же как и в классической, пока не видно никаких фактов, которые помогли бы понять или обосновать экстрасенсорные явления. Если эти явления существуют, то их обоснование следует искать вне физики.
Как работают физики-теоретики на первой, самой важной стадии работы, когда делается качественный анализ поставленной задачи? Как мы увидим, при этом почти без всяких вычислений получаются грубые соотношения между входящими в задачу величинами, прояс
В некоторых случаях многое проясняет простой размерный анализ - размерные оценки входящих в задачу величин и возможные соотношения между ними. Докажем, например, теорему Пифагора из размерных сообра
жений. Из размерности следует, что площадь прямоугольного треугольника можно записать как квадрат гипотенузы с2, умноженный на некую функцию угла f (а) (пусть для определенности а есть угол между гипотенузой с и большим из катетов). То же самое относится к площадям двух подобных прямоугольных треугольников, для которых гипотенузами будут катеты а и b исходного треугольника, а его высота, опущенная из прямого угла, есть общий катет. Поэтому
Сокращая на f (а), получаем теорему Пифагора.
Оценим период колебан-ий маятника. Предположим для простоты, что тяжелый груз с массой m подвешен на легком стержне, массой которого можно пренебречь. Прежде всего выясним, какие величины могут входить в выражение для периода колебаний. Поскольку сила, движущая маятник к положению равновесия, - это сила тяжести, то период может зависеть от ускорения силы тяжести g и от массы маятника т. Кроме того, может войти также длина маятника /. Разумеется, такие величины, как температура и вязкость воздуха, несущественны, если мы пренебрегаем затуханием маятника. Не войдет в задачу также и скорость вращения Земли, если мы не учитываем ускорения Кориолиса, которое возникает от движения точки подвески маятника вместе с Землей. Ничего не поделаешь, чтобы упростить задачу, надо знать, чем можно пренебречь! Из трех оставшихся величин - g, m, l - можно составить только одну комбинацию, имеющую размерность времени. Эта величина равна sqrt(l/g), а следовательно, период Т равен T=asqrt(l/g).
Масса m не вошла в задачу. Безразмерная константа а не может быть найдена из размерных соображений, можно только сказать, что она не очень велика и не очень мала - порядка единицы. Действительно, эта величина должна быть найдена из решения не написанного нами уравнения движения маятника, а числа, возникающие из решения уравнений, встречающихся в физике, как правило, оказываются порядка единицы. Точное вычисление дает для а величину 2л. Таким образом, мы без вычислений, пользуясь только размерным анализом, получили, что период колебаний маятника не зависит от его массы и пропорционален корню квадратному из его длины. Кроме того, мы нашли также и примерную величину периода колебаний.
Обобщенный осциллятор
Во всех областях физики встречаются задачи, связанные с колебаниями около положения равновесия. Такая система независимо от ее устройства называется «осциллятором» - она осциллирует около положения равновесия. Простейший осциллятор - грузик на пружине или маятник; более сложный - натянутая струна, у нее может быть много типов колебаний: колебания с пучностью посередине (основной тон), с одним узлом, двумя узлами и так далее (обертоны). Струна - набор осцилляторов разной частоты. Аналогичный пример - столб воздуха в органной трубе - его можно заставить колебаться с наинизшей частотой - основной тон, - или с более высокой, когда в некоторых точках воздушного столба частицы воздуха будут неподвижны - аналог узлов в колебаниях струны.

Общее для всех осцилляторов заключается в том, что энергия колебательной системы состоит из двух слагаемых. Одно пропорционально квадрату отклонения осциллятора от положения равновесия - это потенциальная энергия. Если q - величина отклонения от положения равновесия, то потенциальная энергия равна
U=\gamma q2/2.
Коэффициент \gamma называется «жестокостью» осциллятора. Второе слагаемое - кинетическая энергия - может быть записано в виде T = \beta q'2/2, где q' - скорость изменения величины q во времени. Величину в можно назвать «массой осциллятора». Если отклонить осциллятор от положения равновесия на величину q0, то запас потенциальной энергии будет U=\gamma q02/2. Поскольку осциллятор стремится вернуться в состояние равновесия, эта потенциальная энергия начнет переходить в кинетическую, а когда осциллятор будет проходить положение равновесия, вся потенциальная энергия перейдет в кинетическую. При этом скорость осциллятора q' максимальна. По инерции он проскочит положение равновесия, и в точке - q0 вся кинетическая энергия перейдет в потенциальную, и затем опять начнется движение в сторону равновесия. Как бы ни был конкретно устроен осциллятор, его угловая частота колебаний \omega (\omega = 2\pi /Т) выражается следующим образом через жесткость \gamma и массу \beta:
\omega =sqrt(\gamma/\beta) , или Т = 2\pi / sqrt(\gamma/\beta).
В случае маятника роль жесткости играла величина g, а «массы» - длина маятника l. Таким образом, можно рассмотреть сразу все осцилляторы независимо от их физической природы.
Вот еще один осциллятор, совсем непохожий на предыдущие, но и к нему применимы те же формулы. Концы катушки из хорошо проводящей проволоки присоединены к конденсатору. Энергия такой системы состоит из двух слагаемых: энергии магнитного поля в катушке и энергии электрического поля, пропорциональной квадрату заряда Q, который в данный момент находится на обкладках конденсатора. Если заряд Q рассматривать как координату осциллятора, то энергия конденсатора будет играть роль потенциальной энергии. Энергия магнитного поля катушки пропорциональна квадрату силы тока, текущего в данный момент по катушке. Но сила тока равна скорости Q' изменения заряда конденсатора со временем. Энергия магнитного поля пропорциональна Q'2 и соответствует кинетической энергии. Такой осциллятор называется «электрическим колебательным контуром».
Если в катушку вдвинуть, а затем вынуть магнит, в цепи возникнут электромагнитные колебания - магнитная энергия будет переходить в электрическую и наоборот. Чем меньше сопротивление проволоки в катушке, тем медленнее будут затухать колебания. Если катушка сделана из сверхпроводника, колебания практически не будут затухать.
Как угадать решение?
Можно иногда выяснить свойства решения, прежде чем будет построена теория, до того как найдены уравнения, описывающие явления. Это пример более сложного анализа размерностей, чем в случае осциллятора.
Одна из труднейших и нерешенных задач теоретической физики - связь гравитационных и электродинамических явлений.
Если такая связь существует, то в результате решения каких-то еще не найденных уравнений будет получено безразмерное число, дающее соотношение между гравитационной постоянной G и величинами, характеризующими электричество, такими, как скорость света с, заряд электрона е и его масса m. Если существенны квантовые явления, в задачу может войти еще постоянная Планка h , которая, как мы видели, характеризует скачки энергии электромагнитных колебаний. Зная размерности величин G, с, е, m, h, нетрудно убедиться, что из этих величин можно составить только две независимые безразмерные комбинации:
Первая из них хорошо известна и называется «постоянной тонкой структуры». Подстановка числовых значений дает \alpha = 1/137; \ksi = 5\cdot 1044. Может ли такое большое
число, как \ksi, возникнуть в результате решения каких-нибудь разумных уравнений? Безразмерные числа, которые получаются в физических задачах, обычно имеют порядок нескольких единиц или долей единицы. Поэтому мы вправе ожидать, что величина \ksi войдет в задачу в такой форме, чтобы в результате получилось число порядка единицы. Пока мы применяли здравый смысл. Теперь нужно сделать небольшой интуитивный логический скачок.
Правдоподобно, что в теорию войдет натуральный логарифм \ksi (ln(\ksi) ~100) в комбинации \alpha ln(\ksi) ~ 1. В этом соотношении уже нет больших чисел. Знание такого соотношения облегчает поиски решения.