Существует ли такое явление, как интегральная йога? Думаю, да. Конечно, это понятие прежде всего связано с именем Шри Ауробиндо [3]. Основная мысль заключается в том, что достижение цели только одним путем может оказаться не достаточным, не очень полным, и потому лучше идти по тройному пути, Тримарге, – одновременно либо последовательно. Мне не известно, насколько действенна интегральная йога, но в самой идее, несомненно, нет ничего плохого.
      Можно ли причислить Шри Ауробиндо к тем, кого называют Просветленными? Что ж, я склонен считать его одним из таких людей. Я не берусь оценивать его величие, равно как и величие любого другого Озаренного, ведь если вершины гор скрываются за облаками, нет смысла пытаться угадать их точную высоту. Обычно, когда человек утверждает, что такой-то и такой-то – величайший из всех (разумеется, этот такой-то неизменно оказывается самым близким для говорящего), в этих словах отражается эго: «Мой Господь, мой учитель, мой гуру». Когда подчеркивается «мой», а затем следует «самый великий», значит, мы имеем дело с утонченной формой эгоизма. Не пытайтесь оценивать величие тех, кто вышел за пределы земного поля зрения. Достаточно сказать, что любой из них способен озарить нам Путь.
      Еще один вопрос: «Что не относится ни к А, ни к не-А?» Самый простой ответ: «Полнота Просветления». Такое отрицание того, что искомое неизбежно окажется либо в А, либо в не-А, означает, что двойственное сознание не способно его постичь, что предмет поиска выходит за рамки подобных ограничений. Наши рассуждения о наблюдаемой вселенной достоверны только в пределах двойственного сознания. В этом-то и сложность. Вы можете сказать: «Я не могу представить себе иное сознание, нечто другое». Да, совершенно верно. Разве ограниченное, двойственное сознание способно вообразить отсутствие двойственности? Дорога к нему проходит через Осознание, а после Осознания вы поймете. До Осознания вы еще ничего не понимаете. Не стоит даже пытаться определять ТО, что находится за любыми границами. Определения применимы только в мире двойственного сознания, но наши концепции не пригодны для ТОГО, что кроется за любыми пределами, и только при искусном обращении они могут дать легкий намек на ТО.
      Следующий вопрос: «Неужели материя не является изменчивой?» Этот вопрос вызывает множество встречных вопросов и приводит к трудному положению. Что вы понимаете под словом «материя»? Вы имеете в виду распространенную гипотезу о слиянии в единое целое всех впечатлений, возникающих благодаря органам чувств? Быть может, вы гипостатируете [4] то, что познаете посредством ощущений – осязания, зрения, слуха, давления, кинестетического напряжения? Нам известно только это. Возможно, вы гипостатируете нечто существующее во внешнем мире независимо от сознания в любом смысле этого слова, то есть нечто лишенное сознания? Если так, то как вы об этом узнали? Нам доступны только ощущения, ничего более.
      Я еще не пользовался словом «материя». Я упомянул о двух функциях, органах или свойствах познания, а именно о чувственном восприятии и умозрительном постижении. Мы знакомы только с их деятельностью. Это нам известно, но разве эти способности могут принести сведения о чем-то таком, что пребывает вне любого сознания? Мы привыкли считать, что так оно и есть, но это беспечность мышления. Если вы прочтете буддийские сутры, то заметите, что они очень точно рассказывают об этом. Будда говорил… во всяком случае, утверждается, что он говорил так: «Качества – вот все, что у нас есть». Под «качествами» он понимал практические ощущения. Больше ничего нет. Говоря о некотором веществе, которое не воспринимается само по себе, но только обладает какими-то качествами, вы недостаточно точны. Этого вы не знаете. Такая привычка легкомысленна. Этот вопрос мог бы увести нас на очень зыбкую почву, и я намерен поговорить об этом позже, после определенной подготовки, так как здесь вы сталкиваетесь с проблемой, которая долгие годы занимала философов.
      По правде говоря, хорошо осведомленный современный ученый никогда не делает метафизических допущений о природе материи. Я имею в виду по-настоящему разумного ученого, а не простого клерка от науки, решающего задачи. Я говорю о людях уровня Эйнштейна [5] или, скажем, Ванневера Буша*. Они понимают, что имеют дело с неким набором определений, пригодным по большей части только для математических формулировок. Опираясь на свои эксперименты, они выдвигают определенные гипотезы, благодаря которым эти опыты складываются в целостную концепцию. Подобные гипотезы оказываются хорошими, если приводят к таким дальнейшим экспериментам или наблюдениям, которые согласуются с гипотетическими предсказаниями и тем самым их подкрепляют. Эти гипотезы терпят крах, если не подтверждаются на практике. Один мой знакомый, физик-теоретик, высказал нечто очевидное для каждого математика: любое явление допускает потенциально бесконечное многообразие возможных объяснений. Я попробую вновь использовать математическую аналогию, чтобы прояснить эту мысль.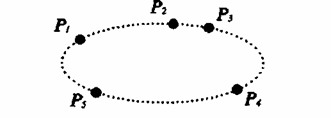
      рис.5
 
      Одним из простейших и прекраснейших примеров в истории науки может служить то, как Кеплер [6] выявил закон движения планет благодаря наблюдениям Тихо Браге [7], то есть определил, что орбиты обращающихся вокруг Солнца планет имеют почти эллиптическую форму.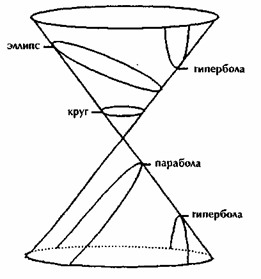
 
      Рис.6
 
      В данном случае, если говорить о пространственных измерениях, он добился достаточно точного результата. Если вы знакомы с коническими сечениями (см. рис. 6) или уравнениями второй степени, решениями которых могут быть окружность, эллипс, парабола, гипербола или две пересекающиеся прямые, то вам известен и тот факт, что произвольные пять точек однозначно определяют одно из конических сечений.
      В данном случае наблюдения показали, что орбиты планет действительно являются эллипсами, хотя и очень близки к окружностям. Несмотря на это, пример послужит неплохой иллюстрацией.
      Предположим, некое уравнение описывает выбранную вами гипотезу, постулированное толкование. Если вы наложите ограничение, требующее, чтобы решением была кривая второй степени, то пять точек будут определять ее однозначно. Но что позволяет вам накладывать такое ограничение на результаты наблюдений?
      Перенесем этот пример на любые результаты наблюдений при решении научной задачи. Неужели решением не может оказаться кривая высшей степени, не обязательно второй? Кривые бывают третьей, четвертой, пятой, n-ой степени, их количество бессчетно, и потому можно найти в буквальном смысле бесконечное число кривых, проходящих через те точки, которые получены в результате наблюдений. Таким образом, теоретически возможно построить гипотетическое толкование или теорию, которая объяснит любые факты научных измерений.
      Кроме того, ученые навязывают гипотезам определенные произвольные правила, которые не объясняются требованиями чистой логики; в частности, гипотезы должны носить такой характер, чтобы они допускали дальнейшую проверку – эксперименты или наблюдения. Это называют требованием операционности. Но можем ли мы быть уверены в том, что природа окончательной истины позволит подвергнуть ее проверке с помощью методов двойственного сознания? Наука предлагает только прагматическую проверку истинности, а не проверку истины как таковой.
      Под словом «прагматическая» я понимаю только то, что она работает, что такие гипотезы приводят к опытам, результаты которых можно предсказать. Например, если вы повернете ключ зажигания, мотор машины заработает. Нечто предсказанное становится правдой. В практическом, прагматическом смысле вы действительно осуществили проверку. Вот и все. Тем не менее истина, справедливая в мире двойственного сознания, совсем не обязательно должна быть окончательной истиной, то есть истиной как таковой, истиной в себе.
      Эйнштейн прекрасно сознавал это и говорил об этом. Одним из тех, кем он больше всего восхищался, был сэр Исаак Ньютон [9], чей философский взгляд на природу мироздания Эйнштейн же и опроверг. Он оказался на шаг впереди Ньютона, так как тот еще верил в метафизическое существование и ввел его в свои гипотезы. Он пользовался концепцией абсолютного времени, равномерно пронизывающего пространство, но при внимательном рассмотрении выяснилось, что эта идея не имеет практического смысла. Многие законы Ньютона справедливы. Они по-прежнему выполняются для большинства повседневных явлений, в мелких масштабах, но уже не действительны – нам известно, что они просто не выполняются, – когда мы имеем дело со скоростями, близкими к скорости света, или с огромными, космическими масштабами, – с такими измерениями, которые были просто невозможны в эпоху Ньютона. Итак, Эйнштейн говорил, что законы Ньютона были первым приближением к истине, а то, что сделал он, Эйнштейн, с точки зрения огромного опыта науки является лишь вторым приближением, после чего могут вновь возникнуть очередные изменения. Он прекрасно понимал, что эти открытия были только первыми приближениями в бесконечной последовательности шагов, ведущих к истине. Вот пример скромности подлинно великого научного ума, осознающего ограниченность собственных методов.
      Одним из наиболее примечательных признаков шага, разделяющего Ньютона и Эйнштейна, стало то, что теперь в картину мироздания вошла эпистемология*. Те способы, посредством которых мы определяем некий факт, например световой сигнал звезды, обусловливают форму знания. Таким образом, знания относительны и определяются ограничениями процесса познания. В сравнении с прежним объединяющим подходом эта позиция отличается большей зрелостью. Во времена Ньютона она была невозможна, так как тогда человек еще не прозрел и не осознал ограниченности собственного процесса познания; это случилось позже. Мы заперты в рамках этой двойственной системы, в пределах ограниченных средств постижения. Как я уже говорил, есть две формы познания: чувственное восприятие и умозрительное постижение -то постижение, которое связано с понятиями и концепциями определенного характера.
      Именно об этом я говорил вчера вечером. Я не упоминал о материи, когда рассказывал о пространстве ниже начерченной линии, когда отождествлял ее с дискретным сознанием, то есть с многообразием отдельных элементов, каждый из которых связан с соседними, как обычные целые числа. Затем я воспользовался идеей непрерывного пространства, чтобы описать то, что находится выше этой черты, за пределами двойственного сознания. При этом я построил лишь приближение к истине, поскольку в конечном счете это непрерывное пространство также дискретно, оно тоже отмечено ограниченностью нашего процесса познания.
      Элементы-песчинки должны быть достаточно небольшими. Вообще говоря, они становятся невероятно крошечными – такими, что их можно назвать «бесконечно малыми». Эту мысль оставил нам Лейбниц, и она стала основой дифференциального исчисления – во всяком случае, в мое время. Мы сталкиваемся с понятием бесконечно малых – в буквальном смысле слова бесконечно малых элементов, совокупность которых образует непрерывное пространство. Однако, поскольку это все-таки отдельные песчинки, такое пространство уже не является чистым потоком.
      Математики так и не смирились с мыслью о существовании чего-то бесконечно малого, ускользающего от любых измерений; эта идея никогда их не удовлетворяла. Говорят, что Вейерштрасс [10] полностью отказался от бесконечно малых. Он считается одним из величайших мыслителей в математическом анализе; этот человек интересен уже тем, что писал как поэт. Ему приписывают такие слова: «Математик, в котором нет ни капли поэта, – не настоящий математик». Возможно, эта фраза поможет вам получить определенное представление об этом человеке. Он, так сказать, избавился от бесконечно малых, но дорогой ценой. Расплатой стал отказ от существования такого явления, как движение; он пришел к тому, что есть только тела, неподвижно покоящиеся в определенных точках пространства в каждый отдельный момент времени. Такое представление работает. Опираясь на него, можно построить дифференциальное исчисление. Лично я не знаком с его выкладками. В мое время они не входили в курс дифференциального исчисления. Наука пошла по пути Лейбница, и теперь вы имеете полное право считать бесконечно малые элементы чем-то совершенно реальным.
      Избавиться от бесконечно малых можно, но при этом придется отбросить представление о существовании самого движения: останутся только тела, занимающие в различные мгновения определенные положения в пространстве. Интуиция заставляет задать вопрос: «Каким образом можно оказаться в ином положении, не перемещаясь в него? Конец бесплатного ознакомительного фрагмента.