Любители поспорить

Зал был набит до отказа.

На помосте стоял большой судейский стол и два маленьких – по бокам. Справа и слева находились площадки, похожие на вышки в бассейне.

Прозвенел звонок, и на сцену поднялись трое судей в красных мантиях.

Главный Судья поднёс к губам рупор и начал:

– Любители поспорить! Открываем наш очередной, два миллиона четыреста сорок первый спор. Его затеяли вчера наши младшие школьники. Спор, начатый в классе, продолжался на улице. У противников появились синяки и шишки. Учительница не сумела справиться с драчунами. И вот мы, любители поспорить, получили приятную возможность перенести этот спор в наш клуб. Да здравствуют спорщики! Что бы мы без них делали? Итак, перехожу к существу: одни утверждают, что дробь 4/7 больше дроби 2/3. Другие, сами понимаете, доказывают обратное. Попрошу капитанов обеих команд занять свои места.

На сцену поднялись две карликанские школьницы – Единица и Пятёрка. Они сели за маленькие столики.

В зале зашумели, засвистели, захлопали.

– Не подкачай, Пятерка! – кричали одни.

– Держись, Единица! – кричали другие.

– Тишина! – крикнул Главный Судья. Зал нехотя затих. – Для полной наглядности прошу обе дроби, послужившие причиной спора, подняться сюда.

Четверо карликан, среди которых была и наша Четвёрка с бантиком, заняли места на боковых площадках, образуя дроби:

«Слово предоставляется Единице», – загремел рупор.

Единица встала, поклонилась судьям и заговорила:

– Утверждаю со всей ответственностью, что 4/7 больше, чем 2/3. (Свист, аплодисменты.) Нечего свистеть! У меня имеется веское доказательство. Вот оно.

Единица подняла над головой палку и угрожающе помахала ею в воздухе. (Шум, оживление в зале.) Потом она подошла к первой дроби и поставила палку рядом с ней.

– Вы видите, – сказала Единица, – эта палка доходит Четвёрке до самого бантика. А теперь измерим вторую дробь… Ага, что я говорила? Палка намного выше верхней цифры 2!

– Это потому, что я сегодня в тапочках! – обиженно пискнула Двойка.

И опять смех, свист, аплодисменты.

С трудом успокоив публику, Главный Судья предоставил слово Пятёрке.

– Не знаю, против чего я должна возражать, – спокойно начала она. – Если мой противник не смеётся над нами, то он, очевидно, глуп.

– Прошу записать в протокол, что меня оскорбили! – заявила Единица.

– Призываю вас к порядку, Пятёрка, – сказал Главный Судья.

– Великий Судья, – обратилась к нему Пятёрка, – разве дроби измеряют палками? Ведь одни школьники пишут большие цифры, другие – маленькие. Если цифры измерять по росту, то Девятка может оказаться меньше Нулика.

– Ах, вам не нравится моя палка! – вскочила с места Единица. – Так бы и сказали. Я могу дать другое доказательство. Положим обе дроби на весы. И вы увидите, что первая весит больше, чем вторая.

– Вы намекаете на то, – закричала упитанная Семёрка, – что я съела сегодня за завтраком слишком много пирожков с мясом?! (Шум, смех, аплодисменты) Я протестую! Прошу занести в протокол, что меня оскорбили.

– Тише, – сказал Судья, – я вам, кажется, не давал слова!… Продолжайте, Пятёрка.

– Мне не о чем говорить, – возразила Пятёрка. – Я знаю, что числа имеют вес, но это надо понимать не в прямом, а в переносном смысле.

– Я возражаю против такого способа спорить, – заявила Единица. – Пятёрка отметает все мои доказательства и не предлагает сама никаких. Потому что у неё их нет! (Свист, аплодисменты.)

– Я могу повторить только то, что сказала вначале, – спокойно ответила Пятёрка. – Величина дроби определяется не весом и не ростом, а значением!

– Способ, способ! – кипятилась Единица. – Вы только болтаете. Вы задавака!

– Прошу отметить в протоколе, что меня оскорбили! – возвысила голос Пятёрка.

– Делаю обоим спорщикам строгое предупреждение! – снова рявкнул Главный Судья. – Спор должен быть взаимно вежливым. Продолжайте.

– Я утверждаю, что 2/3 больше, чем 4/7, – сказала Пятёрка. – И сейчас вам это докажу. Без палок и весов! Попрошу на сцену моих помощников. Двух близнецов. Уважаемый ОЗ, поднимитесь, пожалуйста, сюда имеете со своим братом.

На сцене появились два одинаковых числа – 21.

– Почему она их называет ОЗами? – спросил шёпотом Сева.

– Это, наверное, сокращённые имена, – сказал Олег. – Ну конечно, это же общие знаменатели – ОЗы!

– Эти братья, – продолжала Пятёрка, – не что иное, как произведение знаменателей наших дробей – Тройки и Семёрки. Ведь семь, умноженное на три, равно двадцати одному. Попрошу вас, дорогие близнецы, встать на место знаменателей обеих дробей: вместо Семёрки и Тройки.

– Уважаемая Пятёрка, – возразили в один голос Общие Знаменатели, – мы никак не можем исполнить вашу просьбу. Если мы сейчас займём места знаменателей, вы проиграете спор – первая дробь окажется меньше второй!

– Ага, что я говорила?! – обрадовалась Единица.

– Не радуйтесь преждевременно, – остановила её Пятёрка, – Я просто немного поспешила. Спасибо вам, дорогие ОЗы, за ваше замечание. Конечно, надо одновременно изменить и числители обеих дробей. Я не успела об этом сказать. Ведь при замене знаменателей сами дроби не должны меняться. Итак, заменим одновременно и числители и знаменатели.

И тут произошло нечто необыкновенное: Семёрка поднялась к Двойке, Тройка – к Четвёрке, и между каждой парой мгновенно блеснул знак умножения.

На секунду погас свет, и мы увидели по бокам сцены новые дроби: 14/21 и 12/21.

– Хоть эти дроби и новые, – пояснила Пятёрка, – но величины их ведь не изменились. Как вы думаете? 2/3=14/21, а 4/7=12/21. Так? Единица сделала презрительную гримасу и ничего не ответила.

– Итак, моё доказательство готово! Как видите, знаменатели у дробей одинаковые, а числители разные. Так какая же из этих дробей больше?

– Та, у которой больше числитель! – не выдержал Сева.

– Прошу не подсказывать с места! – загремел Главный Судья.

– Вы совершенно правы, милый школьник, – заметила Пятёрка. – Дробь 14/21, конечно, больше, чем дробь 12/21. Следовательно, истина на моей стороне.

Зрители неистово аплодировали. Судьи, посовещавшись, встали.

– Объявляю решение суда! – протрубил Главный Судья. – Победила Пятёрка! («Молодец!» – пронеслось по залу.) Отныне запрещаю при сравнении дробей пользоваться каким-либо иным способом! Диспут окончен!

– Внимание! – крикнули из зала. – У меня есть объявление! Для участников диспута сегодня состоится цирковое представление. Небывалый трюк – «Дроби на трапециях»! Вход в цирк только по клубным билетам. Нервных просят не приходить.

Толпа хлынула на улицу.

Смертельный атракцион

Оркестр сыграл веселое вступление.

На манеже, у главного входа, выстроились униформисты, и представление началось.

Жонглеров сменяли акробаты, акробатов – гимнасты… Вот на арену выбежала тоненькая, гибкая Тройка; она исполнила пластический этюд: сперва под музыку медленно превратилась в Шестёрку, затем в Девятку и, наконец, в Восьмёрку.

Потом молодая наездница – изящная Пятерка танцевала на спине у лошади, прыгала на полном ходу сквозь обруч и так быстро вертела своей маленькой головкой направо и налево, что никто не мог различить: Пятерка это или Тройка.

Затем на манеж вышел фокусник. Он засучил рукава и предложил каждому зрителю задумать какое-нибудь число.

– Все задумали? – спросил он.

– Все! – ответили зрители хором.

Мои спутники тоже задумали – число 11.

– Попрошу, – сказал фокусник, – умножить задуманное число на 6. Зрители стали в уме умножать на шесть и при этом шевелили губами.

– Одиннадцать на шесть, – шептала Таня, – будет шестьдесят шесть.

– Прибавьте к полученному число 21, – скомандовал фокусник. – Прибавили?

У моих ребят получилось 87.

– Так! – неслось с манежа. – Разделите сумму на 3 («Двадцать девять!» – толкнул меня Сева). Затем вычтите 5 («Останется двадцать четыре», – зашептали ребята). Теперь разделите на 2! – приказал фокусник – Разделили?

– Сейчас, – крикнул кто-то с галерки – Одна минутка. Есть!

– Получается двенадцать, – переглянулись ребята.

– Теперь остается только одно, – заключил фокусник, – отнять единицу. И я вам скажу, какой у кого получился ответ. У каждого получилось то число, которое он задумал. Верно!

– Верно! – крикнул Сева. – Одиннадцать!

– Верно! – неслось со всех сторон. – Восемь! Верно – шесть! Верно – пять, семнадцать, четыре!

Под бурные аплодисменты фокусник долго раскланивался, а потом перешел к следующему фокусу.

– В этом ящике находятся обыкновенные нули. Они вам хорошо знакомы. Беру вот этот топор и разрубаю каждый нуль на любое число частей. (Цирк в ужасе ахнул.) Вот этот нуль на пять частей, этот – на семь, а этот – на тридцать две. Готово! Теперь осмотрите ящик, он совершенно пуст. Бросаю обломки нулей сюда. Накрываю ящик платком. Внимание! – Фокусник ударил по ящику волшебной палочкой и произнес. – Ой, люли, ой, люли! Выходите все нули!

Он быстро сорвал платок – из ящика один за другим выпрыгнули нули: они были целёхоньки!

Зрители неистовствовали.

– Видите, – сказал фокусник, – на сколько бы частей я ни делил нуль, он всегда останется нулем. Нуль, деленный на любое число, есть нуль! А теперь, – продолжал он таинственно, – я вам покажу самый страшный фокус. Попрошу кого-нибудь выйти на манеж. Пусть это будет самый маленький карликан, всё равно. Я на ваших глазах разделю его на нуль! Кто хочет выйти?

Никто не появлялся.

– Ну что ж, – пожал плечами фокусник, – придётся позвать моих ассистентов.

Он хлопнул в ладоши, и на манеж выбежали хрупкая Единица в розовой тюлевой юбочке и Нулик.

– Итак, делю эту Единицу на Нуль! Пугливых прошу отвернуться. Впрочем, я лучше закрою их вот этим покрывалом. Вот так. А теперь передаю им знак деления. Приготовились!

И фокусник произнёс волшебное заклинание:

Блеснула молния, раздался страшный гром барабанов.

Покрывало быстро взвилось кверху, и из-под него вылез… Великан!

Он рос с неимоверной быстротой. Вот его голова уже касается купола цирка. Вот она прорвала парусиновую крышу, а Великан всё рос, рос…

Зрители в страхе жались друг к другу.

– Довольно! – кричали с мест.

Фокусник взмахнул волшебной палочкой – и Великан мигом исчез. На манеже снова стояли хрупкая Единица и маленький Нулик.

– Теперь вы убедились, – сказал фокусник, – как опасно делить на Нуль даже Единицу.

Он изящно раскланялся и под бурные овации покинул манеж.

– Как это он делает? – спросил Сева. – И откуда у него появляется Великан?

– На то и фокусы, чтобы сразу не понять, – ответил я. – Впрочем, этот фокус я объясню потом. А сейчас посмотрим на клоунов.

На арену с разных сторон вышли два клоуна: белый, как мука, Тук и рыжий, как апельсин, Ток.

– Где ты пропадал, Ток? – спросил Тук.

– Я ходил покупать тебе подарок. Абрикосы!

– Я очень люблю абрикосы. Где же они?

– Я их по дороге съел.

– Все?

– Все. А потом я вернулся в магазин и попросил снова продать мне абрикосов. Но только половину того, что купил в первый раз.

– Где же они?

– Съел!

Тук угрожающе замахнулся палкой.

– Подожди, подожди! – закричал Ток. – Я ещё раз вернулся в магазин и попросил продать мне только четверть тех абрикосов, что купил в первый раз.

– И ты их опять съел?

– Съел!… Потом я вернулся и купил одну восьмую. И снова съел. – Ток рассмеялся. – Так я возвращался пять раз. Каждый раз я покупал вдвое меньше, чем в предыдущий. Видишь, я не забывал о тебе.

– Ты мне всё-таки принёс абрикосов или нет?

– Конечно, принёс. Вот, смотри.

– Но здесь всего один абрикос!

– У меня больше не осталось денег.

– Сколько же ты всего съел абрикосов?

– Я не считал. Считай сам!

– Ты ел, а я должен считать?

– Если ты не знаешь арифметики, пусть тебе помогут зрители.

– Друзья, – обратился Тук к зрителям, – вы не знаете, сколько абрикосов съел Ток?

В цирке зашумели, стали считать, спорить. Первым решил задачу Олег:

– Ток съел шестьдесят два абрикоса!

– Неправильно! – закричал Ток. – Шестьдесят три. – Он вырвал у Тука абрикос и тут же съел его. – Это и есть шестьдесят третий!

– Ты всегда был таким обжорой? – спросил Тук.

– Всегда. Вчера я съел двенадцать плиток шоколада, пятнадцать пирожных и двадцать порций мороженого. Вот сколько!

– И что же в сумме получилось?

– Расстройство желудка!

Под конец клоуны стали решать задачу: через сколько времени наполнится бассейн водой, если его наполнять сразу через две трубы. Вместо труб у Тука и Тока были в руках пожарные шланги. Клоуны спотыкались, падали, обливались водой и, так и не решив задачи, мокрые, убежали с манежа.

Из главного выхода появился карликан во фраке и торжественно объявил:

– Смертельный аттракцион! Дроби на трапециях! Из-под купола уже спустили две трапеции. Они покачивались одна против другой.

На манеж выбежали четверо юных карликан: Двойка, Тройка, Четвёрка и Пятёрка. Они ловко забрались по канату на трапеции: Двойка и Тройка – на левую, а Четвёрка и Пятёрка – на правую. Двойка и Четвёрка встали на перекладины и крепко ухватились руками за канаты.

А двое других гимнастов повисли на перекладинах под ними. Они плавно раскачивались и делали красивые движения: выгибались ласточкой, выворачивались на руках, висели вниз головой… Потом они сели на перекладины, чтобы передохнуть, а карликан во фраке объявил:

– Внимание! Заключительный трюк – деление дробей!

И тут же зловеще забила барабанная дробь.

Гимнастки снова заняли первоначальные места, и мы поняли, что они изображают две дроби. Между ними возникли две светящиеся точки – знак деления.

Гимнастки взглянули вниз – сетка была на месте. Без сетки этот номер делать не разрешалось. Секунда внимания, и… «Ап!» – раздалась команда.

И вот уже Пятёрка, сделав в воздухе сальто-мортале, поднялась на вторую трапецию и стала рядом с Двойкой. Одновременно с ней Четвёрка рыбкой полетела вниз и уцепилась за перекладину рядом с Тройкой.

Опять, как во время диспута, между цифрами молниями блеснули два знака умножения. На секунду погас свет, а когда он зажёгся, на первой трапеции уже раскачивалась дробь 10/12. Цирк ревел от восторга.

– Бис! Бис!… – неслось со всех сторон.

Трюк повторили. Однако теперь делимое и делитель поменялись местами.

Когда вновь зажёгся свет, на трапеции раскачивалась новая дробь: 12/10.

– Э-э! – закричал Сева. – Да это та же дробь, только вверх ногами!

– На то и цирк, – резонно заметил Олег.

Артисты легко спустились на манеж. Представление закончилось.

Нашёлся!

Когда мы вышли из цирка на улицу, город был празднично иллюминирован. Несмотря на позднее время, отовсюду слышалась весёлая музыка.

Жители Арабеллы ликовали. То тут, то там раздавались возгласы:

– Нашёлся!

– Какая радость!

– Он не мог пропасть!

– Бедная мама, как она волновалась!

Нетрудно догадаться, о ком говорили карликане. Они радовались возвращению Нулика.

Сегодня утром, когда с площади Добрых Напутствий отправлялась к людям очередная партия карликан, провожавшие дали им наказ: непременно разыскать Нулика. И вот он здесь! Он цел и невредим!

А нашли его так.

Десятка три карликан помогали школьникам второго класса решать задачу на деление целых чисел. Вот уже все ученики отдали тетради учительнице. Прозвенел звонок. Карликане вышли из класса, потому что там должен был начаться урок русского языка, и направились в следующий класс, где изучали обыкновенные дроби.

Весёлой толпой поднимались они по лестнице. Вдруг на площадке послышался жалобный писк. Осмотрелись – никого! Писк повторился.

Тогда одна догадливая Семёрка заглянула за урну, стоявшую в углу. Там она и увидела пропавшего Нулика.

– Я хочу к маме! – хныкал он. – А потом я хочу есть и спать. И вообще я устал.

Ну, его сейчас же обласкали, утёрли носик и глазки. Вот только накормить было пока нечем. Но Нулик и так сразу повеселел, даже немного попрыгал от радости. И все отправились в третий класс помогать детям складывать обыкновенные дроби.

Задача была очень трудная. И Нулику некогда было рассказывать, что с ним произошло. А после надо было спешить на самолёт. И только в самолёте Нулик поведал печальную повесть о своём исчезновении.

Этот рассказ ему пришлось повторять много раз: сперва попутчикам в самолёте, затем встречавшим, потом опоздавшим на встречу и, наконец, тем, кто хотел ещё раз послушать всё, с самого начала. Но так как этого хотели почти все, то в общей сложности Нулик рассказал свою историю 248 раз.

А тут ещё подошли мы и тоже попросили его рассказать. Но Нулик уже охрип, и вместо слов у него получались одни шипящие звуки.

И тогда счастливая мама, толстая Восьмёрка, всё рассказала за него. Она уже успела выучить этот рассказ наизусть.

– Вчера в первый раз я отпустила моего дорогого крошку в такое дальнее путешествие. Но я не смела его удерживать. Ведь он отправлялся к вам, людям, для очень важного дела. И вот привезли его в одну неполную среднюю школу. Я не знаю, почему её называют неполной, но то, что она очень средняя, совершенно ясно: ведь там-то и произошло несчастье с моим дорогим малюткой. И надо же, чтобы мой сыночек попал к самому плохому ученику во всей школе. Он-то и потерял моего Нулика. Да, да, потерял! Словно это иголка! Мыслимое ли дело, потерять такого красавца! – Она поцеловала Нулика в носик. – Учительница задала очень простую задачу: разделить 1836 на 18. Разве это трудно? Конечно, нет! И ответ-то очень простой: 102. Не больше и не меньше. А у этого лентяя получилось 12! Всего лишь 12! Подумайте только – он потерял Нулика! А почему это произошло? Да потому, что разделив 18 на 18 и получив правильно 1, ученик стал вдруг делить на 18 число 36. Надо было сперва разделить 3 на 18, а уж потом 36. Выскажете, что 3 на 18 не делится? Ну и пусть не делится! Если число не делится, то тут-то и надо было вспомнить о моём Нулике и поставить его после единицы. Тогда бы и получился правильный ответ – 102. А мальчишка поленился и стал сразу делить 36 на 18. Вот и выходит: поспешишь – людей насмешишь! А нам не до смеха, нам слёзы.

Ну хорошо. Допустим, ученик ошибся. Ошибки могут быть у всякого. Но ведь он мог себя легко проверить. Вы спрашиваете – как? Стоило только умножить частное 12 на делитель 18. И он бы получил вместо делимого, 1836, всего-навсего 216. Нет, вы только подумайте: вместо 1836 получить 216! Ужас! Спасибо добрым друзьям – карликанам. Если бы не они, так бы и пропал мой сынок.

– Уважаемая Восьмёрка, – заговорил Сева, – всё равно ваш Нулик нашёлся бы. Его обязательно нашла бы учительница. Она ещё просто не успела проверить тетради.

– Да, – ответила толстая Восьмёрка, – учительница, конечно, нашла бы. Но когда? Мой Нулик к тому времени мог умереть с голоду.

И она снова стала обнимать сына, целовать его в носик, в глазки, в ушки…

Мы решили не отвлекать её от этого приятного занятия и тактично удалились. Но через несколько шагов опять услышали знакомый голос:

– Вчера в первый раз я отпустила моего дорогого крошку в такое дальнее…

Счастливая мама по требованию вновь прибывших начала всё сначала.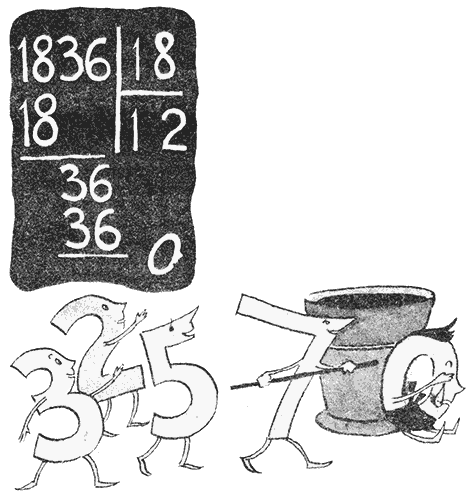

День третий

Спичечный коробок

– Помните, – сказал мне Сева, – вы вчера обещали нам объяснить, как фокусник превратил Единицу в Великана.

– Ну что ж, – ответил я, – обещал, так объясню. Ребята уселись поближе и приготовились слушать.

– Возьмём какое-нибудь число, – начал я, – ну, скажем, сто. И разделим его сперва тоже на сто. Получим единицу, не так ли? Ну, а если мы разделим сто на пятьдесят, что тогда получим?

– Два!

– Правильно, два. Два – это уже больше, чем единица. А потом разделим сто на двадцать пять, получим ещё больше – четыре. Затем – на двадцать. Частное будет пять. А, если мы разделим сто на два, то частное будет ещё больше – пятьдесят. Так? Выходит, чем меньше делитель, тем больше частное. Разделим теперь сто на единицу.

– Так и останется сто, – сказал Сева.

– Нетрудно было догадаться, – продолжал я. – Ну, а если мы станем делить сто на числа, меньшие, чем единица. Что тогда? Частное будет уменьшаться или ещё больше увеличиваться?

– Увеличиваться, – сказала Таня.

– Конечно. Чем меньше делитель, тем всё больше и больше частное. Разделим 100 на 1/2, получим уже 200, а если разделить 100 на 1/5, то частное будет 500.

– Ну конечно, – сказал Олег, – разделить на 1/5 – это всё равно что умножить на 5.

– Молодец, – похвалил я Олега. – Так вот, если мы будем делить число на одну миллионную, то…

– …это всё равно что умножить это число на миллион, – победоносно закончил Сева.

– Вот и подумайте, – снова сказал я, – нуль маленькое число или большое?

– Нуль меньше любого малого числа, – ответил Олег.

– Что же получится, если разделить сто на самое маленькое число? – снова задал я вопрос.

– То же, что получится, если умножить сто на самое большое число, – ответил Сева.

– Правильно, – подтвердил я. – Фокусник разделил единицу на нуль – появился Великан! И никаких фокусов!

Ребята удовлетворённо вздохнули.

– Вот я вам покажу фокус так фокус! – продолжал я после некоторой паузы. – Как вы думаете, сколько чисел может уместиться в этом спичечном коробке?

– Это, смотря как писать, – озабоченно сказал Сева, – крупно или мелко.

– Ну, пусть будет мелко, – решил я великодушно.

– Тогда – много, – ответила Таня.

– Что значит – много?

– Тысяча! – закричал Сева.

– Больше.

– Миллион! – предположила неуверенно Таня.

– Еще больше! – подзадоривал я.

– Ну, это уж сказки! – проворчал недоверчиво Сева.

– Что ж, послушайте мою сказку. Сказку да не сказку. – Я вынул все спички из коробка. – Допустим, что этот коробок разделён на две равные части, ну, хотя бы спичкой. Поместим в одной части число 1.

– Пишите единицу, – деловито предложил Сева и протянул карандаш.

– Нет, – возразил я. – Единица будет воображаемая. Нам, математикам, без воображения нельзя! Итак, в этой половине – единица, а другая пустая.

– Очень неэкономно, – заявил Сева. – Целую половину коробка занимать единицей.

– Ничего, – ответил я, – места хватит. Теперь разделим свободную половину снова пополам. Тоже в воображении, конечно. Можем?

– Можем! – сказали ребята.

Итак, у нас снова два пустых отделения. В одном из них опять-таки мысленно поместим число 2. А свободное отделение ещё раз разделим пополам. И в одну из этих половинок поместим число 3. Потом снова то же самое. Так и будем каждый раз в одно из свободных отделений помещать по числу: 4, затем 5, 6, 7… 100… 1000 и так далее. И каждый раз будем свободное отделение снова делить пополам.

– Нет, – остановил меня Сева, – тут что-то не то. Как же вы будете делить коробок? Если спичками, они туда не влезут.

– А я буду вместо спичек класть волоски, – ответил я.

– Всё равно, – не сдавался Сева, – можно разделить коробок на пятьсот, на тысячу частей, а потом и волосок не полезет!

– Какая же у тебя бедная фантазия! – покачал я головой. – Сумел же кузнец Левша подковать блоху да ещё на каждом гвоздике расписаться! Ведь ещё совсем недавно не было меньшего деления времени, чем секунда. А теперь учёные научились измерять даже миллиардные доли секунды! Раньше, желая похвалить пряху, говорили, что прядёт она нить с паутинку. Тоньше паутинки ничего и представить не могли. А уж измерить паутинку и вовсе не умели. А теперь измеряют размеры молекул, атомов, электронов… Перед ними паутинка что дуб перед мошкой! Так вот. Допустим, найдётся такой искусный мастер, который сумеет разделить наш коробок на самые-самые малые отделеньица. Далеко ходить не надо: разве воображение не лучший мастер на свете? Итак, мастер работает, отделения становятся всё меньше и меньше, вот уж ни в один микроскоп их нельзя разглядеть! А мастер всё делит и делит. Отделения становятся всё меньше, а числа, помещаемые в них, – всё больше. И чем меньше отделение, тем большее число мы в него помещаем. Будет ли этому конец? Нет, не будет! Ведь делить-то можно без конца, да и больших чисел тоже бесконечно много. Вот и выходит, что в этом коробке собрались все бесконечно малые и все бесконечно большие величины. Карлики и великаны!

– Так вот почему эта страна называется Карликанией! – обрадовался Олег.

– Вещий Олег! – сказала Таня.