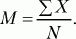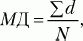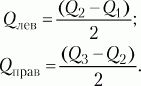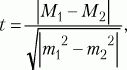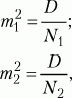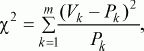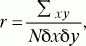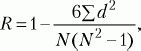Экспериментальная психология: конспект лекций

      С теоретической точки зрения единственным способом установления «внутренней» валидности теста и отдельных заданий является метод факторного анализа (и аналогичные), который позволяет: а) выявлять латентные (скрытые) свойства и вычислять значение «факторных нагрузок» – коэффициенты детерминации свойств тех или иных поведенческих признаков; б) определять меру влияния каждого латентного свойства на результаты тестирования.
       Стандартизация тестазаключается в приведении процедуры оценок к общепринятым нормативам. Стандартизация предполагает преобразование нормальной или искусственно нормализованной шкалы первичных оценок в шкальные оценки (подробнее об этом см. 5.2). Тестовые нормы, полученные в ходе стандартизации, представляют собой систему шкал с характеристиками распределения тестового балла для различных выборок. Они не являются «внутренними» свойствами теста, а лишь облегчают его практическое применение.

6.5. Требования к разработке, проверке и адаптации тестовых методик

      Известны два пути создания психодиагностических методик: адаптация известных методик (зарубежных, устаревших, с иными целями) и разработка новых, оригинальных методик.
       Адаптациятеста – это комплекс мероприятий, обеспечивающих адекватность теста в новых условиях применения. Выделяют следующие этапы адаптации тестов:
      1) анализ исходных теоретических положений автора теста;
      2) для иностранных методик – перевод теста и инструкций к нему на язык пользователя (с обязательной экспертной оценкой соответствия оригиналу);
      3) проверка надежности и валидности в соответствии с психометрическими требованиями;
      4) стандартизация на соответствующих выборках.
      Наиболее серьезные проблемы возникают при адаптации вербальных тестов (опросников, вербальных субтестов в составе тестов интеллекта). Эти проблемы связаны с языковыми и социокультурными различиями народов разных стран. Многовариантность перевода какого-либо термина, невозможность точной передачи идиоматических оборотов – обычное явление при переводах с языка на язык. Иногда бывает настолько сложно подобрать языковые и смысловые аналоги заданий теста, что полная его адаптация становится сопоставимой с разработкой оригинальной методики.
      Понятие адаптации приложимо не только к зарубежным методикам, которые предполагается использовать в условиях нашей страны, но и к устаревшим отечественным методикам. Устаревают они достаточно быстро: в связи с развитием языка и изменчивостью социокультурных стереотипов методики должны корректироваться каждые 5–7 лет, что подразумевает уточнение формулировок вопросов, коррекцию нормативов, обновление стимульного материала, пересмотр интерпретационных критериев.
       Самостоятельная разработкатестовой методики обычно состоит из следующих этапов.
      1. Выбор предмета (явления) и объекта исследования (контингента).
      2. Выбор вида теста (объективный, субъективный, проективный), типа заданий (с предписанными ответами, со свободными ответами) и шкал (числовые, вербальные, графические).
      3. Подбор первичного банка заданий. Он может осуществляться двумя путями: вопросы формулируются исходя из теоретических представлений об измеряемом явлении (факторно-аналитический принцип) или же подбираются в соответствии с их дискриминативностью, т. е. способностью отделять испытуемых по наличию требуемого признака (критериально-ключевой принцип). Второй принцип эффективен при разработке тестов отбора (например, профессионального или клинического).
      4. Оценка заданий первичного банка (содержательной валидности теста, т. е. соответствия каждого из заданий измеряемому явлению, и полноты охвата изучаемого явления тестом в целом). Проводится с помощью метода экспертной оценки.
      5. Предварительное тестирование, формирование банка эмпирических данных.
      6. Эмпирическая валидизация теста. Проводится с помощью корреляционного анализа оценок теста и показателей по внешнему параметру изучаемого свойства (например, школьной успеваемости при валидизации теста интеллекта, врачебного диагноза при валидизации клинических тестов, данных других тестов, валидность которых известна, и др.).
      7. Оценка надежности теста (устойчивости результатов к действию случайных факторов, внешних и внутренних). Наиболее часто оцениваются ретестовая надежность (соответствие результатам повторного тестирования, обычно через несколько месяцев), надежность частей теста (устойчивость результатов отдельных задач или групп задач, например по методу «четное – нечетное») и надежность параллельных форм, если таковые существуют. Методика признается надежной, если коэффициент корреляции результатов (первичного и повторного тестирования, одной и другой частей теста, одной и другой параллельных форм) составляет не менее 0,75. При более низком показателе надежности производятся корректировка заданий теста, переформулирование вопросов, снижающих надежность.
      8. Стандартизация теста, т. е. приведение процедуры и оценок к общепринятым нормативам. Стандартизация оценок подразумевает преобразование нормальной или искусственно нормализованной шкалы первичных оценок (эмпирических значений изучаемого показателя) в оценки шкальные (отражающие место в распределении результатов выборки испытуемых). Виды шкальных оценок: стены (1—10), станайны (1–9), 7-оценки (10—100) и др.
      9. Определение прогностической валидности, т. е. информация о том, с какой степенью точности методика позволяет судить о диагностируемом психологическом качестве спустя определенное время после измерения. Прогностическая валидность также определяется по внешнему критерию, но данные по нему собираются спустя некоторое время после тестирования.
      Таким образом, надежность и валидность – это собирательные понятия, включающие в себя несколько видов показателей, отражающих направленность методики на предмет исследования (валидность) и объект исследования (надежность). Степень надежности и валидности отражают соответствующие коэффициенты, указываемые в сертификате методики.
      Создание методики – трудоемкая работа, требующая развитой системы заказа на методики с соответствующей оплатой труда разработчиков и гонорарами за использование авторских методик.

Тема 7. Обработка данных психологических исследований

7.1. Общее представление об обработке данных

      Обработка данных психологических исследований – отдельный раздел экспериментальной психологии, тесно связанный с математической статистикой и логикой. Обработка данных направлена на решение следующих задач:
      • упорядочивание полученного материала;
      • обнаружение и ликвидация ошибок, недочетов, пробелов в сведениях;
      • выявление скрытых от непосредственного восприятия тенденций, закономерностей и связей;
      • обнаружение новых фактов, которые не ожидались и не были замечены в ходе эмпирического процесса;
      • выяснение уровня достоверности, надежности и точности собранных данных и получение на их базе научно обоснованных результатов.
      Различают количественную и качественную обработку данных. Количественнаяобработка – это работа с измеренными характеристиками изучаемого объекта, его «объективированными» свойствами. Качественнаяобработка представляет собой способ проникновения в сущность объекта путем выявления его неизмеряемых свойств.
      Количественная обработка направлена в основном на формальное, внешнее изучение объекта, качественная – преимущественно на содержательное, внутреннее его изучение. В количественном исследовании доминирует аналитическая составляющая познания, что отражено и в названиях количественных методов обработки эмпирического материала: корреляционный анализ, факторный анализ и т. д. Реализуется количественная обработка с помощью математико-статистических методов.
      В качественной обработке преобладают синтетические способы познания. Обобщение проводится на следующем этапе исследовательского процесса – интерпретационном. При качественной обработке данных главное заключается в соответствующем представлении сведений об изучаемом явлении, обеспечивающем дальнейшее его теоретическое изучение. Обычно результатом качественной обработки является интегрированное представление о множестве свойств объекта или множестве объектов в форме классификаций и типологий. Качественная обработка в значительной мере апеллирует к методам логики.
      Противопоставление друг другу качественной и количественной обработки довольно условно. Количественный анализ без последующей качественной обработки бессмыслен, так как сам по себе не приводит к приращению знаний, а качественное изучение объекта без базовых количественных данных в научном познании невозможно. Без количественных данных научное познание – чисто умозрительная процедура.
      Единство количественной и качественной обработки наглядно представлено во многих методах обработки данных: факторном и таксономическом анализе, шкалировании, классификации и др. Наиболее распространены такие приемы количественной обработки, как классификация, типологизация, систематизация, периодизация, казуистика.
      Качественная обработка естественным образом выливается в описание и объяснение изучаемых явлений, что составляет уже следующий уровень их изучения, осуществляемый на стадии интерпретации результатов. Количественная же обработка полностью относится к этапу обработки данных.

7.2. Первичная статистическая обработка данных

      Все методы количественной обработки принято подразделять на первичные и вторичные.
      Первичная статистическая обработка нацелена на упорядочивание информации об объекте и предмете изучения. На этой стадии «сырые» сведения группируются по тем или иным критериям, заносятся в сводные таблицы. Первично обработанные данные, представленные в удобной форме, дают исследователю в первом приближении понятие о характере всей совокупности данных в целом: об их однородности – неоднородности, компактности – разбросанности, четкости – размытости и т. д. Эта информация хорошо считывается с наглядных форм представления данных и дает сведения об их распределении.
      В ходе применения первичных методов статистической обработки получаются показатели, непосредственно связанные с производимыми в исследовании измерениями.
      К основным методам первичной статистической обработки относятся: вычисление мер центральной тенденции и мер разброса (изменчивости) данных.
      Первичный статистический анализ всей совокупности полученных в исследовании данных дает возможность охарактеризовать ее в предельно сжатом виде и ответить на два главных вопроса: 1) какое значение наиболее характерно для выборки; 2) велик ли разброс данных относительно этого характерного значения, т. е. какова «размытость» данных. Для решения первого вопроса вычисляются меры центральной тенденции, для решения второго – меры изменчивости (или разброса). Эти статистические показатели используются в отношении количественных данных, представленных в порядковой, интервальной или пропорциональной шкале.
       Меры центральной тенденции– это величины, вокруг которых группируются остальные данные. Данные величины являются как бы обобщающими всю выборку показателями, что, во-первых, позволяет судить по ним обо всей выборке, а во-вторых, дает возможность сравнивать разные выборки, разные серии между собой. К мерам центральной тенденции в обработке результатов психологических исследований относятся: выборочное среднее, медиана, мода.
       Выборочное среднее (М) – это результат деления суммы всех значений (X)на их количество (N).

       Медиана (Me) – это значение, выше и ниже которого количество отличающихся значений одинаково, т. е. это центральное значение в последовательном ряду данных. Медиана не обязательно должна совпадать с конкретным значением. Совпадение происходит в случае нечетного числа значений (ответов), несовпадение – при четном их числе. В последнем случае медиана вычисляется как среднее арифметическое двух центральных значений в упорядоченном ряду.
       Мода (Мо) – это значение, наиболее часто встречающееся в выборке, т. е. значение с наибольшей частотой. Если все значения в группе встречаются одинаково часто, то считается, что моды нет. Если два соседних значения имеют одинаковую частоту и больше частоты любого другого значения, мода есть среднее этих двух значений. Если то же самое относится к двум несмежным значениям, то существует две моды, а группа оценок является бимодальной.
      Обычно выборочное среднее применяется при стремлении к наибольшей точности в определении центральной тенденции. Медиана вычисляется в том случае, когда в серии есть «нетипичные» данные, резко влияющие на среднее. Мода используется в ситуациях, когда не нужна высокая точность, но важна быстрота определения меры центральной тенденции.
      Вычисление всех трех показателей производится также для оценки распределения данных. При нормальном распределении значения выборочного среднего, медианы и моды одинаковы или очень близки.
       Меры разброса (изменчивости) – это статистические показатели, характеризующие различия между отдельными значениями выборки. Они позволяют судить о степени однородности полученного множества, его компактности, а косвенно и о надежности полученных данных и вытекающих из них результатов. Наиболее используемые в психологических исследованиях показатели: среднее отклонение, дисперсия, стандартное отклонение.
       Размах(Р) – это интервал между максимальным и минимальным значениями признака. Определяется легко и быстро, но чувствителен к случайностям, особенно при малом числе данных.
       Среднее отклонение(МД) – это среднеарифметическое разницы (по абсолютной величине) между каждым значением в выборке и ее средним.

      где d= |Х – М|, М– среднее выборки, X– конкретное значение, N– число значений.
      Множество всех конкретных отклонений от среднего характеризует изменчивость данных, но если не взять их по абсолютной величине, то их сумма будет равна нулю и мы не получим информации об их изменчивости. Среднее отклонение показывает степень скученности данных вокруг выборочного среднего. Кстати, иногда при определении этой характеристики выборки вместо среднего (М)берут иные меры центральной тенденции – моду или медиану.
       Дисперсия (D)характеризует отклонения от средней величины в данной выборке. Вычисление дисперсии позляет избежать нулевой суммы конкретных разниц (d= Х – М)не через их абсолютные величины, а через их возведение в квадрат:

      где d= |Х – М|, М– среднее выборки, X– конкретное значение, N– число значений.
       Стандартное отклонение(б). Из-за возведения в квадрат отдельных отклонений dпри вычислении дисперсии полученная величина оказывается далекой от первоначальных отклонений и потому не дает о них наглядного представления. Чтобы этого избежать и получить характеристику, сопоставимую со средним отклонением, проделывают обратную математическую операцию – из дисперсии извлекают квадратный корень. Его положительное значение и принимается за меру изменчивости, именуемую среднеквадратическим, или стандартным, отклонением:

 
      где d= |Х– М|, М– среднее выборки, X– конкретное значение, N– число значений.
      МД, Dи ? применимы для интервальных и пропорционных данных. Для порядковых данных в качестве меры изменчивости обычно берут полуквартильное отклонение (Q),именуемое еще полуквартильным коэффициентом. Вычисляется этот показатель следующим образом. Вся область распределения данных делится на четыре равные части. Если отсчитывать наблюдения начиная от минимальной величины на измерительной шкале, то первая четверть шкалы называется первым квартилем, а точка, отделяющая его от остальной части шкалы, обозначается символом QvВторые 25 % распределения – второй квартиль, а соответствующая точка на шкале – Q2. Между третьей и четвертой четвертями распределения расположена точка Q3.Полуквартильный коэффициент определяется как половина интервала между первым и третьим квартилями:

      При симметричном распределении точка Q2совпадет с медианой (а следовательно, и со средним), и тогда можно вычислить коэффициент Qдля характеристики разброса данных относительно середины распределения. При несимметричном распределении этого недостаточно. Тогда дополнительно вычисляют коэффициенты для левого и правого участков:

7.3. Вторичная статистическая обработка данных

      К вторичным относят такие методы статистической обработки, с помощью которых на базе первичных данных выявляют скрытые в них статистические закономерности. Вторичные методы можно подразделить на способы оценки значимости различий и способы установления статистических взаимосвязей.
       Способы оценки значимости различий.Для сравнения выборочных средних величин, принадлежащих к двум совокупностям данных, и для решения вопроса о том, отличаются ли средние значения статистически достоверно друг от друга, используют t-критерий Стьюдента. Его формула выглядит следующим образом:

      где М1, М2– выборочные средние значения сравниваемых выборок, m1, m2– интегрированные показатели отклонений частных значений из двух сравниваемых выборок, вычисляются по следующим формулам:

      где D1, D2– дисперсии первой и второй выборок, N1, N2– число значений в первой и второй выборках.
      После вычисления значения показателя tпо таблице критических значений (см. Статистическое приложение 1), заданного числа степеней свободы ( N1 + N2 – 2) и избранной вероятности допустимой ошибки (0,05, 0,01, 0,02, 001 и т.д.) находят табличное значение t.Если вычисленное значение tбольше или равно табличному, делают вывод о том, что сравниваемые средние значения двух выборок статистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной.
      Если в процессе исследования встает задача сравнить неабсолютные средние величины, частотные распределения данных, то используется ?2 критерий(см. Приложение 2). Его формула выглядит следующим образом:

      где Pk– частоты распределения в первом замере, Vk– частоты распределения во втором замере, m– общее число групп, на которые разделились результаты замеров.
      После вычисления значения показателя ?2по таблице критических значений (см. Статистическое приложение 2), заданного числа степеней свободы ( m– 1) и избранной вероятности допустимой ошибки (0,05, 0,0 ?2 tбольше или равно табличному) делают вывод о том, что сравниваемые распределения данных в двух выборках статистически достоверно различаются с вероятностью допустимой ошибки, меньшей или равной избранной.
      Для сравнения дисперсий двух выборок используется F-критерийФишера. Его формула выглядит следующим образом:

 
      где D1, D2 – дисперсии первой и второй выборок, N1, N2 – число значений в первой и второй выборках.
      После вычисления значения показателя Fпо таблице критических значений (см. Статистическое приложение 3), заданного числа степеней свободы ( N1 – 1, N2– 1) находится Fкр. Если вычисленное значение Fбольше или равно табличному, делают вывод о том, что различие дисперсий в двух выборках статистически достоверно.
       Способы установления статистических взаимосвязей.Предыдущие показатели характеризуют совокупность данных по какому-либо одному признаку. Этот изменяющийся признак называют переменной величиной или просто переменной. Меры связивыявляют соотношения между двумя переменными или между двумя выборками. Эти связи, или корреляции, определяют через вычисление коэффициентов корреляции. Однако наличие корреляции не означает, что между переменными существует причинная (или функциональная) связь. Функциональная зависимость – это частный случай корреляции. Даже если связь причинна, корреляционные показатели не могут указать, какая из двух переменных является причиной, а какая – следствием. Кроме того, любая обнаруженная в психологических исследованиях связь, как правило, существует благодаря и другим переменным, а не только двум рассматриваемым. К тому же взаимосвязи психологических признаков столь сложны, что их обусловленность одной причиной вряд ли состоятельна, они детерминированы множеством причин.
      По тесноте связи можно выделить следующие виды корреляции: полная, высокая, выраженная, частичная; отсутствие корреляции. Эти виды корреляций определяют в зависимости от значения коэффициента корреляции.
      При полнойкорреляции его абсолютные значения равны или очень близки к 1. В этом случае устанавливается обязательная взаимозависимость между переменными. Здесь вероятна функциональная зависимость.
       Высокаякорреляция устанавливается при абсолютном значении коэффициента 0,8–0,9. Выраженнаякорреляция считается при абсолютном значении коэффициента 0,6–0,7. Частичнаякорреляция существует при абсолютном значении коэффициента 0,4–0,5.
      Абсолютные значения коэффициента корреляции менее 0,4 свидетельствуют об очень слабой корреляционной связи и, как правило, в расчет не принимаются. Отсутствие корреляцииконстатируется при значении коэффициента 0.
      Кроме того, в психологии при оценке тесноты связи используют так называемую «частную» классификацию корреляционных связей. Она ориентирована не на абсолютную величину коэффициентов корреляции, а на уровень значимости этой величины при определенном объеме выборки. Эта классификация применяется при статистической оценке гипотез. При данном подходе предполагается, что чем больше выборка, тем меньшее значение коэффициента корреляции может быть принято для признания достоверности связей, а для малых выборок даже абсолютно большое значение коэффициента может оказаться недостоверным.
      По направленностивыделяют следующие виды корреляционных связей: положительная (прямая) и отрицательная (обратная). Положительная(прямая) корреляционная связь регистрируется при коэффициенте со знаком «плюс»: при увеличении значения одной переменной наблюдается увеличение другой. Отрицательная(обратная) корреляция имеет место при значении коэффициента со знаком «минус». Это означает обратную зависимость: увеличение значения одной переменной влечет за собой уменьшение другой.
      По формеразличают следующие виды корреляционных связей: прямолинейную и криволинейную. При прямолинейнойсвязи равномерным изменениям одной переменной соответствуют равномерные изменения другой. Если говорить не только о корреляциях, но и о функциональных зависимостях, то такие формы зависимости называют пропорциональными. В психологии строго прямолинейные связи – явление редкое. При криволинейнойсвязи равномерное изменение одного признака сочетается с неравномерным изменением другого. Эта ситуация для психологии типична.
       Коэффициент линейной корреляции по К. Пирсону (r)вычисляется c помощью следующей формулы:

 
      где х– отклонение отдельного значения Xот среднего выборки (Мх), у– отклонение отдельного значения Y отсреднего выборки (Му), Ьх– стандартное отклонение для X, ? y– стандартное отклонение для Y, N– число пар значений Xи Y.
      Оценка значимости коэффициента корреляции проводится по таблице (см. Статистическое приложение 4).
      При сравнении порядковых данных применяется коэффициент ранговой корреляции по Ч. Спирмену (R):

 
      где d– разность рангов (порядковых мест) двух величин, N– число сравниваемых пар величин двух переменных (X и Y).
      Оценка значимости коэффициента корреляции проводится по таблице (см. Статистическое приложение 5).
      Внедрение в научные исследования автоматизированных средств обработки данных позволяет быстро и точно определять любые количественные характеристики любых массивов данных. Разработаны различные программы для компьютеров, по которым можно проводить соответствующий статистический анализ практически любых выборок. Из массы статистических приемов в психологии наибольшее распространение получили следующие: 1) комплексное вычисление статистик; 2) корреляционный анализ; 3) дисперсионный анализ; 4) регрессионный анализ; 5) факторный анализ; 6) таксономический (кластерный) анализ; 7) шкалирование. Познакомиться с характеристиками этих методов можно в специальной литературе («Статистические методы в педагогике и психологии» Стенли Дж., Гласа Дж. (М., 1976), «Математическая психология» Г.В. Суходольского (СПб., 1997), «Математические методы психологического исследования» А.Д. Наследова (СПб., 2005) и др.).

Тема 8. Интерпретация и представление результатов психологических исследований

8.1. Интерпретация и обобщение результатов исследования

      Методы интерпретации данных корректнее называть подходами, поскольку они являются в первую очередь объяснительными принципами, предопределяющими направление интерпретации результатов исследования. В научной практике получили развитие генетический, структурный, функциональный, комплексный и системный подходы. Использование того или иного метода не означает отбрасывания других.
       Генетическийподход – это способ исследования и объяснения явлений (в том числе психических), основанный на анализе их развития как в онтогенетическом, так и филогенетическом планах. При этом требуется установление: 1) начальных условий возникновения явления; 2) главных этапов и 3) основных тенденций его развития. Цель генетического подхода – выявление связи изучаемых явлений во времени, прослеживание перехода от низших форм к высшим.
      Чаще всего генетический подход применяется при интерпретации результатов в психологии развития: сравнительной, возрастной, исторической. Любое лонгитюдное исследование предполагает применение рассматриваемого подхода.
      Генетический подход рассматривается как методическая реализация одного из основных принципов психологии, а именно принципа развития. При таком видении другие варианты реализации этого принципа рассматриваются как модификации генетического подхода (исторический и эволюционный подходы).
       Структурныйподход – направление, ориентированное на выявление и описание структуры объектов (явлений). Для него характерно: углубленное внимание к описанию актуального состояния объектов; выяснение внутренне присущих им вневременных свойств; интерес не к изолированным фактам, а к отношениям между ними. В итоге строится система взаимосвязей между элементами объекта на различных уровнях его организации.
      Достоинством структурного подхода является возможность наглядного представления результатов в виде различных моделей. Эти модели могут даваться в форме описаний, перечня элементов, графической схемы, классификации и пр. Примеры подобного моделирования можно найти у З. Фрейда, Г. Айзенка и др.
      Структурный подход часто применяется в исследованиях, посвященных изучению конституциональной организации психики и ее материального субстрата – нервной системы. Данный подход привел к созданию И.П. Павловым типологии высшей нервной деятельности, который затем был развит Б.М. Тепловым и В.Д. Небылицыным. Структурные модели человеческой психики в пространственном и функциональном аспектах представлены в работах В.А. Ганзена, В.В. Никандрова и др.
       Функциональныйподход ориентирован на выявление и изучение функций объектов (явлений). Он применяется главным образом при изучении связей объекта со средой. Этот подход исходит из принципа саморегуляции и поддержания равновесия объектов действительности. Примерами реализации функционального подхода в истории науки являются такие известные направления, как функциональная психология и бихевиоризм. Классическим образцом воплощения функционального подхода в психологии является динамическая теория поля К. Левина. В современной психологии функциональный подход обогащается компонентами структурного и генетического анализа. Общеизвестным считается представление о многоуровневости и многофазности всех психических функций человека, действующих одновременно на всех уровнях как единое целое. Элементы структур большинство авторов соответствующих моделей рассматривают также и как функциональные единицы, олицетворяющие определенные связи человека с действительностью.
       Комплексныйподход – это направление, рассматривающее объект исследования как совокупность компонентов, подлежащих изучению с помощью соответствующей совокупности методов. Компоненты могут быть как относительно однородными частями целого, так и его разнородными сторонами, характеризующими изучаемый объект в разных аспектах.
      Часто комплексный подход предполагает изучение сложного объекта методами различных наук, т. е. организацию междисциплинарного исследования. Очевидно, что он предполагает применение в той или иной мере и всех предыдущих интерпретационных методов.
      Яркий пример реализации комплексного подхода в науке – концепция человекознания, согласно которой человек как объект изучения подлежит скоординированному исследованию большого комплекса наук. В психологии эта идея комплексности изучения человека была четко сформулирована Б.Г. Ананьевым. Человек рассматривается одновременно как представитель биологического вида (индивид), носитель сознания и активный элемент познавательной и преобразующей действительность деятельности (субъект), субъект социальных отношений (личность) и уникальное единство социально значимых биологических, социальных и психологических особенностей (индивидуальность).