Компьютерра - Журнал «Компьютерра» №47-48 от 20 декабря 2005 года
ModernLib.Net / Компьютерра Журнал / Журнал «Компьютерра» №47-48 от 20 декабря 2005 года - Чтение
(стр. 9)
При этом методе - называемом еще амплитудной модуляцией - приемлемая передача полутонов возможна даже при относительно грубом растре, и величина линиатуры вообще не применима. И для качества принтера большее значение имеет не само по себе физическое разрешение (конечно, сверх некоего предела, который уже достигнут во всех современных моделях), а минимальный размер капли красителя, который он может выдать. Притом, как известно, поверх этого основного способа в струйных принтерах придумывают еще всякие ухищрения, вроде того, что капля специально делится на множество мелких, что позволяет более тонко регулировать полутона. Теоретики рассуждают так: допустим, принтер имеет такой же строгий растр, как и типографское печатное устройство. Тогда для воспроизведения 256 оттенков нужен квадрат 16х16 точек. Если плотность печати 2400 dpi (HP), то линиатура как раз и получается 150 lpi. Но все это чисто умозрительные рассуждения. Во-первых, квадрат 16х16 для каждого цвета получается исходя из оттенков серого. А цветов в современном фотопринтере даже не четыре, как в модели CMYK, а минимум шесть, притом для каждого можно получить точку диаметром 12 мкм и даже меньше, и они вовсе необязательно будут ложиться рядом, а не поверх друг друга. И красители там не кроющие, а прозрачные. И разрешение в 2400 dpi имеется только по горизонтали (шаг каретки), по вертикали (механизм передвижения бумаги) он раза в два меньше. И не забудем еще, что на бумаге 256 оттенков все равно не получишь (см. врезку), так стоит ли стараться? Производители не декларируют для струйных принтеров никаких линиатур, и правильно делают. Перед нами типичное аналоговое устройство печати (при достаточно высоком физическом разрешении, конечно, но все современные принтеры таковым обладают), и задумываться следует над тем, что нам дает исходная картинка, а не что может воспроизвести принтер. Если у вас сверхчеткое изображение - будьте спокойны, принтер вас не подведет, установите ли вы для него 288, 289 dpi или любую другую цифру, в пределах того, что обеспечивает исходная картинка. Но чтобы при очень качественных оригиналах ничего не потерять, имеет смысл задумываться над алгоритмами растяжения (и даже сжатия) снимков для печати и специально устанавливать разрешение. А для всех любительских камер, и тем более для всех без исключения оригиналов в формате JPEG, этот вопрос не играет ни малейшей роли, и можно спокойно положиться на программу печати и драйвер принтера, которые все сделают за вас, и сделают очень грамотно. А про все эти разрешения лучше вообще забыть, оставив их счастливым обладателям камер класса Canon Mark II.
300 dpi
Цифра в 300 dpi получается в полиграфии из соображений необходимой линиатуры (измеряется в линиях на дюйм, lpi). При типографской печати мы располагаем только одной краской, прозрачность которой регулировать нельзя. Как в таком случае обеспечить полутона? Единственный очевидный способ: там, где изображение светлее, часть точек (лучше всего в случайном порядке) не закрашивать. Те, кто видел советские газеты полувековой давности , отлично понимает, о чем я говорю: там растр был таким грубым, что описанную технику воспроизведения полутонов можно было разглядеть невооруженным взглядом. С повышением разрешения печатающих устройств качество стало более приемлемым, но принцип сохранился (и в цвете он точно такой же, только там не один, а четыре разноцветных растра, наложенные друг на друга под разными углами, по числу красок в модели CMYK). Этот метод передачи полутонов называется частотной модуляцией. Физическое разрешение печатающего устройства (dpi) и заданное разрешение полученного изображения (lpi) оказываются связаны между собой простой зависимостью: число градаций серого = единица плюс квадрат отношения разрешения (dpi) к линиатуре (lpi). Для современных фотонаборных автоматов характерно физическое разрешение в 2540 dpi (100 точек на миллиметр). Что при всех воспроизводимых 256 градациях серого при расчете по формуле, приведенной выше, соответствует линиатуре в 160 lpi или размеру полутоновой точки растра в 0,16 мм - вполне приличная величина, близкая к пределу разрешающей способности глаза на расстоянии комфортного чтения. При желании линиатура может быть установлена и значительно большей, потому что на бумаге с ее динамическим диапазоном максимум в 2 D (то есть контрастом между черным и белым максимум в сто раз) 256 градаций серого никому не нужны, они просто неразличимы. На практике газеты печатают с растром 60-100 lpi, журналы - 133-150 lpi; для специальной печати (например, для дензнаков) используют величины и больше, но там важно уже не столько число оттенков, сколько разрешение само по себе. Ясно, что разрешение исходного снимка (напомню, мы считаем, что оптика нас не лимитирует) должно быть не хуже, чем линиатура. А лучше - с запасом. Если принять двукратный запас, то и получим пресловутые 300 dpi.
ОПЫТЫ: Рождественская милицейская история
Эта история началась осенью 2001-го совершенно буднично, и ничто не предвещало, что она растянется на четыре года и отвлечет на себя значительные силы ростовской милиции. Дело происходило в одном из восточных районов области. Места там степные, засушливые и малонаселенные, живут там в основном крестьяне, занимающиеся разведением овец. Хутора расположены далеко друг от друга, в каждом из них свои устои, порядки и даже власть. В один прекрасный день в районное отделение милиции поступило заявление от жителей одного из хуторов - народ требовал разобраться с пропажей большого количества индюков (любопытный штрих: местные жители почему-то называют этих птиц индю’ки). Участковый, в зону ответственности которого входил хутор, разобрался с делом мгновенно. Этот человек был из породы тех «Анискиных», про которых раньше снимали фильмы, - всё и всех знающий, работающий здесь черт знает сколько лет, пользующийся заслуженным авторитетом у местных жителей… Расследование показало, что во многих семьях двух соседних с обиженным хуторов на обед был суп из птицы, а массовая и прекрасно организованная пропажа индюков - следствие давней затаенной обиды жителей этих селений. Таким образом, вроде как восторжествовала крестьянская справедливость. А чтобы восторжествовал закон, необходимо было всесторонне рассмотреть поступившее от граждан заявление, надлежащим образом все оформить и посадить в тюрьму на срок от трех до пяти лет половину населения двух хуторов. Но ведь жалко… В результате милиционер придумал гениальный ход: рядом с местом, где обычно бродили индюки, проходило железнодорожное полотно и имелся небольшой полустанок. Опрос жителей выявил двух надежных свидетелей, которые дали письменное заявление о том, что видели, как в определенное время на этом полустанке ненадолго остановился товарный состав. При этом индюки, очевидно, движимые любопытством, под воздействием приступа внезапного кретинизма организованно погрузились в вагоны и отбыли в неизвестном направлении. Факт прохождения состава и его остановки подтверждался расписанием движения поездов. На этом расследование можно было считать законченным. Фокус в том, что все, что происходит в поездах, на железнодорожном полотне и на расстоянии девяти метров от него, подпадает под юрисдикцию Управления внутренних дел на транспорте (УВДТ), куда и передается дело для дальнейшего расследования. А это уже другое ведомство, волокита… Отсюда и возникла практика «перетаскивания» неопознанных трупов, найденных в поле, поближе к железнодорожному полотну - вроде как тело выпало из проходящего мимо поезда. К несчастью, как раз в этот момент из столицы прибыла комиссия с инспекторской проверкой, и нераскрытое преступление было совсем ни к чему. Поэтому сотрудники ведомства быстренько провели собственное расследование и установили, что когда интересующий нас состав прибыл на ближайшую крупную станцию, индюков в нем уже не было. Естественно, прилагались свидетельские показания работников станции. Таким образом, следовало, что умные птицы, скорее всего, покинули состав во время одной из остановок на маршруте следования. Список мест остановок тоже прилагался, и дело снова передавалось в районный ОВД. Предполагалось, что индюки будут пытаться вернуться домой. Ну тут уж милиционеры пошли на принцип, и привлеченные участковые быстренько нашли еще двух совершенно надежных свидетелей, которые дали письменные показания о том, что видели, как во время остановки поезда индюки с него слезли и пересели в другой состав, стоявший на соседнем пути. Кроме того, к делу приложили справку известного орнитолога, который утверждал, что индюки - очень умные стайные птицы и что осенью у них мог внезапно пробудиться инстинкт к переселению в теплые края. Дело снова направлялось на дополнительное расследование в УВДТ. Но и в УВДТ, хоть это и другое ведомство, работают не менее упрямые милиционеры. Находились все новые свидетели, клятвенно заверявшие, что индюки проносились мимо них в поездах, пересаживались в другие составы, но упрямо не хотели прибывать ни на одну крупную станцию. В какой-то момент движение индюков стало настолько хаотичным, что контролировать его без привлечения математических алгоритмов обработки информации стало невозможно. И у одного из следователей созрела гениальная мысль назначить компьютерно-техническую экспертизу. Это была лишняя возможность затянуть дело на время производства экспертизы. К сожалению, в тот момент я не знал еще подоплеки и потому ретиво взялся за работу. О боги, я был допущен в диспетчерские Северо-Кавказской железной дороги, получил доступ к специализированному программному обеспечению - мечта хакеров и фанатов Railroad Tycoon. Работа закипела: я отсекал заведомо невозможные маршруты движения индюков, пытался найти логику в их действиях. Я ведь еще не знал, что здесь имеется другая, «высшая» логика. Мои усилия вскоре стали давать результаты, и, думаю, в конце концов, я бы докопался до истины - все шло к тому, что индюки сошли-таки с поезда, причем не так уж далеко от родного хутора. Понимали это и мои оппоненты. А год неумолимо приближался к концу, за халатность при проведении расследования можно было схлопотать выговор, что гарантировало лишение годовой премии и тринадцатой зарплаты. Поэтому на одном из полустанков стая индюков… разделилась. Любой из тех, кто работает с вероятностными алгоритмами, наверняка знает, что подобное действие приводит даже не к удвоению, а к учетверению работы. По наивности и от большого энтузиазма я бы еще справился, но стая продолжила рассредотачиваться, делясь на все более мелкие группы. Когда первые сведения о движении проклятых индюков стали поступать уже с Транссибирской магистрали, я понял, что обречен, и пошел за консультацией к следователю, ведущему это дело. После задушевной беседы, перемежавшейся распитием различного рода напитков, я, наконец, был ознакомлен с подлинным смыслом данного расследования. Совместно был разработан генеральный план продвижения индюков. Теперь, под моим чутким руководством, они неизменно продвигались к югу и покидали границы РФ, переезжая на территорию суверенной и практически никому неподконтрольной Абхазии. Если обнаруживалась группа пернатых, маршрут которой не укладывался в мою схему, предлагалось провести дополнительное расследование. Обычно оказывалось, что это не наши индюки или вообще не индюки. Несколько затруднила мои действия особо упорная группа, движение которой по железнодорожной магистрали наблюдал практически в полном составе некий райотдел милиции (железнодорожная ветка проходила у них под окнами), о чем имелись соответствующие рапорта. Движение этой группы никак не согласовывалось с генеральной линией, и для того, чтобы вернуться на маршрут, от которого они отклонились, не имелось подходящих поездов. Но, в конце концов, с помощью пересадок в трех электричках я решил и эту проблему. К слову, попутно удалось оптимизировать графики движения некоторых поездов Северо-Кавказской железной дороги. Так любимый всеми ростовчанами дополнительный «летний» поезд №642 Ростов-Адлер стал проводить в пути в одну сторону на три часа меньше, а в другую - почти на два. Оказалось, что научно, с использованием компьютерной техники к этому вопросу раньше не подходили. Таким образом, к удовольствию всех заинтересованных лиц, проблему удалось разрешить бескровно. Дело прекратили, никого не наказали, индюки, видимо, ассимилировались в теплых краях и на родину не вернулись. Пару лет спустя, встретившись с одноклассником, избравшим карьеру биолога, после совместного распития неизвестных напитков, я узнал следующую историю. Товарищ рассказал, что бюллетень «Вопросы прикладной орнитологии» недавно напечатал интереснейшую статью одного известного ученого, в которой приводились неопровержимые, даже подкрепленные милицейскими документами факты необычайного поведения домашних птиц, в частности индюков. Автор статьи делал вывод, что птицы, проживая долгое время совместно с человеком, серьезно эволюционируют. В них даже просыпается коллективный разум. Причем сила их разума во многом определялась солнечной активностью. Поэтому на юге России птицы изменялись быстрее. Ученый проводил крайне смелые эксперименты, закончившиеся полным успехом. Результаты их могут привести к настоящей революции в орнитологии. Что же, с нетерпением ожидаю запроса из Академии наук…
Наука:
Проблемы 2000 года: Гипотеза Берча-Свиннертон-Дайера
В одной из предыдущих статей раздела (посвященной гипотезе Ходжа; «КТ» #609) мы уже касались алгебраической геометрии. Тогда же упоминалось, что к ней имеют прямое отношение как минимум три из семи задач на миллион. Об одной из таких задач мы и поговорим: гипотеза Берча-Свиннертон-Дайера касается рациональных точек алгебраических многообразий - иными словами, рациональных решений полиномиальных уравнений.
Введение
Алгебраическую геометрию, как и многие другие области математики, невозможно причислить ни к древним, ни к современным разделам науки. С одной стороны, ничто не ново под луной: еще древних греков, заложивших основы самого метода математического познания, интересовали проблемы, которые и сегодня исследует алгебраическая геометрия. С другой же - о глубине современных методов и задач этой науки древние греки не могли даже догадываться (как зачастую и нынешние математики, работающие в других областях). Ключевые задачи алгебраической геометрии сформулировать и понять совсем не трудно. Вот, например, общее направление, к которому относится и гипотеза Берча-Свиннертон-Дайера: выяснить, сколько у данного полиномиального уравнения решений в рациональных[Имеющих вид p/q, где p, q - целые. - Л.Л.-М.] числах. Но чтобы сформулировать саму гипотезу, требуется изрядная подготовка.
Немного истории
Как мы уже упоминали, общая проблема поиска рациональных решений была поставлена - и в самых простых частных случаях решена - очень давно. Одна из древнейших формулировок, встречающаяся еще в арабских трактатах X века, имеет геометрическую природу. Это так называемая задача о конгруэнтных числах: какие рациональные числа могут быть площадями прямоугольных треугольников с рациональными длинами сторон? Однажды Фибоначчи[Он же Леонардо Пизанский, итальянский ученый и одновременно купец (1170-1250). - Л.Л.-М.], находясь при дворе Фредерика II, не сходя с места нашел такой треугольник с площадью 5; есть и более экзотические примеры. Ответ таков (желающие могут его проверить): n - конгруэнтное число тогда и только тогда, когда число рациональных решений уравнения y2 = x3 - n2x бесконечно. 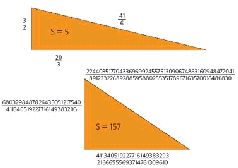 Первым, кто поставил проблему поиска рациональных решений в ее современном смысле, был великий французский математик Анри Пуанкаре. Пуанкаре сделал для развития математики (в том числе алгебраической геометрии) и физики очень многое. О других его достижениях у нас еще будет повод поговорить, ведь именно он сформулировал одну из «задач на миллион», в его честь и названную гипотезой Пуанкаре. Брайан Берч (Bryan Birch) и Питер Свиннертон-Дайер (Peter Swinnerton-Dyer) (да-да, Берч-Свиннертон-Дайер - это два человека, а не три) занимались этой проблемой в начале шестидесятых. Примечательно, что у истоков гипотезы стоит один из ранних компьютеров - кембриджский EDSAC, с помощью которого Берч и Свиннертон-Дайер исследовали поведение так называемых эллиптических кривых (что это такое, поясним чуть позже).
Суть
 Итак, в чем же суть проблемы, о которой мы сегодня рассказываем? Рассмотрим кривую, заданную полиномиальным уравнением с двумя переменными. Одна из важнейших характеристик такой кривой - ее род (genus). Дать здесь классическое определение рода кривой будет трудно, но мы приблизимся к нему с другой стороны. Начнем с поверхностей. Наверное, каждый в детстве читал о топологах, которые не могут отличить кружку от бублика - ведь обе поверхности топологически эквивалентны тору. Так вот, у поверхностей тоже есть род; род бублика, например, равен единице. А вообще род поверхности (если быть точным, род «ориентируемой поверхности») - это количество замкнутых кривых, по которым ее можно разрезать так, чтобы она не распалась на отдельные части. Можете сами попробовать: сферу или плоскость так разрезать нельзя, у них род 0, тор (он же бублик[]) можно разрезать один раз, хоть вдоль, хоть поперек, но после этого останется либо цилиндр, либо кусок плоскости, и второго разреза уже не получится. Все ориентируемые поверхности похожи на сферу с ручками (термин из алгебраической геометрии): сколько у сферы ручек, столько и разрезов можно сделать. Теперь представьте, что уравнение, которое нас интересует, нужно решать в комплексных числах. Тогда множество его решений - это двухмерная поверхность. Ее род в данном случае и называется родом кривой. Итак, род представляет собой целое неотрицательное число; кривые рода 1 - это и есть эллиптические кривые, которые сейчас находят применение в криптографии. О них и идет речь в гипотезе Берча-Свиннертон-Дайера. Кстати, если ограничиться вещественными числами, эллиптические кривые определяются совсем просто: это кривые, заданные одним из уравнений Вейерштрасса y  Как уже упоминалось, гипотеза касается множества рациональных решений данного уравнения. Берч и Свиннертон-Дайер рассматривали функцию L, вычисляемую через количество рациональных решений по модулю простого числа p (в вещественном случае - количество решений уравнения y2 #8801; x3 + ax +b по модулю p). Функция эта строится аналогично дзета-функции Римана, о которой мы уже рассказывали, и свойства имеет соответствующие: L, если рассмотреть ее как функцию комплексного переменного, сходится на полуплоскости, но при этом аналитически продолжается и на другую половину. Вычислить значения L и ее аналитического продолжения для каждой конкретной кривой не очень просто, но вполне возможно; в частности, это можно сделать автоматически, на компьютере. Гипотеза Берча-Свиннертон-Дайера утверждает, что количество и структура множества рациональных решений эллиптической кривой тесно связаны с поведением L-функции в единице[Если быть точным, то по этой гипотезе ранг группы рациональных решений есть степень первого ненулевого члена разложения L в ряд Тейлора в единице; иными словами, L(z) около единицы похожа на (z-1)r, где r - ранг.]. В частности, количество рациональных точек бесконечно тогда и только тогда, когда L(1)=0.  Благодаря работам отечественного математика Виктора Александровича Колывагина, а также доказательству теоремы Ферма Эндрю Уайлсом это утверждение уже доказано в одну сторону: если L(1) #8800; 0, то количество рациональных точек конечно. Доказательство в другую сторону - предмет долгих и безуспешных поисков. Кроме того, открыт путь для обобщений гипотезы - в частности, к изучению рациональных точек не только кривых, но и поверхностей более высокой размерности (то есть уравнений с бульшим количеством переменных). Например, Леонард Эйлер еще в 1769 году выдвинул гипотезу, что уравнение x4 + y4 + z4 = t4 не имеет ненулевых решений. Эту гипотезу, как и похожую на нее гипотезу Ферма, долгое время не могли доказать, но результат в данном случае оказался иным: в 1988 году обнаружился контрпример (точнее, бесконечно много контрпримеров). Вот минимальный из них (проверить легко - но представьте, как трудно было бы его найти без развитой теории): 2682440 4 + 15365639 4 + 18796760 4 = 20615673 4
Приложения
Алгебраическая геометрия - наука, приложения которой, как правило, отнюдь не очевидны. Математикам, чтобы годами биться над интересной задачей, приложения и вовсе не нужны: да, великая теорема Ферма имеет некоторый криптографический смысл, но попытки ее доказательства привели к созданию и развитию нескольких важных разделов современной математики задолго до того, как криптография оформилась как математическая дисциплина. Вот и в случае гипотезы Берча-Свиннертон-Дайера непосредственных приложений, о которых можно было бы здесь рассказать, сразу не видно. Разумеется, в своей области гипотеза занимает центральное место: мы пока не умеем искать рациональные точки алгебраических многообразий (заданных полиномиальными уравнениями множеств), и доказательство гипотезы Берча-Свиннертон-Дайера могло бы доставить математикам новые методы и подходы к этому поиску. Однако история не раз подтверждала, что творения математика переживают столетия лишь тогда, когда он работает без практических применений, а для удовлетворения собственного любопытства. А ориентированные на практику исследования очень редко приносят глубокие, фундаментальные результаты. Кто знает, возможно, гипотеза Берча-Свиннертон-Дайера станет основой теории, которая в очередной раз изменит мир.
ПИСЬМОНОСЕЦ: Happy New Year, бэби!
Доброе время суток, дорогие компьюпилы. Знаете, мне все больше и больше становится жалко Козловского. Мужику все труднее и труднее писать про какие-то новенькие фенечки, это чувствуется… Долго пытался понять почему, и до меня дошло. Когда вы в последний раз с восторгом отзывались о телевизоре? Да-да, о том самом ящике, который стоит в каждом доме. К чему это я? Да к тому, что в последнее время компьютер (проектор, монитор, модем и бла-бла-бла) стали такими же «телевизорами» - незаметными, но незаменимыми (для некоторых) предметами обихода. А писать про то, что есть почти у каждого, неинтересно; трудно привнести в эту среду что-либо новое, оригинальное. Поэтому, как бы мне ни хотелось обратного, но похоже, что года через два «Огород» умрет, зарастет травой. А жаль, будет нехватать…
А «Село» было, есть и будет! А вот что будет с Голубицким - загадка. Возможно, на ниве софта «Голубятня» также загнется, но вот повидло… Его будут «есть» всегда.
Спасибо за возвращенную в конец статей дискетку.
В отличие от своих первых писем, если дадите приз - не откажусь.
ОТ РЕДАКЦИИ: Козловский - это кибернетический организм, отправленный в прошлое, чтобы изменить будущее. Так что я бы на вашем месте был поосторожнее с прогнозами: огородник еще первый аккумулятор только наполовину израсходовал, а у него и второй имеется, с удвоенной емкостью. И не удивляйтесь, если под Новый год на пороге вашей квартиры появится некто с горящими глазами, бородой и пультом управления в ухе и с характерной интонацией поинтересуется: «Паша Кабаев?»
Я являлся читателем «Компьютерры» с 1997 по 2000 год, потом перестал читать, потому что стиль изменился настолько, что мне просто стало неприятно читать. Сначала журнал был замечательный, потом все хуже и хуже. Вот сейчас зашел на сайт, где-то полгода не был, это же ужас! Ребят, вы бы определились с языком, наконец, - если пишете кириллицей, то пишите по-русски, если пишете латинским алфавитом, то по-английски. Когда в одном предложении пять слов антитранслитом, пять - транслитом, пять - по-английски и пять - по-русски, - это просто нереально сложно прочитать, несмотря на то что я одинаково свободно владею русским и английским.
Петр Мордашев
ОТ РЕДАКЦИИ: Знаете, Петр, проблема чистоты русского языка занимала еще Екатерину Вторую, чистокровную немку, которая на закате карьеры потребовала заменить все «чужие» слова на родные, исконные. Власти у нее было с избытком, однако вы, уверен, до сих пор называете клизму «клизмой», а вовсе не «задослабом», как хотелось матушке-императрице. В компьютерной отрасли действительно немало терминов, заимствованных из других языков, но обвинять в этом «Компьютерру» равносильно предположению, что Кеннеди убили Козловский с Голубицким. А претензии ваши можно свести к фразе из интернет-фольклора: «Ниасилил. Очиньмногабуков»
Здравствуйте, друзья! Зацепила меня «13-я комната» в #615 про находящихся на грани разорения мобильных операторах. Идея о миграции в брезентовые палатки - это самое оно. Думаю, на полиграфические шедевры (бесплатные журналы, тарифные планы и пр.) и позолоту лепнины тратятся немалые деньги. Опять же скучающие менеджеры… Плюс к тому непонятное нежелание операторов париться просвещением абонентов, которые зачастую не умеют пользоваться большинством услуг (начиная от SMS и заканчивая GPRS, который используют, в общем-то, только продвинутые полуколхозные пацаны для «закачивания» картинок и мелодий). Несложная пропаганда мобильных e-mail, ICQ и прочего (вкупе с установкой/настройкой/техподдержкой), думаю, резко повысит объемы GPRS-трафика. Полагаю, и с прочими услугами нужно поступать аналогично. Возможно, что в Москве ситуация видится иначе, но у нас в провинциях по-прежнему бытует мнение, что «телефон - чтобы звонить», и ромашки аськи на экране древнего Siemens C60 вводят людей в полнейший ступор («А… Э… А что, можно?!??!»). Что ж, наверное, пришла пора снимать клубные пиджаки и, засучив рукава, пахать… Ну где-то на уровне между водоканалом и горавтотрансом.
С уважением, Кволд
ОТ РЕДАКЦИИ: Я искренне желаю в новом году всем нам разориться, как «разоряются» операторы. Ведь они занервничали лишь из-за того, что у боссов появился риск с черной икры из осетра, который выращен в собственном озерце, где-нибудь в Швейцарии, перейти на банальную баночную. Ну неприятно им так низко опускаться, даже если банка будет с ведро, а икру из нее придется черпать платиновым половником. Одно жаль: как бы мы ни экономили на разговорах, на продолжительности жизни осетров это не скажется.
Антивирусом Dr.Web для Windows 9x-XP - максимально надежной защитой домашнего компьютера - награждается Кволд за понимание тягот жизни состоятельных соотечественников.
Приз предоставлен компанией «Доктор Веб»
. Также победитель получает DVD c фильмом «Doom».
This file was created
with BookDesigner program
bookdesigner@the-ebook.org
04.05.2008
Страницы:
1, 2, 3, 4, 5, 6, 7, 8, 9
|
|





