Программирование на языке пролог

Однако, когда мы говорим, что методом резолюций можно вывести пустой дизъюнкт, это значит, что существует последовательность шагов, на каждом из которых правило резолюций применяется к аксиомам или к дизъюнктам выведенным на предыдущих шагах, и эта последовательность заканчивается выводом дизъюнкта, не содержащего литералов. Единственная проблема – найти соответствующую последовательность шагов. Так как, хотя метод резолюций и говорит о том, как получить следствие двух дизъюнктов, он не сообщает, какие дизъюнкты выбрать для очередного шага и какие литералы в этих дизъюнкциях необходимо «сопоставить». Обычно, если имеется большое количество гипотез, то существует и много вариантов выбора среди них. Более того, на каждом шаге выводится новый дизъюнкт и он тоже становится кандидатом на участие в последующей обработке. Большинство из имеющихся возможностей выбора дизъюнктов и литералов в них не имеют отношения к решаемой задаче и, если не производить тщательного отбора среди кандидатов, то можно потратить слишком много времени на бесплодные поиски, а путь, ведущий к решению, так и не найти.

На решение этих вопросов направлено много различных улучшений исходного принципа резолюций. В следующем разделе рассматриваются некоторые из них.

10.5. Хорновские дизъюнкты

Рассмотрим теперь модификацию метода резолюций, разработанную для случая, когда все дизъюнкты имеют некоторый определенный вид – когда они являются хорновскими дизъюнктами,Хорновский дизъюнкт – это дизъюнкт, содержащий не более одного литерала без отрицания. Оказывается, что если процедура доказательства теорем используется для определения значений вычислимых функций, то вполне достаточно использовать для этого лишь хорновские дизъюнкты. Так как метод резолюций в случае хорновских дизъюнктов также является относительно простым, то естественно выбрать хорновские дизъюнкты в качестве основы для процедуры доказательства теорем, применяемой в практической системе программирования, Рассмотрим коротко, что представляет метод резолюций, если ограничиться хорновскими дизъюнктами.

Прежде всего, очевидно, что существуют два вида хорнов-ских дизъюнктов – дизъюнкты, содержащие один литерал без отрицания и дизъюнкты, не содержащие таких литералов. Будем называть эти два типа хорновских дизъюнктов соответственно дизъюнктами с заголовкоми дизъюнктами без заголовка.Следующие примеры иллюстрируют указанные типы дизъюнктов (необходимо помнить, что литералы без отрицания записываются слева от знака ':-'):

холостяк(Х):- мужчина(Х), неженат(Х).

:- холостяк(Х).

В действительности, рассматривая множества хорновских дизъюнктов (включая целевые утверждения), необходимо выделять лишь такие множества, в которых все дизъюнкты за исключением одного имеют заголовки. Это значит, что каждая разрешимая задача (задача доказательства теоремы), которая может быть выражена с помощью хорновских дизъюнктов, может быть представлена в таком виде, что:

•Имеется только один дизъюнкт без заголовка. Все остальные дизъюнкты имеют заголовки.

Так как совершенно не имеет значения, какие дизъюнкты считать целевыми, то можно принять решение рассматривать дизъюнкт без заголовка как целевой, а все остальные дизъюнкты – как гипотезы. Такое решение выглядит довольно естественно.

Почему мы должны рассматривать лишь такие совокупности хорновских дизъюнктов, которые вписываются в эту схему? Во-первых, легко видеть, что для того, чтобы задача была разрешима, необходимо наличие по крайней мере одного дизъюнкта без заголовка. Это объясняется тем, что в результате применения правила резолюций к двум хорновским дизъюнктам с заголовками вновь получается хорновский дизъюнкт с заголовком. Поэтому, если все дизъюнкты имеют заголовки, то единственное что можно делать – это выводить другие дизъюнкты с заголовками. Так как пустой дизъюнкт не имеет заголовка, то он никогда не будет выведен. Второе требование – это необходим лишь один дизъюнкт без заголовка – обосновать несколько труднее. Од-нако оказывается, что, если среди аксиом имеют несколько дизъюнктов без заголовка, то каждое доказательство нового дизъюнкта методом резолюций может быть преобразовано в доказательство, в котором используется не более чем один из них. Поэтому, если пустой дизъюнкт следует из данного множества аксиом, то он следует и из его подмножества, содержащего все дизъюнкты с заголовками и не более одного дизъюнкта без заголовка.

10.6. Пролог

Давайте подведем итог и посмотрим, как Пролог вписывается в рассмотренную выше схему. Как было показано, некоторые формулы, представленные в виде совокупности дизъюнктов, выглядят в точности так же, как и утверждения в Прологе, в то время как другие формулы имеют несколько отличный вид. Формулы, имевшие вид утверждений Пролога, есть в действительности не что иное, как формулы, представимые в виде хорновских дизъюнктов. При записи хорновского дизъюнкта в соответствии с принятыми соглашениями, количество атомарных формул слева от знака ';-' не может превышать одну. В общем случае, дизъюнкты могут иметь несколько таких формул (они соответствуют литералам, представляющим атомарные формулы без отрицания). В Прологе непосредственно можно представить только хорновские дизъюнкты. Утверждения программы на Прологе соответствуют хорновским дизъюнктам с заголовком (в рамках определенной процедуры доказательства теорем). А что в Прологе соответствует целевому дизъюнкту? Очень просто, вопрос в Прологе

?- A ₁, A ₂,…, A _n

в точности соответствует хорновскому дизъюнкту без заголовка:- A ₁, A ₂,…, А _п

В предыдущем разделе уже говорилось о том, что для решения любой задачи, представленной с помощью хорновских дизъюнктов, достаточно иметь в точности один дизъюнкт без заголовка. В Прологе это соответствует ситуации, когда все утверждения «программы» имеют заголовки и в каждый момент времени рассматривается лишь одно целевое утверждение (не имеющее заголовка).

Пролог-система основывается на процедуре доказательства теорем методом резолюций для хорновских дизъюнктов. Конкретная стратегия, используемая при этом, является разновидностью линейной входной резолюции.При использовании этой стратегии, выбор дизъюнктов для резолюции на каждом шаге ограничен следующими условиями. Процедура начинается с применения правила резолюций к целевому дизъюнкту и к одной из гипотез, что дает новый дизъюнкт. Затем производится резолюция этого дизъюнкта и одной из гипотез, что дает еще один новый дизъюнкт. Затем правило резолюций применяется к последнему полученному дизъюнкту и к одной из гипотез и так далее. На каждом этапе правило резолюций применяется к последнему из вновь полученных дизъюнктов и к одной из исходных гипотез. Правило резолюций никогда не применяется, если оба дизъюнкта были выведены на предыдущих этапах или являются исходными гипотезами. С точки зрения Пролога, последний выведенный дизъюнкт можно рассматривать как конъюнкцию целевых утверждений, которые еще надо доказать (согласовать с базой данных). В начальный момент это вопрос, а в конце процесса, при благоприятных условиях,- это пустое утверждение. На каждом этапе ищется утверждение, заголовок которого сопоставим с одним из целевых утверждений. Если необходимо, происходит конкретизация переменных. Удаляется целевое утверждение, с которым произошло сопоставление, а затем к целевым утверждениям, которые необходимо согласовать, добавляется тело найденного утверждения, в котором произведена конкретизация переменных. Так, например, начав с вопроса

:- мать(джон,Х), мать(Х,Y).

и утверждения

мать(U,V):- родитель(U,V), женщина(V).

получаем

:- родитель(джон,Х), женщина(Х), мать(Х,Y).

В действительности, используемая в Прологе стратегия является более ограниченной по сравнению с общей линейной входной резолюцией. В этом примере для сопоставления был выбран первый литерал целевого дизъюнкта, но с таким же успехом можно было бы сопоставить и второй литерал. В Прологе выбор литерала для сопоставления всегда происходит одним и тем же способом – всегда выбирается первый литерал в целевом дизъюнкте. Кроме того, новые целевые утверждения, полученные при использовании некоторого утверждения помещаются в начале целевого дизъюнкта. Это значит, что Пролог завершит доказательство согласованности всех подцелей прежде чем перейдет к обработке следующих целей.

Все сказанное относится к событиям, происходящим после того, как Пролог выбрал утверждение для сопоставления с первой целью. Но как организуется исследование альтернативных утверждений для удовлетворения той же самой цели? В Прологе используется стратегия поиска вглубь,а не поиска вширь.Это значит, что Пролог в каждый момент времени рассматривает лишь одну альтернативу, упорно следуя подразумеваемому предположению о правильности сделанного выбора. Выбор утверждений для каждой цели производится в строго фиксированном порядке, а пересмотр выбранных ранее утверждений происходит лишь в случае, когда все последующие попытки не привели к решению. В качестве альтернативы можно было бы предложить стратегию, при которой система запоминает одновременно все альтернативные пути решения. При этом система переходила бы по кругу от одной альтернативы к другой, прослеживая каждую альтернативу на небольшую глубину, а затем переходя к следующей. Такая стратегия поиска вширь имеет одно преимущество – если решение существует, то оно обязательно будет найдено. Используемая в Прологе стратегия поиска вглубь может привести к «зацикливанию» и, следовательно, никогда не будут исследованы некоторые альтернативы. С другой стороны такая стратегия намного проще и требует меньших затрат памяти при реализации на вычислительных машинах с традиционной архитектурой.

И наконец, небольшое замечание о возможных различиях между процедурой сопоставления, используемой в Прологе, и процедурой унификации, используемой в методе резолюций. Большинство Пролог-систем допускают обращение с вопросами, подобными следующему:

равны(X,X).

?- равны(foo(Y),Y).

Это возможно по той причине, что в Прологе разрешается сопоставлять некоторый терм с его собственным подтермом. В этом примере foo(Y)сопоставляется с Y, который сам является частью этого терма. В результате этого Yстановится равным foo(Y)что в свою очередь равно foo(foo(Y))(учитывая значение Y), что равно foo(foo(foo(Y)))и так далее. Так что в результате Yобозначает некоторую бесконечную структуру. Заметим, что хотя Пролог-системы могут допускать использование подобных конструкций, большинство из них будут не в состоянии напечатать окончательный результат сопоставления. В соответствии с формальным определением унификации, подобного вида «бесконечные термы» никогда не должны появляться. Так что, Пролог выполняет эту процедуру неправильно в сравнении с тем, как это делается при доказательстве теорем методом резолюций. Для того чтобы сделать процедуру корректной, необходимо добавить проверку условия, заключающегося в том, что переменная не может быть конкретизирована некоторым значением, содержащим эту переменную. Такая проверка, проверка на вхождение,не представляла бы труда для ее реализации, но значительно замедляла бы выполнение программы на Прологе. Так как число программ, в которых может встретиться такая конструкция, невелико, то в большинстве реализаций такая проверка просто не делается.

10.7. Пролог и логическое программирование

В нескольких последних разделах было показано, как используются в Прологе идеи доказательства теорем. Можно видеть, что наши программы довольно похожи на гипотезы о проблемной области, а вопросы очень похожи на теоремы, которые нам хотелось бы доказать. Таким образом, программирование на Прологе имеет мало общего с процессом выдачи машине указаний о том, что и когда следует делать. Оно скорее состоит в передаче машине информации, которая предполагается истинной, и обращении к ней с вопросами о возможных следствиях из этой информации. Идея о том, что программирование должно выглядеть именно так, привлекательна и она привела многих специалистов к исследованию концепции логического программирования,то есть программирования на языке логики,как практической альтернативы обычному. Такой подход резко отличается от использования традиционных языков программирования подобных Фортрану или Лиспу, при программировании на которых необходимо как можно более подробно описать что и когда должна делать вычислительная машина. Преимущества логического программирования должны проявиться в том, что программы станут более понятными. Они не будут содержать затрудняющие понимание детали относительно того какрешать задачу, а скорее будут напоминать описание того, чтособой представляет результат решения. Кроме этого, если программа выглядит как описание (спецификация) того, что предполагается получить, то и относительно проще проверить (вручную или, возможно, используя какие-то автоматические средства), делает ли она в действительности то, что требуется. Подводя итог, можно сказать: преимущества языка логического программирования были бы следствием того, что программы обладают как декларативнойсемантикой, так и процедурной.Мы бы знали чтопрограмма вычисляет, а не какона это делает. Мы не будем здесь рассматривать логическое программирование вообще. Интересующемуся этим вопросом читателю рекомендуем обратиться к книге Ко-walski R. Logic for Problem Solving,North Holland, 1979.

Давайте рассмотрим Пролог как кандидата на место языка логического программирования и посмотрим, насколько хорошо он для этого подходит. Прежде всего, ясно, что некоторые программы на Прологе действительно представляют описание проблемной области на языке логики. Запись:

мать(Х,Y):- родитель(Х,Y), женщина(Y).

можно рассматривать как описание того, что значит быть матерью (это значит быть женщиной и быть одним из родителей). Это утверждение выражает высказывание, которое, как мы предполагаем, должно быть истинным, и, кроме того, указывает, как показать, что кто-то является матерью. Аналогично, утверждения;

присоединить([], X, X).

присоединить([А|В],С[А|D]):- присоединить (B,C,D).

говорят о том, что собой представляет добавление одного списка в начало другого списка. Если пустой список помещается в начало некоторого списка X, то результатом будет X. С другой стороны, если непустой список присоединяется в начало некоторого списка, тоголовой списка-результата будет голова присоединяемого списка. Кроме того, хвостом списка-результата будет список, получаемый в результате присоединения хвоста первого списка ко второму списку. Можно считать, что эти утверждения описывают отношение присоединить, так же как и (возможно) то, как в действительности присоединить один список к другому.

Это все верно лишь для некоторых программ на Прологе. А какое возможное логическое значение можно приписать утверждениям подобным следующим?

memberl(X, List):- var(List),!,fail.

memberl(X,[X|_]).

memberl(X,[_|List]):- memberl(X,List).

print(0):-!.

print(N):- write(N), N1 is N-1, print(N1).

noun(N):- name(N,Name1), append(Name2, [ll5],Namel), name(RootN,Name2), noun(RootN).

implies(Assum,Concl):-asserta(Assum), call(Concl), retract(Concl).

Эта проблема имеет место для всех «встроенных» предикатов, используемых в программах на Прологе. Предикат подобный Var(List)ничего не говорит о принадлежности элемента списку, а проверяет состояние переменной (является ли указанная переменная неконкретизированной), возникающее в процессе доказательства. Аналогично, «отсечение» говорит кое-что о доказательстве высказывания (выбор каких альтернатив можно игнорировать), а не о самом этом высказывании. Два указанных «предиката» можно рассматривать как способ выражения управляющей информации отом, как должно выполняться доказательство. Точно так же, предикаты подобные write(N)не имеют каких-либо интересных логических свойств, но заранее предполагают, что в ходе доказательства будет достигнуто определенное состояние ( Nконкретизируется) и начинают обмен информацией с программистом, сидящим за терминалом. Целевое утверждение name(N, Name1)говорит кое-что о внутренней структуре объекта, который в исчислении предикатов был бы неделимым символом. В Прологе можно преобразовывать символы в строки литер, структуры в списки и в утверждения. Эти операции нарушают замкнутость высказываний исчисления предикатов. В последнем примере, использование предиката assertaозначает, что правило, о котором идет речь, добавляет что-то к множеству аксиом. В логике каждое правило или факт сохраняет истинность независимо от того, существуют ли какие либо другие факты или правила. В данном случае мы имеем дело с правилом, которое грубо нарушает этот принцип. Кроме того, если мы используем это правило, то окажемся в ситуации, когда на разных этапах доказательства имеется различное множество аксиом. Наконец, то что в одном из правил предполагается использовать терм Conclв качестве целевого утверждения, означает, что допускается, чтобы переменная обозначала высказывание, встречающееся в некоторой аксиоме. Такая конструкция не относится к числу тех, которые могут быть выражены на языке исчисления предикатов, но напоминает возможности, которые могут быть представлены логикой более высокого порядка.

На приведенном примере можно видеть, что некоторые программы на Прологе, можно понять лишьв терминах, описывающих что и когда может произойти при выполнении программ и каким образом программы сообщают системе о том, что нужно делать. В качестве крайнего случая, можно привести программу для генатом представленную в гл.7. Вряд ли вообще может быть дана какая-либо декларативная интерпретация этой программы. Имеет ли тогда смысл рассматривать Пролог как язык логического программирования? Можем ли мы реально надеяться на какие-то преимущества логического программирования применительно к нашим программам на Прологе? На оба этих вопроса можно дать положительный ответ и основанием для этого служит то, что приняв соответствующий стиль программирования, мы все же можем получить некоторые преимущества благодаря связи Пролога с логикой. Ключевым моментом является использование разбиения программ на части, ограничивающие использование нелогических операций небольшим множеством утверждений. В качестве примера в гл. 4 было показано, как в некоторых случаях «отсечение» может быть заменено предикатом not.В результате таких замен, программу, содержавшую целый ряд «отсечений» можно свести к программе, в которой «отсечение» используется лишь однажды (в определении not).Использование предиката notдаже если он не совсем точно соответствует логическому '~' позволяет восстановить часть логической основы программы. Аналогично, ограничивая область применения предикатов assertaи retractопределениями небольшого числа предикатов (таких как генатоми найтивсе),можно добиться того, что в целом программа становится более понятной по сравнению с программой, в которой эти предикаты свободно используются где угодно.

Таким образом, с появлением Пролога конечная цель, состоящая в создании языка логического программирования, не была достигнута. Тем не менее, Пролог дал практическую систему программирования, обладающую в некоторой степени свойствами, которыми должен обладать язык логического программирования – ясностью и декларативностью. Между тем ведутся работы по разработке улучшенных версий Пролога, которые более близки к логике чем имеющиеся в настоящее время. К числу наиболее важных работ в этой области относятся работы по созданию практической системы программирования, в которой нет необходимости использовать «отсечение» и которая имеет вариант предиката notточно соответствующий логическому понятию отрицания.

ГЛАВА 11. ПРОГРАММНЫЕ ПРОЕКТЫ НА ПРОЛОГЕ

В этой главе рассматривается перечень программных проектов, которые вы могли бы попытаться осуществить для развития навыков программирования на Прологе. Некоторые из этих проектов довольно просты, зато другие вполне могут быть предложены в качестве «курсовой работы» в рамках учебного курса по Прологу. Более простые проекты следует использовать как дополнение к упражнениям, приведенным в предыдущих главах. В целом при перечислении проектов мы не придерживались какого-то определенного порядка, хотя те из них, что содержатся в разд. 11.2, в большей мере допускают расширения, содержат вызов честолюбию, но и требуют некоторой подготовки или знакомства с литературой по различным вопросам искусственного интеллекта и информатики. Небольшая часть проектов требует знаний из определенных разделов науки, поэтому если вы не специалист в области математической физики, то не отчаивайтесь, если не сможете написать программу дифференцирования трехмерных векторных полей.

Целая подборка Пролог-программ опубликована в отчете Coehlo H., Cotta J. С, Pereira L. M. How to solve it with Prolog,Laboratorio Nacional de Engenharia Civil, Lisbon, Portugal. В нем содержится свыше ста небольших примеров, задач и упражнений из таких областей как вывод умозаключений на основе базы данных, естественный язык, символьное решение уравнений, и т. д. Этот отчет по своему характеру не рассчитан на использование для обучения, поэтому приведенные в нем Пролог-программы снабжены лишь краткими пояснениями.

11.1. Простые проекты

1.Определить предикат линдля «линеаризации» списка путем построения нового списка, не содержащего списков в качестве элементов, но включающего все атомы исходного списка. Например, следующее целевое утверждение будет согласовано с базой данных:

?- лин([а,[b,с],[[d],[],е]], [a,b,c,d,e]).

Существует по меньшей мере шесть различных способов написания этой программы.

2.Составить программу для вычисления интервала (в днях) между двумя датами, заданными в формате День-Месяц, считая что обе они относятся к одному и тому же невисокосному году. Заметим, что '-' это просто инфиксная форма задания 2-х местного функтора. Например, следующее целевое утверждение будет согласованос базой данных:

интервал(3-март, 7-апрель, 35).

3.В главе 7 приведены сведения, достаточные для составления программ дифференцирования и упрощения арифметических выражений. Усовершенствуйте эти программы так, чтобы они могли обрабатывать выражения с тригонометрическими функциями и, если есть желание, с операциями дифференциальной геометрии, такими как div, grad и rot.

4.Написать программу, осуществляющую символическое отрицание выражения исчисления высказываний. Это выражение строится из атомов, одноместного функтора notи двухместных функторов and(и), or(или) и implies(импликация). Задать соответствующие описания операторов для этих функторов. Выражение, являющееся результатом отрицания, должно быть представлено в простейшей форме, когда notприменяется только к атомам. Например, отрицание выражения

р implies (q and not r)

должно выглядеть следующим образом: р and (not q or r)

5.Частотный словарь – это перечень слов, встречающихся в данном тексте, выписанный в алфавитном порядке с указанием числа вхождений каждого слова в тексте. Написать программу составления частотного словаря по списку слов, представленных в виде строк Пролога. Учтите, что строки – это списки кодов ASCII.

6.Написать программу, воспринимающую простые английские предложения, имеющие следующий формат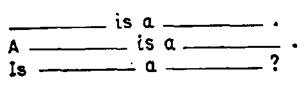

На основе ранее введенных предложений программа должна выдавать соответствующий ответ (yes (да), no (нет), ok (принято), unknown (неизвестно)). Например,

John is a man.

ok

A man is a person.

ok

Is John a person?

yes

Is Mary a person?

unknown

Каждое предложение должно транслироваться в утверждение Пролога, которое затем в зависимости от его характера, либо помещается в базу данных, либо выполняется как целевое. Так, результаты трансляции предложений приведенного выше примера выглядят следующим образом:

man(john).

person(X):- man(X).?- person (john).?- person(mary).

Если это окажется удобным, используйте правила грамматики. Головное утверждение дляуправления диалогом может иметь вид:

беседа:- repeat, read (Предложение), анализ(Предложение, Утверждение), ответ(Утверждение), Утверждение = stop.

7. Альфа-бета (±-І) алгоритм – это один из методов обхода дерева игры, который упоминается во многих книгах по искусственному интеллекту. Реализуйте альфа-бета алгоритм на Прологе.

8.Задача об N-ферзях также широко распространена в литературе по программированию. Реализовать программу нахождения всех способов размещения 4 ферзей на шахматной доске размером 4?4, причем так, чтобы ни один ферзь не угрожал другому. Один из возможных подходов состоит в создании генератора перестановок, который затем проверяет каждую перестановку, чтобы убедиться, что все ферзи размещены правильно.

9.Написать программу, которая переписывает выражение исчисления высказываний (см. задачу 4), заменяя все вхождения and, or, impliesи notединственной связкой nand. Определение связки nand задается следующим тождеством

(± nand І) a(±'І)

10.Один из способов представления целых положительных чисел состоит в том, чтобы представлять их в виде термов Пролога с использованием целого числа 0 и функтора Sс одним аргументом. Так, число 0 представляет само себя, 1 представляется как S(0), 2 как S(S(0))и т. д. (каждое число представляется в виде функтора S примененного к представлению числа, на единицу меньшего, чем данное). Написать определение стандартных арифметических операций: сложение, умножение и вычитание, использующих указанное представление чисел. Например, нужно определить предикат plusкоторый действует следующим образом:

?- plus(s(s(0)),s(s(s(0))),X)

X=s(s(s(s(s(0)))))

(2+3=5). Для вычитания нужно ввести соглашение о том, что делать, когда результат операции не является положительным целым числом. Определите также предикат «меньше чем». Какие аргументы нужно конкретизировать, чтобы ваши определения работали правильно? Что произойдет, если этого не сделать? Как это соотносится со стандартными арифметическими операциями Пролога? Попытайтесь определить более сложные арифметические операции, такие как деление нацело и извлечение квадратного корня.

11.2. Более сложные проекты

Может показаться, что некоторые проекты данного раздела невозможно выполнить до конца, однако все они были реализованы на Прологе. Некоторые из них просто являются усложнениями программ, которые рассматривались ранее, а другие – совершенно новые и требуют знакомства с литературой по искусственному интеллекту или по информатике.

1.Дана карта, которая описывает дороги, соединяющие города. Написать программу планирования поездки между двумя городами, которая выдает расписание предполагаемой поездки. Данные, описывающие карту, могут включать расстояния, состояние дороги, уклон дороги, возможность заправки топливом вдоль разных дорог.

2.В существующих Пролог-системах встроенные арифметические операции предусмотрены только для целых чисел. Разработайте пакет программ, поддерживающий арифметические операции над рациональными числами, представленными в виде целой и дробной частей или в виде мантиссы и порядка.

3.Написать процедуры обращения и умножения матриц.

4.Компиляцию с языка высокого уровня на язык низкого уровня можно представить себе как последовательное преобразование синтаксических деревьев. Написать такой компилятор сначала для компиляции арифметических выражений. Затем добавить управляющие структуры (типа if- then-else).Точное соблюдение синтаксиса ассемблера в данном случае не столь существенно. Например, арифметическое выражение х+1 может быть «упрощено» до ассемблерной операции inc x, где incопределена как одноместная операция. Проблема распределения регистров может быть отложена на потом за счет предположения, что объектный код предназначен для выполнения на машине с магазинной (стековой) памятью (безадресная машина),

5. Разработать представление для сложной настольной игры, такой как шахматы или го, и разобраться в том, как возможности Пролога в части сопоставления образцов могут быть использованы при реализации стратегий для этих игр.

6.Разработать формализм для описания набора аксиом, например, из теории групп, евклидовой геометрии, денотационной семантики, и исследовать проблему создания программы доказательства теорем для этих областей.

7. Интерпретатор утверждений Пролога может быть написан на самом Прологе. Напишите интерпретатор, реализующий иные семантики выполнения Пролога, такие как более гибкий порядок выполнения (вместо жесткого слева-направо), возможно, с использованием какого-нибудь «расписания» или планировщика.