Параллельные миры

Глэшоу попросили прокомментировать заявление Виттена о том, что струнная теория может занять доминирующее положение в физике на ближайшие полвека подобно тому, как квантовая механика лидировала на протяжении последних пятидесяти лет. Тот ответил, что струнная теория будет занимать такое же лидирующее положение, как и теория Калуцы — Клейна (которую он считает полным бредом) на протяжении последних пятидесяти лет, что совсем не соответствует действительности. Он старался не пускать в Гарвард ученых, работающих над струнной теорией. Но поскольку следующее поколение физиков переметнулось на сторону струнной теории, даже одинокий голос Нобелевского лауреата был вскоре заглушён. (С тех пор Гарвард пригласил на работу нескольких ученых, работающих в области струнной теории.)

Космическая музыка

      Эйнштейн однажды сказал, что если теория не представляет такой физической картины, которая понятна даже ребенку, то она, скорее всего, бесполезна. К счастью, за струнной теорией стоит четкая физическая картина — картина, основанная на музыке.
      Согласно струнной теории, если бы у нас был сверхмощный микроскоп и мы могли вглядеться в сердце электрона, то мы бы увидели вовсе не точечную частицу, а вибрирующую струну. (Струна чрезвычайно маленькая — около длины Планка, которая составляет Ю" 33см, — в миллиарды миллиардов раз меньше протона, а потому все субатомные частицы выглядят как точки.) Если бы мы задели эту струну, то характер вибрации изменился бы — электрон мог бы превратиться в нейтрино. Заденьте струну снова — и он, возможно, превратится в кварк. В сущности, если задеть струну достаточно сильно, то она могла бы превратиться в любую из известных субатомных частиц. Таким образом, струнная теория может легко объяснить, почему существует так много субатомных частиц. Они представляют собой не что иное, как «ноты», которые можно сыграть на суперструне. Для аналогии, на скрипичной струне ноты ля, си или до-диез не являются основными. Просто, играя на струне различным способом, мы можем получить все ноты музыкальной гаммы. Например, си-бемоль является не более основной, чем соль. Все они представляют собой лишь ноты, которые можно сыграть на скрипичной струне. Подобным образом, ни кварки, ни электроны не являются основными частицами — основой является сама струна. В сущности, все субчастицы Вселенной можно рассматривать в качестве различных вибраций струны. «Гармонией» струны являются законы физики.
      Струны могут взаимодействовать путем расщепления и воссоединения, создавая таким образом взаимодействия, которые мы наблюдаем в атомах между электронами и протонами. В общем, с помощью струнной теории мы можем воспроизвести все законы атомной и ядерной физики. «Мелодии», которые могут быть сыграны на струнах, соотносятся с законами химии. Всю Вселенную теперь можно рассматривать как необъятную струнную симфонию.
      Струнная теория не только дает объяснение частиц квантовой теории как музыкальных нот Вселенной, она также объясняет теорию относительности Эйнштейна: самая низкая вибрация струны, частица со спином «двойка» и нулевой массой, может интерпретироваться как гравитон — частица или квант гравитации. Если мы подсчитаем взаимодействия этих гравитонов, то в точности получим старую добрую теорию гравитации Эйнштейна в квантовом виде, Двигаясь, расщепляясь и изменяя форму, струна налагает огромные ограничения на пространство-время. При анализе этих ограничений мы опять-таки приходим к старой доброй общей теории относительности Эйнштейна. Таким образом, струнная теория четко объясняет теорию Эйнштейна без ненужных дополнительных усилий. Эдвард Виттен сказал, что если бы Эйнштейн не открыл теорию относительности, то его теория была бы открыта как побочный продукт струнной теории. В каком-то смысле, общая теория относительности является к ней бесплатным приложением.
      Прелесть струнной теории состоит в том, что ее можно уподобить музыке. Музыка дает нам метафору, с помощью которой можно понять природу Вселенной как на субатомном, так и на космическом уровне. Как когда-то написал великий скрипач Иегуди Менухин, «Музыка создает порядок из хаоса; ибо ритм придает единодушие разобщенности; мелодия придает связность разрозненности; а гармония придает совместимость несовместимому».
      Эйнштейн писал, что его поиски единой теории поля в конечном счете позволят ему «узреть замысел Божий». Если струнная теория верна, то мы увидим, что замысел Бога — это космическая музыка, резонирующая во всех десяти измерениях гиперпространства. Готфрид Лейбниц однажды сказал: «Музыка — это скрытые арифметические упражнения души, которая не ведает о том, что занимается вычислениями».
      Исторически связь между музыкой и наукой установилась в V веке до н. э., когда греки-пифагорейцы открыли законы гармонии и свели их к математике. Они обнаружили, что высота тона задетой струны лиры соотносится с ее длиной. Если длину струны лиры увеличивали вдвое, то тон становился на октаву ниже. Если длину струны уменьшали до двух третей, то тон менялся на квинту. Исходя из этих данных, законы музыкальной гармонии могли быть сведены к точным отношениям между числами. Неудивительно, что девизом пифагорейцев была следующая фраза: «Всё есть числа». Изначально они были так довольны полученным результатом, что попытались применить выведенные законы гармонии ко всей Вселенной. Однако все их усилия были напрасны, поскольку такая задача отличалась чрезвычайной сложностью. И все же, работая со струнной теорией, физики в каком-то смысле возвращаются к мечте пифагорейцев.
      Комментируя эту историческую связь, Джейми Джеймс однажды сказал: «Музыка и наука [когда-то] были настолько тесно связаны, что любого, кто предположил бы существование какого-либо коренного различия между ними, посчитали бы невеждой, [однако сегодня] любой, предположивший, что у них есть нечто общее, рискует показаться мещанином одной стороне и дилетантом — второй; и, что самое неприятное, обе группы сочтут его человеком, популяризирующим их идеи».

Проблемы в гиперпространстве

      Но если дополнительные измерения и вправду существуют в природе, а не только в чистейшей математике, то ученым, занимающимся струнной теорией, придется заняться той же проблемой, что неотступно преследовала Теодора Калуцу и Феликса Клейна в 1921 году, когда они сформулировали первую теорию дополнительных измерений: где же находятся эти измерения?
      Калуца, впрошломмалоизвестньгйматематик, написал Эйнштейну письмо, в котором предлагал переписать уравнения Эйнштейна применительно к пяти измерениям (одно измерение времени и четыре измерения пространства). С математической точки зрения это никакой проблемы не представляло, поскольку уравнения Эйнштейна могли быть легко переписаны для любого количества измерений. Но в письме содержалось поразительное замечание: если выделить четырехмерные части, содержащиеся в уравнениях, записанных для пяти измерений, то мы автоматически, будто по волшебству, получим теорию света Максвелла! Иными словами, если мы всего лишь добавим пятое измерение, то из уравнений Эйнштейна для гравитации получается теория электромагнитного взаимодействия Максвелла.
      Хотя мы не можем видеть само пятое измерение, на его поверхности образуется рябь, которая соответствует световым волнам! Это был приятный результат, поскольку на протяжении последних 150 лет целым поколениям физиков и инженеров приходилось заучивать сложные уравнения Максвелла. Сегодня эти сложные уравнения без всяких усилий выводятся как простейшие вибрации, которые можно обнаружить в пятом измерении.
      Представьте себе рыб, плавающих в мелком пруду прямо под листьями кувшинок. Они считают, что их «вселенная» двумерна. Наш трехмерный мир может находиться за пределами их знания. Но существует способ, с помощью которого они могут уловить присутствие третьего измерения. Если идет дождь, то они отчетливо видят тень волн ряби, расходящихся по поверхности пруда. Подобным образом и мы не можем видеть пятого измерения, но рябь в пятом измерении предстает перед нами как свет.
      (Теория Калуцы была прекрасным и глубоким открытием, касающимся симметрии. Позднее было замечено, что если мы добавим еще больше измерений к прежней теории Эйнштейна и заставим их вибрировать, то тогда эти вибрации дополнительных измерений будут представлять W- и Z-бозоны и глюоны, обнаруженные в сильном и слабом ядерном взаимодействии! Если путь, предложенный Калуцой, был верным, то Вселенная была явно намного проще, чем изначально предполагали ученые. Просто, вибрируя все «выше», измерения представляли многие взаимодействия, правящие миром.)
      Хотя Эйнштейна потряс этот результат, он был слишком хорош, чтобы быть правдой. Спустя годы были обнаружены проблемы, которые сделали идею Калуцы бесполезной. Во-первых, его теория была усеяна противоречиями и аномалиями, что весьма типично для теорий квантовой гравитации. Во-вторых, тревожил гораздо более важный физический вопрос: почему же мы не видим пятого измерения? Когда мы пускаем стрелы в небо, мы не видим, чтобы они исчезали в другом измерении. Возьмем дым, который медленно проникает во все области пространства. Поскольку никогда не было замечено, чтобы дым исчезал в высшем измерении, физики поняли, что дополнительные измерения, если они вообще существуют, должны быть меньше атома. За последнее столетие идеей о дополнительных измерениях развлекались мистики и математики; что же касается фи-
      зиков, то они с пренебрежением относились к этой идее, поскольку никто и никогда не видел, чтобы предметы пропадали в пятом измерении.
      Для спасения теории физикам пришлось предположить, что эти дополнительные измерения настолько малы, что их нельзя наблюдать в природе. Поскольку наш мир четырехмерен, это предполагало, что пятое измерение должно быть свернуто в крошечный шарик размером меньше атома — слишком маленький, чтобы его можно было наблюдать в ходе эксперимента.
      Струнной теории приходится сталкиваться с той же проблемой. Мы должны свернуть все эти нежелательные дополнительные измерения в крошечный шарик (этот процесс называется компактифи-кацией). Согласно струнной теории, изначально Вселенная была десятимерной, а все взаимодействия в ней были объединены струной. Однако десятимерное гиперпространство было неустойчивым, и шесть из десяти измерений начали сворачиваться в крошечный шарик, а остальные четыре расширились в Большом Взрыве. Причиной, по которой мы не видим эти другие измерения, является то, что они намного меньше атома, а потому ничто не может в них проникнуть. (Например, садовый шланг и соломинка издалека кажутся одномерными объектами, основной характеристикой которых является их длина. Но если рассмотреть их поближе, то мы обнаружим, что они, в сущности, являются двумерными поверхностями или цилиндрами, но второе измерение свернулось таким образом, что мы его не видим.)

Почему струны?

      Хотя все предыдущие попытки построить единую теорию поля с треском провалились, струнная теория до сих пор выдержала все испытания. В сущности, ей нет равных. Существуют две причины, по которым струнная теория преуспела там, где все остальные теории потерпели поражение.
      Во-первых, будучи основанной на протяженном предмете (струне), струнная теория избегает многих отклонений, связанных с точечными частицами. Как заметил Ньютон, гравитационное взаимодействие, окружающее точечную частицу, при приближении к ней становится бесконечным. (В знаменитом законе обратных квадратов Ньютона гравитационное взаимодействие увеличивается пропорционально зависимости 1/г 2, так что оно стремится к бесконечности, когда мы приближаемся к точечной частице; то есть когда г стремится к нулю, гравитационное взаимодействие возрастает и стремится к 1/0, что представляет собой бесконечность.)
      Даже в квантовой теории эта сила остается бесконечной, если мы приблизимся к квантовой точечной частице. За многие десятилетия Фейнман и другие ученые создали ряд хитрых правил, с помощью которых эти и многие другие противоречия можно было замести под ковер. Но для того, чтобы исключить все бесконечности в квантовой теории гравитации, недостаточно даже мешка ухищрений, собранного Фейнманом. Проблема в том, что точечные частицы бесконечно малы, а это означает, что их силы и энергии потенциально бесконечны.
      Но при внимательном рассмотрении струнной теории мы увидим, что есть два способа, при помощи которых мы можем избавиться от этих противоречий. Первый способ исходит из топологии струн, а второй из-за своей симметрии называется суперсимметрией.
      Топология струнной теории носит совершенно другой характер, чем топология точечных частиц, а отсюда различны и возникающие противоречия. (Грубо говоря, поскольку струна обладает конечной длиной, это означает, что силы не стремятся к бесконечности при приближении к струне. Рядом со струной силы возрастают пропорционально зависимости 1 /L 2, где L — это длина струны, соизмеримая с длинной Планка, порядка 10" 33см. Эта длина L позволяет отсечь все противоречия.) Поскольку струна не является точечной частицей, обладая определенным размером, можно показать, что противоречия «размазаны» вдоль всей струны, и отсюда все физические величины становятся конечными.
      Хотя интуитивно кажется совершенно очевидным, что все противоречия струнной теории «размазаны» и потому конечны, точное математическое выражение этого факта довольно сложно и представлено «эллиптической модулярной функцией», одной из самых странных функций математики. Ее история настолько захватывающа, что ей даже довелось играть ключевую роль в одном из голливудских фильмов. «Умница Уилл Хантинг» — это история о неотесанном пареньке из рабочей семьи с окраин Кембриджа (его играл Мэтт Дэймон), который демонстрировал потрясающие способности к математике.
      В сущности, фильм «Умница Уилл Хантинг» основан на жизни Сринивазы Рамануджана, величайшего математического гения двадцатого столетия. Он вырос в бедности и изоляции от основных научных достижений возле Мадраса в Индии на рубеже ХГХ и XX веков. Поскольку юноша жил в условиях оторванности от научного мира, ему пришлось до многого доходить самому, основываясь на европейской математике ХГХ века. Его карьера была подобна взрыву сверхновой, мимолетно осветившей небеса его математической гениальностью. Его смерть была трагична: он умер от туберкулеза в 1920 году в возрасте 37 лет. Подобно Мэтту Дэймону из фильма «Умница Уилл Хантинг», Рамануджан грезил математическими уравнениями, в данном случае эллиптической модулярной функцией: написанная для двадцати четырех измерений, она обладает причудливыми, но красивыми математическими свойствами. Математики и по сей день пытаются расшифровать «утерянные записи Рамануджана», обнаруженные после его смерти. Оглядываясь на работу Рамануджана, мы видим, что ее можно обобщить и свести к восьми измерениям, которые напрямую применимы к струнной теории. Физики добавляют еще два измерения для построения физической теории. (Например, создание поляризованных солнцезащитных очков основано на том факте, что свет обладает двумя физическими поляризациями: он может вибрировать влево-вправо или вверх-вниз. Но математическая формулировка света в уравнениях Максвелла представлена четырьмя компонентами. Две из этих четырех вибраций, в сущности, лишние.) Если мы добавим еще два измерения к функциям Рамануджана, то «волшебными числами» математики становятся 10 и 26, которые являются «волшебными числами» и в струнной теории. Таким образом выходит, что в каком-то смысле Рамануджан занимался струнной теорией еще до Первой мировой войны!
      Сказочные свойства этих эллиптических модулярных функций объясняют, почему теория должна существовать в десяти измерениях. Только в таком количестве измерений будто по волшебству исчезает большая часть противоречий, наводняющих все остальные теории. Но сама по себе топология струн не обладает достаточной «властью», чтобы исключить все эти противоречия. Остальные противоречия струнной теории устраняются при помощи второй ее характеристики — суперсимметрии.

Суперсимметрия

       Вструне заключены некоторые величайшие симметрии, известные науке. Обсуждая инфляционное расширение Вселенной и Стандартную модель в главе 4, мы видели, что симметрия предоставляет нам прекрасный способ организации субатомных частиц в приятные и изящные модели. Три типа кварков могут быть организованы согласно симметрии SU(3), которая позволяет кваркам меняться между собой местами. В теории ТВО считается, что пять типов кварков и лептонов могли бы быть организованы согласно симметрии SU(5).
      В струнной теории благодаря этим симметриям уходят оставшиеся противоречия и аномалии. Поскольку симметрии представляют собой одно из наиболее прекрасных и мощных средств, имеющихся в нашем распоряжении, то вполне можно было бы ожидать, что теория Вселенной должна обладать наиболее изящной и мощной симметрией, какая только известна науке. Логичной была бы симметрия, которая позволила бы менять местами не только кварки, но и все частицы, которые можно встретить в природе. Это значит, что все уравнения должны оставаться неизменными, если мы изменим положение всех частиц относительно друг друга. Такой подход в точности описывает симметрия суперструны, называемая суперсимметрией. Это единственный вид симметрии, который позволяет менять местами все известные физикам субатомные частицы. Такая симметрия является идеальным претендентом на место симметрии, которая организует все частицы Вселенной в единое, изящное целое.
      Если рассматривать все взаимодействия и частицы Вселенной, то мы увидим, что, в зависимости от спина, все они делятся на две категории — «фермионы» и «бозоны». Они ведут себя как волчки, которые могут вращаться с различными скоростями. К примеру, спин фотона, частицы, являющейся носителем электромагнитного взаимодействия, равен единице. Гравитон, частица гравитации, имеет спин, равный двум. Все частицы, обладающие спином, выражающимся целым числом, называют бозонами. Подобным образом, частицы вещества описываются при помощи субатомных частиц, спин которых выражается полуцелыми значениями — 1/2, 3/2, 5/2 и так далее. (Частицы с полуцелыми значениями спина называют фермионами. К ним относятся электрон, нейтрино и кварки.) Таким образом, супер симметрия изящно выражает дуализм, возникающий между бозонами и фермионами, между взаимодействиями и веществом.
      В теории, основанной на суперсимметрии, у каждой частицы есть напарник: каждый фермион находится в паре с бозоном. Хотя мы никогда не наблюдали этих суперсимметричных партнеров в природе, физики окрестили партнера электрона «сэлектроном», который обладает спином, равным нулю. (Физики добавляют «с» для описания суперпартнера какой-либо частицы.) Слабые взаимодействия включают в себя частицы, называемые лептонами: их суперпартнеров называют слептонами. Подобным образом и у кварка может быть партнер с нулевым спином, который называется скварком. В целом, партнеры всех известных частиц (кварков, лептонов, гравитонов, фотонов и так далее) называются счастицами, или суперчастицами. Эти счастицы нам еще только предстоит обнаружить при помощи ускорителей частиц (возможно, наше оборудование еще не достаточно мощное, чтобы мы могли получить эти частицы).
      Но поскольку все субатомные частицы являются либо фермионами, либо бозонами, то в теории суперсимметрии содержится потенциал объединения всех известных субатомных частиц одной простой симметрией. Теперь у нас есть достаточно обширная симметрия, которая включит в себя целую Вселенную.
      Представьте себе снежинку. Пусть каждый из шести ее кончиков представляет субатомную частицу, при этом бозоны расположены через один и за каждым бозоном следует фермион. Красота этой «суперснежинки» состоит в том, что при вращении она остается неизменной. Таким образом, эта суперснежинка объединяет все частицы и их счастицы. Поэтому, если мы попытаемся построить гипотетическую единую теорию поля, в которой есть лишь шесть частиц, то вполне естественно, что лучшим претендентом на эту роль явится супер снежинка.
      Суперсимметрия помогает устранить все оставшиеся бесконечности, которые для других теорий оказывались роковыми. Ранее мы уже упоминали о том, что большая часть отклонений устраняется благодаря топологии струны — то есть, поскольку струна обладает конечной длиной, силы не стремятся к бесконечности при приближении к самой струне. При рассмотрении оставшихся отклонений мы видим, что они делятся на два типа, исходя из взаимодействий бозонов и фермионов. Однако два типа действий, производимых этими частицами, всегда имеют противоположный знак, а потому действие фермиона всегда компенсируется действием бозона! Иными словами, поскольку действия бозона и фермиона всегда имеют противоположный знак, то оставшиеся в теории противоречия взаимоустраня-юхся. Таким образом, суперсимметрия — это не просто витринное крашение. Это не только симметрия, которая дарит эстетическое удовольствие, — это неотъемлемый элемент для устранении отклонений в струнной теории.
      Вспомним аналогию конструирования гладкой ракеты, в которой вибрации могут возрасти настолько, что в конечном счете у нее оторвет крылья. Одним из решений этой проблемы является применение силы симметрии для корректировки конструкции крыльев — таким образом, чтобы вибрации, возникающие в одном крыле, компенсировали вибрации в другом. Когда одно крыло вибрирует по часовой стрелке, второе крыло должно вибрировать против часовой стрелки, что уравновешивает вибрацию первого крыла. Таким образом, симметрия ракеты — казалось бы, всего лишь искусственный художественный элемент — имеет ключевое значение в устранении и балансировке нагрузок на крылья ракеты. Подобным образом и суперсимметрия устраняет отклонения благодаря тому, что бозонная и фермионная части полностью компенсируют действие друг друга.
      (Суперсимметрия также решает ряд сложных технических проблем, фатальных для ТВО. Для устранения математических противоречий в ТВО необходима суперсимметрия.)
      Хотя суперсимметрия несет в себе очень мощную идею, в настоящее время не существует никаких экспериментальных доказательств ее истинности. Это может объясняться тем, что суперпартнеры известных нам электронов и протонов могут попросту обладать слишком большой массой, чтобы мы могли получить их на современных ускорителях частиц. Однако существует очень даже привлекательное доказательство существования суперсимметрии. Мы знаем, что три квантовых взаимодействия различны по силе. В сущности, при малых энергиях сильное взаимодействие в 30 раз сильнее слабого взаимодействия и в сотню раз сильнее электромагнетизма. Однако так было не всегда. Мы предполагаем, что в момент Большого Взрыва все три взаимодействия были равны по силе. Возвращаясь назад во времени, физики могут вычислить силы трех взаимодействий в начале времен. Анализируя Стандартную модель, физики обнаружили, что силы трех взаимодействий, видимо, стремились к равенству в момент Большого Взрыва. Но они не в точности равняются друг другу. Зато когда мы добавляем суперсимметрию, то все три взаимодействия в точности совпадают друг с другом по силе, а это именно то, что предполагается в единой теории поля. И хотя этот факт не является прямым доказательством в пользу суперсимметрии, он все же показывает, что суперсимметрия, по крайней мере, вписывается в рамки известной физики.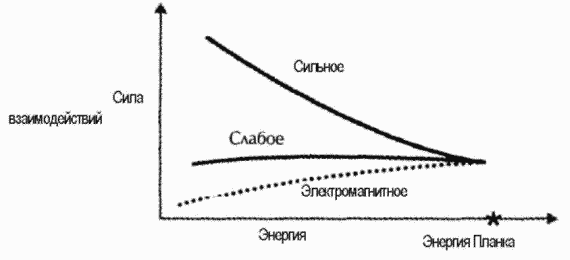

       Силы слабого, сильного и электромагнитного взаимодействия не являются эквивалентными по силе в современном нам мире. Однако при энергиях Большого Взрыва силы этих взаимодействий должны полностью совпадать. Это совпадение имеет место при применении теории суперсимметрии. Таким образом, суперсимметрия может оказаться ключевым элементом для любой единой теории поля.

Вывод Стандартной модели

      Хотя в суперструнах в принципе не существует настраиваемых параметров, струнная теория может предложить решения, удивительно близкие к Стандартной модели с ее пестрым собранием причудливых субатомных частиц и девятнадцатью «гуляющими» параметрами (такими, как массы частиц и их силы взаимодействия). Кроме того, в Стандартной модели существуют три идентичные (и лишние) копии всех кварков и лептонов, что кажется совершенно бесполезным. Ксчастью, струнная теория может без напряжения вывести многие качественные характеристики Стандартной модели. В 1984 году Филип Канделас из Техасского университета, Гари Хоровиц и Эндрю Стромингер из Калифорнийского университета в Санта-Барбаре, а также Эдвард Виттен показали, что если свернуть шесть из десяти измерений струнной теории и при этом сохранить суперсимметрию в оставшихся четырех измерениях, то крошечный шестимерный мир можно описать при помощи того, что математики называют многообразием Калаби-Яу. Взяв несколько примеров из пространств Калаби-Яу, они показали, что симметрию струны можно свести к теории, которая удивительно близка к Стандартной модели.
      Таким образом, струнная теория дает нам простой ответ на то, почему в Стандартной модели существуют три излишних поколения. В струнной теории количество поколений или излишеств в кварковой модели связано с количеством «отверстий», которые мы обнаруживаем в многообразии Калаби-Яу. (Например, возьмем пончик, велосипедную камеру и кофейную чашку — все они являются поверхностями с одним отверстием. В оправе для очков два отверстия. В пространствах Калаби-Яу может существовать произвольное количество отверстий.) Таким образом, просто выбрав многообразие Калаби-Яу, в котором есть определенное количество отверстий, мы можем построить Стандартную модель с различными поколениями лишних кварков. (Поскольку мы никогда не видим пространства Калаби-Яу из-за того, что оно очень маленькое, мы также никогда не видим и того факта, что это пространство, подобно пончику, пронизано отверстиями.) В течение многих лет группы физиков пытались каталогизировать все возможные пространства
      Калаби-Яу, осознавая тот факт, что топология этого шестимерного пространства определяет кварки и лептоны нашей четырехмерной Вселенной.

М-теория

      Всеобщее увлечение струнной теорией, имевшее место в 1984 году, не могло продолжаться вечно. К середине 1990-х годов триумфальное шествие теории суперструн начало сбавлять темп. Легкие проблемы, которые решала эта теория, были уже все выбраны, и остались только сложные. Одной из таких проблем было открытие миллиардов решений струнных уравнений. При компактификации, или свертывании пространства-времени различным образом, струнные решения можно было записывать в любом измерении, а не только в четырех. Каждое из миллиардов струнных решений соответствовало математически непротиворечивой Вселенной.
      Физики внезапно начали тонуть в струнных решениях. Что примечательно, многие из этих решений выглядели очень похожими на нашу Вселенную. Выбрав подходящее пространство Калаби-Яу, можно было относительно несложно воспроизвести многие из существенных черт Стандартной модели с ее причудливым скоплением кварков и лептонов, даже с ее любопытным набором поколений. Однако чрезвычайно сложной задачей (неразрешенной и по сей день) было обнаружить первоначальную Стандартную модель с определенными значениями ее девятнадцати параметров и тремя излишними поколениями. (Ошеломляющее количество струнных решений, вообще-то, приветствовалось физиками, которые поддерживали идею Мультивселенной, поскольку каждое решение представляет полностью непротиворечивую параллельную вселенную. Однако удручал тот факт, что физики испытывали сложности в обнаружении именно нашей Вселенной в этих джунглях вселенных.)
      Одной из причин сложности этого предприятия является то, что в конечном счете суперсимметрию все же нужно разрушить, поскольку в нашем мире низких энергий мы этой симметрии не наблюдаем. К примеру, мы не видим в природе сэлектрона — суперпартнера электрона. Если оставить супер симметрию нетронутой, то масса каждой частицы должна быть эквивалентна массе ее суперчастицы.
      Физики считают, что суперсимметрия была нарушена, и результатом этого является то, что массы суперчастиц огромны и, таким образом, суперчастицы находятся вне пределов досягаемости современных ускорителей частиц. Но в настоящее время никто еще не предложил правдоподобного механизма для нарушения суперсимметрии.
      Дэвид Гросс из Института теоретической физики Кавли в Санта-Барбаре заметил, что существуют миллионы и миллионы решений струнной теории в трех пространственных измерениях, что несколько смущает, поскольку нет способа, с помощью которого мы можем выбирать среди них.
      Были и другие вопросы, в частности то, что существовало пять непротиворечивых струнных теорий. Было сложно представить, что Вселенная могла позволять существование пяти отдельных единых теорий поля. Эйнштейн считал, что у Бога не было выбора при создании Вселенной, так почему же Бог должен был создать целых пять вселенных?
      Первоначальная теория, основанная на формуле Венециано, описывает то, что называют суперструнной теорией типа I. В теории типа I фигурируют как открытые струны (с двумя концами), так и замкнутые струны (свернутые в окружность). Эту теорию очень активно разрабатывали в начале 1970-х годов. (Используя струнную теорию поля, Киккаве и мне удалось каталогизировать полный набор струнных взаимодействий типа I. Мы показали, что струны типа I требуют пять взаимодействий. Что касается замкнутых струн, то мы показали, что там необходим только один член взаимодействия.)
      Мы с Киккавой также показали, что возможно построение полностью непротиворечивых теорий только с замкнутыми струнами (то есть похожими на петлю). Сегодня такие теории называются струнными теориями типа II, где струны взаимодействуют путем расщепления на две струны меньшего размера (этот процесс напоминает митоз в клетках).
      Наиболее реалистичной струнной теорией считается теория гете-ротических струн, сформулированная группой ученых из Принстона (в том числе Дэвидом Гроссом, Эмилем Мартинеком, Райаном Ромом и Джеффри Харви). Теория гетеротических струн может содержать в себе группы симметрии, называемые Е(8)хЕ(8) или 0(32), которые достаточно велики, чтобы включить в себя теории'ТВО.

       Взаимодействие струн типа I может проходить в пяти различных вариантах. В ходе этих взаимодействий струны могут разрываться, соединяться и расщепляться. Для замкнутых струн характерно лишь последнее взаимодействие, которое напоминает процесс митоза в клетках.