1. ПРАВИЛЬНОЕ РАССУЖДЕНИЕ

Слово «логика» употребляется довольно часто, но в разных значениях.

Нередко говорят о логике событий, логике характера и т.п. В этих случаях имеется в виду определённая последовательность и взаимозависимость событий или поступков, наличие в них некоторой общей линии.

Слово «логика» употребляется также в связи с процессами мышления. Так, мы говорим о логичном и нелогичном мышлении, имея в виду присутствие или отсутствие таких его свойств, как последовательность, доказательность и т.п.

В третьем смысле «логика» является именем особой науки о мышлении, называемой также формальной логикой.

Трудно найти более многогранное и сложное явление, чем человеческое мышление. Оно изучается многими науками, и логика — одна из них. Её предмет — логические законы и логические операции мышления. Принципы, устанавливаемые логикой, необходимы, как и все научные законы. Мы можем не осознавать их, но вынуждены следовать им.

Формальная логика — наука о законах и операциях правильного мышления.

Основной задачей логики является отделение правильных способов рассуждения (выводов, умозаключений) от неправильных.

Правильные выводы называются также обоснованными, последовательными или логичными.

Рассуждение представляет собой определённую, внутренне обусловленную связь утверждений. От нашей воли зависит, на чем остановить свою мысль. В любое время мы можем прервать начатое рассуждение и перейти к другой теме. Но если мы решим провести его до конца, то сразу же попадём в сети необходимости, стоящей выше нашей воли и желаний. Согласившись с одними утверждениями, мы вынуждены принять и те, что из них следуют, независимо от того, нравятся они нам или нет, способствуют нашим целям или, напротив, препятствуют им. Допустив одно, мы тем самым автоматически лишаем себя возможности утверждать другое, несовместимое с уже допущенным.

Если мы убеждены, что все жидкости упруги, мы должны признать также, что вещества, не являющиеся упругими, не относятся к жидкостям. Убедив себя, что каждое водоплавающее существо обязательно дышит жабрами, мы исключаем из разряда водоплавающих дышащих лёгкими — китов и дельфинов.

В чем источник этой логической необходимости? Что именно следует считать несовместимым с принятыми уже утверждениями и что должно приниматься вместе с ними? Из размышления над этими вопросами и выросла особая наука о мышлении — логика. Отвечая на вопрос «что из чего следует?», она отделяет правильные способы рассуждения от неправильных и систематизирует первые.

Правильным является следующий вывод, использовавшийся в качестве стандартного примера ещё в Древней Греции:

Все люди смертны; Сократ — человек; следовательно, Сократ смертен.

Первые два высказывания — это посылки вывода, третье — его заключение.

Правильным будет, очевидно, и такое рассуждение:

Всякий металл электропроводен; натрий — металл; значит, натрий электропроводен.

Сразу же можно заметить сходство данных двух выводов, но не в содержании входящих в них утверждений, а в характере связи этих утверждений между собою. Можно даже почувствовать, что с точки зрения правильности эти выводы совершенно идентичны: если правильным является один из них, то таким же будет и другой, и притом в силу тех же самых оснований.

Ещё один пример правильного вывода, связанного со знаменитым опытом Фуко:

Если Земля вращается вокруг своей оси, маятники, качающиеся на её поверхности, постепенно изменяют плоскость своих колебаний; Земля вращается вокруг своей оси; значит, маятники на её поверхности постепенно изменяют плоскость своих колебаний.

Как протекает это рассуждение о Земле и маятниках? Сначала устанавливается условная связь между вращением Земли и изменением плоскости колебания маятников. Затем констатируется, что Земля действительно вращается. Из этого выводится, что маятники в самом деле постепенно изменяют плоскость своих колебаний. Это заключение вытекает с какой-то принудительной силой. Оно как бы навязывается всем, кто принял посылки рассуждения. Именно поэтому можно было бы сказать также, что маятники должны изменять плоскость своих колебаний, с необходимостью делают это.

Схема данного рассуждения проста: если есть первое, то есть второе; имеет место первое; значит, есть и второе.

Принципиально важным является то, что, о чем бы мы ни рассуждали по такой схеме — о Земле и маятниках, о человеке или химических элементах, о мифах или богах, рассуждение останется правильным.

Чтобы убедиться в этом, достаточно подставить в схему вместо слов «первое» и «второе» два утверждения с любым конкретным содержанием.

Изменим несколько данную схему и будем рассуждать так: если есть первое, то имеется второе; имеет место второе; значит, есть и первое.

Например:

Если идёт дождь, земля мокрая; земля мокрая; следовательно, идёт дождь.

Этот вывод, очевидно, неправилен. Верно, что всякий раз, когда идёт дождь, земля мокрая. Но из этого условного утверждения и того факта, что земля мокрая, вовсе не вытекает, что идёт дождь. Земля может оказаться мокрой и без дождя, её можно намочить, скажем, из шланга, она может быть мокрой после таяния снега и т.д.

Ещё один пример рассуждения по последней схеме подтвердит, что она способна приводить к ложным заключениям:

Если у человека повышенная температура — он болен; человек болен; значит, у него повышенная температура.

Однако такое заключение не вытекает с необходимостью: люди с повышенной температурой действительно больны, но далеко не у всех больных такая температура.

Отличительная особенность правильного вывода заключается в том, что от истинных посылок он всегда ведёт к истинному заключению.

Этим объясняется тот огромный интерес, который логика проявляет к правильным выводам. Они позволяют из уже имеющегося знания получать новое знание, и притом с помощью «чистого» рассуждения, без всякого обращения к опыту, интуиции и т.п. Правильное рассуждение как бы разворачивает и конкретизирует наши знания. Оно даёт стопроцентную гарантию успеха, а не просто обеспечивает ту или иную — быть может, и высокую — вероятность истинного заключения.

Если посылки, или хотя бы одна из них, являются ложными, правильное рассуждение может давать в итоге как истину, так и ложь. Неправильные рассуждения могут от истинных посылок вести как к истинным, так и к ложным заключениям. Никакой определённости здесь нет. С логической необходимостью заключение вытекает только в случае правильных, обоснованных выводов.

Логика занимается, конечно, не только связями утверждений в правильных выводах, но и другими проблемами. В числе последних — смысл и значение выражений языка, различные отношения между понятиями, определение понятий, вероятностные и статистические рассуждения, софизмы и парадоксы и др. Но главная и доминирующая тема формальной логики — это, несомненно, анализ правильности рассуждения, исследование «принудительной силы речей», как говорил основатель этой науки — древнегреческий философ и логик Аристотель.

2. ЛОГИЧЕСКАЯ ФОРМА

Формальная логика, как уже говорилось, отделяет правильные способы рассуждения от неправильных и систематизирует первые.

Своеобразие формальной логики связано прежде всего с её основным принципом, в соответствии с которым правильность рассуждения зависит только от его логической формы.

Самым общим образом форму рассуждения можно определить как способ связи входящих в это рассуждение содержательных частей.

Основной принцип формальной логики предполагает — и это следует специально подчеркнуть, что каждое наше рассуждение, каждая мысль, выраженная в языке, имеет не только определённое содержание, но и определённую форму. Предполагается также, что содержание и форма отличаются друг от друга и могут быть разделены. Содержание мысли не оказывает никакого влияния на правильность рассуждений, и поэтому от него следует отвлечься. Для оценки правильности мысли существенной является лишь её форма. Её необходимо выделить в чистом виде, чтобы затем на основе такой «бессодержательной» формы решить вопрос о правильности рассматриваемого рассуждения.

Как известно, все предметы, явления и процессы имеют как содержание, так и форму. Наши мысли не являются исключением из этого общего правила. То, что они обладают определённым, меняющимся от одной мысли к другой содержанием, известно каждому. Но мысли имеют также форму, что обычно ускользает от внимания.

Смысл понятия логической формы лучше всего раскрыть на примерах.

Сравним два высказывания:

«Все вороны — птицы»,

»Все шахматисты — гроссмейстеры».

По содержанию они совершенно различны, к тому же первое является истинным, а второе ложным. И тем не менее сходство их несомненно. Это сходство, а точнее говоря, тождество, в их строении, форме. Чтобы выявить такое сходство, нужно отвлечься от содержания высказываний, а значит и от обусловленных им различий. Оставим поэтому в стороне ворон и шахматистов, птиц и гроссмейстеров. Заменим все содержательные компоненты высказываний латинскими буквами, скажем S и Р, не несущими никакого содержания. В итоге получим в обоих случаях одно и то же:

«Все S есть Р ».

Это и есть форма рассматриваемых высказываний. Она получена в результате отвлечения от конкретного их содержания. Но сама эта форма имеет все-таки некоторое содержание. Из неё мы узнаем, что у всякого предмета, обозначаемого буквой S, есть признак, обозначаемый буквой Р. Это не особенно богатое, но все-таки содержание, «формальное содержание».

Этот простой пример хорошо показывает одну из особенностей подхода формальной логики к анализу рассуждений — его высокую абстрактность.

В самом деле, все началось с очевидной мысли, что утверждения о воронах, которые являются птицами, и о шахматистах, сплошь являющихся гроссмейстерами, совершенно различны. И если бы не цели логического анализа, на этом различии мы и остановились бы, не увидев ничего общего между высказываниями «Все вороны — птицы» и «Все шахматисты — гроссмейстеры».

Отвлечение от содержания и выявление формы привело нас, однако, к прямо противоположному мнению: рассматриваемые высказывания имеют одну и ту же логическую форму и, следовательно, они полностью совпадают. Начав с мысли о полном различии высказываний, мы пришли к выводу об абсолютной их тождественности.

Рассмотрим далее два более сложных высказывания:

«Если число делится на 2, то оно чётное»,

»Если сейчас ночь, то сейчас темно».

Для выявления логической формы этих высказываний подставим вместо их содержательных компонентов слова «первое» и «второе», не несущие конкретного содержания. В результате получим, что оба эти высказывания имеют одну и ту же логическую форму:

«Если первое, то второе», т.е. каждое из них устанавливает условную связь, выражаемую словами «если, то», между двумя ситуациями, обозначаемыми словами «первое» и «второе». Если вместо последних слов использовать буквенные переменные, скажем, А и В, получим:

«Если А, то В ».

Это и есть логическая форма данных сложных высказываний.

Легко понять, что такое пространственная форма. Скажем, форма здания характеризует не то, из каких элементов оно сложено, а только то, как эти элементы связаны друг с другом. Здание одной и той же формы может быть и кирпичным, и железобетонным.

Достаточно просты также многие непространственные представления о форме. Говорят, например, о форме классического романа, предполагающего постепенную завязку действия, кульминацию и, наконец, развязку. Все такие романы, независимо о их содержания, сходны в своей форме, способе связи содержательных частей.

В сущности, не намного более сложным для понимания является и понятие логической формы. Наши мысли слагаются из некоторых содержательных частей, как здание из кирпичей, блоков, панелей и т.п. Эти «кирпичики» мысли определённым образом связаны друг с другом. Способ их связи и представляет собой форму мысли.

Для выявления формы надо отвлечься от содержания мысли, заменить содержательные её части какими-нибудь пробелами или буквами. Останется только связь этих частей. В обычном языке она выражается словами: «все … есть …», «некоторые … есть…», «если…, то…», «… и …», «… или …», «неверно, что …» и т.п.

3. ДЕДУКЦИЯ И ИНДУКЦИЯ

Умозаключение — это логическая операция, в результате которой из одного или нескольких принятых утверждений (посылок) получается новое утверждение — заключение (следствие).

В зависимости от того, существует ли между посылками и заключением связь логического следования, можно выделить два вида умозаключений.

В дедуктивном умозаключении эта связь опирается на логический закон, в силу чего заключение с логической необходимостью вытекает из принятых посылок. Как уже отмечалось, отличительная особенность такого умозаключения в том, что оно от истинных посылок всегда ведёт к истинному заключению.

К дедуктивным относятся, например, такие умозаключения:

Если данное число делится на 6, то оно делится на 3.

Данное число делится на 6.

Данное число делится на 3.

Если гелий металл, он электропроводен.

Гелий не электропроводен.

Гелий не металл.

Черта, отделяющая посылки от заключения, заменяет слово «следовательно».

В индуктивном умозаключении связь посылок и заключения опирается не на закон логики, а на некоторые фактические или психологические основания, не имеющие чисто формального характера. В таком умозаключении заключение не следует логически из посылок и может содержать информацию, отсутствующую в них. Достоверность посылок не означает поэтому достоверности выведенного из них индуктивно утверждения. Индукция даёт только вероятные, или правдоподобные, заключения, нуждающиеся в дальнейшей проверке.

Примерами индукции могут служить рассуждения:

Аргентина является республикой; Бразилия — республика; Венесуэла — республика;

Эквадор — республика.

Аргентина, Бразилия, Венесуэла, Эквадор — латиноамериканские государства.

Все латиноамериканские государства являются республиками.

Италия — республика; Португалия — республика; Финляндия — республика;

Франция — республика.

Италия, Португалия, Финляндия, Франция — западноевропейские страны.

Все западноевропейские страны являются республиками.

Индукция не даёт полной гарантии получения новой истины из уже имеющихся. Максимум, о котором можно говорить, это определённая степень вероятности выводимого утверждения. Так, посылки и первого и второго индуктивного умозаключения истинны, но заключение первого из них истинно, а второго — ложно. Действительно, все латиноамериканские государства — республики; но среди западноевропейских стран имеются не только республики, но и монархии, например, Англия, Бельгия и Испания.

Особенно характерными дедукциями являются логические переходы от общего знания к частному. Во всех случаях, когда требуется рассмотреть какое-то явление на основании уже известного общего принципа и вывести в отношении этого явления необходимое заключение, мы умозаключаем в форме дедукции (Все поэты — писатели; Лермонтов — поэт; следовательно, Лермонтов — писатель).

Рассуждения, ведущие от знания о части предметов к общему знанию обо всех предметах определённого класса, — это типичные индукции, поскольку всегда остаётся вероятность того, что обобщение окажется поспешным и необоснованным (Платон — философ; Аристотель — философ; значит, все люди — философы).

Нельзя вместе с тем отождествлять дедукцию с переходом от общего к частному, а индукцию — с переходом от частного к общему. Дедукция — это логический переход от одной истины к другой, индукция — переход от достоверного знания к вероятному. К индуктивным умозаключениям относятся не одни обобщения, но и уподобления, или аналогии, заключения о причинах явлений и др.

Дедукция играет особую роль в обосновании утверждений. Если рассматриваемое положение логически следует из уже установленных положений, оно обосновано и приемлемо в той же мере, что и последние. Это — собственно логический способ обоснования утверждений, использующий чистое рассуждение и не требующий обращения к наблюдению, интуиции и т.д.

Подчёркивая важность дедукции в процессе обоснования, не следует, однако, отрывать её от индукции или недооценивать последнюю. Почти все общие положения, включая, конечно, и научные законы, являются результатом индуктивного обобщения. В этом смысле индукция — основа нашего знания. Сама по себе она не гарантирует его истинности и обоснованности. Но она порождает предположения, связывает их с опытом и тем самым сообщает им определённое правдоподобие, более или менее высокую степень вероятности. Опыт — источник и фундамент человеческого знания. Индукция, отправляющаяся от того, что постигается в опыте, является необходимым средством его обобщения и систематизации.

Дедукция — это выведение заключений, столь же достоверных, как и принятые посылки.

В обычных рассуждениях дедукция только в редких случаях предстаёт в полной и развёрнутой форме. Чаще всего мы указываем не все используемые посылки, а лишь некоторые из них. Общие утверждения, о которых можно предполагать, что они хорошо известны, как правило, опускаются. Не всегда явно формулируются и заключения, вытекающие из принятых посылок. Сама логическая связь, существующая между исходными и выводимыми утверждениями, лишь иногда отмечается словами, подобными «следовательно» и «значит».

Нередко дедукция является настолько сокращённой, что о ней можно только догадываться. Восстановить её в полной форме, с указанием всех необходимых элементов и их связей бывает нелегко.

Проводить дедуктивное рассуждение, ничего не опуская и не сокращая, обременительно. Человек, указывающий все предпосылки своих заключений, создаёт впечатление какого-то педанта. И вместе с тем всякий раз, когда возникает сомнение в обоснованности сделанного вывода, следует возвращаться к самому началу рассуждения и воспроизводить его в возможно более полной форме. Без этого трудно или даже просто невозможно обнаружить допущенную ошибку.

Многие литературные критики полагают, что Шерлок Холмс был «списан» А.Конан-Дойлом с профессора медицины Эдинбургского университета Джозефа Белла. Последний был известен как талантливый учёный, обладавший редкой наблюдательностью и отлично владевший методом дедукции. Среди его студентов был и будущий создатель образа знаменитого детектива.

Однажды, рассказывает в своей автобиографии Конан-Дойл, в клинику пришёл больной, и Белл спросил его:

— Вы служили в армии?

— Так точно! — став по стойке смирно, ответил пациент.

— В горно-стрелковом полку?

— Так точно, господин доктор!

— Недавно ушли в отставку?

— Так точно!

— Были сержантом?

— Так точно! — лихо ответил больной.

— Стояли на Барбадосе?

— Так точно, господин доктор!

Студенты, присутствовавшие при этом диалоге, изумлённо смотрели на профессора. Белл объяснил, насколько просты и логичны его выводы.

Этот человек, проявив при входе в кабинет вежливость и учтивость, все же не снял шляпу. Сказалась армейская привычка. Если бы пациент был в отставке длительное время, то давно усвоил бы гражданские манеры. В осанке властность, по национальности он явно шотландец, а это говорит за то, что он был командиром. Что касается пребывания на Барбадосе, то пришедший болен элефантизмом (слоновостью) — такое заболевание распространено среди жителей тех мест.

Здесь дедуктивное рассуждение чрезвычайно сокращено. Опущены, в частности, все общие утверждения, без которых дедукция была бы невозможной.

Введённое ранее понятие «правильное рассуждение (умозаключение)» относится только к дедуктивному умозаключению. Лишь оно может быть правильным или неправильным. В индуктивном умозаключении вывод не связан логически с принятыми посылками. Поскольку «правильность» — это характеристика логической связи между посылками и заключением, а индуктивным умозаключением данная связь не предполагается, такое умозаключение не может быть ни правильным, ни неправильным. Иногда на этом основании индуктивные рассуждения вообще не включаются в число умозаключений.

4. ИНТУИТИВНАЯ ЛОГИКА

Под интуитивной логикой обычно понимают интуитивные представления о правильности рассуждений, сложившиеся стихийно в процессе повседневной практики мышления.

Интуитивная логика, как правило, успешно справляется со своими задачами в повседневной жизни, но совершенно недостаточна для критики неправильных рассуждений. Правильно ли рассуждает человек, когда говорит: «Если бы барий был металлом, он проводил бы электрический ток; барий проводит электрический ток; следовательно, он металл?». Чаще всего на основе логической интуиции отвечают: правильно, барий металл, и он проводит ток. Этот ответ, однако, неверен. Логическая правильность, как гласит теория, зависит только от способа связи утверждений. Она не зависит от того, истинны используемые в выводе утверждения или нет. Хотя все три утверждения, входящие в рассуждение, верны, между ними нет логической связи. Рассуждение построено по неправильной схеме: «Если есть первое, то есть второе; второе есть; значит, есть и первое». Такая схема от истинных исходных положений может вести не только к истинному, но и к ложному заключению, она не гарантирует получения новых истин из имеющихся. В рассуждении: «Если у человека повышенная температура, он болен; человек болен; следовательно, у него повышенная температура» обе посылки могут быть истинными, а заключение ложным: многие болезни протекают без повышения температуры. Другой пример: «Если бы шёл дождь, земля была бы мокрой; но дождя нет; значит, земля не мокрая». Это рассуждение интуитивно обычно оценивается как правильное, но достаточно небольшого рассуждения, чтобы убедиться, что это не так. Верно, что в дождь земля всегда мокрая; но если дождя нет, из этого вовсе не следует, что она сухая: земля может быть просто полита или быть мокрой после таяния снега. Рассуждение опять-таки идёт по неправильной схеме: «Если первое, то второе; но первого нет; значит, нет и второго». Эта схема может привести от истинных посылок к ошибочному заключению: «Если человек художник, он рисует; человек рисует; значит, человек художник». Эти простые примеры показывают, что логика, усвоенная стихийно, даже в обычных ситуациях может оказаться ненадёжной.

Обычно мы применяем логические законы, не задумываясь о них, нередко не подозревая о самом их существовании. Но бывает, что использование даже простой схемы сталкивается с известными трудностями.

Эксперименты, проводившиеся психологами с целью сопоставления мышления людей разных культур, наглядно показывают, что чаще всего причина трудностей в том, что схема рассуждения, его форма не выделяется в чистом виде. Вместо этого для решения вопроса о правильности рассуждения привлекаются не относящиеся к делу содержательные соображения. Обычно они связаны с какой-то конкретной ситуацией.

Вот как описывают ход одного из экспериментов, проводившихся в Африке, М.Коул и С.Скрибнер в книге «Культура и мышление».

Экспериментатор. Однажды паук пошёл на праздничный обед, ему сказали, что прежде чем приступить к еде, он должен ответить на один вопрос. Вопрос такой: «Паук и чёрный олень всегда едят вместе. Паук ест. Ест ли олень?»

Испытуемый. Они были в лесу?

Экспериментатор. Да.

Испытуемый. Они вместе ели?

Экспериментатор. Паук и олень всегда едят вместе. Паук ест. Ест ли олень?

Испытуемый. Но меня там не было. Как я могу ответить на такой вопрос?

Экспериментатор. Не можете ответить? Даже если вас там не было, вы можете ответить на этот вопрос. (Повторяет вопрос.)

Испытуемый. Да, да, чёрный олень ест.

Экспериментатор. Почему вы говорите, что чёрный олень ест?

Испытуемый. Потому что чёрный олень всегда весь день ходит по лесу и ест зеленые листья. Потом он немного отдыхает и снова встаёт, чтобы поесть.

Здесь очевидная ошибка. У испытуемого нет общего представления о логической правильности вывода. Чтобы дать ответ, он стремится опереться на какие-то факты, а когда экспериментатор отказывается помочь ему в поисках таких фактов, сам придумывает их.

Ещё пример из этого же исследования.

Экспериментатор. Если Флюмо или Йакпало пьют сок тростника, староста деревни сердится. Флюмо не пьёт сока тростника. Йакпало пьёт сок тростника. Сердится ли староста деревни?

Испытуемый. Люди не сердятся на других людей.

Экспериментатор повторяет задачу.

Испытуемый. Староста деревни в тот день не сердился.

Экспериментатор. Староста деревни не сердился? Почему?

Испытуемый. Потому что он не любит Флюмо.

Экспериментатор. Он не любит Флюмо? Скажи почему?

Испытуемый. Потому что, когда Флюмо пьёт сок тростника, это плохо. Поэтому староста деревни сердится, когда Флюмо так делает. А когда Йакпало иногда пьёт сок тростника, он ничего плохого не делает людям. Он идёт и ложится спать. Поэтому люди на него не сердятся. Но тех, кто напьётся сока тростника и начинает драться, староста не может терпеть в деревне».

Испытуемый имеет в виду скорее всего каких-то конкретных людей или просто выдумал их. Первую посылку задачи он отбросил и заменил её другим утверждением: люди не сердятся на других людей. Затем он ввёл в задачу новые данные, касающиеся поведения Флюмо и Йакпало. Ответ испытуемого на экспериментальную задачу был неправилен. Но он был результатом вполне логичных рассуждений на основе новых посылок.

Для анализа задачи, поставленной в первом эксперименте, переформулируем её так, чтобы были выявлены логические связи утверждений: «Если ест паук, то ест и олень; если ест олень, то ест и паук; паук ест; следовательно, олень тоже ест». Здесь три посылки. Вытекает ли из двух («Если ест паук, олень также ест» и «Паук ест») заключение «Олень ест?». Конечно. Рассуждение идёт по упоминавшейся уже схеме: «Если есть первое, то есть второе; есть первое; значит, есть второе». Она представляет собой логический закон. Правильность этого рассуждения не зависит, разумеется, от того, происходит ли все в лесу, присутствовал ли при этом испытуемый и т.п.

Несколько сложнее схема, по которой идёт рассуждение во второй задаче: «Если Флюмо или Йакпало пьют сок тростника, староста деревни сердится. Флюмо не пьёт сок тростника. Йакпало пьёт сок тростника. Сердится ли староста деревни?» Отвлекаясь от конкретного содержания, выявляем схему рассуждения: «Если есть первое или второе, то есть третье; первого нет, но есть второе; следовательно, есть третье». Эта схема является логическим законом, и, значит, рассуждение правильно. Схема близка указанной ранее схеме: «Если есть первое, то есть второе; есть первое; следовательно, есть второе». Различие только в том, что в качестве «первого» в более сложном рассуждении указываются две альтернативы, одна из которых тут же исключается.

Навык правильного мышления не предполагает каких-либо теоретических знаний, умения объяснить, почему что-то делается именно так, а не иначе. К тому же сама интуитивная логика, как правило, беззащитна перед лицом критики.

Усвоение языка есть одновременно и усвоение общечеловеческой, не зависящей от конкретных языков, логики. Без неё, как и без грамматики, нет, в сущности, владения языком. В дальнейшем стихийно сложившееся знание грамматики систематизируется и шлифуется в процессе школьного обучения. На логику же специального внимания обычно не обращается, её совершенствование остаётся стихийным процессом. Нет поэтому ничего странного в том, что, научившись на практике последовательно и доказательно рассуждать, человек затрудняется ответить, какими принципами он при этом руководствуется. Почувствовав сбой в рассуждении, он оказывается, как правило, не способным объяснить, какая логическая ошибка допущена. Это под силу только теории логики.

5. НЕКОТОРЫЕ СХЕМЫ ПРАВИЛЬНЫХ РАССУЖДЕНИЙ

В правильном рассуждении заключение вытекает из посылок с логической необходимостью, и общая схема такого рассуждения представляет собой логический закон.

Логические законы лежат, таким образом, в основе логически совершённого мышления. Рассуждать логически правильно — значит рассуждать в соответствии с законами логики.

Число схем правильного рассуждения (логических законов) бесконечно. Многие известны нам из практики рассуждения. Мы применяем их интуитивно, не отдавая себе отчёта, что в каждом правильно проведённом умозаключении мы используем тот или иной логический закон.

Вот некоторые, наиболее часто используемые, схемы.

Если есть первое, то есть второе; есть первое; следовательно, есть второе. Эта схема позволяет от утверждения условного высказывания и утверждения его основания перейти к утверждению следствия. По этой схеме протекает, в частности, рассуждение: «Если лёд нагревают, он тает; лёд нагревают; значит, он тает».

Это логически корректное движение мысли иногда путается со сходным, но логически неправильным её движением от утверждения следствия условного высказывания к утверждению его основания: «Если есть первое, то есть второе; есть второе; значит, есть первое». Последняя схема не является логическим законом, от истинных посылок она может привести к ложному заключению. Скажем, идущее по этой схеме рассуждение «Если человеку восемьдесят лет, он стар; человек стар; следовательно, человеку восемьдесят лет» ведёт к ошибочному заключению, что старику ровно восемьдесят лет.

Если есть первое, то есть второе; но второго нет; значит, нет первого. Посредством этой схемы от утверждения условного высказывания и отрицания его следствия осуществляется переход к отрицанию основания высказывания. Например: «Если наступает день, то становится светло; но сейчас не светло; следовательно, день не наступил». Иногда эту схему смешивают с логически некорректным движением мысли от отрицания основания условного высказывания к отрицанию его следствия: «Если есть первое, есть и второе; но первого нет; значит, нет и второго».

Если есть первое, то есть второе; следовательно, если нет второго, то нет и первого. Эта схема позволяет, используя отрицание, менять местами высказывания. К примеру, из высказывания «Если есть гром, есть также молния» получается высказывание «Если нет молнии, то нет и грома».

Есть по меньшей мере или первое или второе; но первого нет; значит, есть второе. Например: «Бывает день или ночь; сейчас ночи нет; следовательно, сейчас день».

Либо имеет место первое, либо второе; есть первое; значит, нет второго. Посредством этой схемы от утверждения двух взаимоисключающих альтернатив и установления того, какая из них присутствует, осуществляется переход к отрицанию другой альтернативы. Например: «Достоевский родился либо в Москве, либо в Петербурге; он родился в Москве; значит, неверно, что он родился в Петербурге». В американском вестерне «Хороший, плохой и злой» Бандит говорит: «Запомни, Однорукий, что мир делится на две части: тех, кто держит револьвер, и тех, кто копает. Револьвер сейчас у меня, так что бери лопату». Это рассуждение также опирается на рассматриваемую схему.

Неверно, что есть и первое, и второе; следовательно, нет первого или нет второго; Есть первое или есть второе; значит, неверно, что нет первого и нет второго. Эти и близкие им схемы позволяют переходить от утверждений с союзом «и» к утверждениям с союзом «или», и наоборот. Используя данные схемы, от утверждения «Неверно, что сегодня ветер и дождь» можно перейти к утверждению «Неверно, что сегодня ветер или неверно, что сегодня дождь» и от утверждения «Амундсен или Скотт был первым на Южном полюсе» перейти к утверждению «Неверно, что ни Амундсен, ни Скотт не является первым человеком, побывавшим на Южном полюсе».

Таковы некоторые схемы правильного рассуждения. В дальнейшем эти и другие схемы будут рассмотрены более детально и представлены с использованием специальной логической символики.

6. ТРАДИЦИОННАЯ И СОВРЕМЕННАЯ ЛОГИКА

История логики охватывает около двух с половиной тысячелетий. «Старше» формальной логики, пожалуй, только философия и математика.

В длинной и богатой событиями истории развития логики отчётливо выделяются два основных этапа. Первый — от древнегреческой логики до возникновения во второй половине прошлого века современной логики. Второй — с этого времени до наших дней.

На первом этапе, обычно называемом традиционной логикой, формальная логика развивалась очень медленно. Обсуждавшиеся в ней проблемы мало чем отличались от проблем, поставленных ещё Аристотелем. Это дало повод немецкому философу И.Канту (1724-1804) в своё время придти к выводу, что формальная логика является завершённой наукой, не продвинувшейся со времени Аристотеля ни на один шаг.

Кант не заметил, что ещё с XVII в. стали назревать предпосылки для научной революции в логике. Именно в это время получила ясное выражение идея представить доказательство как вычисление, подобное вычислению в математике.

Эта идея связана главным образом с именем немецкого философа и математика Г.Лейбница (1646-1716). По Лейбницу, вычисление суммы или разности чисел осуществляется на основе простых правил, принимающих во внимание только форму чисел, а не их смысл. Результат вычисления однозначно предопределяется этими, не допускающими разночтения правилами, и его нельзя оспорить. Лейбниц мечтал о времени, когда умозаключение будет преобразовано в вычисление. Когда это случится, споры, обычные между философами, станут так же невозможны, как невозможны они между вычислителями. Вместо спора они возьмут в руки перья и скажут: «Будем вычислять».

Идеи Лейбница не оказали, однако, заметного влияния на его современников. Энергичное развитие логики началось позже, в XIX в.

Немецкий математик и логик Г.Фреге (1848-1925) в своих работах стал применять формальную логику для исследования оснований математики. Фреге был убеждён, что «арифметика есть часть логики и не должна заимствовать ни у опыта, ни у созерцания никакого обоснования». Пытаясь свести математику к логике, он реконструировал последнюю. Логическая теория Фреге — провозвестник всех нынешних теорий правильного рассуждения.

Идея сведения всей чистой математики к логике была подхвачена английским логиком и философом Б.Расселом (1872-1970). Но последующее развитие логики показало неосуществимость этой грандиозной по своему замыслу попытки. Она привела, однако, к сближению математики и логики и к широкому проникновению плодотворных методов первой во вторую.

В России в конце прошлого — начале нынешнего века, когда научная революция в логике набрала силу, ситуация была довольно сложной. И в теории, и в практике преподавания господствовала так называемая «академическая логика», избегавшая острых проблем и постоянно подменявшая науку логику невнятно изложенной методологией науки, истолкованной к тому же по заимствованным и устаревшим образцам. И тем не менее были люди, стоявшие на уровне достижений логики своего времени и внёсшие в её развитие важный вклад. Прежде всего это доктор астрономии Казанского университета, логик и математик П.С.Порецкий. Сдержанное общее отношение к математической логике, разделявшееся многими русскими математиками, во многом осложнило его творчество. Часть своих работ он вынужден был опубликовать за границей. Но его идеи оказали в конечном счёте существенное влияние на развитие алгебраически трактуемой логики как в нашей стране, так и за рубежом. Порецкий первым в России начал читать лекции по современной логике, о которой он говорил, что это «по предмету своему есть логика, а по методу математика». Исследования Порецкого продолжают оказывать стимулирующее влияние на развитие алгебраических теорий логики и в наши дни.

Одним из первых (ещё в 1910 г.) сомнения в неограниченной приложимости логического закона противоречия, о котором пойдёт речь далее, высказал логик Н.А.Васильев. «Предположите, — говорил он, — мир осуществлённого противоречия, где противоречия выводились бы, разве такое познание не было бы логическим?» Васильев, подобно Ломоносову, наряду с научными статьями, писал порой и стихи. В них своеобразно преломлялись его логические идеи, в частности идея воображаемых (возможных) миров:

… Мне грезится безвестная планета,

Где все идёт иначе, чем у нас.

В качестве логики воображаемого мира он предложил свою теорию без закона противоречия, долгое время считавшегося центральным принципом логики. Васильев полагал необходимым ограничить и действие закона исключённого третьего, о котором также говорится в дальнейшем. В этом смысле Васильев явился одним из идейных предшественников логики наших дней. Идеи Васильева при его жизни подвергались жёсткой критике, в результате он оставил занятия логикой. Потребовалось полвека, прежде чем его «воображаемая логика» без законов противоречия и исключённого третьего была оценена по достоинству. Идеи, касающиеся ограниченной приложимости закона исключённого третьего и близких ему способов математического доказательства, были развиты математиками А.Н.Колмогоровым, В.А.Гливенко, А.А.Марковым и др. В результате возникла так называемая конструктивная логика, считающая неправомерным перенос ряда логических принципов, применимых в рассуждениях о конечных множествах, на область бесконечных множеств.

Известный русский физик П.Эренфест первым высказал гипотезу о возможности применения современной ему логики в технике. В 1910 г. он писал:

«Символическая формулировка даёт возможность „вычислять“ следствия из таких сложных систем посылок, в которых при словесном изложении почти или совершенно невозможно разобраться. Дело в том, что в физике и технике действительно существуют такие сложные системы посылок. Пример: пусть имеется проект схемы проводов автоматической телефонной станции. Надо определить: 1) будет ли она правильно функционировать при любой комбинации, могущей встретиться в ходе деятельности станции; 2) не содержит ли она излишних усложнений. Каждая такая комбинация является посылкой, каждый маленький коммутатор есть логическое „или-или“, воплощённое в эбоните и латуни; все вместе — система чисто качественных (сети слабого тока, поэтому не количественных) „посылок“, ничего не оставляющая желать в отношении сложности и запутанности. Следует ли при решении этих вопросов раз и навсегда удовлетвориться рутинным способом преобразования на графике? Правда ли, что, несмотря на существование уже разработанной алгебры логики, своего рода „алгебра распределительных схем“ должна считаться утопией?»

В дальнейшем гипотеза Эренфеста получила воплощение в теории релейно-контактных систем.

В общем, оглядываясь на историю распространения логики, можно сказать, что лучшие русские логики всегда стремились стоять на уровне современных им мировых теорий и концепций, органически чуждаясь всякого рода логического сектантства и сепаратизма.

Современную логику нередко называют математической, подчёркивая тем самым своеобразие новых её методов в сравнении с использовавшимися ранее в традиционной логике.

Одна из характерных черт этих методов — широкое использование разнообразных символов вместо слов и выражений обычного языка. Символы применял в ряде случаев ещё Аристотель, а затем и все последующие логики. Однако теперь в использовании символики был сделан качественно новый шаг. В логике стали использоваться специально построенные языки, содержащие только специальные символы и не включающие ни одного слова обычного разговорного языка.

Широкое использование символических средств послужило основанием того, что, новую логику стали называть символической. Названия «математическая логика» и «символическая логика», обычно употребляемые и сейчас, обозначают одно и то же — современную формальную логику. Она занимается тем же, чем всегда занималась логика — исследованием правильных способов рассуждения.

7. СОВРЕМЕННАЯ ЛОГИКА И ДРУГИЕ НАУКИ

С момента своего возникновения логика была самым тесным образом связана с философией. В течение многих веков логика считалась, подобно психологии, одной из «философских наук». И только во второй половине xix в. формальная — к этому времени уже математическая — логика «отпочковалась», как принято выражаться, от философии. Примерно в это же время от философии отделилась и стала самостоятельной научной дисциплиной психология. Но если отделение психологии было связано прежде всего с проникновением в неё опыта и эксперимента и сближением её с другими эмпирическими науками, то в отделении логики решающую роль сыграло проникновение в неё математических методов и сближение с математикой.

Математическая логика возникла, в сущности, на стыке двух столь разных наук, как философия, или точнее — философская логика, и математика. И тем не менее, взаимосвязь новой логики с философией не только не оборвалась, но, напротив, парадоксальным образом даже окрепла. Обращение к философии является необходимым условием прояснения логикой своих оснований. С другой стороны, использование в философии понятий, методов и аппарата современной логики несомненно способствует более ясному пониманию самих философских понятий, принципов и проблем.

Тесная связь современной логики с математикой придаёт особую остроту вопросу о взаимных отношениях этих двух наук. Среди многих точек зрения, высказывавшихся по этому поводу, были и две крайних, ведущих в общем-то к тому же самому конечному результату — объединению математики и логики в единую научную дисциплину, сведению их в одну науку.

Согласно Г.Фреге, Б.Расселу и их последователям, математика и логика — это всего лишь две ступени в развитии той же самой науки. Математика может быть полностью сведена к логике, и такое чисто логическое обоснование математики позволит установить её истинную и наиболее глубокую природу. Этот подход к обоснованию математики получил название логицизма.

Сторонники логицизма добились определённых успехов в прояснении основ математики. В частности, было показано, что математический словарь сводится к неожиданно краткому перечню основных понятий, которые принадлежат словарю чистой логики. Вся существующая математика была сведена к сравнительно простой и унифицированной системе исходных, принимаемых без доказательства положений, или аксиом, и правил вывода из них следствий, или теорем.

Однако в целом логицизм оказался утопической концепцией. Математика не сводима к логике, поскольку для построения математики необходимы аксиомы, устанавливающие существование в реальности определённых объектов. Но такие аксиомы имеют уже внелогическую природу.

Другой формой объединения математики и логики в одну науку было объявление математической, или современной, логики одним из разделов современной математики. Многие математики и сейчас ещё считают главной — если не единственной — задачей математической логики уточнение понятия математического доказательства.

Тенденция включать математическую логику в число математических дисциплин и видеть в ней только теорию математического доказательства является, конечно, ошибочной. На самом деле задачи логики гораздо шире. Она исследует основы всякого правильного рассуждения, а не только строгого математического доказательства, и её интересует связь между посылками и следствиями в любых областях рассуждения и познания.

Современная логика тесно связана также с кибернетикой — наукой о закономерностях управления процессами и системами в любых областях: в технике, в живых организмах, в обществе. Основоположник кибернетики, американский математик Н.Винер не без оснований подчёркивал, что само возникновение кибернетики было бы немыслимо без математической логики. Автоматика и электронно-вычислительная техника, применяемые в кибернетике, были бы невозможны без использования алгебры логики — этого возникшего первым раздела современной логики. В управляющих системах, применяемых в кибернетике, значительное место занимают релейно-контактные схемы, моделирующие логические операции. Описание таких операций, даваемое логикой, способствует детальному анализу логического строения мысли и открывает поразительные перспективы автоматизации логических процессов.

Помимо кибернетики современная логика находит широкие приложения и во многих других областях науки и техники.

1. ЯЗЫК КАК ЗНАКОВАЯ СИСТЕМА

Язык представляет собой необходимое условие существования абстрактного мышления.

Язык возникает одновременно с сознанием и мышлением. Являясь чувственно воспринимаемой оболочкой мышления, язык обеспечивает мысли человека реальное существование. Вне такой оболочки мысль недоступна для других. Язык — это непосредственная действительность мысли.

Логический анализ мышления всегда имеет форму исследования языка, в котором оно протекает и без которого оно не является возможным. В этом плане логика — наука о мышлении — есть в равной мере и наука о языке.

Мышление и язык — две предполагающие друг друга стороны процессов познания и общения. Язык участвует не только в выражении мысли, но и в самом её формировании. Нельзя противопоставлять «чистое», внеязыковое мышление и его «вербализацию», последующее выражение в языке.

Вместе с тем язык и мышление не тождественны. Каждая из сторон единства, составляемого ими, относительно самостоятельна и обладает своими специфическими законами.

Иногда предполагается, что единственным способом получения подлинной истины является мистическое «вживание» в предмет, позволяющее в одном акте постичь его. При этом мышлению с помощью языка противопоставляется непосредственное, внеязыковое познание. Задача языка сводится к передаче — и притом с необходимостью в более или менее искажённой форме — результатов интуитивного постижения. Очевидно, что настаивание на интуитивном характере нашего познания ведёт так или иначе к противопоставлению мышления и языка.

Язык представляет собой систему знаков, используемую для целей коммуникации и познания.

Системность языка выражается в том, что каждый язык, помимо словаря, имеет также синтаксис и семантику.

Синтаксические правила языка устанавливают способы образования сложных выражений из простых.

Семантические правила определяют способы придания значений выражениям языка. Это достигается указанием тех обстоятельств, в которых должны приниматься предложения определённого вида.

Правила значения обычно делятся на три группы: аксиоматические, дедуктивные и эмпирические.

Аксиоматические правила требуют принятия предложений определённого вида во всех обстоятельствах. Примером могут служить правила русского языка, предписывающие всем говорящим на этом языке всегда принимать предложения «Каждый холостяк не женат», «Сантиметр равен одной сотой метра», «Красное не есть чёрное» и т.п.

Дедуктивные правила требуют принятия следствий, вытекающих из некоторых посылок, если приняты сами посылки. Таково, например, правило, согласно которому, приняв предложения «Если Иван Ильич человек, то он смертен», и «Иван Ильич человек», следует принять также предложение «Иван Ильич смертен».

И наконец, ситуация принятия предложений, указываемая эмпирическими правилами значения, предполагает выход за пределы языка и внеязыковое наблюдение. Примерами таких правил являются правила, требующие принятия предложения «Больно» в случае ощущения боли, предложения «Этот предмет — красный» — при восприятии красного предмета и т.п.

Языки, включающие эмпирические правила значения, принято называть эмпирическими. Очевидно, что ни язык логики, ни язык математики не требуют при принятии или отбрасывании своих предложений обращения к непосредственному опыту и ощущению. В этом смысле данные языки не являются эмпирическими.

Все языки могут быть разделены, далее, на естественные, искусственные и частично искусственные.

Первые, называемые также «повседневными», «разговорными», «обычными» и т.п., складываются стихийно и постепенно. История каждого такого языка неотделима от истории народа, владеющего им. Искусственные языки сознательно создаются людьми для каких-либо специальных целей. Таковы, например, языки математики, логики, алгоритмические языки программирования для ЭВМ, шифры и т.п. Языки естественных и гуманитарных наук относятся к частично искусственным. Скажем, учебник биологии написан всегда на том или ином естественном языке: русском, английском, немецком и т.п. Вместе с тем, помимо слов этого языка, учебник обязательно включает собственно биологическую терминологию и символику, являющуюся по преимуществу интернациональной.

Одна из особенностей искусственных языков состоит в строгой определённости их словаря, синтаксиса и семантики. Во многих случаях эта особенность оказывается несомненным преимуществом таких языков в сравнении с естественными языками, аморфными как со стороны словаря, так и со стороны правил образования и значения.

Искусственные языки генетически и функционально вторичны в отношении естественного языка: первые возникают на базе второго и могут функционировать только в связи с ним.

Традиционная логика пользуется для описания мышления обычным языком.

Этот язык, возникший как средство общения людей, претерпел долгую и противоречивую эволюцию. Многое в нем остаётся невыявленным, а только молчаливо предполагается.

Все это не означает, конечно, что обычный язык никуда не годен, и его следует заменить во всех областях какой-то искусственной символикой. Он вполне справляется с многообразными своими функциями. Но, решая многие задачи, он лишается способности точно передавать форму нашей мысли.

Для целей логики необходим искусственный язык, строящийся по строго сформулированным правилам. Этот язык не предназначен для общения. Он должен служить только одной задаче — выявлению логических связей наших мыслей, но решаться она должна с предельной эффективностью.

Принципы построения искусственного логического языка разработаны в современной логике. Создание его имело примерно такое же значение в области мышления для техники логического вывода, какие в области производства имел переход от ручного труда к труду механизированному.

Специально созданный для целей логики язык получил название формализованного. Слова обычного языка заменяются в нем отдельными буквами и различными специальными символами. Формализованный язык — это «насквозь символический» язык.

Введение его означает принятие особой теории логического анализа рассуждений.

В обычном языке деление на синтаксис и семантику во многом условно. И синтаксические, и семантические правила этого языка расплывчаты и всегда имеют исключения. В нем нет, например, ясного определения осмысленного предложения, нет перечня тех частей, которые должны быть в каждом предложении, чтобы оно могло считаться правильно построенным, и т.д.

2. ОСНОВНЫЕ ФУНКЦИИ ЯЗЫКА

Основные функции, или употребления, языка — это те основные) задачи, которые решаются языком в процессе коммуникации и познания.

В числе этих задач особое место занимает описание — сообщение о реальном положении вещей. Если это сообщение соответствует действительности, оно является истинным. Сообщение, не отвечающее реальному положению дел, ложно. К примеру, описание «Снег белый» является истинным, а описание «Кислород — металл» ложно. Иногда допускается, что описание может быть неопределённым, лежащим между истиной и ложью. К неопределённым можно отнести многие описания будущего: «Через год в этот день будет пасмурно» и т.п.

Описательное употребление языка иногда выделяется словами «истинно», «верно», «на самом деле» и т.п.

Долгое время считалось, что описание — это единственная функция языка или, во всяком случае, та его функция, к которой может быть сведено любое иное его употребление. Предполагалось, что любое грамматически правильное повествовательное предложение является описательным, и значит, истинным или ложным.

Как мы убедимся далее, описание, несмотря на всю его важность, — не единственная задача, решаемая с помощью языка. Оно не является даже главной задачей. Перед языком стоят многие другие задачи, не сводимые к описанию.

Ещё одна функция языка — попытка заставить что-то сделать. Выражения, в которых реализуется намерение говорящего добиться того, чтобы слушающий совершил нечто, разнообразны. Это — команды, приказы, требования, предписания, законы, правила и т.п., короче говоря, нормы. Их примерами могут служить выражения: «Прекратите говорить!», «Старайтесь приносить максимум пользы как можно большему числу людей», «Следует быть стойким» и т.п. Нормы, в отличие от описаний, не являются истинными или ложными, но они могут быть обоснованными или необоснованными, полезными или бесполезными, способствующими достижению каких-то целей или нет и т.п.

Язык может служить также для выражения разнообразных чувств: «Сожалею, что разбудил вас», «Искренне сочувствую вам», «Поздравляю с праздником», «Приветствую всех, кто пришёл», «Извините, но не смогу быть» и т.п. Выражения чувств называются экспрессивами. В них выражаются определённые психические состояния и идёт речь о каком-то свойстве (не обязательно действии), приписываемом либо говорящему, либо слушающему. К примеру, я вправе поздравить вас с победой на соревнованиях, если вы действительно победили и если я на самом деле рад вашей победе. В этом случае поздравление будет искренним, и его можно считать истинным, т.е. соответствующим внешним обстоятельствам и моим чувствам. Если же я поздравляю вас с тем, что вы хорошо выглядите, хотя на самом деле вы выглядите неважно, моё поздравление неискренне. Оно не соответствует реальности, и если я знаю об этом, то не соответствует и моим чувствам. Такое поздравление можно оценить как ложное. Ложным было бы и поздравление с тем, что вы открыли квантовую механику: и мне, и вам заведомо известно, что это не так, и поздравление выглядело бы насмешкой.

Язык может использоваться, далее, для изменения мира словом. Именно эта задача решается, например, выражением: «Назначаю вас председателем», «Ухожу в отставку», «Я заявляю: Наш договор (настоящим) расторгнут», «Увольняю вас», «Объявляю военное положение», «Обручаю вас» («Объявляю вас мужем и женой») и т.п. Такие выражения называются декларациями и выполняют специальную функцию: они меняют существовавшее до их произнесения положение вещей. Если я успешно осуществляю акт назначения вас председателем, вы становитесь председателем, а до этого акта вы не были им; если я успешно выполняю акт производства вас в генералы, в мире сразу же становится одним генералом больше и т.д. Когда футбольный арбитр говорит: «Вы удаляетесь с поля», вы оказываетесь вне игры, и она, по всей очевидности, меняется.

Декларации не описывают некоторое существующее положение дел. В отличие от норм они не направлены на то, чтобы кто-либо в будущем создал предписываемое положение вещей. Декларации непосредственно меняют мир, и делают это самим фактом своего произнесения. Очевидно, что декларации не являются истинными или ложными. Но они, подобно нормам, могут быть обоснованными или необоснованными (я могу назначить кого-то председателем, если у меня есть право делать это), способствующими достижению каких-то целей или нет и т.п.

Язык может использоваться также для обещаний, т.е. для того, чтобы возложить на говорящего обязательство совершить некоторое будущее действие или придерживаться определённой линии поведения. Обещаниями являются, к примеру, выражения: «Обещаю вести себя примерно», «Клянусь говорить правду и только правду», «Буду всегда вежлив» и т.п. Обещания можно истолковать как просьбы к самому себе, т.е. как нормы, адресованные говорящим самому себе и в чем-то предопределяющие его поведение в будущем. Как и все нормы, обещания не являются истинными или ложными. Они могут быть обдуманными или поспешными, целесообразными или нецелесообразными и т.п.

Язык может использоваться, наконец, для оценок, т.е. для выражения положительного, отрицательного или нейтрального отношения к рассматриваемому объекту или, если сопоставляются два объекта, для выражения предпочтения одного из них другому или утверждения равноценности их друг другу. Оценками являются, например, выражения: «Хорошо, что погас свет», «Плохо, когда кто-то опаздывает», «Лучше прийти раньше, чем опоздать» и т.п. Подробнее об оценках мы поговорим в дальнейшем, здесь же отметим только, что оценки столь же фундаментальны и ни к чему не сводимы, как и описания. Но в отличие от описаний они не являются истинными или ложными, а могут быть только глубокими или поверхностными, общепринятыми или нет, эффективными или нет и т.п.

Имеется, таким образом, шесть разных употреблений языка, или разных задач, решаемых с его помощью: сообщение о положении дел (описание), попытка заставить что-то сделать (норма), выражение чувств (экспрессив), изменение мира словом (декларация), принятие обязательства что-то сделать (обещание) и выражение позитивного или негативного отношения к чему-то (оценка).

Выделение функций языка зависит от тех целей, для которых используется противопоставление языковых выражений. В разных случаях могут выделяться и противопоставляться разные функции. С точки зрения логики, важным является проведение различия между двумя основными функциями языка: описательной и оценочной. Все другие употребления языка, если отвлечься от психологических и иных, несущественных с логической точки зрения обстоятельств, сводятся либо к описаниям, либо к оценкам.

Экспрессивы представляют собой своеобразные описания, и как все описания, являются истинными или ложными.

Обещание — это норма, адресованная самому себе. Декларация — норма, адресованная всем, кого она касается и кто должен будет считаться с тем изменением мира, которое произошло, благодаря произнесённым словам. Сами же нормы представляют собой частный случай оценок: это оценки с предполагаемым потенциальным наказанием. К примеру, норма (команда): «Организуйте комиссию!» означает, что создание комиссии оценивается положительно, и если она не будет создана, последует какое-то наказание.

Описание и оценка являются, таким образом, двумя полюсами, к которым тяготеют все другие употребления языка. Анализ последних интересен сам по себе, он может оказываться полезным во многих областях. Но он движется в рамках исходного и фундаментального противопоставления описаний и оценок.

За оппозицией «описание — оценка» стоит в конечном счёте оппозиция «истина — ценность», и первая не может быть ясно понята без прояснения второй.

Большинство рассуждений о ценностях, в том числе и о ценностях в науке, имеет существенный недостаток. Обычно упускается из виду, что категория ценности столь же универсальна, как и категория истины.

Всякая человеческая деятельность неразрывно связана с постановкой целей, следованием нормам и правилам, систематизацией и иерархизацией рассматриваемых и преобразуемых объектов, подведением их под образцы или стандарты, отделением важного и фундаментального от менее существенного и второстепенного и т.д. Все эти понятия — «цель», «норма», «правило», «система», «иерархия», «образец», «стандарт», «фундаментальное», «второстепенное» и т.п. — являются оценочными или несут важное оценочное содержание.

Ценности — неотъемлемый элемент всякой деятельности, а значит и всей человеческой жизни, в каких бы формах она ни протекала.

Вопрос о соотношении истины и ценности — один из аспектов более общей проблемы взаимосвязи теории и практики, созерцания и действия.

Существуют десятки определений понятия ценности. Они различаются деталями, но суть большинства из них одна: ценностью объявляется предмет некоторого интереса, желания, стремления и т.п., или, короче, объект, значимый для человека или группы лиц. На всех этих определениях сказывается обычное убеждение, что истина — это свойство мыслей, правильно отображающих реальность, а ценность — свойство самих вещей, отвечающих каким-то целям, намерениям, планам и т.п.

Однако, ценность, как и истина, является не свойством, а отношением между мыслью и действительностью.

Утверждение и его объект могут находиться между собой в двух противоположных отношениях: истинностном и ценностном. В первом случае отправным пунктом сопоставления является объект, утверждение выступает его описанием и характеризуется с точки зрения истинностных понятий. Во втором случае исходным является утверждение, функционирующее как оценка, стандарт, план. Соответствие ему объекта характеризуется в оценочных понятиях.

Позитивно ценным является объект, соответствующий высказанному о нем утверждению, отвечающий предъявленным к нему требованиям.

Понимание истины как соответствия утверждений описываемым ими ситуациями — это так называемое «классическое» её определение. Определение ценности как соответствия самих объектов утверждениям о них также восходит к античности и с таким же правом может быть названо классическим.

Ценность, как и истина, не существует вне связи мысли и действительности.

К примеру, сопоставляются строящийся город и его план. Если за исходное принимается сам город, то несоответствие плана городу должно характеризоваться как ложность плана, а соответствие — как его истинность. Если же за исходное принимается план, то город рассматривается как его реализация и расхождение между планом и городом оценивается как недостаток города, а соответствие его плану — как его достоинство. План, соответствующий городу, является истинным; город, отвечающий плану, является хорошим, т.е. таким, каким он должен быть.

Ещё один пример возможности двух разных направлений соответствия между словами и миром. Предположим, что некий покупатель наполняет в супермаркете свою тележку, ориентируясь на имеющийся у него список. Другой человек, наблюдающий за ним, составляет список отобранных им предметов. При выходе из магазина в руках у покупателя и его наблюдателя могут оказаться два одинаковых списка, имеющих совершенно разные функции. Цель списка покупателя в том, чтобы, так сказать, приспособить мир к словам; цель списка наблюдателя — привести слова в согласие с действительностью. Для покупателя отправным пунктом служит список; мир, преобразованный в соответствии с последним, будет позитивно ценным (хорошим). Для наблюдателя исходным является мир; список, соответствующий ему, будет истинным. Если покупатель допускает ошибку, для её исправления он предпринимает предметные действия, видоизменяя плохой, не отвечающий списку мир. Если ошибается наблюдатель, он вносит изменения в ложный, не согласующийся с миром список.

Цель описания — сделать так, чтобы слова соответствовали миру, цель оценки — сделать так, чтобы мир отвечал словам. Это — две диаметрально противоположные функции. Очевидно, что они не сводимы друг к другу. Нет оснований также считать, что описательная функция языка является первичной или более фундаментальной, чем его оценочная функция.

Описание и оценка являются двумя точками тяготения всех других употреблений языка. Между «чистыми» описаниями и «чистыми» оценками существует масса переходов. Как в повседневном языке, так и в языке науки имеются многие разновидности и описаний, и оценок. «Чистые» описания и «чистые» оценки довольно редки, большинство языковых выражений носит двойственный, или смешанный, описательно-оценочный характер. Все это должно, разумеется, учитываться при изучении множества способов употребления языка. Но надо учитывать и то, что всякий более тонкий анализ употреблений языка движется в рамках исходного и фундаментального противопоставления описаний и оценок и является всего лишь его детализацией.

3. ЛОГИЧЕСКАЯ ГРАММАТИКА

Из грамматики хорошо известно деление предложений на части речи — существительное, прилагательное, глагол и т.д. Деление языковых выражений на семантические категории, широко используемое в логике, напоминает это грамматическое подразделение и в принципе произошло из него. На этом основании теорию семантических категорий иногда называют «логической грамматикой». Её задача — предотвращать смешение языковых выражений разных типов, которое ведёт к образованию бессмысленных выражений, подобных «Квадратичность пьёт воображение» или «Если дует ветер, то звезда».

Идея семантических категорий была выдвинута в начале этого века Э.Гуссерлем, называвшим их «категориями значения». Как логико-философская доктрина, имеющая обширные приложения в исследованиях языка, теория категорий была детально развита польскими логиками С.Лесневским, К.Айдукевичем и А.Тарским.

Подразделение речевых оборотов на семантические категории производится в зависимости от того, что эти обороты означают. Два выражения считаются относящимися к одной и той же семантической категории рассматриваемого языка, если замена одного из них другим в произвольном осмысленном предложении не превращает это предложение в бессмысленное. Наоборот, два выражения всегда относятся к разным категориям, если подстановка одного из них вместо другого ведёт к утрате осмысленности.

Например, имена Сократ и Платон относятся к одной и той же семантической категории: замена одного из них другим в любом осмысленном предложении даёт опять-таки осмысленное предложение. Скажем, предложение «Платон был учителем Аристотеля» является осмысленным и истинным. Получаемое из него путём замены предложение «Сократ был учителем Аристотеля» будет ложным, но осмысленным.

Выражения же «Сократ» и «стоит» принадлежат разным семантическим категориям, поскольку из предложения «Сократ стоит» при замене слова «стоит» словом «Сократ» образуется выражение «Сократ Сократ», не являющееся вообще предложением.

Ещё несколько примеров. Выражения «либо…, либо…» и «если…, то…» относятся к одной и той же категории, так как при преобразовании, допустим, предложения «Либо идёт дождь, либо дует ветер» в предложение «Если идёт дождь, то дует ветер» осмысленность сохраняется. Слова «больше» и «старше» также принадлежат одной и той же семантической категории, поскольку всякое предложение, осмысленное с одним из этих слов, будет осмысленным и с другим.

Выражения же «больший» и «либо» относятся к разным категориям: замена первого выражения вторым в осмысленном, хотя и ложном, предложении «Мадрид больше Парижа» даёт бессмысленное целое «Мадрид либо Парижа». Сходным образом, замена «либо» на «каждый» ведёт к превращению осмысленного предложения в бессмысленное, и поэтому «либо» и «каждый» принадлежат разным семантическим категориям.

Очевидно, что осмысленность не тождественна истинности. Имеют смысл, а значит являются осмысленными, не только истинные, но и ложные высказывания.

Согласно теории семантических категорий, каждое правильно построенное выражение языка принадлежит одной и только одной из семантических категорий. В принципе этих категорий бесконечное число, и они составляют весьма разветвлённую иерархию.

В неё входят две основные категории и бесконечная совокупность так называемых функторных категорий. К основным относятся категория имён и категория предложений (высказываний), включающие также имена и предложения с переменными (подобные «брат некоторого S » и «Если Аристотель был учеником Платона, то А », где S — какое-то имя, а А — предложение). Функторные категории различаются в зависимости от того, к чему применяется операция, называемая функтором, и что возникает в результате её применения.

К примеру «Солнце» — это имя, «Солнце греет» — предложение. Слово «есть» — функтор, образующий предложение из двух других предложений и т.д.

Имеются функторы, преобразующие имена в предложения, предложения в предложения, имена в имена и предложения в имена. Имеются также более сложные функторы, преобразующие одни функторы в другие.

В разных языках число семантических категорий является разным. Существуют, например, языки с одной-единственной категорией имён, и имеются языки с несколькими категориями имён.

В обычном языке нет таких жёстких границ между речевыми оборотами как те, которые предполагаются теорией семантических категорий. Кроме того, может оказаться, что в языках разных народов границы между выражениями проводятся по разному. Скажем, в русском языке говорить о «каждом Аристотеле» не вполне естественно. Но из этого ещё не следует, что и в любом другом языке этот оборот будет резать слух.

Ограниченная применимость теории семантических категорий к естественным языкам не исключает, разумеется, что с её помощью нельзя получить интересных наблюдений и заключений, относящихся к этим языкам.

Оставляя в стороне сложные и спорные детали теории семантических категорий, можно ограничиться выделением трех основных категорий языковых выражений: имён, предложений (высказываний) и функторов.

Именами являются языковые выражения, подстановка которых в форму « Sесть Р» вместо переменных Sи Рдаёт осмысленное предложение.

Именами являются, к примеру, выражения «звёздная ночь», «Волга», «Тамбов» и «вечерние сумерки». Подставив данные выражения в указанную форму мы получим осмысленные (хотя и не обязательно истинные) предложения: «Тамбов есть Волга», «Вечерние сумерки есть звёздная ночь», «Звёздная ночь есть Волга» и т.п.

Предложение (высказывание) — это языковое выражение являющееся истинным или ложным.

Высказываниями являются, например, выражения «Ниобий — это инертный газ», «5 есть простое число», «Если металлический стержень нагревается, его длина увеличивается». Первое из этих высказываний ложно, два других истинны.

Функтор — это языковое выражение, не являющееся ни именем, ни высказыванием и служащее для образования новых имён или высказываний из уже имеющихся.

Например, слово «есть» — это функтор, поскольку оно не представляет собой имени или высказывания, но позволяет из двух имён получить высказывание (скажем, высказывание «Ньютон есть физик»). Выражения «все … есть …», «некоторые … есть …», «все … не есть …» и «некоторые … не есть …» также являются функторами: это не имена и не высказывания, но с их помощью, подставляя на места многоточий какие-то имена, можно получить высказывания (к примеру, «Все инертные газы есть летучие», «Некоторые металлы есть жидкости», «Все киты не есть рыбы» и «Некоторые музыканты не есть композиторы»).

Выражения «… и …», «… или …», «либо …, либо …», «если …, то …», «…, если и только если …» — это функторы, дающие из двух высказываний новое высказывание («Идёт снег и дует ветер», «Мы идём в кино или мы остаёмся дома», «Либо Киев стоит на Днепре, либо Киев стоит на Сене», «Если имеется причина, то имеется и следствие», «Число делится на 6, если и только если число делится на 2 и на 3» и т.п.).

Выражение «неверно, что …» (или просто «не»), не будучи именем или высказыванием, позволяет получить из одного высказывания другое высказывание (позволяет, к примеру, из высказывания «Все учёные рассеянны» получить высказывание «Неверно, что все учёные рассеянны», или «Не все учёные являются рассеянными»).

Функторы, позволяющие из имён или высказываний получать новые высказывания называются пропозициональными (от латинского слова propositio — высказывание, суждение).

В дальнейшем из всех возможных функторов особое внимание будет уделено именно пропозициональным функторам.

1. ВИДЫ ИМЁН

Имена — необходимое средство познания и общения. Обозначая предметы и их совокупности, имена связывают язык с реальным миром.

Имена естественны и привычны, как те вещи, с которыми они связаны. Настолько естественны, что когда-то они казались принадлежащими самим вещам, подобно цвету, тяжести и другим свойствам.

Первобытные люди рассматривали свои имена как нечто конкретное, реальное и часто священное. Психолог Л.Леви-Брюль, создавший в начале этого века концепцию первобытного мышления, считал такое отношение к именам важным фактором, подтверждающим мистический и внелогический характер мышления наших предков. Он указывал, в частности, что «индеец рассматривает своё имя не как простой ярлык, но как отдельную часть своей личности, как нечто вроде своих глаз или зубов. Он верит, что от злонамеренного употребления его имени он так же верно будет страдать, как от раны, нанесённой какой-нибудь части его тела. Это верование встречается у разных племён от Атлантического до Тихого океана». На побережье Западной Африки «существуют верования в реальную и физическую связь между человеком и его именем; можно ранить человека, пользуясь его именем… Настоящее имя царя является тайным…»

Эти наивные представления об именах как свойствах вещей удивительно живучи. Астроном В.Воронцов-Вельяминов вспоминает, например, что на популярных лекциях слушатели не раз задавали ему вопрос: «Мы допускаем, то можно измерить и узнать размеры, расстояние и температуру небесных тел; но как, скажите, узнали вы названия небесных светил?»

Ответ на такой вопрос прост. Астрономы узнают имена открытых ими небесных тел так же, как родители узнают имена своих детей — давая им эти имена. Но сам факт подобного вопроса показывает, что иллюзия «приклеенности», «привинченности» имён к вещам нуждается в специальном объяснении.

Роль имён в языке настолько велика и заметна, что иногда даже в науке о языке придание имён вещам считается едва ли не единственной задачей языка. Связь языка с миром представляется при этом как какое-то развешивание имён-ярлыков. В частности, существует и пользуется известностью логическая теория, явно склонная видеть среди выражений языка по преимуществу одни имена. Даже предложения оказываются для неё не описаниями каких-то ситуаций или требованиями каких-то действий, а только именами особых «абстрактных предметов» — истины и лжи.

Исследованием имён как одного из основных понятий и естественных и формализованных языков занимаются все науки, изучающие язык. И прежде всего логика, для которой имя — одна из основных семантических категорий.

В разных научных дисциплинах под именем понимаются разные, а порой и несовместимые вещи. Логика затратила немало усилий на прояснение того, что представляет собой имя и каким принципам подчиняется операция именования, или обозначения. Нигде, пожалуй, имена не трактуются так всесторонне, глубоко и последовательно, как в логических исследованиях.

В общем случае имя — это выражение языка, обозначающее отдельный предмет, совокупность сходных предметов, свойства, отношения и т.п.

Например, слово «Цезарь» обозначает отдельный предмет — первого римского императора Цезаря; слово «учёный» обозначает класс людей, каждый из которых занят научными исследованиями; слово «чёрный» может рассматриваться как обозначение свойства черноты; слово «дальше» — как обозначение определённого отношения между предметами и т.п.

Имя можно определить по его роли в структуре предложения. Выражение языка является именем, если оно может использоваться в качестве подлежащего или именной части сказуемого в простом предложении «S есть Р» (S — подлежащее, Р — сказуемое). Скажем, «Амундсен», «Скотт» и «человек, открывший Южный полюс» — это имена, поскольку подстановка их вместо букв S и Р даёт осмысленные предложения: «Амундсен есть человек, открывший Южный полюс», «Скотт есть человек, открывший Южный полюс» и т.п.

Имена различаются между собой в зависимости от того, сколько предметов они означают. Единичные имена обозначают один и только один предмет. Общие имена обозначают более чем один предмет. Единичным именем является к примеру слово «Солнце», обозначающее единственную звезду в Солнечной системе. Единичным является и имя «естественный спутник Земли», поскольку оно обозначает Луну, являющуюся единственным таким спутником Земли. К общим относятся имена «человек», «женщина», «школьник» и т.п. Все эти имена связаны с множествами, или классами, предметов. При этом имя относится не к множеству как единому целому, а к каждому входящему в него предмету. Слово «человек» обозначает не всех людей вместе, а каждого в отдельности, о ком можно сказать: «Это человек». В отличие от понятия «человек», слово «человечество» не общее, а единичное имя: объект, который можно назвать «человечеством», всего один. Слово «галактика» является общим именем, поскольку во Вселенной есть, помимо нашей Галактики, и другие галактики. Слово же «Вселенная» — единичное имя, так как Вселенная является единственной.

Среди общих имён особое значение имеют понятия.

Понятие представляет собой общее имя с относительно ясным и устойчивым содержанием, используемое в обычном языке или в языке науки.

Понятиями являются, к примеру, «дом», «квадрат», «молекула», «кислород», «атом», «любовь», «бесконечный ряд» и т.п. Отчётливой границы между теми именами, которые можно назвать понятиями, и теми, которые не относятся к понятиям, не существует. «Атом» уже с античности является достаточно оформившимся понятием, в то время как «кислород» и «молекула» до XVIII в. вряд ли могли быть отнесены к понятиям.

Имя «понятие» широко используется и в повседневном, и в научном языке. Однако в истолковании содержания этого имени единства мнений нет. В одних случаях под «понятиями» имеют в виду все имена, включая и единичные. К понятиям относят не только «столицу» и «европейскую реку», но и «столицу Белоруссии» и «самую большую реку Европы». В других случаях понятия понимаются как общие имена, отражающие предметы и явления в их существенных признаках. Иногда понятие отождествляется с содержанием общего имени, со смыслом, стоящим за таким именем.

Далее под понятиями понимаются все общие имена, для которых имеется какое-то определение или содержание которых является относительно ясным. Слово «понятие» будет использоваться, таким образом, в своём обычном или близком к обычному смысле, а не в качестве специального логического термина.

Имена можно разделить также на пустые, или беспредметные, и непустые. Пустое имя не обозначает ни одного реально существующего предмета. Имя, не являющееся пустым, отсылает хотя бы к одному реальному объекту. К пустым относятся, к примеру, имена «Зевс», «Пегас», «кентавр», «русалка», «нимфа», созданные мифологией и обозначающие вымышленных, отсутствующих в реальном мире существ. Пустыми являются также имена «идеальный газ», «абсолютно чёрное тело», «идеально упругое тело», «несжимаемая жидкость», «точка», «линия», «материальная точка», используемые в физике и математике и обозначающие не реально существующие, а идеализированные предметы. Пустое имя может отсылать к одному единственному несуществующему предмету («король, правивший во Франции в начале этого века», дед Мороз, Снегурочка и т.п.) или к двум и более таким предметам (леший, домовой, гном и т.п.).

Имена подразделяются далее на конкретные и абстрактные. Конкретное имя обозначает физические тела или живые существа. Абстрактное имя обозначает объекты, не являющиеся индивидами. К конкретным относятся, например, имена «стол», «тетрадь», «лес», «звезда», «ангел», «речной вокзал», «Казань» и т.п. Абстрактными являются имена свойств, отношений, классов, чисел и т.п.: слово «чёрный» может рассматриваться как обозначение свойства «черноты»» слово «ближе» как обозначение определённого отношения между предметами и т.п. Абстрактными являются также имена «человечность», «справедливость», «законность» и т.п.

2. ОТНОШЕНИЯ МЕЖДУ ИМЕНАМИ

Содержание имени — это совокупность тех свойств, которые присущи всем предметам, обозначаемым данным именем, и только им.:

К примеру, склероз — это, как известно, уплотнение каких-либо органов, вызванное гибелью специфических для этих органов элементов и заменой их соединительной тканью. Перечисленные свойства составляют содержание имени «склероз». Они позволяют в относительно любой ситуации решить, можно ли назвать происшедшие в органе изменения склерозом или нет. Содержание имени «стул» составляют свойства «быть предметом мебели, предназначенным для сидения» и «иметь ножки, сидение и спинку». Этими свойствами, относящимися к функциям стула и его строению, обладает каждый стул и не обладает ничто иное. Если изъять из числа структурных частей стула, скажем, спинку, получим содержание уже иного имени («табурет»). В содержание имени «стол» входят признаки «быть предметом мебели, предназначенным для сидения за ним» и «иметь ножки и крышку».

Помимо содержания, или смысла, имя имеет также объём.

Объём имени — это совокупность, или класс, тех предметов, которые обладают признаками, входящими в содержание имени.

Например, в объём имени «склероз» входят все случаи склеротического изменения органов, в частности склероз мозга. Объём имени «стул» включает все стулья, объём имени «стол» — все столы. Нетрудно заметить, что объёмы даже таких простых имён, как «стул» и «стол», являются неопределёнными, размытыми, а значит, сами эти имена относятся к неточным. Входит ли стул или стол, который только задумал сделать столяр, в объём имени «стул» или «стол»? В «Ревизоре» Н.Гоголя упоминается учитель, который, рассказывая об Александре Македонском, так горячился, что ломал стулья. Входят ли эти поломанные стулья в объём имени «стул»? На эти и подобные вопросы трудно ответить однозначно.

Понимание имени как того, что имеет определённый объём и определённое содержание, широко распространено в логике. Нетрудно заметить, что это понимание существенно отличается от употребления понятия «имя» в обычном языке. Имя в обычном смысле — это всегда или почти всегда собственное имя, принадлежащее индивидуальному, единственному в своём роде предмету. Например, слово «Наполеон» является в обычном словоупотреблении типичным именем. Но уже выражения «победитель под Аустерлицем» и «побеждённый под Ватерлоо» к именам обычно не относятся. Тем более не относятся к ним такие типичные с точки зрения логики имена, как «квадрат», «человек», «самый высокий человек» и т.п. Во всяком случае, если бы кто-то на вопрос о своём имени ответил: «Моё имя — человек», вряд ли такой ответ считался бы уместным. И даже ответ: «Моё имя — самый высокий человек в мире» — не показался бы удачным.

То, что логика заметно расширяет обычное употребление слова «имя», объясняется многими причинами, и прежде всего её стремлением к предельной общности своих рассуждений.

Имена находятся в различных отношениях друг к другу. Между объёмами двух произвольных имён, которые есть какой-то смысл сопоставлять друг с другом, имеет место одно и только одно из следующих отношений: равнозначность, пересечение, подчинение (два варианта) и исключение.

Равнозначными являются два имени, объёмы которых полностью совпадают. Иными словами, равнозначные имена отсылают к одному и тому же классу предметов, но делают это разными способами.

Равнозначны, к примеру, имена «квадрат» и «равносторонний прямоугольник»: каждый квадрат является равносторонним прямоугольником, и наоборот.

Равнозначность означает совпадение объёмов двух имён, но не их содержаний. Например, объёмы имён «сын» и «внук» совпадают (каждый сын есть чей-то внук и каждый внук — чей-то сын), но содержания их различны.

Отношения между объёмами имён можно геометрически наглядно представить с помощью круговых схем. Они называются по имени математика XVIII в. Л.Эйлера «кругами Эйлера». Каждая точка круга представляет один предмет, входящий в объём рассматриваемого имени. Точки вне круга представляют предметы, не подпадающие под это имя.

Отношение между двумя равнозначными именами изображается в виде двух полностью совпадающих кругов.

Равнозначность

В отношении пересечения находятся два имени, объёмы которых частично совпадают.

Пересекаются, в частности, объёмы имён «лётчик» и «космонавт»: некоторые лётчики являются космонавтами (они представлены заштрихованной частью кругов), есть лётчики, не являющиеся космонавтами, и есть космонавты, не являющиеся лётчиками.

Пересечение

В отношении подчинения находятся имена, объём одного из которых полностью входит в объём другого.

В отношении подчинения находятся, к примеру, имена «треугольник» и «прямоугольный треугольник»: каждый прямоугольный треугольник является треугольником, но не каждый треугольник прямоугольный.

Подчинение

В этом же отношении находятся имена «дедушка» и «внук»: каждый дедушка есть чей-то внук, но не каждый внук является дедушкой. «Внук» — подчиняющее имя, «дедушка» — подчинённое.

Если в отношении подчинения находятся общие имена, то подчиняющее имя называется родом, а подчинённое — видом. Имя «треугольник» есть род для вида «прямоугольный треугольник», а имя «внук» — род для вида «дедушка».

В отношении исключения находятся имена, объёмы которых полностью исключают друг друга.

Исключают друг друга имена «трапеция» и «пятиугольник», «человек» и «планета», «белое» и «красное» и т.п.

Исключение

Можно выделить два вида исключения:

1. Исключающие объёмы дополняют друг друга так, что в сумме дают весь объём рода, видами которого они являются. Имена, объёмы которых исключают друг друга, исчерпывая объём родового понятия, называются противоречащими.

Противоречащими являются, например, имена «умелый» и «неумелый», «стойкий» и «нестойкий», «красивый» и «некрасивый» и т.п. Противоречат друг другу также имена «простое число» и «число, не являющееся простым», исчерпывающие объём родового имени «натуральное число», имена «красный» и «не являющийся красным», исчерпывающие объём родового имени «предмет, имеющий цвет», и т.п.

2. Исключающие имена составляют в сумме только часть объёма того рода, видами которого они являются. Имена, объёмы которых исключают друг друга, не исчерпывая объём родового имени, называются противоположными.

Противоречащие имена Противоположные имена

К противоположным относятся, в частности, имена «простое число» и «чётное число», не исчерпывающие объёма родового имени «натуральное число», имена «красный» и «белый», не исчерпывающие объёма родового имени «предмет, имеющий цвет» и т.п.

Круговые схемы могут применяться для одновременного представления объёмных отношений более, чем двух имён. Такова, к примеру, приводимая на рисунке схема, представляющая отношения между объёмами имён: «планета» (S), «планета Солнечной системы»(P ), «Земля» (M ), «спутник» (L), «искусственный спутник» (N), «Луна»(O ) и «небесное тело» ®. Согласно этой схеме существуют, в частности, небесные тела, не являющиеся ни планетами, ни их спутниками, планеты, не входящие в Солнечную систему, спутники, не являющиеся искусственными, и т.д. Объёмы единичных имён представляются точками.

3. ОПРЕДЕЛЕНИЕ

Определение — логическая операция, раскрывающая содержание имени. Определить имя — значит указать, какие признаки входят в его содержание.

Определяя, например, манометр, мы указываем, что это, во-первых, прибор, и во-вторых, именно тот, с помощью которого измеряется давление. Давая определение имени «графомания», мы говорим, что это болезненное пристрастие к писанию, к многословному, пустому, бесполезному сочинительству.

Важность определений подчёркивал ещё Сократ, говоривший, что он продолжает дело своей матери, акушерки, и помогает родиться истине в споре. Анализируя вместе со своими оппонентами различные случаи употребления конкретного понятия, он стремился прийти в конце концов к его прояснению и определению.

Определение решает две задачи. Оно отличает и отграничивает определяемый предмет от всех иных. Скажем, определение манометра позволяет однозначно отграничить манометры от всех предметов, не являющихся приборами, и отделить манометры по присущим только им признакам от всех иных приборов. Далее, определение раскрывает сущность определяемых предметов, указывает те их основные признаки, без которых они не способны существовать и от которых в значительной мере зависят все иные их признаки.

С этой второй задачей как раз и связаны основные трудности определения конкретных имён.

Дать хорошее определение — значит раскрыть сущность определяемого объекта. Но сущность, как правило, не лежит на поверхности. Кроме того, за сущностью первого уровня всегда скрывается более глубокая сущность второго уровня, за той — сущность третьего уровня и так до бесконечности. Эта возможность неограниченного углубления в сущность даже простого объекта делает понятными те трудности, которые встают на пути определения, и объясняет, почему определения, казалось бы, одних и тех же вещей меняются с течением времени. Углубление знаний об этих вещах ведёт к изменению представлений об их сущности, а значит, и их определений.

Необходимо также учитывать известную относительность сущности: существенное для одной цели может оказаться второстепенным с точки зрения другой цели.

Скажем, в геометрии для доказательства разных теорем могут Использоваться разные, не совпадающие между собой определения понятия «линия». И вряд ли можно сказать, что одно из них раскрывает более глубокую сущность этого понятия, чем все остальные.

Писатель И.Рат-Вег в своей «Комедии книги» упоминает некоего старого автора, чрезвычайно не любившего театр. Отношение к театру этот автор считал настолько важным, что определял через него все остальное. Рай, писал он, это место, где нет театра; дьявол — изобретатель театра и танцев; короли — люди, которым особенно позорно ходить в театр и покровительствовать актёрам, и т.п. Разумеется, эти определения поверхностны со всех точек зрения. Со всех, кроме одной: тому, кто всерьёз считает театр источником всех зол и бед, существующих в мире, определения могут казаться схватывающими суть дела.

Определение может быть более глубоким и менее глубоким, и его глубина зависит прежде всего от уровня знаний об определяемом предмете. Чем лучше, глубже мы знаем предмет, тем больше вероятность, что нам удастся найти хорошее его определение.

Конкретные формы, в которых практически реализуется операция определения, чрезвычайно разнообразны.

Прежде всего нужно отметить различие между явными и неявными определениями.

Первые имеют форму равенства — совпадения двух имён (понятий). Общая схема таких определений: «5 есть (по определению) Р ». Здесь S и Р — два имени, причём не имеет значения, выражается каждое из них одним словом или сочетанием слов. Явными являются, к примеру, определения: «Антигены — это чуждые для организма вещества, вызывающие в крови и других тканях образование „антител“» и «Пропедевтика есть введение в какую-либо науку». В последнем определении приравниваются друг другу, или отождествляются, два имени: «пропедевтика» и «введение в какую-либо науку».

Неявные определения не имеют формы равенства двух имён.,

Особый интерес среди неявных определений имеют контекстуальные и остенсивные определения.

Всякий отрывок текста, всякий контекст, в котором встречается интересующее нас имя, является в некотором смысле неявным его определением. Контекст ставит имя в связь с другими именами и тем самым косвенно раскрывает его содержание.

Допустим, нам не вполне ясно, что такое удаль. Можно взять текст, в котором встречается слово «удаль», и попытаться уяснить, что именно оно означает.

«Удаль. В этом слове, — пишет Ф.Искандер, — ясно слышится — даль. Удаль — это такая отвага, которая требует для своего проявления пространства, дали.

В слове «мужество» — суровая необходимость, взвешенность наших действий, точнее, даже противодействий. Мужество от ума, от мужчинства. Мужчина, обдумав и осознав, что в тех или иных обстоятельствах жизни, защищая справедливость, необходимо проявить высокую стойкость, проявляет эту высокую стойкость, мужество. Мужество ограничено целью, цель продиктована совестью.

Удаль, безусловно, предполагает риск собственной жизнью, храбрость.

Но, вглядевшись в понятие «удаль», мы чувствуем, что это неполноценная храбрость. В ней есть самонакачка, опьянение. Если бы устраивались состязания по мужеству, то удаль на эти соревнования нельзя было бы допускать, ибо удаль пришла бы, хватив допинга.

Удаль требует пространства, воздух пространства накачивает искусственной смелостью, пьянит. Опьянённому жизнь — копейка. Удаль — это паника, бегущая вперёд. Удаль рубит налево и направо. Удаль — возможность рубить, все время удаляясь от места, где уже лежат порубленные тобой, чтобы не задумываться: а правильно ли я рубил?

А все-таки красивое слово: удаль! Утоляет тоску по безмыслию».

В этом отрывке отсутствует явное определение удали. Но можно хорошо понять, что представляет собой удаль и как она связана с отвагой и мужеством.

В «Словаре русского языка» С.И.Ожегова «охота» определяется как «поиски, выслеживание зверей, птиц с целью умерщвления или ловли». Это определение звучит сухо и отрешённо. Оно никак не связано с горячими спорами о том, в каких крайних случаях оправданно убивать или заточать в неволю зверей или птиц. В коротком стихотворении «Формула охоты» поэт В.Бурич так определяет охоту и своё отношение к ней:

Черта горизонта

Птицы в числителе

Рыбы в знаменателе

Умноженные на дробь выстрела

и переменный коэффициент удочки

дают произведение

доступное каждой посредственности.

Завзятый охотник может сказать, что эта образная характеристика охоты субъективна и чересчур эмоциональна. Но тем не менее она явно богаче и красками, и деталями, относящимися к механизму охоты, чем сухое словарное определение.

Контекстуальные определения всегда остаются в значительной мере неполными и неустойчивыми. Не ясно, насколько обширным должен быть контекст, познакомившись с которым, мы усвоим значение интересующего нас имени. Никак не определено также то, какие иные имена могут или должны входить в этот контекст. Вполне может оказаться, что ключевых слов, особо важных для раскрытия содержания имени, в избранном нами контексте как раз нет.

Почти все определения, с которыми мы встречаемся в обычной жизни, — это контекстуальные определения.

Услышав в разговоре неизвестное ранее слово, мы не уточняем его определение, а стараемся установить его значение на основе всего сказанного. Встретив в тексте на иностранном языке одно-два неизвестных слова, мы обычно не спешим обратиться к словарю, а пытаемся понять текст в целом и составить примерное представление о значениях неизвестных слов.

Никакой словарь не способен исчерпать всего богатства значений отдельных слов и всех оттенков этих значений. Слово познаётся и усваивается не на основе сухих и приблизительных словарных разъяснений. Употребление слов в живом и полнокровном языке, в многообразных связях с другими словами — вот источник полноценного знания как отдельных слов, так и языка в целом. Контекстуальные определения, какими бы несовершенными они ни казались, являются фундаментальной предпосылкой владения языком.

Остенсивные определения — это определения путём показа.

Нас просят объяснить, что представляет собой зебра. Мы, затрудняясь сделать это, ведём спрашивающего в зоопарк, подводим его к клетке с зеброй и показываем: «Это и есть зебра».

Определения такого типа напоминают обычные контекстуальные определения. Но контекстом здесь является не отрывок какого-то текста, а ситуация, в которой встречается объект, обозначаемый интересующим нас понятием. В случае с зеброй — это зоопарк, клетка, животное в клетке и т.д.

Остенсивные определения, как и контекстуальные, отличаются некоторой незавершённостью, неокончательностью.

Определение посредством показа не выделяет зебру из её окружения и не отделяет того, что является общим для всех зебр, от того, что характерно для данного конкретного их представителя. Единичное, индивидуальное слито в таком определении с общим, тем, что свойственно всем зебрам.

Остенсивные определения — и только они — связывают слова с вещами. Без них язык — только словесное кружево, лишённое объективного, предметного содержания.

Определить путём показа можно, конечно, не все имена, а только самые простые, самые конкретные. Можно предъявить стол и сказать: «Это — стол, и все вещи, похожие на него, тоже столы». Но нельзя показать и увидеть бесконечное, абстрактное, конкретное и т.п. Нет предмета, указав на который можно было бы заявить: «Это и есть то, что обозначается словом „конкретное“». Здесь нужно уже не остенсивное, а вербальное определение, т.е. чисто словесное определение, не предполагающее показа определяемого предмета.

В явных определениях отождествляются, приравниваются друг к другу два имени. Одно — определяемое имя, содержание которого требуется раскрыть, другое — определяющее имя, решающее эту задачу.

Обычное словарное определение гиперболы: «Гипербола — это стилистическая фигура, состоящая в образном преувеличении, например: „Наметали стог выше тучи“». Определяющая часть выражается словами «стилистическая фигура, состоящая…» и слагается из двух частей. Сначала понятие гиперболы подводится под более широкое понятие «стилистическая фигура». Затем гипербола отграничивается от всех других стилистических фигур. Это достигается указанием признака («образное преувеличение»), присущего только гиперболе и отсутствующего у иных стилистических фигур, с которыми можно было бы спутать гиперболу. Явное определение гиперболы дополняется примером.

Явные определения этого типа принято называть определениями через род и видовое отличие. Поскольку такие определения чрезвычайно распространены и являются как бы образцами определения вообще, их иногда называют также классическими определениями.

Общая схема классических определений: «S есть Р и М ». Здесь S — определяемое имя, Р — имя, более общее по отношению к S (род), М — такие признаки, которые выделяют предметы, обозначаемые именем S среди всех предметов, обозначаемых именем Р (вид).

Родо-видовое, или классическое, определение — одно из самых простых и распространённых определений. В словарях и энциклопедиях подавляющее большинство определений относится именно к этому типу. Иногда даже считают, что всякое определение является родо-видовым. Разумеется, это неверно.

К явным определениям и, в частности, к родо-видовым предъявляется ряд достаточно простых и очевидных требований. Их называют обычно правилами определения.

1. Определяемое и определяющее понятия должны быть взаимозаменяемы. Если в каком-то предложении встречается одно из этих понятий, всегда должна существовать возможность заменить его другим. При этом предложение, истинное до замены, должно остаться истинным и после неё.

Для определений через род и видовое отличие это правило формулируется как правило соразмерности определяемого и определяющего понятий: совокупности предметов, охватываемые ими, должны быть одними и теми же.

Соразмерны, например, имена «гомотипия» и «сходство симметричных органов» (скажем, правой и левой руки). Соразмерны также «голкипер» и «вратарь», «нонсенс» и «бессмыслица». Встретив в каком-то предложении имя «нонсенс», мы вправе заменить его на «бессмыслицу» и наоборот.

Если объём определяющего понятия шире, чем объём определяемого, говорят об ошибке слишком широкого определения. Такую ошибку мы допустили бы, определив, к примеру, ромб просто как плоский четырехугольник. В этом случае к ромбам оказались бы отнесёнными и трапеции, и все прямоугольники, а не только те, у которых равны все стороны.

Если объём определяющего понятия уже объёма определяемого, имеет место ошибка слишком узкого определения. Такую ошибку допускает, в частности, тот, кто определяет ромб как плоский четырехугольник, у которого все стороны и все углы равны. Ромб в этом случае отождествляется со своим частным случаем — квадратом, и из числа ромбов исключаются четырехугольники, у которых не все углы равны.

2. Нельзя определять имя через само себя или определять его через такое другое имя, которое, в свою очередь, определяется через него. Это правило запрещает порочный круг.

Содержат очевидный круг определения «Война есть война» и «Театр — это театр, а не кинотеатр». Задача определения — раскрыть содержание ранее неизвестного имени и сделать его известным. Определение, содержащее круг, разъясняет неизвестное через него же. В итоге неизвестное так и остаётся неизвестным. Истину можно, к примеру, определить как верное отражение действительности, но только при условии, что до этого верное отражение действительности не определялось как такое, которое даёт истину.

3. Определение должно быть ясным. Это означает, что в определяющей части могут использоваться только имена, известные и понятные тем, на кого рассчитано определение. Желательно также, чтобы в ней не встречались образы, метафоры, сравнения, т.е. все то, что не предполагает однозначного и ясного истолкования.

Можно определить, к примеру, пролегомены как пропедевтику. Но такое определение будет ясным лишь для тех, кто знает, что пропедевтика — это введение в какую-либо науку.

Не особенно ясны и такие определения, как «Дети — это цветы жизни», «Архитектура есть застывшая музыка», «Овал — круг в стеснённых обстоятельствах», и т.п. Они образны, иносказательны, ничего не говорят об определяемом предмете прямо и по существу, каждый человек может понимать их по-своему.

Ясность не является, конечно, абсолютной и неизменной характеристикой. Ясное для одного может оказаться не совсем понятным для другого и совершенно тёмным и невразумительным для третьего. Представления о ясности меняются и с углублением знаний. На первых порах изучения каких-то объектов даже не вполне совершённое их определение может быть воспринято как успех. Но в дальнейшем первоначальные определения начинают казаться все более туманными. Встаёт вопрос о замене их более ясными определениями, соответствующими новому, более высокому уровню знания.

Определение всегда существует в некотором контексте. Оно однозначно выделяет и отграничивает множество рассматриваемых вещей, но делает это только в отношении известного их окружения. Чтобы отграничить, надо знать не только то, что останется в пределах границы, но и то, что окажется вне её.

Интересно отметить, что наши обычные загадки представляют собой, в сущности, своеобразные определения. Формулировка загадки — это половина определения, его определяющая часть. Отгадка — вторая его половина, определяемая часть.

«Утром — на четырех ногах, днём — на двух, вечером — на трех. Что это?» Понятно, что это — человек в разные периоды своей жизни. Саму загадку можно переформулировать так, что она станет одним из возможных его определений.

Контекстуальный характер определений хорошо заметён на некоторых вопросах, подобных загадкам. Сформулированные для конкретного круга людей, они могут казаться странными или даже непонятными за его пределами.

Древний китайский буддист Дэн Инь-фэн однажды задал такую загадку. «Люди умирают сидя и лёжа, некоторые умирают даже стоя. А кто умер вниз головой?» — «Мы такого не знаем», — ответили ему. Тогда Дэн встал на голову и… умер.

Сейчас такого рода «загадка» кажется абсурдом. Но в то давнее время, когда жил Дэн, в атмосфере полемики с существующими обычаями и ритуалом его «загадка» и предложенная им «разгадка» показались вполне естественными. Во всяком случае его сестра, присутствовавшая при этом, заметила только: «Живой ты, Дэн, пренебрегал обычаями и правилами и вот теперь, будучи мёртвым, опять нарушаешь общественный порядок!»

4. ДЕЛЕНИЕ

Деление — это операция распределения на группы тех предметов, которые мыслятся в исходном имени.

Получаемые в результате деления группы называются членами деления. Признак, по которому производится деление, именуется

основанием деления. В каждом делении имеются, таким образом, делимое понятие, основание деления и члены деления.

Посредством операции деления раскрывается объём того или иного имени, выясняется, из каких подклассов состоит класс, соответствующий делимому имени.

Так, по строению листьев класс деревьев может быть подразделён на два подкласса: лиственные деревья и хвойные. По признаку величины угла все треугольники могут быть подразделены на остроугольные, прямоугольные и тупоугольные.

К операции деления приходится прибегать едва ли не в каждом рассуждении. Определяя имя, мы раскрываем его содержание, указываем признаки предметов, мыслимых в этом имени. Производя деление имени, мы даём обзор того круга предметов, который отображён в нем.

Важно уметь не только определять содержание имени, но и прослеживать те группы, из которых слагается класс предметов, обозначаемых именем.

Простой пример из энтомологии — науки о насекомых — ещё раз подтвердит эту мысль. На столе энтомолога коробочки с наколотыми на тонкие булавки маленькими мухами-серебрянками. Ножницами с иголочно-тонкими лезвиями учёный общипывает у этих мух «хвостики» и наклеивает на крошечные стекла. Зачем? В ряде случаев только по «хвостикам» — по особенностям строения отдельных органов — можно точно определить, к какому именно виду относится насекомое. А роспись насекомых по видам и определение территории их обитания важны не только для удовлетворения научной любознательности. Ведь иные из них — потенциальные переносчики ряда болезней, другие — вредители культурных растений, третьи — напротив, враги этих вредителей. Например, трихограммы — крошечные, в полмиллиметра длиной, родственники всем известных пчёл, шмелей и ос. Трихограммы широко применяются в биологической борьбе с вредителями урожая. Однако недавние исследования показали, что до последнего времени на биофабриках разводили не один вид этого насекомого, а «смесь» из трех видов. Но у каждого свои привязанности: один предпочитает поле, другой — сад, третий — огород. И в каждом случае лучше разводить именно тот вид, который подходит для местных условий.

Требования, предъявляемые к делению, достаточно просты.

1. Деление должно вестись только по одному основанию.

Это требование означает, что избранный вначале в качестве основания отдельный признак или совокупность признаков не следует в ходе деления подменять другими признаками.

Правильно, например, делить климат на холодный, умеренный и жаркий. Деление его на холодный, умеренный, жаркий, морской и континентальный будет уже неверным: вначале деление производилось по среднегодовой температуре, а затем — по новому основанию. Неверными являются деления людей на мужчин, женщин и детей; обуви — на мужскую, женскую и резиновую; веществ — на жидкие, твёрдые, газообразные и металлы и т.п.

2. Деление должно быть соразмерным, или исчерпывающим, т.е. сумма объёмов членов деления должна равняться объёму делимого понятия.

Это требование предостерегает против пропуска отдельных членов деления.

Ошибочными, неисчерпывающими будут, в частности, деление треугольников на остроугольные и прямоугольные (пропускаются тупоугольные треугольники); деление людей с точки зрения уровня образования на имеющих начальное, среднее и высшее образование (пропущены те, кто не имеет никакого образования); деление предложений на повествовательные и побудительные (пропущены вопросительные предложения).

3. Члены деления должны взаимно исключать друг друга.

Согласно этому правилу, каждый отдельный предмет должен находиться в объёме только одного видового понятия и не входить в объёмы других видовых понятий.

Нельзя, к примеру, разбивать все целые числа на такие классы: числа, кратные двум; числа, кратные трём; числа, кратные пяти, и т.д. Эти классы пересекаются, и, допустим, число 10 попадает и в первый и в третий классы, а число 6 — и в первый и во второй классы. Ошибочно и деление людей на тех, которые ходят в кино, и тех, которые ходят в театр: есть люди, которые ходят и в кино и в театр.

4. Деление должно быть непрерывным.

Это правило требует не делать скачков в делении, переходить от исходного понятия к однопорядковым видам, но не к подвидам одного из таких видов.

Например, правильно делить людей на мужчин и женщин, женщин — на живущих в Северном полушарии и живущих в Южном полушарии. Но неверно делить людей на мужчин, женщин Северного полушария и женщин Южного полушария. Среди позвоночных животных выделяются такие классы: рыбы, земноводные, рептилии (гады), птицы и млекопитающие. Каждый из этих классов делится на дальнейшие виды. Если же начать делить позвоночных на рыб, земноводных, а вместо указания рептилий перечислить все их виды, то это будет скачком в делении.

Можно заметить, что из третьего правила вытекает первое. Так, деление обуви на мужскую, женскую и детскую нарушает не только первое правило, но и третье: члены деления не исключают друг друга. Деление королей на наследственных, выборных и трефовых не согласуется опять-таки как с первым, так и с третьим правилом.

Частным случаем деления является дихотомия (буквально: разделение надвое). Дихотомическое деление опирается на крайний случай варьирования признака, являющегося основанием деления: с одной стороны, выделяются предметы, имеющие этот признак, с другой — не имеющие его.

В случае обычного деления люди могут подразделяться, к примеру, на мужчин и женщин, на детей и взрослых и т.п. При дихотомии множество людей разбивается на мужчин и «немужчин», детей и «недетей» и т.п.

Дихотомическое деление имеет свои определённые преимущества, но в общем-то оно является слишком жёстким и ригористичным. Оно отсекает одну половину делимого класса, оставляя её, в сущности, без всякой конкретной характеристики. Это удобно, если мы хотим сосредоточиться на одной из половин и не проявляем особого интереса к другой. Тогда можно назвать всех тех людей, которые не являются мужчинами, просто «немужчинами» и на этом закончить о них разговор. Далеко не всегда, однако, такое отвлечение от одной из частей целесообразно. Отсюда ограниченность использования дихотомий.

Обычные деления исторических романов — наглядный пример «делений надвое». Мир сегодняшней исторической романистики очень широк по спектру проблем, хронологических времён и мест действия, стилевых и композиционных форм, способов ведения рассказа.

Можно попытаться провести всеохватывающую классификацию исторических романов по одному основанию, но она неизбежно окажется сложной, не особенно ясной и, что главное, практически бесполезной. Текучесть «материи» романа на темы истории диктует особую манеру деления: не стремясь к единой классификации, дать серию в общем-то не связанных между собой дихотомических делений. «Есть романы — „биографии“ и романы — „эссе“» романы документальные и романы — «легенды», «философии истории»» романы, концентрирующие узловые моменты жизни того или иного героя или народа, и романы, разворачивающиеся в пространные хроникально-циклические повествования, в которых есть и интенсивность внутреннего движения, и глубина, а вовсе не «растекание» мысли». Эта характеристика «поля» исторического романа, взятая из литературоведческой работы, как раз тяготеет к серии дихотомий.

Дихотомические деления были особенно популярны в прошлом, в средние века. Это объяснялось, с одной стороны, ограниченностью и поверхностностью имевшихся в то время знаний, а с другой стороны — неуёмным стремлением охватить и упорядочить весь мир, включая и «внеземную» его часть, которая предполагалась существующей, но недоступной слабому человеческому уму.

Вот как делил, например, философ того времени Григорий Великий «все то, что есть»: «… Все, что есть, либо существует, но не живёт; либо существует и живёт, но не имеет ощущений; либо и существует, и живёт, и чувствует, но не понимает и не рассуждает; либо существует, живёт, чувствует, понимает и рассуждает. Камни ведь существуют, но не живут. Растения существуют, живут, однако не чувствуют… Животные существуют, живут и чувствуют, но не разумеют. Ангелы существуют, живут и чувствуют и, обладая разумением, рассуждают. Итак, человек, имея с камнями то общее, что он существует, с древесами — то, что живёт, с животными — то, что чувствует, с ангелами — то, что рассуждает, правильно обозначается именем вселенной…»

Здесь все делится сначала на существующее и несуществующее, затем существующее — на живущее и неживущее, живущее — на чувствующее и нечувствующее и, наконец, чувствующее — на рассуждающее и нерассуждающее. Эта классификация призвана показать, по замыслу автора, что человек имеет что-то общее со всеми видами существующих в мире вещей, а потому его справедливо называют «вселенной в миниатюре».

Для создания подобного рода делений нет, разумеется, никакой необходимости в конкретном исследовании каких-то объектов. А вывод — глобален: человек есть отражение всей вселенной и вершина всего земного. Однако научная ценность таких делений ничтожна.

Классификация — это многоступенчатое, разветвлённое деление.

Результатом классификации является система соподчинённых имён: делимое имя является родом, новые имена — видами, видами видов (подвидами) и т.д.

Наиболее сложные и совершённые классификации даёт наука, систематизирующая в них результаты предшествующего развития каких-либо областей знания и намечающая одновременно перспективу дальнейших исследований.

Пример из биологии показывает, какую несомненную пользу способна принести удачная классификация, объединяющая в одну группу животных, казавшихся ранее не связанными между собой.

«Среди современных животных, — пишет зоолог Д.Симпсон, — броненосцы, муравьеды и ленивцы столь не похожи друг на друга, их образ жизни и поведение настолько различны, что едва ли кому-нибудь пришло бы в голову без морфологического изучения объединить их в одну группу». Но было обнаружено, что в позвоночнике этих животных имеются дополнительные сочленения, из-за которых они получили имя «ксенантры» — странно сочленённые млекопитающие».

После открытия необычных сочленений был тут же открыт целый ряд других сходных особенностей этих животных: сходное строение зубов, сходные конечности с хорошо развитыми когтями и очень большим когтем на третьем пальце передней конечности и т.д. «Сейчас никто не сомневается, — заключает Симпсон, — что ксенантры, несмотря на их значительное разнообразие, действительно образуют естественную группу и имеют единое происхождение. Вопрос о том, кто именно был их предком и когда и где он существовал, связан с большими сомнениями и ещё не разгаданными загадками…» Предпринятые тщательные поиски общего предка ксенантр позволили обнаружить их предположительных родичей в Южной Америке, Западной Европе.

Таким образом, объединение разных животных в одну группу систематизации позволило не только раскрыть многие другие их сходные черты, но и высказать определённые соображения об их далёком предке.

Говоря о проблемах классификации другой группы живых организмов — вирусов, учёные-вирусологи Д.Г.Затула и С.А.Мамедова пишут: «Без знания места, которое занимает объект исследования в ряду ему подобных, учёным трудно работать. Классификация нужна в первую очередь для того, чтобы экономить время, силы и средства, чтобы, раскрыв тайны одного вируса или разработав меры борьбы с каким-либо вирусным заболеванием, применить на других подобных вирусах и болезнях. Частые открытия в вирусологии, бурно развивающейся науке, вынуждают пересматривать законы и свойства, по которым сгруппированы вирусы… Учёные не считают какую-либо классификацию вирусов единственно верной и законченной. Конечно, будут ещё обнаружены новые свойства, которые уточнят и расширят таблицу вирусов, а может быть, и позволят создать новую классификацию».

Все сказанное о выгодах, даваемых классификацией вирусов, и об изменениях её с развитием вирусологии справедливо и в отношении классификаций других групп живых организмов. Это верно и применительно ко всем вообще классификациям, разрабатываемым наукой.

Затруднения с классификацией имеют чаще всего объективную причину. Дело не в недостаточной проницательности человеческого ума, а в сложности окружающего нас мира, в отсутствии в нем жёстких границ и ясно очерченных классов. Всеобщая изменчивость вещей, их «текучесть» ещё более усложняет и размывает эту картину.

Именно поэтому далеко не все и не всегда удаётся чётко классифицировать. Тот, кто постоянно нацелен на проведение ясных разграничительных линий, постоянно рискует оказаться в искусственном, им самим созданном мире, имеющем мало общего с динамичным, полным оттенков и переходов реальным миром.

Наиболее сложным объектом для классификации является, без сомнения, человек. Типы людей, их темпераменты, поступки, чувства, стремления, действия и т.д. — все это настолько тонкие и текучие «материи», что попытки их типологизации только в редких случаях приводят к полному успеху.

Сложно классифицировать людей, взятых в единстве присущих им свойств. С трудом поддаются классификации даже отдельные стороны психической жизни человека и его деятельности.

В начале прошлого века Стендаль написал трактат «О любви», явившийся одним из первых в европейской литературе опытов конкретно-психологического анализа сложных явлений духовной жизни человека. Есть четыре рода любви, говорится в этом сочинении. «Любовь-страсть» заставляет нас жертвовать всеми нашими интересами ради неё. «Любовь-влечение» — «это картина, где все, вплоть до теней, должно быть розового цвета, куда ничто неприятное не должно вкрасться ни под каким предлогом, потому что это было бы нарушением верности обычаю, хорошему тону, такту и т.д. …В ней нет ничего страстного и непредвиденного, и она часто бывает изящнее настоящей любви, ибо ума в ней много…» «Физическая любовь» — «…какой бы сухой и несчастный характер ни был у человека, в шестнадцать лет он начинает с этого». И наконец «любовь-тщеславие», подобная желанию обладать предметом, который в моде, и часто не приносящая даже физического удовольствия.

Эта классификация приводится в хрестоматиях по психологии, и она в самом деле проницательна и интересна. Отвечает ли она, однако, хотя бы одному из тех требований, которые принято предъявлять к делению? Вряд ли. По какому признаку разграничиваются эти четыре рода любви? Не очень ясно. Исключают ли они друг друга? Определённо — нет. Исчерпываются ли ими все разновидности любовного влечения? Конечно, нет.

В этой связи нужно помнить, что не следует быть излишне придирчивым к классификациям того, что по самой своей природе противится строгим разграничениям.

Любовь — очень сложное движение человеческой души. Но даже такое внешне, казалось бы, очень простое проявление психической жизни человека, как смех, вызывает существенные затруднения при попытке разграничения разных его видов. Какие вообще существуют разновидности смеха? Ответа на этот вопрос нет, да и не особенно ясно, по каким признакам их можно было бы различить.

Это не удивительно, поскольку даже смех конкретного человека трудно охарактеризовать в каких-то общих терминах, сопоставляющих его со смехом других людей.

Перу А.Ф.Лосева принадлежит интересная биография известного философа и оригинального поэта конца прошлого века В.С.Соловьёва. В ней, в частности, сделана попытка проанализировать своеобразный смех Соловьёва, опираясь на личные впечатления и высказывания людей, близко знавших философа.

«Случалось ему знавать и нужду, — пишет сестра Соловьёва, — и он потом, рассказывая о ней, заливался безудержным радостным смехом, потому что у матери было уж очень выразительно скорбное лицо». «Много писали о смехе Вл.Соловьёва, — говорит другой. — Некоторые находили в этом смехе что-то истерическое, жуткое, надорванное. Это неверно. Смех B.C. был или здоровый олимпийский хохот неистового младенца, или мефистофелевский смешок хе-хе, или и то и другое вместе». В этом же духе говорит о смехе Соловьёва и писатель А.Белый: «Бессильный ребёнок, обросший львиными космами, лукавый черт, смущающий беседу своим убийственным смешком: хе-хе…». В другом месте Белый пишет: «Читаются стихи. Если что-нибудь в стихах неудачно, смешно, Владимир Сергеевич разразится своим громовым исступлённым „ха-ха-ха“, подмывающим сказать нарочно что-нибудь парадоксальное, дикое».

Подводя итог, Лосев пишет: «Смех Вл.Соловьёва очень глубок по своему содержанию и ещё не нашёл для себя подходящего исследователя. Это не смешок Сократа, стремившегося разоблачить самовлюблённых и развязных претендентов на знание истины. Это не смех Аристофана или Гоголя, где под ним крылись самые серьёзные идеи общественного и морального значения. И это не романтическая ирония Жан-Поля, когда над животными смеётся человек, над человеком ангелы, над ангелами архангелы и над всем бытием хохочет абсолют, который своим хохотом и создаёт бытие, и его познает. Ничего сатанинского не было в смехе Вл.Соловьёва, и это уже, конечно, не комизм оперетты или смешного водевиля. Но тогда что же это за смех? В своей первой лекции на высших женских курсах Герье Вл.Соловьёв определял человека не как существо общественное, но как существо смеющееся».

Интересны термины, употребляемые в этих высказываниях для характеристики конкретного смеха. В большинстве своём они не дают прямого его описания, а только сопоставляют его с какими-то иными, как будто более известными разновидностями смеха. Рассматриваемый смех то уподобляется «здоровому олимпийскому хохоту» или «мефистофелевскому смешку», то противопоставляется «смеху Аристофана», «смешку Сократа», «иронии Жан-Поля» и т.д. Все это, конечно, не квалификационные понятия, а только косвенные, приблизительные описания.

Встречаются такие термины, которые характеризуют, как кажется, именно данный смех. Среди них «радостный», «истерический», «убийственный», «исступлённый» и т.п. Но и их нельзя назвать строго квалификационными. Значение их расплывчато, и они опять-таки не столько говорят о том, чем является сам по себе этот смех, сколько сравнивают его с чем-то: состоянием радости, истерики, исступления и т.п.

Все это, конечно, не случайно, и дело не в недостаточной проницательности тех, кто пытался описать смех. Источник затруднений — в сложности смеха, отражающей сложность и многообразие тех движений души, внешним проявлением которых он является. Именно это имеет, как кажется, в виду Лосев, когда он заканчивает своё описание смеха Соловьёва определением человека как «смеющегося существа». Если смех связан с человеческой сущностью, он столь же сложен, как и сама эта сущность. Классификация смеха оказывается в итоге исследованием человека со всеми вытекающими из этого трудностями.

Речь шла только о смехе, но все это относится и к другим проявлениям сложной внутренней жизни человека.

И в заключение — один пример явно несостоятельной классификации, грубо нарушающей требования, предъявляемые к делению.

Писатель Х.Л.Борхес приводит отрывок из «некой китайской энциклопедии». В нем даётся классификация животных и говорится, что они «подразделяются на: а) принадлежащих императору; б) бальзамированных; в) приручённых; г) молочных поросят; д) сирен; е) сказочных; ж) бродячих собак; з) заключённых в настоящую классификацию; и) буйствующих, как в безумии; к) неисчислимых; л) нарисованных очень тонкой кисточкой из верблюжьей шерсти; м) и прочих; н) только что разбивших кувшин; о) издалека кажущихся мухами».

Чем поражает эта классификация? Почему с самого начала становится очевидным, что подобным образом нельзя рассуждать ни о животных, ни о чем-либо ином?

Дело, разумеется, не в отдельных рубриках, какими бы необычными они ни казались. Каждая из них имеет вполне определённое конкретное содержание. В числе животных упоминаются, правда, фантастические существа — сказочные животные и сирены, но это делается, пожалуй, с целью отличить реально существующих животных от существующих только в воображении. К животным относятся и нарисованные, но мы и в самом деле обычно называем их животными.

Невозможными являются не отдельные указанные разновидности животных, а как раз соединение их в одну группу, перечисление их друг за другом, так что рядом встают живые и умершие животные, буйствующие и нарисованные, фантастические и приручённые, классифицируемые и только что разбившие кувшин. Сразу возникает чувство, что нет такой единой плоскости, на которой удалось бы разместить все эти группы, нет общего, однородного пространства, в котором могли бы встретиться все перечисленные животные.

Классификация всегда устанавливает определённый порядок. Она разбивает рассматриваемую область объектов на группы, чтобы упорядочить эту область и сделать её хорошо обозримой. Но классификация животных из «энциклопедии» не только не намечает определённой системы, но, напротив, разрушает даже те представления о гранях между группами животных, которые у нас есть. В сущности, эта классификация нарушает все те требования, которые предъявляются к разделению какого-то множества объектов на составляющие его группы. Вместо системы она вносит несогласованность и беспорядок.

Ясно, что классификация вообще не придерживается никакого твёрдого основания, в ней нет даже намёка на единство и неизменность основания в ходе деления. Каждая новая группа животных выделяется на основе собственных своеобразных признаков, безотносительно к тому, по каким признакам обособляются другие группы. Связь между группами оказывается почти полностью разрушенной, никакой координации и субординации между ними установить невозможно. Можно предполагать, что сирены относятся к сказочным животным, а молочные поросята и бродячие собаки не принадлежат ни к тем, ни к другим. Но относятся ли сирены, сказочные животные, молочные поросята и бродячие животные к тем животным, что буйствуют, как в безумии, или к неисчислимым, или к тем, которые нарисованы тонкой кисточкой? Как соотносятся между собой животные, только что разбившие кувшин, и животные, издалека кажущиеся мухами? На подобные вопросы невозможно ответить, да их и бессмысленно задавать, поскольку очевидно, что никакого единого принципа в основе этой классификации не лежит. Далее, члены деления здесь не исключают друг друга. Всех перечисленных животных можно нарисовать, многие из них издалека могут казаться мухами, все они включены в классификацию и т.д. Относительно того, что перечисленные виды животных исчерпывают множество всех животных, можно говорить только с натяжкой: те животные, которые не упоминаются прямо, свалены в кучу в рубрике «и прочие». И наконец, очевидны скачки, допускаемые в данном делении. Различаются как будто сказочные и реально существующие животные, но вместо особого упоминания последних перечисляются их отдельные виды — поросята и собаки, причём не все поросята, а только молочные, и не все собаки, а лишь бродячие.

Классификации, подобные этой, настолько сумбурны, что возникает даже сомнение, следует ли вообще считать их делениями каких-то понятий. О возможности усовершенствования таких классификаций, придании им хотя бы видимости системы и порядка не приходится и говорить.

Но что интересно, даже такого рода деления, отличающиеся путаницей и невнятностью, иногда могут оказываться практически небесполезными. Неправильно делить, к примеру, обувь на мужскую, женскую и резиновую (или детскую), но во многих обувных магазинах она именно так делится, и это не ставит нас в тупик. Нет ничего невозможного в предположении, что и классификация животных, подобная взятой из «энциклопедии», может служить каким-то практическим, разнородным по самой своей природе целям. Теоретически, с точки зрения логики, она никуда не годится. Однако далеко не все, что используется повседневно, находится на уровне требований высокой теории и отвечает стандартам безупречной логики.

Нужно стремиться к логическому совершенству, но не следует быть педантичным и отбрасывать с порога все, что представляется логически не вполне совершённым.

1. ПРОСТЫЕ И СЛОЖНЫЕ ВЫСКАЗЫВАНИЯ.

ОТРИЦАНИЕ, КОНЪЮНКЦИЯ, ДИЗЪЮНКЦИЯ

Высказывание — грамматически правильное предложение, взятое вместе с выражаемым им смыслом (содержанием) и являющееся истинным или ложным.

Высказывание — более сложное образование, чем имя. При разложении высказываний на части, мы всегда получаем те или иные имена. Скажем, высказывание «Солнце есть звезда» включает в качестве своих частей имена «Солнце» и «звезда».

Понятие высказывания — одно из ключевых в логике. Как таковое, оно не допускает точного определения, в равной мере приложимого в разных её разделах. Ясно, что всякое высказывание описывает определённую ситуацию, что-то утверждая или отрицая о ней, и является истинным или ложным.

Высказывание считается истинным, если даваемое им описание соответствует реальной ситуации, и ложным, если не соответствует ей. «Истина» и «ложь» называются истинностными значениями высказывания.

Из отдельных высказываний разными способами можно строить новые высказывания. Так, из высказываний «Дует ветер» и «Идёт дождь» можно образовать более сложные высказывания «Дует ветер и идёт дождь», «Либо дует ветер, либо идёт дождь», «Если идёт дождь, дует ветер» и т.п. Слова «и», «либо, либо», «если, то» и т.п., служащие для образования сложных высказываний, называются логическими связками.

Высказывание называется простым, если оно не включает других высказываний в качестве своих частей.

Высказывание является сложным, если оно получено с помощью логических связок из нескольких более простых высказываний.

Может показаться, что знакомство с высказываниями естественнее всего начать с изучения простых высказываний и их частей, и уже затем приступить к изучению того, как из простых высказываний образуются сложные. В логике, однако, подход является обратным. Сначала рассматриваются способы построения сложных высказываний из более простых, при этом простое высказывание берётся как неразложимое далее целое (как «атом»), и только затем переходят к выявлению строения простых высказываний. Анализ структуры сложных высказываний предшествует анализу структуры простых. Объясняется это следующим: для того, чтобы понимать способы сочетания высказываний, вовсе не обязательно знать, что такое простое высказывание; достаточно учитывать только то, что последнее имеет определённое значение истинности. Простые высказывания чрезвычайно разнообразны, выявление составляющих их частей во многом зависит от принятого способа их анализа. Некоторые логические связи между высказываниями не зависят от строения простых высказываний. Разумно поэтому поступить так, как если бы мы знали все о простых высказываниях, т.е. оставить вопрос об их структуре на время в стороне и заняться логическими связями высказываний. Последняя задача является относительно лёгкой.

Та часть логики, в которой описываются логические связи высказываний, не зависящие от структуры простых высказываний, называется общей теорией дедукции.

Перейдём теперь к рассмотрению наиболее важных способов построения сложных высказываний.

Отрицание — логическая связка, с помощью которой из данного высказывания получается новое, причём, если исходное высказывание истинно, его отрицание будет ложным, и наоборот. Отрицательное высказывание состоит из исходного высказывания и отрицания, выражаемого обычно словами «не», «неверно, что». Отрицательное высказывание является, таким образом, сложным высказыванием: оно включает в качестве своей части отличное от него высказывание. Например, отрицанием высказывания «10 — чётное число» является высказывание «10 не есть чётное число» (или: «Неверно, что 10 есть чётное число»).

Будем обозначать высказывания буквами А, В, С, …, отрицание высказывания — символом ~. Полный смысл понятия отрицания высказывания задаётся условием: если высказывание Л истинно, его отрицание А ложно, и если А ложно, его отрицание, ~А, истинно. Например, так как высказывание «1 есть целое положительное число» истинно, его отрицание «1 не является целым положительным числом» ложно, а так как «1 есть простое число» ложно, его отрицание «1 не есть простое число» истинно.

Определению отрицания можно придать форму таблицы истинности, в которой «и» означает «истинно» и «л» — «ложно».

В результате соединения двух высказываний при помощи слова «и», мы получаем сложное высказывание, называемое конъюнкцией. Высказывания, соединяемые таким способом, называются членами конъюнкции. Например, если высказывания «Сегодня жарко» и «Вчера было холодно» соединить связкой «и» получится конъюнкция «Сегодня жарко и вчера было холодно».

Конъюнкция истинна только в случае, когда оба входящих в неё высказывания являются истинными; если хотя бы один из её членов ложен, то и вся конъюнкция ложна.

Высказывание А может быть либо истинным, либо ложным, и то же самое можно сказать о высказывании В. Следовательно, возможны четыре пары значений истинности для этих высказываний.

Обозначим конъюнкцию символом &. Таблица истинности для конъюнкции приведена ниже.

Определение конъюнкции, как и определения других логических связок, служащих для образования сложных высказываний, основывается на следующих двух предположениях:

1) каждое высказывание (как простое, так и сложное) имеет одно и только одно из двух значений истинности: оно является либо истинным, либо ложным;

2) истинностное значение сложного высказывания зависит только от истинностных значений входящих в него высказываний и способа их логической связи между собой.

Эти предположения кажутся простыми. Приняв их, нужно, однако, отбросить идею, что, наряду с истинными и ложными высказываниями, могут существовать также высказывания неопределённые с точки зрения своего истинностного значения (такие, как, скажем, «Через пять лет в это время будет идти дождь с громом» и т.п.). Нужно отказаться также от того, что истинностное значение сложного высказывания зависит от «связи по смыслу» соединяемых высказываний.

В обычном языке два высказывания соединяются союзом «и», когда они связаны между собой по содержанию, или смыслу. Характер этой связи не вполне ясен, но понятно, что мы не рассматривали бы конъюнкцию «Он шёл в пальто и я шёл в университет» как выражение, имеющее смысл и способное быть истинным или ложным. Хотя высказывания «2 — простое число» и «Москва — большой город» истинны, мы не склонны считать истинной также их конъюнкцию «2 — простое число и Москва — большой город», поскольку составляющие её высказывания не связаны между собою по смыслу.

Упрощая значение конъюнкции и других логических связок и отказываясь для этого от неясного понятия «связь высказываний по смыслу», логика делает значение этих связок одновременно и более широким, и более ясным.

Соединяя два высказывания с помощью слова «или», мы получаем дизъюнкцию этих высказываний. Высказывания, образующие дизъюнкцию, называются членами дизъюнкции.

Слово «или» в повседневном языке имеет два разных смысла. Иногда оно означает «одно или другое или оба», а иногда «одно или другое, но не оба вместе». Высказывание «В этом сезоне я хочу пойти на „Пиковую даму“ или на „Аиду“» допускает возможность двукратного посещения оперы. В высказывании же «Он учится в Московском или в Саратовском университете» подразумевается, что упоминаемый человек учится только в одном из этих университетов.

Первый смысл «или» называется неисключающим. Взятая в этом смысле дизъюнкция двух высказываний означает только, что по крайней мере одно из этих высказываний истинно, независимо от того, истинны они оба или нет. Взятая во втором, исключающем, смысле дизъюнкция двух высказываний утверждает, что одно из них истинно, а второе — ложно.

Символ v будет обозначать дизъюнкцию в неисключающем смысле, для дизъюнкции в исключающем смысле будет использоваться символ V. Таблицы для двух видов дизъюнкции показывают, что неисключающая дизъюнкция истинна, когда хотя бы одно из входящих в неё высказываний истинно, и ложна, только когда оба её члена ложны; исключающая дизъюнкция истинна, когда истинным является только один из её членов, и она ложна, когда оба её члена истинны или оба ложны.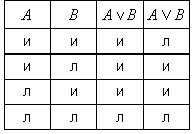

В логике и математике слово «или» всегда употребляется в неисключающем значении.

Разложение некоторого высказывания на простые, далее неразложимые части даёт два вида выражений, называемых собственными и несобственными символами. Особенность собственных символов в том, что они имеют какое-то содержание, даже взятые сами по себе. К ним относятся имена (обозначающие некоторые объекты), переменные (отсылающие к какой-то области объектов), высказывания (описывающие какие-то ситуации и являющиеся истинными или ложными). Несобственные символы не имеют самостоятельного содержания, но в сочетании с одним или несколькими собственными символами образуют сложные выражения, уже имеющие самостоятельное содержание. К несобственным символам относятся, в частности, логические связки, используемые для образования сложных высказываний из простых: «… и …», «… или …», «либо …, либо …», «если …, то …», «… тогда и только тогда, когда …», «ни …, ни …», «не …, а …», «…, но не …», «неверно, что …» и т.п. Само по себе слово, скажем «или», не обозначает никакого объекта. Но в совокупности с двумя собственными, обозначающими символами это слово даёт новый обозначающий символ: из двух высказываний «Письмо получено» и «Телеграмма отправлена» — новое высказывание «Письмо получено или телеграмма отправлена».

Центральная задача логики — отделение правильных схем рассуждения от неправильных и систематизация первых. Логическая правильность определяется логической формой. Для её выявления нужно отвлечься от содержательных частей рассуждения (собственных символов) и сосредоточить внимание на несобственных символах, представляющих эту форму в чистом виде. Отсюда интерес формальной логики к таким, обычно не привлекающим внимания, словам, как «и», «или», «если, то» и т.п.[1]

2. УСЛОВНОЕ ВЫСКАЗЫВАНИЕ, ИМПЛИКАЦИЯ, ЭКВИВАЛЕНТНОСТЬ

Условное высказывание — сложное высказывание, формулируемое обычно с помощью связки «если …, то …» и устанавливающее, что одно событие, состояние и т.п. является в том или ином смысле основанием или условием для другого. Например: «Если есть огонь, то есть дым», «Если число делится на 9, оно делится на 3» и т.п.

Условное высказывание слагается из двух простых высказываний. То, которому предпослано слово «если», называется основанием, или антецедентом (предыдущим); высказывание, идущее после слова «то», называется следствием, или консеквентом (последующим).

Утверждая условное высказывание, мы прежде всего имеем в виду, что не может быть так, чтобы то, о чем говорится в его основании, имело место, а то, о чем говорится в следствии, отсутствовало. Иными словами, не может случиться, чтобы антецедент был истинным, а консеквент — ложным.

В терминах условного высказывания обычно определяются понятия достаточного и необходимого условия: антецедент (основание) есть достаточное условие для консеквента (следствия), а консеквент — необходимое условие для антецедента. Например, истинность условного высказывания «Если выбор рационален, то выбирается лучшая из имеющихся альтернатив» означает, что рациональность — достаточное основание для избрания лучшей из имеющихся возможностей, и что выбор такой возможности есть необходимое условие его рациональности.

Типичной функцией условного высказывания является обоснование одного высказывания ссылкой на другое высказывание. К примеру, то, что серебро электропроводно, можно обосновать ссылкой на то, что оно металл: «Если серебро — металл, оно электропроводно».

Выражаемую условным высказыванием связь обосновывающего и обосновываемого (основания и следствия) трудно охарактеризовать в общем виде и только иногда природа её относительно ясна. Эта связь может быть, в частности, связью логического следования, имеющей место между посылками и заключением правильного умозаключения («Если все живые многоклеточные существа смертны, а медуза является таким существом, то она смертна»). Связь может представлять собой закон природы («Если тело подвергнуть трению, оно начнёт нагреваться») или причинную связь («Если Луна в новолуние находится в узле своей орбиты, наступает солнечное затмение»). Рассматриваемая связь может иметь также характер социальной закономерности, правила, традиции и т.п. («Если меняется общество, меняется также человек», «Если совет разумен, он должен быть выполнен»).

Со связью, выражаемой условным высказыванием, обычно соединяется убеждение, что консеквент с определённой необходимостью «вытекает» из антецедента и что имеется некоторый общий закон, сформулировав который, мы могли бы логически вывести консеквент из антецедента. Например, условное высказывание «Если висмут металл, он пластичен» как бы предполагает общий закон «Все металлы пластичны», делающий консеквент данного высказывания логическим следствием его антецедента.

И в обычном языке, и в языке науки условное высказывание, кроме функции обоснования, может выполнять также целый ряд других задач. Оно может формулировать условие, не связанное с каким-либо подразумеваемым общим законом или правилом («Если захочу, разрежу свой плащ»), фиксировать какую-то последовательность («Если прошлое лето было сухим, то в этом году оно дождливое»), выражать в своеобразной форме неверие («Если вы решите эту задачу, я докажу великую теорему Ферма»), противопоставлять («Если в огороде растёт бузина, то в Киеве живёт дядька») и т.п. Многочисленность и разнородность функций условного высказывания существенно затрудняют его анализ.